铧强中学高2017届高考模拟测试卷(6)(附件)
2017年普通高等学校招生全国统一考试模拟(六)数学(理)试题Word版含答案

核 心 八 模2017年普通高等学校招生全国统一考试模拟试题数学(理科)(六) 第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.已知集合()(){}{}|210,|11A x x x B x Z x =-+<=∈-≤≤,则A B =A. {}1,0-B. {}0,1C. {}1,0,1-D. {}1,2-2.方程26130x x ++=的一个根是A. 32i -+B. 32i +C.23i -+D.23i +3.已知()f x 是定义在R a 满足()(12a f f -> A. 1,2⎛⎫-∞ ⎪⎝⎭B. 3,2⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭3,2⎛⎫+∞ ⎪⎝⎭4.如图,设区域(){,1,0D x y x y =≤≤y =235.86s =,则判断框内的正整数的D.8,96.向量,a b 满足23a b a +=,且()0a b a -⋅=,则,a b 的夹角的余弦值为A. 0B. 13C. 12D. 27.已知等差数列{}n a 中,n S 为其前n 项和,若()244n S an n a a R =++-∈,记数列1n S ⎧⎫⎨⎬⎩⎭的前项和为n T ,则10T = A.18 B. 14 C. 940 D.5228.已知,,a b c 均为正数,且()()2a c b c ++=,则23a b c ++的最小值是9.3,则正视图中10.SAC ⊥平面ABC ,若该三棱锥的四个顶点都在同一球面上,则该球的体积为11.已知点,F F 22a bP2122,3OP PF PF =≥,则双曲线C 的离心率的取值范围为⎫+∞⎪⎪⎭ C. 1,2⎛ ⎝⎦ D.51,2⎛⎤⎥⎝⎦ 12.已知函数()()()[)11,,232,2,x x f x f x x ⎧--∈-∞⎪=⎨-∈+∞⎪⎩,则函数()()cos g x f x x π=-在区间[]0,8内所有零点的和为A. 16B. 30C. 32D. 40第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题5分,共20分.13.已知,x y 满足约束条件20220220x y x y x y +-≤⎧⎪--≤⎨⎪-+≥⎩,若20x y k ++≥恒成立,则实数k 的取值范围为 . 14.若()()2015201501201512x a a x a x x R -=+++∈,则12201522015a a a +++= .15.已知点A,F 分别是椭圆()2222:10x y C a b a b+=>>的上顶点和左焦点,若AF 与圆22:4O x y +=相切于点T ,且点T 是线段AF 靠近点A 的三等分点,则椭圆C 的标准方程为 .16.若数列{}n a 满足2133431n n a a a a a a a a +->->->>->,则称数列{}n a 为“差递减”数列.若数列{}n a 是“差递减”数列,且其通项n a 与其前n 项和()n S n N *∈满足()2321n n S a n N λ*=+-∈,则实数λ的取值范围为 .三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程. 17.(本题满分12分)在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且a c >,已知12,cos , 3.3BA BC B b ⋅===,求:(1)a 和c 的值; (2)()cos B C -的值.18.中,DO 垂直平分AB ,且2AB =,现将ADO ∆沿DO(1)求证:直线AO ⊥平面OBCD ;(2)求平面AOD 与平面ABC 所成角(锐角)的余弦值.19.(本题满分12分)在一个盒子里有6张卡片,上面分别写着如下定义域为R 的函数:()()()())()21234251,,sin ,log ,cos ,f x x f x x f x x f x x f x x x =+====+()6sin 2.f x x x =-(1)现从盒子中任取两张卡片,记事件A 为“这两张卡片上函数相加,所得新函数是奇函数”,求事件A 的概率;(2)从盒子中不放回逐一抽取卡片,若取到一张卡片上的函数是偶函数,则停止抽取,否则继续进行,记停止时抽取次数为ξ,写出ξ的分布列并求其数学期望E ξ.20.(本题满分12分)已知曲线C 上的任意一点到点()0,1F 的距离减去它到x 轴的距离的差都是1.(1)求曲线C 的方程;(2)设直线()0y kx m m =+>与曲线C 在x 轴及x 轴上方部分交于A,B 两点,若对于任意的k R ∈都有FA FB ⋅21.(本题满分12)0. (1)当1a =(2)若不等式()()1ln f x a x ≥-在[)1,x ∈+∞时恒成立,求实数a 的取值范围.请考生在第22、23两题中任选一题作答,如果两题都做,则按照所做的第一题给分;作答时,请用2B 铅笔将答题卡上相应的题号涂黑。
(最新整理)2017届高三地理模拟试卷

2017届高三地理模拟试卷2017届高三地理模拟试卷编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017届高三地理模拟试卷)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017届高三地理模拟试卷的全部内容。
12017届高三地理模拟试卷(一)一、选择题桌状山是顶平似桌面、四周被陡崖围限的方形山体。
南非桌山是南非的平顶山,海拔1087米耸立于高而多岩石的开普半岛北端,可俯瞰开普敦市和桌湾.图1示意开普敦位置及某野外地质考察队在考察南非桌山过程中拍摄的相片,读图回答1~3题.1.南非桌山形成过程中的地质作用的先后顺序是A.沉积作用一地壳运动一变质作用 B.沉积作用一地壳运动一侵蚀作用C.岩浆活动一沉积作用一地壳运动 D.侵蚀作用一岩浆活动一沉积作用2.该野外地质考察队可在南非桌山上看到的景观是A.山顶云雾缭绕 B.林海雪原 C.角马迁徙大军D.雪山连绵3.图中M海域鱼类资源丰富,其主要成因是A。
有大河注入 B.寒、暖流交汇 C.上升补偿流D.高、低盐水交汇正屋正脊是指主屋屋顶最高处的一条屋脊.图2示意海南岛东北部地区的某乡村正屋正脊线与等高线的关系,图中等高距为30米.读图回答4~6题.24.该乡村的相对高差可能是A。
40米 B.60米 C.100米 D.120米5.该乡村建筑的排列是正屋沿等高线平行或与等高线有一定角度排列,这样排列的主要目的是A。
通风排水 B.便于采光 C.拦截水源 D.获得更多太阳能6.夏至日前后,站在甲处正屋的房门口能看到A。
太阳从正前方山头处升起 B.太阳从正前方山头处落下C.太阳从左前方山头出升起 D.太阳从右前方山头处落下城市商品房“去库存”已被确定为我国201 6年五大经济任务之一。
2017年普通高等学校招生全国统一考试高考数学模拟试题(六)理(PDF)

% 方程 # %! )" #)! .'$ 的一个根是
*& (.)% /
+& .)% /
,& (%). /
-& %). /
已知 % 是定义在 上的偶函数 且在区 间 上 单 调 递 增 若实 # (0 $ .!
&(! " " 则实数 & 的取值范围是 数满足 % % (槡 % '%
核!心!八!模 年普通高等学校招生全国统一考试模拟试题
数学 理科 六
选择题 和第 卷 非选择题 两部分 满分 ! 考 # $分 !! 本试卷分第 卷 试时间 ! 分钟 % $ &
第 卷 ! 选择题 ! 共 " $ 分
一 选择题 本大题 ! 每小题 # 分 共" 在每 小题给出 的四个 选 % 小题 $ 分 项中 只有一项是符合题目要求的 & 已知集合 "' 则 "&$' !! # #( % #) ! $ $' #$ ( ! #% ! " # " % *& (! $ +& $ ! ,& (! $ ! -& (! %
! *& (0 % ! . ,& % %
! . +& (0 )0 ( % % . -& )0 %
如图 设区域 '' 向 1! # $%#%! $%(%! " ( 区域内随机投一点 且投入到区 域内 任一 点 都 是 等
% 可能的 则点落到由曲线 ('槡 所 围成 阴 #与('#
2017年高考模拟试卷(6)

开始结束输出S n ←1, S ←0S < 100 n ←n + 1S ←S + 2n NY (第5题)2017年高考模拟试卷(6)第Ⅰ卷(必做题,共160分)一、填空题:本大题共14小题,每小题5分,共70分 . 1. 设集合A = {1,x },B = {2,3,4},若A ∩B ={4},则 x = ▲ .2. 若复数z 1=2+i ,z 1·-z 2=5,则z 2= ▲ .3. 从数6,7,8,9,10,11六个数中,任取两个不同的数, 则两个数互质的概率是 ▲ .4.已知一组数据x 1,x 2,…,x 100的方差是2,则数据 3x 1,3x 2,…,3x 100 的标准差为 ▲ .5.执行右边的程序框图,则输出的S 的值为 ▲ .6.设正四棱柱ABCD —A 1B 1C 1D 1的底面ABCD 是单位正方形,其表面积14,则AA 1= ▲ . 7.不等式组⎩⎨⎧y ≤x +2y ≥x0≤y ≤4x ≥0表示的平面区域的面积为S ,则S 的值为 ▲ .8.函数y =sin(ωx +π4)(ω>0)的图象在[0,1]上恰有三个最高点,则ω的取值范围是 ▲ .9.若两个非零向量a ,b 的夹角为60°,且(a +2b )⊥(a -2b ),则向量a +b 与a -b 的夹角的余弦值是 ▲ .10.已知函数f (x )=e x -1-tx ,∃x 0∈R ,f (x 0)≤0,则实数t 的取值范围 ▲ .11.已知数列{a n }是一个等差数列,首项a 1>0,公差d ≠0,且a 2、a 5、a 9依次成比数列,则 使a 1+a 2+…+a n >100a 1的最小正整数k 的值是 ▲ .12.抛物线y 2=2px (p >0)和双曲线x 2a 2-y 2b2=1(a >0,b >0)有一个相同的焦点F 2(2,0),而双曲线的另一个焦点F 1,抛物线和双曲线交于点B 、C ,若△BCF 1是直角三角形,则双曲线的离心率是 ▲ .13.△ABC 中,∠A 、∠B 、∠C 的对边分别为a 、b 、c ,若a 2cos A =b 3cos B =c 6cos C,则cos A cos B cos C = ▲ .14.已知函数f (x )=2x 3+7x 2+6x x 2+4x +3,x ∈[0,4],则f (x )最大值是 ▲ .AA 1B 1 CD 1 B C 1D MO 115.(本小题满分14分)已知α∈(0,π),且sin(α+π3)=6-24.(1)求sin(α-π4)的值;(2)求cos(2α-π3)的值.16.(本小题满分14分)如图,四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 是菱形,M 是AB的中点,O 1是A 1C 1与B 1D 1的交点. (1)求证:O 1M ∥平面BB 1C 1C ;(2)若平面AA 1C 1C ⊥平面ABCD ,求证:四边形BB 1D 1D 是矩形.17.(本小题满分14分)如图所示,一根绳穿过两个定滑轮,且两端分别挂有3(N)、2(N)的重物.现在两个滑轮之间的绳上挂一个重量为m (N)的重物,恰好使系统处于平衡状态. (1)若∠AOB =120°,求m 的值; (2)求m 的取值范围.18. 椭圆C :x 2+y 2=1的左、右顶点分别为A 、B ,F 为椭圆C 的右焦点,在椭圆C 上任取异ABO 3Nm (N)2N于A 、B 的点P ,直线P A 、PB 分别与直线x =3交于点M ,N ,直线MB 与椭圆C 交于点Q . (1)求FM →·FN →的值;(2)证明:A 、Q 、N 三点共线.19.(本小题满分16分)已知数列{}n a 满足123n n a a n ++=-,n *∈N .(1)若数列{}n a 为等差数列,求1a ;(2)设1(0)a a a =>,2n n *∀∈N ≥,,不等式22113n n n n a a a a ++++≥成立,求实数a 的最小值.20.(本小题满分16分)已知二次函数f (x )=ax 2+bx +1,g (x )=a 2x 2+bx +1.(1)若f (x )≥g (x )对任意实数x 恒成立,求实数a 的取值范围;(2)若函数f (x )有两个不同零点x 1,x 2;函数g (x )有两个不同零点x 3,x 4. (i)若x 3<x 1<x 4,试比较x 2,x 3,x 4的大小关系; (ii)若x 1=x 3<x 2,m 、n 、p ∈1(,)x -∞,()()()()()()f m f n f pg n g p g m '''==,求证m =n =p .第Ⅱ卷(附加题,共40分)21.[选做题]本题包括A 、B 、C 、D 四小题,每小题10分;请选定其中两题,并在相应的答题区域.................内作答.... A .(选修4-1:几何证明选讲)如图,AB 是半圆的直径,C 是半圆上一点,D 是弧AC 的中点,DE ⊥AB 于E ,AC 与DE 交于M ,求证:AM =DM . AEBCDMB .(选修4-2:矩阵与变换)已知二阶矩阵M 属于特征值3的一个特征向量为a =⎣⎡⎦⎤11,并且矩阵M 对应的变换将点(-1,2)变成点(9,15),求出矩阵M..C .(选修4-4:坐标系与参数方程)已知圆C 的极坐标方程是4cos ρθ=,以极点为平面直角坐标系的原点,极轴为x 轴的正半轴,建立平面直角坐标系,直线l 的参数方程是2222x t m y t ⎧=+⎪⎪⎨⎪=⎪⎩(t 是参数).若直线l 与圆C 相切,求实数m 的值.D .(选修4-5:不等式选讲)设函数()|1||1|f x x x =-++,若不等式|||2|||()a b a b a f x +--≤⋅对任意,a b R ∈且0a ≠恒成立,求实数x 的范围.【必做题】第22题、第23题,每题10分,共计20分.请在答题卡指定区域内作答..........,解答时应写出文字说明、证明过程或演算步骤.22.(本小题满分10分) 如图,在四棱锥O -ABCD 中,底面ABCD 是边长为1的菱形,∠ABC =45°,OA ⊥底面ABCD ,OA =2,M 为OA 的中点. (1)求异面直线AB 与MD 所成角的大小; (2)求平面OAB 与平面OCD 所成锐二面角的余弦值.23.设a 0<a 1<a 2<…<a n (i ∈N *,i =1,2,…,n ),以[b ,c ]表示正整数b ,c 的最小公倍数.求证:1[a 0,a 1]+1[a 1,a 2]+…+1[a n -1,a n ]≤1-12n .2017年高考模拟试卷(5)参考答案M D O A B C1.{1,2,3,6}. 2.1i +. 3. 391. 4. 18. 5.29.6.充分不必要. 7.4. 8.76. 9.10.10.已知函数()sin(2)3f x x π=+(0x <π≤),且1()()3f f αβ==(βα≠),则=+βα ▲ .10.76π.由0x <π≤,知2333x ππ7π+≤≤,因为31()()32f f αβ==<,所以()()3π222332αβππ+++=⨯, 所以76αβπ+=.11.(1,2]. f (f (x ))=⎩⎪⎨⎪⎧x 2-2x ,x <0,2-x 2,0≤x <1,x 4-2x 2,x ≥1.作出函数f (f (x ))的图像可知,当1<k ≤2时,函数y=f (f (x ))-k 有3个不同的零点.12.12.由2AB AC AO +=可得OB OC +=0,即BO OC =,所以圆心在BC 上,且AB AC ⊥. 注意到||||=2AB AO =,所以ππ,,4,2336B C BC AC ====,所以12CA CB ⋅=.13.212-.由()a a b c bc ++=,得1b c b c a a a a ++=⋅,设,b c x y a a ==,则1x y xy ++=, 1a b c x y =++,因为21()2x y x y xy +++=≤,所以222x y ++≥,所以a b c +的最大值为212-.14.设a 为实数,记函数f (x )=ax -ax 3(x ∈[12,1])的图象为C .如果任何斜率不小于1的直线与C 都至多有一个公共点,则a 的取值范围是 ▲ .14.1,42⎡⎤-⎢⎥⎣⎦.由任何斜率不小于1的直线与C 都至多有一个公共点,也即x ∈[12,1]时,曲线()y f x =上任意两点连线的斜率都小于1,所以()1f x '≤在x ∈[12,1]上恒成立.由2()31f x a ax '=-≤,即2310ax a -+≥,设()31g t at a =-+,1,14t ⎡⎤∈⎢⎥⎣⎦,只需1()04g ≥,且(1)0g ≥,所以142a -≤≤.15.解:(1)由正弦定理知,b sin A =a sin B =2,①又a cos B =1, ②①,②两式平方相加,得(a sin B )2+(a cos B )2=3, 因为sin 2B +cos 2B =1, 所以a =3(负值已舍);(2)由(1)中①,②两式相除,得sin B cos B=2,即tan B =2,因为A -B =π4,所以tan A =tan(B +π4)=tan B +tanπ41-tan B tanπ4 =1+21-2=-3-22.(14分)16.证:(1)方法1:取线段PD 的中点M ,连结FM 、AM .因为F 为PC 的中点,所以FM ∥CD ,且FM =12CD .因为四边形ABCD 为矩形,E 为AB 的中点,所以EA ∥CD ,且EA =12CD .所以FM ∥EA ,且FM =EA .所以四边形AEFM 为平行四边形.所以EF ∥AM . 又AM ⊂平面P AD ,EF ⊄平面P AD ,所以EF ∥平面P AD .方法2:连结CE 并延长交DA 的延长线于N ,连结PN .因为四边形ABCD 为矩形,所以AD ∥BC , 所以∠BCE =∠ANE ,∠CBE =∠NAE . 又AE =EB ,所以△CEB ≌△NEA . 所以CE =NE .又F 为PC 的中点,所以EF ∥NP . 又NP ⊂平面P AD ,EF ⊄平面P AD , 所以EF ∥平面P AD .方法3:取CD 的中点Q ,连结FQ 、EQ .在矩形ABCD 中,E 为AB 的中点,所以AE =DQ ,且AE ∥DQ .所以四边形AEQD 为平行四边形, 所以EQ ∥AD .又AD ⊂平面P AD ,EQ ⊄平面P AD , 所以EQ ∥平面P AD .(2分)因为Q 、F 分别为CD 、CP 的中点,又PD ⊂平面P AD ,FQ ⊄平面P AD ,所以FQ ∥平面P AD .又FQ 、EQ ⊂平面EQF ,FQ ∩EQ =Q ,所以平面EQF ∥平面P AD .(5分) 因为EF ⊂平面EQF ,所以EF ∥平面P AD . (2) 设AC 、DE 相交于G .在矩形ABCD 中,因为AB =2BC ,E 为AB 的中点,所以DA AE =CDDA= 2.又∠DAE =∠CDA ,所以△DAE ∽△CDA , 所以∠ADE =∠DCA .又∠ADE +∠CDE =∠ADC =90°, 所以∠DCA +∠CDE =90°. 由△DGC 的内角和为180°,得∠DGC =90°. 即DE ⊥AC .因为点P 在平面ABCD 内的正投影O 在直线AC 上,所以PO ⊥平面ABCD . 因为DE ⊂平面ABCD ,所以PO ⊥DE . 因为PO ∩AC =O ,PO 、AC ⊂平面P AC , 所以DE ⊥平面P AC ,又DE ⊂平面PDE ,所以平面P AC ⊥平面PDE .17.解:(1)设n *()n ∈N 年内所建安置房面积之和首次不低于3 000万m 2, 依题意,每年新建安置房面积是以200为首项,50为公差的等差数列, 从而n 年内所建安置房面积之和为(1)200502n n n -⎡⎤+⨯⎢⎥⎣⎦m 2, 则(1)200502n n n -+⨯≥3 000,整理得,271200n n +-≥, 解得8 (15)n n -≤≥舍去.答:8年内所建安置房面积之和首次不低于3 000万m 2.(2)依题意,每年新建住房面积是以500为首项,1.1为公比的等比数列, 设第m 年所建安置房面积占当年新建住房面积的比为()p m , 则1120050(1)3()500(10.1)10 1.1m m m m p m --+-+==⋅+⨯, 由()(1)p m p m =+得,13410 1.110 1.1m mm m -++=⨯⨯,解得7m =.答:第7年和第8年,所建安置房面积占当年新建住房面积的比保持不变. ·····14分 18.解:(1)分别过点A 、B 作直线l 的垂线,垂足为11,B A , 由题意得11BB AA =,由点到直线距离公式得112a AA BB ==,因为圆A 以1AF 为半径,所以半径为c ,被直线l 截得的弦长为222()2a c -,圆B 以OB 为半径,∴半径为a ,被直线l 截得的弦长为222()2a a -.因为直线l :33y x =-被圆A 和圆B 截得的弦长之比为156,所以()222222241563324a c c a a a --==,解得a c 34=(a >c >0). 因为c e a=,所以所求的离心率为34,(2)存在点P ,使得过点P 有无数条直线被圆A 和圆B 截得的弦长之比为34,设点0(,0)P x ,由题意可得直线方程为0()y k x x =-, 直线截圆A 所得的弦长为2202|(7)|21k x c k ⎛⎫--- ⎪+⎝⎭, 直线截圆B 所得的弦长为2202|(7)|21k x a k ⎛⎫-- ⎪+⎝⎭,[][]22022220220202(7)2(1)(7)134(1)(7)(7)21k x c k c k x k k a k x k x a k ⎛⎫+- ⎪+-++⎝⎭==+--⎛⎫-- ⎪+⎝⎭,化简得22222220016(7)9(7)(1)(169)k x k x k c a +--=+-(*),由(1)离心率为34,得22169c a =,即方程(*)为0)1)(49(002=++x x k ,解得10-=x 或490-=x , 即存在2个点)0,1(-和)0,49(-;当10-=x 时,22||61||81k c kk a k ⎧<+⎪⎨<+⎪⎩,解得7157151515k -<<,当490-=x 时,22||421||561k c kk a k⎧<+⎪⎨<+⎪⎩,解得7772121k -<<,即有无数条直线;故存在2个点P ,使得过点P 有无数条直线被圆A 和圆B 截得的弦长之比为34.19.解:(1)∵()()e ,0x f x x k x '=->.(i )当0k ≤时,()0恒成立'>f x ,∴()f x 的递增区间是0+(,)∞,无递减区间;无极值.(ii )当0>k 时,由()0'>f x 得,>x k ;由()0'<f x 得,0<<x k ;∴()f x 的递减区间是(0,)k ,递増区间是(,+)∞k ,()f x 的极小值为()e k f k =-,无极大值. (2)①由()4f x x <,可得(1)e 40x x k x ---<,因为e 0x >,所以41e x x x k --<,即41ex x k x >--对任意[1,2]x ∈恒成立, 记4()1ex xg x x =--,则4(1)e 4(1)()1e e x x x x x g x -+-'=-=, 因为[1,2]x ∈,所以()0g x '>,即()g x 在[1,2]x ∈上单调递增,故2max228e 8()(2)1e e g x g -==-=.所以实数k 的取值范围为22e 8(,)e-+∞.②由已知1212()()()f x f x x x =≠,结合(1)可知, 0k >,()f x 在(,)-∞k 上单调递减,在(,+)∞k 上单调递增,又(1)0+=f k ,1<+x k 时,()0<f x .不妨设121<<<+x k x k ,此时2x k >,12->k x k ,故要证122+<x x k ,只要证122k x x ->,只要证12(2)()f k x f x ->, 因12()()f x f x =,即证11(2)()f k x f x ->.设()(2)()h x f k x f x =--2(1)(1)()k xxx k x k x k -+-=---<e e e ,2()e ()()e e k xxx k h x x k -'=--22()()k x x x k --=e e e , ∴当<x k 时,()0h x '<,()h x 在(,)-∞k 上单调递减,∴(,)x k ∈-∞时,()()0k k h x h k >=-+=e e , 故当<x k 时,(2)()->f k x f x ,即11(2)()->f k x f x 成立,∴122+<x x k .20.解:(1)111312A B d ===,,;222413A B d ===,,;333716A B d ===,,. …………………………………………………………………3分(2)① 当1n =时,11(1)1a a λλ-=-+,所以11a =;当2n ≥时,由21(1)33n n S a n λλ-=-++,则1121(1)(1)33n n S a n λλ---=-+-+, 两式相减得12(1)3n n n a a a λλλ--=-++,即123n n a a λ-=+, 所以11122233(1)3(1)n n n n b a a b λλλλλ---⎡⎤=++=+==⎢⎥--⎣⎦.……………………………6分 因为112313(1)3(1)b a λλλ-=+=--,所以当13λ≠时,数列{}n b 满足1n n bb λ-=(2n ≥),即数列{}n b 是以313(1)λλ--为首项,λ为公比的等比数列;当13λ=时,数列{}n b 不是等比数列. …………………………………………………8分② 由①知,当13λ≠时,13123(1)3(1)n n a λλλλ--=⋅---;当13λ=时,23(1)n a λ=--.……………………………………………………………10分又{}{}1212max min i i i i n d a a a a a a ++=-,,,,,,, {}{}112123max min i i i i n d a a a a a a ++++=-,,,,,,.由于{}{}1223min min i i n i i n a a a a a a ++++,,,≤,,,,所以由1i i d d +>可得,{}{}12121max max i i a a a a a a +<,,,,,,.所以{}1211max i i a a a a ++=,,,对任意的正整数1232i n =-,,,,恒成立, 即数列{}n a 的前1n -项单调递增是题设成立的必要条件,易知13λ≠.………………12分因为1i i i d a a +=-,112i i i d a a +++=-,所以1212i i i i i d d a a a +++-=+-1231(12)3(1)i λλλλλ--=⋅+--1231(1)3(1)i λλλλ--=⋅--.当1λ>时,由1n n a a +>,得3103(1)λλ->-,解得1λ>, 此时10i i d d +-≥,不符合1i i d d +>,舍去;当01λ<<,由1n n a a +>,得3103(1)λλ-<-,解得113λ<<,此时10i i d d +-<,符合1i i d d +>.综上所述,λ的取值范围是()113,. ……………………………………………………16分第II 卷(附加题,共40分)21A .证:因为P A 是圆O 在点A 处的切线,所以∠P AB =∠ACB .因为PD ∥AC ,所以∠EDB =∠ACB , 所以∠P AE =∠P AB =∠ACB =∠BDE .又∠PEA =∠BED ,故△P AE ∽△BDE . …………………… 10分21B .解:设点(x 0,y 0)为曲线|x |+|y |=1上的任意一点,在矩阵10103M ⎛⎫⎪= ⎪ ⎪⎝⎭对应的变换作用下得到的点为(,)x y '',则0010103x x y y ⎛⎫'⎡⎤⎡⎤ ⎪=⎢⎥⎢⎥ ⎪' ⎪⎣⎦⎣⎦⎝⎭,所以003x x y y ='⎧⎨='⎩ ……5分 所以曲线|x |+|y |=1在矩阵10103M ⎛⎫⎪= ⎪ ⎪⎝⎭对应的变换作用下得到的曲线为|x |+3|y |=1, 所围成的图形为菱形,其面积为1222233⨯⨯= .……10分21C .解:(1)将(2,3)M 及对应的参数3πϕ=代入cos ,(0,sin x a a b y b ϕϕϕ=⎧>>⎨=⎩为参数),得2cos 33sin 3a b ππ⎧=⎪⎪⎨⎪=⎪⎩,所以42a b =⎧⎨=⎩,所以曲线1C 的普通方程为221164x y +=. ……4分 (2)曲线1C 的极坐标方程为2222cos sin 1164ρθρθ+=,将12(,),(,)2A B πρθρθ+代入得222211cos sin 1164ρθρθ+=,222222sin cos 1164ρθρθ+=,所以221211516ρρ+=. ……10分21D .解:因为a >0,b >0,a +b =1,所以(2a +1)+(2b +2)=5,从而(12a +1+2b +1 )[(2a +1)+(2b +2)]=1+4+2b +22a +1+4(2a +1)2b +2≥5+22b +22a +1×4(2a +1)2b +2=9. …………………… 6分 所以12a +1+2b +1≥95.当且仅当2b +22a +1=4(2a +1)2b +2,且a +b =1,即a =13,b =23 时,12a +1+2b +1取得最小值95. …………………… 10分22.解:因为在直三棱柱111ABC A B C -中,AB AC ⊥,所以分别以AB 、AC 、1AA 所在的直线为x 轴、y 轴、z 轴,建立空间直角坐标系, 则111(0,0,0),(2,0,0),(0,4,0),(0,0,3),(2,0,3),(0,4,3)A B C A B C ,因为D 是BC 的中点,所以(1,2,0)D ,……………………………………………………2分 (1)因为111(0,4,0),(1,2,3)AC A D ==-,设平面11A C D 的法向量1111(,,)n x y z =, 则1111100n AC n A D ⎧⋅=⎪⎨⋅=⎪⎩,即111140230y x y z =⎧⎨+-=⎩,取111301x y z =⎧⎪=⎨⎪=⎩,所以平面11A C D 的法向量1(3,0,1)n =,而1(1,2,3)DB =-, 所以111111335cos ,35n DB n DB n DB ⋅<>==⋅, 所以直线1DB 与平面11A C D 所成角的正弦值为33535;…………………………………5分 (2)11(2,0,0)A B =,1(1,2,3)DB =-,设平面11B A D 的法向量2222(,,)n x y z =, 则2112100n A B n DB ⎧⋅=⎪⎨⋅=⎪⎩,即222220230x x y z =⎧⎨-+=⎩,取22232x y z =⎧⎪=⎨⎪=⎩,平面11B A D 的法向量2(0,3,2)n =,所以121212130cos ,65n n n n n n ⋅<>==⋅, 二面角111B A D C --的大小的余弦值13065.……………………………………………10分 23.(1)证明:0)(121)2()(31222222>-=+-++=-b a b a b ab a B A (2)证明:11,1B A n ==;,)2(,11,311nn n n n b a B b a b a n A n +=--+=≥++令,,y b a x b a =-=+且0,>y x ,于是,)2(],)()[()1(21)2()2(1111111n n n n n n n n x B y x y x y n y y x y x n A =--++=--++=+++++ 因为y x C y x C y x C y x y x nn n n n n n n 11323111112)22(])()[(+-++++≥++=--+ ,所以n n n n n n n n B x x y x C y n A ===⋅+≥++)2(22)1(21111.。
2017年高考模拟试卷(1)参考答案

2017年高考模拟试卷(1)参考答案一、填空题1.()12,.A B =()12,.2.12. (2)(1)2i 13.1i (1)(1)2i i iz i i ++++===--+,则复数z 的实部为 12.3.(-9,+∞).函数5()log (9)f x x =+的单调增区间(-9,+∞).4. 536.点数之和是6包括(15)(24)(33)(42)(15),,,,,,,,,共5种情况,则所 求概率是536.5. 8.若613x =,则1326x =>,不符;若513x +=,则82x =>.6. 0. 244.这组数据的平均数为10,方差为222221(109.4)(109.7)(109.8)(1010.3)(1010.8)0.245⎡⎤-+-+-+-+-=⎣⎦. 7. 76.函数()f x 的周期4(3T π=⨯)43π7π+=,又Τω2π=,所以ω的值为76.8. π.依题意,2220+⋅-=a a b b ,又1==a b ,故1⋅=a b ,则a 与b 的夹角为π. 9. 113.()()()()11tan tan 25tan tan 111tan tan 125αββααββαββ--+=-+===⎡⎤⎣⎦---⨯-113. 10. 115⎡⎤-⎢⎥⎣⎦,.因为不等式2 >0ax bx c ++的解集为()1 5-,,所以(1)(5)>0a x x +-,且0a <,即245>0ax ax a --,则45b a c a =-=-,,则2 0cx bx a ++≤即为254 0ax ax a --+≤,从而254 1 0x x +-≤,故解集为115⎡⎤-⎢⎥⎣⎦,. 11.3.由121x y +=得,02y x y =>-,则()222222222log log log log log 22y y x y xy y y -++===-- ()224log 24log 832y y ⎡⎤=-++=⎢⎥-⎣⎦≥. 12. 5.易得圆C :22(1)9x y -+=,定点A (10)-,,EA ED =,则3EC EA EC ED +=+=, 从而三角形AEC 的周长为5.13. 2027.易得数列{}n b :1,3,5,6,7,9,10,11,12,13,14,15,17,…,则1137++++…12121k k k ++-=--,当10k =,12120372017k k +--=>,2037201720-=,从而第2017项为1121202027--=. 14. ()()5114-∞-,,.{}()max 11f x x x =-+,2()()g x x k k =+∈R 恰有4个零点, 当54k =时,()f x 与()g x 相切.如图,结合图形知,实数k 的取值范围是())5114-∞-,,. 二、解答题15. (1)因为cos cos 02C C +=,所以22cos cos 1022C C +-=,解得cos 12C =-或1cos 22C =, 又0C π<< ,故22C π0<<,从而23C π=,即23C π=.(2)由余弦定理2222cos c a b ab C =+-得,221a b ab ++=, ① 由三角形ABC 的面积1sin 2ab C ==13ab =, ②由①②得,a b ==.16. (1)因为AB //DE ,又AB ⊄平面DEF , DE ⊂平面DEF ,所以AB //平面DEF , 同理BC //平面DEF , 又因为ABBC C =,A B B C ⊂,平面ABC ,所以平面ABC //平面DEF . (2)因为CAB ∠是二面角C -AD -E 的平面角,所以CA AD BA AD ⊥⊥,, 又因为CA AB A =, AB ,CA ⊂平面ABC ,所以DA ⊥平面ABC , 又DA ⊂平面DABE ,所以平面ABC ⊥平面DABE .17. (1)过点P 分别作AB ,AD 的垂线,垂足分别为E ,F , 则△PNF 与△MPE 相似,从而PF NF EM PE=,所以2121n m -=-,即211m n+=. 欲使剩下木板的面积最大,即要锯掉的三角形废料MAN 的面积 12S mn =最小.由211m n =+≥8mn ≥ (当且仅当21m n =,即4m =,2n =时,“=”成立),此时min 4S =(平方分米). (2)欲使剩下木板的外边框长度最大,即要m n +最小.由(1)知,()()212333n m m n m n m n m n +=++=++=≥,(当且仅当2n m m n =即2m =,1n 时,“=”成立),答:此时剩下木板的外边框长度的最大值为33-分米.18. (1)由椭圆C :2221x y a+=(a >1)知, 焦距为2=, 解得a =因为a >1,所以a =(第17题)(2)设直线1y kx =+被椭圆截得的线段长为ΑΡ, 由22211y kx x y a=+⎧⎪⎨+=⎪⎩,,得()2222120a k x a kx ++=, 解得10x =,222221a kx a k=-+.因此2122221a kΑΡx a k=-=+. (3)因为圆与椭圆的公共点有4个,由对称性可设y 轴左侧的椭圆上有2个不同的公共点为P ,Q ,满足AP AQ =.记直线AP ,AQ 的斜率分别为1k ,2k ,且1k ,20k >,12k k ≠. 由(2)知,1AP2AQ ,12,所以22222222121212)1(2)0k k k k a a k k ⎡⎤-+++-=⎣⎦(,因为1k ,20k >,12k k ≠,所以22222212121(2)0k k a a k k +++-=, 变形得,()()22221211111(2)a a k k ++=+-, 从而221+(2)1a a ->,解得a则)1c e a =. 19. (1)因为函数()f x 为偶函数,所以()()f x f x -=-,即()()()323222x a x b x c x ax bx c -+-+-+=----, 整理得,20ax c +=,所以0a c ==,从而3()2f x x bx =+,又函数()f x 图象过点(12)-,,所以4b =-. 从而3()24f x x x =-.(2)①32()2()f x x ax bx c a b c =+++∈R ,,的导函数2()62f x x ax b '=++. 因为()f x 在1x =和2x =处取得极值,所以(1)0(2)0f f ''==,, 即6202440a b a b ++=⎧⎨++=⎩,,解得912a b =-=,. ②由(1)得32()2912()f x x x x c c =-++∈R ,()6(1)(2)f x x x '=--. 列表:显然,函数()f x 在[0,3]上的图象是一条不间断的曲线.由表知,函数()f x 在[0,3]上的最小值为(0)f c =,最大值为(3)9f c =+. 所以当0c >或90c +<(即9c <-)时,函数()f x 在区间[03],上的零点个数为0. 当50c -<<时,因为(0)(1)(5)0f f c c =+<,且函数()f x 在(0,1)上是单调增函数,所以函数()f x 在(0,1)上有1个零点.当54c -<<-时,因为(1)(2)(5)(4)0f f c c =++<,且()f x 在(1,2)上是单调减函数, 所以函数()f x 在(1,2)上有1个零点.当94c -<<-时,因为(2)(3)(4)(9)0f f c c =++<,且()f x 在(2,3)上是单调增函数, 所以函数()f x 在(2,3)上有1个零点.综上,当0c >或9c <-时,函数()f x 在区间[03],上的零点个数为0;当95c -<-≤或40c -<≤时,零点个数为1; 当4c =-或5c =-时,零点个数为2;当54c -<<-时,零点个数为3.20.(1)依题意,11111166022a a a aa b ++=- (当且仅当111a a =时,等号成立).(2)易得()1342n n --=--,当n 为奇数时,()13420n n --=--<,所以43n <,又*n ∈N ,故1n =,此时111a b ==-;当n 为偶数时,()13420n n --=-->,所以43n >,又*n ∈N ,故246n =,,,…若2n =,则222a b ==,若4n =,则448a b ==, 下证:当6n ≥,且n 为偶数时,()1342n n --<--,即()12134n n --->-.证明:记()12()34n p n n ---=-,则()()()112434(2)341()32322n n n p n n p n n n +----+-=⋅=>++--, 所以()p n 在6n ≥,且n 为偶数时单调递增, 从而17()(6)17p n p >=>.综上,124n =,,,所以m 的值为3. (3)证明:假设3m =,不妨123n n n <<,满足11n n a b =,22n n a b =,33n n a b =, 设1(1)n a a n d =+-,11n n b b q -=,其中0q >,且1q ≠, 记11()(1)xb f x a x d q q=+--⋅, 则1()ln x b f x d q q q '=-⋅,()21()ln x b f x q q q''=-⋅,由参考结论,知112()n n ξ∃∈,,1()0f ξ'=,223()n n ξ∃∈,,2()0f ξ'=, 同理,12()ηξξ∃∈,,()0f η''=,即()21()ln 0b f q q qηη''=-⋅=, 这与()21()ln 0b f q q qηη''=-⋅≠矛盾,故假设不成立,从而3m ≠.第Ⅱ卷(附加题,共40分)A .因为ABCD 是圆的内接四边形,所以DAE BCD ∠=∠,FAE BAC BDC ∠=∠=∠. 因为BC BD =,所以BCD BDC ∠=∠, 所以DAE FAE ∠=∠,所以AE 是四边形ABCD 的外角DAF ∠的平分线. B .因为1002⎡⎤=⎢⎥⎣⎦A ,11201⎡⎤⎢⎥=⎢⎥⎣⎦B , 所以11101122020102⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦AB .由逆矩阵公式得,1114()102-⎡⎤-⎢⎥=⎢⎥⎢⎥⎣⎦AB . C .以极点O 为原点,极轴Ox 为x 轴正半轴建立平面直角坐标系xOy . 则圆24sin 50ρρθ--=化为普通方程22450x y y +--=,即22(2)9x y +-=.直线π()3θρ=∈R化为普通方程y =0y -=.圆心(02),0y -=的距离为1d ==,于是所求线段长为 D .由柯西不等式可得,(()22222215⎤++=⎦≤,(当且仅当=16[34]5x =∈,时,“=”成立.) 22. (1)依题意,将(12)C ,代入22(0)y px p =>得,2p =; (2)因为 90BCA ∠=︒,所以0CA CB ⋅=,其中2(122)CA a a =--,,2(122)CB b b =--,, 从而22(1)(1)4(1)(1)0a b a b --+--=,化简得,51a b a +=-+;(3)易得直线AB 的方程为222()y a x a b a-=-+, 令5x =得,22(5)2251y a a a a a =-+=-+-++. 23.当2n =时,1,2,3排成一个三角形有:12 31 32 2 13 2 3 13 1 23 2 1共有6种,其中满足12M M <的有如下4种:所以24263p ==;(2)设当n k =时,12k M M M <<⋅⋅⋅的概率为k p ,则当1n k =+时,121k k M M M M +<<⋅⋅⋅<的概率为1k p +, 而1k +排在第1k +行的概率为12(1)(11)22k k k k +=++++, 所以12(2)2k k p p k k +=+≥,即12(2)2k k p k p k +=+≥, 故3224p p =,4325p p =,5426p p =,…,121n n p p n -=+, 叠乘,得()22214n n p p n n -=+⨯⨯⋅⋅⋅⨯,其中24263p ==, 所以n p 2(1)!n n =+.1 2 31 3 22 1 32 3 1。
2017高考模拟试卷理数及答案
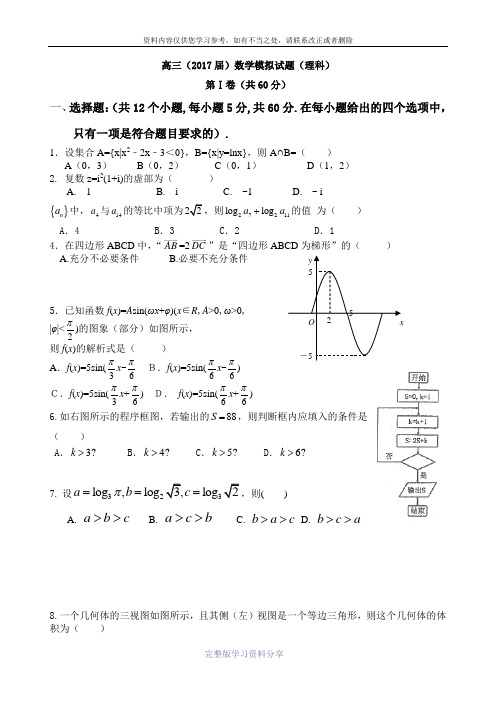
高三(2017届)数学模拟试题(理科)第Ⅰ卷(共60分)一、选择题:(共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.设集合A={x|x 2﹣2x ﹣3<0},B={x|y=lnx},则A ∩B=( )A (0,3)B (0,2)C (0,1)D (1,2) 2. 复数z=i 2(1+i)的虚部为( )A. 1B. iC. -1D. - i{}n a 中,4a 与14a 的等比中项为22,则27211log log a a +的值 为( )A .4B .3C .2D .1 4.在四边形ABCD 中,“AB =2DC ”是“四边形ABCD 为梯形”的( ) A.充分不必要条件 B.必要不充分条件 5.已知函数f (x )=A sin(ωx +φ)(x ∈R ,A >0,ω>0, |φ|<2π)的图象(部分)如图所示,则f (x )的解析式是( )A .f (x )=5sin(3πx -6π B.f (x )=5sin(6πx -6π)C.f (x )=5sin(3πx +6π) D. f (x )=5sin(6πx +6π)6.如右图所示的程序框图,若输出的88S =,则判断框内应填入的条件是( )A .3?k >B .4?k >C .5?k >D .6?k >7. 设323log ,log 3,log 2a b c π===,则( )A.a b c >>B.a cb >>C.b ac >> D. b c a >>8.一个几何体的三视图如图所示,且其侧(左)视图是一个等边三角形,则这个几何体的体积为( )x -5y O 5 2 5A .433 B .533 C .23 D .833x y 、满足121y y x x y m ≥⎧⎪≤-⎨⎪+≤⎩,如果目标函数z x y =-的最小值为-1,则实数m =( )A .6B .5C .4D .3 10.函数()2sin f x x x =+的部分图象可能是( )11. 已知双曲线()222210,0x y C a b a b-=>>:的右焦点为F ,过F 且斜率为3的直线交C 于A B 、两点,若4AF FB =,则C 的离心率为A .95 B. 75 C. 58 D. 6512、已知定义在R 上的可导函数f(x)的导函数为/()f x ,满足/()f x <()f x ,且()(2)f x f x -=+,(2)1f =,则不等式()x f x e <的解集为( )A. ()2,-+∞B. (0,+∞)C.(1, +∞)D.(2, +∞)第Ⅱ卷(非选择题 共90分)二、填空题:(本大题共4个小题,每小题5分,共20分). 13. (4y x 的展开式中33x y 的系数为 。
四川省眉山市仁寿县铧强中学2023届高三高考前模拟文综历史试题(含解析)
四川省眉山市仁寿县铧强中学2023届高三高考前模拟文综历史试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.西周时,穆王曾在游牧部族的引导下,带着“六师之人”,沿着黄河上游西行穿越戎狄地区,互赠礼品,并赐子戎狄部族首领“宗正”一职,以示安抚和奖励。
据此可知当时A.黄河上游普遍实行分封制B.西周军队战斗力明显强于戎狄C.西周重视边远地区的管理D.宗法制度在西周境内得以落实2.发端于先秦时期的道家和儒家思想,在中国传统文化中留下了深刻的烙痕。
下列言论,按时间先后顺序排列,正确的是①“从天而颂之,孰与制天命而用之!望时而待之,孰与应时而使之!”②“合抱之木,生于毫末;九层之台,起于累土;千里之行,始于足下。
”③“天生民性,有善质而未能善,于是为之立王以善之,此天意也”A.①②③B.①③②C.②①③D.③②①3.宋人张方平在《论钱禁铜法事》中说:“边关重车而出,海舶饱载而回……钱本中国宝货,今乃与四夷共用。
”这说明宋代A.商业革命影响邻国经济发展B.经济交流推动铜钱“国际化”C.经济强盛使得交子广泛流通D.国际流通造成铸币严重短缺4.宣德八年,明政府回赠日本贡使礼品,除常例白金三百两、皇室精制丝绸一百二十二匹以外,特另增戗金桥、床,银制酒具,古铜花瓶、香炉等四十二种,装柜六十只。
对于日本贡舶附带货物,明政府均以优价收买。
明朝与日本的往来()A.冲破了海禁政策限制B.可扩大中国海外影响力C.有效缓解了倭患问题D.推动了手工业技艺革新5.下图为明代和清代两个时期对异域人物的不同描绘,这反映了A.清代宫廷绘画流行写实画风B.西方人从野蛮时代走向文明社会C.天朝上国的观念已经被打破D.中外交流拓展了国人的世界视野6.下表是1890~1918年外商银行在中国发行与流通的纸币数量约略统计情况(单位:万元)。
年份数量发行银行A.采取新经济政策并取得初步成果B.在帝国历史与现实政治之间妥协C.注重提高艺术品的意识形态价值D.经济实力增强但外汇储量备不足充斥西方,已成为西方国家政治主流。
2017年普通高等学校招生全国统一考试模拟(六)理科综合物理试题
2017年普通高等学校招生全国统一考试模拟(六)理科综合物理试题二、选择题(本大题共8小题;每小题6分,共48分。
在每小题中给出的四个选项中,其中14-18题只有一个选项正确,19-21题有多个选项正确,全部选对的得6分,选不全的得3分,有选错或不答的得0分。
)14. 如图为氢原子能级的示意图,现有大量的氢原子处于n=4的激发态,当向低能级跃迁时辐射出若干不同频率的光.关于这些光,下列说法正确的是A.最容易表现出衍射现象的光是由n=4能级跃迁到n=1能级产生的B.频率最小的光是由n=2能级跃迁到n=1能级产生的C.这些氢原子总共可辐射出3种不同频率的光D.用n = 2能级跃迁到n=1能级辐射出的光照射逸出功为6.34eV金属铂能发生光电效应15. 如图所示,正方形线框以速度v0沿光滑水平面进入宽度为d的匀强磁场,已知线框恰好能穿过磁场,则线框进入磁场和穿出磁场的过程中产生的热量之比Q1:Q2为A.1:1B. 2:1C.3:1D.4:116. —金属容器置于绝缘板上,带电小球用绝缘细线悬挂于容器中,容器内的电场线分布如图所示。
容器内表面为等势面,A、B为容器内表面上的两点,下列说法正确的是A. A点的电场强度比B点的大B. 小球表面的电势比容器内表面的低C. B 点的电场强度方向与该处内表面垂直D. 将检验电荷从A 点沿不同路径到B 点,电场力所做的功不同17. 如图所示,正六边形abcdef 区域内有垂直于纸面的匀强磁场.一带正电的粒子从f 点沿fd 方向射入磁场区域,当速度大小为v b 时,从b 点离开磁场,在磁场中运动的时间为t b ,当速度大小为v c 时,从C 点离开磁场,在磁场中运动的时间为t c , 不计粒子重力.则A.:1:2,:2:1b c b c v v t t ==B. :2:2,:1:2b c b c v v t t ==C. :2:1,:2:1b c b c v v t t ==D. :1:2,:1:2b c b c v v t t ==18.如图,由某种粗细均匀的总电阻为3R 的金属条制成的矩形线框abcd ,固定在水平面内且处于方向竖直向下的匀强磁场B 中.一接入电路电阻为R 的导体棒PQ ,在水平拉力作用下沿ab 、dc 以速度v 匀速滑动,滑动过程PQ 始终与ab 垂直,且与线框接触良好,不计摩擦.在PQ 从靠近ad 处向bc 滑动的过程中A. PQ 中电流先增大后减小B. PQ 两端电压先减小后增大C. PQ 上拉力的功率先减小后增大D. 线框消耗的电功率先减小后增大19、P 1P 2为相距遥远的两颗行星,距各自表面相同高度处各有一颗卫星s 1、s 2、做匀速圆周运动.图中纵坐标表示行星对周围空间各处物体的引力产生的加速度a ,横坐标表示物体到行星中心的距离r 的平方,两条曲线分别表示P 1P 2周围的a 与r 2的反比关系,它们左端点横坐标相同.则A. P1的平均密度比P2的大B. P1的“第一宇宙速度”比P2的小C. s1的向心加速度比s2的大D. s1的公转周期比s2的大20. 两根足够长的光滑导轨竖直放置,间距为L,底端接阻值为R的电阻.将质量为m的金属棒悬挂在一个固定的轻弹簧下端,金属棒和导轨接触良好,导轨所在平面与磁感应强度为B的匀强磁场垂直,如图所示.除电阻R外其余电阻不计.现将金属棒从弹簧原长位置由静止释放.则A.释放瞬间金属棒的加速度等于重力加速度gB.金属棒向下运动时,流过电阻R的电流方向为a→bC.金属棒的速度为v时.所受的安培力大小为F22B L v FRD.电阻R上产生的总热量等于金属棒重力势能的减少量21. 如图所示,一滑块从底端冲上固定的足够长粗糙斜面,到达某一高度后返回.下列各图分别表示滑块在斜面上运动的位移s、速度v、加速度a、机械能E随时间变化的图像,可能正确的是三、非选择题(包括必考题和选考题两部分,第22-32题为必考题,每个小题考生都必须作答,第33-40题为选考题,考生根据要求作答.)(一)必考题(共11题,共129分)22. (6分)某同学设计了一个用电磁打点计时器验证动量守恒定律的实验:在小车A的前端粘有橡皮泥,推动小车A使之做匀速运动,然后与原来静止在前方的小车B相碰并粘合成一体,继续做匀速运动.他设计的装置如图(a)所示.在小车A后连着纸带,电磁打点计时器所用电源频率为50 Hz,长木板下垫着小木片以平衡摩擦力.(1)若已测得打点的纸带如图(b)所示,并测得各计数点的间距(已标在图上).A为运动的起点,则应选段来计算A碰撞前的速度,应选段来计算A和B碰后的共同速度(以上两空选填“AB”“BC”“CD”或“DE”).(2) 已测得小车A的质量rn1=0. 4 kg,小车B的质量rn2=0. 2 kg,则碰前两小车的总动量大小为kg∙m/s,碰后两小车的总动量大小为kg ∙ m/s.23. (9分)某研究小组收集了两个电学元件:电阻R0(约为2 kΩ)和手机中的锂电池(电动势E标称值为3. 7V,允许最大放电电流为100 mA).实验室备有如下器材A.电压表V(量程3V,电阻Rv约为4.0 k))B.电流表A1 (量程100 mA,电阻R A1约为5Ω)C.电流表A2 (量程2 mA,电阻R A2约为50 Ω)D.滑动变阻器R1(0-40Ω),额定电流1 A)E.电阻箱R2(0-999. 9Ω)F.开关S—只、导线若干(1)为了测定电阻R0的阻值,小明设计了一电路,如图1所示为其对应的实物图,图中的电流表A应选(选填“A1’或“A2”),请将实物连线补充完整.(2)为测量锂电池的电动势E 和内电阻r ,小红设计了如图所示的电路图,根据测量数据作出211U R 图像,如图3所示.若该图线的斜率为k ,纵轴截距为b ,则该锂电池的电动势E= ,内阻r= (用k 、b 和R 2表示).该实验的测量值偏小,造成此系统误差的主要原因是 .24. (14分)如图所示,在同一竖直平面内的两正对着的相同半圆光滑轨道, 相隔一定的距离,虚线沿竖直方向,一小球能在其间运动,今在最高点A 与最低点B 各放置一个压力传感器,测试小球对轨道的压力,并通过计算机显示出来,当轨道距离变化时,测得两点的压力差与距离x 的图像如图,g=10m/s 2,不计空气阻力,求:(1)小球的质量为多少?(2) 若小球的最低点B 的速度为20 m/s ,为使小球能沿轨道运动,x 的最大值为多少?25.如图所示,在平面直角坐标系xoy 中,第一象限存在沿y 轴正方向的匀强电场,直线PQ 与x 轴负方向的夹角为a ,且tan α= 12,O 、P 之间的距离为L;第三象限存在平行x 轴的匀强电场(未画出)第四象限存在垂直于坐标平面向里的勻强磁场.一质量为m 、电荷量为q 的带电粒子 从P 点以速度v 0沿x 轴正方向射入电场,经x 轴上的Q 点射入磁场,最后从y 轴负半轴上的M 点(未画出)射出磁场,且进入第三象限后粒子做匀减速直线运动.已知第一象限和第三象限的匀强电场的场强大小相等,粒子的重力不计.(1) 求第一象限内匀强电场的场强大小E ,写出粒子从 Q 点射入磁场的方向与PQ 的夹角θ和α的关系.(2) 求勻强磁场的磁感应强度大小B.(3) 粒子从M 点进入第三象限后,能否再回到P 点? 如果能,说明理由;如不能,请你求出粒子从第1次 进入第四象限到第3次进入第四象限所用的时间.(二)选考题(共15分.请考生从给出的2道物理题、2道化学题、2道生物题中每科任选一题作答,如果多做,则每学科按所做的第一题计分.)33.[物理选修3-3](15分)(1) 下列叙述正确的有(填正确答案标号.选对1个得2分,选对2个得1分,选对3个得5分.每选错1个扣3分,最低得分为0分)A. 在过程a→b中,气体不一定吸热B. p c=P b>P aC.在过程b→c中,气体分子势能不断增大D.在过程b→c中,气体分子的平均速率减小E.在过程c→a中,气体从外界吸收的热量等于气体对外做的功(2) (10分)如图所示,长为100 cm、粗细均匀的细玻璃管的一端开口另一端封闭,在与水平面成θ=30°角放置时,一段长为h = 30cm的水银柱封闭着一定质量的理想气体,管内气柱长度为L1=60cm,大气压强p0=75 cmHg,环境温度t1=27℃.(ⅰ)如果将玻璃管沿逆时针方向缓慢转60°同时温度缓慢降到t2=7℃.求转动过程中管内气柱长度的最小值. (ii)如果将玻璃管沿顺时针方向缓慢转过30°保持温度不变,管内是否还有水银?如有,求最后水银柱的长度;如没有,请说明原因.34.[物理——选修3-4](15分)(1)(6分)如图,一束光沿半径方向射向一块半圆柱形玻璃砖,在玻璃砖底面上的入射角为θ经折射后射出ab两束光线.则A.在玻璃中,a 光的传播速度小于b 光的传播速度B.在真空中,a 光的波长小于b 光的波长C. 玻璃砖对a 光的折射率小于对b 光的折射率D.若改变光束的入射方向使θ角逐渐变大,则折射光线a 首先消失E.分别用ab 光在同一个双缝干涉实验装置上做实验,a 光的干涉条纹间距大于b 光的干涉条纹间距(2) (9分)某时刻的波形图如图所示,波沿x 轴正方 向传播,质点P 的横坐标x = 0. 32 m.从此时刻开始计时:(i )若P 点经0. 4s 第一次到达最大正位移处,求波速大小;(ii )若P 点经0. 4 s 到达平衡位置,波速大小又如何?答案:14.D 15.C 16.C 17.A 18.C 19.AC 20.AC 21.BC22.(1)BC DE (2)0.420;0.41723.(1)A 2 图示:(2)1;k b b;电压表的分流 24.(1)设轨道半径为R ,由机械能守恒可知:2211(2)22B A mv mg R x mv =++ 对B 点:2B N v F mg m R-= 对A 点:2A N v F mg m R+=联立解得两点的压力差:1226N N N mgx F F F mg R ∆=-=+由图像得:截距6mg=3 可得m=0.05kg(2)因为图像的斜率21mg k R== 得R=1m 。
2017届高三上学期第二次模拟考试理科综合试卷
某某省五个一联盟(某某一中、某某一中、某某一中、某某一中、某某一中)2017届高三上学期第二次模拟考试理科综合试卷可能用到的相对原子质量:H-1 C-12 O-16 Cl-35.5 Na-23 Fe-56 Ti-48第Ⅰ卷(选择题共126分)一、选择题:本题共13小题,每小题6分。
在每小题给出的四个选项中,只有一项是符合题目要求。
1.下列有关生物科学史的叙述,错误的是()A.1880年,恩格尔曼以水绵为实验材料,发现了光合作用的场所B.1910年,摩尔根以白眼雄果蝇为实验材料,发现了基因的分离定律C.1958年,斯图尔德以胡萝卜韧皮部为实验材料,证明了植物细胞具有全能性D.1970年,科学家用荧光物质标记细胞膜上的蛋白质,证明了细胞膜上的蛋白质是可以运动的2.下图甲表示由磷脂分子合成的人工膜的结构示意图,下图乙表示人的红细胞膜的结构示意图及葡萄糖和乳酸的跨膜运输情况,图丙中A为1mol/L的葡萄糖溶液,B为1mol/L的乳酸溶液,下列说法不正确的是()A.由于磷脂分子具有亲水的头部和疏水的尾部,图甲人工膜在水中磷脂分子排列成单层B.若图乙所示细胞放在无氧环境中,葡萄糖和乳酸的跨膜运输都不会受到影响C.若用图甲所示人工膜作为图丙中的半透膜,当液面不再变化时,左侧液面等于右侧液面D.图丁中①为信号分子,与靶细胞细胞膜上的②特异性结合,体现了细胞膜的信息交流功能3.研究发现,正常干细胞中两种关键蛋白质“失控”发生越位碰撞后,正常干细胞会变成肿瘤干细胞。
下列有关叙述正确的是()A.干细胞分化形成各种类型的细胞体现了细胞的全能性B.干细胞在癌变过程中细胞膜上的甲胎蛋白会减少C.干细胞分化导致基因的选择性表达,细胞种类增多D.干细胞分化后的逐渐衰老是由细胞中基因决定的正常的生命历程4.已知A、a是一对等位基因。
右图①~③分别表示某种动物3个种群A基因频率的变化情况,3个种群的初始个体数依次为26260和2600且存在地理隔离。
2017年高考理科数学模拟试卷(全国卷)【精选文档】
2017年普通高等学校招生全国统一模拟考试理科数学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22~24题为选考题,其它题为必考题。
全卷满分150分.考试时间120分钟。
注意事项:⒈答题前,考生务必把自己的姓名、考生号等填写在答题卡相应的位置上。
⒉做选择题时,必须用2B 铅笔把答题卷上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
⒊非选择题必须使用黑色字迹钢笔或签字笔,将答案写在答题卡规定的位置上. ⒋所有题目必须在答题卡上指定位置作答,不按以上要求作答的答案无效。
⒌考生必须保持答题卡的整洁.考试结束后,将答题卡交回。
参考公式:柱体体积公式:V Sh = (其中S 为底面面积,h 为高)锥体体积公式:13V Sh =(其中S 为底面面积,h 为高) 球的表面积、体积公式:2344,3S R V R ==ππ (其中R 为球的半径)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数12iz i-+=(i 是虚数单位)在复平面上对应的点位于 ( )A . 第一象限B . 第二象限C . 第三象限D . 第四象限 2.已知集合M={x |y=lg},N={y|y=x 2+2x+3},则(∁R M )∩N= ( )A . {x|0<x <1}B . {x |x >1}C . {x|x≥2}D . {x|1<x <2}3、采用系统抽样方法从960人中抽取32人做问卷调查为此将他们随机编号为1,2 .。
.960,分组后在第一组采用简单随机抽样的方法抽到的号码为9,抽到的32人中,编号落入区间[1,450]的人做问卷A ,编号落人区间[451,750]的人做问卷B ,其余的人做问卷C 。
则抽到的人中,做问卷C 的人数为 ( ) A. 15 B 。
10 C 。
9 D. 7 4.设{n a } 是公差为正数的等差数列,若12315a a a ++=,且12380a a a =,则111213a a a ++等于( )A .120B . 105C . 90D .755.由2y x =和23y x =-所围成图形面积是 ( )A.B 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
铧强中学高2017届高考物理模拟测试卷(6)
一、选择题:本题共8小题,每小题6分。
在每小题给出的四个选项中,第1~5 题只有一项符合题
目要求,第6~8 题有多项符合题目要求。
全部选对的得6分,选对但不全的得3 分,有选错的得0分
1、核能作为一种新能源在现代社会中已不可缺少,我国在完善核电安全基础上将加大核
电站建设.核泄漏中的钚(Pu)是一种具有放射性的超铀元素,它可破坏细胞基因,提高患
癌的风险.已知钚的一种同位素239
94
PU的半衰期为24100年,其衰变方程为239
94
PU→X+4
2
He+
γ,下列有关说法正确的是()
A.衰变发出的γ射线是波长很短的光子,穿透能力很强
B.X原子核中含有92个中子
C.8个239
94
PU经过24100年后一定还剩余4个
D.由于衰变时释放巨大能量,根据E=mc2,衰变过程总质量不变
2、如图,顶端固定着小球的直杆固定在小车上,当小车向右做匀加速
运动时,球所受杆的作用力的方向沿图中的()
A、OA方向
B、OB方向
C、OC方向
D、OD方向
3、研究“蹦极”运动时,在运动员身上装好传感器,用于测量运动员
在不同时刻下落的高度及速度。
如图甲所示,运动员
及所携带的全部设备的总质量为60kg,弹性绳原长为
10m。
运动员从蹦极台自由下落,根据传感器测到的数
据,得到如图乙所示的速度—位移(v—l)图像。
不计
空气阻力,重力加速度g取10m/s2。
下列判断正确的
是()
A.运动员下落运动轨迹为一条抛物线
B.运动员下落速度最大时绳的弹性势能也为最大
C.运动员下落加速度为0时弹性势能为0
D.运动员下落到最低点时弹性势能为18000J
4、如图,某空间站在轨道半径为R的近地圆轨道I上围绕地球运行,一宇宙飞船与空间
站对接后,在轨道I上围绕地球运行多圈后又与空间站分离,进入椭圆轨道II运行。
已
知椭圆轨道的远地点到地球球心的距离为3.5R,地球质量为M,
万有引力常量为G,则()
A.空间站在圆轨道I上运行的周期为
GM
R3
2π
B.空间站与飞船对接后在圆轨道I上运行的周期变小
C.飞船在椭圆轨道远地点的速率是近地点的3.5倍
D.飞船与空间站分离后在远离地球过程中其机械能不断增大
5、如图所示,一水平面内固定两根足够长的光滑平行金属导轨,导轨上面横放着两根完
全相同的铜棒ab和cd,构成矩形回路,在整个导轨平面内都有竖直向上的匀强磁场B。
开始时,棒cd静止,棒ab有一个向左的初速度v0,则关于两棒以后的运动,下列说法正
确的是()
A.ab棒做匀减速直线运动,cd棒做匀加速直线运动
B.ab棒减小的动量等于cd棒增加的动量
C.ab棒减小的动能等于cd棒增加的动能
D.两棒一直运动,机械能不断转化为电能
6、如图所示,F-t图象表示某物体所受的合外力,随时间的变化关系,t=0时物体的初速
度为零,则下列说法正确的是()
A.前4s内物体的速度变化量为零
B.前4s内物体的位移为零
C.物体在0-2s内的位移大于2-4s内的位移
D.0-2s内F所做的功等于2-4s内物体克服F所做的功
7、在光滑绝缘水平面上,一条绷紧的轻绳拉着一个带电小球绕轴O在匀强磁场中作逆时针
方向匀速圆周运动,磁场方向竖直向下,其俯视图如图所示.若小球运动到A点时,绳子忽
然断开.关于小球在绳断开后可能的运动情况,下列说法中正确的
是()
A.小球仍作逆时针匀速圆周运动,半径不变
B.小球作顺时针匀速圆周运动,半径不变
C.小球仍作逆时针匀速圆周运动,但半径减小
D.小球作顺时针匀速圆周运动,半径减小
8、如图所示,一直角三角形处于平行于纸面的匀强电场中,∠CAB=90°,∠CBA=30°,AC
长为L,已知A点电势为ϕ(ϕ>0),B点电势为2ϕ,C点电势为0,一带电的粒子从C点
以v0的速度出发,方向如图所示(与AC边成60°),不计粒
子重力,下列说法中正确的是()
A.电场强度的方向由B指向C
B
C.若粒子能击中图中的A点,则该粒子的比荷为
2
6mv
ϕ
D.无论粒子速度多大都不可能击中图中B点
9、某同学利用图甲所示的装置进行恒力做功与物体动能变化的关系实验,水平桌面上放
上小物块,在适当重物牵引下运动,重物落地后,物块再运动一段距离停在桌面上。
通过
实验得到如图乙所示的纸带,纸带上O点为物体运动起始时刻打的点,选取时间间隔为
0.1s。
实验时物块的质量为0.5kg,力的传感器测得物块所受的拉力为1.98N,g=9.80m/s2.
(1)物块与桌面的;动摩擦因数μ= .
(2)物块从O点到D点,所受的合外力做的功为 J,动能的变化量△E
K
= J(保
留三位有效数字)
10、为了描绘小灯泡的伏安特性曲线,实验室可供选择的器材如下:
A.待测小灯泡(6V 500mA)
B.电流表A(0﹣0.6A 内阻约0.5Ω)
C.电压表V(0﹣3V 内阻5kΩ)
D.滑动变阻器R
1
(0﹣lkΩ 100mA)
E.滑动变阻器R
2
(0﹣5Ω 1.5A)
II
F .电阻箱R 3(0﹣9999.9Ω)
G .直流电源E (约6V ,内阻不计) H .开关S ,导线若干
(1)将电压表量程扩大为6V ,与它串联的电阻箱的阻值应调为 k Ω.
(2)图甲中画出了实验的部分电路,请你补全电路图;滑动变阻器应选用 (选填“R l “或“R 2“).
(3)实验中,变阻器滑动触头P 在ab 间移动时,发现小灯泡两端的电压只能在3.5V ﹣6.0V 间变化,则电路中出现的故障可能是 .
(4)排除故障后,测量出多组数据以灯泡两端的电压U 为横轴,电流表的示数I 为纵轴,描点作出小灯泡的伏安特性曲线如图乙所示.由于电压表V 内阻分流的影响,则小灯泡实际的伏安特性曲线应在所画图线的 (选填“上方“或“下方“).
11小物块质量m=0.99kg ,静止在光滑水平面上,—颗质量为m 0=0.01kg 的子弹以速度v 0=400m/s 从左边射入小物块,之后小物块滑上一倾角为37°的斜坡,最后返回水平面。
水平面与斜坡的连接处有一小段光滑圆弧,小物块与斜坡的动摩擦因数μ=0.5,重力加速度g=10m/s 2。
(sin37°=0.6,cos37°=0.8)求:(1)小物块被打入子弹后沿斜坡上滑的最大距离;(2)小物块返回水平面的速度。
12、如图所示,在平面直角坐标系xOy 内,第二、三象限内存在沿y 轴正方向的匀强电场,第一、四象限内存在半径为L 的圆形匀强磁场,磁场方向垂直于坐标平面向外。
一个比荷(q
m
)为K 的带正电的粒子从第三象限中的Q (-2L ,-L )点以速度v 0沿x 轴正方向射出,恰好从坐标原点O 进入磁场,从P (2L ,0)点射出磁场。
不计粒子重力,求:(1)电场强度E.(2)从P 点射出时速度的大小.(3)粒子在磁场与电场中运动时间之比
.
选修3-4
I 、如图为半圆形的玻璃砖,C 为AB 的中点,OO ′过C 点且与AB 面垂直,a 、b 两束不同频率的单色可见细光束垂直AB 边从空气射入玻璃砖,两束光在AB 面上的入射点到C 点的距离相等,两束光折射后相交于图中的P 点,以下判断正确的是( ) A.a 光的频率大于b 光的频率
B.b 光比a 光更容易发生衍射现象
C.在半圆形的玻璃砖中,a 光的折射率小于b 光的折射率
D.a 光在此玻璃中的传播速度小于b 光在此玻璃中的传播速度
E.若a 、b 两束光从同一介质射入真空过程中,a 光发生全反射的临界角大于b 光发生全反射的临界角
II 、一列简谐横波在介质中沿x 轴正方向传播,波长不小于10cm 。
O 和A 是介质中平衡位置分别位于x=0和x=5cm 处的两个质点。
t=0时刻观察,此时质点O 的位移y=4cm ,质点A
处于波峰位置;t=1
3
s,质点O 第一次回到平衡位置,t=1s 时质点A 第一次回到平衡位置。
求(1)简谐波的周期、波长和波速;(2)质点O 的位移随时间变化的关系式。
