高等数学上册复习提纲培训资料
高等数学上复习提纲

高等数学上复习提纲高数第七版教材第一章函数与极限知识要点:函数的定义域、函数的几种特性、极限的定义、左右极限、无穷小量的比较、极限的运算、两个重要极限、极限存在准则、函数的连续性与间断点P16 D1(5)(9),D6; P26 D1; P33 D2, D3; P44例8;P45 D1(5)(7)(14); D3(1);P52 D1(5)(6), D2(2)(4), D4(1);P55 D3,D5(1)(3);P59 例4,例5;P61 D3( 1 ); P66 D3(7), D5;P70总习题D1(1)(4), D3(2), D9(2)(4);第二章导数与微分知识要点:导数,函数的求导法则,高阶导数,复合函数的求导,隐函数求导,微分(含复合函数的微分),基本初等函数的求导公式,可导与连续的关系等P81 例9; P97 例4;P99 例8;P101例1、2;P108 1(3)、(4);P115 例4、5;第三章微分中值定理与导数的应用知识要点:罗尔定理,拉格朗日中值定理,洛必达法则,函数的单调性、凸凹性,函数的极值与最值P132 D6、D8、D12;P134 例3;P136 例8、例10;P137 D1(13);P146例4;P148例6;P148例8、例9;P181 D2;总复习三D2;第四章不定积分知识要点:不定积分的概念与性质;第一、二换元法,分部积分法,基本积分表P189 例7;P190 例8;P192 D2(15) (17) (25);P207 D2(35);P197 例11;P212例9;P214 例2;P222 D4(4);第五章定积分知识要点:定积分的性质,变上限函数的定义,导数及其应用,牛-莱公式,定积分换元法和分部积分,反常积分P236 D7; P243 例8;P244 D8(8); P245 D11(1);P249例5;P253例12;P255 D1(17,19,23);P262 D1(3);P273 D14;题型分布:选择10题,共20分;填空5题,共10分;计算10题,共50分;应用2题,共20分。
高数讲义上册总复习

a
0
若 f (x) 为偶函数,即 f (x ) f ( x )
a
a
a f (x)d x 2 0 f (x)d x
若 f (x) 为奇函数,即 f (x ) f ( x )
a
a f (x)d x 0
例1:求
5 5
x 3 sin 2x x4 x2 1
d
x
例2:求 2 ( x 3 sin 2 x ) cos 2 x d x
(特别关注)
4.已知函数 f (x) 满足:
1
0
f
(ux)d u
1 2
f
(x) 1,
1
0 f ( x)d x
1,
求 f (x) .
答案: f ( x) 2(1 x).
2。二阶常系数非齐次微分方程的通解
(非齐项为 e x Pm ( x) 类型)
重点: y py qy e x Pm ( x)
六、综合证明题
(1)用单调性证明不等式
(2)利用积分中值定理和罗尔定理 证明含有中值的等式
(3)零点定理(熟练掌握函数的构造方法)
所确定,
求
d2 dx
y
2
.
求由方程
x y
a cos3 a sin3
t t
表示的函数的 设
4. 函数的单调性判别,极值 5. 求曲线的凹凸区间及拐点, 例如:
例1 设 y 1 arctan 1 x2 1 ln 1 x2 1 ,
2
4 1 x2 1
求 y.
例 2 计算由曲线 y x3 6x 和 y x2 所围成
的图形的面积.
例3:求曲线
y x2, 2
y
1 1 x
2
高等数学上册复习资料

高等数学(上册)复习资料一:函数的两个要素: 定义域 对应法则1 两个函数相同: (1)定义域相同 (2)对应法则相同 至于自变量与因变量用什么符合来表示无所谓。
例如:sin y x x =-∞<<+∞ 与sin u t t =-∞<<+∞是同一个函数。
2 函数的几种特性(1)有界性 ()y f x x D =∈如果存在实数1k ,使得1()f x k ≤ ,则称()f x 在D 上有上界 如果存在实数2k ,使得1()f x k ≥ ,则称()f x 在D 上有下界。
有界:既有上界 ,又有下界 。
即存在实数1k ,2k 使得21()k f x k ≤≤ 等价于存在0k > ,使得()f x k x D ≤∈(2)单调性若对区间I 内任意两点12x x < ,都有12()()()f x f x ≤≥ ,则称()y f x =在I 内单调增加(减少)。
若将“()≤≥ ”改成“()<>”称为严格单调增加(减少)。
(3)奇偶性设函数()y f x =的定义域关于原点对称 如果 ()()f x f x -= ,则称 ()f x 为偶函数 如果()()f x f x -=- ,则称 ()f x 为奇函数 (4) 周期性若()()f x l f x += 则称()f x 是以l 为周期的函数 注:周期通常指的是它的最小正周期 3复合函数设()y f u =的定义域为1D ,又()u g x =的定义域为D ,且1()g D D ⊂ ,则函数[]()y f g x x D =∈称为由函数()u g x =和 函数 ()y f u =构成的复合函数。
u 称为中间变量,记为:[]()()()f g x f g x = 4 基本初等函数:(1)幂函数 y x μ= (2)指数函数 (0,1)xy a a a =>≠(3)对数函数log a y x = 特例,ln a e y x == (4)三角函数 sin ,cos y x y x == 等 (5)反三角函数 arcsin ,arccos y x y x ==等5 初等函数:由常数和基本初等函数经过有限次四则运算和有限次复合运算得到的并可以用一个式子表示的函数。
高等数学上册总复习

高等数学第一学期总复习资料(工科)《高等数学》上册总复习 〈一〉 内容提要第一章 函数与极限一、函数1. 知道集合、映射的概念2. 理解函数的定义,并会求函数的定义域、函数值 (注:求定义域时注意:1°:分母不为0;2°:真数大于0;3°:开偶次方数不小于0;4°:u arcsin 、u arccos 中||u ≤1)3. 会判断(证明)函数的特性(单调性、有界性、奇偶性、周期性)4. 理解反函数的定义,知道直接函数与其反函数的关系,会求函数的反函数。
5. 熟练掌握基本初等函数的形式、定义域、特性等。
(基本初等函数是指幂函数、指数函数、对数函数、三角函数、反三角函数)6. 理解复合函数的定义,能熟练分解复合函数为基本初等函数链7. 理解初等函数的定义,并知道基本初等函数、分段函数与初等函数的区别与联系 二、极限1. 知道并理解数列的极限、函数极限的三个分析定义⎪⎩⎪⎨⎧∞→-→-∞→-)()()(0x X x x n N εδεε,且能作几何解释2. 知道左、右极限定义和极限存在定理3. 知道并会应用极限运算法则求极限(主要和、差、积、商及复合函数的极限)4. 理解无穷小定义,知道无穷小与无穷大的关系,并会作无穷小的比较、无穷小运算(注意有极限函数与无穷小的关系) 5. 熟记极限存在准则和两个重要极限(1sin lim 0=→x x x 及1)()(sin lim 0)(=→x x x ϕϕϕ;e x xx =⎪⎭⎫ ⎝⎛+∞→11lim 及e x x x =⎪⎪⎭⎫ ⎝⎛+∞→)()()(11lim ϕϕϕ;()e x xx =+→11lim 及[]e x x x =+→)(10)()(1lim ϕϕϕ)6. 能熟练求出所给函数(或数列)在某趋势下的极限 注:常用求极限的方法:1°:利用极限运算法则求极限(注意分式函数在∞→x 时的求法); 2°:利用左、右极限求极限(即:用极限存在定理求极限); 3°:利用无穷小与无穷大的关系求极限; 4°:利用极限存在准则求极限; 5°:利用重要极限求极限;6°:利用无穷小等价代换求极限; 7°:利用初等函数的连续性求极限;8°:利用洛必塔法则求极限 三、函数的连续性1. 理解函数的连续性定义,并会判断函数的连续性 2. 会求函数的间断点,并能判断间断点的类3. 知道连续函数的运算(即连续函数的和、差、积、商以及复合函数、初等函数的连续性) 4. 熟记闭区间上连续函数的性质,并会利用这些性质解决有关问题这里是指:最大最小值定理、有界性定理、零点定理、介值定理及其推论。
高等数学上册复习.doc

第一章复习提要 第一节 映射与函数1、注意几个特殊函数:符号函数,取整函数,狄利克雷函数;这些函数通常用于判断题中的反例2、注意无界函数的概念3、了解常用函数的图像和基本性质(特别是大家不太熟悉的反三角函数) 第二节 数列的极限 会判断数列的敛散性 第三节 函数的极限1、函数极限存在的充要条件:左右极限存在并相等。
(重要)2、水平渐近线的概念,会求函数的水平渐近线(p37)。
(重要)3、了解函数极限的局部有界性、局部保号性。
第四节 无穷大和无穷小1、无穷小和函数极限的关系:⇔=∞→→A x f x x x )(lim 0α+=A x f )(,其中α是无穷小。
2、无穷大和无穷小是倒数关系3、铅直渐近线的概念(p41), 会求函数的铅直渐近线4、无界与无穷大的关系:无穷大一定无界,反之不对。
5、极限为无穷大事实上意味着极限不存在,我们把它记作无穷大只是为了描述函数增大的这种状态 第五节 极限的运算法则1、极限的四则运算法则:两个函数的极限都存在时才能用。
以乘法为例比如x x g x x f 1)(,)(==。
0)(lim 0=→x f x ,∞=→)(lim 0x g x 。
但是1)()(lim 0=⨯→x g x f x2、会求有理分式函数)()(x q x p 的极限(P47 例3-例7)(重要) 0x x →时:若分母0)(0≠x q ,则极限为函数值若分子和分母同时为零,则为型极限,约去公因子 若只是分母为零,则极限为无穷大。
(p75页9(1))∞→x 时,用抓大头法,分子、分母同时约去x 的最高次幂。
第六节 极限存在的准则,两个重要极限(重要) 1、利用夹逼准则求极限: 例 p56也习题4(1)(2),及其中考试题(B )卷第三题(1) 2、利用两个重要极限求其他的极限(p56习题2)3 注意下面几个极限:01sin lim 0=→x x x ;0sin lim=∞→x x x ;1sin lim 0=→xxx 第七节 无穷小的比较(重要)1、会比较两个无穷之间的关系(高阶、低阶、同阶,k 阶还是等价穷小)2、常见的等价无穷小:x x x x ~arcsin ,tan ,sin ;2~cos 12x x -x e x ~1-;nx x n~)1(1+ 3、若)(x ϕ为无穷小,则)(~)(sin x x ϕϕ,nx x n )(~))(1(1ϕϕ+,)(~))(1ln(x x ϕϕ+,)(~1)(x e x ϕϕ-。
高等数学上册第一到第三章复习资料
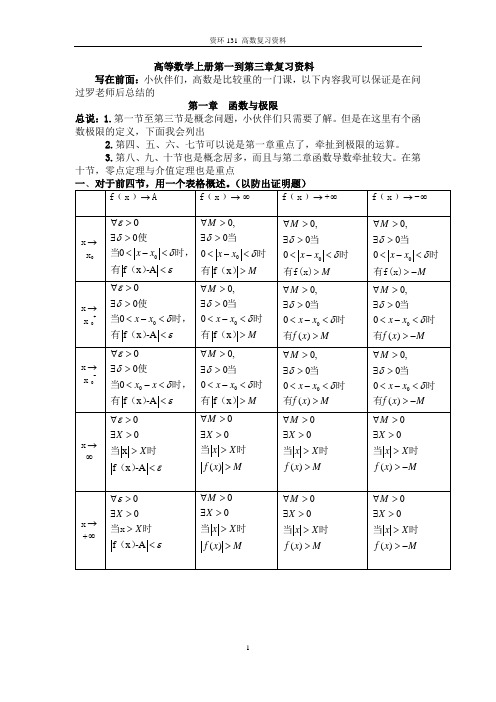
高等数学上册第一到第三章复习资料写在前面:小伙伴们,高数是比较重的一门课,以下内容我可以保证是在问过罗老师后总结的第一章函数与极限总说:1.第一节至第三节是概念问题,小伙伴们只需要了解。
但是在这里有个函数极限的定义,下面我会列出2.第四、五、六、七节可以说是第一章重点了,牵扯到极限的运算。
3.第八、九、十节也是概念居多,而且与第二章函数导数牵扯较大。
在第十节,零点定理与介值定理也是重点二、极限运算的各种定理与推论(极限运算的基础)x 0是x 0+ x 0- 1.定理1:有限个无穷小的和也是无穷小2.定理2:有界函数与无穷小的乘积是无穷小3.定理3:如果limf ﹙x ﹚=A ,limg ﹙x ﹚=B ,那么:﹙1﹚lim[f ﹙x ﹚±g ﹙x ﹚]=lim f ﹙x ﹚±limg ﹙x ﹚=A +B ﹙2﹚lim[f ﹙x ﹚·g ﹙x ﹚]= lim f ﹙x ﹚·limg ﹙x ﹚=A ·B﹙3﹚若有B ≠0,则 lim [f ﹙x ﹚/ g ﹙x ﹚]= limf ﹙x ﹚/ limg ﹙x ﹚=A/B 4.定理4:设有数列﹛x n ﹜和﹛y n ﹜,如果lim n →∞x n =A , lim n →∞y n =B 那么:(1)lim n →∞(x n ±y n ﹚=A ±B(2) lim n →∞x n ·y n =A ·B(3)当n x 0(1,2,3...)B 0lim n n nAy n y B →∞≠=≠=且时, 5.定理5:[][][]00000,00()()lim (),lim (),(),g(x)u ,lim ()lim ()x xu u x x u u y f g x g x g x u f u A x f g x f u Aδ→→→→===∈≠== 设函数是由函数u=g(x)与函数y=f(u)复合而成,f 在点x 的某去心邻域内有定义,若且存在x 有则:4.推论1:常数与无穷小的乘积是无穷小5.推论2:有限个无穷小的乘积也是无穷小6.推论3:如果limf(x)存在,而c 为常数,则:[]lim ()lim ()cf x c f x =7.推论4:如果limf(x)存在,而n 是正整数,则:[][]lim ()lim ()nnf x f x = 二、无穷小的比较处公式:(可根据题干变换x )11nx 等价于 arcsinx x 等价于 sinx x 等价于211-cos x 2x 等价于 1sec cos x x等价于 tan tx x等价于三、重要极限:0sin lim1x x x →= 1lim 1xx e x →∞⎛⎫+= ⎪⎝⎭四、零点定理与介值定理:1.零点定理:设函数f(x)在闭区间[a ,b ]上连续,且f(a)与f(b)异号,那么在开区间﹙a ,b ﹚内至少有一点ξ ,使:f(ξ)=02.介值定理:设函数f(x)在闭区间[a ,b ]上连续,且在这区间的端点取不同的值f (a )=A f(b)=B,那么,对于A 与B 之间的任意一个数C ,在开区间(a,b ) 内至少有一点ξ ,使:f(ξ)=C (a<ξ<b )第二章 导数与微分总说:这一章可以说是前半本书的重点,它不仅与极限联系,而且与后面的积分息息相关,这章必须融会贯通。
《高等数学上册》复习重点
《高等数学上册》复习重点(注意:此文件仅供教师复习课用,不能给学生拷贝!即教师上复习课时以此为纲,让学生通过听课记笔记(而不是抄或拷贝)了解此重点。
)第一章函数与极限1.朴素的极限概念,极限四则运算法则2.两个重要极限3.无穷小定义,无穷小的阶,等价无穷小代换4.求间断点及判别间断点的类型5.连续和极限的关系,连续函数的极限6.利用零点定理验证解的存在性第二章导数与微分1.导数的定义和几何意义2.导数的四则运算法则和复合函数的求导法则3.二阶导数4.隐函数求导5.参数方程所确定的函数的求导6.微分的定义和几何意义,求微分,一阶微分形式不变性7.连续、可导与可微的关系第三章微分中值定理与导数的应用1.拉格朗日中值定理及其应用2.利用洛必达法则求未定式的极限3.判断函数的单调性,利用单调性证明不等式4.判断函数图形的凹凸性,求拐点5.求函数极值点和极值,求解较简单的最值应用问题第四章不定积分1.原函数与不定积分的概念,不定积分的性质2.不定积分的第一换元法(简单的凑微分法)3.不定积分的第二换元法(不含三角代换)4.典型的分部积分法问题,换元法与分部法的结合5.简单的有理函数的积分(简单地试凑可分解为部分分式的)第五章定积分1.定积分的概念及性质2.变限积分的概念及其求导3.牛顿-莱布尼兹公式,定积分的换元法和分部积分法4.简单的无穷限的反常积分第六章定积分的应用1.平面图形面积(直角坐标方程)2.绕坐标轴旋转的旋转体的体积(直角坐标方程)第七章微分方程(注意:讲课按教学大纲要求讲,不可删减内容)1.微分方程解的概念,线性微分方程解的结构2.可分离变量的微分方程3.一阶线性微分方程4.二阶常系数齐次线性微分方程5.二阶常系数非齐次线性微分方程的特解形式6.简单的微分方程应用问题。
高等数学(上)复习大纲
《高等数学》(上)复习大纲一、函数与极限1、了解函数、单射、满射及双射的概念;掌握反函数与复合函数的概念;掌握函数的有界性、单调性、奇偶函数、周期性的概念;了解初等函数的概念.2、了解数列极限的直观定义;掌握数列极限的N -ε定义, 会证明01l i m =∞→nn 和)1|(|0lim <=∞→q q n n ; 了解收敛数列的唯一性、有界性、保号性及与子数列的关系.3、掌握函数极限A x f x x =→)(lim 0的δε-定义, 会证明c c x x =→0lim 和00lim x x x x =→; 了解函数的左、右极限的定义;掌握函数极限A x f x =∞→)(lim 的X -ε定义, 会证明01lim=∞→xx ;了解A x f x =-∞→)(lim 和A x f x =+∞→)(lim 的定义;了解函数极限的唯一性和局部保号性.4、了解无穷小的概念以及函数极限与无穷小的关系;了解无穷大的概念以及无穷大与无穷小的关系.5、掌握无穷小与有界函数乘积是无穷小的定理;掌握极限的四则运算法则,会使用一定的技巧计算一些函数的极限. 了解复合函数的极限的计算方法.6、了解夹逼准则,记住重要极限1sin lim0=→xxx ;了解单调有界准则,记住重要极限e 11lim =⎪⎭⎫⎝⎛+∞→xx x 及其变形()e 1lim 10=+→x x x .7、了解高阶无穷小、同阶无穷小、k 阶无穷小、等价无穷小的概念.8、了解增量的概念;掌握函数f (x )在点x 0处连续的定义及判定方法;了解初等函数在其定义域内连续的结论;了解函数点x 0处左、右连续的概念;了解函数的常见的几种间断点(无穷间断点、振荡间断点、可去间断点及跳跃间断点)及函数的第一类间断点与第二类间断点;. 9、了解函数的和、差、积、商的连续性及反函数、复合函数的连续性. 10、掌握闭区间上连续函数的最值定理(有界性定理)、介值定理(零点定理).二、导数与微分1、结合速度问题和切线问题掌握)(x f 在点0x 的导数的概念;会推导简单函数的求导公式;了解单侧(左、右)导数的概念;掌握)(0'x f 的几何意义;了解可导与连续的关系. 2、掌握函数的和、差、积、商的求导法则;掌握反函数以及复合函数的求导法则;掌握常见函数(x x x x x x C x f xarctan ,arcsin ,ln ,e ,cos ,sin ,,)(μ=)的求导公式.3、了解高阶导数的计算.4、掌握隐函数及由参数方程所确定的函数的求导方法.5、掌握函数)(x f y =在点0x 处的微分y d 的定义;了解可微与连续的关系;掌握微分与导数的关系,特别是xyx f d d )('=的含义;了解微分的几何意义;掌握常见函数的微分公式以及函数的和、差、积、商及复合的微分法则.(本节内容是以后学习积分等有关内容的基础.)三、微分中值定理与导数的应用1、了解罗尔定理、拉格朗日中值定理以及柯西中值定理.2、掌握使用洛必达法则计算未定式极限的方法.3、了解泰勒公式(泰勒中值定理).4、掌握利用导数对函数的单调性判定的方法,会证明一些不等式;了解函数的凹凸性的判定方法以及曲线拐点的计算.5、掌握函数的极大(小)值的计算;了解函数的最大(小)值的计算.6、了解根据函数的特性描绘函数图形的方法.7、了解曲率的概念.8、了解方程的近似计算.四、不定积分1、掌握不定积分的定义及性质;记住常见函数⎰⎰⎰⎰⎰⎰⎰⎰+-≠x x osx x x x x x x x x x x x k xd e ,d c ,d sin ,d 11,d -11,d 1),1(d ,d 22μμ的积分公式(尽管不定积分本质上与求导公式相同).2、掌握第一类换元法(凑微分方法)与第二类换元法( 变量替换法),了解积分公式:()⎰⎰++-=-+++=+,ln d 1,ln d 122222222C a x x x a x C a x x x a x()⎰⎰+++++=++=-.ln 22d ,2arcsin 2d 2222222222C a x x a a x x x a x C x a x x a3、掌握分部积分公式.4、掌握有理函数以及可以化为有理函数的积分.5、了解积分表的使用.五、定积分1、结合曲边梯形的面积计算理解定积分的定义;理解定积分的性质.2、掌握积分上限函数⎰=xax x f x Φd )()(的性质;掌握牛顿-莱布尼茨公式.3、掌握定积分的换元法和分部积分法.4、了解反常积分.六、定积分的应用1、了解定积分元素法的思想.2、理解利用定积分计算平面图形的面积、(旋转体、平行截面面积已知的)立体的体积、平面曲线的弧长的方法.3、了解定积分在物理上的应用.七、空间解析几何与向量代数1、了解向量的概念及其线性运算;了解空间直角坐标系的建立;掌握向量的坐标表示及利用坐标做线性运算的方法;掌握向量的长度(模)、两点间的距离公式、向量的方向角及方向余弦.2、掌握向量的数量积(内积)及向量积的定义及计算.3、了解曲面的概念;掌握旋转曲面(特别是球面)、柱面(特别是圆柱面)的方程;了解其他二次曲面的方程.4、掌握空间曲线的一般方程及参数方程;掌握空间曲线在坐标面上的投影.5、掌握平面的点法式方程及一般方程;了解两平面间的夹角;掌握点到平面的距离.6、掌握空间直线的一般方程、点向式方程及经过两点的直线方程;了解两直线的夹角及直线与平面的夹角.。
高数复习知识点及提纲
高数复习知识点及提纲第一篇:高数复习知识点及提纲高数复习知识点及提纲1.瑕积分的判别,广义积分和Γ(n)的计算。
6分2.罗必达法则求未定式。
6分3.利用导数研究函数的单调性和极值,凸凹性和拐点。
10’4.利用定积分求解封闭图形的面积7分5.多元函数连续与可微的关系3分6.多元函数的一阶、二阶偏导数的计算;二元函数的全微分,多元函数复合函数的求导及隐函数求导。
20分7.二元函数极值的经济应用7分8.二重积分的计算以及交换积分次序10分9.利用级数的收敛性证明极限,求幂级数的收敛域和函数,函数的幂级数展开18分10.微分方程解的概念,一阶线性的微分方程的求解。
13’--------------------第二篇:高数知识点高等数学B2知识点1、二元函数的极限、连续、偏导数、全微分;微分法在几何上的应用;二元函数的方向导数与梯度;二元函数的极值。
2、二重积分的计算(直角坐标、极坐标);三重积分的计算(直角坐标、柱面坐标)。
3、曲线积分、曲面积分的计算;格林公式;高斯公式。
4、数项级数收敛性的判别;幂级数的收敛半径、收敛域。
第三篇:高数知识点总结高数重点知识总结1、基本初等函数:反函数(y=arctanx),对数函数(y=lnx),幂函数(y=x),指数函数(y ax),三角函数(y=sinx),常数函数(y=c)2、分段函数不是初等函数。
x2+xx=lim=13、无穷小:高阶+低阶=低阶例如:limx→0x→0xxsinx4、两个重要极限:(1)lim=1x→0x(2)lim(1+x)=ex→01x⎛1⎫lim 1+⎪=e x→∞⎝x⎭g(x)x经验公式:当x→x0,f(x)→0,g(x)→∞,lim[1+f(x)]x→x0=ex→x0limf(x)g(x) 例如:lim(1-3x)=ex→01xx→0⎝⎛3x⎫lim -⎪x⎭=e-35、可导必定连续,连续未必可导。
例如:y=|x|连续但不可导。
6、导数的定义:lim∆x→0f(x+∆x)-f(x)=f'(x)∆xx→x0limf(x)-f(x0)=f'(x0)x-x07、复合函数求导:df[g(x)]=f'[g(x)]•g'(x)dx例如:y=x+x,y'=2x=2x+1 2x+x4x2+xx1+18、隐函数求导:(1)直接求导法;(2)方程两边同时微分,再求出dy/dx x2+y2=1例如:解:法(1),左右两边同时求导,2x+2yy'=0⇒y'=-x ydyx法(2),左右两边同时微分,2xdx+2ydy⇒=-dxy9、由参数方程所确定的函数求导:若⎨⎧y=g(t)dydy/dtg'(t)==,则,其二阶导数:dxdx/dth'(t)⎩x=h(t)d(dy/dx)d[g'(t)/h'(t)]dyd(dy/dx)dtdt===2dxdxdx/dth'(t)210、微分的近似计算:f(x0+∆x)-f(x0)=∆x•f'(x0)例如:计算sin31︒11、函数间断点的类型:(1)第一类:可去间断点和跳跃间断点;例如:y=sinx(x=0x是函数可去间断点),y=sgn(x)(x=0是函数的跳跃间断点)(2)第二类:振荡间断点和无穷间断点;例如:f(x)=sin ⎪(x=0是函数的振荡间断点),y=数的无穷间断点)12、渐近线:水平渐近线:y=limf(x)=cx→∞⎛1⎫⎝x⎭1(x=0是函xlimf(x)=∞,则x=a是铅直渐近线.铅直渐近线:若,x→a斜渐近线:设斜渐近线为y=ax+b,即求a=limx→∞f(x),b=lim[f(x)-ax]x→∞xx3+x2+x+1例如:求函数y=的渐近线x2-113、驻点:令函数y=f(x),若f'(x0)=0,称x0是驻点。
大一高数上册知识点提纲
大一高数上册知识点提纲数列与数学归纳法1. 数列的概念和表示方法2. 等差数列的性质和通项公式3. 等比数列的性质和通项公式4. 斐波那契数列的性质和递推公式5. 数学归纳法的基本思想和应用函数与极限1. 函数的基本概念和性质2. 基本初等函数及其性质3. 极限的概念和性质4. 极限的运算法则5. 无穷大与无穷小6. 函数的连续性及其运算法则导数与微分1. 导数的定义和计算方法2. 基本初等函数的导数3. 函数的导数与可导性4. 高阶导数与导数公式5. 隐函数与参数方程的导数6. 微分的概念和计算方法微分中值定理与导数的应用1. 罗尔中值定理及其证明2. 拉格朗日中值定理及其证明3. 柯西中值定理及其特殊情况4. 应用题:极值问题、函数图像的描绘等不定积分与定积分1. 不定积分的概念和基本性质2. 基本初等函数的不定积分3. 第一类换元积分法4. 分部积分法及其应用5. 定积分的概念和性质6. 定积分的计算方法:换元法和分部积分法定积分的应用1. 曲线长度与曲面积的计算2. 物理应用:质量、质心和转动惯量的计算3. 概率应用:概率密度函数与累积分布函数常微分方程1. 基本概念:微分方程、初值问题、通解和特解2. 可分离变量的一阶微分方程3. 齐次方程和一阶线性微分方程4. 二阶常系数齐次线性微分方程5. 指数函数、三角函数和特殊函数的微分方程以上是大一高数上册的知识点提纲,涵盖了数列与数学归纳法、函数与极限、导数与微分、微分中值定理与导数的应用、不定积分与定积分、定积分的应用以及常微分方程等内容。
希望这份提纲可以帮助你系统地理解和掌握这些知识点,为之后的学习打下坚实的基础。
祝你学习顺利!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
9、 求 导 法 则 、 、本复公合式函 数 、 隐 函 参数方程求导;
10、高阶导数及公式 11、中值定理及泰勒及公其式应用;
12、函数的单调、性最、值极应值用、点凹 13、不等式的5证 种明 常( 用方法);
14、方程根的讨论。
7、定积分的计算;
8、对称区间上的积 2si分 nn x及 dx 0
高等数学上册 复习提纲
函数、极限、连续元及函一数微分学
一、基本题型 :
1、基本函数问题;
2、极限的求1法 0多(种); 3、连续性及间断点的讨论; 4、无穷小的比较及无 等穷 价小;
5、闭区间上连续函 性数 质的 及应用; 6、 导 数 、 微 分 的 定几义何及意 义 ;
7、左右极限、左 及右 左连 右续 导数的应 8、 极 限 、 连 续 可 导微及的可关 系 ;
9、积分等式和不等式证的明;
10、广义积分。
11、定积分在几何上的应用
12、定积分在物理上的应用
预祝同学们考出好成绩!
