辽宁省朝阳县柳城高级中学高中数学 函数导学案 新人教A版必修1
新课标高中数学人教A版必修1全册导学案及答案(145页)

§1.1.1集合的含义及其表示[自学目标]1.认识并理解集合的含义,知道常用数集及其记法;2.了解属于关系和集合相等的意义,初步了解有限集、无限集、空集的意义; 3.初步掌握集合的两种表示方法—列举法和描述法,并能正确地表示一些简单的集合. [知识要点] 1. 集合和元素 (1)如果a 是集合A 的元素,就说a 属于集合A,记作a A ∈;(2)如果a 不是集合A 的元素,就说a 不属于集合A,记作a A ∉.2.集合中元素的特性:确定性;无序性;互异性.3.集合的表示方法:列举法;描述法;Venn 图.4.集合的分类:有限集;无限集;空集.5.常用数集及其记法:自然数集记作N ,正整数集记作*N 或N +,整数集记作Z ,有理数集记作Q ,实数集记作R . [预习自测]例1.下列的研究对象能否构成一个集合?如果能,采用适当的方式表示它. (1)小于5的自然数; (2)某班所有高个子的同学; (3)不等式217x +>的整数解; (4)所有大于0的负数;(5)平面直角坐标系内,第一、三象限的平分线上的所有点.分析:判断某些对象能否构成集合,主要是根据集合的含义,检查是否满足集合元素的确定性.例2.已知集合{},,M a b c =中的三个元素可构成某一个三角形的三边的长,那么此三角形 一定是 ( )A.直角三角形B.锐角三角形C.钝角三角形D.等腰三角形例3.设()()(){}22,,2,,5,a N b N a b A x y x a y a b ∈∈+==-+-=若()3,2A ∈,求,a b 的值.分析: 某元素属于集合A,必具有集合A 中元素的性质p ,反过来,只要元素具有集合A 中元素的性质p ,就一定属于集合A.例4.已知{}2,,M a b =,{}22,2,N a b =,且M N =,求实数,a b 的值.[课内练习]1.下列说法正确的是( )(A )所有著名的作家可以形成一个集合 (B )0与 {}0的意义相同 (C )集合⎭⎬⎫⎩⎨⎧∈==+N n n x x A ,1是有限集 (D )方程0122=++x x 的解集只有一个元素 2.下列四个集合中,是空集的是( )A .}33|{=+x xB .},,|),{(22R y x x y y x ∈-= C .}0|{2≤x x D .}01|{2=+-x x x 3.方程组20{=+=-y x y x 的解构成的集合是( )A .)}1,1{(B .}1,1{C .(1,1)D .}1{.4.已知}1,0,1,2{--=A ,}|{A x x y y B ∈==,则B =5.若}4,3,2,2{-=A ,},|{2A t t x xB ∈==,用列举法表示B= . [归纳反思]1.本课时的重点内容是集合的含义及其表示方法,难点是元素与集合间的关系以及集合元素的三个重要特性的正确使用;2.根据元素的特征进行分析,运用集合中元素的三个特性解决问题,叫做元素分析法。
3.1.1 函数的概念第二课时-【新教材】人教A版(2019)高中数学必修第一册导学案

§3.1.1 函数的概念(第二课时)导学目标:1.了解构成函数的三要素,能求具体函数及抽象函数的定义域. 2.了解构成函数的三要素,理解函数值域的含义,能求简单函数的值域.(预习教材P 62~ P 63,回答下列问题) 回忆:函数的三要素是什么? 问题:已知函数()f x x =(1)求函数的定义域;(2)求()1f x -的表达式?你能求()1f x -的定义域吗? (3)你能直接求出()21f x +的定义域吗?【知识点一】函数定义域的求法 (1)具体函数的定义域求法 ①1x出现时要求0x ≠;②x 出现时要求0x ≥;③0x 出现时要求0x ≠. 自我检测1:求函数0()5(1)4f x x x x =++++的定义域;(2)抽象函数的定义域求法形如()1f x -、()21f x +、()()()211F x f x f x =++-这类函数而言,未直接给出对应法则f 对所施加对象作用后的具体表达形式,我们称之为抽象函数.第三章 函数的概念与性质- 2 -通过观察,若函数()f x =()1f x -=①函数()f x 与()1f x -的自变量都是自身表达式中的x (定义域是自变量的取值集合); ②在同一题中,对应法则f 的含义一致(即法则f 对施加对象的约束条件相同). 自我检测2:若函数()f x 的定义域为[)0,+∞,则函数()1f x -的定义域是 .(3)实际问题中的自变量还要考虑实际要求:自我检测3:某种笔记本的单价为3元,小明手里有100元钱,设小明一共买了x 个该笔记本,花费为y 元,你能正确写出该问题中自变量x 的约束条件吗?【知识点二】函数值域的求法函数()y f x =的值域即为函数值y 的取值集合,其取值范围受自变量x 的取值范围和对应法则f 共同决定,所以在求值域时,一定要注意定义域以及函数的结构. 常用的求值域的方法有:①图像法(如一次函数、二次函数、反比例函数等已知图像的函数) ②换元法(利用整体换元的思想,将未知函数结构转化成已知函数结构求解)自我检测4:你能将四次函数()4223f x x x =--转化成二次函数模型吗?前后函数自变量有何改变?题型一 函数的定义【例1-1】求下列函数的定义域 (1)求函数221()121f x x x x x =+--+的定义域. (2)求函数21()x f x --=的定义域.【例1-2】求下列函数的定义域(1)已知函数()y f x =定义域是[]1,3-,求()1y f x =-的定义域. (2)已知函数(1)y f x =-定义域是[]1,3-,求()y f x =的定义域. (3)已知函数(1)=-y f x 定义域是[]1,3-,求()21y f x =+的定义域.第三章 函数的概念与性质- 4 -【例1-3】求下列函数的定义域(1)已知函数()f x 的定义域为[1,2]-,求()()()g x f x f x =+-的定义域. (2)已知函数()f x 的定义域[]4,2-,求()()21f xg x x =+的定义域.【例1-4】求下列函数的定义域一枚炮弹发射后,经过26s 落地后击中目标.炮弹的射高为845m ,且炮弹距地面高度h (单位:m )与时间t (单位:s )的关系为21305h t t =-. 则该函数的定义域为 .题型二 函数的值域【例2-1】求下列函数的值域(1)函数(){}1,1,1,2f x x x =+∈- ; (2)函数()223f x x x =-+,x R ∈ ;(若将定义域改为{1,0,1,2}x ∈-、[)1,4x ∈-,又将如何?) (3)函数()1f x x =,11,2x ⎡⎫∈--⎪⎢⎣⎭ .【例2-2】求下列函数的值域 已知函数()af x x x=+,()0a >的图像如右图所示,请回答: (1)当1a =,(0,)x ∈+∞时,求此函数()f x 的值域; (2)当4a =,[1,3]x ∈时,求此函数()f x 的值域.【例2-3】求下列函数的值域(1)函数()4223f x x x =--,()0,2x ∈的值域为_________________.(2)函数()12g x x x =--的值域为_________________.(3)函数2()(1)1x h x x x =>-的值域为_________________.第三章 函数的概念与性质- 6 -1.已知函数1()f x x x=+,则( ) A .函数()f x 的定义域为{|0}x x ≠,值域为{|2}y y ≥ B .函数()f x 的定义域为{|0}x x ≠,值域为{|22}y y y ≥≤-或 C .函数()f x 的定义域为{|0}x x ≠,值域为R D .函数()f x 的定义域为R ,值域为R2.已知函数()f x 的定义域为[]1,4,求12f x ⎛⎫+ ⎪⎝⎭的定义域.3.已知函数()f x 的定义域是[0,2],求11()22g x f x f x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭的定义域.4.求下列函数的值域(1)函数()242f x x x =-+-,[)0,3x ∈的值域是___________.(2)求函数()63f x x x =-在区间[]2,4上的值域.§3.1.1 函数的概念(第二课时)参考答案(预习教材P 62~ P 63,回答下列问题) 回忆:函数的三要素是什么? 问题:已知函数()f x x =(1)求函数的定义域;(2)求()1f x -的表达式?你能求()1f x -的定义域吗? (3)你能直接求出()21f x +的定义域吗? 【答案】(1)[)0,+∞(2)()1f x x =-,[)1,+∞(3)1,2⎡⎫-+∞⎪⎢⎣⎭【知识点一】函数定义域的求法 (1)具体函数的定义域求法 ①1x出现时要求0x ≠;②x 出现时要求0x ≥;③0x 出现时要求0x ≠. 自我检测1:求函数0()5(1)4f x x x x =++++的定义域; 【答案】要使函数有意义,应有504010x x x +≥⎧⎪+≠⎪⎨⎪⎪+≠⎩即541x x x ≥-⎧⎪≠-⎨⎪≠-⎩所以函数的定义域是[)()()54411-----+∞,,,.(2)抽象函数的定义域求法形如()1f x -、()21f x +、()()()211F x f x f x =++-这类函数而言,未直接给出对应法则f 对所施加对象作用后的具体表达形式,我们称之为抽象函数.第三章 函数的概念与性质- 8 -通过观察,若函数()f x x =,则函数()11f x x -=-,我们可有如下结论:①函数()f x 与()1f x -的自变量都是自身表达式中的x (定义域是自变量的取值集合); ②在同一题中,对应法则f 的含义一致(即法则f 对施加对象的约束条件相同). 自我检测2:若函数()f x 的定义域为[)0,+∞,则函数()1f x -的定义域是 . 【答案】[)1,+∞(3)实际问题中的自变量还要考虑实际要求:自我检测3:某种笔记本的单价为3元,小明手里有100元钱,设小明一共买了x 个该笔记本,花费为y 元,你能正确写出该问题中自变量x 的约束条件吗? 【答案】{}033x x x N ≤≤∈且 【知识点二】函数值域的求法函数()y f x =的值域即为函数值y 的取值集合,其取值范围受自变量x 的取值范围和对应法则f 共同决定,所以在求值域时,一定要注意定义域以及函数的结构. 常用的求值域的方法有:①图像法(如一次函数、二次函数、反比例函数等已知图像的函数) ②换元法(利用整体换元的思想,将未知函数结构转化成已知函数结构求解)自我检测4:你能将四次函数()4223f x x x =--转化成二次函数模型吗?前后函数自变量有何改变?【答案】 令2t x =,由x R ∈,可得0t ≥,223y t t =--,0t ≥;前后函数自变量改变,相应的取值范围也改变.题型一 函数的定义【例1-1】求下列函数的定义域 (1)求函数221()121f x x x x x =+--+的定义域.(2)求函数()f x =的定义域.【答案】(1)11|22x x x ⎧+⎪<->⎨⎪⎪⎩⎭;(2){}|13x x x <>或;【例1-2】求下列函数的定义域(1)已知函数()y f x =定义域是[]1,3-,求()1y f x =-的定义域. (2)已知函数(1)y f x =-定义域是[]1,3-,求()y f x =的定义域. (3)已知函数(1)=-y f x 定义域是[]1,3-,求()21y f x =+的定义域. 【答案】(1)[]0,4 (2)[]2,2- (3)31,22⎡⎤-⎢⎥⎣⎦(3)13,212x x -≤≤∴-≤-≤,故()f x 的定义域为[2,2]-, 所以令2212x -≤+≤,解得3122x -≤≤, 故()21y f x =+的定义域是31,22⎡⎤-⎢⎥⎣⎦.【例1-3】求下列函数的定义域(1)已知函数()f x 的定义域为[1,2]-,求()()()g x f x f x =+-的定义域. 【答案】[1,1]-由题意,函数()f x 的定义域为[1,2]-,第三章 函数的概念与性质- 10 -则函数()()()g x f x f x =+-满足1212x x -≤≤⎧⎨-≤-≤⎩,解得1221x x -≤≤⎧⎨-≤≤⎩,即11x -≤≤,即函数()g x 的定义域为[1,1]-.(2)已知函数()f x 的定义域[]4,2-,求()()21f xg x x =+的定义域. 【答案】[)(]2,11,1---;函数()f x 的定义域[]4,2-,即422x -≤≤,可得21x -≤≤ 又分母10x +≠,可得1x ≠-. ∴()()21f xg x x =+的定义域为[)(]2,11,1---.【例1-4】求下列函数的定义域一枚炮弹发射后,经过26s 落地后击中目标.炮弹的射高为845m ,且炮弹距地面高度h (单位:m )与时间t (单位:s )的关系为21305h t t =-. 则该函数的定义域为 .【答案】{}026t t ≤≤题型二 函数的值域【例2-1】求下列函数的值域(1)函数(){}1,1,1,2f x x x =+∈- ; (2)函数()223f x x x =-+,x R ∈ ;(若将定义域改为{1,0,1,2}x ∈-、[)1,4x ∈-,又将如何?) (3)函数()1f x x =,11,2x ⎡⎫∈--⎪⎢⎣⎭ .【答案】(1){}0,2,3(2)[)2,+∞,{}6,3,2,[)2,11(3)(]2,1--【例2-2】求下列函数的值域 已知函数()af x x x=+,()0a >的图像如右图所示,请回答: (1)当1a =,(0,)x ∈+∞时,求此函数()f x 的值域; (2)当4a =,[1,3]x ∈时,求此函数()f x 的值域. 【答案】(1)[)2,+∞;(2)[]4,5【例2-3】求下列函数的值域(1)函数()4223f x x x =--,()0,2x ∈的值域为_________________.(2)函数()12g x x x =--的值域为_________________.(3)函数2()(1)1x h x x x =>-的值域为_________________.【答案】(1)[)4,5- (2)1(,]2-∞ (3)[4,)+∞(2)()()224321f x x x x =-+=--,因为1-≤x ≤1,所以3-≤x −2≤1-,所以1≤(x −2)2≤9,则0≤(x −2)21-≤8.故函数()[]243,1,1f x x x x =-+∈-的值域为[0,8].函数()g x 的定义域为1,2⎛⎤-∞ ⎥⎝⎦,令()2112,02t t x x t -=-=≥,得21122y t t =--+,故1,2y ⎛⎤∈-∞ ⎥⎝⎦,所以函数()12g x x x =--的值域为1,2⎛⎤-∞ ⎥⎝⎦.(3)()()()2212111124111x x x h x x x x x -+-+===-++≥---.当且仅当x =2时“=”第三章 函数的概念与性质- 12 -成立,故函数()2(1)1x h x x x =>-的值域为[)4,+∞.1.已知函数1()f x x x=+,则( ) A .函数()f x 的定义域为{|0}x x ≠,值域为{|2}y y ≥ B .函数()f x 的定义域为{|0}x x ≠,值域为{|22}y y y ≥≤-或 C .函数()f x 的定义域为{|0}x x ≠,值域为R D .函数()f x 的定义域为R ,值域为R 【答案】B2.已知函数()f x 的定义域为[]1,4,求12f x ⎛⎫+⎪⎝⎭的定义域. 【答案】(,1]-∞-∪1,2⎡⎫+∞⎪⎢⎣⎭.由1124x ≤+≤,得112x -≤≤,即110x -≤<或102x<≤, 解得x ≤ 1-,或12x ≥.∴函数的定义域为(-∞,1-]∪[12,+∞).3.已知函数()f x 的定义域是[0,2],求11()22g x f x f x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭的定义域.【答案】13,22⎡⎤⎢⎥⎣⎦.()f x 的定义域是[0,2],且11()22g x f x f x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭,102,2102,2x x ⎧+⎪⎪∴⎨⎪-⎪⎩则13,2215,22x x ⎧-≤≤⎪⎪⎨⎪≤≤⎪⎩ 即1322x .()g x ∴的定义域为13,22⎡⎤⎢⎥⎣⎦. 4.求下列函数的值域(1)函数()242f x x x =-+-,[)0,3x ∈的值域是___________.【答案】 [2,2]-(2)求函数()3f x x =在区间[]2,4上的值域.【答案】12,4⎤-⎦t =,则26x t =- ∵[]2,4x ∈,2t ≤≤那么函数()f x 转化为()22()36318g t t t t t =--=+-其对称轴16t =-, 故得()f x 的值域为12,4⎤-⎦.。
人教A版高中数学必修一全册导学案指数函数(1)

2.2.2指数函数(1)【自学目标】1. 掌握指数函数的概念、图象和性质;2. 能借助于计算机画指数函数的图象;3. 能由指数函数图象归纳出指数函数的性质。
【知识描述】1.指数函数的定义。
【预习自测】例1.下列函数中是指数函数的是 。
⑴2x y =; ⑵x 3y =;⑶x 4y -=; ⑷x )4(y -=; ⑸x x y =; ⑹x e y =; ⑺1x 3y -=; ⑻x )1a 2(y -=(21a >,1a ≠)例2.已知指数函数)x (f y =的图象经过点(1,π),求下列各个函数值:⑴)0(f ; ⑵)1(f ; ⑶)(f π。
例3.比较大小:⑴5.27.1和37.1; ⑵1.08.0-与2.025.1; ⑶3.07.1与1.39.0。
例4.作出下列函数的图象,并说明它们之间的关系:⑴x 3y =; ⑵1x 3y -=; ⑶1x 3y +=。
【课堂练习】1.在下列六个函数中: ①x a y 2=;②2+=x a y ;③3+=x a y ;④x a y =;⑤x a y )(-=;⑥x ay )1(=。
若0a >,且1a ≠,则其中是指数函数的有( )A .0个B .1个C .2个D .3个 2.函数323+=-x y 恒过定点 。
3.函数x ay )1(=和)1,0(≠>=a a a y x 的图象关于 对称。
4.已知函数x a y =(0a >,1a ≠)在[0,1]上的最大和最小值之和是3,求实数a 的值。
5.设4323)5.0(2--≤x x ,求x 的取值范围。
【归纳反思】1.要根据指数函数的图象特征来熟记和研究指数函数的性质,并根据需要,对底数a 分两种情况加以讨论,体会其中的数形结合和分类讨论思想;2.注意图象的的平移变换的方法和规律,并能正确地运用这一方法和规律解有关函数图象的问题,加深对指数函数的图象和性质的认识和理解。
【巩固提高】1.若集合}R x ,2y |y {A x ∈==,}R x ,x y |y {B 2∈==,则 ( ) A .A B B .B A ⊆ C .B A D .B A = 2.已知1b ,1a 0-<<<,则函数b a y x +=的图象不经过( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限3.图中曲线4321,,,C C C C 分别是指数函数x x x x d y c y b y a y ====,,,的图象,则d c b a ,,,与1的大小关系是( ) A .d c b a <<<<1 B .c d b a <<<<1 C .d c a b <<<<1 D .c d a b <<<<14.已知0a >,且1a ≠,1a a 3a M ++=,1a a 2a N ++=,则( )A .N M >B .N M =C .N M <D .M 、N 大小关系不确定 5.函数xy -=)41(的值域是 ;6.若指数函数x a y )1(2-=在R 上是减函数,则a 的取值范围是 。
新课标高中数学人教A版必修1全册导学案及答案

§集中的含意及其表示之阳早格格创做[自教目标]1.认识并明黑集中的含意,知讲时常使用数集及其记法;2.相识属于关系战集中相等的意思,收端相识有限集、无限集、空集的意思;3.收端掌握集中的二种表示要领—枚举法战形貌法,并能精确天表示一些简朴的集中. [知识重心]1. 集中战元素 (1)A 的元素,A,(2)A 的元素,A,2.集中中元素的个性:决定性;无序性;互同性.3.集中的表示要领:枚举法;形貌法;Venn 图.4.集中的分类:有限集;无限集;空集.5.时常使用数集及其记法:整数[预习自测]例1.下列的钻研对付象是可形成一个集中?如果能,采与适合的办法表示它.(1)小于5的自然数;(2)某班所有下身材的共教; (3; (4)所有大于0的背数;(5)仄里曲角坐标系内,第一、三象限的仄分线上的所有面.分解:推断某些对付象是可形成集中,主假如根据集中的含意,查看是可谦脚集中元素的决定性.例2.,那么此三角形一定是 ( )A.曲角三角形B.钝角三角形C.钝角三角形D.等腰三角形例3.. 分解: 某元素属于集中A,必具备集中A 反过去,只消元素具备集中A 便一定属于集中A.例4..[课内训练]1.下列道法精确的是()(A B )0(CD 个元素2AB C D 3AB C .(1,1) D4B =5B=. [归纳深思]1.原课时的沉面真量是集中的含意及其表示要领,易面是元素与集中间的关系以及集中元素的三个要害个性的精确使用;2.根据元素的个性举止分解,使用集中中元素的三个个性办理问题,喊搞元素分解法.那是办理有关集中问题的一种要害要领;3.决定的对付象才搞形成集中.可依据对付象的个性大概个数的几去表示集中,如个数较少的有限集中可采与枚举法,而其余的普遍采与形貌法. 4.要特天注意数教谈话、标记的典型使用. [坚韧普及]1.已知下列条件:①小于60的部分有理数;②某校下一年级的所有教死;③与2的所有解.其中不不妨表示集中的有--------------------() A .1个 B .2个 C .3个 D .4个2-----------------------------------------()A 3()A B C D4.已知集中A 是() A .0B .-1C .1D .25.圆程组3254x yx y =+⎧⎨+=⎩的解的集中是---------------------------------------()A .(){}1,1-B .(){}1,1-C .()(){},1,1x y -D .{}1,1-6.用枚举法表示不等式组240121x x x +>⎧⎨+≥-⎩的整数解集中为:7.设215022x x ax ⎧⎫∈--=⎨⎬⎩⎭,则集中21902x x x a ⎧⎫--=⎨⎬⎩⎭中所有元素的战为: 8、用枚举法表示下列集中:⑴(){},3,,x y x y x N y N +=∈∈⑵{}3,,y x y x N y N +=∈∈9.已知A ={1,2,x 2-5x +9},B ={3,x 2+ax +a },如果A ={1,2,3},2 ∈B ,供真数a 的值.10.设集中{},3A n n Z n =∈≤,集中{}21,B y y x x A ==-∈,集中,试用枚举法分别写出集中A 、B 、C.子集、齐集、补集[自教目标]1.相识集中之间包罗关系的意思.2.明黑子集、真子集的观念.3.相识齐集的意思,明黑补集的观念. [知识重心]1.子集的观念:如果集中A 中的任性一个元素皆是集中B 中的元素(若a A ∈,则a B ∈),那么称集中A 为集中B 的子集(subset ),记做B A ⊆大概A B ⊇,.B A ⊆还不妨用Venn 图表示.咱们确定:A ∅⊆.即空集是所有集中的子集. 根据子集的定义,简单得到:⑴所有一个集中是它自己的子集,即A A ⊆.⑵子集具备传播性,即若B A ⊆且B C ⊆,则A C ⊆.2.真子集:如果B A ⊆且A B ≠,那时集中A 称为集中B 的真子集(proper subset ).记做:A B⑴确定:空集是所有非空集中的真子集. ⑵如果A B, B C ,那么A C3.二个集中相等:如果B A ⊆与B A ⊆共时创造,那么,A B 中的元素是一般的,即A B =.4.齐集:如果集中S 包罗有咱们所要钻研的各个集中,那时S 不妨瞅A B (){}2,1,C x y y x x A ==-∈做一个齐集(Universal set ),齐集常常记做U.5.补集:设A S ⊆,由S 中不属于A 的所有元素组成的集中称为S 的子集A 的补集(complementary set ), 记做:S A (读做A 正在S 中的补集),即 补集的Venn 图表示: [预习自测]例1.推断以下关系是可精确:⑴{}{}a a ⊆;⑵{}{}1,2,33,2,1=;⑶{}0∅⊆; ⑷{}00∈;⑸{}0∅∈;⑹{}0∅=;例2.设{}13,A x x x Z =-<<∈,写出A 的所有子集.例3.已知集中{},,2M a a d a d =++,{}2,,N a aq aq =,其中0a ≠且MN =,供q 战d的值(用a 表示).例4.设齐集{}22,3,23U a a =+-,{}21,2A a =-,{}5U C A =,供真数a 的值. 例5.已知{}3A x x =<,{}B x x a =<. ⑴若B A ⊆,供a 的与值范畴; ⑵若A B ⊆,供a 的与值范畴; ⑶若R C A R C B ,供a 的与值范畴. [课内训练]1. 下列关系中精确的个数为()①0∈{0},②Φ{0},③{0,1}⊆{(0,1)},④{(a ,b )}={(b ,a )}A )1(B )2 (C )3(D )42.集中{}8,6,4,2的真子集的个数是()(A )16 (B)15 (C)14 (D) 133.集中{}正方形=A ,{}矩形=B ,{}平行四边形=C ,{}梯形=D ,则底下包罗关系中不精确的是()(A )B A ⊆ (B) C B ⊆ (C) D C ⊆ (D) C A ⊆4.若集中 ,则_____=b .5.已知M={x| 2≤x ≤5}, N={x| a+1≤x ≤2a 1}.(Ⅰ)若M ⊆N ,供真数a 的与值范畴; (Ⅱ)若M ⊇N ,供真数a 的与值范畴. [归纳深思]1.那节课咱们教习了集中之间包罗关系及补集的观念,沉面明黑子集、真子集,补集的观念,注意空集与齐集的相关知识,教会数轴表示数集. 2. 深刻明黑用集中谈话道述的数教命题,并能准确天把它翻译成相关的代数谈话大概几许谈话,抓住集中谈话背笔墨谈话大概图形谈话转移是挨启解题大门的钥匙,办理集中问题时要注意充分使用数轴战韦恩图,收挥数形分离的思维要领的巨大能力. [坚韧普及]1.四个关系式:①∅}0{⊂;②0}0{∈;③}0{∈∅;④}0{=∅.其中表述精确的是[ ] A .①,② B .①,③ C .①,④ D .②,④2.若U={x ∣x 是三角形},P={ x ∣x 是曲角三角形},则=P C U ----------------------[ ]A .{x ∣x 是曲角三角形}B .{x ∣x 是钝角三角形}C .{x ∣x 是钝角三角形}D .{x ∣x 是钝角三角形大概钝角三角形}3.下列四个命题:①{}0∅=;②空集不子集;③所有一个集中必有二身材集;④空集是所有一个集中的子集.其中精确的有---------------------------------------------------[ ]A.0个 B.1个 C.2个 D.3个4.谦脚关系{}1,2A ⊆{}1,2,3,4,5的集中A的个数是--------------------------[ ] A.5 B.6 C.7 D.8 5.若,x y R ∈,(){},A x y y x ==,(),1y B x y x ⎧⎫==⎨⎬⎩⎭,则,A B 的关系是---[ ] A.A B B.A B C.A =B D.A ⊆B6.设A={}5,x x x N ≤∈,B={x ∣1< x <6,x }N ∈,则=B C A7.U={x ∣},01582R x x x ∈=+-,则U 的所有子集是8.已知集中}5|{<<=x a x A ,x x B |{=≥}2,且谦脚B A ⊆,供真数a 的与值范畴.9.已知集中P={x ∣},062R x x x ∈=-+,S={x ∣},01R x ax ∈=+, 若S ⊆P ,供真数a 的与值集中.10.已知M={x ∣x ,0>R x ∈},N={x ∣x ,a >R x ∈} (1)若M N ⊆,供a 得与值范畴;(2)若M N⊇,供a得与值范畴;(3)若MC R,供a得与值范畴.C R N接集、并集[自教目标]1.明黑接集、并集的观念战意思2.掌握相识区间的观念战表示要领3.掌握有关集中的术语战标记[知识重心]1.接集定义:A∩B={x|x∈A且x∈B}运算本量:(1)A∩B A,A∩B B(2) A∩A=A,A∩φ=φ(3) A∩B= B∩A(4) A B A∩B=A2.并集定义:A∪B={x| x∈A大概x∈B }运算本量:(1) A (A∪B),B (A∪B)(2) A∪A=A,A∪φ=A(3) A∪B= B∪A (4) A B A∪B=B[预习自测]1.设A={x|x>—2},B={x|x<3},供 A∩B战A∪B2.已知齐集U={x|x与不大于30的量数},A、B是U的二身材集,且A∩C U B={5,13,23},C U A∩B={11,19,29},C U A∩C U B={3,7},供A,B.3.设集中A={|a+1|,3,5},集中B={2a+1,a2+2a,a2+2a—1}当A∩B={2,3}时,供A∪B[课内训练]1.设A=(]3,1-,B=[)4,2,供A∩B2.设A=(]1,0,B={0},供A∪B3.正在仄里内,设A、B、O为定面,P为动面,则下列集中表示什么图形(1){P|PA=PB} (2) {P|PO=1}4.设A={(x,y)|y=—4x+b},B={(x,y)|y=5x—3 },供A∩B5.设A={x|x=2k+1,k∈Z},B={x|x=2k—1,k∈Z},C= {x|x=2k,k∈Z},供A∩B,A∪C,A∪B[归纳深思]1.集中的接、并、补运算,不妨借帮数轴,还不妨借帮文氏图,它们皆是数形分离思维的体现2.分类计划是一种要害的数教思维法,精确分类计划思维,掌握分类计划思维要领.[坚韧普及]1.设齐集U={a,b,c,d,e},N={b,d,e}集中M={a,c,d},则C U(M∪N)等于2.设A={ x|x<2},B={x|x>1},供A∩B战A∪B3.已知集中A B,供真数a 的与值范畴4.供谦脚{1,3}∪A={1,3,5}的集中A5.设A={x|x2—x—2=0},A∩B6、设A={(x,y)| 4x+m y =6},B={(x,y)|y=nx—3 }且A∩B={(1,2)},则m= n=7、已知A={2,—1,x2—x+1},B={2y,—4,x+4},C={—1,7}且A ∩B=C,供x,y的值8、设集中2+3px+2=0},B={x|2x2+x+q=0},其中p,q,x∈R,且A∩时,供p的值战A∪B9、某车间有120人,其中乘电车上班的84人,乘汽车上班的32人,二车皆乘的18人,供:⑴只乘电车的人数⑵不乘电车的人数⑶乘车的人数⑷只乘一种车的人数10、设集中A={x|x2+2(a+1)x+a2—1=0},B={x|x2+4x=0}⑴若A∩B=A,供a的值⑵若A∪B=A,供a的值集中复习课[自教目标]1.加深对付集中关系运算的认识2.对付含字母的集中问题有一个收端的相识[知识重心]1.数轴正在解集中题中应用2.若集中中含有参数,需对付参数举止分类计划 [预习自测]1.含有三个真数的集中可表示为⎭⎬⎫⎩⎨⎧1,,a b a ,也可表示为{}0,,2b a a +,供20042003b a +2.已知集中A={}21|>-<x x x 或,集中B={}04|<+p x x ,当B A ⊇时,供真数p 的与值范畴3.已知齐集U={1,3,x x x 2323++},A={1,|2x —1|},若C U A={0},则那样的真数x 是可存留,若存留,供出x 的值,若不存留,证明缘由 [课内训练]1.已知A={x|x<3},B={x|x<a} (1)若B A ,供a 的与值范畴 (2)若A B ,供a 的与值范畴(3)若C R A C R B ,供a 的与值范畴2.若P={y|y=x 2,x ∈R},Q={y| y=x 2+1,x ∈R },则P ∩Q =3.若P={y|y=x 2,x ∈R},Q={(x ,y )| y=x 2,x ∈R },则P ∩Q = 4.谦脚{a ,b} A {a ,b ,c ,d ,e}的集中A 的个数是 [归纳深思]1.由条件给出的集中要明黑它所表示的含意,即元素是什么?2.含参数问题需对付参数举止分类计划,计划时央供既不沉复也不遗漏.[坚韧普及]1.已知集中M={x|x 3—2x 2—x+2=0},则下列各数中不属于M 的一个是()A .—1B .1C .2D .—22.设集中A= {x|—1≤x <2},B={ x|x<a },若A ∩B ≠φ,则a 的与值范畴是()A .a <2B .a >—2C .a >—1D .—1≤a ≤23.集中A 、B 各有12个元素,A ∩B 中有4个元素,则A ∪B 中元素个数为4.数集M={x|N k k x ∈+=,41},N={ x|N k k x ∈-=,412},则它们之间的关系是⊂ ≠⊂≠5.已知集中M={(x,y )|x+y=2 },N={(x,y )|x —y=4},那么集中M ∩N=6.设集中A={x|x 2—px+15=0},B={x|x 2—5x+q=0},若A ∪B={2,3,5},则A=B=7.已知齐集U=R ,A={x|x ≤3},B={ x|0≤x ≤5},供(C U A )∩B8.已知集中A={x|x 2—3x+2=0},B={x|x 2—mx+(m —1)=0},且B A ,供真数m 的值9.已知A={x|x 2+x —6=0},B={x|mx+1=0},且A ∪B=A ,供真数m 的与值范畴10.已知集中A={x|—2<x <—1大概x >0},集中B={ x|a ≤x ≤b},谦脚A ∩B={x|0<x ≤2},A ∪B={x|x >—2},供a 、b 的值§函数的观念与图象(1)[自教目标]1.体验函数是形貌变量之间的依好关系的要害数教模型,明黑函数的观念;2.相识形成函数的果素有定义域、值域与对付应规则; [知识重心]12.函数观念的三果素:定义域、值域与对付应规则. 3.函数的相等. [预习自测]例1(1(2(2(3(4应,单值对付应的关键是元素对付应的存留性战唯一性.例2.下列各图中表示函数的是------------------------------------------[ ]⊂ ≠A B C D例3.正在下列各组函数中,)(x f 与)(x g 表示共一函数的是------------------[ ]A .)(x f =1,)(x g =0xB .x y =与2x y =C .2x y =与2)1(+=x yD .)(x f =∣x ∣,)(x g =2x63-x (x ≥0)例4 已知函数=)(x f 供)1(f 及)]1([f f 5+x (x 0<), [课内训练]1.下列图象中表示函数y=f(x)关系的有--------------------------------( )A.(1)(2)(4)B.(1)(2)C.(2)(3)(4)D.(1)(4)2.下列四组函数中,表示共一函数的是----------------------------------( ) A .24129y x x =-+战32y x =-B .2y x =战y x x = C .y x =战2y x=D .y x =战()2y x =3.下列四个命题(1)f(x)=x x -+-12蓄意思;(2))(x f 表示的是含有x 的代数式(3)函数y=2x(x N ∈)的图象是背去线;(4)函数y=⎪⎩⎪⎨⎧<-≥0,0,22x x x x 的图象是扔物线,其中精确的命题个数是()A .1B .2C .3D .04.已知f(x)=221(1)1(1)x x x x ⎧->⎪⎨-<⎪⎩,则f(33)=;5.已知f 谦脚f (ab )=f (a )+ f (b),且f (2)=p ,q f =)3(那么)72(f =[归纳深思]1.原课时的沉面真量是函数的定义与函数暗号()f x 的意思,易面是函数观念的明黑战精确应用;xy xy x yxy OOO O2.推断二个函数是可是共一函数,是函数观念的一个要害应用,要能紧扣函数定义的三果素举止分解,进而精确天做出推断.[坚韧普及]1--------------------[ ]A B C D2.下列各项中表示共一函数的是ABCD3) ] AB.1C.24--------------------------------[ ]ABCD5678910[自教目标]掌握供函数定义域的要领以及步调;[知识重心]1、函数定义域的供法:(1)由函数的剖析式决定函数的定义域;(2)由本量问题决定的函数的定义域;(3). [预习自测]例1.供下列函数的定义域:(1)()1f x x x =+-(2))(x f =xx -1(3)1()21f x x=+(4))(x f =+-x 5x-21分解:如果()f x 是整式,那么函数的定义域是真数集R ;如果()f x 是分式,那么函数的定义域是使分母0≠的真数的集中;如果()f x 是二次根式,那么函数的定义域是使根号内的表黑式≥0的真数的集中.★注意定义域的表示不妨是集中大概区间.例2.周少为l 的铁丝直成下部为矩形,上部为半圆形的框架(如图),若矩形底边少为2x ,供此框架围成的里积y 与x 的函数关系式,并指出其定义域例3.若函数=y )(x f 的定义域为[]1,1- (1)供函数(1)f x +的定义域; (2)供函数=y )41()41(-++x f x f 的定义域.[课内训练]1.函数()1f x x x=-的定义域是―――――――――――――――――()A.(),0-∞B.()0,+∞C.[0,)+∞D.R 2.函数f(x)的定义域是[12,1],则y=f(3-x)的定义域是―――――――――()A [0,1]B [2,52] C [0,52] D (),3-∞3.函数()f x =()011x x -+-的定义域是:4.函数)5lg()(-=x x f 的定义域是5.函数()()1log 143++--=x x xx f 的定义域是 [归纳深思]1.函数定义域是指受节造条件下的自变量的与值;2.供函数的定义域时常是归纳为解不等式战不等式组; [坚韧普及]1.函数y =21x -+12-x 的定义域是----------------------------[ ] A .[1-,1] B .(),1[]1,+∞-∞- C .[0,1] D .{1,1-}2.已知)(x f 的定义域为[2,2-],则)21(x f -的定义域为------------[ ] A .[2,2-] B .[]23,21- C .[]3,1- D .[,2-]233------------------------------------[ ]A45.6.7.供下列函数的定义域328.9.用少为30cm的铁丝围成矩形,试将矩形里积S.10黑式.§函数的观念与图象(3)[自教目标]掌握供函数值域的基原供法;[知识重心]函数值域的供法函数的值域是由函数的定义域与对付应规则决定的,果此,央供函数的值域,普遍要从函数的定义域与对付应规则进脚分解,时常使用的要领有:(1)瞅察法;(2)图象法;(3)配要领;(4)换元法.[预习自测]例1.供下列函数的值域:(1(2(3(4(5(6分解:供函数的值域,一种时常使用的要领便是将函数的剖析式做适合的变形,通过瞅察大概利用死知的基原函数(如一次函数、二次函数等)的值域,进而逐步推出所供函数的值域(瞅察法);大概者也不妨利用换元法举止转移供值域.例2.畴[1A2.函数y=2x2-4x-3,0≤x≤3的值域为 ( )∞)3 ( )A45.供函数[归纳深思]供函数的值域是教习中的一个易面,要领机动百般,初教时只消掌握几种时常使用的要领,如瞅察法、图象法、配要领、换元法等,正在以去的教习中还会有一些新的要领(比圆使用函数的单调性、配要领、分段计划法、不等式法等等),不妨逐步天深进战普及.[坚韧普及---------------------------------------[ ]1.A2.下列函数中,值域是的是A3.--------[ ]:.5.:.6.:.7.供下列函数的值域23(1(4568.§函数的观念与图象(4)[自教目标]1.会使用描面法做出一些简朴函数的图象,从“形”的角度进一步加深对付函数观念的明黑;2.通过对付函数图象的描画战钻研,培植数形分离的意识,普及使用数形分离的思维要领办理数教问题的本领. [知识重心]1.函数图象的观念每一个值时,便得到一系列那样的面.所有那些面组成的集中(面2.函数图象的画法画函数的图象,时常使用描面法,其基原步调是:⑴列表;⑵描面;⑶连线.正在画图历程中,一定要注意函数的定义域战值域. 3.会做图,会读(用)图 [预习自测]例1.画出下列函数的图象,并供值域:,2];;例2y =3x 2-6x |图象的接面个数为() (A )4个(B )3个(C )2个(D )1个例3.下图中的A. B. C. D 四个图象中,用哪三个分别形貌下列三件事最符合,并请您为剩下的一个图象写出一件事. 离启家的距离(m) 离启家的距离(m) 时间(min )时间(min )A B离启家的距离(m) 离启家的距离(m) 时间(min )时间(min )C D(1) 尔离启家不暂,创造自己把做业原记正在家里了,停下去念了一会仍旧返回家与了做业原再上教;(2) 尔骑着车一路匀速止驶,不过正在途中逢到一次接通阻碍,延误了一些时间;(3) 尔出收后,心情沉快,缓缓前进,厥后为了赶时间加快了速度. [课堂训练]1.下列四个图像中,是函数图像的是( )A 、(1)B 、(1)、(3)、(4)C 、(1)、(2)、(3) D 、(3)、(4)2.曲线x a =()a R ∈战函数21y x =+的图象的接面个数 ( )A 至多一个B 起码有一个C 有且仅有一个D 有一个大概二个以上3.函数y=|x+1|+1的图象是 ( )4.某企业近几年的年产值如图,则年删少率最下的是( )(年删少率=年删少值/年产值)A )97年B )98年C )99年D )00年5.做出函数223(1y x x x =--≤-大概2x >)的图象;[归纳深思] 根据函数的剖析式画函数的图象,基原要领是描面法,但是值得指出的是:一要注意函数的定义域,二要注意对付函数剖析式的个性加以分解,充分利用已知函数的图象普及做图的速度战准确性; 函数的图象是表示函数的一种要领,通过函数的图象不妨曲瞅天表示x 与y 的对付应关系以及二个变量变更历程中的变更趋势,以去咱们会时常天使用函数剖析式与函数图象二者的有机分离去钻研函数xOyxxxyyyOOO(1)(2)(3)(4)0099989796(年)2004006008001000(万元)的本量. [坚韧普及]1.某教死离家去书院,由于怕早退,所以一启初便跑步,等跑乏了再走做余下的路,正在 下图中纵轴表示离书院距离,横轴表示出收后的时间,则下图中较切合教死走法的是( ) d d d dO t O t O t O t A B C D 2.某工厂八年去产品C (即前t 年年产量之战)与时间t(年)的函数如下图,下列四种道法:(1)前三年中,产量删少的速度越去越快; (2)前三年中,产量删少的速度越去越缓; (3)第三年后,年产量脆持稳定; (4)第三年后,年产量逐步删少. 其中道法精确的是()A .(2)与(3)B .(2)与(4)C .(1)与(3)D .(1)与(4)3.下列各图象中,哪一个不可能是函数)(x f y =的图象()xA .B .xxC .D .4.函数)0(≠+=kb b kx y 的图象短亨过第一象限,则b k ,谦脚-----------[ ] A .k 0,0><b B .0,0<<b k C .0,0<>b k D .0,0>>b k5.函数c bx ax y ++=2与b ax y +=()0≠ab 的图象只大概是---------[ ]A .B .C .D .6.函数1+=x y 的图象是----------------------------------------[ ]A .B .C .D . 7.函数1(13-=x y ≤x ≤2)的图象是xy0 0xxxxxx x xyyyyy yyy8.一次函数的图象通过面(2,0)战(-2,1),则此函数的剖析式为9.10.(1(2[自教目标]1.相识表示函数有三种基原要领:图象法、列表法、剖析法;明黑函数关系的三种表示要领具备内正在的通联,正在一定的条件下是不妨互相转移的.2.相识供函数剖析式的一些基原要领,会供一些简朴函数的剖析式.3.相识简朴的分段函数的个性以及应用.[知识重心]1.表示函数的要领,时常使用的有:剖析法,列表法战图象法.正在表示函数的基原要领中,列表法便是间接列表表示函数,图象法便是间接做图表示函数,而剖析法是通过函数剖析式表示函数.2.供函数的剖析式,普遍有三种情况⑴根据本量问题修坐函数的关系式;⑵已知函数的典型供函数的剖析式;⑶使用换元法供函数的剖析式;3.分段函数正在定义域内分歧部分上,有分歧的剖析表黑式的函数常常喊搞分段函数;注意:①分段函数是一个函数,而不是几个函数;;值范畴的并集[例题分解]例1.买买某种饮料x听,所需钱数为y元.若每听2元,试分别用剖成的函数,并指出该析法、列表法、图象法将y表示例2.(1)已知f(x)是一次函数,且f(f(x))=4x-1,供f(x)的表黑式;(2)已知,供f(x)的表黑式;例3︱的图象 变题③供函数f(x)=︱x+1︱+︱x-2︱的值域变题④做出函数f(x)=︱x+1︱+︱x-2︱的图象,是可存得通太过类计划,将剖析式化为不含有千万于值的式子.做出f(x)的图象例4(1)供f(-3)、f[f(-3)] ; (2)若供a 的值.[课堂训练]1.用少为30cm 的铁丝围成矩形,试将矩形里积S一边少x (cm )的函数,并画出函数的图象.2.若f(f(x))=2x -1,其中f(x)为一次函数,供f(x)的剖析式.3.已知f(x-3)f(x+3) 的表黑式.4.如图,根据的图象,写出y=f(x)的剖析式. [归纳深思]1. 函数关系的表示要领主要有三种: 剖析法,列表法战图象法.那三种表示要领各有劣缺面,千万不克不迭误认为惟有剖析式表示出去的对付应关系才是函数;2. 函数的剖析式是函数的一种时常使用的表示要领,央供二个变量间的函数关系,一是央供出它们之间的对付应规则,二是央供出函数的定义域;3. 无论使用哪种要领表示函数,皆不克不迭忽略函数的定义域;对付于分段函数,还必须注意正在分歧的定义范畴内,函数有分歧的对付应关系,必须先分段钻研,再合并写出函数的表黑式. [坚韧普及]1.函数f(x)=︱x+3︱的图象是------------------------------------------------------------( )2--------------------------------------------------( )A.32x + B.3x + C.32x + D.23x +3.已知一次函数的图象过面()1,0以及()0,1,则此一次函数的剖析式为------()A .1y x =-+B .1y x =+C .1y x =-D .1y x =--4.已知函数()()()221122(2)x x y f x x x x x +≤-⎧⎪==-<<⎨⎪>⎩,且()3f a =,则真数a 的值为---()A .1B .1.5C .3-D .35.若函数()2,(),(1)1,f x x mx n f n m f =-+==-则()5f -= 6.某航空公司确定,乘机所携戴止李的沉量(kg )与其运费(元)由如图的一次函数图象决定,那么搭客免费可携戴止李的最大沉量为7.画出函数2x0,f(x)=x0,x x ≥⎧⎨<⎩的图象,并供f(32+)+f(32-的值. 8.画出下列函数的图象(1) y=x -︱1-x ︱ (2) 21,02,0x x y x x ⎧+≤=⎨->⎩9.供函数y=1-︱1-x ︱的图象与x 轴所围成的启关图形的里积.。
高中必修第一册统编人教A版《3.1函数的概念及其表示》优秀教学导学案
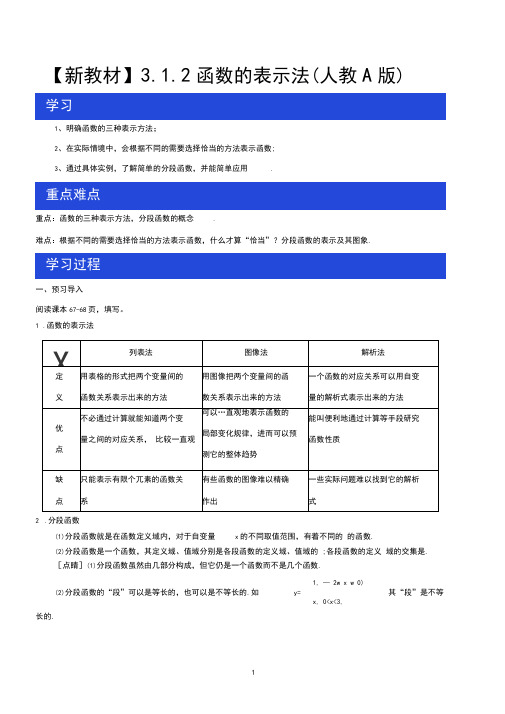
【新教材】3.1.2函数的表示法(人教A版)1、明确函数的三种表示方法;2、在实际情境中,会根据不同的需要选择恰当的方法表示函数;3、通过具体实例,了解简单的分段函数,并能简单应用.重点:函数的三种表示方法,分段函数的概念.难点:根据不同的需要选择恰当的方法表示函数,什么才算“恰当”?分段函数的表示及其图象.一、预习导入阅读课本67-68页,填写。
1.函数的表示法2.分段函数(1)分段函数就是在函数定义域内,对于自变量x的不同取值范围,有着不同的的函数.(2)分段函数是一个函数,其定义域、值域分别是各段函数的定义域、值域的 ;各段函数的定义域的交集是.[点睛](1)分段函数虽然由几部分构成,但它仍是一个函数而不是几个函数.1, — 2w x w 0)(2)分段函数的“段”可以是等长的,也可以是不等长的.如y= 其“段”是不等x, 0<x<3,长的.1.判断(正确的打“,”,错误的打“X”)(1)任何一个函数都可以同上述三种方法表示. ( )(2)函数f(x) = 2x+ 1不能用列表法表示. ( )(3)函数的图象一定是定义区间上一条连续不断的曲线. ( )(4)分段函数由几个函数构成. ( )x+ 1, x< 1,(5)函数f(x)= 是分段函数.( )-x+ 3, x>12.函数y = f(x)的图象如图,则f(x)的定义域是( )A.RB.( —8, 1) U (1 , +OO)C.( —8, 0) U (0 , +OO)D.(― 1,0)3.已知反比例函数 f (x)满足f(3) =—6, f (x)的解析式为题型一函数的定义例1某种笔记本的单价是5元,买x (x C {1 , 2, 3,4, 5})个笔记本需要y元.试用三种表示法表示函数y=f(x).跟踪训练一1 .已知函数f(x) , g(x)分别由下表给出.123£(X)321则f( g(1)) 的值为;当g ( f (x)) =2 时,x=题型二分段函数求值|x-1|-2, |x|<1,例2 已知函数f (x) = 1寸x|>1.(1)求f(?N??)的值;(2)若f(x) =1 ,求x的值 3跟踪训练二x2+2, x<2,1. 函数f(x)= 4 若f(x o) = 8,则x0= .二x , x> 2.5题型三求函数解析式例 3 (1)已知f(x+1)= ??-3x+2,求f(x);(2)已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x, 求f(x)的解析式;(3)已知函数f(x)对于任意的x都有f(x)+2f(-x)=3x-2, 求f(x).跟踪训练三1.已知f(x)是一次函数,且f(f(x))=2x-1, 求f(x)的解析式;2.已知f( vx+1)=x+2 vx,求f(x)的解析式;3.设函数f(x)满足f(x)+2f (-) =x(x w 0),求f(x). x题型四函数的图像及应用例4 1.函数f(x) = |x - 1|的图象是( )B C D2.给定函数 f(x) = x + 1,g(x) = (x + 1)2,x CR(1)在同一直角坐标系中画出函数 f (x ) ,g (x )的图像;(2) ?x CR,用M(x)表示f(x),g(x)中的较大者,记为 M(x) = max{f(x) ,g(x)}.请分别用图像法和解析法表示函数M(x).跟踪训练四1 .已知函数f(x)的图象如右图所示,则 f(x)的解析式是 .b, a>b,2.若定义运算 aOb=则函数f(x) =xO(2—x)的值域为 ______________ .a, a< b.题型五 函数的实际应用例5下表是某校高一(1)班三位同学在高一学年度几次数学测试的成绩及班级及班级平均分表:A 次 第二次 第三次 第四次 第五次 第六次王伟 98 87 91 92 88人 95 张城 90 76 88 75 86 80 赵 磊 68 65 73 72 75 82 班平均分88. 278. 385. 480. 375. 782. 6请你对这三们同学在高一学年度的数学学习情况做一个分析.堂检测2.已知 f(W)=x,贝Uf(x)=()1+x1.若 f(x)={x-3, x >10, ,f(f(x+ 6)), x<则f(5)的值为(10 ,A.8B.9C.10D.11B二1+x D.M x x+13.若f(x)对于任意实数x恒有3f(x)-2f(-x)=5x+1, 则f(x)=( A.x+1 B.x-1C.2x+1D.3x+34.函数f(x)=2x , 0 < x < 1,{2, 1 < ??< 2,的值域是( ) 3, x >2A.RB.[0,+ 8)C.[0,3]5.已知函数D.[0,2] U {3}f(x)6.已知f(x) 为二次函数,其图象的顶点坐标为(1,3),且过原点,求f(x)的解析式.7.某商场新进了10台彩电,每台单价3 000元,试求售出台数x与销售额y之间的函数关系,分别用列表法、图象法、解析法表示出来答案小试牛刀1 . (1) X (2) ,(3) X (4) X (5 ),2. C一183. y =——x自主探究例1【答案】见解析【解析】这个函数的定义域是数集{1,2, 3,4, 5}.用解析法可将函数y=f (x)表示为y=5x, x C {1 , 2, 3,4, 5}用列表法可将函数y=f(x)表示为用图像法可将函数 y=f(x)表示为25 -g20 -•15 -*10 -■5 - •1I1K 1 ."(7] |2~3~4~5^跟踪训练一【答案】1 1【解析】由于函数关系是用表格形式给出的,知 g (1) =3,,f ( g(1)) =f (3) =1.由于g (2) =2,,f (x)=2, ■. x = 1.例2 【答案】(1) A (2)±\211,3 【解析】(1)因为f 2 = 2-1 -2=-2,=;,若 |x| < 1,则 |x - 1| —2=;,得 x=;或 x=一:. 3 3 3 3因为|x| < 1,所以x 的值不存在;若|x|>1 ,则彳导 x =±\2,符合 |x| >1.I i- x 3所以若f(x) =1, x 的值为士 \2.3跟踪训练二【答案】—m 或10【解析】解析:当 xo<2时,f(x o)=x0+2=8,即x2=6,xo= 一 \ 6或 xo= 6(舍去);~ ,1所以f f 2 =f3 14— = -------------- = ---23 2131 +— -2-(2)f(x), , 4当Xo>2 时,f(x 0)= -Xo , Xo= 10. 5综上可知,Xo=—{§或Xo= 1 0.例3【答案】见解析【解析】(1)(方法一)令x+1=t,则x=t-1.将x=t-1 代入f(x+1)= ?%3x+2,得f(t尸(?? 1)2-3(t-1)+2= /5t+6, f(x)= ??-5x+6.(方法二)「f(x+1)= ?f -3x+2= ?f+2x+1-5x-5+6= (?4 1)2-5(x+1)+6, • . f(x户?f-5x+6.(2)设所求的二次函数为f(x)=a ?5+bx+c(a w。
人教A版高中数学必修一全册导学案函数及其表示

课题:1.2 函数及其表示 (习题课)一、三维目标:知识与技能:对函数()f x 记号的理解与运用,会根据条件求函数的解析式,理解函数的三种表示法及其简单应用,掌握函数的图像及其简单应用。
过程与方法:通过本节内容的学习,使学生加深对函数及其应用的理解、初步体会学习函数的方法。
情感态度与价值观:激发学习兴趣,培养学生合作探究学习的能力。
二、学习重、难点:重点:函数()f x 记号的理解与运用,会根据条件求函数的解析式,掌握函数的图像及应用。
难点:函数的图像及其应用。
三、知识链接:1、函数的概念 :2、函数的三种表示方法:四、学法指导:回顾前几节函数知识的内容,认真学习导学案中的例题,灵活运用函数知识解决问题,并注意方法规律总结。
五、学习过程:A1. 函数()f x 记号的理解与运用:已知函数)(x f =4x+3,g(x)=x 2,求f[4] g[6].,f[g(x)],g[f(x)]。
B2.解析式法及应用:例1求函数的解析式:(1)已知f (2x +1)=x 2+1,求f (x );解:(1)设t =2x +1,则x =t -12, ∴f (t )=(t -12)2+1.从而f (x )=(x -12)2+1.(2)已知f (1x )=x1-x 2,求f (x ).解法一:设t =1x , 则x =1t (t ≠0),代入f (1x )=x1-x 2,得f (t )=1t 1-(1t)2=t t 2-1, 故f (x )=xx 2-1(x ≠0).解法二:∵f (1x )=x 1-x 2=1x (1x)2-1, ∴f (x )=xx 2-1(x ≠0).(3)已知f (x )是一次函数,且满足3f (x +1)-2f (x -1)=2x +17,求f (x );解:设f (x )=ax +b (a ≠0),则3f (x +1)-2f (x -1)=3ax +3a +3b -2ax +2a -2b =ax +b +5a =2x +17, ∴a =2,b =7,∴f (x )=2x +7. (4)已知)(x f 满足12()()3f x f x x+=,求)(x f . 解:2f (x )+f (1x)=3x ①,把①中的x 换成1x ,得2f (1x )+f (x )=3x②,①×2-②得3f (x )=6x -3x ,∴f (x )=2x -1x.方法总结:第(1)题用代入法;第(2)题用配凑法;第(3)题已知一次函数,可用待定系数法;第(4)题用方程组法。
人教A版高中数学必修一学新导学案第一章集合与函数的概念复习,

第一章 集合与函数的概念(复习)1. 理解集合有关概念和性质,掌握集合的交、并、补等三种运算的,会利用几何直观性研究问题,如数轴分析、Venn 图;2. 深刻理解函数的有关概念,理解对应法则、图象等有关性质,掌握函数的单调性和奇偶性的判定方法和步骤,并会运用解决实际问题.245复习1:集合部分.① 概念:一组对象的全体形成一个集合② 特征:确定性、互异性、无序性③ 表示:列举法{1,2,3,…}、描述法{x |P }④ 关系:∈、∉、⊆、、=⑤ 运算:A ∩B 、A ∪B 、U C A⑥ 性质:A ⊆A ; ∅⊆A ,….⑦ 方法:数轴分析、Venn 图示.复习2:函数部分.① 三要素:定义域、值域、对应法则;② 单调性:()f x 定义域内某区间D ,12,x x D ∈,12x x <时,12()()f x f x <,则()f x 的D 上递增;12x x <时,12()()f x f x >,则()f x 的D 上递减.③ 最大(小)值求法:配方法、图象法、单调法.④ 奇偶性:对()f x 定义域内任意x ,()()f x f x -=- ⇔ 奇函数;()()f x f x -= ⇔ 偶函数.特点:定义域关于原点对称,图象关于y 轴对称.二、新课导学※ 典型例题例1设集合22{|190}A x x ax a =-+-=,2{|560}B x x x =-+=,2{|280}C x x x =+-=.(1)若A B =A B ,求a 的值;(2)若φA B ,且A C =∅,求a 的值;(3)若A B =A C ≠∅,求a 的值.例2 已知函数()f x 是偶函数,且0x ≤时,1()1x f x x+=-. (1)求(5)f 的值; (2)求()0f x =时x 的值;(3)当x >0时,求()f x 的解析式.例3 设函数221()1x f x x +=-. (1)求它的定义域; (2)判断它的奇偶性;(3)求证:1()()f f x x=-;(4)求证: ()f x 在[1,)+∞上递增.※动手试试练1. 判断下列函数的奇偶性:(1)222()1x xf xx+=+;(2)3()2f x x x=-;(3)()f x a=(x∈R);(4)(1)()(1)x xf xx x-⎧=⎨+⎩0,0.xx≥<练2. 将长度为20 cm的铁丝分成两段,分别围成一个正方形和一个圆,要使正方形与圆的面积之和最小,正方形的周长应为多少?三、总结提升※学习小结1. 集合的三种运算:交、并、补;2. 集合的两种研究方法:数轴分析、Venn图示;3. 函数的三要素:定义域、解析式、值域;4. 函数的单调性、最大(小)值、奇偶性的研究.※知识拓展要作函数()y f x a=+的图象,只需将函数()y f x=的图象向左(0)a>或向右(0)a<平移||a个单位即可. 称之为函数图象的左、右平移变换.要作函数()y f x h=+的图象,只需将函数()y f x=的图象向上(0)h>或向下(0)h<平移||h 个单位即可. 称之为函数图象的上、下平移变换.※ 自我评价 你完成本节导学案的情况为( ).A. 很好B. 较好C. 一般D. 较差※ 当堂检测(时量:5分钟 满分:10分)计分:1. 若{}2|0A x x =≤,则下列结论中正确的是( ).A. 0A =B. 0AC. A =∅D. ∅A2. 函数||y x x px =+,x R ∈是( ).A .偶函数B .奇函数C .不具有奇偶函数D .与p 有关3. 在区间(,0)-∞上为增函数的是( ).A .1y =B .21x y x=+- C .221y x x =--- D .21y x =+4. 某班有学生55人,其中音乐爱好者34人,体育爱好者43人,还有4人既不爱好体育也不爱好音乐,则班级中即爱好体育又爱好音乐的有 人.0x >时,()1f x =,则当0x <,()f x = .1. 数集A 满足条件:若,1a A a ∈≠,则11A a∈+. (1)若2A ∈,则在A 中还有两个元素是什么;(2)若A 为单元集,求出A 和a .2. 已知()f x 是定义在R 上的函数,设()()()2f x f x g x +-=,()()()2f x f x h x --=. (1)试判断()()g xh x 与的奇偶性; (2)试判断(),()()g x h x f x 与的关系;(3)由此你猜想得出什么样的结论,并说明理由?。
人教A版高中数学必修一第一轮高效复习导学案第三课时函数的单调性新人教

函数的图象【学习目标】1. 理解函数单调性的概念。
2. 学会利用定义判断证明函数单调性,并能应用。
3. 以极度的热情投入学习,体会成功的快乐。
【学习重点】函数单调性的概念。
【学习难点】判断证明函数单调性方法。
[自主学习] 一、单调性1.定义:如果函数y =f (x )对于属于定义域I 内某个区间上的任意两个自变量的值x 1、、x 2,当x 1、<x 2时,①都有 ,则称f (x )在这个区间上是增函数,而这个区间称函数的一个 ;②都有 ,则称f (x )在这个区间上是减函数,而这个区间称函数的一个 .若函数f (x )在整个定义域l 内只有唯一的一个单调区间,则f (x )称为 . 2.判断单调性的方法:(1) 定义法,其步骤为:① ;② ;③ .(2) 导数法,若函数y =f (x )在定义域内的某个区间上可导,①若 ,则f (x )在这个区间上是增函数;②若 ,则f (x )在这个区间上是减函数.二、单调性的有关结论1.若f (x ), g (x )均为增(减)函数,则f (x )+g (x ) 函数; 2.若f (x )为增(减)函数,则-f (x )为 ; 3.互为反函数的两个函数有 的单调性;4.复合函数y =f [g(x )]是定义在M 上的函数,若f (x )与g(x )的单调相同,则f [g(x )]为 ,若f (x ), g(x )的单调性相反,则f [g(x )]为 .5.奇函数在其对称区间上的单调性 ,偶函数在其对称区间上的单调性 .【基础过关】1 下列函数中,在区间(0,2)上递增的有______________①xy 1-= ②y=-x ③y=|x-1| ④y=122++x x 2 函数)34(212log )(-+-=x x x f 的递减区间为_______________3 已知函数2)1(2)(2+-+=x a x x f 在区间(-∞,4]上是减函数,则a 的取值范围为___________________4 已知f(x)是定义在R 上的偶函数,且在[0,+∞]上是增函数,0)31(=f ,则不等式)(log 81xf 的解集为_____________[典型例析](A )例1 求证:函数11)(--=xx f 在区间(-∞,0)上是单调增函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一问题情境:我们已经利用对数求出了方程0.840.5x
=的近似解,即0.84lg 0.5log 0.5 4.lg 0.84
x ==≈问题(1)如果利用图像能求出0.840.5x =的近似解吗? 问题(2)利用什么方法可求出方程lg 3x x =-的近似解呢?
二 建构数学:下列每组题目中的两个问题,其结果怎样?
(1)①求一元二次方程2230x x --=的解.____________
②求二次函数223y x x =--的图像与x 轴的交点的横坐标.________________
(2)①方程2
2750x x -+=有没有实数解?有几个解?_______,_________.
②二次函数2275y x x =-+的图像与x 轴有没有交点?有几个交点?_____,______.
我发现(1)中的两个结果______;(2)中的两个结果__________.
由此我们可以知道:一元二次方程2
0(0)ax bx c a ++=≠的实数根就是二次函数2(0)y ax bx c a =++≠的函数值___y =时的自变量x 的值.也就是二次函数2(0)y ax bx c a =++≠的图像与_____轴的交点的_____坐标.因此,一元二次方程20(0)ax bx c a ++=≠的实数根也称为函数2(0)y ax bx c a =++≠的_________.
当0a >时,可以得到方程20(0)ax bx c a ++=≠的根与函数2
(0)y ax bx c a =++≠的图像之间的关系(如下表) 24b ac ∆=-
0∆> 0∆= 0∆< 20(0)ax bx c a ++=>的
根
2y ax bx c =++
(0)a >的图像
2y ax bx c =++
的零点
一般地,我们把使函数()y f x =的值为0的实数x 称为函数()y f x =的零点,即方程()0f x =的实数根叫做函数()y f x =的零点。
例1:(1)函数()f x x b =+的零点是 ;
(2)函数245y x x =--的零点是 ;
(3)函数2()22x f x =-
的零点是 ; (4)函数3()3f x x x =-的零点是 。
例2:求证:二次函数2
234y x x =+-有两个不同的零点.
例3:判断函数()222f x x x =--在区间()2,3上是否存在零点.
一般地,若函数()y f x =在区间[],a b 上的图像是一条不间断的曲线,且()()0,f a f b ⨯<则函数()y f x =在区间(),a b 上有________.
例3:求证函数()32
1f x x x =++在区间()2,1--上存在零点.
思考:如果0x 是二次函数()y f x =的零点,且0,m x n <<那么()()0f m f n ⨯<一定成立吗?
三、课堂练习:
1.画出函数22y x x =--的图像,并指出函数2
2y x x =--的零点.
2.证明:(1)函数264y x x =++有两个不同的零点;
(2)函数()331f x x x =+-在区间()0,1上有零点.
第二十二课时 函数的零点 (学案)
1.函数2y x =-的零点是 。
2.函数2
()2f x x x a =-+有两个零点,则实数a 的取值范围是 。
3.若(),,()()y f x x R f x f x =∈-=-,当0x >时,()y f x =单调递增,(1)(2)0f f •<,则方程()0f x =的根的个数为 。
4.如果二次函数()y f x =的零点是1-和5,试比较()()()()21,36f f f f -⨯⨯与0的大小关系为 。
5.在二次函数()y f x =中,如果已知()()210,f f -⨯<()()360,f f ⨯<试判断函数两个零点的范围. 。
6.(1)求证:方程210x x ++=没有实数根.
(2) 求证方程322360x x x +--=在区间()1,2上有根。
(3)求证:方程2
5710x x --=的根一个在区间()1,0-上,另一个在区间()1,2上.
7.判断下列函数是否存在零点,如果存在,请求出。
(1)2
()871f x x x =-++;
(2)2()2f x x x =++;
(3)3()1f x x =+;
(4)2412()2
x x f x x +-=-。
8.关于x 的方程2
2(3)2140mx m x m ++++=有两实根,且一个大于4,一个小于4,求m 的取值范围。
9.已知关于x 的二次方程22210,x mx m +++=若方程有两根,其中一根在区间()1,0-,另一根在区间()1,2内,求m 的取值范围.。
