初二旋转知识点归纳
初中旋转知识点及类型题
初中旋转知识点及类型题
1、 旋转:把一个平面图形绕着平面内某一点
O 转动一个角度,就叫做图形的旋转。点
O
叫做旋转中心,转动的角叫做旋转角,如果图形上的点
P 经过旋转变为点 P’,那么这
两个点叫做这个旋转的对应点。
2、 旋转的性质:对应点到旋转中心的距离相等。
对应点与旋转中心所连线段的夹角等于旋转角。
.
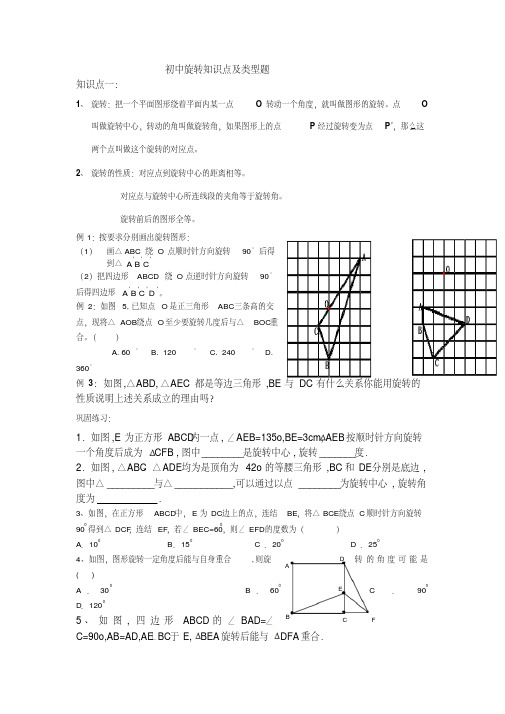
3、如图,在正方形 ABCD中, E 为 DC边上的点,连结 BE,将△ BCE绕点 C 顺时针方向旋转
900 得到△ DCF,连结 EF,若∠ BEC=600,则∠ EFD的度数为(
)
A. 100
B. 150
C . 200
D . 250
4、如图,图形旋转一定角度后能与自身重合 ()
, 则旋
A
A . 300
)
4、( 2013?德州)民族图案是数学文化中的一块瑰宝.下列图案中,既不是中心对称图形也 不是轴对称图形的是
5、( 2013 凉山州)下列图案中,既是轴对称图形又是中心对称图形的是(
)
A
B.
C.
D
A.
B.
C.
D. 6、( 2013?眉山)下列图形是中心对称图形的是
A
B
C
D
7、( 2013?遂宁)下列图案由正多边形拼成,其中既是轴对称图形又是中心对称图形的是
A1个 .
B2 个 .
C3 个 .
D4 个 .
14、( 2013?毕节) 在下列图形中既是轴对称图形又是中心对称图形的是(
D
①线段 ②角 ③等边三角形 ④ 圆 ⑤平行四边形 ⑥矩形
A. ③④⑥ B. ①③⑥ D. ④⑤⑥ D.
旋转知识点总结

旋转知识点总结知识点一旋转的概念1.旋转的定义:把一个图形绕着某一O转动一个角度的图形变换叫做旋转点O叫做旋转中心,转动的角叫做旋转角.如果图形上的点A经过旋转变为点A′,那么,这两个点叫做这个旋转的对应点.重点突出旋转的三个要素:旋转中心、旋转方向和旋转角度.2.旋转的性质:?(1)对应点到旋转中心的距离相等;(2)对应点与旋转中心所连线段的夹角等于旋转角;(3)旋转前后的图形全等3.作图:?在画旋转图形时,要把握旋转中心与旋转角这两个元素.确定旋转中心的关键是看图形在旋转过程中某一点是“动”还是“不动”,不动的点则是旋转中心;确定旋转角度的方法是根据已知条件确定一组对应边,看其始边与终边的夹角即为旋转角作图的步骤:1)连接图形中的每一个关键点与旋转中心;?(2)把连线按要求绕旋转中心旋转一定的角度(旋转角);?(3)在角的一边上截取关键点到旋转中心的距离,得到各点的对应点;?(4)连接所得到的各对应点.知识点二、中心对称与中心对称图形?1.中心对称:把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心.这两个图形中的对应点叫做关于中心的对称点.2.中心对称的两条基本性质:(1)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心所平分.(2)关于中心对称的两个图形是全等图形.?3.中心对称图形把一个图形绕着某一个点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形叫做中心对称图形,这个点就是它的对称中心.??4.中心对称和中心对称图形的区别与联系?中心对称中心对称图形区别?①指两个全等图形之间的相互位置关系①指一个图形本身成中心对称②对称中心不定②对称中心是图形自身或内部的点联系:?如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形.?如果把中心对称图形对称的部分看成是两个图形,那么它们又关于中心对称.?5.?关于原点对称的点的坐标特征:关于原点对称的两个点的横、纵坐标均互为相反数.即P(x,y)关于原点的对称点Q(-x,-y)的坐标为,反之也成立知识点三、平移、轴对称、旋转?1.平移、旋转、轴对称之间的对比?三、规律方法指导1.在学习了图形平移、轴对称的基础上,学习图形旋转的有关知识,要注意处理好如下三个问题:(1)先复习图形平移、轴对称的有关内容,学习时要采用对比的方法;?(2)在对图形旋转性质探索过程中,要从图形变换前后的形状、大小和位置关系上入手分析,发现图形旋转的特性、对应关系、旋转中心和旋转方向;(3)利用旋转设计简单的图案,通过具体画图操作,掌握旋转图形的方法、技巧2.学习中心对称时,注意采用如下方法进行探究:(1)实物分析法:观察具体事物的特征,结合所学知识,分析它们的共同特征和联系;(2)类比分析法:中心对称是一个图形旋转180°后能和另一个图形重合,离不开旋转的知识,因此要类比着进行学习,以提升对图形变换知识的掌握;(3)理论联系实际:在学习中可以通过具体画图操作,以及对具体事物的分析、归纳总结出中心对称的有关知识。
数学旋转的知识点

数学旋转的知识点数学中的旋转是一种基本的几何变换,它可以使我们更好地理解和解决各种问题。
在这篇文章中,我将为您介绍数学旋转的几个重要知识点,帮助您更好地理解和应用它们。
一、旋转的基本概念在数学中,旋转是指围绕一个中心点按照一定的角度将物体或坐标系转动。
旋转可以是顺时针或逆时针方向,角度可以是正数或负数。
二、旋转矩阵旋转可以用一个矩阵来表示,这个矩阵被称为旋转矩阵。
一个二维平面上的旋转矩阵可以写成如下形式:cosθ -sinθsinθ cosθ其中,θ表示旋转的角度。
对于三维空间中的旋转,旋转矩阵会稍有不同。
三、旋转的性质旋转具有一些重要的性质,这些性质有助于我们更好地理解和应用旋转。
1.旋转是保角的:旋转不改变物体之间的角度关系,两个物体的夹角在旋转前后保持不变。
2.旋转是保距的:旋转不改变物体上两点之间的距离,两点间的距离在旋转前后保持不变。
3.旋转是可逆的:旋转可以通过逆向旋转来恢复到原来的状态。
四、旋转的应用旋转在数学和其他科学领域有着广泛的应用。
1.几何学:旋转可以用来解决各种几何问题,如求解物体的位置和姿态,计算点、直线和曲线的旋转等。
2.物理学:旋转在物理学中也有着重要的应用,如刚体转动、天体运动等。
3.计算机图形学:旋转是计算机图形学中的基本操作之一,用于实现物体的旋转、变形和动画效果。
4.人工智能:旋转在人工智能领域也有着广泛的应用,如图像处理、模式识别和机器人导航等。
五、旋转的实例下面给出一个简单的旋转实例,以帮助读者更好地理解旋转的应用。
假设有一个平面上的点A(2, 3),我们要将这个点绕原点逆时针旋转60度。
根据旋转矩阵的公式,我们可以得到旋转后的坐标B(x, y),计算过程如下:x = 2 * cos60° - 3 * sin60° = 1y = 2 * sin60° + 3 * cos60° = 4.196所以,点A(2, 3)绕原点逆时针旋转60度后的坐标为B(1, 4.196)。
初二物理旋转知识点归纳总结

初二物理旋转知识点归纳总结旋转是物体的一种运动形式,它在我们日常生活中无处不在。
物体的旋转运动涉及到很多重要的物理概念和知识点。
在初二物理学习中,我们学习了许多与旋转相关的内容。
本文将对初二物理旋转知识点进行归纳总结,并深入解释其中的原理与应用。
一、刚体的旋转刚体是指在受到外力作用时形状和大小保持不变的物体。
刚体的旋转运动有以下几个基本概念和原理:1.转轴与转动轴转轴是指物体绕其旋转的轴线,转动轴则是物体旋转时其各个部分所处的轨迹。
在刚体的旋转运动中,转轴和转动轴一般不重合。
2.转动力矩转动力矩是产生旋转运动的力矩。
它与力的大小、作用点到转动轴的距离以及作用方向有关。
转动力矩的大小可以通过以下公式计算:M = F × d其中,M代表转动力矩,F代表力的大小,d代表力的作用点到转动轴的距离。
3.转动惯量物体旋转时具有旋转惯性,刚体旋转的难易程度与其转动惯量有关。
转动惯量与物体的质量以及物体质量分布的形状和大小有关。
常用的转动惯量公式有:I = m × r^2其中,I代表转动惯量,m代表物体的质量,r代表物体质心到转动轴的距离。
二、角度与弧长在物体的旋转运动中,角度和弧长是非常重要的概念。
下面我们将介绍它们的定义和关系:1.角度角度是用来度量旋转程度的物理量。
我们常用度(°)作为角度的单位。
一个完整的圆周角为360°,1°相当于圆周的1/360。
当物体旋转一周时,它的角度为360°。
2.弧长弧长是指在圆周或弧上的一段长度。
我们常用弧度(rad)作为弧长的单位。
一个完整的圆周的弧长为2πr(r为圆的半径),弧长和角度之间的关系可以通过以下公式得到:l = r × θ其中,l代表弧长,r代表圆的半径,θ代表角度。
三、角速度与角加速度角速度和角加速度是描述旋转运动快慢以及加速度大小的物理量。
它们在旋转运动的描述和计算中起着重要作用。
1.角速度角速度是指物体单位时间内旋转的角度。
认识旋转知识点总结初中

认识旋转知识点总结初中一、旋转的基本概念1. 旋转的定义旋转是物体围绕某一固定轴线或者某一固定点进行的运动。
在旋转运动中,物体的各个点围绕着轴线或者固定点进行圆周运动,同时保持相对位置不变。
2. 旋转的方向围绕轴线进行旋转运动的物体,其运动可以是顺时针方向或者逆时针方向。
在物理学中,通常将顺时针方向定为正向,逆时针方向定为负向。
3. 旋转的角度旋转运动可以用角度来描述。
一个完整的旋转是360度,也可以表示为2π弧度。
物体围绕轴线或者固定点所经过的角度称为旋转角。
二、旋转运动的基本定律1. 旋转惯量旋转惯量是描述物体围绕轴线旋转运动的一种物理量,它与物体的质量和几何形状有关。
物体的旋转惯量越大,其旋转运动越难以改变。
2. 角动量在旋转运动中,角动量是描述物体旋转运动的一种物理量,它等于物体的旋转惯量乘以物体围绕轴线旋转的角速度。
3. 旋转运动的动能物体进行旋转运动时,具有旋转动能。
其大小等于物体的旋转惯量乘以物体所具有的角速度的平方再除以2。
4. 角速度角速度是描述物体围绕轴线旋转运动的物理量,它等于物体围绕轴线旋转的角度变化量与时间的比值。
5. 动量定理在旋转运动中,动量定理也适用。
它可以描述物体围绕轴线旋转运动时所受到的力和物体的角加速度之间的关系。
三、旋转运动的应用1. 陀螺的原理陀螺是一种利用旋转运动原理制作的玩具。
它的工作原理是利用陀螺的高速旋转使得陀螺保持一定的平衡状态,从而能够在平滑的表面上保持稳定的旋转运动。
2. 自行车轮的稳定性自行车的骑行稳定性也与旋转运动有关。
自行车前轮的旋转运动可以使得自行车保持稳定的前进方向,而不会出现侧倾的情况。
3. 地球自转和公转运动地球自转和公转运动也是旋转运动的一种应用。
地球每天围绕自己的轴线旋转一圈,并且围绕太阳做公转运动,这些运动都是旋转运动的应用。
四、旋转运动的实验1. 旋转惯量实验通过测量不同物体的旋转惯量,可以观察到物体的形状和质量对旋转惯量的影响,从而了解旋转运动的基本定律。
旋转知识点总结

旋转知识点总结旋转知识点归纳知识点1:旋转的定义及其有关概念在平面内,将一个图形绕一个定点O沿某个方向转动一个角度,这样的图形运动称为旋转。
定点O称为旋转中心,转动的角称为旋转角。
如果图形上的点P经过旋转到点P',那么这两个点叫做这个旋转的对应点。
如图1,线段AB绕点O顺时针转动90度得到AB',这就是旋转,点O就是旋转中心,∠BOB'和∠AOA'都是旋转角。
说明:旋转的范围是在平面内旋转,否则有可能旋转为立体图形,因此“在平面内”这一条件不可忽略。
决定旋转的因素有三个:一是旋转中心;二是旋转角;三是旋转方向。
知识点2:旋转的性质由旋转的定义可知,旋转不改变图形的大小和形状,这说明旋转前后的两个图形是全等的。
由此得到如下性质:⑴经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了相同的角度,对应点的排列次序相同。
⑵任意一对对应点与旋转中心的连线所成的角都是旋转角。
⑶对应点到旋转中心的距离相等。
⑷对应线段相等,对应角相等。
例1:如图2,D是等腰Rt△ABC内一点,BC是斜边,如果将△ADB绕点A逆时针方向旋转到△ADC的位置,则∠ADD'的度数是()。
分析:抓住旋转前后两个三角形的对应边相等、对应角相等等性质,本题就很容易解决。
由△ADC是由△ADB旋转所得,可知△ADB≌△ADC,∴AD=AD',∠DAB=∠D'AC,∵∠DAB+∠___,∴∠D'AC+∠___,∴∠ADD'=45,故选D。
评注:旋转不改变图形的大小与形状,旋转前后的两个图形是全等的,紧紧抓住旋转前后图形之间的全等关系,是解决与旋转有关问题的关键。
知识点3:旋转作图1.明确作图的条件:(1)已知旋转中心;(2)已知旋转方向与旋转角。
2.理解作图的依据:(1)旋转的定义:在平面内,将一个图形绕一个定点O沿某个方向转动一个角度的图形变换叫做旋转;(2)旋转的性质:经过旋转,图形上的每一点都绕旋转中心沿相同的方向转动了相同的角度,任意一对对应点与旋转中心的连线所组成的角都是旋转角,对应点到旋转中心的距离相等。
旋转现象知识点总结

旋转现象知识点总结1. 旋转现象的基本原理旋转现象基本原理是物体围绕自身中心轴进行旋转运动。
这种运动形式是刚体运动的一种,而刚体的旋转运动是以固定点为轴心,刚体的各点都做圆周运动的运动形式。
在旋转中,刚体上所有点都作圆周运动,而且速度和加速度都不相同。
这种运动可以通过角位移、角速度和角加速度来描述。
角位移表示旋转的角度大小,角速度表示旋转的快慢,而角加速度则表示旋转的加速或减速程度。
在物理学中,旋转现象的基本原理受到角动量守恒定律的影响。
根据角动量守恒定律,如果没有外力矩作用,旋转态的角动量守恒,即角动量大小和方向保持不变。
这就意味着在旋转过程中,如果没有外力矩的作用,物体的角速度和角动量会保持不变。
除了角动量守恒,旋转现象还受到转动惯量的影响。
转动惯量是描述物体抵抗转动的能力,它和物体的形状、质量分布有关。
转动惯量的大小和形状、质量分布都有关系,例如,长杆的转动惯量要比球体的小。
转动惯量的大小影响着物体旋转的难易程度,而且其大小还决定了物体在旋转中的动能大小。
2. 旋转现象的应用旋转现象在工程学、医学、航天航空等领域都有着广泛的应用。
在工程学领域,旋转现象被广泛应用于机械系统中,例如发动机、泵、风力发电机等设备。
这些设备都是通过旋转来实现能量转换和传递的。
旋转还在制造业中用于车床、铣床等机床设备,加工工件时通过旋转实现切削加工。
此外,旋转还在交通运输行业中应用广泛,例如汽车、飞机、船舶等交通工具都需要通过发动机和车轮的旋转来实现运动。
在医学方面,旋转现象也有着重要的应用。
例如,MRI(核磁共振成像)技术就是基于旋转原理的一种诊断技术,它通过物质原子核的旋转运动产生信号,来获取人体组织的影像。
此外,旋转还在手术器械、假肢等医疗器械中有着广泛的应用。
在航天航空领域,旋转现象也被广泛应用于飞行器的姿态控制、推进系统等方面。
例如,飞行器通过调整旋转状态来实现姿态控制,通过发动机旋转来产生推进力。
此外,还有卫星、航天飞行器等载具通过旋转来调整轨道、实现定位和导航等任务。
旋转的知识点归纳总结

旋转的知识点归纳总结旋转的知识点主要包括旋转的基本概念、旋转的运动规律、旋转的动力学和静力学分析、以及旋转在工程技术中的应用等方面。
本文将对这些知识点进行系统归纳总结,希望能够帮助读者更全面地理解旋转的相关概念和原理。
一、旋转的基本概念1. 旋转的定义旋转是物体在围绕某一点或轴线上旋转的运动形式。
在旋转过程中,每一个点都有一个不同的速度和加速度,这是与直线运动的显著区别。
在旋转过程中,我们通常用角度来描述物体的位置和方向。
2. 旋转的基本量在描述旋转运动时,我们通常会涉及到一些基本量,比如角度、角速度和角加速度。
角度用来描述物体在旋转过程中沿着轴线或者绕着某一点旋转的程度,通常用弧度或者度来表示。
角速度用来描述物体在旋转过程中单位时间内转过的角度,通常用弧度/秒或者度/秒来表示。
角加速度用来描述物体在旋转过程中单位时间内角速度的变化,通常用弧度/秒^2或者度/秒^2来表示。
3. 旋转的方向在旋转过程中,我们通常也会关注物体旋转的方向。
旋转的方向通常可以用飞轮定则来描述,即如果按照顺时针方向旋转,则对应的角速度和角加速度都为正值,如果按照逆时针方向旋转,则对应的角速度和角加速度都为负值。
二、旋转的运动规律1. 旋转平衡在旋转过程中,物体可能存在平衡和不平衡的情况。
当物体的旋转力矩和惯性矩平衡时,物体就处于旋转平衡状态;否则,物体就处于旋转不平衡状态。
旋转平衡是旋转运动稳定进行的前提,因此对于旋转平衡的分析和判断是非常重要的。
2. 旋转的动力学在旋转运动中,我们通常会涉及到力矩、惯性矩和角加速度等概念。
力矩用来描述物体在旋转过程中受到的力的作用,通常用力和力臂的乘积来表示。
惯性矩用来描述物体在旋转过程中惯性对旋转运动的阻碍程度,通常用质量和半径的平方的乘积来表示。
角加速度用来描述物体在旋转过程中单位时间内角速度的变化,通常用力矩和惯性矩的比值来表示。
根据牛顿第二定律,力矩等于惯性矩乘以角加速度,即力矩=惯性矩*角加速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
旋转知识点归纳
1、旋转的定义及其有关概念: 旋转中心、旋转角、对应点.如图,线
段AB 绕点O 顺时针转动0
90得到B A '',这就是旋转,点O 就是旋转中
心,A AO B BO '∠'∠,都是旋转角.
决定旋转的因素有三个:一是旋转中心;二是旋转角;三是旋转方向.
2、旋转的性质:不改变图形的大小和形状(两个图形是全等的).由此得到如下性质: ⑴经过旋转,图形上的每一点都绕旋转中心沿相同方向转动了相同的角度,对应点的排列次序相同.
⑵任意一对对应点与旋转中心的连线所成的角都是旋转角. ⑶对应点到旋转中心的距离相等. ⑷对应线段相等,对应角相等.
例1 、如图2,D 是等腰Rt △ABC 内一点,BC 是斜边,如果将△ADB 绕点A 逆时针方向旋转到△C D A '的位置,则ADD '∠的度数是()D
A.25o
B.30o
C.35o
D.45o
3、旋转作图:略
4:钟表的旋转问题:钟表的时针与分针每时每刻都以轴心为旋转中心作旋转运动,其中时针
12小时旋转一周,则每小时旋转,301236000=这样时针每分钟旋转;5.00
分针每小时旋转一周,则每分钟旋转.660
36000
= 例3 从1点到1点25分,分针转了多少度角时针转了多少度角1点25分时时针与分针的夹角是多少度
解: 分析:(1)时针每分钟旋转0
5.0;(2)分针每分钟旋转.60
分针旋转的角度为;15025600=⨯时针旋转的角度为;5.12255.000=⨯ 分针与时针的夹角为.5.1075.12301500000=--
A '
图
图2
五.典例剖析
1、如图1,该图形围绕自己的旋转中心,按下列角度旋转后,不能..与其自身重合的是( )
A.72o
B.108o
C.144o D.216o
2、如图2,ABC △是等腰直角三角形,90AB AC BAC ==︒,∠,D 是BC 上一点,ACD △经过
旋转后到达ABE △的位置. (1)旋转中心是哪一点 (2)旋转了多少度
(3)若P 是AC 的中点,那么经过上述旋转后,点P 旋转到了什么位置
(解:(1)点A 是旋转中心;(2)顺时针旋转了90︒;(3)点P 旋转到了AB 的中点.) 3、求旋转90°后点的坐标
例1、如图,在平面直角坐标系中,点A 的坐标为(1,4),将线段OA 绕点O 顺时针旋转90°得到线段OA′,则点A′的坐标是 .
解:如图所示,做出OA 绕点O 顺时针旋转90°后得到的线段OA′,则A ′的坐标为(4,-1)
规律总结:已知点A 的坐标为()a b ,,O 为坐标原点,连结OA ,将线段OA 绕点O 按顺时针方向旋转90°得1OA ,则点1A 的坐标为()b a -,,将线段OA 绕点O 按逆时针方向旋转90°得2A ,则点2A 的坐标为()b a -,, 2、求旋转180°后点的坐标
例2、在平面直角坐标系xOy 中,已知点A (2,3),若将OA 绕原点O 逆时针旋转180°得到0A ′,则点A ′在平面直角坐标系中的位置是在
A 第一象限
B 第二象限 c 第三象限 D 第四象限
图1
B E 图2
规律总结:已知点A 的坐标为()a b ,,O 为坐标原点,连结OA ,将线段OA 绕点O 按顺时针方向(或逆时针方向)旋转180°得1OA ,则点1A 的坐标为,)a b --(, 3、求旋转135°后点的坐标
例3、点A 的坐标为(2,0),把点A 绕着坐标原点顺时针旋转135º到点B ,那么点B 的坐标是 _________ .
解:点A 的坐标为(2,0),则点A 在x 轴的正半轴上,把点A 绕着坐标原点顺时针
旋转135º到点B ,则点B 在第三象限且在第三象限的角平分线上,由于OB =OA 点B 就在边长为1的格点正方形的顶点上,则点B 的坐标为(-1,1)
4、求多次旋转后点的坐标
例4、如图,在直角坐标系中,已知点,,对△连续作旋转变换,依次得到三角形①、②、③、④…,则三角形⑩的直角顶点的坐标为________ 答案(36,0)
旋转常见错解剖析
例1 分析图1的旋转现象. 错解:本题是由图案的
1
4
绕图案中心分别旋转四次,每次旋转90°形成的. 正解:是由一个梯形绕图案中心依次旋转90°,180°,270°而形成的,也可以看做是由两个相邻的梯形绕图案的中心旋转180°而形成的.
二、弄错图形的旋转方向
例2如图2,将网格中的△ABC 绕C 逆时针旋转90°,画出旋转后的图形.
错解:作∠ACD =∠BCE =90°并截取CA /
=CA ,CB /
=CB ;连结CB /
、B /A /
、CA /
就得到了旋转后的图形△CB /A /
.
剖析:这种作法显然没有注意到是逆时针方向旋转,同学们可以按照逆时针方向作一下,看看是不是与图3所示一样. 三、忽视分类讨论
例3在△ABC 中,∠B =45°,∠C =60°,将△ABC 绕点A 旋转30°后与△AB 1C 1重合,求∠BAC 1的度数.
错解:如图4,因为在△ABC 中,∠B =45°,∠C =60°,所以∠BAC =75°.所以∠BAC 1=∠BAC +∠CAC 1=75°+30°=105°.
A A C 1
B 1
C B C C 1 B 1 B 图4 图5
正解:当△ABC 绕点A 逆时针方向旋转30°时,作法同错解;当△ABC 绕点A 顺时针方向旋转30°时,如图9,∠BAC 1=∠BBAC -∠CAC 1=75°-30°=45°.
A A
A /
A /
B B B
/
B /
C C E
D 图2
图3。
