第八章 t检验.
合集下载
医学统计学：第八章 t检验
作为总体指标）
（1）建立检验假设
H0：μ ＝μ0 ，即该托儿所男婴的体重发育状
况与全国九城市的同期水平相同。
H1： μ≠μ0 ，即该托儿所男婴的体重发育状
况与全国九城市的同期水平不同。
α ＝0.05(双侧)
（2）计算u值 本例因总体标准差σ已知，故
可用u检验。
本例n=47, 样本均数=11, 总体均数=11.18,总
验）
一、单样本t检验（样本均数与总体均数比较的t检验）
即样本均数代表的未知总体均数与已知的 总体均数（一般为理论值、标准值或经过大量 观察所得的稳定值等）进行比较。
这时检验统计量t值的计算在H0成立的前提
条件下为：
t X 0
Sn
例3.3 根据调查，已知健康成年男子脉搏的 均数为72次/分钟，某医生在一山区随机测量 了25名健康成年男子脉搏数，求得其均数为 74.2次/分钟，标准差为6.5次/分钟，能否认 为该山区成年男子的脉搏数与一般健康成年 男子的脉搏数不同？
二、配对资料的t检验
配对实验设计得到的资料称为配对资料。
医学科研中配对资料的四种主要类型： ➢ 同一批受试对象治疗前后某些生理、生化指标
的比较； ➢ 同一种样品，采用两种不同的方法进行测定，
来比较两种方法有无不同； ➢ 配对动物试验，各对动物试验结果的比较等。 ➢ 同一观察对象的对称部位。
配对资料的 t 检验
之间收缩压均数有无差别？
（1)建立检验假设
H0：μ1 ＝μ2 ，即该地20～24岁健康女子和
男子之间收缩压均数相同；
H1: μ1≠μ2 ，即该地20～24岁健康女子和男
子之间收缩压均数不同。 α ＝0.05（双侧）
（2）计算u值
（1）建立检验假设
H0：μ ＝μ0 ，即该托儿所男婴的体重发育状
况与全国九城市的同期水平相同。
H1： μ≠μ0 ，即该托儿所男婴的体重发育状
况与全国九城市的同期水平不同。
α ＝0.05(双侧)
（2）计算u值 本例因总体标准差σ已知，故
可用u检验。
本例n=47, 样本均数=11, 总体均数=11.18,总
验）
一、单样本t检验（样本均数与总体均数比较的t检验）
即样本均数代表的未知总体均数与已知的 总体均数（一般为理论值、标准值或经过大量 观察所得的稳定值等）进行比较。
这时检验统计量t值的计算在H0成立的前提
条件下为：
t X 0
Sn
例3.3 根据调查，已知健康成年男子脉搏的 均数为72次/分钟，某医生在一山区随机测量 了25名健康成年男子脉搏数，求得其均数为 74.2次/分钟，标准差为6.5次/分钟，能否认 为该山区成年男子的脉搏数与一般健康成年 男子的脉搏数不同？
二、配对资料的t检验
配对实验设计得到的资料称为配对资料。
医学科研中配对资料的四种主要类型： ➢ 同一批受试对象治疗前后某些生理、生化指标
的比较； ➢ 同一种样品，采用两种不同的方法进行测定，
来比较两种方法有无不同； ➢ 配对动物试验，各对动物试验结果的比较等。 ➢ 同一观察对象的对称部位。
配对资料的 t 检验
之间收缩压均数有无差别？
（1)建立检验假设
H0：μ1 ＝μ2 ，即该地20～24岁健康女子和
男子之间收缩压均数相同；
H1: μ1≠μ2 ，即该地20～24岁健康女子和男
子之间收缩压均数不同。 α ＝0.05（双侧）
（2）计算u值
医学统计学第3版第八章t检验
⑴ 建立检验假设，确定检验水准 H0:µd=0，即两方法检测结果相同 H1:µd≠0，即两方法检测结果不同
α= 0.05 ,双侧检验
⑵ 选定检验方法，计算检验统计量 根据题目资料类型，可见，该资料差值构成样本与总体之间的比较，可用样本-总
体的t检验。依公式计算检验统计量：
d2 ( d)2 3882(130)2
4
13.3
5
12.0
6
12.0
7
14.6
8
14.6
9
12.0
10 12.3
合计
பைடு நூலகம்12.0 13.3 10.6 12.0 12.0 10.6 10.6 14.6 12.7 13.3 Σd =12.7
4.0 -1.3 4.0 1.3 0.0 1.4 4.0 0.0 -0.7 0.00 Σd2 =53.83
16.00 1.69 16.00 1.69 0.00 1.96 16.00 0.00 0.49 0.00
⑴ 建立检验假设，确定检验水准 H0:µd=0，即手术前后舒张压无变化 H1:µd≠0，即手术前后舒张压有变化
α= 0.05 ,双侧检验
⑵ 选定检验方法，计算检验统计量 根据题目资料类型，可见，该资料差值构成样本与总体之间的比较，可用样本-总
s
x2(x)/n
107.397(11.376)2/12 0.29
n1
121
txu0 9.489.32.15 s/ n 0.29/ 12
n112111
（3）确定P 值，作出统计推断
以
查t 界值表，得单测t0.05,11= 1.796，
11 本案例的统计量t = 2.15＞1.796，因此P ＜ 0.05,
5 t检验
– 自身对照(self control)
• 同一对象(生物学标本)分两份接受不同处理 • 同一对象身体不同部位分别接受不同处理 • 同一对象接受处理或不同阶段前后
应用条件及其考察 不满足条件时的处理 本章总结 本章要求 课后作业
返回
配对设计观察性研究
概念和用途
• 研究血清IL-6与银屑病的关系
– 处于进行期的银屑病患者与正常人 – 血清标本进行IL-6 – 考虑性别、年龄的影响
未知 d ~ N ( , d2 )
d 0 t ~ t (n 1) Sd
例题分析
• 分析目的：儿童皮肤对两种不同结核菌素的反应性有无差别
– 研究假设：儿童皮肤对两种不同结核菌素的反 应性不同，即差值不等于0
• 若差值服从正态分布，即d0
• 设计方法：试验研究，配对设计 • 效应指标变量类型：定量变量 • 已知条件：样本数据
2.已知 d 15.6g/L，若进行假设检验，关于H0的说法正确的是：
3.若计算结果t =2.15，经查表 t0.05/2, 8=2.31、t0.05, 8=1.86，按 =0.05 水准，下列说法正确的是：
A 由于2.15<2.31，P>0.05，与11g/L的差异无统计学意义
1 2 3 4 5 6 7 8 9 10 11 12 … ∞
单侧 双侧
0.250 0.Biblioteka 00 1.000 0.816 0.765 0.741
0.200 0.400 1.376 1.061 0.978 0.941
0.100 0.200 3.078 1.886 1.638 1.533
0.150 0.300 1.963 1.386 1.250 1.190
第8章思考与练习0801217
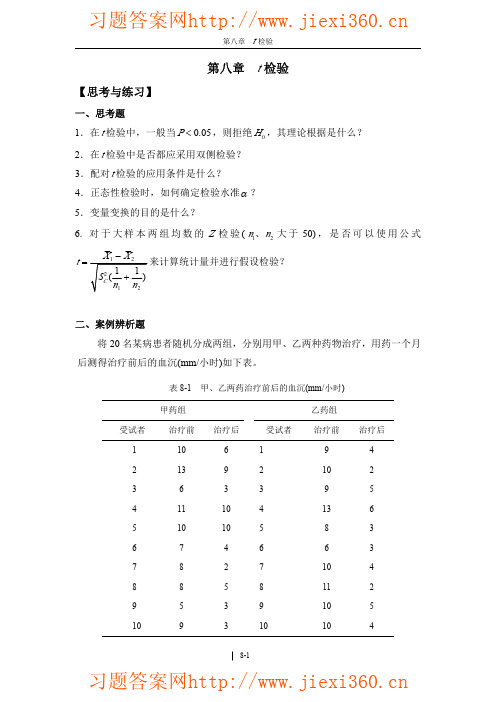
Z KURT = 0.360 1.334 < 1.96 Z KURT = 0.232 1.334 < 1.96
故，甲药，、乙药两组资料的差值 d1、d 2 均服从正态分布。 (2) 方差齐性检验 1) 建立检验假设，确定检验水准
2 ，两差值总体方差相等 H 0 ：σ 12 = σ 2
2 ，两差值总体方差不等 H1：σ 12 ≠ σ 2
g d Valid N (listwise) d Valid N (listwise)
Group Statist ic s Std. Error Std. Deviation Mean 1.93218 .61101 1.81353 .57349
g d
N 10 10
Mean 3.2000 5.8000
8-3
习题答案网
习题答案网
第八章
t 检验
7. 为研究两种方法的检测效果，将 24 名患者配成 12 对，采用配对 t 检验进行统 计分析，则其自由度为： A. 24 B. 12 C. 11 D. 23 E. 2 四、综合分析题 1. 大量研究表明健康成年男子脉搏的均数为 72 次/min。某医生在某山区随机调 查了 16 名健康成年男子，测得其脉搏(次/min)资料如下： 69 72 74 68 73 74 80 73 75 74 73 75 74 79 72 74
Z KURT = 1.403 1.334 < 1.96 Z KURT = 0.751 1.334 < 1.96
Z SKEW = 0.088 0.687 < 1.96
故，甲、乙两组资料均服从正态分布。 (2) 假设检验
2 2 由甲、乙两组数据得： X甲 = 5.5， X 乙 = 3.8， S甲 = 3.12 ， S乙 = 1.32
医学统计学第七、八章 假设检验的基本概念和t检验
S x 1 − x 2 为两样本均数差值的标准误
Sx −x
1
2
⎛1 1⎞ ⎟ = S ⎜ + ⎜n n ⎟ 2 ⎠ ⎝ 1
2 c
在两总体方差相等的条件下，可将两方差合并， 求合并方差(pooled variance) S c2
2 ⎡ ( Σ x1 ) ⎤ 2 ⎢ Σ x1 − ⎥ + n1 ⎦ ⎣ = n1 − 1 + 2 ⎡ ( Σx2 ) ⎤ 2 ⎢Σ x2 − ⎥ n2 ⎦ ⎣ n2 − 1
t 检验的应用条件:
① 单样本t检验中，σ 未知且n 较小，样本取自 正态总体； ② 两小样本均数比较时，两样本均来自正态分 布总体，两样本的总体方差相等；若两总体 方差不齐可用t’检验； ③ 两大样本均数比较时，可用Z检验。
1、样本均数与总体均数比较的 t 检验
• 使用范围：用于样本均数与已知总体均数（一 般为理论值、标准值或经过大量观察所得的稳 定值等）的比较。 • 分析目的：推断样本所代表的未知总体均数 μ 与已知总体均数 μ0有无差别。 • 若 n 较大，则 tα .ν ≈ tα .∞ , 可按算得的 t 值用 v = ∞ 查 t 界值表( t 即为 Z )得P值。
回到例子:
2.计算统计量
已知μ0＝ 3min，n＝50, X=4min
4−3 t= = 4 .7140 1 .5 / 50
υ = 50 − 1 = 49
3、确定 P 值，作出统计推断 根据算出的检验统计量如 t、z 值，查 相应的界值表，即可得到概率 P。 P值是在H0成立前提下，抽得比现有样 本统计量更极端的统计量值的概率。 P值越小只能说明：作出拒绝H0 ，接受 H1的统计学证据越充分。
X −μ X −μ 用公式：t = 或z = σX SX
第八章t检验6讲
数均数的标准误。
2020/6/7
8
例8.2 对24名接种卡介苗。胺同年龄、同性别配成12对， 每对重的2名儿童分别接种两种结核菌素，一种为标准品，另 一种为新制品。72小时后记录两种结核菌素的皮肤反应平均 直径，数据见表8.1。问儿童对两种不同结核菌素的皮肤反应 直径有无不同？
（1）建立检验假设 ，确定检验水准
2020/6/7
12
S 2 (n1 1)S12 (n2 1)S22 n1 n2 2
上式如果n1=n2，则
S X1X 2
S12
S
2 2
n1 n2
t | X1 X2 | S12 S22 n1 n2
2020/6/7
13
例8.3 某医生研究血清白介素-6（IL-6）与银屑病的关系， 见表8.2结果。问银屑病患者与正常人的血清IL-6平均水平是否 不同？
2020/6/7
21
2020/6/7
22
(二) 统计检验法 1.W检验和D检验：两种方法的检验假设为： H0：样本来自正态分布，H1：样本不来自正态分布。 由于两种方法的计算公式繁琐，一般用SAS或SPSS统计软
件处理，当P>0.05，则不拒绝H0； P≤0.05，则拒绝H0。
注意：SAS规定，当样本含量n ≤2000时，以W检验结果为 准；当样本含量n >2000时，以D检验结果为准。
2020/6/7
23
如例4.2 120名9岁男孩的肺活量资料，通过SAS进行正 态性检验，其结果如下：
2020/6/7
24
2.矩法检验 分别对总体分布的偏度和峰度进行检验。
(1)偏度检验：主要计算偏度系数（coefficient of skewness ,SKEW），一般用g1来表示。检验假设为：
2020/6/7
8
例8.2 对24名接种卡介苗。胺同年龄、同性别配成12对， 每对重的2名儿童分别接种两种结核菌素，一种为标准品，另 一种为新制品。72小时后记录两种结核菌素的皮肤反应平均 直径，数据见表8.1。问儿童对两种不同结核菌素的皮肤反应 直径有无不同？
（1）建立检验假设 ，确定检验水准
2020/6/7
12
S 2 (n1 1)S12 (n2 1)S22 n1 n2 2
上式如果n1=n2，则
S X1X 2
S12
S
2 2
n1 n2
t | X1 X2 | S12 S22 n1 n2
2020/6/7
13
例8.3 某医生研究血清白介素-6（IL-6）与银屑病的关系， 见表8.2结果。问银屑病患者与正常人的血清IL-6平均水平是否 不同？
2020/6/7
21
2020/6/7
22
(二) 统计检验法 1.W检验和D检验：两种方法的检验假设为： H0：样本来自正态分布，H1：样本不来自正态分布。 由于两种方法的计算公式繁琐，一般用SAS或SPSS统计软
件处理，当P>0.05，则不拒绝H0； P≤0.05，则拒绝H0。
注意：SAS规定，当样本含量n ≤2000时，以W检验结果为 准；当样本含量n >2000时，以D检验结果为准。
2020/6/7
23
如例4.2 120名9岁男孩的肺活量资料，通过SAS进行正 态性检验，其结果如下：
2020/6/7
24
2.矩法检验 分别对总体分布的偏度和峰度进行检验。
(1)偏度检验：主要计算偏度系数（coefficient of skewness ,SKEW），一般用g1来表示。检验假设为：
第八章 t检验(6讲)
7
配对资料的t检验(paired samples t-test)先求出各对子的差值d的均值 , 若两种处理的效应无差别，理论上
差值d的总体均数 应为0。所以这类资料的比较可看作是样本均数
d 分布为正态分布。t检验的公式为：
d
与总体均数0的比较。要求差值的总体
d
t | d d | | d 0 | | d |
第八章 t 检验 景学安
2019/12/29
1
[学习要求] 了解：正态性检验和变量变换的基本概念。 熟悉：方差齐性检验的基本概念；两样本方差齐性检验的计算；t’检验的计算。 掌握：t检验的步骤和t分布的关系；样本均数和总体均数比较、配对设计均数的比较、两样本均 数的比较t检验的方法与步骤。
2019/12/29
2
t检验（t test）亦称Student’s t test，是以t分布理论为基础，定量资料分析常用的假设检验方法。小样本的样 本均数与总体均数的比较以及两个样本均数的比较要用t检验。t 检验的适用条件：①样本来自正态总体或近似 正态总体；②两样本总体方差相等。
第一节 样本均数与总体均数的比较
亦称为单样本t检验（one sample t-test）。即样本均数代表的未知总体均数μ与已知的总体均数μ0（一般为 理论值、标准值或经过大量观察所得的稳定值等）进行比较。
2019/12/29
10
第三节 两样本均数比较
两本均数比较的t检验亦称为成组t检验，又称为独立样本t检验（independent samples t-test）。适用于比较
按完全随机设计而得到的两组资料，比较的目的是推断两样本均数各自所代表的总体均数μ1和μ2是否相等。两 样本含量可以相等也可以不相等，但在总例数不变的条件下，当两样本含量相等时，统计检验的效率最高。本
第8章t检验
第八章 t 检验t 检验(t test)亦称Student’s t 检验，是以t 分布为基础定量资料分析中常用的假设检验方法，用于两均数间的比较。
t 检验的应用条件为：①在单样本t 检验中，总体标准差σ未知且样本含量较小，要求样本来自正态分布总体；②配对t 检验是单样本t 检验的特殊情况，配对设计是指同质受试对象配成对子分别接受两种不同处理或同一受试对象分别接受两种不同处理；③两小样本均数比较时，要求两样本均来自正态分布总体，且两样本总体方差相等；若两样本总体方差不相等，则用t '检验；④对两大样本(12n n 、均大于50)的均数比较，可用Z 检验。
但在实际应用时，与上述条件略有偏差，只要其分布为单峰且近似对称分布即可。
第一节 样本均数与总体均数的比较样本与总体均数比较的检验亦称为单样本t 检验(one sample t test)，用于样本均数代表的未知总体均数μ与已知总体均数0μ(一般为理论值或标准值)的比较。
在00:H μμ=成立的条件下，检验统计量的计算公式如下01X X X t v n S μ-===- (8.1) 式中，X 为样本均数，S 为样本标准差，v 为自由度。
例8.1 已知某地新生儿出生体重均数为3.36 kg 。
从该地农村随机抽取40名新生儿，测得其平均体重为3.27 kg ，标准差为0.44 kg ，问该地农村新生儿出生体重是否与该地新生儿平均出生体重不同？1．建立检验假设，确定检验水准0: 3.36H μ=，该地农村新生儿体重与该地新生儿平均出生体重相同 1: 3.36H μ≠，该地农村新生儿体重与该地新生儿平均出生体重不同0.05α=2．计算检验统计量 由式(8.1)，得1.294140139X X X t S v n μ-====-=-=-= 3．确定P 值，作出统计推断根据39v =和 1.294t =-的绝对值查t 界值表(附表3)，得0.20.4P <<，则按0.05α=的检验水准，不拒绝0H ，差异无统计学意义，尚不能认为该地农村新生儿体重与该地新生儿平均出生体重不同。
第八章 t检验
S n 7.2 16 1.8 查 附 表 2 t 界 值 表 得 ， t0.05/2(15)= 2.131， t > t0.05/2(15)，
P<,拒 绝 H0， 接 受 H1。 认 为 常 年 锻 炼 的 中 学 男 生 心 率
与一般中学男生不同。
f (t)
P ＝0.0003
－4.65
0t
4.65
H1： 孪 生 兄 弟 体 重 不 同 ， 即 d 0。
双 侧 检 验 ,=0.05
d
=0.063，
s d
=0.027，
n=15。
将
数
据
代
入
式
(5-3)得
t 0.063 0 0.063 2.33
0.104 15 0.027
, =n-1=14
查 附 表 2t 界 值 表 得 ， t0.05/2(14)=， t t0.05/2(14) =2.145，
尚不能认为两种药的疗效不等。
第四节 正态性检验与方差齐性检验
正态性检验：即检验样本是否来自正态 总体。
检验方法：
1.图示法：方格坐标纸图
正态概率纸图
P-P图：若所分析数据服从 正态分布，则在P-P图上数据点应在左 下到右上的对角直线上。
优点：简单易行。 缺点：较粗糙。
2.统计检验方法 （1)W检验：适用于n≤50 (2) 矩法检验：分别对总体的偏度和 分度进行检验
当t<t/2()时，P>，不拒绝H0。
例 5-5 表 5-2 国 产 与 进 口 两 药 物 治 疗 绝 经 后 妇 女
骨 质 疏 松 症 第 2-4 腰 椎 骨 密 度 改 善 值 (mg/cm2)
国产药
进口药
P<,拒 绝 H0， 接 受 H1。 认 为 常 年 锻 炼 的 中 学 男 生 心 率
与一般中学男生不同。
f (t)
P ＝0.0003
－4.65
0t
4.65
H1： 孪 生 兄 弟 体 重 不 同 ， 即 d 0。
双 侧 检 验 ,=0.05
d
=0.063，
s d
=0.027，
n=15。
将
数
据
代
入
式
(5-3)得
t 0.063 0 0.063 2.33
0.104 15 0.027
, =n-1=14
查 附 表 2t 界 值 表 得 ， t0.05/2(14)=， t t0.05/2(14) =2.145，
尚不能认为两种药的疗效不等。
第四节 正态性检验与方差齐性检验
正态性检验：即检验样本是否来自正态 总体。
检验方法：
1.图示法：方格坐标纸图
正态概率纸图
P-P图：若所分析数据服从 正态分布，则在P-P图上数据点应在左 下到右上的对角直线上。
优点：简单易行。 缺点：较粗糙。
2.统计检验方法 （1)W检验：适用于n≤50 (2) 矩法检验：分别对总体的偏度和 分度进行检验
当t<t/2()时，P>，不拒绝H0。
例 5-5 表 5-2 国 产 与 进 口 两 药 物 治 疗 绝 经 后 妇 女
骨 质 疏 松 症 第 2-4 腰 椎 骨 密 度 改 善 值 (mg/cm2)
国产药
进口药
医学统计学——t检验课件
医学统计学——t检验课件xx年xx月xx日contents •t检验的基本概念•t检验的原理•t检验的步骤•t检验的应用•t检验的注意事项•t检验的实例演示目录01 t检验的基本概念统计假设检验的一种，用于比较两个独立样本的平均数是否有显著差异，或一个样本的平均数与一个已知的参考值之间是否有显著差异。
t检验常用于小样本数据，特别是两个独立样本的比较。
t检验的定义t检验的适用范围适用于小样本数据，特别是两个独立样本的比较；常用于检验一个样本的平均数与一个已知的参考值之间是否有显著差异；可用于二分类变量和等级变量的比较。
两个独立样本来自的总体服从正态分布；两个独立样本来自的总体方差相等；样本数据是随机样本。
t检验的假设条件02 t检验的原理两独立样本t检验适用条件样本应来自正态分布总体，且方差相等。
结果解释根据t值和自由度，结合临界值表，确定P值，判断是否拒绝原假设。
统计假设比较两组独立样本的均值是否存在显著差异，即H0：μ1=μ2与H1：μ1≠μ2。
两配对样本t检验统计假设比较两组配对样本的差值均值是否显著非零，即H0：μ1-μ2=0与H1：μ1-μ2≠0。
适用条件样本应来自正态分布总体，且方差相等。
结果解释根据t值和自由度，结合临界值表，确定P值，判断是否拒绝原假设。
单因素方差分析t检验统计假设比较三组或多组独立样本的均值是否存在显著差异，即H0：μ1=μ2=…=μn与H1：μ1≠μ2≠…≠μn。
适用条件样本应来自正态分布总体，且方差相等。
结果解释根据F值和自由度，结合临界值表，确定P值，判断是否拒绝原假设。
如果P值小于预设显著性水平α，则认为各组均值存在显著差异；否则，认为无显著差异。
03 t检验的步骤明确研究目的明确研究目的是t检验的首要步骤，决定了数据的类型和数量。
数据筛选对数据进行筛选，去除异常值和缺失值，以确保数据的有效性和可靠性。
数据分组根据研究目的，将数据分成两组或以上，以便进行比较和分析。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
95th%ethDCeiofDfneifrfiefdenercenencceeInterval of
LowLeorwer the DiffeUrepUnpceperper
Lo.1w5e.31r53
1U.0p12p.40e2r4
8
.014
.5889
.153
1.024
图6-5 例6-1独立样本检验结果
图8-5 例8-1独立样本检验结果
应用条件： ① 样本个体测量值相互独立。 ② 两 个样本所代表的总体均数均服从正态分布，即正 态性(normality)。 ③两总体方差相等，即方差齐 性(homogeneity of variance)。
【例8-3】 测定功能性子宫出血症中实热组与虚寒组的免 疫功能，其淋巴细胞转化率如表8-2.试比较实热组与虚寒 组的淋巴细胞转化率均数是否不同。
第二节 配对设计资料均数的t检验
配对设计：将受试对象按某些重要特征相同或相近的原 则配成对子（以消除其对研究结果的影响），再将每对 中的个体按随机分配的原则给予不同的处理。 配对设计可以减小实验误差，提高研究效率。
配对设计的几种类型： ① 同一对的两个受试对象分别接受不同处理 ② 同一样品用两种不同方法测试 ③ 同一受试对象处理前后的比较或不同部位测定值比较
n 1 9 1 8 ③ 确定P值、作出统计推论。
t＞t0.05/2，8＝2.306，P<0.05
weigwhetight
weight
tt
t 3.1138.118
3.118
OnOOen-nSeea-SmapmlepplTleeesTTetesstt
TesTteVsatlVuealu=e8=.98.9
Lower -3.487
Upper 22.154
图8-10 例8-2配对检验结果
t 1.602
Sig. df (2-tailed)
11
.137
第三节 独立样本的方差齐性检验与t检验
独立样本t检验：亦称两样本t检验或成组t检验， 适用于完全随机化设计两独立样本的均数比较。
目的：检验两独立样本均数所代表的未知总体均 数是否有差别。
Test Value = 8.9
df df
SigS. i(g2-.t(a2i-letadi)led) MeManeDaniffDeirfefenrceence
df 8 8 Sig. (2-t.a0i1le4.0d1)4 Mean Dif.f5e8r.8e59n8c89e
95%95C%oCnfoidnefindceencIneteInrtvearlvoafl of
第八章 t检验
t检验的应用条件
① 每个样本来自正态或近似正态总体 ② 两样本均数比较时，还要求相应的两总体方差齐
同。
第一节 单样本t检验
目的：用于从正态总体中获得一份含量为n的样本，算得 均数和标准差，判断其总体均数是否与某个已知总体均数 相同。
已知总体均数：一般为标准值、理论值或经大量观察得到 的较稳定的指标值。
a. Lil li efors Si gni fi cance Correcti on
图6-3 例6-1正态性检验结果
图8-3 例8-1正态性检验结果
Sig. .832
（2）单样本t检验
① 建立检验假设、确定检验水准： H0 ： = 0 H1 ： 0 ＝0.05
② 选择检验方法、计算统计量：
t x 0 s n 9.49 8.9 0.57 9 3.118
t＜t0.05/2，11＝2.201 ，P>0.05
Paired Samples Test
PairPaired Differences
Std. Deviation
20.178
Std. Error Mean 5.825
95% Confidence Interval of the Difference
原法 60 142 195 80 242 220 190 25 212 38 236 95
新法 80 152 243 82 240 220 205 38 243 44 200 100
差值d 20
10 48
2
-2
0
15 13 31
6 -36
5
统计量t的计算公式
t d 0 sd n
n 1
应用条件：变量的差值服从正态分布。
解：（1）单样本的正态性检验
Tests of Normality
a
Kolmogorov-Smirnov
Shapiro-Wilk
weight
Statistic .153
df 9
Sig. .200*
Statistic .963
df 9
*. T hi s is a l ower bound of the true significance.
例8.2的假设检验
（1）研究变量的差值d的的正态性检验
Tests of Normality
a
Kolmogorov-Smirnov
(
Statistic
df
Sig.
d
.204
12
.181
a. Liliefors Significance Correction
Shapiro-Wilk
Statistic .931
【例 8-2】 对 12 份血清分别用原方法(检测时间 20 分钟)和新方法(检测时间 10 分钟)
测谷丙转氨酶( nmol • s1 / L )，结果见表 6-1。问两法所得结果有无差别？
表8-1 两种方法测得12份血清的谷丙转氨酶含量( nmol • s1 / L )
编号
1
2
3
4
5
6
7
8
9
10 11 12
应用条件：资料服从正态分布或近似正态分布。
统计量t的计算公式：
t x 0 s n
=n-1
【例8-1】 某中药厂用旧设备生产的六味地黄丸，药丸重的 均数是8.9g，更新设备后，从所生产的产品中随机抽取9 丸，其重量为：9.2，10.0，9.6，9.8，8.6，10.3，9.9， 9.1，8.9g。问：设备更新后生产的丸药的平均重量有无 变化？
df 12
图8-9 例8-2正态性检验结果
Sig. .392
（2）配对设计数值变量的t检验
① 建立检验假设、确定检验水准：
H0 ： d 0 H1 ： d 0
＝0.05 ② 选择检验方法、计算统计量：
t d 0 s n 9.33 0 20.18 12 1.602
ν＝11
③ 确定P值、作出统计推论。
LowLeorwer the DiffeUrepUnpceperper
Lo.1w5e.31r53
1U.0p12p.40e2r4
8
.014
.5889
.153
1.024
图6-5 例6-1独立样本检验结果
图8-5 例8-1独立样本检验结果
应用条件： ① 样本个体测量值相互独立。 ② 两 个样本所代表的总体均数均服从正态分布，即正 态性(normality)。 ③两总体方差相等，即方差齐 性(homogeneity of variance)。
【例8-3】 测定功能性子宫出血症中实热组与虚寒组的免 疫功能，其淋巴细胞转化率如表8-2.试比较实热组与虚寒 组的淋巴细胞转化率均数是否不同。
第二节 配对设计资料均数的t检验
配对设计：将受试对象按某些重要特征相同或相近的原 则配成对子（以消除其对研究结果的影响），再将每对 中的个体按随机分配的原则给予不同的处理。 配对设计可以减小实验误差，提高研究效率。
配对设计的几种类型： ① 同一对的两个受试对象分别接受不同处理 ② 同一样品用两种不同方法测试 ③ 同一受试对象处理前后的比较或不同部位测定值比较
n 1 9 1 8 ③ 确定P值、作出统计推论。
t＞t0.05/2，8＝2.306，P<0.05
weigwhetight
weight
tt
t 3.1138.118
3.118
OnOOen-nSeea-SmapmlepplTleeesTTetesstt
TesTteVsatlVuealu=e8=.98.9
Lower -3.487
Upper 22.154
图8-10 例8-2配对检验结果
t 1.602
Sig. df (2-tailed)
11
.137
第三节 独立样本的方差齐性检验与t检验
独立样本t检验：亦称两样本t检验或成组t检验， 适用于完全随机化设计两独立样本的均数比较。
目的：检验两独立样本均数所代表的未知总体均 数是否有差别。
Test Value = 8.9
df df
SigS. i(g2-.t(a2i-letadi)led) MeManeDaniffDeirfefenrceence
df 8 8 Sig. (2-t.a0i1le4.0d1)4 Mean Dif.f5e8r.8e59n8c89e
95%95C%oCnfoidnefindceencIneteInrtvearlvoafl of
第八章 t检验
t检验的应用条件
① 每个样本来自正态或近似正态总体 ② 两样本均数比较时，还要求相应的两总体方差齐
同。
第一节 单样本t检验
目的：用于从正态总体中获得一份含量为n的样本，算得 均数和标准差，判断其总体均数是否与某个已知总体均数 相同。
已知总体均数：一般为标准值、理论值或经大量观察得到 的较稳定的指标值。
a. Lil li efors Si gni fi cance Correcti on
图6-3 例6-1正态性检验结果
图8-3 例8-1正态性检验结果
Sig. .832
（2）单样本t检验
① 建立检验假设、确定检验水准： H0 ： = 0 H1 ： 0 ＝0.05
② 选择检验方法、计算统计量：
t x 0 s n 9.49 8.9 0.57 9 3.118
t＜t0.05/2，11＝2.201 ，P>0.05
Paired Samples Test
PairPaired Differences
Std. Deviation
20.178
Std. Error Mean 5.825
95% Confidence Interval of the Difference
原法 60 142 195 80 242 220 190 25 212 38 236 95
新法 80 152 243 82 240 220 205 38 243 44 200 100
差值d 20
10 48
2
-2
0
15 13 31
6 -36
5
统计量t的计算公式
t d 0 sd n
n 1
应用条件：变量的差值服从正态分布。
解：（1）单样本的正态性检验
Tests of Normality
a
Kolmogorov-Smirnov
Shapiro-Wilk
weight
Statistic .153
df 9
Sig. .200*
Statistic .963
df 9
*. T hi s is a l ower bound of the true significance.
例8.2的假设检验
（1）研究变量的差值d的的正态性检验
Tests of Normality
a
Kolmogorov-Smirnov
(
Statistic
df
Sig.
d
.204
12
.181
a. Liliefors Significance Correction
Shapiro-Wilk
Statistic .931
【例 8-2】 对 12 份血清分别用原方法(检测时间 20 分钟)和新方法(检测时间 10 分钟)
测谷丙转氨酶( nmol • s1 / L )，结果见表 6-1。问两法所得结果有无差别？
表8-1 两种方法测得12份血清的谷丙转氨酶含量( nmol • s1 / L )
编号
1
2
3
4
5
6
7
8
9
10 11 12
应用条件：资料服从正态分布或近似正态分布。
统计量t的计算公式：
t x 0 s n
=n-1
【例8-1】 某中药厂用旧设备生产的六味地黄丸，药丸重的 均数是8.9g，更新设备后，从所生产的产品中随机抽取9 丸，其重量为：9.2，10.0，9.6，9.8，8.6，10.3，9.9， 9.1，8.9g。问：设备更新后生产的丸药的平均重量有无 变化？
df 12
图8-9 例8-2正态性检验结果
Sig. .392
（2）配对设计数值变量的t检验
① 建立检验假设、确定检验水准：
H0 ： d 0 H1 ： d 0
＝0.05 ② 选择检验方法、计算统计量：
t d 0 s n 9.33 0 20.18 12 1.602
ν＝11
③ 确定P值、作出统计推论。