江苏省灌南县实验中学九年级数学《第三章小结与思考》练习题(无答案) 人教新课标版
九年级数学上学期10月练习试卷5含解析新人教版

2015-2016学年江苏省连云港市灌南实验中学九年级(上)练习数学试卷5一、选择1.下列直线是圆的切线的是()A.与圆有公共点的直线B.到圆心的距离等于半径的直线C.到圆心的距离大于半径的直线D.到圆心的距离小于半径的直线2.⊙O的半径为R,直线l与⊙O有公共点,如果圆心到直线l的距离为d,那么d与R的大小关系是()A.d≥R B.d≤R C.d>R D.d<R3.Rt△ABC中,∠C=90°,AC=3,CB=4,给出下列三个结论:①以点C为圆心,1.3长为半径的圆与AB相离;②以点C为圆心,2.4长为半径的圆与AB相切;③以点C为圆心,2.5长为半径的圆与AB相交.上述结论正确的个数是()A.0个B.1个C.2个D.3个4.已知⊙O的半径为3cm,点P是直线l上一点,OP长为5cm,则直线l与⊙O的位置关系为()A.相交B.相切C.相离D.相交、相切、相离都有可能5.已知Rt△ABC的直角边AC=BC=4cm,若以C为圆心,以3cm为半径作圆,则这个圆与斜边AB所在直线的位置关系是()A.相交B.相切C.相离D.不能确定6.如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与∠A的关系是()A.∠FDE与∠A相等B.∠FDE与∠A互补C.∠FDE与∠A互余D.无法确定7.如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,AB=4,OM=1,则PA的长为()A.B.C.2 D.4三、解答题8.如图.⊙O的半径为2,AB、AC是⊙O的两条弦,AB=2,AC=4,如果以O为圆心,作一个与直线AC相切的圆,那么:(1)所作的圆的半径是多少?(2)所作的圆与直线AB有怎样的位置关系?为什么?9.在某张航海图上,标明了三个观测点的坐标,如图,O(0,0),B(6,0),C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.(1)求圆形区域的面积;(2)某时刻海面上出现一渔船A,在观察点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,那么当渔船A向正西方向航行时,是否会进入海洋生物保护区?10.如图,AB是⊙O的直径,AC=AB,⊙O交BC于D.DE⊥AC于E,DE是⊙O的切线吗?为什么?11.已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.求证:(1)AD=BD;(2)DF是⊙O的切线.12.已知:如图⊙O是Rt△CDE的外接圆,BC⊥CE,BD和CE的延长线交于点A,且OB∥ED.(1)求证:AD是⊙O的切线;(2)若BC=6,AD=4,求⊙O的半径r.13.如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.求证:(1)AC是⊙D的切线;(2)AB+EB=AC.14.如图:AB是⊙O的直径,以OA为直径的⊙O1与⊙O的弦AC相交于D,DE⊥OC,垂足为E.(1)求证:AD=DC;(2)求证:DE是⊙O1的切线;(3)如果OE=EC,请判断四边形O1OED是什么四边形,并证明你的结论.15.由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴的侵袭.近日,A城气象局测得沙尘暴中心在A城的正西方向240km的B处,以每时12km的速度向北偏东60°方向移动,距沙尘暴中心150km的范围为受影响区域.(1)A城是否受到这次沙尘暴的影响?为什么?(2)若A城受这次沙尘暴影响,那么遭受影响的时间有多长?16.如图,已知PA,PB为⊙O的切线,A,B为切点,∠P=60°.AB=4,求∠C的度数和⊙O 的半径.17.如图,I是△ABC的内心,∠BAC的平分线和△ABC的外接圆相交于点D.BD与ID相等吗?为什么?2015-2016学年江苏省连云港市灌南实验中学九年级(上)练习数学试卷5(10月份)参考答案与试题解析一、选择1.下列直线是圆的切线的是()A.与圆有公共点的直线B.到圆心的距离等于半径的直线C.到圆心的距离大于半径的直线D.到圆心的距离小于半径的直线【考点】切线的判定.【分析】根据切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线,可判定C、D错误;由切线的定义:到圆心距离等于圆的半径的直线是圆的切线,可判定A错误,B正确.注意排除法在解选择题中的应用.【解答】解:A、与圆只有一个交点的直线是圆的切线,故本选项错误;B、到圆心距离等于圆的半径的直线是圆的切线,故本选项正确;C、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误;D、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误.故选B.【点评】此题考查了切线的判定.此题难度不大,注意掌握切线的判定定理与切线的定义是解此题的关键2.⊙O的半径为R,直线l与⊙O有公共点,如果圆心到直线l的距离为d,那么d与R的大小关系是()A.d≥R B.d≤R C.d>R D.d<R【考点】直线与圆的位置关系.【分析】直接根据直线与圆的位置关系进行解答即可.【解答】解:∵直线l与⊙O有公共点,∴直线与圆相切或相交,即d≤R.故选B.【点评】本题考查的是直线与圆的位置关系,即判断直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,当d<r时,直线l和⊙O相交;当d=r时,直线l和⊙O 相切;当d>r时,直线l和⊙O相离.3.Rt△ABC中,∠C=90°,AC=3,CB=4,给出下列三个结论:①以点C为圆心,1.3长为半径的圆与AB相离;②以点C为圆心,2.4长为半径的圆与AB相切;③以点C为圆心,2.5长为半径的圆与AB相交.上述结论正确的个数是()A.0个B.1个C.2个D.3个【考点】直线与圆的位置关系.【分析】根据题意可以求得斜边AB的长度及斜边AB上的高的长度,从而可以判断题目中的三个判断是否正确,从而可以解答本题.【解答】解:∵在Rt△ABC中,∠C=90°,AC=3,CB=4,∴AB==5,∴斜边AB上的高是:,∴以点C为圆心,1.3长为半径的圆与AB相离,故①正确;以点C为圆心,2.4长为半径的圆与AB相切,故②正确;以点C为圆心,2.5长为半径的圆与AB相交,故③正确;故选D.【点评】本题考查直线与圆的位置关系,解题的关键是明确题意,找出所求问题需要的条件.4.已知⊙O的半径为3cm,点P是直线l上一点,OP长为5cm,则直线l与⊙O的位置关系为()A.相交B.相切C.相离D.相交、相切、相离都有可能【考点】直线与圆的位置关系.【分析】直线和圆的位置关系与数量之间的联系:若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.【解答】解:因为垂线段最短,所以圆心到直线的距离小于等于5.此时和半径3的大小不确定,则直线和圆相交、相切、相离都有可能.故选D.【点评】判断直线和圆的位置关系,必须明确圆心到直线的距离.特别注意:这里的5不一定是圆心到直线的距离.5.已知Rt△ABC的直角边AC=BC=4cm,若以C为圆心,以3cm为半径作圆,则这个圆与斜边AB所在直线的位置关系是()A.相交B.相切C.相离D.不能确定【考点】直线与圆的位置关系.【分析】根据勾股定理可以求得斜边AB的长度,由等腰三角形的性质可知底边上的中线和高线重合于一条,从而可以求得直角顶点C到斜边AB的长度,从而可以解答本题.【解答】解:∵Rt△ABC的直角边AC=BC=4cm,∴斜边AB=4cm,∴斜边AB上的中线与高重合,长度为:2cm,∵2,即2<3,∴这个圆与斜边AB所在直线的位置关系是相交,故选A.【点评】本题考查直线与圆的位置关系、等腰三角形的性质,勾股定理,解题的关键是明确题意,找出所求问题需要的条件.6.如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与∠A的关系是()A.∠FDE与∠A相等B.∠FDE与∠A互补C.∠FDE与∠A互余D.无法确定【考点】三角形的内切圆与内心.【分析】根据切线的性质得出∠AFI=∠AEI=90°,进而得出∠A+∠EIF=180°,即可得出∠A+∠FIE=90°,进而得出答案.【解答】解:连接FI,IE,∵△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,∴∠AFI=∠AEI=90°,∴∠A+∠EIF=180°,∵∠FDE=∠FIE,∴∠A+∠FIE=90°,∴∠A+∠FDE=90°.故选:C.【点评】此题主要考查了切线的性质以及四边形内角和定理、圆周角定理等知识,根据已知得出∠A+∠EIF=180°是解题关键.7.如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,AB=4,OM=1,则PA的长为()A.B.C.2 D.4【考点】切线的性质.【分析】先根据垂径定理得AM=AB=2,则利用勾股定理可计算出OA=,再根据切线的性质得∠OAP=90°,即∠PAM+∠OAM=90°,利用等角的余角相等得∠P=∠OAM,于是可判断Rt△PAM ∽Rt△AOM,然后利用相似比可计算出PA的长.【解答】解:∵AB⊥OP,∴AM=BM=AB=×4=2,在Rt△AOM中,OA===,∵PA切⊙O于点A,∴OA⊥PA,∴∠OAP=90°,即∠PAM+∠OAM=90°,而∠PAM+∠P=90°,∴∠P=∠OAM,∴Rt△PAM∽Rt△AOM,∴=,即=,∴PA=2.故选C.【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了相似三角形的判定与性质.三、解答题8.如图.⊙O的半径为2,AB、AC是⊙O的两条弦,AB=2,AC=4,如果以O为圆心,作一个与直线AC相切的圆,那么:(1)所作的圆的半径是多少?(2)所作的圆与直线AB有怎样的位置关系?为什么?【考点】直线与圆的位置关系.【分析】(1)作OE⊥AC于E,连接OA,根据垂径定理和勾股定理求出OE的长,根据直线与圆的位置关系得到答案;(2)求出OF的长,根据直线与圆的位置关系进行判定.【解答】解:(1)作OE⊥AC于E,连接OA,则AE=AC=2,则OE==2,答:以O为圆心,作一个与直线AC相切的圆,所作的圆的半径是2;(2)作OF⊥AB于F,则AF=AB=,∴OF==,∵>2,∴所作的圆与直线AB相离.【点评】本题考查的是直线与圆的位置关系,如果圆心到直线的距离为d,圆的半径为r,若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.9.在某张航海图上,标明了三个观测点的坐标,如图,O(0,0),B(6,0),C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.(1)求圆形区域的面积;(2)某时刻海面上出现一渔船A,在观察点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,那么当渔船A向正西方向航行时,是否会进入海洋生物保护区?【考点】解直角三角形的应用-方向角问题.【分析】(1)根据题意可以求得圆心的坐标和圆的半径,从而可以求得圆形区域的面积;(2)根据题意可以求得点A的纵坐标,然后与4+5=9比较,从而可以解答本题.【解答】解:(1)∵O(0,0),B(6,0),C(6,8),∴圆心的坐标为(3,4),∴圆的半径是:,∴圆形区域的面积是:π×52=25π,即圆形区域的面积是25π;(2)∵观察点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,圆的半径为5,圆心为(3,4),设点A的坐标为(a,b),∴OB=,即,解得,b=9+3≈14,4+5=9<14,∴当渔船A向正西方向航行时,不会进入海洋生物保护区.【点评】本题考查解直角三角形的应用﹣方向角问题,解题的关键是明确题意,找出所求问题需要的条件.10.(2012秋漳县校级期中)如图,AB是⊙O的直径,AC=AB,⊙O交BC于D.DE⊥AC于E,DE是⊙O的切线吗?为什么?【考点】切线的判定.【分析】DE是⊙O的切线,接OD,只要证明OD⊥DE即可.【解答】答:DE是⊙O的切线,理由如下:证明:连接OD,∵OD=OB,∴∠B=∠ODB,∵AB=AC,∴∠B=∠C,∴∠C=∠ODB,∴OD∥AC,∴∠ODE=∠DEC;∵DE⊥AC,∴∠DEC=90°,∴∠ODE=90°,即DE⊥OD,∴DE是⊙O的切线.【点评】本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.11.已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.求证:(1)AD=BD;(2)DF是⊙O的切线.【考点】切线的判定;圆周角定理.【分析】(1)由于AC=AB,如果连接CD,那么只要证明出CD⊥AB,根据等腰三角形三线合一的特点,我们就可以得出AD=BD,由于BC是圆的直径,那么CD⊥AB,由此可证得.(2)连接OD,再证明OD⊥DE即可.【解答】证明:(1)连接CD,∵BC为⊙O的直径,∴CD⊥AB.∵AC=BC,∴AD=BD.(2)连接OD;∵AD=BD,OB=OC,∴OD是△BCA的中位线,∴OD∥AC.∵DE⊥AC,∴DF⊥OD.∵OD为半径,∴DF是⊙O的切线.【点评】本题主要考查了切线的判定,等腰三角形的性质等知识点.要注意的是要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.12.已知:如图⊙O是Rt△CDE的外接圆,BC⊥CE,BD和CE的延长线交于点A,且OB∥ED.(1)求证:AD是⊙O的切线;(2)若BC=6,AD=4,求⊙O的半径r.【考点】切线的判定;切割线定理.【分析】(1)要证明AD是圆的切线,只需连接OD,证明OD⊥AB;(2)根据切线长定理和勾股定理计算得到AC的长,再进一步根据切割线定理进行计算.【解答】(1)证明:连接OD.∵OB∥ED,∴∠CFO=∠CDE=90°.又∵CD是⊙O的弦,∴OB垂直平分CD.∴∠BCF=∠BDF.又∵∠2=∠1,∴∠1+∠BDF=∠2+∠BCF=∠BCO=90°.∴∠BDO=90°.∴AD是⊙O的切线.(2)解:设AE=k.∵BC,BD是⊙O的切线,∴BD=BC=6.∵AD=4,∴AB=10,∴由勾股定理求出:AC==8.又∵AD是⊙O的切线,∴AD2=AEAC.∴16=8k,k=2.∴2r=8﹣2=6,∴r=3.∴该圆的半径是3.【点评】此题综合运用了切线长定理、切割线定理、圆周角定理的推论、平行线的性质和等腰三角形的性质.13.如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.求证:(1)AC是⊙D的切线;(2)AB+EB=AC.【考点】切线的判定;直角三角形全等的判定.【分析】(1)过点D作DF⊥AC于F,求出BD=DF等于半径,得出AC是⊙D的切线.(2)先证明△BDE≌△FCD(HL),根据全等三角形对应边相等及切线的性质的AB=AF,得出AB+EB=AC.【解答】证明:(1)过点D作DF⊥AC于F;∵AB为⊙D的切线,AD平分∠BAC,∴BD=DF,∴AC为⊙D的切线.(2)∵AC为⊙D的切线,∴∠DFC=∠B=90°,在Rt△BDE和Rt△FCD中;∵BD=DF,DE=DC,∴Rt△BDE≌Rt△FCD(HL),∴EB=FC.∵AB=AF,∴AB+EB=AF+FC,即AB+EB=AC.【点评】本题考查的是切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线;及全等三角形的判断,全等三角形的对应边相等.14.如图:AB是⊙O的直径,以OA为直径的⊙O1与⊙O的弦AC相交于D,DE⊥OC,垂足为E.(1)求证:AD=DC;(2)求证:DE是⊙O1的切线;(3)如果OE=EC,请判断四边形O1OED是什么四边形,并证明你的结论.【考点】切线的判定;正方形的判定.【分析】(1)连OD可得OD⊥AC,又有OA=OC,所以第一问可求解;(2)证明O1D⊥DE即可;(3)如果OE=EC,又D为AC的中点,所以四条边相等,再根据角之间的关系,即可得出其形状.【解答】证明:(1)连接OD,∵AO为圆O1的直径,则∠ADO=90°.∵AC为⊙O的弦,OD为弦心距,∴AD=DC.(2)∵D为AC的中点,O1为AO的中点,∴O1D∥OC.又DE⊥OC,∴DE⊥O1D∴DE与⊙O1相切.(3)如果OE=EC,又D为AC的中点,∴DE∥O1O,又O1D∥OE,∴四边形O1OED为平行四边形.又∠DEO=90°,O1O=O1D,∴四边形O1OED为正方形.【点评】熟练掌握切线的性质及正方形的判定,会运用其性质进行一些简单的证明求解问题.15.由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴的侵袭.近日,A城气象局测得沙尘暴中心在A城的正西方向240km的B处,以每时12km的速度向北偏东60°方向移动,距沙尘暴中心150km的范围为受影响区域.(1)A城是否受到这次沙尘暴的影响?为什么?(2)若A城受这次沙尘暴影响,那么遭受影响的时间有多长?【考点】勾股定理的应用.【分析】(1)过点A作AC⊥BM,垂足为C,在Rt△ABC中,由题意可知∠B=30°,由此可以求出AC的长度,然后和150比较大小即可判断A城是否受到这次沙尘暴的影响;(2)如图,设点E,F是以A为圆心,150km为半径的圆与MB的交点,根据勾股定理可以求出CE的长度,也就求出了EF的长度,然后除以沙尘暴的速度即可求出遭受影响的时间.【解答】解:(1)过点A作AC⊥BM,垂足为C,在Rt△ABC中,由题意可知∠CBA=30°,∴AC=AB=×240=120(km),∵AC=120<150,∴A城将受这次沙尘暴的影响;(2)设点E,F是以A为圆心,150km为半径的圆与MB的交点,连接AE,AF,由题意得CE=(km),∴EF=2CE=2×90=180(km),∴A城受沙尘暴影响的时间为:180÷12=15(时),答:A城将受到这次沙尘暴的影响,影响的时间为15时.【点评】此题考查了直角三角形中30°的角所对的直角边等于斜边的一半及勾股定理的应用,当然首先正确理解题意,把握好题目的数量关系是解决问题的前提.16.如图,已知PA,PB为⊙O的切线,A,B为切点,∠P=60°.AB=4,求∠C的度数和⊙O 的半径.【考点】切线的性质.【分析】连接OB,OA,根据切线的性质定理以及四边形的内角和定理得到∠AOB=180°﹣∠P=120°,再根据等边对等角以及三角形的内角和定理求得∠BAC的度数,最后用锐角三角函数求出半径.【解答】解:如图,连接OB,OA,∵PA、PB是⊙O的切线,A、B为切点,∴∠PAO=∠PBO=90°,∴∠AOB=360°﹣∠P﹣∠PAO﹣∠PBO=120°,∴∠BAC=∠AOB=60°,∵OA=OB,∴∠OAB=30°过点O作OD⊥AB,∴AD=AB=2,∴cos∠OAB=,∴,∴OC=4.【点评】此题综合运用了切线的性质定理、四边形的内角和定理、等边对等角以及三角形的内角和定理,锐角三角函数,求出∠AOB是解本题的关键.17.如图,I是△ABC的内心,∠BAC的平分线和△ABC的外接圆相交于点D.BD与ID相等吗?为什么?【考点】三角形的内切圆与内心;三角形的外接圆与外心.【分析】首先连接BI,由I是△ABC的内心,可得∠BAD=∠CAD,∠ABI=∠CBI,又由圆周角定理,可证得∠BAD=∠CBD,继而可证得∠BID=∠IBD,则可证得结论.【解答】解:BD=ID.理由:连接IB,∵I是△ABC的内心,∴∠BAD=∠CAD,∠ABI=∠CBI,∵∠CBD=∠CAD,∴∠BAD=∠CBD,∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,∴∠BID=∠IBD,∴BD=ID.【点评】此题考查了三角形内心的性质、等腰三角形的判定以及圆周角定理.注意准确作出辅助线是解此题的关键.。
江苏省淮安市淮阴区棉花中学九年级数学下册 第三章 中心对称图形《小结与思考》同步练习(无答案) 新人

D
A
B C B'D A B C C'B'A B C C'B'
2.如图,C 是线段AB 上一点,分别以AC 、BC 为边在线段AB 同侧作正方形ACDE 和BCF G,连接AF 、BD .
⑴AF 与BD 是否相等?为什么?
⑵如果点正方形BGFC 在正方形ACDE 的内部,⑴中结论是否成立?请画图,并说明理由.
1. 如图,⊿ABC 和⊿DB C 都是等边三角形,点B ’在BC 上,沿BC 方向将⊿DBC 平移到⊿
D ’B ’C ’的位置,此时,四边形ABD ’C ’是平行四边形吗,为什么?
2. 如图,在⊿ABC 中,点O 是AC 上的任意一点(不与点A 、C 重合),过点O 作直线m//BC,F D
m O A D F C E A
C D O F
A D
B
C E C
B D A
A 1G H 且直线m 与∠BCA 的平分线相交于点E,与∠DCA 相交于点F.
(1) OE 与OF 相等吗,为什么?
(2) 探索:当点O 在何处时,四边形AECF 为矩形,请说明理由。
3. 如图,在直角梯形ABCD 中,O 为CD 的中点,分别度量点A,B 到点O 的距离,它们相
等吗,说明理由?
4. 在矩形纸片ABCD 中,AB=6,BC=8.
(1) 将矩形纸片沿BD 折叠,使点A 落在点E 处(左图),设DE 与BC 相交于点F,求BF 的长。
(2) 将矩形纸片折叠,使点B 与点D 重合(右图),求折痕GH 的长。
江苏省连云港市灌南实验中学九年级数学上学期10月练习试卷5(含解析) 新人教版

2015-2016学年江苏省连云港市灌南实验中学九年级(上)练习数学试卷5一、选择1.下列直线是圆的切线的是()A.与圆有公共点的直线B.到圆心的距离等于半径的直线C.到圆心的距离大于半径的直线D.到圆心的距离小于半径的直线2.⊙O的半径为R,直线l与⊙O有公共点,如果圆心到直线l的距离为d,那么d与R的大小关系是()A.d≥R B.d≤R C.d>R D.d<R3.Rt△ABC中,∠C=90°,AC=3,CB=4,给出下列三个结论:①以点C为圆心,1.3长为半径的圆与AB相离;②以点C为圆心,2.4长为半径的圆与AB相切;③以点C为圆心,2.5长为半径的圆与AB相交.上述结论正确的个数是()A.0个B.1个C.2个D.3个4.已知⊙O的半径为3cm,点P是直线l上一点,OP长为5cm,则直线l与⊙O的位置关系为()A.相交B.相切C.相离D.相交、相切、相离都有可能5.已知Rt△ABC的直角边AC=BC=4cm,若以C为圆心,以3cm为半径作圆,则这个圆与斜边AB所在直线的位置关系是()A.相交B.相切C.相离D.不能确定6.如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与∠A的关系是()A.∠FDE与∠A相等B.∠FDE与∠A互补C.∠FDE与∠A互余D.无法确定7.如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,AB=4,OM=1,则PA的长为()A.B.C.2D.4三、解答题8.如图.⊙O的半径为2,AB、AC是⊙O的两条弦,AB=2,AC=4,如果以O为圆心,作一个与直线AC相切的圆,那么:(1)所作的圆的半径是多少?(2)所作的圆与直线AB有怎样的位置关系?为什么?9.在某张航海图上,标明了三个观测点的坐标,如图,O(0,0),B(6,0),C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.(1)求圆形区域的面积;(2)某时刻海面上出现一渔船A,在观察点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,那么当渔船A向正西方向航行时,是否会进入海洋生物保护区?10.如图,AB是⊙O的直径,AC=AB,⊙O交BC于D.DE⊥AC于E,DE是⊙O的切线吗?为什么?11.已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.求证:(1)AD=BD;(2)DF是⊙O的切线.12.已知:如图⊙O是Rt△CDE的外接圆,BC⊥CE,BD和CE的延长线交于点A,且OB∥ED.(1)求证:AD是⊙O的切线;(2)若BC=6,AD=4,求⊙O的半径r.13.如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.求证:(1)AC是⊙D的切线;(2)AB+EB=AC.14.如图:AB是⊙O的直径,以OA为直径的⊙O1与⊙O的弦AC相交于D,DE⊥OC,垂足为E.(1)求证:AD=DC;(2)求证:DE是⊙O1的切线;(3)如果OE=EC,请判断四边形O1OED是什么四边形,并证明你的结论.15.由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴的侵袭.近日,A城气象局测得沙尘暴中心在A城的正西方向240km的B处,以每时12km的速度向北偏东60°方向移动,距沙尘暴中心150km的范围为受影响区域.(1)A城是否受到这次沙尘暴的影响?为什么?(2)若A城受这次沙尘暴影响,那么遭受影响的时间有多长?16.如图,已知PA,PB为⊙O的切线,A,B为切点,∠P=60°.AB=4,求∠C的度数和⊙O的半径.17.如图,I是△ABC的内心,∠BAC的平分线和△ABC的外接圆相交于点D.BD与ID相等吗?为什么?2015-2016学年江苏省连云港市灌南实验中学九年级(上)练习数学试卷5(10月份)参考答案与试题解析一、选择1.下列直线是圆的切线的是()A.与圆有公共点的直线B.到圆心的距离等于半径的直线C.到圆心的距离大于半径的直线D.到圆心的距离小于半径的直线【考点】切线的判定.【分析】根据切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线,可判定C、D错误;由切线的定义:到圆心距离等于圆的半径的直线是圆的切线,可判定A错误,B正确.注意排除法在解选择题中的应用.【解答】解:A、与圆只有一个交点的直线是圆的切线,故本选项错误;B、到圆心距离等于圆的半径的直线是圆的切线,故本选项正确;C、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误;D、经过半径的外端且垂直于这条半径的直线是圆的切线,故本选项错误.故选B.【点评】此题考查了切线的判定.此题难度不大,注意掌握切线的判定定理与切线的定义是解此题的关键2.⊙O的半径为R,直线l与⊙O有公共点,如果圆心到直线l的距离为d,那么d与R的大小关系是()A.d≥R B.d≤R C.d>R D.d<R【考点】直线与圆的位置关系.【分析】直接根据直线与圆的位置关系进行解答即可.【解答】解:∵直线l与⊙O有公共点,∴直线与圆相切或相交,即d≤R.故选B.【点评】本题考查的是直线与圆的位置关系,即判断直线和圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d,当d<r时,直线l和⊙O相交;当d=r时,直线l和⊙O 相切;当d>r时,直线l和⊙O相离.3.Rt△ABC中,∠C=90°,AC=3,CB=4,给出下列三个结论:①以点C为圆心,1.3长为半径的圆与AB相离;②以点C为圆心,2.4长为半径的圆与AB相切;③以点C为圆心,2.5长为半径的圆与AB相交.上述结论正确的个数是()A.0个B.1个C.2个D.3个【考点】直线与圆的位置关系.【分析】根据题意可以求得斜边AB的长度及斜边AB上的高的长度,从而可以判断题目中的三个判断是否正确,从而可以解答本题.【解答】解:∵在Rt△ABC中,∠C=90°,AC=3,CB=4,∴AB==5,∴斜边AB上的高是:,∴以点C为圆心,1.3长为半径的圆与AB相离,故①正确;以点C为圆心,2.4长为半径的圆与AB相切,故②正确;以点C为圆心,2.5长为半径的圆与AB相交,故③正确;故选D.【点评】本题考查直线与圆的位置关系,解题的关键是明确题意,找出所求问题需要的条件.4.已知⊙O的半径为3cm,点P是直线l上一点,OP长为5cm,则直线l与⊙O的位置关系为()A.相交B.相切C.相离D.相交、相切、相离都有可能【考点】直线与圆的位置关系.【分析】直线和圆的位置关系与数量之间的联系:若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.【解答】解:因为垂线段最短,所以圆心到直线的距离小于等于5.此时和半径3的大小不确定,则直线和圆相交、相切、相离都有可能.故选D.【点评】判断直线和圆的位置关系,必须明确圆心到直线的距离.特别注意:这里的5不一定是圆心到直线的距离.5.已知Rt△ABC的直角边AC=BC=4cm,若以C为圆心,以3cm为半径作圆,则这个圆与斜边AB所在直线的位置关系是()A.相交B.相切C.相离D.不能确定【考点】直线与圆的位置关系.【分析】根据勾股定理可以求得斜边AB的长度,由等腰三角形的性质可知底边上的中线和高线重合于一条,从而可以求得直角顶点C到斜边AB的长度,从而可以解答本题.【解答】解:∵Rt△ABC的直角边AC=BC=4cm,∴斜边AB=4cm,∴斜边AB上的中线与高重合,长度为:2cm,∵2,即2<3,∴这个圆与斜边AB所在直线的位置关系是相交,故选A.【点评】本题考查直线与圆的位置关系、等腰三角形的性质,勾股定理,解题的关键是明确题意,找出所求问题需要的条件.6.如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与∠A的关系是()A.∠FDE与∠A相等B.∠FDE与∠A互补C.∠FDE与∠A互余D.无法确定【考点】三角形的内切圆与内心.【分析】根据切线的性质得出∠AFI=∠AEI=90°,进而得出∠A+∠EIF=180°,即可得出∠A+∠FIE=90°,进而得出答案.【解答】解:连接FI,IE,∵△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,∴∠AFI=∠AEI=90°,∴∠A+∠EIF=180°,∵∠FDE=∠FIE,∴∠A+∠FIE=90°,∴∠A+∠FDE=90°.故选:C.【点评】此题主要考查了切线的性质以及四边形内角和定理、圆周角定理等知识,根据已知得出∠A+∠EIF=180°是解题关键.7.如图,PA切⊙O于点A,弦AB⊥OP,垂足为M,AB=4,OM=1,则PA的长为()A.B.C.2D.4【考点】切线的性质.【分析】先根据垂径定理得AM=AB=2,则利用勾股定理可计算出OA=,再根据切线的性质得∠OAP=90°,即∠PAM+∠OAM=90°,利用等角的余角相等得∠P=∠OAM,于是可判断Rt △PAM∽Rt△AOM,然后利用相似比可计算出PA的长.【解答】解:∵AB⊥OP,∴AM=BM=AB=×4=2,在Rt△AOM中,OA===,∵PA切⊙O于点A,∴OA⊥PA,∴∠OAP=90°,即∠PAM+∠OAM=90°,而∠PAM+∠P=90°,∴∠P=∠OAM,∴Rt△PAM∽Rt△AOM,∴=,即=,∴PA=2.故选C.【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了相似三角形的判定与性质.三、解答题8.如图.⊙O的半径为2,AB、AC是⊙O的两条弦,AB=2,AC=4,如果以O为圆心,作一个与直线AC相切的圆,那么:(1)所作的圆的半径是多少?(2)所作的圆与直线AB有怎样的位置关系?为什么?【考点】直线与圆的位置关系.【分析】(1)作OE⊥AC于E,连接OA,根据垂径定理和勾股定理求出OE的长,根据直线与圆的位置关系得到答案;(2)求出OF的长,根据直线与圆的位置关系进行判定.【解答】解:(1)作OE⊥AC于E,连接OA,则AE=AC=2,则OE==2,答:以O为圆心,作一个与直线AC相切的圆,所作的圆的半径是2;(2)作OF⊥AB于F,则AF=AB=,∴OF==,∵>2,∴所作的圆与直线AB相离.【点评】本题考查的是直线与圆的位置关系,如果圆心到直线的距离为d,圆的半径为r,若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.9.在某张航海图上,标明了三个观测点的坐标,如图,O(0,0),B(6,0),C(6,8),由三个观测点确定的圆形区域是海洋生物保护区.(1)求圆形区域的面积;(2)某时刻海面上出现一渔船A,在观察点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,那么当渔船A向正西方向航行时,是否会进入海洋生物保护区?【考点】解直角三角形的应用-方向角问题.【分析】(1)根据题意可以求得圆心的坐标和圆的半径,从而可以求得圆形区域的面积;(2)根据题意可以求得点A的纵坐标,然后与4+5=9比较,从而可以解答本题.【解答】解:(1)∵O(0,0),B(6,0),C(6,8),∴圆心的坐标为(3,4),∴圆的半径是:,∴圆形区域的面积是:π×52=25π,即圆形区域的面积是25π;(2)∵观察点O测得A位于北偏东45°,同时在观测点B测得A位于北偏东30°,圆的半径为5,圆心为(3,4),设点A的坐标为(a,b),∴OB=,即,解得,b=9+3≈14,4+5=9<14,∴当渔船A向正西方向航行时,不会进入海洋生物保护区.【点评】本题考查解直角三角形的应用﹣方向角问题,解题的关键是明确题意,找出所求问题需要的条件.10.(2012秋漳县校级期中)如图,AB是⊙O的直径,AC=AB,⊙O交BC于D.DE⊥AC于E,DE是⊙O的切线吗?为什么?【考点】切线的判定.【分析】DE是⊙O的切线,接OD,只要证明OD⊥DE即可.【解答】答:DE是⊙O的切线,理由如下:证明:连接OD,∵OD=OB,∴∠B=∠ODB,∵AB=AC,∴∠B=∠C,∴∠C=∠ODB,∴OD∥AC,∴∠ODE=∠DEC;∵DE⊥AC,∴∠DEC=90°,∴∠ODE=90°,即DE⊥OD,∴DE是⊙O的切线.【点评】本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.11.已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.求证:(1)AD=BD;(2)DF是⊙O的切线.【考点】切线的判定;圆周角定理.【分析】(1)由于AC=AB,如果连接CD,那么只要证明出CD⊥AB,根据等腰三角形三线合一的特点,我们就可以得出AD=BD,由于BC是圆的直径,那么CD⊥AB,由此可证得.(2)连接OD,再证明OD⊥DE即可.【解答】证明:(1)连接CD,∵BC为⊙O的直径,∴CD⊥AB.∵AC=BC,∴AD=BD.(2)连接OD;∵AD=BD,OB=OC,∴OD是△BCA的中位线,∴OD∥AC.∵DE⊥AC,∴DF⊥OD.∵OD为半径,∴DF是⊙O的切线.【点评】本题主要考查了切线的判定,等腰三角形的性质等知识点.要注意的是要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.12.已知:如图⊙O是Rt△CDE的外接圆,BC⊥CE,BD和CE的延长线交于点A,且OB∥ED.(1)求证:AD是⊙O的切线;(2)若BC=6,AD=4,求⊙O的半径r.【考点】切线的判定;切割线定理.【分析】(1)要证明AD是圆的切线,只需连接OD,证明OD⊥AB;(2)根据切线长定理和勾股定理计算得到AC的长,再进一步根据切割线定理进行计算.【解答】(1)证明:连接OD.∵OB∥ED,∴∠CFO=∠CDE=90°.又∵CD是⊙O的弦,∴OB垂直平分CD.∴∠BCF=∠BDF.又∵∠2=∠1,∴∠1+∠BDF=∠2+∠BCF=∠BCO=90°.∴∠BDO=90°.∴AD是⊙O的切线.(2)解:设AE=k.∵BC,BD是⊙O的切线,∴BD=BC=6.∵AD=4,∴AB=10,∴由勾股定理求出:AC==8.又∵AD是⊙O的切线,∴AD2=AEAC.∴16=8k,k=2.∴2r=8﹣2=6,∴r=3.∴该圆的半径是3.【点评】此题综合运用了切线长定理、切割线定理、圆周角定理的推论、平行线的性质和等腰三角形的性质.13.如图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.求证:(1)AC是⊙D的切线;(2)AB+EB=AC.【考点】切线的判定;直角三角形全等的判定.【分析】(1)过点D作DF⊥AC于F,求出BD=DF等于半径,得出AC是⊙D的切线.(2)先证明△BDE≌△FCD(HL),根据全等三角形对应边相等及切线的性质的AB=AF,得出AB+EB=AC.【解答】证明:(1)过点D作DF⊥AC于F;∵AB为⊙D的切线,AD平分∠BAC,∴BD=DF,∴AC为⊙D的切线.(2)∵AC为⊙D的切线,∴∠DFC=∠B=90°,在Rt△BDE和Rt△FCD中;∵BD=DF,DE=DC,∴Rt△BDE≌Rt△FCD(HL),∴EB=FC.∵AB=AF,∴AB+EB=AF+FC,即AB+EB=AC.【点评】本题考查的是切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线;及全等三角形的判断,全等三角形的对应边相等.14.如图:AB是⊙O的直径,以OA为直径的⊙O1与⊙O的弦AC相交于D,DE⊥OC,垂足为E.(1)求证:AD=DC;(2)求证:DE是⊙O1的切线;(3)如果OE=EC,请判断四边形O1OED是什么四边形,并证明你的结论.【考点】切线的判定;正方形的判定.【分析】(1)连OD可得OD⊥AC,又有OA=OC,所以第一问可求解;(2)证明O1D⊥DE即可;(3)如果OE=EC,又D为AC的中点,所以四条边相等,再根据角之间的关系,即可得出其形状.【解答】证明:(1)连接OD,∵AO为圆O1的直径,则∠ADO=90°.∵AC为⊙O的弦,OD为弦心距,∴AD=DC.(2)∵D为AC的中点,O1为AO的中点,∴O1D∥OC.又DE⊥OC,∴DE⊥O1D∴DE与⊙O1相切.(3)如果OE=EC,又D为AC的中点,∴DE∥O1O,又O1D∥OE,∴四边形O1OED为平行四边形.又∠DEO=90°,O1O=O1D,∴四边形O1OED为正方形.【点评】熟练掌握切线的性质及正方形的判定,会运用其性质进行一些简单的证明求解问题.15.由于过度采伐森林和破坏植被,我国部分地区频频遭受沙尘暴的侵袭.近日,A城气象局测得沙尘暴中心在A城的正西方向240km的B处,以每时12km的速度向北偏东60°方向移动,距沙尘暴中心150km的范围为受影响区域.(1)A城是否受到这次沙尘暴的影响?为什么?(2)若A城受这次沙尘暴影响,那么遭受影响的时间有多长?【考点】勾股定理的应用.【分析】(1)过点A作AC⊥BM,垂足为C,在Rt△ABC中,由题意可知∠B=30°,由此可以求出AC的长度,然后和150比较大小即可判断A城是否受到这次沙尘暴的影响;(2)如图,设点E,F是以A为圆心,150km为半径的圆与MB的交点,根据勾股定理可以求出CE的长度,也就求出了EF的长度,然后除以沙尘暴的速度即可求出遭受影响的时间.【解答】解:(1)过点A作AC⊥BM,垂足为C,在Rt△ABC中,由题意可知∠CBA=30°,∴AC=AB=×240=120(km),∵AC=120<150,∴A城将受这次沙尘暴的影响;(2)设点E,F是以A为圆心,150km为半径的圆与MB的交点,连接AE,AF,由题意得CE=(km),∴EF=2CE=2×90=180(km),∴A城受沙尘暴影响的时间为:180÷12=15(时),答:A城将受到这次沙尘暴的影响,影响的时间为15时.【点评】此题考查了直角三角形中30°的角所对的直角边等于斜边的一半及勾股定理的应用,当然首先正确理解题意,把握好题目的数量关系是解决问题的前提.16.如图,已知PA,PB为⊙O的切线,A,B为切点,∠P=60°.AB=4,求∠C的度数和⊙O的半径.【考点】切线的性质.【分析】连接OB,OA,根据切线的性质定理以及四边形的内角和定理得到∠AOB=180°﹣∠P=120°,再根据等边对等角以及三角形的内角和定理求得∠BAC的度数,最后用锐角三角函数求出半径.【解答】解:如图,连接OB,OA,∵PA、PB是⊙O的切线,A、B为切点,∴∠PAO=∠PBO=90°,∴∠AOB=360°﹣∠P﹣∠PAO﹣∠PBO=120°,∴∠BAC=∠AOB=60°,∵OA=OB,∴∠OAB=30°过点O作OD⊥AB,∴AD=AB=2,∴cos∠OAB=,∴,∴OC=4.【点评】此题综合运用了切线的性质定理、四边形的内角和定理、等边对等角以及三角形的内角和定理,锐角三角函数,求出∠AOB是解本题的关键.17.如图,I是△ABC的内心,∠BAC的平分线和△ABC的外接圆相交于点D.BD与ID相等吗?为什么?【考点】三角形的内切圆与内心;三角形的外接圆与外心.【分析】首先连接BI,由I是△ABC的内心,可得∠BAD=∠CAD,∠ABI=∠CBI,又由圆周角定理,可证得∠BAD=∠CBD,继而可证得∠BID=∠IBD,则可证得结论.【解答】解:BD=ID.理由:连接IB,∵I是△ABC的内心,∴∠BAD=∠CAD,∠ABI=∠CBI,∵∠CBD=∠CAD,∴∠BAD=∠CBD,∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,∴∠BID=∠IBD,∴BD=ID.【点评】此题考查了三角形内心的性质、等腰三角形的判定以及圆周角定理.注意准确作出辅助线是解此题的关键.。
江苏省灌南县实验中学九年级数学《第二章小结与思考》复习学案(无答案) 人教新课标版
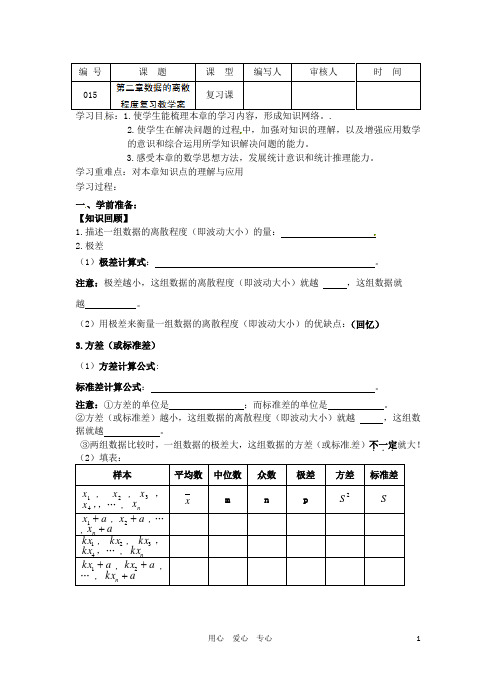
编 号 课 题 课 型 编写人 审核人时 间 015复习课学习目标:1.使学生能梳理本章的学习内容,形成知识网络。
.2.使学生在解决问题的过程中,加强对知识的理解,以及增强应用数学的意识和综合运用所学知识解决问题的能力。
3.感受本章的数学思想方法,发展统计意识和统计推理能力。
学习重难点:对本章知识点的理解与应用 学习过程: 一、学前准备: 【知识回顾】1.描述一组数据的离散程度(即波动大小)的量:2.极差(1)极差计算式: 。
注意:极差越小,这组数据的离散程度(即波动大小)就越 ,这组数据就越 。
(2)用极差来衡量一组数据的离散程度(即波动大小)的优缺点:(回忆) 3.方差(或标准差) (1)方差计算公式:标准差计算公式: 。
注意:①方差的单位是 ;而标准差的单位是 。
②方差(或标准差)越小,这组数据的离散程度(即波动大小)就越 ,这组数据就越 。
③两组数据比较时,一组数据的极差大,这组数据的方差(或标准差)不一定...就大! 样本平均数 中位数众数 极差 方差标准差1x , 2x ,3x ,4x ,,… , n xx m n p 2SSa x +1,a x +2,…,a x n +1kx , 2kx , 3kx ,4kx ,… , n kxa kx +1,a kx +2,… , a kx n +4、本章疑难摘要: 。
二、探究活动:(一)师生探究·合作交流1. 已知数据1,2,3,4,5的方差为2,则11,12,13,14,15的方差为_________ ,标准差为_______ 。
2.若一组数据1x , 2x ,… , n x 的极差为2、方差为9,则数据321-x ,322-x ,…,32-n x 的极差是 ,标准差是____ .5、某同学使用计算器求30个数据的平均数时,错将其中一个数据105输入为15,那么所求出平均数与实际平均数的差是( ) A 、3.5 B 、3 C 、0.5 D 、-36.一组数据中若最小数与平均数相等,那么这组数据的方差为 . (二)独立思考·解决问题例1.为了解某小区居民的日用电情况,居住在该小区的一名同学随机抽查了l5户家庭的日用电量,结果如下表:日用电量 (单位:度) 5 6 7 8 10 户 数2543l则关于这l5户家庭的日用电量,下列说法错误的是( )A .众数是6度B .平均数是6.8度C .极差是5度D .中位数是6度例2.为了从甲、乙两名学生中选拔一人参加竞赛,•学校每个月对他们的学习进行一次测验,如图是两人赛前5次测验成绩的折线统计图.(1)分别求出甲、乙两名学生5次测验成绩的平均数、极差及方差;(2)如果你是他们的辅导教师,应选派哪一名学生参加这次竞赛.•请结合所学习的统计知识说明理由. 练一练:1.已知甲、乙两组数据的平均数分别是80x =甲,90x =乙,方差分别是210S =甲,25S =乙,比较这两组数据,下列说法正确的是( )A .甲组数据较好B .乙组数据较好C .甲组数据的极差较大D .乙组数据的波动较小2.(08,河南)样本数据3,6,a , 4,2的平均数是5,则这个样本的方差是 。
苏科版数学九年级上册《小结与思考》说课稿3

苏科版数学九年级上册《小结与思考》说课稿3一. 教材分析苏科版数学九年级上册《小结与思考》这一章节,是在学生已经学习了概率的初步知识、二次函数、相似三角形等数学知识的基础上进行讲解的。
本章主要内容包括:几何图形的对称性、圆的性质、函数的性质、概率的性质等。
这些内容是学生进一步学习高中数学的基础,也是培养学生逻辑思维、空间想象、抽象概括能力的重要环节。
二. 学情分析九年级的学生已经具备了一定的数学基础,对于一些基本的数学概念和运算规则有一定的了解。
但是,学生在学习过程中,对于一些抽象的数学概念和理论的理解还不够深入,需要通过大量的练习来巩固。
此外,学生的学习兴趣和学习习惯也影响着他们的学习效果,因此在教学过程中,需要关注学生的学习兴趣,培养良好的学习习惯。
三. 说教学目标根据教材内容和学情分析,本节课的教学目标如下:1.理解并掌握本章所涉及的几何图形的对称性、圆的性质、函数的性质、概率的性质等基本概念和性质。
2.培养学生的逻辑思维、空间想象、抽象概括能力。
3.提高学生的数学运用能力,使他们在解决实际问题时,能够灵活运用所学的数学知识。
4.激发学生的学习兴趣,培养他们积极主动探究数学问题的习惯。
四. 说教学重难点1.教学重点:理解和掌握本章所涉及的几何图形的对称性、圆的性质、函数的性质、概率的性质等基本概念和性质。
2.教学难点:对于一些抽象的数学概念和理论的理解,以及如何在实际问题中灵活运用所学的数学知识。
五. 说教学方法与手段为了达到本节课的教学目标,我将采用以下教学方法和手段:1.讲授法:对于一些基本的数学概念和性质,我将通过讲解来引导学生理解和掌握。
2.案例分析法:通过分析一些实际问题,让学生学会如何灵活运用所学的数学知识。
3.小组讨论法:学生进行小组讨论,培养他们的合作意识和团队精神。
4.多媒体教学:利用多媒体课件,直观地展示一些几何图形的对称性、圆的性质等,帮助学生更好地理解和掌握。
六. 说教学过程1.导入:通过复习前几章的内容,引导学生进入本章的学习。
九年级数学下册第三章圆章末考点复习与小结习题8

◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
◆考点突破 ◆考前过三关 ( ◎第一关 ◎第二关 ◎第三关 )
江苏省连云港市灌南实验中学九年级数学上学期10月练习
2015-2016学年江苏省连云港市灌南实验中学九年级(上)练习数学试卷12(10月份)一、选择题1.二次函数y=x2﹣x+1的图象与x轴的交点个数是()A.0个B.1个C.2个D.不能确定2.图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是()A.y=﹣2x2B.y=2x2C.y=﹣x2D.y=x23.已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则有()A.a>0,b>0 B.a>0,c>0 C.b>0,c>0 D.a,b,c都小于04.若抛物线y=ax2﹣6x经过点(2,0),则抛物线顶点到坐标原点的距离为()A. B. C. D.5.如图,二次函数y=x2﹣4x+3的图象交x轴于A,B两点,交y轴于C,则△ABC的面积为()A.6 B.4 C.3 D.16.已知抛物线y=ax2+bx+c如图所示,则关于x的方程ax2+bx+c﹣8=0的根的情况是()A.有两个不相等的正实数根B.有两个异号实数根C.有两个相等的实数根D.没有实数根7.二次函数y=4x2﹣mx+5,当x<﹣2时,y随x的增大而减小;当x>﹣2时,y随x的增大而增大,那么当x=1时,函数y的值为()A.﹣7 B.1 C.17 D.258.如图所示,阳光中学教学楼前喷水池喷出的抛物线形水柱,其解析式为y=﹣x2+4x+2,则水柱的最大高度是()A.2 B.4 C.6 D.2+二、填空题:9.如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1=﹣1,x2=3③a+b+c>0 ④当x>1时,y随x的增大而增大.正确的说法有.10.抛物线y=x2﹣4x+3的顶点及它与x轴的交点三点连线所围成的三角形面积是.11.已知二次函数y=ax2+bx+c(a≠0)的顶点坐标(﹣1,﹣3.2)及部分图象(如图),由图象可知关于x的方程ax2+bx+c=0的两个根分别是x1=1.3和x2= .12.将抛物线y=ax2向右平移2个单位,再向上平移3个单位,移动后的抛物线经过点(3,﹣1),那么移动后的抛物线的关系式为.13.若二次函数y=(m+5)x2+2(m+1)x+m的图象全部在x轴的上方,则m的取值范围是.14.如图,⊙O的半径为2,C1是函数y=x2的图象,C2是函数y=﹣x2的图象,则阴影部分的面积是.三、解答题:15.某学校在一次投掷铅球时,刚出手时铅球离地面的m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图所示:(1)求抛物线的函数关系式;(2)这名学生此次投掷成绩大约是多少?16.如图所示,过点A(a,0)(a>0)且平行于y轴的直线分别与抛物线y=x2及y=x2交于C、B两点.(1)求点C、B的坐标;(2)求线段AB与BC的比;(3)若正方形BCDE的一边DE与y轴重合,求此正方形BCDE的面积.17.有一条长7.2米的木料,做成如图所示的“日”字形的窗框,问窗的高和宽各取多少米时,这个窗的面积最大?(不考虑木料加工时损耗和中间木框所占的面积)18.某公司生产的A种产品,每件成本是2元,每件售价是3元,一年的销售量是10万件.为了获得更多的利润,公司准备拿出一定资金来做广告.根据经验,每年投入的广告费为x(万元)时,产品的年销售量是原来的y倍,且y是x的二次函数,公司作了预测,知x与y(2)如果把利润看成是销售总额减去成本和广告费,请你写出年利润S(万元)与广告费x (万元)的函数关系式;(3)从上面的函数关系式中,你能得出什么结论?19.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;(3)若球一定能越过球网,又不出边界,求h的取值范围.2015-2016学年江苏省连云港市灌南实验中学九年级(上)练习数学试卷12(10月份)参考答案与试题解析一、选择题1.二次函数y=x2﹣x+1的图象与x轴的交点个数是()A.0个B.1个C.2个D.不能确定【考点】抛物线与x轴的交点.【分析】利用“二次函数的图象和性质与一元二次方程之间的关系”解答即可.【解答】解:判断二次函数图象与x轴的交点个数,就是当y=0时,方程x2﹣x+1=0解的个数,∵△=(﹣1)2﹣4×1×1=﹣3<0,此方程无解,∴二次函数y=x2﹣x+1的图象与x轴无交点.故选A.2.图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是()A.y=﹣2x2B.y=2x2C.y=﹣x2D.y=x2【考点】根据实际问题列二次函数关系式.【分析】由图中可以看出,所求抛物线的顶点在原点,对称轴为y轴,可设此函数解析式为:y=ax2,利用待定系数法求解.【解答】解:设此函数解析式为:y=ax2,a≠0;那么(2,﹣2)应在此函数解析式上.则﹣2=4a即得a=﹣,那么y=﹣x2.故选:C.3.已知抛物线y=ax2+bx+c(a≠0)在平面直角坐标系中的位置如图所示,则有()A.a>0,b>0 B.a>0,c>0 C.b>0,c>0 D.a,b,c都小于0【考点】二次函数图象与系数的关系.【分析】根据函数图象可以得到以下信息:a<0,b>0,c>0,再结合函数图象判断各选项.【解答】解:由函数图象可以得到以下信息:a<0,b>0,c>0,A、错误;B、错误;C、正确;D、错误;故选C.4.若抛物线y=ax2﹣6x经过点(2,0),则抛物线顶点到坐标原点的距离为()A. B. C. D.【考点】二次函数图象上点的坐标特征.【分析】由抛物线y=ax2﹣6x经过点(2,0),求得a的值,再求出函数顶点坐标,求得顶点到坐标原点的距离.【解答】解:由于抛物线y=ax2﹣6x经过点(2,0),则4a﹣12=0,a=3,抛物线y=3x2﹣6x,变形,得:y=3(x﹣1)2﹣3,则顶点坐标M(1,﹣3),抛物线顶点到坐标原点的距离|OM|==.故选B.5.如图,二次函数y=x2﹣4x+3的图象交x轴于A,B两点,交y轴于C,则△ABC的面积为()A.6 B.4 C.3 D.1【考点】二次函数综合题.【分析】根据解析式求出A、B、C三点的坐标,即△ABC的底和高求出,然后根据公式求面积.【解答】解:在y=x2﹣4x+3中,当y=0时,x=1、3;当x=0时,y=3;即A(1,0)、B(3,0)、C(0,3)故△ABC的面积为:×2×3=3;故选C.6.已知抛物线y=ax2+bx+c如图所示,则关于x的方程ax2+bx+c﹣8=0的根的情况是()A.有两个不相等的正实数根B.有两个异号实数根C.有两个相等的实数根D.没有实数根【考点】抛物线与x轴的交点.【分析】把抛物线y=ax2+bx+c向下平移8个单位即可得到y=ax2+bx+c﹣8的图象,由此即可解答.【解答】解:∵y=ax2+bx+c的图象顶点纵坐标为8,向下平移8个单位即可得到y=ax2+bx+c ﹣8的图象,此时,抛物线与x轴有一个交点,∴方程ax2+bx+c﹣8=0有两个相等实数根.7.二次函数y=4x2﹣mx+5,当x<﹣2时,y随x的增大而减小;当x>﹣2时,y随x的增大而增大,那么当x=1时,函数y的值为()A.﹣7 B.1 C.17 D.25【考点】二次函数的性质.【分析】因为当x<﹣2时,y随x的增大而减小;当x>﹣2时,y随x的增大而增大,那么可知对称轴就是x=﹣2,结合顶点公式法可求出m的值,从而得出函数的解析式,再把x=1,可求出y的值.【解答】解:∵当x<﹣2时,y随x的增大而减小,当x>﹣2时,y随x的增大而增大,∴对称轴x=﹣=﹣=﹣2,解得m=﹣16,∴y=4x2+16x+5,那么当x=1时,函数y的值为25.故选D.8.如图所示,阳光中学教学楼前喷水池喷出的抛物线形水柱,其解析式为y=﹣x2+4x+2,则水柱的最大高度是()A.2 B.4 C.6 D.2+【考点】二次函数的应用.【分析】求最大高度,就要把抛物线解析式的一般形式改写成顶点式后,求顶点的纵坐标.【解答】解:y=﹣x2+4x+2=﹣(x﹣2)2+6,∵﹣1<0∴当x=2时,最大高度是6.故选C.二、填空题:9.如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0的根是x1=﹣1,x2=3③a+b+c>0 ④当x>1时,y随x的增大而增大.正确的说法有①②③.【考点】二次函数图象与系数的关系.【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.【解答】解:∵抛物线的开口向下,∴a<0,∵与y轴的交点为在y轴的正半轴上,∴c>0,∴ac<0,故①正确;∵对称轴为x=1,抛物线与x轴的一个交点为(3,0),∴另一个交点为(﹣1,0),∴方程ax2+bx+c=0的根是x1=﹣1,x2=3,故②正确;当x=1时,y=a+b+c>0,故③正确;∴a、b异号,即b<0,当x>1时,y随x的增大而减小,故④错误.∴其中正确的说法有①②③;故答案为:①②③.10.抛物线y=x2﹣4x+3的顶点及它与x轴的交点三点连线所围成的三角形面积是 1 .【考点】抛物线与x轴的交点.【分析】抛物线y=x2﹣4x+3的顶点及它与x轴的交点三点连线所围成的三角形中:底边长为与x轴的两交点之间的距离,高为抛物线的顶点的纵坐标的绝对值,再利用三角形的面积公式即可求出b的值.【解答】解:由题意可得:抛物线的顶点的纵坐标为=﹣1,∴底边上的高为1;∵x2﹣4x+3=0,解得x1=1,x2=3,∴抛物线与x轴的交点为(1,0)、(3,0);由题意得:底边长=|x1﹣x2|=2,∴抛物线y=x2﹣4x+3的顶点及它与x轴的交点三点连线所围成的三角形面积为:×2×1=1.11.已知二次函数y=ax2+bx+c(a≠0)的顶点坐标(﹣1,﹣3.2)及部分图象(如图),由图象可知关于x的方程ax2+bx+c=0的两个根分别是x1=1.3和x2= ﹣3.3 .【考点】图象法求一元二次方程的近似根.【分析】先根据图象找出函数的对称轴,得出x1和x2的关系,再把x1=1.3代入即可得x2.【解答】解:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(﹣1,﹣3.2),则对称轴为x=﹣1;所以=﹣1,又因为x1=1.3,所以x2=﹣2﹣x1=﹣2﹣1.3=﹣3.3.故答案为:﹣3.312.将抛物线y=ax2向右平移2个单位,再向上平移3个单位,移动后的抛物线经过点(3,﹣1),那么移动后的抛物线的关系式为y=﹣4(x﹣2)2+3 .【考点】二次函数图象与几何变换.【分析】易得新抛物线的顶点,根据顶点式及所给的坐标可得新抛物线的解析式.【解答】解:原抛物线的顶点为(0,0),向右平移2个单位,再向上平移3个单位,那么新抛物线的顶点为(2,3);可设新抛物线的解析式为y=a(x﹣h)2+k,把(3,﹣1)代入得a=﹣4,∴y=﹣4(x﹣2)2+3.13.若二次函数y=(m+5)x2+2(m+1)x+m的图象全部在x轴的上方,则m的取值范围是m>.【考点】抛物线与x轴的交点.【分析】由题意二次函数y=(m+5)x2+2(m+1)x+m的图象全部在x轴的上方,可知(m+5)x2+2(m+1)x+m=0,方程二次项系数(m+5)>0,方程根的判别式△<0,根据以上条件从而求出m的取值范围.【解答】解:∵二次函数y=(m+5)x2+2(m+1)x+m的图象全部在x轴的上方,∴(m+5)>0,△<0,∴m>﹣5,4(m+1)2﹣4(m+5)×m<0,解得m>.故m>14.如图,⊙O的半径为2,C1是函数y=x2的图象,C2是函数y=﹣x2的图象,则阴影部分的面积是2π.【考点】二次函数的图象.【分析】不规则图形面积通过对称转化为可求的图形面积.【解答】解:由图形观察可知,把x轴上边的阴影部分的面积对称到下边就得到一个半圆阴影面积,则阴影部分的面积s==2π.故答案为:2π.三、解答题:15.某学校在一次投掷铅球时,刚出手时铅球离地面的m,铅球运行的水平距离为4m时,达到最高,高度为3m,如图所示:(1)求抛物线的函数关系式;(2)这名学生此次投掷成绩大约是多少?【考点】二次函数的应用.【分析】(1)由题意知铅球运行的水平距离为4m时,达到最高,高度为3m,故能知道顶点坐标,设抛物线的函数关系式y=a(x﹣b)2+c,代入题干数据解得a、b、c,(2)令二次函数解析式y=0,就出x.【解答】解:(1)由题意知铅球运行的水平距离为4m时,达到最高,高度为3m,故能知道顶点坐标为(4,3);设抛物线的函数关系式y=a(x﹣4)2+3,代入点(0,),解得a=﹣,故抛物线的函数关系式y=﹣(x﹣4)2+3;(2)令y=0,即=﹣(x﹣4)2+3=0,解得x1=10,x2=﹣2(舍去).答:这名学生此次投掷成绩大约是10m.16.如图所示,过点A(a,0)(a>0)且平行于y轴的直线分别与抛物线y=x2及y=x2交于C、B两点.(1)求点C、B的坐标;(2)求线段AB与BC的比;(3)若正方形BCDE的一边DE与y轴重合,求此正方形BCDE的面积.【考点】二次函数综合题.【分析】(1)根据已知得出B,C两点横坐标为:a,代入解析式即可得出B,C纵坐标;(2)表示出)|AB|=a2,|BC|=a2,进而求出比值;(3)由已知得出正方形BCDE的边长为a和a2,求出a的值即可得答案.【解答】解:(1)∵过点A(a,0)(a>0)且平行于y轴的直线分别与抛物线y=x2及y=x2交于C、B两点.∴B,C两点横坐标为:a,∴分别代入二次函数解析式即可;∴y=a2,y=,∴C(a,a2) B(a,);(2)∵|AB|=a2,|BC|=a2﹣a2=a2,∴|AB|:|BC|=1:3;(3)∵正方形BCDE的边长为a和a2,由a=a2,解得:a=,所以正方形BCDE的面积.17.有一条长7.2米的木料,做成如图所示的“日”字形的窗框,问窗的高和宽各取多少米时,这个窗的面积最大?(不考虑木料加工时损耗和中间木框所占的面积)【考点】二次函数的应用.【分析】设窗框的宽为x米,窗框的高为,则窗框的面积为S=x•,再求得面积的最大值即可.【解答】解:设窗框的宽为x米,则窗框的高为米.则窗的面积S=x•S=.当x==1.2(米)时,S有最大值.此时,窗框的高为=1.8(米)18.某公司生产的A种产品,每件成本是2元,每件售价是3元,一年的销售量是10万件.为了获得更多的利润,公司准备拿出一定资金来做广告.根据经验,每年投入的广告费为x(万元)时,产品的年销售量是原来的y倍,且y是x的二次函数,公司作了预测,知x与y(2)如果把利润看成是销售总额减去成本和广告费,请你写出年利润S(万元)与广告费x (万元)的函数关系式;(3)从上面的函数关系式中,你能得出什么结论?【考点】二次函数的应用.【分析】(1)设所求函数关系式为y=ax2+bx+c,代入三点求出a、b、c,(2)由利润看成是销售总额减去成本和广告费列出关系式,(3)把二次函数化成顶点坐标式,观察S随x的变化.【解答】解:(1)设所求函数关系式为y=ax2+bx+c,把(0,1),(1,1.5),(2,1.8)分别代入上式,得解得∴y=﹣x2+x+1(2)S=(3﹣2)×10y﹣x=(﹣x2+x+1)×10﹣x=﹣x2+5x+10.(3)∵S=﹣x2+5x+10=﹣.∴当0≤x≤2.5时,S随x的增大而增大.因此当广告费在0﹣2.5万元之间时,公司的年利润随广告费的增大而增大19.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣6)2+h.已知球网与O点的水平距离为9m,高度为2.43m,球场的边界距O点的水平距离为18m.(1)当h=2.6时,求y与x的关系式(不要求写出自变量x的取值范围)(2)当h=2.6时,球能否越过球网?球会不会出界?请说明理由;(3)若球一定能越过球网,又不出边界,求h的取值范围.【考点】二次函数的应用.【分析】(1)利用h=2.6将点(0,2),代入解析式求出即可;(2)利用当x=9时,y=﹣(x﹣6)2+2.6=2.45,当y=0时,,分别得出即可;(3)根据当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),以及当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2)时分别得出h的取值范围,即可得出答案.【解答】解:(1)∵h=2.6,球从O点正上方2m的A处发出,∴抛物线y=a(x﹣6)2+h过点(0,2),∴2=a(0﹣6)2+2.6,解得:a=﹣,故y与x的关系式为:y=﹣(x﹣6)2+2.6,(2)当x=9时,y=﹣(x﹣6)2+2.6=2.45>2.43,所以球能过球网;当y=0时,,解得:x1=6+2>18,x2=6﹣2(舍去)故会出界;(3)当球正好过点(18,0)时,抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:,解得:,此时二次函数解析式为:y=﹣(x﹣6)2+,此时球若不出边界h≥,当球刚能过网,此时函数解析式过(9,2.43),抛物线y=a(x﹣6)2+h还过点(0,2),代入解析式得:,解得:,此时球要过网h≥,故若球一定能越过球网,又不出边界,h的取值范围是:h≥.。
九年级数学下册 第三章 圆小结与复习练习课件

第十五页,共二十九页。
2021/12/8
第十六页,共二十九页。
2021/12/8
第十七页,共二十九页。
2021/12/8
第十八页,共二十九页。
2021/2/8
第十九页,共二十九页。
2021/12/8
第二十页,共二十九页。
2021/12/8
第二十一页,共二十九页。
2021/12/8
第二十二页,共二十九页。
2021/12/8
第二十三页,共二十九页。
2021/12/8
第二十四页,共二十九页。
2021/12/8
第二十五页,共二十九页。
2021/12/8
第二十六页,共二十九页。
2021/12/8
第二十七页,共二十九页。
2021/12/8
第二十八页,共二十九页。
内容 总结 (nèiróng)
九年级数学(shùxué)下册(BS)
No Image
12/8/2021
第二十九页,共二十九页。
2021/12/8
第八页,共二十九页。
2021/12/8
第九页,共二十九页。
2021/12/8
第十页,共二十九页。
2021/12/8
第十一页,共二十九页。
2021/12/8
第十二页,共二十九页。
2021/12/8
第十三页,共二十九页。
2021/12/8
第十四页,共二十九页。
2021/12/8
2021/12/8
第一页,共二十九页。
九年级数学(shùxué)下册(BS)
2021/12/8
第二页,共二十九页。
2021/12/8
第三页,共二十九页。
2021/12/8
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省灌南县实验中学九年级数学《第三章小结与思考》(2)
人教新课标版
班级 姓名 学号 得分
一.选择题:(每题4分,共28分)
1.如果a 是实数,下列各式一定有意义的是 ( ) A .a B .
2
1a
C . 122+-a a
D .2a -
2.下列各式中,不成立的是 ( ) (A)
B 、5552⋅=
C 、
()552
=- D 、
()552
-=-
3.能与2cm 和3cm 的线段组成直角三角形的第三条线段的长是( ) A .5 B .1 C .7 D .5或1
4.下列二次根式中,最简二次根式是 ( ) (A )8a (B )5a (C )
3
a (D )22a a
b +
5.下列根式中与23可以合并的是 ( ) A .12 B .27 C .72 D .1.0
6.下列计算正确的是 ( )
A .235+=
B .2
36=· C .84= D .2(3)3-=- 7.已知a <0,那么a a 22-可化简为 ( )
(A )-a (B )a (C )-3a (D )3a 二. 填空题:(每题4分,共32分) 1.当x 时,式子
1
2--x x
在实数范围内有意义。
2. 3
4
22c abc a b
字母均大于0)= . 3.已知2
51-=
x ,则x
x 1
-
的值等于___________.
4. 将a
a 1
-
(a <0)根号外的因式移入根号内的结果是 。
5.若长方形的面积为302
cm ,且宽为5cm ,则长为 。
6.若a+4 +a+2b -2 =0,则ab = 。
7.解方程:
3
22123x x =
+,得x = .
8.若x<2,化简x x -+-3)2(2
的正确结果是 三.计算题:(每小题7分,共计42分) 1. 3
1
13112-- 2. )52453204(52+- 3. 32
218+- 4.
2
2
23
3
3-
-
-
5.1322
1355⨯÷; 6. 3122a b b a b ⎛⎫•÷ ⎪ ⎪⎝⎭
四. 解答题(28分)
1.(8分)已知:31,31x y =+=-,求22
x y -.
2. (10分)化简并求值: x
x x x x x x 1
12122÷⎪⎭⎫ ⎝⎛+---+,其中12+=x .
3.(10分)已知: Rt ⊿ABC 中,∠C=90°3232求 (1)Rt ⊿ABC 的面积; (2)斜边AB 的长.
五.提高题:(10+10=20)
1.数a 、b 在数轴上的位置如图所示,化简:()()()2
2
2
11b a b a ---+
+
2.因为
(
)
223122
-=-,
所以12223-=-,因为(
)
223122
+=+,
所以12223+=+,因为()
3473
22
-=-,所以32347-=-,
请你根据以上规律,结合你的经验化简下列各式:
(1)625- (2)24
9
+
1
2
3
-1
-2 -3。
