中考真题专题汇编-综合计算题

合集下载

中考计算真题专项练习100题

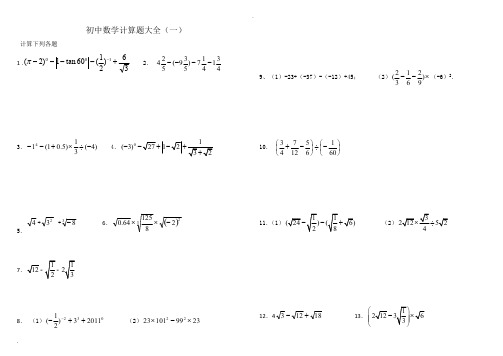
第 1 页中考计算真题专项练习100题12．6-6） 34．解下列方程：（1（256（用配方法解） 78．（本题4分）计算910．（1（2）已知：tan60°·sinα.11．计算(1).(2).-36） 12－313．解方程（1）532436x x-=-；（2）431.60.20.5x x +--=- 14．计算：0323||()tan 60823ππ+-++︒+--．15．解不等式组，并把它们的解集在数轴上表示出来.(1)33213(1)8x x x x -⎧+≥⎪⎨⎪--<-⎩ （2）⎪⎩⎪⎨⎧<+>-3)4(2112x x 16．()()241940-+---17．（－5）×（－8）－（－28）÷4 18．12)1276521(⨯-+ 19．－22－（－2）2－23×（－1）2011 20．4932÷-+|－4|×0.52+292×（－121）2 21．（10分）计算：121()24234-+-⨯-.22．先化简，再求值：(21+a 1)212+-a a ，其中a ＝13+．23．先化简，再求值xx x x x x 41)111(22+÷-+++其x足方程0122=--x x ．24．计算：0011124sin 60(3()3--+---π）25．计算：()0432--+-．26．21233(2)(2)x y x y ---÷第 3 页27．11122-+--+a aa a a 28．计算：2sin30°+4cos30°·tan60°-cos 245°29．先化简，再求值：)211(342--⋅--a a a ，其中3-=a ． 30．（1−16 +34）×（−48）31．计算： |－4|2÷－（2－3）0＋2)21(-- 32．计算221()a ba b a b b a-÷-+-33．计算 1a a-÷1a a a 22---1a 1- 34．解方程=--3x x 21-x31-35．先化简后求值。

中考化学真题分类汇编计算题(含解析)-人教版初中九年级全册化学试题

综合计算题(一)1.(18某某)尿素[CO(NH2)2]是一种常见的氮肥，工业上制备反应如下：CO2+2NH3CO(NH2)2+H2O，请计算：（1）尿素中氮元素的质量分数。

（2）生产6t尿酸理论上需要氨气的质量是多少？化学试题参考答案及评分标准【答案】（1）46.7%t。

【解析】（1）尿素中氮元素的质量分数为：×100%=46.7%（2）设理论上需要氮气的质量为x。

CO2+2NH3CO(NH2)2+H2O3460x6tx tt。

2.(18某某)一种新型“人造树叶”可吸收二氧化碳并转化为乙醇(C2H5OH)燃料，化学方程式为2CO2+3H2O C2H5OH+3O2。

研究显示，一升“人造树叶”每天可从空气中吸收968gCO2。

(1)一升“人造树叶”工作一天可得到乙醇的质量是________?(2)若每天一棵树平均可吸收2，则一升“人造树叶”吸收的CO2相当于_______棵树吸收的CO2。

【答案】(1).506g(2).20【解析】根据反应的化学方程式计算解答。

(1)设一升“人造树叶”工作一天可得到乙醇的质量为x。

2CO2+3H2O C2H5OH +3O28846968gxx=506g(2)968g÷48.4g=20答：(1)一升“人造树叶”工作一天可得到乙醇的质量是506g；(2)若每天一棵树平均可吸收2，则一升“人造树叶”吸收的CO2相当于20棵树吸收的CO2。

3.(18某某)用溶质质量分数为5%的NaOH溶液中和73g的稀盐酸，反应过程中溶液的酸碱度变化如下图所示。

请计算:(1)用质量分数为10％的氢氧化钠溶液配制5％的氢氧化钠溶液100g，需要水__________克.(2)当a为80g时，所得溶液中溶质的质量分数是___________(结果精确到0.1%)?【答案】(1)50(2)3.8%【解析】(1)设需要水的质量为x，根据溶质在稀释前后质量不变。

100g×5%=(100g-x)×10%x=50g；(2)根据图像可知，当a为80g时，盐酸与氢氧化钠恰好完全反应。

中考数学真题《计算综合》专项测试卷(附答案)

中考数学真题《计算综合》专项测试卷(附答案)学校:___________班级：___________姓名：___________考号：___________1．（2024·北京海淀·二模）计算：020242sin 45|3|8-︒+-【答案】42【分析】本题主要考查实数的混合运算掌握零次幂特殊角的三角函数值的计算二次根式的性质化简绝对值的性质化简等知识是解题的关键．【详解】解：020242sin 4538-︒+-21232=-++42=2．（2024·北京海淀·二模）解不等式组：532342(1)x x x x +⎧<⎪⎨⎪->+⎩【答案】6x >【分析】本题考查了解一元一次不等式组熟练掌握不等式组的解法是解题关键．先分别求出两个不等式的解集再找出它们的公共部分即为不等式组的解集．【详解】解：由532x x +< 解不等式可得1x > 由342(1)x x ->+解不等式可得6x >综上可得不等式组的解集为6x >．3．（2024·北京海淀·二模）已知2230m n --= 求代数式2()2()m n n m n +-+的值．【答案】3【分析】本题主要考查了已知式子的值求代数式的值根据2230m n --=可得出223m n -= 代数式2()2()m n n m n +-+提因式得到()()2m n m n n ++- 再用平方差公式即可得出22m n - 即可得到答案．【详解】解：2230m n --= 即223m n -= 2()2()m n n m n +-+()()2m n m n n =++- ()()m n m n =+-22m n =-3=4．（2024·北京东城·()13112tan6022-⎛⎫+--- ⎪⎭︒⎝．36【分析】本题考查了实数的混合运算利用二次根式的性质特殊角的三角函数值负整数指数幂乘方的意义进行化简再计算加减即可掌握运算法则是解此题的关键．()13112tan6022-⎛⎫+--- ⎪⎭︒⎝()()23328=---36=．5．（2024·北京东城·二模）解不等式组：()2154,611.3x x x x ⎧+<-⎪⎨+≥-⎪⎩【答案】2x >【分析】本题主要考查解一元一次不等式组根据不等式的性质求出不等式的解集根据找不等式组解集的规律找出不等式组的解集即可．【详解】解：()21546113x x x x ⎧+<-⎪⎨+≥-⎪⎩①② 解不等式① 得 2x > 解不等式① 得 43x ≥-所以不等式组的解集为：2x >6．（2024·北京朝阳·二模）计算：113tan3027233-⎛⎫︒+- ⎪⎝⎭【答案】3【分析】本题考查特殊角的三角函数值负整数指数幂二次根式化简以及去绝对值正确计算是解答本题的关键．先计算特殊角的三角函数值负整数指数幂化简二次根式以及去绝对值再计算加减即可．【详解】解：113tan3027233-⎛⎫︒+- ⎪⎝⎭333333=+-333323=-3=．7．（2024·北京朝阳·二模）解不等式345(2)x x +<+ 并写出它的所有负整数解．【答案】不等式的解集是3x >- 其中所有负整数解为2- 1-【分析】此题考查一元一次不等式的整数解解题关键在于掌握运算法则．先解出不等式的解集再求其负整数解．【详解】解：34510x x +<+．移项得 35104x x -<-．合并同类项得 26x -<．系数化为1得 3x >-．所以原不等式的所有负整数解为2- 1-．8．（2024·北京门头沟·()213220212sin 602π-⎛⎫-+++ ⎪⎝⎭°．【答案】5【分析】本题考查了含特殊角的三角函数值的实数的混合运算根据相应的运算法则计算即可．()213220212sin 602π-⎛⎫-++︒+ ⎪⎝⎭23134=5=．9．（2024·北京门头沟·二模）解分式方程26111x x x -=+-【答案】5x =-【分析】本题考查了解分式方程正确掌握解分式方程的法则及步骤是解题的关键．将分式方程去分母化为整式方程解整式方程求出解并检验即可．【详解】解：26111x x x -=+- 方程两边乘以(1)(1)x x +-得：(1)6(1)(1)--=+-x x x x 去括号：2261x x x --=- 移项：2216x x x --=-+ 合并同类项：5x -= 系数化1：5x =-．经检验：5x =-是原方程的解． ∴原方程的解是5x =-．10．（2024·北京门头沟·二模）已知：0x y -= 求()2222x yx y x xy y -⋅+++的值．【答案】2x y x y -+ 12- 【分析】本题考查分式化简求值问题先通分计算括号里的再除法转化成乘法计算括号外的最后把x y =的值代入计算即可．【详解】解：()2222x yx y x xy y -⋅+++()()22x yx y x y -=⋅++2x yx y-=+ ①0x y -= ①x y = ①原式212x x x x -==-+． 11．（2024·北京昌平·1182sin 45122-⎛⎫-︒+ ⎪⎝⎭.【答案】2+1【分析】本题考查了二次根式绝对值负指数幂特殊角的三角函数值的运算熟悉运算法则是解题的关键．根据二次根式绝对值负指数幂特殊角的三角函数值的运算化简计算即可．【详解】解：原式222221=- 222221=221=．12．（2024·北京昌平·二模）解不等式组：38312x x x x -≥⎧⎪⎨->⎪⎩①②．【答案】4x ≥【分析】本题考查解一元一次不等式组．先解出每个不等式的解集即可得到不等式组的解集．【详解】解：38312x x x x -≥⎧⎪⎨->⎪⎩①②．解不等式①得 4x ≥ 解不等式①得 1x >所以这个不等式的解集为4x ≥．13．（2024·北京昌平·二模）已知220x x +-= 求代数式212111x x ⎛⎫+÷ ⎪--⎝⎭的值．【答案】1【分析】本题考查的是分数的混合运算．将212111x x ⎛⎫+÷ ⎪--⎝⎭化简为22x x+ 再整体代入求值．【详解】解：原式211211x x x +-=÷--(1)(1)12x x x x +-=⋅-22x x += 220x x +-= 22x x ∴+=∴原式1=.14．（2024·北京顺义·二模）计算：13tan 302|1|12.︒--+-【答案】132【分析】本题考查实数的运算熟练掌握特殊角的三角函数值负整指数幂的运算法则是解题的关键．先把特殊角的三角函数值代入并运用负整指数幂的运算法则计算和求绝对值化简二次根式再计算乘法最后计算加减即可．【详解】解：13tan302112--+-3131232=+-13231232=+-132=15．（2024·北京顺义·二模）解不等式：2123x x -≥ 并求它的正整数解．【答案】2x ≤ 正整数解是2 1．【分析】此题考查了一元一次不等式的整数解正确解不等式求出解集是解答本题的关键解不等式的基本步骤：去分母去括号移项合并同类项系数化为1 解不等式应根据不等式的基本性质．首先解不等式然后确定不等式的解集中的正整数值即可．【详解】解：342x x ≥-2x -≥-2x ≤正整数解是2 1．16．（2024·北京房山·二模）计算：()0π34sin60212--+-︒【答案】3【分析】本题主要考查了特殊角三角函数值和实数的混合运算熟练掌握运算法则和特殊角三角函数值是解答本题的关键．先求出特殊角的三角函数值幂的运算并对绝对值二次根式化简再进行计算即可．【详解】()0π34sin60212--+-︒31423=-++3=．17．（2024·北京房山·二模）解不等式组：12822x x x x +⎧<⎪⎨⎪->+⎩．【答案】1x <【分析】本题考查了解一元一次不等式组熟练掌握知识点是解题的关键．先解每一个一元一次不等式再取解集的公共部分即可．【详解】解：原不等式组为12822x x x x +⎧<⎪⎨⎪->+⎩①② 解不等式① 得1x < 解不等式① 得2x < ∴原不等式组的解集为1x <．18．（2024·北京房山·二模）已知2210x x +-= 求代数式()()223x x x ++-的值．【答案】5【分析】本题考查了代数式求值完全平方公式整式的乘法解决本题的关键是利用整体的思想求解．先将代数式展开得到224x x ++ 再将2210x x +-=化简为221x x += 整体代入求值即可．【详解】解：()()223x x x ++- 22443x x x x =+++-224x x =++．2210x x +-= 221x x ∴+=∴原式2245x x =++=．19．（2024·北京·二模）计算：0(π2024)4sin 60512-+︒+-【答案】6【分析】本题考查实数的运算熟练掌握相关运算法则是解题的关键．利用特殊锐角三角函数值二次根式的性质零整数指数幂绝对值的性质计算即可【详解】解：0(π2024)4sin 60512-+︒+-314523=+-6=．20．（2024·北京·二模）解不等式组：2123x x x x -≤⎧⎪⎨+>⎪⎩【答案】31-<≤x【分析】本题考查的是解一元一次不等式组熟知“同大取大同小取小大小小大中间找大大小小找不到”的原则是解答此题的关键．分别求出每一个不等式的解集根据口诀：同大取大同小取小大小小大中间找大大小小无解了确定不等式组的解集．【详解】解：原不等式组为2123x x x x -≤⎧⎪⎨+>⎪⎩①②解不等式① 得1x ≤ 解不等式① 得3x >-①原不等式组的解集为31-<≤x ．21．（2024·北京·二模）已知340m n +-= 求代数式2226+69m nm mn n ++的值．【答案】12【分析】本题考查了分式的化简求值熟练掌握因式分解是解题的关键．先算对分子分母进行因式分解再约分然后根据340m n +-=可以得到34m n +=然后代入化简后的式子即可．【详解】解：2226+69m nm mn n ++22(3)(3)m n m n +=+23m n=+． ①340m n +-= ①34m n +=①原式21 42==．22．（2024·北京大兴·311232sin602-⎛⎫+--︒⎪⎝⎭．35【分析】本题考查了实数的运算分别根据二次根式化简负整数指数幂的运算法则化简绝对值特殊角的三角函数值计算出各数再进行合并计算即可熟知二次根式化简负整数指数幂的运算法则化简绝对值特殊角的三角函数值是解题的关键．【详解】解：原式3 3832=+-353 =35=．23．（2024·北京大兴·二模）解不等式组：()213 412x xxx⎧-<+⎪⎨+>⎪⎩【答案】152x -<<【分析】本题考查解一元一次不等式组分别解出每个不等式的解集然后确定不等式组的解集熟练掌握不等式组的解法是解题的关键．【详解】解：()213412x x x x ⎧-<+⎪⎨+>⎪⎩①② 解不等式① 得5x < 解不等式① 得12x >-①原不等式组的解集为：152x -<<．24．（2024·北京大兴·二模）已知50x y --= 求代数式2222x y x yy x x ⎛⎫+--÷ ⎪⎝⎭的值．【答案】10【分析】本题考查分式的化简求值熟练掌握分式的混合运算法则是解题关键．先根据分式减法法则计算括号内的式子再根据分式除法法则化简得出最简结果把50x y --=变形后整体代入即可得答案．【详解】解：2222x y x yy x x ⎛⎫+--÷ ⎪⎝⎭ 2222x y xy xx x x y ⎛⎫+=-⋅⎪-⎝⎭ 2222x y xy x x x y⎛⎫+-=⋅⎪-⎝⎭()22x y xxx y-=⋅- ()2x y =-．①50x y --= ①5x y -=①原式()2=10x y =-．25．（2024·北京石景山·()0276tan3012024︒--+．3【分析】本题主要考查了实数的运算求特殊角三角函数值 27=33 3tan 30︒=11-= 02024=1 再计算即可.【详解】解：原式333611=+ 333=326．（2024·北京石景山·二模）解不等式组：3452924x x xx -<+⎧⎪⎨-<⎪⎩【答案】31x -<<【分析】本题考查的是解一元一次不等式组分别求出各不等式的解集再求出其公共解集即可．熟知“同大取大同小取小大小小大中间找大大小小找不到”的原则是解答此题的关键．【详解】解：原不等式组为3452924x x xx -<+⎧⎪⎨-<⎪⎩①② 解不等式① 得3x >-．解不等式① 得1x <．∴原不等式组的解集为31x -<<．27．（2024·北京丰台·．【答案】解：原式=22+3-2-2×22=22+3-2-2=2+1． 28．（2024·北京丰台·二模）解不等式组：【答案】解：解不等式① 得2<x解不等式① 得21->x∴不等式组的解集为221<<-x ．29．（2024·北京丰台·二模）已知22360a a --= 求代数式(12)(12)3(12)a a a a +---的值．【答案】解：原式=221436a a a --+=2123a a +-．①22360a a --= ①2236a a -=．①原式=16+=7．30．（2024·北京西城·二模）计算：4cos45°−√18+|−√2|−(π+3)0．118|3|2sin 452（）°-+---22345，．x x x x +⎧<⎪⎨⎪-<+⎩【答案】31．（2024·北京西城·二模）解不等式组{3x−2＜x+4x≥2x−35并写出它的所有整数解．【答案】32．（2024·北京西城·二模）已知x2+x﹣3＝0 求代数式(1+3x−1)⋅3x2+4x+4的值．【答案】33．（2024•顺义区二模）如果1m n+=那么代数式22(1)m m nm n n--⋅-的值为()A．1-B．1C．2-D．2【答案】A【考点】分式的化简求值【分析】将所求式子化简然后将m n+的值代入计算即可．【解答】解：1m n +=∴22(1)m m n m n n--⋅- ()()m n m m n m n m n n--+-=⋅-()()n m n m n m n n-+-=⋅- ()m n =-+1=-故选：A ．34．（2024•朝阳区二模）已知2220x x +-=，则代数式22(1)(1)(1)2x x x x +++-+的值为( ) A ．4B ．2C ．1D ．0【答案】A【考点】整式的混合运算—化简求值【分析】先根据完全平方公式和平方差公式进行计算再合并同类项求出222x x += 最后代入求出答案即可．【解答】解：22(1)(1)(1)2x x x x +++-+ 2222112x x x x =+++-+ 242x x =+ 2220x x +-= 222x x ∴+=∴原式22(2)224x x =+=⨯=．故选：A ．35．（2024•东城区二模）在下列各式中从左到右计算结果正确的是( ) A 862B ．22(1)1x x -=- C 2(2)2--D ．12111x x x -+=++ 【答案】D【考点】二次根式的加减法完全平方公式二次根式的性质与化简分式的加减法【分析】直接利用二次根式的加减运算法则完全平方公式二次根式的性质分式的加减运算法则分别化简进而得出答案．【解答】解：A 86 故此选项不合题意B ．22(1)21x x x -=-+ 故此选项不合题意C 2(2)2- 故此选项不合题意D ．12111x x x -+=++ 故此选项符合题意．故选：D ．36．（2024•石景山区二模）若2310x x -+=，则代数式(2)(2)(6)x x x x +-+-的值为．【答案】6-．【考点】整式的混合运算—化简求值【分析】先根据平方差公式和单项式乘多项式法则进行计算再合并同类项求出231x x -=- 最后代入求出答案即可．【解答】解：(2)(2)(6)x x x x +-+- 2246x x x =-+- 2264x x =-- 2310x x -+= 231x x ∴-=-∴原式22(3)42(1)4246x x =--=⨯--=--=-．故答案为：6-．37．（2024•东城区二模）若250m m +-=，则代数式22111()10m m m m--÷的值为．【答案】2．【考点】分式的化简求值【分析】先利用异分母分式加减法法则计算括号里再算括号外然后把25m m +=代入化简后的式子进行计算即可解答．【解答】解：22111()10m m m m--÷第 21 页共 21 页 2110(1)(1)m m m m m -=⋅+- 10(1)m m =+ 210m m=+ 250m m +-= 25m m ∴+= ∴当25m m +=时原式1025== 故答案为：2．。

(完整版)初中数学中考计算题复习含答案

1 .23621601214314175395243 40431511454233862328125647--8123220113212399101232210601651274311121241318123214 1531246612131321620212529363181712312712661833218243352741581920112|4120131124212223231|1|3333325=14-9=5387431511441312318118741-44011536414233832527------813229200121012-992(101-99)21220091-3;210121-23+-37--12+45410-30=-45-606512743606560127604335+50=-3011121212121312131431323157.21113262969276161212233633231212122312231712233411851451424334155275424335274155424335274158019-2.+2-=-2.1. 2.201212352122232------------------------------------------------------------------63253--------71　220130　3|1|012013567　8　10　111213+|3|+1　151612120130+||222+412　17112013|7|+0121819122012302452211|3|+162320130222122312+124122512+12612272829201322012420113011一．解答题（共3011211+12121211101220130+1+13|1|01201312+1111212451141144362744421811139210+31111111212原式第一项利用立方根的定义化简，第二项利用负数的绝对值等于它的相反数计算法则计算，第四项利用负指数幂法则计算，第五项利用1181311321132132214 3.140+|3|+120131415221612120130+||222+412121122424242+4　17112013|7|+01211211115218原式第一项利用立方根的定义化简，第二项利用二次根式的化简公式化简，第三项利用零指数幂法则计算，1451912121114+1+|12|142121112012302452121222311416314211|3|+16232013021）原式第一项利用负数的绝对值等于它的相反数计算，第二项先计算乘方运算，再计算除法运算，第2131234622212121121313122312+11）原式第一项利用负数的绝对值等于它的相反数计算，第二项利用特殊角的三212172+1+324121）原式第一项利用绝对值的代数意义化简，第二项利用零指数幂法则计算，第三项利用负指数幂法则21+13+3213212512+112112+126121）原式第一项利用特殊角的三角函数值化简，第二项利用零指数幂法则计算，212211118272282129201322012420112011201122420112242011+522420110301819126-6 3020151351251513 223113415322 2215113656 709422023432852213222330 920121451012456011 ---3622337956347181213343144201232221113．解方程（本小题共61 2532436431.60.20.5140||6015 233218342101216241940 17582818 192221121276521223201120+|4|×0.5+21 21 49322922121212423424 25 0116033230148 31|4|201634232212117538131383171. 2. 3. 4. 5.62-36:-363-17.=-1+1-9-8=-174172312x-2=3x+5 2x-3x=2+5x=-7262(2x+1)-(5x-1)=6x=-354113【解析】先把第二个方程去分母得3x-4y=-2,4113622114211222212221117363236322182323931410123211212111-192-111=-9÷9-18=-1-18=-192753796418=-28+30-27+14=-111221311326313 1532436112171217129128122121543326452431.60.20.529362762732661361263616220561235414试题分析：原式第一项利用零指数幂法则计算，第二项利用绝对值的代数意义化简，第三项利用特殊角的三角函数值计算，最后一项利用立方根定义化简计算即可得到2. 3.153222123x-3+6≥2x332181-3x+3-8+x 0-23223421012122221161747 189190 2021-40--19-24=-40+19-24=-45 2-5-8--28 3-1256712=6+10-74-22--22-23-12011=-4-4+85-32+|-4|×0.52+2-12942912=-4+1+521 312124234 712166 102244124322421 1212423412166224001160341313200116034131322425 =2-1+230-76=-48+8-36=-76316412 95。

中考化学计算题综合题汇编含详细答案

一、中考初中化学计算题1．实验室有一瓶未知浓度的BaCl2溶液，某同学取出150g该溶液于烧杯中，向其中逐滴加入溶质质量分数为26.5%的Na2CO3溶液。

反应过程中生成沉淀的质量与所用Na2CO3溶液质量的关系如图所示。

已知：BaCl2＋Na2CO3=BaCO3↓＋2NaCl。

请计算：(1)配制26.5%的Na2CO3溶液80g，需要Na2CO3固体___g。

(2)BaCl2溶液的溶质质量分数是____？(写出计算过程，结果保留到0.1%)【答案】(1) 21.2g；（2）13.9%【解析】试题分析：（1）根据溶质质量分数计算的表达式：配制26．5%的Na2CO3溶液80g，需要Na2CO3固体质量=80g×26．5%=21．2g（2）从图甲中获知，当BaCl2完全转化为沉淀时消耗Na2CO3溶液的质量为40g,再根据化学反应方程式：BaCl2＋Na2CO3＝BaCO3↓＋2NaCl中Na2CO3与BaCl2的质量关系，可求出BaCl2的质量，进而可求解BaCl2溶液的溶质质量分数解：设BaCl2的质量为xBaCl2＋Na2CO3＝BaCO3↓＋2NaCl208106x40g×26．5%208∶106＝X∶(40g×26．5%)x＝208×40g×26．5%/106＝20．8g该BaCl2溶液的溶质质量分数＝（20．8g/150g）×100%=13．9%答：该BaCl2溶液的溶质质量分数为13．9%考点：溶质质量分数计算，根据化学方程式计算2．某中学化学课外活动小组对某工厂排放的含少量硫酸的废水进行抽样检测．取一定量的废水，用质量分数为1%的氢氧化钡溶液中和(其它物质不与氢氧化钡反应)，当恰好中和时，消耗氢氧化钡溶液的质量为171g，过滤后，测得滤液的质量为268.67g．(不考虑过滤时滤液质量损失)(计算结果保留二位小数)求：①反应中生成沉淀的质量为多少？②该工厂排放的废水中所含硫酸的质量分数为多少？【答案】①2.33g ②0.98%【解析】解：①设生成沉淀的质量为x，废水样品中所含硫酸质量为y；H2SO4+Ba(OH)2═BaSO4↓+2H2O98 171 233 y 171g×1% x1711711%=233g x ⨯，x=2.33g ； 98=1711711%y g ⨯，y=0.98g ； ②根据质量守恒定律知：所取废水样品质量=（268.67+2.33）g-171g=100g ，该工厂排放的废水中硫酸的质量分数=0.98100gg×100%=0.98%；答：①反应中生成沉淀的质量为2.33g ；②该工厂排放的废水中所含硫酸的质量分数为0.98%。

汇总)初中数学中考计算题(最全)-含答案

汇总)初中数学中考计算题(最全)-含答案.doc1.解答题（共30小题）1.1 计算题：① 2+3=5；②解方程：x+5=10，解得x=5.1.2 计算：π+（π﹣2013）=2π-2013.1.3 计算：|1﹣|﹣2cos30°+（﹣）×（﹣1）2013|=|1-|-2cos30°+（-1）×（-1）2013||=|1-|-2×√3/2+1||=|1-√3+1|=|2-√3|。

1.4 计算：﹣（-2）+（-3）=1.1.5 计算：√（5+2√6）+√（5-2√6）=√2+√3.1.6 计算：（2+√3）（2-√3）=1.1.7 计算：（1+√2）²=3+2√2.1.8 计算：（1-√3）²=4-2√3.1.9 计算：（√2+1）²=3+2√2.1.10 计算：（√2-1）²=3-2√2.1.11 计算：（3+√5）（3-√5）=4.1.12 计算：（√3+1）（√3-1）=2.1.13 计算：（√2+√3）²=5+2√6.1.14 计算：﹣（π﹣3.14）+|﹣3|+（﹣1）2013+tan45°=0.1.15 计算：√3+√2-√6=√3-√2+√6.1.16 计算或化简：1）计算2﹣1﹣tan60°+（π﹣2013）+|﹣|=-tan60°-2011；2）（a﹣2）²+4（a﹣1）﹣（a+2）（a﹣2）=-3a²+10a-6.1.17 计算：1）（﹣1）2013﹣|﹣7|+（√2）﹣1=-√2-8；2）（2+√3）÷（√3-1）=1+√3.1.18 计算：（1+√2）（1-√2）=﹣1.1.19 解方程：x²+2x+1=0，解得x=-1.1.20 计算：1）tan45°+sin230°﹣cos30°•tan60°+cos245°=√2-1；2）（√2+1）²-（√2-1）²=4√2.1.211）|﹣3|+16÷（﹣2）³+（2013﹣）﹣tan60°=2010；2）解方程：（1-2x）²=3，解得x=√2﹣1.1.222）求不等式组：{x²-2x0}，解得0<x<1.1.232）先化简，再求值：（√3+1）÷（√3-1）=2.1.241）计算：tan30°=√3/3；2）解方程：x²-2x+1=0，解得x=1.1.25 计算：1）√2-√3+√6=（√2-1）（√3-1）；2）先化简，再求值：（√2+1）²+（√2-1）²=8.1.261）计算：（1-√2）÷（1+√2）=-1+√2；2）解方程：x²-2x+2=0，解得x=1-√3.1.27 计算：1）（√2+√3）²-（√2-√3）²=4√6；2）先化简，再求值：（x²+2x+1）÷（x²-1）=1+x。

专题05解答基础题：计算综合(原卷版+解析)

专题05 计算综合题一、解答题（28题）专题05 计算综合题一、解答题（28题）1．（2023·重庆·统考中考真题）计算：(1)()()()211a a a a -++-； (2)22.211x x x x x x ⎛⎫÷- ⎪+++⎝⎭【答案】(1)21a - (2)11x + 【分析】（1）先计算单项式乘多项式，平方差公式，再合并同类项即可；（2）先通分计算括号内，再利用分式的除法法则进行计算．【详解】（1）解：原式2221a a a =-+-21a =-；（2）原式()222.11x x x x x x ⎛⎫+-=÷ ⎪++⎝⎭ ()22211x x x x =÷++ ()22211x x x x +=⋅+ 11x =+．【点睛】本题考查整式的混合运算，分式的混合运算．熟练掌握相关运算法则，正确的计算，是解题的关键．2．（2023·重庆·统考中考真题）计算：(1)()()263x x x ++-； (2)2293n m n m m -⎛⎫+÷ ⎪⎝⎭．【答案】(1)229x + (2)13m n- 【分析】（1）先根据单项式乘以多项式的法则、完全平方公式计算，再合并同类项；（2）根据分式混合运算的法则解答即可．【详解】（1）解：()()263x x x ++-22669x x x x =++-+229x =+；（2）解：2293n m n m m -⎛⎫+÷ ⎪⎝⎭ ()()333m n m m m n m n +=⋅+-13m n=-．【点睛】本题考查了整式和分式的运算，属于基本计算题型，熟练掌握整式和分式混合运算的法则是解题的关键．3．（2022·重庆·统考中考真题）计算：(1)()()(2)x y x y y y +-+-； (2)2244124m m m m m -+⎛⎫-÷ ⎪⎝⎭-+．【答案】(1)22x y - (2)22m - 【分析】（1）根据平方差公式和单项式乘多项式法则进行计算，再合并同类项即可；（2）先将括号里通分计算，所得的结果再和括号外的分式进行通分计算即可．【详解】（1）解：()()(2)x y x y y y +-+-=2222x y y y -+-=22x y -（2）解： 2244124m m m m m -+⎛⎫-÷ ⎪⎝⎭-+ =()()()222222m m m m m m -+-÷++- =()()()222222m m m m +-⨯+- =22m - 【点睛】本题考查了平方差公式、单项式乘多项式、合并同类项、分式的混合运算等知识点，熟练掌握运算法则是解答本题的关键．4．（2022·重庆·统考中考真题）计算：(1)()()224x x x ++-； (2)2212a a b b b -⎛⎫-÷ ⎪⎝⎭．【答案】(1)224x + (2)2a b+ 【分析】（1）先计算乘法，再合并，即可求解；（2）先计算括号内的，再计算除法，即可求解．【详解】（1）解：原式22444x x x x =+++-224x =+（2）解：原式2()()a b b b a b a b -=⨯+- 2a b =+ 【点睛】本题主要考查了整式的混合运算，分式的混合运算，熟练掌握相关运算法则是解题的关键． 5．（2021·重庆·统考中考真题）计算（1）()()22x y x x y -++；（2）2241244a a a a a -⎛⎫-÷ ⎪+++⎝⎭．【答案】（1）222x y +；（2）22a - 【分析】（1）利用完全平方公式和整式的乘法运算法则计算即可；（2）根据分式混合运算的运算法则计算即可．【详解】解：（1）()()22x y x x y -++=x 2﹣2xy +y 2+x 2+2xy=2x 2+y 2；（2）2241244a a a a a -⎛⎫-÷ ⎪+++⎝⎭ =22(2)(2))22(2)a a a a a a a ++--÷+++（ =22(2)2(2)(2)a a a a +⨯++- =22a -．【点睛】本题考查整式的混合运算、分式的混合运算、平方差公式、完全平方公式，熟练掌握运算法则是解答的关键．6．（2021·重庆·统考中考真题）计算：（1）2(23)()a a b a b ++-；（2）22293211x x x x x x ⎛⎫--÷+ ⎪+++⎝⎭．【答案】（1）223++a ab b ；（2）-31x x + 【分析】（1）根据单项式乘以多项式以及完全平方公式计算即可；（2）利用分式的混合运算法则进行计算即可．【详解】解：（1）2(23)()a a b a b ++-2222+3+2+=a ab a ab b -22=3++a ab b（2）22293211x x x x x x ⎛⎫--÷+ ⎪+++⎝⎭()()()222+3-3+3=11+x x x x x x x ⎛⎫-÷ ⎪++⎝⎭()()()2+3-31=31x x x x x +++ -3=1x x + 【点睛】本题考查了整式的混合运算和分式的混合运算，熟练掌握运算法则是解题的关键．7．（2023·重庆沙坪坝·重庆八中校考一模）计算(1)()()()2223x y y x x y +-+-(2)2121211x x x x +⎛⎫÷+ ⎪-+-⎝⎭ 【答案】(1)22562x xy y -+(2)11x - 【分析】（1）根据平方差公式与完全平方公式将原式展开，再合并同类项即可；（2）现将分式中的多项式因式分解，以及通分括号里的式子，再根据分式的除法法则求解即可．【详解】（1）解：原式()()()2223y x y x x y =+-+-()()22222323y x x x y y =-+-⨯⋅+2222496y x x xy y =-+-+ ()()2222496x x xy y y =-+-++22562x xy y =-+．（2）解：原式()2112111x x x x x +-⎛⎫=÷+ ⎪--⎝⎭- ()21111x x x x ++⎛⎫=÷ ⎪-⎝⎭- ()21111x x x x +-=⋅+- 11x =-．【点睛】本题考查了整式与分式的化简，需要熟练掌握平方差公式与完全平方公式，以及分式的混合运算，熟练掌握运算法则是解答本题的关键．8．（2023·重庆沙坪坝·重庆一中校考一模）计算：(1)()()2225x y x x y --- (2)221651m n n m n m n -⎛⎫÷- ⎪++⎝⎭ 【答案】(1)22xy y +(2)4m n +【分析】（1）根据完全平方公式，单项式乘以多项式进行计算即可求解；（2）根据分式的混合运算进行化简即可求解．【详解】（1）解：()()2225x y x x y ---()2222225x xy y x xy =-+-+ 22224225x xy y x xy =-+-+22xy y =+；（2）解：221651m n n m n m n -⎛⎫÷- ⎪++⎝⎭()()445m n m n m n n m n m n+-+-=÷++ ()()444m n m n m n m n m n+-+=⨯+- 4m n =+．【点睛】本题考查了整式的乘法以及分式的混合运算，熟练掌握整式的乘法运算以及分式的运算法则是解题的关键．9．（2023·重庆九龙坡·重庆市育才中学校考一模）计算：(1)()()22x y x y x +--； (2)224221121a a a a a a -⎛⎫-+÷ ⎪--+⎝⎭．【答案】(1)222x y + (2)12a + 【分析】（1）根据完全平方公式，单项式乘以多项式进行计算即可求解；（2）根据分式的加减进行计算，同时将除法转化为乘法，根据分式的混合运算进行化简即可求解．【详解】（1）解：()()22x y x y x +--22222x xy y xy x =++-+ 222x y =+；（2）解：224221121a a a a a a -⎛⎫-+÷ ⎪--+⎝⎭()()()222141121a a a a a -+-=⨯-- ()()()()22+111211a a a a a -=⨯--+ 12a +=．【点睛】本题考查了整式的化简，分式的混合运算，熟练掌握整式的运算法则以及分式的运算法则是解题的关键．10．（2023·重庆九龙坡·重庆实验外国语学校校考一模）计算：(1)(2)(2)(4)a b a b b a b +---； (2)222623969x x x x x ⎛⎫+÷ ⎪---+⎝⎭．【答案】(1)2a ab - (2)33x x --+ 【分析】（1）根据平方差公式与单项式乘以多项式进行计算即可求解；（2）根据分式的混合运算进行计算即可求解．【详解】（1）(2)(2)(4)a b a b b a b +---22244a b ab b =--+2a ab =-；（2）222623969x x x x x ⎛⎫+÷ ⎪---+⎝⎭ ()()()()26233332x x x x x -+-=⨯+- ()()()232332x x x x x--=⨯+- 33x x -=-+．【点睛】本题考查了整式的乘法运算，分式的混合运算，熟练掌握以上运算法则是解题的关键． 11．（2023·重庆南岸·统考一模）计算：(1)()()212x x x ++-； (2)293()a a a a --÷ 【答案】(1)221x +(2)2a 3a +【分析】(1）根据完全平方公式、单项式乘以多项式法则计算解答即可；(2）根据分式乘除法则进行计算即可．【详解】（1）解：()()212x x x ++-=22212x x x x +++-=221x +．（2）解：293()a a a a --÷ =2(3)(3)3a a a a a +-⨯-【点睛】此题考查整式、分式的混合计算，关键是根据整式、分工的混合计算顺序和完全平方公式进行解答．12．（2023·重庆沙坪坝·统考一模）计算：(1)()()221x x x -++； (2)24122m m m -⎛⎫+÷ ⎪⎝⎭．【答案】(1)41x + (2)2m m - 【分析】（1）先根据单项式乘以多项式，完全平方公式去括号，然后合并同类项即可；（2）根据分式的混合计算法则求解即可．【详解】（1）解：原式22221x x x x =-+++41x =+．（2）解：原式()()22222m m m m +-+=÷ ()()22222m m m m +=⋅+- 2m m =-．【点睛】本题主要考查了分式的混合计算，知识的混合计算，熟知相关计算法则是解题的关键． 13．（2023·重庆开州·校联考一模）计算：(1)()()224--+x y x x y ； (2)2214411a a a a a -+⎛⎫-÷ ⎪--⎝⎭．【答案】(1)284-+xy y (2)2a a - 【分析】（1）先根据完全平方公式，单项式乘多项式进行计算，再合并同类项即可；（2）先根据分式的减法法则进行计算，再根据分式的除法法则把除法变成乘法，最后根据分式的乘法法则进行计算即可．【详解】（1）解：()()224--+x y x x y＝222444-+--x xy y x xy（2）解：2214411a a a a a -+⎛⎫-÷ ⎪--⎝⎭＝()()211112-----a a a a a ＝()()21212----a a a a a ＝2a a - 【点睛】本题考查整式的混合运算和分式的混合运算，能正确根据整式的运算法则和分式的运算法则进行化简是解此题的关键，注意运算顺序．14．（2023·重庆合川·校考一模）计算：(1)(2)()(3)x y x y x x y ++-+；(2)2344(1)11x x x x x -+--÷++．【答案】(1)22y(2)22x x +- 【分析】（1）先去括号再合并同类项即可；（2）先计算括号内的再乘以后面的式子的倒数即可．【详解】（1）解：原式222223x xy xy y x xy =+++--22y =．（2）解：原式2(1)(1)3111(2)x x x x x x -++⎡⎤=-⋅⎢⎥++-⎣⎦ 2(2)(2)11(2)x x x x x +-+=⋅+- x 2x 2+=-．【点睛】本题考查了多项式乘以多项式，单项式乘以多项式，分式的混合运算，正确的计算是解题的关键． 15．（2023·重庆九龙坡·统考一模）化简：(1)()()()x y x y x x y -+--(2)22221211a a a a a a a ⎛⎫-÷-- ⎪-+-⎝⎭【答案】(1)2y xy -+ (2)1a a - 【分析】（1）先根据平方差公式和单项式乘多项式法则计算，再合并同类项即可；（2）根据分式的混合运算法则计算即可．【详解】（1）解：()()()x y x y x x y -+--222x y x xy =--+2y xy =-+；（2）解：22221211a a a a a a a ⎛⎫-÷-- ⎪-+-⎝⎭ 222(12)21(1)11a a a a a a a a ⎛⎫--+=÷- ⎪---⎝⎭ 2(12)12(1)1a a a a a --=÷-- 2(12)1(1)12a a a a a--=⨯-- 1a a =-．【点睛】本题考查整式的混合运算，分式的混合运算．掌握各运算法则是解题关键．16．（2023·重庆九龙坡·重庆市育才中学校联考三模）化简(1)()()23x y x x y -++ (2)222111a a a a a a --⎛⎫+-÷ ⎪++⎝⎭ 【答案】(1)222x xy y ++ (2)1a a- 【分析】（1）根据完全平方公式及单项式乘以多项式的运算法则即可解答；（2）根据分式的混合运算法则即可解答．【详解】（1）解；()()23x y x x y -++()22223x xy y x xy =-+++22223x xy y x xy =-+++ 222x xy y =++；（2）解：222111a a a a a a --⎛⎫+-÷ ⎪++⎝⎭ ()()21122+111a a a a a a a a +-⎛⎫--=÷ ⎪+++⎝⎭ 2222111a a a a a a -+--=÷++ ()()21111a a a a a -=-÷++ ()()21111a a a a a -=+⨯+- 1a a-=；【点睛】本题考查了完全平方差公式，单项式乘以多项式运算法则，分式的混合运算法则，掌握对应法则是解题的关键．17．（2023·重庆渝中·重庆巴蜀中学校考一模）计算：(1)()()232x x y x y -+- (2)22411369a a a a -⎛⎫-÷ ⎪+++⎝⎭ 【答案】(1)2275y xy x +- (2)31a a +-+ 【分析】()1原式利用单项式乘多项式法则，以及完全平方公式化简，去括号合并即可得到结果； ()2原式括号中两项通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分即可得到结果.【详解】（1）原式222344x xy x xy y =-+-+2257x xy y =-+（2）原式()()()21143333a a a a a a +-+⎛⎫=-÷ ⎪++⎝⎭+ ()()()2343311a a a a a +--=⋅++- ()()()231311a a a a a +-=-⋅++- 3.1a a +=-+【点睛】此题考查了分式的混合运算，单项式乘多项式，以及完全平方公式，熟练掌握运算法则及公式是解本题的关键.18．（2023·重庆沙坪坝·重庆南开中学校考二模）计算：(1)()223()31b ab a b b a ⋅+--+； (2)2222132193a a a a a a a ⎛⎫++++÷+- ⎪-+⎝⎭．【答案】(1)22a ab - (2)13a a+- 【分析】（1）先根据单项式乘法法则、完全平方公式、单项式乘多项式法则进行展开，然后再合并同类项即可；（2）根据分式的基本性质和去括号法则进行分析判断，然后化简即可．【详解】（1）()223()31b ab a b b a ⋅+--+22222323ab a ab b ab b =+-+--22a ab =-（2）2222132193a a a a a a a ⎛⎫++++÷+- ⎪-+⎝⎭ ()()()()()2121÷1333a a a a a a a ⎡⎤+++=+-⎢⎥+-+⎣⎦ ()()()()()()()211321÷3333a a a a a a a a a ⎡⎤+++++=-⎢⎥+-++⎣⎦()()()()()()()211321333÷a a a a a a a a +++-++=+-+ ()()()()()()()213·331321a a a a a a a a ++=+-++-++ ()()()()()()213·33132a a a a a a a ++=+-⎡⎤++-+⎣⎦ ()211·31a a a +=-+ 13a a+=-．【点睛】本题主要考查分式的混合运算，掌握相关知识，及运算法则是解题的关键．19．（2023·重庆九龙坡·重庆市育才中学校联考二模）计算：(1)()()224a b a a b +-+； (2)22221121m m m m +⎛⎫+÷ ⎪--+⎝⎭．【答案】(1)24b ； (2)12m - 【分析】（1）利用完全平方公式和单项式乘多项式的运算法则计算乘方和乘法，然后合并同类项进行化简；（2）先将小括号内的式子进行通分计算，然后再算括号外面的除法．【详解】（1）解：原式222444a ab b a ab =++--24b =；（2）解：原式()()22121111m m m m m +-⎛⎫=+÷ ⎪--⎝⎭- ()()211121m m m m -+=-+ 12m -= 【点睛】本题考查整式的混合运算，分式的混合运算，掌握完全平方公式、分式混合运算的运算顺序（先算乘方，然后算乘除，最后算加减，有小括号先算小括号里面的）和计算法则是解题关键．20．（2023·重庆渝中·重庆巴蜀中学校考二模）计算：(1)()()()()32242422a b a b b a b a b a b -++-÷-(2)222623969x x x x x ⎛⎫+÷ ⎪+--+⎝⎭．【答案】(1)2a ab +(2)33x x -+ 【分析】（1）根据整式的混合运算法则计算即可；（2）根据分式的运算法则计算即可．【详解】（1）解：原式222244ab ab b a b =-++-2a ab =+（2）解：原式22(3)6(3)(3)(3)(3)(3)2x x x x x x x ⎡⎤--=+⋅⎢⎥+-+-⎣⎦ 22(3)(3)(3)2x x x x x-=⋅+- 33x x -=+ 【点睛】本题考查了整式混合运算和分式混合运算，熟练掌握整式除法、完全平方公式、平方差公式以及整式的运算法则，分式的运算法则是解题的关键．21．（2023·重庆·重庆实验外国语学校校考二模）化简：(1)()()()21214x x x x -+-+ (2)2192122x x x x --⎛⎫-÷ ⎪++⎝⎭ 【答案】(1)2341x x -- (2)23x -- 【分析】（1）先计算平方差、单项式乘多项式，再合并同类项；（2）先将括号内式子通分，再将分式除法变形为乘法，最后约分化简．【详解】（1）解：()()()21214x x x x -+-+()22=414x x x --+22=414x x x ---2=341x x --（2）解：2192122x x x x --⎛⎫-÷ ⎪++⎝⎭ ()()()33122121x x x x x x +----=÷++ ()()()()321133x x x x x -++=⋅++-23x =-- 【点睛】本题考查整式的混合运算，平方差公式的应用，分式的混合运算，掌握运算法则和运算顺序是解题的关键．22．（2023·重庆九龙坡·统考二模）化简：(1)()()()x y x y x x y -+-- (2)22221211a a a a a a a ⎛⎫-÷-- ⎪-+-⎝⎭【答案】(1)2y xy -+ (2)1a a - 【分析】（1）先计算平方差公式、单项式乘以多项式，再计算整式的加减法即可得；（2）先计算括号内的分式减法，再计算分式的除法即可得．【详解】（1）解：原式222x y x xy =--+2y xy =-+．（2）解：原式()()()222121111a a a a a a a --=÷--⎡⎤⎢⎥⎢-⎣⎦-⎥ ()()2221221111a a a a a a a a -⎛⎫-+=÷- ⎪---⎝⎭ ()()2121211a a a a a --=÷-- ()()2121121a a a a a --=⋅-- 1a a =-．【点睛】本题考查了整式的混合运算、分式的减法与除法运算，熟练掌握整式和分式的运算法则是解题关键．23．（2023·重庆大渡口·统考二模）计算：(1)()()222x y y x y x -+-+； (2)22241244a a a a -⎛⎫+÷ ⎪--+⎝⎭．【答案】(1)22x (2)2a a + 【分析】（1）根据完全平方公式和整式加减的运算法则计算即可；（2）根据分式的加减运算法则及乘除法运算法则计算即可．【详解】（1）()()222x y y x y x -+-+222222x xy y xy y x =-++-+ 22x x =+22x =；（2）22241244a a a a -⎛⎫+÷ ⎪--+⎝⎭ 222(2)2(2)(2)a a a a a -+-=⋅-+- 2a a =+．【点睛】本题主要考查了整式及分式的混合运算，解题的关键是熟练运用整式与分式的混合运算法则，属于基础题．24．（2023·重庆江津·重庆市江津中学校校考二模）计算：(1)2(2)()()x y x y x y ---+； (2)2211211x x x x x -⎛⎫÷+ ⎪-+-⎝⎭．【答案】(1)254y xy -(2)1【分析】（1）根据完全平方公式以及平方差公式即可求出答案；（2）先对前半部分分子分母进行因式分解，括号里的部分进行通分，再将分式除法转化为乘法，进行约分化简即可．【详解】（1）觧：2(2)()()x y x y x y ---+，222244x xy y x y =-+-+，254y xy =-；（2）2211211x x x x x -⎛⎫÷+ ⎪-+-⎝⎭， 2(1)11(1)11x x x x x x --⎛⎫=÷+ ⎪---⎝⎭， 2(1)(1)1x x x x x -=÷--， 2(1)1(1)x x x x x--=⋅-， 1=．【点睛】本题考查了整式的混合运算，分式的混合运算，解题的关键是熟练运用完全平方公式、平方差公式、分式运算法则是解答本题的关键．25．（2023·重庆渝中·统考二模）计算：(1)()()()233x x x x +--+；(2)（a b +﹣2b a b+）22241a b a ab -÷+．【答案】(1)29x + (2)22a a b- 【分析】（1）先计算单项式乘多项式，再利用平方差公式计算，然后合并即可；（2）先把括号内通分和除法运算化为乘法运算，再把分子分母因式分解，然后约分即可．【详解】（1）()()()233x x x x +--+()2229x x x =+--2229x x x =+-+ 29x =+；（2）22224()b a b a b a b a ab-+-÷++ 22()()(2)(2)a b b a a b a b a b a b +-+=⋅++- ()()()222222a a b a ab b b a b a b a b +++-=⋅++- ()2a a b a b +=+()()()22a a b a b a b +⋅+- ＝22a a b-．【点睛】本题考查了分式的混合运算：先乘方，再乘除，然后加减，有括号的先算括号里面的．也考查了完全平方公式．26．（2023·重庆九龙坡·重庆实验外国语学校校考三模）计算：(1)()()2a b a a b +-+ (2)283111m m m m m -⎛⎫+-÷ ⎪--⎝⎭ 【答案】(1)2ab b +(2)3m m+ 【分析】（1）根据完全平方公式和单项式乘以多项式进行运算，再合并同类项即可．（2）括号内的式子通分，根据分式的混合运算顺序进行运算即可.【详解】（1）解：原式2222a ab b a ab =++--2ab b =+；（2）解：原式()2318111m m m m m m -⎛⎫-=-÷ ⎪---⎝⎭ ()29113m m m m m --=⋅-- ()()()33113m m m m m m +--=⋅-- 3m m+=．【点睛】本题考查了整式的混合运算以及分式的混合运算，熟练掌握运算法则及运算顺序是解题的关键． 27．（2023·重庆沙坪坝·重庆一中校考三模）计算：(1)()()222a b b b a a a ---+⋅ (2)2221214421x x x x x x x x x --++⎛⎫÷-⋅ ⎪++⎝⎭ 【答案】(1)23a a + (2)21x x +- 【分析】（1）根据完全平方公式，单项式乘以单项式，同底数幂的乘法进行计算即可求解；（2）根据分式的加减计算括号内的，同时将除法转化为乘法，再根据分式的性质化简【详解】（1）解：原式222322a ab b b ab a =-+-++23a a =+；（2）解：原式()()()()221122121x x x x x x x x x +-+-+=÷⋅++()()()()()22112211x x x x x x x x +-+=⨯++-21x x +=-．【点睛】本题考查了整式的乘法与分式的混合运算，熟练掌握乘法公式以及分式的运算法则是解题的关键． 28．（2023·重庆渝中·重庆巴蜀中学校考三模）计算(1)()()()32242a a b a b a b ÷-++- (2)22311x x x x x -⎛⎫÷-+ ⎪++⎝⎭【答案】(1)224a ab - (2)212x x-+ 【分析】（1）先计算幂的乘方、单项式乘多项式、完全平方公式，再计算同底数幂的除法，然后计算加减法即可得；（2）先计算括号内的分式加法，再计算分式的除法即可得．【详解】（1）解：原式6422222a a ab b a ab b =÷--+-+224a a ab =+-224a ab =-．（2）解：原式()()()1112311x x x x x x x ⎡⎤-+-=÷+⎢⎥++⎣⎦+ ()2213111x x x x x x ⎛⎫--=÷+ ⎪++⎝⎭+ ()22411x x x x x --=÷++ ()()()12122x x x x x x -+=⋅+-+ ()12x x =-+ 212x x =-+．【点睛】本题考查了幂的乘方、单项式乘多项式、完全平方公式、同底数幂的除法、分式的混合运算，熟练掌握各运算法则是解题关键．。

2024全国各地区数学中考真题汇编《第一期》

数学几何图形的相关计算1.（2024达州10题4分）如图，△ABC是等腰直角三角形，∠ABC=90°，AB=4，点D，CE，则下列E分别在AC，BC边上运动，连接AE，BD交于点F，且始终满足AD=√=√2；②∠DFE=135°；③△ABF面积的最大值是4√2-4；④CF的最小值是结论：①2√10-2√2.其中正确的是( )A.①③B.①②④C.②③④D.①②③④第1题图【推荐地区：安徽】解图①解图②第1题解图解直角三角形及其应用2.（2024遂宁19题8分）小明的书桌上有一个L型台灯，灯柱AB高40cm，他发现当灯带BC与水平线BM夹角为9°时(图①)，灯带的直射宽DE(BD⊥BC，CE⊥BC)为35cm，但此时灯的直射宽度不够，当他把灯带调整到与水平线夹角为30°时(图②)，直射宽度刚好合适，求此时台灯最高点C到桌面的距离.(结果保留1位小数)(sin9°≈0.16，cos9°≈0.99，tan9°≈0.16)图①图②第2题图【推荐地区：安徽、山西、浙江】【参考答案】2.解：如题图，∵BD⊥BC，CE⊥BC，∴BD∥CE.∵BM∥DE，∴四边形BDEM为平行四边形，∴BM=DE=35cm，∴BC=BM·cos9°≈34.65cm，如解图，过点C作D’E’的垂线分别交BM与点F，交D’E’于点G.在Rt△BCF中，CF=BC·sin30°≈17.3cm，∴CH=sin30°×cos9°×BM=×0.99×35=17.3(m)，∴此时台灯最高处到左面的距离CG=CF+AB=17.3+40=57.3(cm).第2题解图一次函数与反比例函数的综合应用3.（2024自贡24题10分）如图，在平面直角坐标系中，一次函数y=kx+b的图象与反比例函数myx=的图象交于A（-6，1），B（1，n）两点．第3题图（1）求反比例函数和一次函数的解析式；（2）P是直线x=-2上的一个动点，△PAB的面积为21，求点P坐标；（3）点Q在反比例函数myx=位于第四象限的图象上，△QAB的面积为21，请直接写出Q点坐标．【推荐地区：安徽、江西、浙江】第3题解图，统计与概率4．（2024重庆B卷20题10分）数学文化有利于激发学生数学兴趣．某校为了解学生数学文化知识掌握的情况，从该校七、八年级学生中各随机抽取10名学生参加了数学文化知识竞赛，并对数据（百分制）进行整理、描述和分析（成绩均不低于70分，用x表示，共分三组：A．90≤x≤100，B．80≤x＜90，C．70≤x＜80），下面给出了部分信息：七年级10名学生的竞赛成绩是：76，78，80，82，87，87，87，93，93，97．八年级10名学生的竞赛成绩在B组中的数据是：80，83，88，88．八年级抽取的学生竞赛成绩扇形统计图七、八年级抽取的学生竞赛成绩统计表第4题图根据以上信息，解答下列问题：（1）填空：a=________，b=________，m=________；（2）根据以上数据，你认为该校七、八年级中哪个年级学生数学文化知识较好？请说明理由（写出一条理由即可）；（3）该校七年级学生有500人，八年级学生有400人．估计该校七、八年级学生中数学文化知识为“优秀”（x≥90）的总共有多少人？【推荐地区：安徽、江西、浙江、湖南】【参考答案】4.（1）88，87，40；【解法提示】∵八年级10名学生的竞赛成绩在C组的有10×20%=2名，∴将八年级10名学生的竞赛成绩按照从小到大的顺序进行排列，在中间的两个数分别是88，88，∴=88；∵七年级10名学生的竞赛成绩中87出现的次数最多，∴b=87；∵八年级a=10名学生的竞赛成绩在B组的有4名，∴在A组的有10-2-4=4名，∴A组所占百分比为40%，即m=40.（2）八年级的数学文化知识较好，理由：七、八年级10名学生的竞赛成绩平均数相同，八年级的中位数和众数均大于七年级；（3）500×+400×40%=310（人）.∴估计该校七、八年级学生中数学文化知识为“优秀”（x≥90）的总共有310人.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2018中考真题专题汇编——综合计算题1.(2018甘肃）某化学兴趣小组同学为回收一块质量为40 g 的铜锌合金中的铜，将该合金放人烧杯中，逐渐加入稀硫酸至不再产生气泡时，恰好用去稀硫酸100 g ，烧杯内剩余固体27 g 。

请完成下列计算：（1）40 g 铜锌合金中锌的质量是________g 。

（2）计算所用稀硫酸中溶质的质量分数。

【答案】（1）40 g 铜锌合金中锌的质量为40 g-27 g=13 g （2）解：设所用稀硫酸中溶质的质量为x 。

Zn+H 2SO 4═ZnSO 4+H 2↑ 65 98 13 g xx98g 1365= x=19.6 g所用稀硫酸中溶质的质量分数：%6.19%100g100g19.6=⨯。

答：所用稀硫酸中溶质的质量分数是19.6%。

2.（2018安顺）某锥形瓶盛有盐酸和氯化铜的混合溶液100g ，向其中逐滴加入溶质质量分数为10％的氢氧化钠溶液，锥形瓶内溶液质量与滴入的氢氧化钠溶液的质量的变化关系如图所示。

请计算：（l ）反应至A 点时加入氢氧化钠溶液的质量为__________；（2）计算反应至B 点时锥形瓶内所得溶液的溶质质量分数为多少？（计算结果保留至0.1%）【答案】（1）40g （1分）；（2）10.4%3.（2018河南）将30.9 g 氯酸钾（KClO 3）和二氧化锰的固体混合物装入试管中，加热制取氧气，同时生成氯化钾。

待反应完全后，将试管冷却，称量，可以得到21.3 g 固体物质。

请计算原固体混合物中氯酸钾的质量。

【答案】生成氧气的质量为30.9g －21.3g=9.6g ，设原混合物中氯酸钾的质量为x2KClO 32KCl+3O 2↑245 96x 9.6g96245=gx 6.9 解得x= 24.5g 4.（2018黄石）向l33.4克稀盐酸中加入锌粉（仅含不溶于酸的杂质），所加锌粉的质量与产生气体的质量的关系如下图所示。

求：（1）此过程产生气体的最大质量是______________；（2）原稀盐酸中溶质的质量分数为多少？（诗写出计算过程）【答案】（1）0.4 （2）10.9%5.(2018武汉)钢是铁的合金。

为测定某钢样中铁的质量分数，取11.4g 钢样，向其中加入稀硫酸，产生氢气的质量与加入稀硫酸的质量关系如图所示（不考虑钢样中其它成分与稀硫酸的反应）。

（1）钢_____(填“是”或“不是”)金属材料。

（2）计算此钢样中铁的质量分数。

【答案】（1）是（2）98%6.（2018襄阳）把干燥、纯净的氯酸钾和二氧化锰的混合物31.5g装入大试管中，加热制取氧气。

待完全反应后，将试管冷却、称量，得到21.9g固体物质。

计算制得氧气多少克？21.9g固体物质中含有哪些物质？各多少克？【答案】9.6g；氯化钾14.9g、二氧化锰7g。

7.（2018孝感）某工厂排放的废水中含有亚硫酸钠（Na2SO3）未经处理，会造成污染。

化学兴趣小组的同学对废水处理设计了如图所示的实验方案：试计算：（l）反应完后生成亚硫酸钙沉淀的质量为_______g。

（2）废水中亚硫酸钠的质量分数（请写出计算过程）。

（温馨提示：Na2SO3＋CaC12=CaSO3↓+2NaCl；氯化钙不与废水中的其它杂质反应）【答案】（1）6g；（2）12.6%。

8.（2107邵阳）某同学在实验室用氯酸钾和二氧化锰的混合物制取氧气，并对反应后固体剩余物进行回收、利用，实验操作流程及数据记录如下：请回答下列问题：（1）滤液可作化肥使用，你认为它属于_______肥。

（2）该同学制得氧气的质量_______g。

（3）计算滤液中溶质质量分数。

【答案】（1）钾或 K（1分）（2）4.8（1分）（3）14.9%9.（2018长沙）将适量二氧化碳通入100g氢氧化钠溶液中，恰好完全反应后，得到108.8g碘酸钠溶液。

请计算：（1）参加反应的二氧化碳的质量为_______g；（2）氢氧化钠溶液的溶质质量分数_________．【答案】（1） 8.8；（2）16%10.（2018宿迁）牙膏中的摩擦剂可以增强牙膏对牙齿的摩擦作用和去污效果。

己知某品牌牙膏中的摩擦剂是CaCO3和SiO2(SiO2不溶于水也不与稀盐酸反应)。

为了测定摩擦剂中CaCO3的质量分数，通过实验测得如图数据：（1）生成CO2质量为______g；（2）求摩擦剂中CaCO3的质量分数。

【答案】（1）2.2；（2）50%11.(2018江西)学习小组测定某工业废水（含有H2SO4、HNO3，不含固体杂质）中H2SO4的含量。

取100g废水于烧杯中，加入100gBaCl2溶液，恰好完全反应，经过滤得到176.7g溶液。

（可溶性杂质不参加反应，过滤后滤液的损失忽略不计）（1）充分反应后生成沉淀的质量为_______g；（2）该工业度水中硫酸的质量分数为多少？（写出计算过程）[来源:学科网]（3）为避免工业废水污染环境，排放前应对废水进行中和处理，需加入的物质是________。

【答案】（1）100g+100g－176.7g＝23.3g解：设100 g工业废水中硫酸的质量x（2）H2SO4+BaCl2=BaSO4↓+2HCl98 233x 23.3g98/233 = x/23.3gx = 9.8g9.8g/100g×100% = 9.8%答：该工业废水中硫酸的质量分数为9.8%。

（3）氢氧化钙等12.（2018呼和浩特）铁的氧化物有三种，分别是FeO、Fe2O3和Fe3O4。

某固体粉未可能含有一种或两种铁的氧化物。

取23.2克固体粉未，向其中通入足量一氧化碳并加热（假设固体完全反应），将反应生成的气体通入足量的澄清石灰水中。

生成40.0克沉淀。

试计算：（l）反应生成二氧化碳的质量为多少克？（要求写出计算过程）（2）固体粉末中含有的铁的氧化物可能为______或_______。

【答案】（1）17.6g；（2）Fe3O4；或FeO和Fe2O3。

13.（2018枣庄）一化工厂产生的废液中含有硫酸亚铁和硫酸铜（不考虑其它物质），为回收铜和硫酸亚铁，研究人员设计出“用铁处理”的发案，取100g上述废液，向其中加入2.8g铁粉，恰好完全反应，测得反应后溶液中溶质的质量分数为15%，求：（1）回收得到铜的质量为 g（2）回收得到硫酸亚铁的质量是多少？（写出计算过程）【答案】解：设2.8g铁完全反应生成的铜的质量为xFe+CuSO4=FeSO4+Cu56 642.8g x=x=3.2g硫酸亚铁质量为×15%=14.94g答：（1）回收得到铜的质量为 3.2gg（2）回收得到硫酸亚铁的质量是14.94g．14.（2018达州）NaCl和Na2CO3的固体混合物与一定质量的稀盐酸恰好完全反应，得到4.4gCO2和100g21.1%的NaCl溶液，求：⑴稀盐酸中溶质的质量为 g。

⑵原混合物中NaCl的质量分数（写出计算过程）。

【答案】⑴7.3g ⑵47%解：设碳酸钠的质量为x，反应生成的氯化钠质量为y，参加反应的盐酸中溶质质量为z。

Na2CO3+2HCl=2NaCl+H2O+CO2↑106 73 117 44x z y 4.4g106 x =73z=117y=444.4gx=10.6g y=11.7g z=7.3g原混合物中氯化钠的质量为：100g×21.1%-11.7g =9.4g原混合物中NaCl的质量分数=9.4g9.4g+10.6g×100%=47%15.（2018南充）某化学兴趣小组欲测定一瓶过氧化氢溶液中溶质的质量分数，实验操作及相关数据如图所示：（1）生成氧气的质量 g；（2）这瓶过氧化氢溶液中溶质的质量分数是多少?（写出计算过程）. 解：（1）根据质量守恒定律，反应生成氧气的质量=68g+2g-68.4g=1.6g；故填：1.6（2）设68g过氧化氢溶液中含有过氧化氢的质量为x．2H2O22H2O + O2↑68 32x 1.6g解得，x=3.4g过氧化氢溶液的溶质的质量分数为16.(2018雅安) 化学兴趣小组用一瓶久置的过氧化氢溶液制取氧气并测量过氧化氢质量分数。

称量 68g 过氧化氢溶液和 0. 1g 二氧化锰进行实验, 反应前后质量随时间变化关系如图。

计算:( 1) 制得氧气的质量是 g。

( 2) 过氧化氢质量分数是多少?【答案】（1）0.8克（2分）（2）设参加反应的过氧化氢质量为x。

2H2O2 MnO2△2H2O + O2↑68 32x 0.8g68∶32=x∶0.8gx=1.7g过氧化氢质量分数：1.7g/68g *100%=2.5%答：过氧化氢质量分数是2.5%。

17.(2018湖州)军事上常用氢化锂( LiH)来制取氢气，反应的化学方程式为:LiH+H2O=LiOH+ H2↑现将12克氢化锂与991克水反应，反应后所得溶液中无LiOH析出。

求：（1）生成氢气的质量．（2）所得溶液的溶质质量分数。

【答案】（1）3g；（2）3.6%18.（2018温州）实验室有一变质的氢氧化钠样品（样品中只含碳酸钠杂质，且成分均匀），为测量样品中Na2CO3的质量分数，小明进行了如下实验。

①取质量、大小相同的3个烧杯，分别加入一定质量分数的稀盐酸100克，②向上述3个烧杯中分别加入3 份质量不同的样品；③充分反应后，再用电子天平称量烧杯及烧杯内物质的总质量（假设产生的气体完全逸出）。

实验数据记录如下：实验一实验二实验三反应前稀盐酸+烧杯质量（克）150 150 150反应前固体样品质量（克） 4 8 12反应后烧杯内物质+烧杯质量（克）m 155.8 158.7已知实验中发生的化学反应：NaOH+HCl=NaCl+H2ONa2CO3+ 2HCl=2NaCl+H2O+ CO2↑（1）分析表中教据，写出判断实验二中的样品已完全反应的理由__________。

（2）表中的m 值为________。

（3）根据实验二的数据计算样品中Na2CO3的质量分数。

【答案】（1）因为实验三产生的气体质量为150+12-158.7=3.3（克），实验三产生的气体质量为150+8-155.8=2.2（克），实验三产生的气体质量大于实验二，所以实验二中稀盐酸有剩余，8克样品已完全反应。

（2）152.9 （3）66.25%19.（2018重庆A）合成氨工业中，常用碳酸钾溶液吸收产生的二氧化碳得到碳酸氢钾，反应的化学方程式为：K2CO3+CO2+H2O=2KHCO3.现向碳酸钾溶液中通入二氧化碳，恰好完全反应，得到溶质的质量分数为10%的溶液50g，试计算：（1）碳酸钾中钾元素、碳元素、氧元素的质量比为_____________。

（2）若把该50g溶液，稀释为质量分数为4%的溶液，需要加入水的质量。