《线性代数》第9讲-第2章第6节
合集下载
线性代数教材讲解ppt课件

a11
A
a21
a12
a22
a1n a2n
am1 am1 amn
矩阵A的
m, n元
简记为
A Amn
aij
mn
aij
.
这m n个数称为A的元素,简称为元.
元素是实数的矩阵称为实矩阵,
元素是复数的矩阵称为复矩阵.
例如
1 9
0 6
3 4
5 3
是一个 2 4 实矩阵,
0
0
单位阵.
0 0 1
线性变换
x1 y1
cosx siny, sinx cosy.
对应 cos sin sin cos
这是一个以原点为中心
旋转 角的旋转变换.
Y P1 x1, y1
Px, y
O
X
三、小结
(1)矩阵的概念 m行n列的一个数表
a11
A
a21
a12
且对应元素相等,即
aij bij i 1,2,,m; j 1,2,,n,
则称矩阵 A与B相等,记作 A B.
(8)线性变换与矩阵之间关系:
例1 n个变量x1, x2,, xn与m个变量y1, y2,, ym之
间的关系式
y1 a11x1 a12 x2 a1n xn ,
y2 a21x1 a22 x2 a2n xn ,
13 2
6 2
2i 2
是一个
33
复矩阵,
2 2 2
1 2 是一个 3 1 矩阵,
4
2 3 5 9
4
是一个 1 4 矩阵,
是一个 11 矩阵.
矩阵与行列式有本质的区别, 行列式是一个算式, 其行数和列数相同,一个数字行列式经过计算 可求得其值, 而矩阵仅仅是一个数表, 它的行数和 列数可以不同.
《线性代数》(同济第六版)课件

0 0 a33 a43
a14 a24 = a11a22a33a44 a34 a44
0 0 = a14a23a33a41 0 a44
a11 0 a21 a22 D4 = a32 a32 a41 a42
四个结论: (1) 对角行列式
a11 D= a22
= a11a22ann
ann
(2)Leabharlann a1nD= an1
规律:
1.三阶行列式共有6项,即3!项. 2.每一项都是位于不同行不同列的三个元素的乘积.
p p
是1、2、3的某个排列.
4.当p1p2p3 是偶排列时,对应的项取正号; 当 p1p2p3 是奇排列时,对应的项取负号.
所以,三阶行列式可以写成
a11 a12 D = a21 a22 a31 a32
a13 a23 = a11a22a33 +a12a23a31 +a13a21a32 a33 a13a22a31 a12a21a33 a11a23a32
3
第一章 行列式
�
内容提要
§1 §2 §3 §4 §5
•行列式是线性代数 的一种工具! •学习行列式主要就 是要能计算行列式 的值.
§6 §7
二阶与三阶行列式 全排列及其逆序数 行列式的概念. n 阶行列式的定义 对换(选学内容) 行列式的性质 行列式的性质及计算. 行列式按行(列)展开 克拉默法则 —— 线性方程组的求解.
注意:对角线法则只适用于二阶与三阶行列式.
例2 计算行列式
1 2 -4 D = -2 2 1 -3 4 -2
解
按对角线法则,有
D = 1×2×( 2)+ 2×1×( 3)+ ( 4)×( 2)×4
a14 a24 = a11a22a33a44 a34 a44
0 0 = a14a23a33a41 0 a44
a11 0 a21 a22 D4 = a32 a32 a41 a42
四个结论: (1) 对角行列式
a11 D= a22
= a11a22ann
ann
(2)Leabharlann a1nD= an1
规律:
1.三阶行列式共有6项,即3!项. 2.每一项都是位于不同行不同列的三个元素的乘积.
p p
是1、2、3的某个排列.
4.当p1p2p3 是偶排列时,对应的项取正号; 当 p1p2p3 是奇排列时,对应的项取负号.
所以,三阶行列式可以写成
a11 a12 D = a21 a22 a31 a32
a13 a23 = a11a22a33 +a12a23a31 +a13a21a32 a33 a13a22a31 a12a21a33 a11a23a32
3
第一章 行列式
�
内容提要
§1 §2 §3 §4 §5
•行列式是线性代数 的一种工具! •学习行列式主要就 是要能计算行列式 的值.
§6 §7
二阶与三阶行列式 全排列及其逆序数 行列式的概念. n 阶行列式的定义 对换(选学内容) 行列式的性质 行列式的性质及计算. 行列式按行(列)展开 克拉默法则 —— 线性方程组的求解.
注意:对角线法则只适用于二阶与三阶行列式.
例2 计算行列式
1 2 -4 D = -2 2 1 -3 4 -2
解
按对角线法则,有
D = 1×2×( 2)+ 2×1×( 3)+ ( 4)×( 2)×4
线性代数各章知识及脉络图

M M
0 0
0
,n 3
Dn
A
B
a1
b1
,n 1
a1 a2 b1 b2 , n 2
-5-
○2 加边法专辑
加边法的应用:通过升阶获得一些特殊的元素值,从而消去某些元素,使得行列式形式更加简单且特殊,
从而实现计算的简化。
此种方法其实是反向利用 Laplace 展开定理,看似复杂化,其实阶数的增加反倒可以将行列式简单化,更 易发现规律。同时应当注意加边的类型及加边后行列式值不能改变。
1 n2
○3 爪型行列式专辑
爪型行列式形如:
方法:将 D 的第 i+1 列乘以 ci i 1, 2,L , n都加到第 1 列,得
ai
有些行列式经过适当的变化可以化为行列式,再采用上述方法计算。
a1 x x L x a2 x L 【例】: Dn x x a3 L M M MO
x x xL
【例】:计算行列式
令 Dn C C AB ,
a2 1 0 L
a2 1 0 L
C
M
MM
a2 1 0 L
a2 1 0 L
0 1 1 L 0b1 b2 L M 0 0 L 0 M M 0 0 0 L
1 1
bn1 bn
0
0
【例】:
1、设行列式 det A 的元素为 aij ,行列式
n
试证: det D det A x Aij ,其中 Aij 为 aij 在 det A 中的代数余子式。 i, j1
证明:把 det D 升阶得到
n
n
n
线性代数第9讲精品PPT课件

r3 3r1 0 2 6 3 0 1 r3 r2
r1 r2 r3 r2
1 0 2 1 1 0 r1 2r3 0 2 5 2 1 0 0 0 1 1 1 1 r2 5r3
aj2
a jn
第
i
行
ai1
ai 2
ain
第
j
行
am1 am2 amn
相当于对矩阵 A 施行第一种初等行变换 :
把 A 的第 i 行与第 j 行对调 (ri rj ).
类似地,
以 n 阶初等矩阵 En(i, j) 右乘矩阵 A,
a11
AEn
(i,
j)
a21
a1 j
a2 j
a12
a1
ai1
ka
j1
ai 2 ka j2
ain
a
jn
a j1
aj2
a jn
am1
am 2
amn
把 A的第 j 行乘 k 加到第 i 行上 (ri krj ).
类似地,以 En(ij(k)) 右乘矩阵 A,其结果相当于 把 A 的第i列乘 k 加到第 j 列上 (c j kci ).
就称这两个线性方程组等价
二、初等矩阵的概念
矩阵的初等变换是矩阵的一种基本运算,应 用广泛. 定义 由单位矩阵 E 经过一次初等变换得到的方 阵称为初等矩阵.
三种初等变换对应着三种初等方阵.
1. 对调两行或两列; 2.以数 k 0 乘某行或某列; 3.以数 k 乘某行(列)加到另一 行(列)上去.
同理可定义矩阵的初等列变换(所用记号是 把“r”换成“c”).
定义2 矩阵的初等列变换与初等行变换统称为 初等变换.
初等变换的逆变换仍为初等变换, 且变换类型 相同.
r1 r2 r3 r2
1 0 2 1 1 0 r1 2r3 0 2 5 2 1 0 0 0 1 1 1 1 r2 5r3
aj2
a jn
第
i
行
ai1
ai 2
ain
第
j
行
am1 am2 amn
相当于对矩阵 A 施行第一种初等行变换 :
把 A 的第 i 行与第 j 行对调 (ri rj ).
类似地,
以 n 阶初等矩阵 En(i, j) 右乘矩阵 A,
a11
AEn
(i,
j)
a21
a1 j
a2 j
a12
a1
ai1
ka
j1
ai 2 ka j2
ain
a
jn
a j1
aj2
a jn
am1
am 2
amn
把 A的第 j 行乘 k 加到第 i 行上 (ri krj ).
类似地,以 En(ij(k)) 右乘矩阵 A,其结果相当于 把 A 的第i列乘 k 加到第 j 列上 (c j kci ).
就称这两个线性方程组等价
二、初等矩阵的概念
矩阵的初等变换是矩阵的一种基本运算,应 用广泛. 定义 由单位矩阵 E 经过一次初等变换得到的方 阵称为初等矩阵.
三种初等变换对应着三种初等方阵.
1. 对调两行或两列; 2.以数 k 0 乘某行或某列; 3.以数 k 乘某行(列)加到另一 行(列)上去.
同理可定义矩阵的初等列变换(所用记号是 把“r”换成“c”).
定义2 矩阵的初等列变换与初等行变换统称为 初等变换.
初等变换的逆变换仍为初等变换, 且变换类型 相同.
线性代数(人大版)第9讲60页PPT

k1a1+k2a2+k3a3=b, 或者写为
1 0 2 1
k1
2 3
k2
1 4
k3
63
1 5
. 也
就
是说线性
1 0 2 x1 1
方程组
2 3
1 4
3 6
x2 x3
1 5
是否有解.
02.06.2020
线性代数
17
102 由于 2 1 3 4 0故该线性方程组有唯一
bn
kan
称这两种运算为线性运算, 其运算规律遵从
矩阵的相关运算律
02.06.2020
线性代数
6
例 3.2 已知向量 x 满足条件: 2x+3a=5x+2b,
1 3
其中α
23
,
β
0 3
,试求向量
x.
解 由题意得
1 3 9 3
3x
3α
2β
3
2 3
2
0 3
63
,
x2 1.02.06.2020线性代数
7
例3.3 给定线性方程组
a11x1 a12x2 L a1nxn b1
a21x1
a22x2 L LLL
a2nxn L
b2
am1x1 am2x2 L amnxn bn
a11 a12 L Aa21 a22 L
M M am1 am2 L
a1n x1 b1
第三章 向量组的线性相关性 §1 向量与向量组
一,向量的概念及其运算 定义3.1 n1矩阵
a1
α
a
2
M
a
n
称为n维列向量,
而1n矩阵aT=(a1,a2, ,an)称为n维行向量, n
麻省理工上课讲义 线性代数[第9集]线性相关性、基、维数
![麻省理工上课讲义 线性代数[第9集]线性相关性、基、维数](https://img.taocdn.com/s3/m/b68112f1856a561252d36fba.png)
Bases of a column space and nullspace
Suppose: ⎤ 1 2 3 1 A = ⎣ 1 1 2 1 ⎦. 1 2 3 1 By definition, the four column vectors of A span the column space of A. The third and fourth column vectors are dependent on the first and second, and the first two columns are independent. Therefore, the first two column vectors are the pivot columns. They form a basis for the column space C ( A). The matrix has rank 2. In fact, for any matrix A we can say: rank( A) = number of pivot columns of A = dimension of C ( A). (Note that matrices have a rank but not a dimension. Subspaces have a dimen sion but not a rank.) The column vectors of this A are not independent, so the nullspace N ( A) contains more than just the zero vector. Because the third column is the sum ⎡
1
Example: R3 �� One basis for R3 is � c1
线性代数第九讲PPT课件

向量的减法定义为
()(a1b 1,a2b2, ,anbn)T
11
向量的线性运算 定义3.3 数 与n维向量 (a1,a2, ,an)T
的乘积,称为向量的数乘. 记作
或
即
(a 1,a 2, ,a n)
12
易验证,向量的运算满足如下八条基本规律: 1) 加法交换律 + = + ; 2) 加法结合律 ( + ) + = ( + ) + ;
(其中 , , 为任意 n 维向量, k, l 为实数).
13
例3.1设
0
1
3
1 1,2 1,3 4.
1
0
0
求
1
,
2
2a13a2 a3
解
0 1 1
1 2 11 0 .
1 0 1
0
21 32 3 1.
2
14
§2 向量组的线性相关性
一.向量组的线性组合 二.向量组的等价 三.向量组的线性相关性 四.向量组线性相关性的判定 五.向量组线性相关性的性质
求矩阵秩的一种常用方法 即利用初等变换将矩阵化为行阶梯形矩阵, 行阶梯形矩阵中非零行的行数 就为所求矩阵的秩。
4
§1 n维向量及其线性运算
5
定义3.1
由n个有次序的数a1 a2 an所组成的数组
称为一n维、向向量.量的定义
这n个数称为该向量的n个分量(或坐标) 第i个数ai称为第i个分量
6
n 维向量可写成一行:a 1,a 2, ,a n
1 3 2 0 2 1 0 2 0 1
1 2 2 0 1 3 0 2 1 5
1 32 0 2 30 2 0 5
RA2
()(a1b 1,a2b2, ,anbn)T
11
向量的线性运算 定义3.3 数 与n维向量 (a1,a2, ,an)T
的乘积,称为向量的数乘. 记作
或
即
(a 1,a 2, ,a n)
12
易验证,向量的运算满足如下八条基本规律: 1) 加法交换律 + = + ; 2) 加法结合律 ( + ) + = ( + ) + ;
(其中 , , 为任意 n 维向量, k, l 为实数).
13
例3.1设
0
1
3
1 1,2 1,3 4.
1
0
0
求
1
,
2
2a13a2 a3
解
0 1 1
1 2 11 0 .
1 0 1
0
21 32 3 1.
2
14
§2 向量组的线性相关性
一.向量组的线性组合 二.向量组的等价 三.向量组的线性相关性 四.向量组线性相关性的判定 五.向量组线性相关性的性质
求矩阵秩的一种常用方法 即利用初等变换将矩阵化为行阶梯形矩阵, 行阶梯形矩阵中非零行的行数 就为所求矩阵的秩。
4
§1 n维向量及其线性运算
5
定义3.1
由n个有次序的数a1 a2 an所组成的数组
称为一n维、向向量.量的定义
这n个数称为该向量的n个分量(或坐标) 第i个数ai称为第i个分量
6
n 维向量可写成一行:a 1,a 2, ,a n
1 3 2 0 2 1 0 2 0 1
1 2 2 0 1 3 0 2 1 5
1 32 0 2 30 2 0 5
RA2
线性代数第9讲
定理4 矩阵方程AX=B有解的充分必要件是R(A)=R(A, B).
补充例题 首页 上页 返回 下页 结束 铃
向量组的等价 若向量组B: b1, b2, ⋅⋅⋅, bl中的每个向量都能由向量组A: a1, a2, ⋅⋅⋅, am线性表示, 则称向量组B能由向量组A线性表示. 若向量组A与B能相互表示, 则称这两个向量组等价. 定理2 向量组B: b1, b2, ⋅⋅⋅, bl能由向量组A: a1, a2, ⋅⋅⋅, am线性表示 的充分必要条件是R(A)=R(A, B). 分析: 向量组B能由向量组A线性表示 存在矩阵X,使得B=AX R(A)=R(A,B)
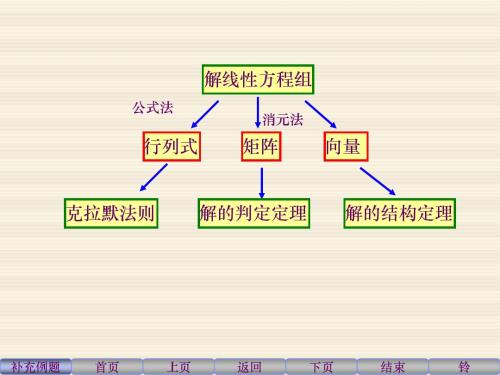
解线性方程组
公式法 消元法
行列式 克拉默法则
矩阵 解的判定定理
向量 解的结构定理
补充例题
首页
上页
返回
下页
结束
铃
第四章 向量组的线性相关性
§1 向量组及其线性组合 §2 向量组的线性相关性 §3 向量组的秩 §4 线性方程组的解的结构 §5 向量空间
引例
首页
上页
返回
下页
结束
铃
§4.1 向量组及其线性组合
上页下页铃结束返回首页补充例题解线性方程组公式法行列式矩阵克拉默法则解的判定定理解的结构定理向量消元法第四章向量组的线性相关性上页下页返回引例首页结束铃12345向量组及其线性组合向量组的线性相关性向量组的秩线性方程组的解的结构向量空间41向量组及其线性组合anaa21a或ata1a2an向量n个有次序的数a1a2an所组成的数组称为n维向量这n个数称为该向量的n个分量第i个数ai称为第i个分量由数组a1a2an所组成的n维向量可记为其中a称为列向量即列矩阵at称为行向量即行矩阵上页下页铃结束返回补充例题首页上页下页下页铃结束返回首页补充例题1列向量用黑体小写字母ab等表示行向量则用atbttt等表示所讨论的向量在没有指明是行向量还是列向量时都当作列向量anaa21a或ata1a2an向量n个有次序的数a1a2an所组成的数组称为n维向量这n个数称为该向量的n个分量第i个数ai称为第i个分量由数组a1a2an所组成的n维向量可记为其中a称为列向量即列矩阵at称为行向量即行矩阵?说明上页下页下页铃结束返回首页补充例题2分量全为实数的向量称为实向量分量为复数的向量称为复向量3规定行向量与列向量都按矩阵的运算规则进行运算anaa21a或ata1a2an向量n个有次序的数a1a2an所组成的数组称为n维向量这n个数称为该向量的n个分量第i个数ai称为第i个分量由数组a1a2an所组成的n维向量可记为?说明其中a称为列向量即列矩阵at称为行向量即行矩阵上页下页下页铃结束返回首页补充例题m12111aaam22212aaamnnnaaa21向量n个有次序的数a1a2an所组成的数组称为n维向量这n个数称为该向量的n个分量第i个数ai称为第i个分量向量组若干个同维数的列向量或同维数的行向量所组成的集合叫做向量组向量举例一个mn矩阵对应一个m维列向量组也对应一个n维行向量组mnmmnnaaaaaaaaa212222111211上页下页下页铃结束返回首页补充例题向量n个有次序的数a1a2an所组成的数组称为n维向量这n个数称为该向量的n个分量第i个数ai称为第i个分量向量组若干个同维数的列向量或同维数的行向量所组成的集合叫做向量组向量举例一个mn矩阵对应一个m维列向量组也对应一个n维行向量组mnmmnnaaaaaaaaa212222111211mna1n222221112a11mmnaaaaaaa上页下页下页铃结束返回首页补充例题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
该定理揭示了初等变换与初等矩阵、矩阵乘法之间的联系 该定理揭示了初等变换与初等矩阵、矩阵乘法之间的联系.
第二章
7
例1. 设 A是 n 阶可逆矩阵,将 A 的第 行与第 行对换后所 的第i行与第 行与第j行对换后所 是 阶可逆矩阵,
得的矩阵记为B 得的矩阵记为 . (1) 证明 B 可逆 . (2) 求AB-1 .
§2.6 矩阵的初等变换
一、初等变换与初等矩阵 二、矩阵的标准型 三、求逆矩阵的初等行(列)变换法 求逆矩阵的初等行 列 变换法
第二章
1
一、初等变换与初等矩阵
定义 对矩阵施以下列三种变换,称为矩阵的初等变换. 对矩阵施以下列三种变换,称为矩阵的初等变换 初等变换. (1) 交换: 交换: (2) 数乘: 数乘: (3) 倍加: 倍加: 记作 ri↔rj (ci↔cj) × 记作 ri←k×ri (ci←k×ci) × 记作 ri←ri+kr(ci←ci+kcj) j
A 初等列变换 I I A-1
第二章
13
上例也可使用初等列变换法求得逆矩阵: 上例也可使用初等列变换法求得逆矩阵: 注:
A = I
0 1 2 1 0 0 1 2 1 4 −1 0 0 0 1 0 0 1
2 = 4 3 − 2
−1 −2 1
1 1 1 − 2
第二章
12
算法: 算法:求逆矩阵的初等列变换法
⋅⋅⋅ 可逆, 若A可逆, A-1也可逆,故存在初等矩阵 1,G2,⋅⋅⋅ ,Gk,使 可逆 则 也可逆,故存在初等矩阵G A-1 = G1G2⋅⋅⋅ Gk , 则 AA-1 = A G1G2⋅⋅⋅ Gk , 即 I = A G1G2⋅⋅⋅ Gk , (对A 施以若干次初等列变换化为 I ) 施以若干次初等列变换 初等列变换化为 A-1 = I G1G2⋅⋅⋅ Gk , (对 I 施以同样的初等列变换化为 A-1) 施以同样的初等列变换 初等列变换化为
1 ⋱ (i) 1 k I( i, j(k) ) = ⋱ (j) 1 ⋱ 1
意义: 意义: 行列式: 行列式: 逆矩阵: 逆矩阵:
(i) (j)
第二章
6
定理 设 A 是一个 m×n 矩阵, × 矩阵,
(1) 对A施行一次初等行变换等于用相应的 阶初等矩阵左乘A; 施行一次初等行 阶初等矩阵左 施行一次初等 变换等于用相应的m阶初等矩阵 ; (2) 对A施行一次初等列变换等于用相应的 阶初等矩阵右乘A. 施行一次初等列 施行一次初等 变换等于用相应的n 阶初等矩阵右
第二章
15
(i) (j)
第二章
4
2) 对 I 施以第二种初等变换得到的初等矩阵为: 施以第二种初等变换得到的初等矩阵为:
1 ⋱ (i) I( i(k) ) = 1 k ⋱ 1
意义: 意义: 行列式: 行列式: 逆矩阵: 逆矩阵:
(i)
第二章
5
3) 对 I 施以第三种初等变换得到的初等矩阵为: 施以第三种初等变换得到的初等矩阵为:
初等变换
记法: A 记法:
B
第二章
2
例:
a11 a12 a13 a14 r1↔r3 A = a21 a22 a23 a24 a a a a 31 32 33 34 a11 a12 a13 a14 c3←kc3 A = a21 a22 a23 a24 a a a a 31 32 33 34 a31 a32 a33 a34 a21 a22 a23 a24 a a a a 11 12 13 14 a11 a12 ka13 a14 a21 a22 ka23 a24 a a ka a 33 34 31 32
1 0 只能用列 0 → ⋯⋯ → 的初等变换 2 4 - 3 2
0 1 0 0 1 -1 1 -2 1 1 1 - 2 0
第二章
14
小结
交换、数乘、 1. 初等行/列变换:交换、数乘、倍加 初等行/ :对单位矩阵施以初等变换得到 初等矩阵 初等变换与初等矩阵、 初等变换与初等矩阵、矩阵乘法之间的关系 2. 矩阵的标准型 :可逆矩阵的标准型是单位阵 n阶矩阵 可逆 阶矩阵A可逆 阶矩阵 A可以表示为若干初等矩阵的乘积 可以表示为若干初等矩阵的乘积. 可以表示为若干初等矩阵的乘积 3. 矩阵的又一种求逆算法:初等行/列变换法 矩阵的又一种求逆算法:初等行
初等行变换
(A I)
(I
A-1 )
第二章
11
1 0 1 例3. 求矩阵 A= 2 1 0 的逆矩阵 的逆矩阵. −3 2 −5
-2.5 1 -0.5 A-1 = 5 -1 1 3.5 -1 0.5
.
0 A = 1 例4. 2
1 1 −1
2 4, 0
求 A −1 .
A −1
第二章
8
二、矩阵的标准型
定理 任意一个矩阵 Am×n = (aij)m×n 经过若干次初等变换,可以化 × 经过若干次初等变换, × 为下列形式的矩阵 D : D = 标准型. 称 D 为矩阵 A 的标准型 Ir Or×(n−r) × − O(m−r)×r O(m−r)×(n−r) − × − × − ,
2 1 2 3 例2. A = 4 1 3 5 2 0 1 2
……
1 0 0 0 0 1 0 0 0 0 0 0
第二章
9
推论 设 A 为 n 阶方阵, 阶方阵, 则 A 可逆 A 经过若干次初等变换,可以化为 In 经过若干次初等变换, A 可以表示为若干初等矩阵的乘积 .
第二章
10
三、求逆矩阵的初等行(列)变换法 求逆矩阵的初等行 列 变换法 算法: 算法:求逆矩阵的初等行变换法
⋅⋅⋅ 可逆, 若A可逆, A-1也可逆,故存在初等矩阵 1,G2,⋅⋅⋅ ,Gk,使 可逆 则 也可逆,故存在初等矩阵G A-1 = G1G2⋅⋅⋅ Gk , 则 A-1A = G1G2⋅⋅⋅ Gk A, , 即 I = G1G2⋅⋅⋅ Gk A, (对 A施以若干次初等行变换化为 I) , 施以若干次初等行变换 施以若干次初等行变换化为 ) A-1 = G1G2⋅⋅⋅ Gk I, (对 I 施以同样的初等行变换化为 A-1) , 施以同样的初等行变换 初等行变换化为
第二章
3
定义
初等矩阵. 初等矩阵.
1) 对 I 施以第一种初等变换得到的初等矩阵为: 施以第一种初等变换得到的初等矩阵为:
1 ⋱ (i) 1 1 0 I( i, j ) = ⋱ 0 1 1 ⋱ (j) 1
意义: 意义: 行列式: 行列式: 逆矩阵: 逆矩阵:
第二章
7
例1. 设 A是 n 阶可逆矩阵,将 A 的第 行与第 行对换后所 的第i行与第 行与第j行对换后所 是 阶可逆矩阵,
得的矩阵记为B 得的矩阵记为 . (1) 证明 B 可逆 . (2) 求AB-1 .
§2.6 矩阵的初等变换
一、初等变换与初等矩阵 二、矩阵的标准型 三、求逆矩阵的初等行(列)变换法 求逆矩阵的初等行 列 变换法
第二章
1
一、初等变换与初等矩阵
定义 对矩阵施以下列三种变换,称为矩阵的初等变换. 对矩阵施以下列三种变换,称为矩阵的初等变换 初等变换. (1) 交换: 交换: (2) 数乘: 数乘: (3) 倍加: 倍加: 记作 ri↔rj (ci↔cj) × 记作 ri←k×ri (ci←k×ci) × 记作 ri←ri+kr(ci←ci+kcj) j
A 初等列变换 I I A-1
第二章
13
上例也可使用初等列变换法求得逆矩阵: 上例也可使用初等列变换法求得逆矩阵: 注:
A = I
0 1 2 1 0 0 1 2 1 4 −1 0 0 0 1 0 0 1
2 = 4 3 − 2
−1 −2 1
1 1 1 − 2
第二章
12
算法: 算法:求逆矩阵的初等列变换法
⋅⋅⋅ 可逆, 若A可逆, A-1也可逆,故存在初等矩阵 1,G2,⋅⋅⋅ ,Gk,使 可逆 则 也可逆,故存在初等矩阵G A-1 = G1G2⋅⋅⋅ Gk , 则 AA-1 = A G1G2⋅⋅⋅ Gk , 即 I = A G1G2⋅⋅⋅ Gk , (对A 施以若干次初等列变换化为 I ) 施以若干次初等列变换 初等列变换化为 A-1 = I G1G2⋅⋅⋅ Gk , (对 I 施以同样的初等列变换化为 A-1) 施以同样的初等列变换 初等列变换化为
1 ⋱ (i) 1 k I( i, j(k) ) = ⋱ (j) 1 ⋱ 1
意义: 意义: 行列式: 行列式: 逆矩阵: 逆矩阵:
(i) (j)
第二章
6
定理 设 A 是一个 m×n 矩阵, × 矩阵,
(1) 对A施行一次初等行变换等于用相应的 阶初等矩阵左乘A; 施行一次初等行 阶初等矩阵左 施行一次初等 变换等于用相应的m阶初等矩阵 ; (2) 对A施行一次初等列变换等于用相应的 阶初等矩阵右乘A. 施行一次初等列 施行一次初等 变换等于用相应的n 阶初等矩阵右
第二章
15
(i) (j)
第二章
4
2) 对 I 施以第二种初等变换得到的初等矩阵为: 施以第二种初等变换得到的初等矩阵为:
1 ⋱ (i) I( i(k) ) = 1 k ⋱ 1
意义: 意义: 行列式: 行列式: 逆矩阵: 逆矩阵:
(i)
第二章
5
3) 对 I 施以第三种初等变换得到的初等矩阵为: 施以第三种初等变换得到的初等矩阵为:
初等变换
记法: A 记法:
B
第二章
2
例:
a11 a12 a13 a14 r1↔r3 A = a21 a22 a23 a24 a a a a 31 32 33 34 a11 a12 a13 a14 c3←kc3 A = a21 a22 a23 a24 a a a a 31 32 33 34 a31 a32 a33 a34 a21 a22 a23 a24 a a a a 11 12 13 14 a11 a12 ka13 a14 a21 a22 ka23 a24 a a ka a 33 34 31 32
1 0 只能用列 0 → ⋯⋯ → 的初等变换 2 4 - 3 2
0 1 0 0 1 -1 1 -2 1 1 1 - 2 0
第二章
14
小结
交换、数乘、 1. 初等行/列变换:交换、数乘、倍加 初等行/ :对单位矩阵施以初等变换得到 初等矩阵 初等变换与初等矩阵、 初等变换与初等矩阵、矩阵乘法之间的关系 2. 矩阵的标准型 :可逆矩阵的标准型是单位阵 n阶矩阵 可逆 阶矩阵A可逆 阶矩阵 A可以表示为若干初等矩阵的乘积 可以表示为若干初等矩阵的乘积. 可以表示为若干初等矩阵的乘积 3. 矩阵的又一种求逆算法:初等行/列变换法 矩阵的又一种求逆算法:初等行
初等行变换
(A I)
(I
A-1 )
第二章
11
1 0 1 例3. 求矩阵 A= 2 1 0 的逆矩阵 的逆矩阵. −3 2 −5
-2.5 1 -0.5 A-1 = 5 -1 1 3.5 -1 0.5
.
0 A = 1 例4. 2
1 1 −1
2 4, 0
求 A −1 .
A −1
第二章
8
二、矩阵的标准型
定理 任意一个矩阵 Am×n = (aij)m×n 经过若干次初等变换,可以化 × 经过若干次初等变换, × 为下列形式的矩阵 D : D = 标准型. 称 D 为矩阵 A 的标准型 Ir Or×(n−r) × − O(m−r)×r O(m−r)×(n−r) − × − × − ,
2 1 2 3 例2. A = 4 1 3 5 2 0 1 2
……
1 0 0 0 0 1 0 0 0 0 0 0
第二章
9
推论 设 A 为 n 阶方阵, 阶方阵, 则 A 可逆 A 经过若干次初等变换,可以化为 In 经过若干次初等变换, A 可以表示为若干初等矩阵的乘积 .
第二章
10
三、求逆矩阵的初等行(列)变换法 求逆矩阵的初等行 列 变换法 算法: 算法:求逆矩阵的初等行变换法
⋅⋅⋅ 可逆, 若A可逆, A-1也可逆,故存在初等矩阵 1,G2,⋅⋅⋅ ,Gk,使 可逆 则 也可逆,故存在初等矩阵G A-1 = G1G2⋅⋅⋅ Gk , 则 A-1A = G1G2⋅⋅⋅ Gk A, , 即 I = G1G2⋅⋅⋅ Gk A, (对 A施以若干次初等行变换化为 I) , 施以若干次初等行变换 施以若干次初等行变换化为 ) A-1 = G1G2⋅⋅⋅ Gk I, (对 I 施以同样的初等行变换化为 A-1) , 施以同样的初等行变换 初等行变换化为
第二章
3
定义
初等矩阵. 初等矩阵.
1) 对 I 施以第一种初等变换得到的初等矩阵为: 施以第一种初等变换得到的初等矩阵为:
1 ⋱ (i) 1 1 0 I( i, j ) = ⋱ 0 1 1 ⋱ (j) 1
意义: 意义: 行列式: 行列式: 逆矩阵: 逆矩阵:
