大学物理习题与综合练习答案详
成都大学_大学物理(2)综合练习题及参考答案1(振动波光近代)
．一质点同时参与了两 个同方向的简谐振动， 它们的振动 9 0.05 cos(t １ )( SI )，x2 0.05 cos(t )( SI )， 方程分别为 x1 4 12 其合成运动的运动方程 为x __________ __________ ____ ．
8
解法三： 旋转矢量法
由旋转矢量图知, A1 A2 ,
A A1 A2 0.05 2 (m)
2 2
0
4
4
2
合振动方程x A cos(t 0 ) 即x 0.05 2 cos(t )( SI ) 2
光学
一、选择题
1．在双缝干涉实验中，屏幕E上的P点处是明纹．若将缝S 2盖住， 并在S1S 2连线的垂直平分面处放一高折射率介质反射面M，如图所示， 则此时（ ）．
2 2 3 C. x2 A cos(t ) D. x2 A cos(t ) 2
由题意作两简谐振动的旋转矢量图如下 解：
要写出质点2的振动方程， 应先求出其初相 2
2 ( )
2
x2 A cos(t 2 ) A cos[t ( )] A cos(t ) 2 2 (选B)
t ， 解： 由图可知， 2s时 x 0
2 2 v A A 6 3 (cm s 1 ) T 4
答案： 3cm.s 0；
1
7
．一弹簧振子系统具有 1.0 J的振动能量、 0.10 m的振幅和
×1的最大速率，则弹簧的 劲度系数为 _____ ，振子的振动 1.0 m s 频率为 _______ ． 1 2 E 2 1.0 解： E kA2 , 得k 2 由 200( N .m 1 ), 2 A 0.12
大学物理习题及综合练习答案详解
库仑定律 7-1 把总电荷电量为Q 的同一种电荷分成两部分，一部分均匀分布在地球上，另一部分均匀分布在月球上，使它们之间的库仑力正好抵消万有引力，已知地球的质量M ＝ 5.98l024kg ，月球的质量m =7.34l022kg 。
（1）求 Q 的最小值；（2）如果电荷分配与质量成正比，求Q 的值。
解：（1）设Q 分成q 1、q 2两部分，根据题意有 2221r MmG r q q k=，其中041πε=k即 2221q k q GMm q q Q +=+=。
求极值，令0'=Q ，得 0122=-kq GMmC 1069.5132⨯==∴k GMm q ，C 1069.51321⨯==k q GMm q ，C 1014.11421⨯=+=q q Q （2）21q m q M =Θ，k GMm q q =21 kGMm m q mq Mq ==∴2122 解得C 1032.61222⨯==kGm q ， C 1015.51421⨯==m Mq q ，C 1021.51421⨯=+=∴q q Q 7-2 三个电量为 –q 的点电荷各放在边长为 l 的等边三角形的三个顶点上，电荷Q （Q ＞0）放在三角形的重心上。
为使每个负电荷受力为零，Q 值应为多大？解：Q 到顶点的距离为 l r 33=，Q 与-q 的相互吸引力为 20141rqQ F πε=， 两个-q 间的相互排斥力为 220241l q F πε=据题意有 10230cos 2F F =，即 2022041300cos 412rqQl q πεπε=⨯，解得：q Q 33= 电场强度7-3 如图7-3所示，有一长l 的带电细杆。
（1）电荷均匀分布，线密度为+，则杆上距原点x 处的线元d x 对P 点的点电荷q 0 的电场力为何？q 0受的总电场力为何？（2）若电荷线密度=kx ，k 为正常数，求P 点的电场强度。
解：（1）线元d x 所带电量为x q d d λ=，它对q 0的电场力为200200)(d 41)(d 41d x a l x q x a l q q F -+=-+=λπεπεq 0受的总电场力 )(4)(d 4000200a l a l q x a l xq F l+=-+=⎰πελπελ00>q 时，其方向水平向右；00<q 时，其方向水平向左q 0 图7-3a λ lP x q-q-q-ll rQ rr（2）在x 处取线元d x ，其上的电量x kx x q d d d ==λ，它在P 点的电场强度为2020)(d 41)(d 41d x a l xkx x a l q E P -+=-+=πεπε)ln (4)(d 40020al aa l k x a l x x kE lP ++=-+=∴⎰πεπε 方向沿x 轴正向。
吉林大学大学物理作业答案综合练习题(下)(二)
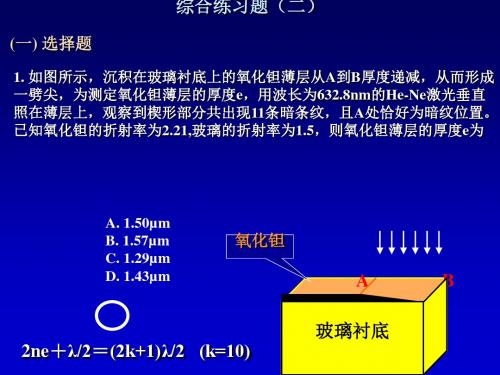
(一) 选择题
1. 如图所示，沉积在玻璃衬底上的氧化钽薄层从A到B厚度递减，从而形成 一劈尖，为测定氧化钽薄层的厚度e，用波长为632.8nm的He-Ne激光垂直 照在薄层上，观察到楔形部分共出现11条暗条纹，且A处恰好为暗纹位置。 已知氧化钽的折射率为2.21,玻璃的折射率为1.5，则氧化钽薄层的厚度e为
2 a b 10 2 4 0 0 n m s i n 3 0
1
4.一平面透射光栅，当用白光垂直照射时，能在30°衍射方向上观察到600nm的第 二级干涉主极大，并能在该处分辨△λ=0.05nm的两条光谱线，但在此30°方向上却 测不到400nm的第三级主极大，计算此光栅的缝宽a和缝距b以及总缝数N 。
6.氢原子中核外电子所处状态的角量子数是l＝2，其绕核运动的角动量的 大小 ；该角动量的空间取向可能有 5 种。 一级明
6
a sin 3 ;
a sin k; 2
k1 .5
9.一电磁波在空气中通过某点时，该点某一时刻的电场强度 为E，则同时刻的磁场强度H＝ ，能流密度S＝ 。
光栅对第k级主极大的分辨本领为
对于 ＝600nm的第二级主极大有
0 . 0 5 n m
所以,光栅总缝数
R kN
6 0 0 N 6 0 0 0 k 2 0 . 0 5
5. 在惯性系K中观测到相距 的两地点相隔 8 发生两事 x 9 1 0m 件，而在相对于K系沿x轴正向以匀速度运动的 系中发现此两事件 恰好发生在同一地点，试求在 系中此两事件的时间间隔。 t 5s
m向下拉x时，
kx a J m 2 R k 2 J m 2 R
T2 k ( x x 0 ) mg T 1 ma T R T R J 2 1 a R
大学物理学课后习题答案
习题及解答（全）习题一1-1 ｜r ∆｜与r ∆有无不同?t d d r 和t d d r 有无不同? t d d v 和t d d v有无不同?其不同在哪里?试举例说明．解：（1）r ∆是位移的模，∆r 是位矢的模的增量，即r ∆12r r -=，12r r r -=∆； （2）t d d r 是速度的模，即t d d r ==v tsd d .t rd d 只是速度在径向上的分量.∵有r r ˆr =（式中r ˆ叫做单位矢），则t ˆr ˆt r t d d d d d d r rr += 式中t rd d 就是速度径向上的分量，∴t r t d d d d 与r 不同如题1-1图所示.题1-1图(3)t d d v 表示加速度的模，即t v a d d =，t v d d 是加速度a 在切向上的分量. ∵有ττ (v =v 表轨道节线方向单位矢），所以t v t v t v d d d d d d ττ +=式中dt dv就是加速度的切向分量.(t tr d ˆd d ˆd τ 与的运算较复杂，超出教材规定，故不予讨论) 1-2 设质点的运动方程为x =x (t )，y =y (t )，在计算质点的速度和加速度时，有人先求出r ＝22y x +，然后根据v =t rd d ，及a ＝22d d t r 而求得结果；又有人先计算速度和加速度的分量，再合成求得结果，即v =22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x 及a =222222d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛t y t x 你认为两种方法哪一种正确？为什么？两者差别何在？解：后一种方法正确.因为速度与加速度都是矢量，在平面直角坐标系中，有j y i x r+=，jt y i t x t r a jt y i t x t r v222222d d d d d d d d d d d d +==+==∴故它们的模即为222222222222d d d d d d d d ⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=+=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x a a a t y t x v v v y x y x而前一种方法的错误可能有两点，其一是概念上的错误，即误把速度、加速度定义作22d d d d t r a trv ==其二，可能是将22d d d d t r tr 与误作速度与加速度的模。
大学物理练习题及答案详解
大学物理练习题及答案详解-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN大学物理学(上)练习题第一编 力 学 第一章 质点的运动1．一质点在平面上作一般曲线运动，其瞬时速度为,v瞬时速率为v ，平均速率为,v 平均速度为v，它们之间如下的关系中必定正确的是(A) v v ≠，v v ≠； (B) v v =，v v ≠；(C) v v =，v v =； (C) v v ≠，v v = [ ]2．一质点的运动方程为26x t t =-(SI)，则在t 由0到4s 的时间间隔内，质点位移的大小为 ，质点走过的路程为 。
3．一质点沿x 轴作直线运动，在t 时刻的坐标为234.52x t t =-（SI ）。
试求：质点在（1）第2秒内的平均速度； （2）第2秒末的瞬时速度； （3）第2秒内运动的路程。
4．灯距地面的高度为1h ，若身高为2hv 沿水平直线行走，如图所示，则他的头顶在地上的影子M 面移动的速率M v = 。
5．质点作曲线运动，r表示位置矢量，s 表示路程，t a 表示切向加速度，下列表达式（1）dv a dt =， （2）dr v dt =， （3）ds v dt =， （4）||t dv a dt=. （A ）只有（1）、（4）是对的； （B ）只有（2）、（4）是对的； （C ）只有（2）是对的； （D ）只有（3）是对的. [ ]6．对于沿曲线运动的物体，以下几种说法中哪一种是正确的。
（A ）切向加速度必不为零； （B ）法向加速度必不为零（拐点处除外）；（C ）由于速度沿切线方向；法向分速度必为零，因此法向加速度必为零； （D ）若物体作匀速率运动，其总加速度必为零；（E ）若物体的加速度a为恒矢量，它一定作匀变速率运动. [ ]Av B vvv7．在半径为R 的圆周上运动的质点，其速率与时间的关系为2v ct =（c 为常数），则从0t =到t 时刻质点走过的路程()s t = ；t 时刻质点的切向加速度t a = ；t 时刻质点的法向加速度n a = 。
大学物理静电学综合练习题(含答案)
解：利用高斯定理
r
a ： E1
=
Qr 4 0a 3
；r
a ： E2
=
Q 4 0r 2
we
=
1 E 2 ， 2
W
=
0a
1 2
0
E12
dV
+
a
1 2
ቤተ መጻሕፍቲ ባይዱ
0
E
2 2
dV
=
3Q 2 20 0a
12．一个半径为 R1 的金属球带有正电荷 Q ，球外包围着一层同心的相对介电常数为 r 的均 匀 电 介 质 球 壳 层 ， 其 内 半 径 为 R1 ， 外 半 径 为 R2 ， 在 电 介 质 内 的 点 a 距 离 球 心 为
(A) 0 ； (B) − q ； (C) r1 q ； (D) − r1 q 。
r2
r2
4-3
解：球心电势
U0
=
q 4 0r2
+ q 4 0r1
= 0，q = − r1 q r2
10．如图所示，一个封闭的空心导体，观察者 A (测量仪器)和电
荷 Q1 置于导体内，而观察者 B 和电荷 Q2 置于导体外，下列说
解：在圆环上任取一段d l ，d l 到o 点的连线与 x 轴夹角为 ，则d l 段
=
q0q 4 0
1 d
−
0
−
q0q 4 0
1 d
−
0
=
0
或 Ao = q0(Uo − U ) = 0
4．长度为 L 的细玻璃棒，沿着长度方向均匀地分布着电 荷，总电量为 Q ，如图所示。在棒的轴向有一点 P ，离 棒 左 端 的 距 离 为 r ， 则 P 点 的 电 势 P•
吉林大学大学物理练习册综合练习二答案
c′
V
8．1mol刚性双原子分子理想气体，当温度为 时，其 ． 刚性双原子分子理想气体， 刚性双原子分子理想气体 当温度为T时 内能为
3 A . RT 2 3 B . kT 2
5 C . RT 2
5 D . kT 2
4
9．对于室温下的双原子分子理想气体，在等压 ．对于室温下的双原子分子理想气体， 膨胀的情况下， 膨胀的情况下，系统对外所作的功与从外界吸 收的热量之比 A/Q 等于 A. 1/3 B. 1/4 C. 2/5 D. 2/7 10．一定量的理想气体向真空作绝热自由膨 ． 体积由V 增至V 胀，体积由 1增至 2，在此过程中气体的 A. 内能不变，熵增加 内能不变， B. 内能不变，熵减少 内能不变， C. 内能不变，熵不变 内能不变， D. 内能增加，熵增加 内能增加，
m mg µl M f = 2∫ ⋅ dr ⋅ gµr = 0 2l 2
l
M f ⋅ ∆t = 0 − Iω 0 ⇒ 2 lω 0 ∆t = 3 µg
8
5． 如图所示 ， 质点 的质量为 ． 如图所示， 质点P的质量为 的质量为2kg， 位置矢量 ， r r r 的作用。 为 r ，速度为 υ ，它受到力 F 的作用。这三个 −1 量均在xOy平面内，且r = 3m， = 4.0m ⋅ s ， 平面内， 量均在 平面内 ， υ r F=2N。 则该质点对 点的角动量 12kkgm2s−1， 点的角动量=_________， 。 则该质点对O点的角动量 r 作用在质点上的力对O点的力矩 点的力矩=___________。 作用在质点上的力对 点的力矩 3kNm 。
角动量（动量矩） 角动量（动量矩）
r r r L = r × mυ
r r r M = r ×F
大学物理综合练习答案
擦不计，物体与台面间摩擦系数为，试计算台面对物体的摩擦力
的功以及物体的初速V0 。
L
V0
解:当物体滑至前端到达
x时摩擦力可表示为
f
滑道
m
xg
i
L
mg i
x (0 x L)
( x L)
L
台面
S
则全过程摩擦力的功为：
Af
f dl
L
0
m L
xg dx
S
mg dx
L
mg(S
L) 2
2.质量m=1Kg的物体，在坐标原点处从静止出发在水平面内沿X轴
运动，其所受合力方向与运动方向相同，合力大小为F=3+2x(SI)，
那么物体在开始运动的3m内，合力所做功W=
其速率V=
6m/s
。
a F /m 3 2x
a dV / dt V dV / dx
18J
F
dr;且 03x(3=32mx)时i d，x i
移到相应的b、c、d 各点，设移动过程中电场力所做功分别为A1、
A2、A3，则三者的大小关系是： A1 A2 A3 。a
A q0U AB ，球面为-Q的一个等势面
5.在一个不带电的导体球壳内，先放进一电量为
Q
o
b c
d
填空题4
+q的点电荷，点电荷不与球壳内壁接触，然后使该球壳与地接触一
下，再将点电荷+q取走，此时球壳的电量为 -q ，电场分布的范
m l
x1g
T1
m l
x1a
(T1
T2 )R
J
(1 MR2 2
m R R2 )
l
a
S
工科大学物理练习答案及解析(含综合卷)
16
t 2
k4
V 4t 2
Vt 1 4m/s
a R
d dV 2kt 8t dt dt
an 2 R 2 16t 4
F
O
F
1题图
M J
M 0
2.质量为m的小孩站在半径为R的水平平台边缘上，平台可以绕通过 其中心的竖直光滑轴自由转动，转动惯量为J，开始时平台和小孩 均静止，当小孩突然以相对地面为V的速率在台边缘沿顺时针转向
走动时，此平台相对地面旋转的角速度和旋转方向分别为 ：
(A)
mR 2 V ( ) J R
M J k 2 J 0 / 2
k 2 J
d dt
2.一长为l的轻质细棒，两端分别固定质量为m和
2m的小球如图，此系统在竖直平面内可绕过中点 O且与棒垂直的水平光滑固定轴(O轴)转动。开始 时棒与水平成60°角并处于静止状态。无初转速 地释放以后，棒、球组成的系统绕O轴转动，系 3 ml 2 统绕O轴转动惯量J= 4 ，释放后，当棒转到 1 mgl 水平位置时，系统受到的合外力矩M= 2 ， 角加速度 =
a2 10 18 2 26(SI )
2.一质点沿X轴运动，其加速度a与位置坐标x的关系为a=3+6x2(SI), 如果质点在原点处的速度为零，试求其在任意位置处的速度。 dV dx dV 2 dV a ( 3 6 x ) i V 解： dt dx dt dx
k t ( AV0 ) m V Ae
mg F A k
西工大大学物理习题与综合练习
资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载西工大大学物理习题与综合练习地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容大学物理习题1 ．质点运动学一、选择题1 ．质点在 xoy 平面内作曲线运动，则质点速率的正确表达式为：A ．B ．C ．D ．E ．（）2 ．质点作匀速圆周运动，下列各量中恒定不变的量是A ．B ．C ．D ．E ．F ． . （）3 ．下列表述中正确的是：A ．质点沿轴运动，若加速度，则质点必作减速运动；B ．在曲线运动中，质点的加速度必定不为零；C ．若质点的加速度为恒矢量，则其运动轨道必为直线；D ．当质点作抛体运动时，其法向加速度、切向加速度是不断变化的，因此也是不断变化的。
（）4 ．在离水面高度为 h 的湖岸边上，有人用绳子拉船靠岸。
若人以匀速率v 0 收绳，则船在水中的运动为：A ．匀速运动，且 v = v 0 ；B ．加速运动，且 v > v 0 ；C ．加速运动，且 v < v 0 ；D ．减速运动。
（）5 ．已知质点的运动方程为：式中 A 、 B 、θ 均为恒量，且，，则质点的运动为：A ．一般曲线运动；B ．匀速直线运动；C ．圆周运动；D ．匀减速直线运动；E ．椭圆运动；F ．匀加速直线运动。
（）6 ．下列说法中正确的是A ．作曲线运动的物体，必有切向加速度；B ．作曲线运动的物体，必有法向加速度；C ．具有加速度的物体，其速率必随时间改变。
（）7 ．在相对地面静止的坐标系内， A 、 B 两船都以 2 的速率匀速行驶，A 船沿 x轴正向， B 船沿 y 轴正向。
今在 A 船上设置与静止坐标系方向相同的坐标系（ x 、 y 方向的单位矢量用 i ， j 表示），那么在 A 船上的坐标系中， B 船的速度（以为单位）为A ．B ．C ．D ．（）8 ．下列各种情况中，不可能存在的是A ．速率增加，加速度减小；B ．速率减小，加速度增大；C ．速率不变而有加速度；D ．速率增大而无加速度；E ．速率增大，而法向加速度的大小不变。
吉林大学大学物理练习册综合练习一答案
R1
R2O
λ1 r P
λ2
D. 0
9. 真空中一半径为 的球面均匀带电 ，在球心 处有一 真空中一半径为R的球面均匀带电 的球面均匀带电Q，在球心O处有一 带电量为q的点电荷 如图所示。 的点电荷， 带电量为 的点电荷，如图所示。设无穷远处为电 势零 则在球内离球心O距离为 距离为r的 点处电势为 点，则在球内离球心 距离为 的P点处电势为
二、填空题 x = 6 t − t 2 ( SI) ,则在 由0至4 s的 1. 一质点的运动方程为 则在t由 至 的 则在 时间间隔内， 时间间隔内，质点的位移大小为 8m ，在t由0到4 s 由 到 的时间间隔内质点走过的路程为 10m 。 2. 半径为 半径为30cm的飞轮 从静止开始以 的飞轮,从静止开始以 的飞轮 从静止开始以0.5rad/s2的匀角加速 度转动， 度转动，则飞轮边缘上一点在飞轮转过 240°时的切向 ° 法向加速度的大小a 加速度的大小 at＝ 0.15 m/s2 ， 法向加速度的大小 n ＝ 0.4π m/s2 。 3．一定量的理想气体处于热动平衡状态时，此热力学 ．一定量的理想气体处于热动平衡状态时， 系统不随时间变化的三个宏观量是____________, 系统不随时间变化的三个宏观量是 P,V ,T 2 1 而随时间不断变化的微观量是_________________. 而随时间不断变化的微观量是 υ, 2 mυ , mυ等
m dMf = rµ gdm = rµ g 2 2π rdr πR
mg 2 Mf = ∫ rµ 2 2πrdr = mgµ R 3 πR 0
R
1 2 − Mf θ = 0 − Iω0 2
n =θ
3Rω = 2π 16πµ g
2 0
3. 一卡诺热机 可逆的 ，当高温热源的温度为 一卡诺热机(可逆的 当高温热源的温度为127oC, 低温 可逆的)， 热源温度为27 时 其每次循环对外作净功8000J。今维 热源温度为 oC时，其每次循环对外作净功 。 持低温热源的温度不变，提高高温热源温度， 持低温热源的温度不变，提高高温热源温度，使其每次 循环对外作净功10000J 。若两个卡诺循环都工作在相同 循环对外作净功 的两条绝热线之间，试求： 的两条绝热线之间，试求： (1) 第二个循环热机的效率； 第二个循环热机的效率； (2) 第二个循环的高温热源的温度。 第二个循环的高温热源的温度。 T1 − T2 A 解： = η = ⇒Q2 = 24000J T1 Q2 + A 两循环工作在相同的两条绝热线之间， 两循环工作在相同的两条绝热线之间，且低温热源的 温度不变， 不变。 温度不变，故Q2不变。
吉林大学大学物理练习册综合练习一答案
B
成60o角，如图所示。则通过以该圆周为边线的如图所示
的任意曲面 Biblioteka 的磁通量 Φm1 s B dS BS cos 60o n R
任意曲面S
1 BR2
2
Φm2
s B dS
1 2
BR2
60 B
S
B
B
三、计算题
1. 如图所示，质点P在水平面内沿一半径为R = 2m的圆轨道转动。转动的角速度与时间t的函 数关系为=kt2(k为常数)。已知t=2s时，质点的 速度值为32m/s。试求t=1s时，质点P的速度与加 速度的大小。
半径为r具有光滑轴的定滑轮边缘绕一细绳绳下端挂一质量为m的物体绳的质量可以忽略绳与定滑轮之间无相对滑动若物体下落的加速度为a则定滑轮对轴的转动惯量jmg?arma2b?n?rb?b?任意曲面s?60s???sbs2m??d2rb21???d1三计算题1
3．一个人站在正在旋转的转台上，当他从转台 边缘沿半径向中心走去时，则转台的角速度 将
E Q (1 1 )
4 L R R2 L2
若Q 0 E沿x轴负方向
5. 图示为一个均匀带电的球层，其电荷体密度为
球层内表面半径为R1 ，外表面半径为R2 。设
无穷远处为电势零点，求空腔内任一点的电势。
解： dU 1 dq
4 0 r
dq 4 r2dr
R1
2
O
R2
E0
,B=
4 3
0
E0
.
A
B
E0
A 2 0
B 2 0
1 3
E0
A 2 0
大学物理课后习题答案详解
⼤学物理课后习题答案详解第⼀章质点运动学1、(习题 1.1)：⼀质点在xOy 平⾯内运动，运动函数为2x =2t,y =4t 8-。
（1）求质点的轨道⽅程；（2）求t =1 s t =2 s 和时质点的位置、速度和加速度。
解：（1）由x=2t 得，y=4t 2-8 可得： y=x 2-8 即轨道曲线（2）质点的位置： 22(48)r ti t j =+- 由d /d v r t =则速度： 28v i tj =+ 由d /d a v t =则加速度： 8a j =则当t=1s 时，有 24,28,8r i j v i j a j =-=+= 当t=2s 时，有 48,216,8ri j v i j a j =+=+=2、（习题1.2）：质点沿x 在轴正向运动，加速度kv a -=，k 为常数．设从原点出发时速度为0v ，求运动⽅程)(t x x =.解：kv dtdv -= ??-=t v v kdt dv v 001 tk e v v -=0t k e v dtdx-=0 dt e v dx t k t x -??=000 )1(0t k e k v x --=3、⼀质点沿x 轴运动，其加速度为a = 4t (SI)，已知t = 0时，质点位于x 0=10 m 处，初速度v 0 = 0．试求其位置和时间的关系式．解： =a d v /d t 4=t d v 4=t d t ?=vv 0d 4d tt t v 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020= x 2= t 3 /3+10 (SI)4、⼀质量为m 的⼩球在⾼度h 处以初速度0v ⽔平抛出，求：（1）⼩球的运动⽅程；（2）⼩球在落地之前的轨迹⽅程；（3）落地前瞬时⼩球的d d r t ，d d v t ，tv d d . 解：（1） t v x 0= 式（1）2gt 21h y -= 式（2） 201()(h -)2r t v t i gt j =+（2）联⽴式（1）、式（2）得 22v 2gx h y -=（3）0d -gt d rv i j t = ⽽落地所⽤时间 gh2t = 所以 0d -2gh d r v i j t =d d v g j t=- 2202y 2x )gt (v v v v -+=+= 2120212202)2(2])([gh v gh g gt v t g dt dv +=+=5、已知质点位⽮随时间变化的函数形式为22r t i tj =+，式中r 的单位为m ，t 的单位为s .求：（1）任⼀时刻的速度和加速度；（2）任⼀时刻的切向加速度和法向加速度。
大学基础教育《大学物理（一）》综合练习试题 附答案
大学基础教育《大学物理（一）》综合练习试题附答案姓名：______ 班级：______ 学号：______考试须知：1、考试时间：120分钟，本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
一、填空题（共10小题，每题2分，共20分）1、一质点作半径为0.1m的圆周运动，其运动方程为：（SI），则其切向加速度为＝_____________。
2、一圆盘正绕垂直于盘面的水平光滑固定轴O转动，如图射来两个质量相同，速度大小相同，方向相反并在一条直线上的子弹，子弹射入圆盘并留在盘内，则子弹射入后的瞬间，圆盘的角速度_____。
3、两列简谐波发生干涉的条件是_______________，_______________，_______________。
4、从统计的意义来解释, 不可逆过程实质上是一个________________的转变过程, 一切实际过程都向着________________ 的方向进行。
5、质量为M的物体A静止于水平面上，它与平面之间的滑动摩擦系数为μ，另一质量为的小球B以沿水平方向向右的速度与物体A发生完全非弹性碰撞．则碰后它们在水平方向滑过的距离L＝__________。
6、质量为m的物体和一个轻弹簧组成弹簧振子，其固有振动周期为T．当它作振幅为A的自由简谐振动时，其振动能量E＝__________。
7、简谐振动的振动曲线如图所示，相应的以余弦函数表示的振动方程为__________。
8、静电场中有一质子(带电荷) 沿图示路径从a点经c点移动到b点时，电场力作功J．则当质子从b点沿另一路径回到a点过程中，电场力作功A＝___________；若设a点电势为零，则b点电势＝_________。
9、两根相互平行的“无限长”均匀带正电直线1、2，相距为d，其电荷线密度分别为和如图所示，则场强等于零的点与直线1的距离a为_____________ 。
10、花样滑冰运动员绕通过自身的竖直轴转动，开始时两臂伸开，转动惯量为，角速度为；然后将两手臂合拢，使其转动惯量变为，则转动角速度变为_______。
大学物理综合练习题及答案
⼤学物理综合练习题及答案综合练习题AII⼀、单项选择题（从每⼩题给出的四个备选答案中，选出⼀个正确答案，并将其号码填在题⼲后的括号内，每⼩题2分，共计20分）。
1、关于⾼斯定理，下⾯说法正确的是：（）A. ⾼斯⾯内不包围电荷，则⾯上各点的电场强度E 处处为零；B. ⾼斯⾯上各点的E 与⾯内电荷有关，与⾯外的电荷⽆关；C. 穿过⾼斯⾯的电通量，仅与⾯内电荷有关；D. 穿过⾼斯⾯的电通量为零，则⾯上各点的E 必为零。
2、真空中有两块互相平⾏的⽆限⼤均匀带电平板，其中⼀块的电荷⾯密度为+σ，另⼀块的电荷⾯密度为－σ，两板间的电场强度⼤⼩为：（）A. 0；B. 023εσ；C. 0εσ；D. 02εσ。
3、图1所⽰，P 点在半圆中⼼处，载流导线旁P 点的磁感应强度B 的⼤⼩为：（） A. µ0I(r r 2141+π)； B. µ0I(r r2121+π)； C. µ0I(r r 4141+π)； D. µ0I(r r 4121+π) 。
4、⼀带电粒⼦以速率V 垂直射⼊某匀强磁场B 后，运动轨迹是圆，周期为T 。
若以速率2V 垂直射⼊，则周期为：（） A. T/2； B. 2T ； C. T ； D. 4T 。
5、根据洛仑兹⼒的特点指出下列叙述错误的为：（） A. 洛仑兹⼒与运动电荷的速度相垂直； B. 洛仑兹⼒不对运动电荷做功； C. 洛仑兹⼒始终与磁感应强度相垂直；D. 洛仑兹⼒不改变运动电荷的动量。
6、在杨⽒双缝⼲涉实验中，两条狭缝相距2mm ，离屏300cm ，⽤600nm 光照射时，⼲涉条纹的相邻明纹间距为：（）A. 4.5mm ；B. 0.9mm ；C. 3.12mm ；D. 4.15mm 。
7、若⽩光垂直⼊射到光栅上，则第⼀级光谱中偏离中⼼最远的光是：（）A. 蓝光；B. 黄光；C. 红光；D. 紫光。
8、⼀束光是⾃然光和线偏振光的混合光，让它垂直通过⼀偏振⽚。
大学物理电磁学综合练习题(含答案)
解：选择电流元
d I = I dl = I d R
d B = 0 d I = 0 I d 2R 2R
d Bx = − d B sin
=
−
0I 2 2R
sin
d
d By = d B cos
=
0I 2 2R
cos
d
Bx
=
0 d Bx
=
− 0I 2R
I • P•
o• L2
(D) M = 。
解：线圈 1（或 2）的电流变化不会引起线圈 2（或 1）的磁
通量的变化。
二、填充题(单位制为 SI)
1．
电流回路如图所示，弧线
AD
、
BC
为同心半圆环。某时刻一电子以速度
v
沿水平向左
的方向通过圆心 o 点，则电子在该点受到的洛仑兹力大小为 Fm
=
0I 4
ev
5-5
则此导线中的感生电动势 i
=
5 2
BR 2 ；
O 点电势高。
解：添 ob 后，整个线圈的感应电动势为零，所以
oacb
=
ob
=
ob(v
B) dl
=
− obrB
d
r
=
−
0
5R
rB
d
r
=
=
−
5 2
R2B
5．如图所示，一无限长圆柱体半径为 R ，均匀通过电流 I ，则穿过图中阴影部分的磁通量
解：产生涡旋电场，据 i = E K d l 可判断。
10．两个自感应系数分别为 L1 、 L2 ，半径均为 R 的圆
L1
《大学物理》习题训练与详细解答一(质点运动学练习一、二)
2 3 2 3 x x0 t 10 t 3 3
6．如图2所示，质点p在水平面内沿一半径为R =2m的圆轨道转动,转动的角速度ω与时间的关系 2 示为 kt （k为常数）。 已知t=2s时，质点P的速度值为32m/s. 试求 t=1s时，质点P的速度与加速度的大小
w v k 2 2 4 t Rt
（A）(1)、(4)是正确的 (C) (2) 是正确的 (B) (2)、(4)是正确的 (D) (3)是正确的
3.一质点沿x轴作直线运动，它的运动方程为 x=3+5t+6t2-t3 (SI) 则 5m/s (1) 质点在t=0时刻的速度V0=________; (2)加速度为零时，该质点的速度v=________. 17m/s
dv dv 2 kv t 2 ktdt dt v v t 1 1 2 ( ) ( kt ) v0 0 v 2
.
3.一质点作直线运动，其坐标x与时间t的函数曲线如图 3 秒瞬时速度为零；在第 1所示，则该质点在第______ 3 6 ______ 秒至第______ 秒间速度与加速度同方向。
大学物理Ⅳ-习题课1
练习一 质点运动学（一）
1.一质点在平面上作一般曲线运动，其瞬时速度为 ， 瞬时速率为v，某一段时间内的平均速度为v ，平均速 率为v ,它们之间的关系必定有 [ ] D (A) | v | = v， | v | = v (B) | v | ≠v, | v | = v (C) | v | ≠v,
r 平均速度： v , t s 平均速率： v , t dr 瞬时速度： v , dt d r ds 瞬时速率： v dt dt
v
|v≠ | v
(D)
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
库仑定律7-1 把总电荷电量为Q 的同一种电荷分成两部分，一部分均匀分布在地球上，另一部分均匀分布在月球上，使它们之间的库仑力正好抵消万有引力，已知地球的质量M ＝5.98⨯l024kg ，月球的质量m =7.34⨯l022kg 。
（1）求Q 的最小值；（2）如果电荷分配与质量成正比，求Q 的值。
解：（1）设Q 分成q 1、q 2两部分，根据题意有 2221r MmG r q q k=，其中041πε=k即 2221q k q GMm q q Q +=+=。
求极值，令0'=Q ，得 0122=-kq GMmC 1069.5132⨯==∴k GMm q ，C 1069.51321⨯==k q GMm q ，C 1014.11421⨯=+=q q Q （2）21q m q M =，k GMm q q =21kGMm m q mq Mq ==∴2122 解得C 1032.61222⨯==kGm q ， C 1015.51421⨯==m Mq q ，C 1021.51421⨯=+=∴q q Q 7-2 三个电量为 –q 的点电荷各放在边长为l 的等边三角形的三个顶点上，电荷Q （Q ＞0）放在三角形的重心上。
为使每个负电荷受力为零，Q 值应为多大？ 解：Q 到顶点的距离为 l r 33=，Q 与-q 的相互吸引力为 20141rqQF πε=， 两个-q 间的相互排斥力为 220241l q F πε=据题意有 10230cos 2F F =，即 2022041300cos 412rqQl q πεπε=⨯，解得：q Q 33= 电场强度7-3 如图7-3所示，有一长l 的带电细杆。
（1）电荷均匀分布，线密度为+λ，则杆上距原点x 处的线元d x对P 点的点电荷q 0 的电场力为何？q 0受的总电场力为何？（2）若电荷线密度λ=kx ，k 为正常数，求P 点的电场强度。
解：（1）线元d x 所带电量为x q d d λ=，它对q 0的电场力为200200)(d 41)(d 41d x a l x q x a l q q F -+=-+=λπεπεq 0受的总电场力 )(4)(d 4000200a l a l q x a l xq F l+=-+=⎰πελπελ00>q 时，其方向水平向右；00<q 时，其方向水平向左q 0 图7-3q -q-（2）在x 处取线元d x ，其上的电量x kx x q d d d ==λ，它在P 点的电场强度为2020)(d 41)(d 41d x a l xkx x a l q E P -+=-+=πεπε)ln (4)(d 40020al aa l k x a l x x kE lP ++=-+=∴⎰πεπε 方向沿x 轴正向。
7-4一半径为R 的绝缘半圆形细棒，其上半段均匀带电量+q ，下半段均匀带电量-q ，如图7-4所示，求半圆中心处电场强度。
解：建立如图所示的坐标系，由对称性可知，+q 和-q 在O 点电场强度沿x 轴的分量之和为零。
取长为d l的线元，其上所带电量为θπθππλd 2d 2d 21d d q R R q l R q l q ====，20d 41d R q E πε=∴ 方向如图y 方向的分量 θεπθθπεcos 2d cos d 41d 20220R q R q E y -=-=j R qj R q E20220202d cos 22επθθεππ-=⨯-=∴⎰7-5一半径为R 的半球壳，均匀带有电荷，电荷面密度为σ，求球心处电场强度。
解：沿半球面的对称轴建立x 轴，坐标原点为球心O 。
在球面上取半径为r 、宽为d l 的环带，如图，其面积为θππd 2d 2d R r l r S ⋅==，所带电荷 θπσσd 2d d R r S q ⋅⋅==d q 在O 处产生的电场强度为，2322023220)(d 2)(d 41d r x xr R r x qx E +=+=θεσπε θsin R r = ，θcos R x =θθθεσd cos sin 2d 0=∴E 因为球面上所有环带在O 处产生的电场强度方向相同，i i E204d cos sin 2εσθθθεσπ==∴⎰7-6一无限大均匀带电薄平板，面电荷密度为σ，平板中部有一半径为R 的圆孔,如图7-6所示。
求圆孔中心轴线上的场强分布。
（提示：利用无穷大板和圆盘的电场及场强叠加原理） 解：利用补偿法，将圆孔看作由等量的正、负电荷重叠而成，即等效为一个完整的带电无穷大平板和一个电荷面密度相反的圆盘叠加而成。
无穷大平板的电场为 n e E12εσ= 图7-4圆盘激发的电场为 n e R x x E )1(22202+--=εσ，其中n e为平板外法线的单位矢量。
圆孔中心轴线上的电场强度为 n e R x x E E E220212+=+=εσ电通量7-7电场强度为E的匀强电场，其方向与半径为R 的半球面的对称轴平行，如图7-7所示，求通过该半球面的电场强度通量。
解：作半径为R 的平面S ’与半球面S 构成一个闭合曲面，由于该闭合曲面内无电荷，由高斯定理0d d d ''=⋅+⋅=⋅=Φ⎰⎰⎰+S SS S S E S E S EE R R E S E S E S SS 22'cos d d πππ=⋅-=⋅-=⋅=Φ∴⎰⎰7-8一边长为a 的立方体置于直角坐标系中，如图7-8所示。
现空间中有一非均匀电场j E i kx E E21)(++=，E 1、E 2为常量，求电场对立方体各表面及整个立方体表面的电场强度通量。
解：0=z E 0=Φ=Φ∴DEFG OABC⎰⎰==⋅++=⋅=ΦSSABGF a E S E j S j E i kx E S E 22221)(d ])[(d⎰⎰-=-⋅++=⋅=ΦSSCDEO a E j S j E i kx E S E 2221)d (])[(d⎰⎰-=-⋅+=⋅=ΦSSAOEF a E i S j E i E S E 2121)d ()(d⎰⎰+=⋅++=⋅=ΦSSBCDGa ka E i S j E i ka E S E 2121)()(d ])[(d整个立方体表面的电场强度通量 3ka ii=Φ=Φ∑高斯定理7-9有两个同心的均匀带电球面，内外半径分别为R 1和R 2，已知外球面的电荷面密度为+σ，其外面各处的电场强度都是零。
试求：（1）内球面上的电荷面密度；（2）外球面以内空间的电场分布。
解：作一半径为r 的同心球面为高斯面。
设内球面上的电荷面密度为'σ。
（1）2R r >处：因为外球面外的电场强度处处为零，由高斯定理有0)4'4(11d 212203=⋅+⋅==⋅∑⎰R R q S E ii Sπσπσεε，得 σσ212)('R R -= （2）由高斯定理011=<E R r图7-821R r R <<21024'1d R S E Sπσε⋅=⋅⎰即 210224'14R r E πσεπ⋅=⋅2022202121220212)(44'rR r R R R r R E εσεσπεπσ-=⋅-=⋅=∴ 方向沿径向反向 7-10一对无限长的均匀带电共轴直圆筒，内外半径分别为R 1和R 2，沿轴线方向单位长度的电量分别为λ1和λ2。
（1）求各区域内的场强分布；（2）若λ1＝-λ2，情况如何？画出此情形下的E ～ r 的关系曲线。
解：（1）作一半径为r 、长为h 的共轴圆柱面为高斯面，由高斯定理有011=<E R r21R r R <<h S E S1021d λε=⋅⎰h rh E 10212λεπ=⋅∴，得 rrE ˆ2012 πελ=2R r >h S E S )(1d 2103λλε+=⋅⎰ 得 r r E ˆ20213 πελλ+= （2）21λλ-=时，01=E，r rE ˆ2012 πελ=，03=E7-11设半径为R 的球体，电荷体密度ρ ═ kr （r ≤R ），其中k 为常量，r 为距球心的距离。
求电场分布，并画出E ～ r 的关系曲线。
解：作一半径为r 的同心球面为高斯面。
根据高斯定理Rr <402011d 41d 1d kr r r kr V S E rVSπεπερε=⋅==⋅⎰⎰⎰即 402114kr r E πεπ=⋅ 得 rkr E ˆ4021 ε= R r >402021d 41d kR r r kr S E RSπεπε=⋅=⋅⎰⎰即 402214kR r E πεπ=⋅ 得 r rkR E ˆ42042 ε= 7-12一厚度为d =0.5cm 的无限大平板，均匀带电，电荷体密度ρ ═ 1.0⨯10-4C/m 3，求（1）平板内外的电场分布；（2）讨论平板中央以及平板内与其表面相距0.1cm 处的电场强度。
解：（1）设中心平面为S 0。
根据对称性，在距S 0处为x 处对称地取两面积均为S ∆的底面作一圆柱形高斯面，其侧面与板面垂直（如图所示），即侧面的电通量为零。
2d x <时S x S E S E S∆⋅=∆=⋅⎰ρε212d 011 ， x E 01ερ=∴122d x >时S d S E S E S ∆⋅⋅=∆=⋅⎰2212d 022ρε ， 02ερd E =∴ （2）平板中央 0=x ，00=∴E平板内与表面相距0.1cm 处，cm 15.0=x4123401069.11085.8105.1100.1⨯=⨯⨯⨯⨯==∴---ερx E V/m 7-13一个电荷体密度为ρ（常量）的球体。
（1）证明球内距球心r 处一点的电场强度为r E3ερ=；（2）若在球内挖去一个小球，如图7-13所示，证明小球空腔内的电场是匀强电场a E3ερ=，式中a 是球心到空腔中心的距离矢量。
证：（1）作与球体同心的球面为高斯面，根据高斯定理⎰⎰=⋅V SV S E d 1d 0ρε 即 302344r r E περπ⋅=⋅ r E 03ερ=∴ 矢量式 r E3ερ= 得证（2）填充法：设在空腔中填充电荷密度分别为ρ和-ρ的电荷球体，形成电荷密度分别为ρ和-ρ的大球体和小球体。
对腔内任一点P （如图），由（1）的结果有大球 r E P 013ερ=； 小球 '302r E Pερ-= a r r E E E P P0213)'(3ερερ=-=+= 得证静电场的环路定理7-14若电场中某一部分电场线的形状是以O 点为中心的同心圆弧。
证明该部分上各点的电场强度都应与该点离O 点的距离成反比，即E 1 r 1 = E 2 r 2。