附和导线计算例题
导线测量—附合导线测量的内业计算(水利水电工程测量课件)

CD 603644 603801 1 17
f CD
60 6 147
f 容 60 n
12560627
坐标方位角
5
2364428
2110753
1002711
二、附合导线坐标计算
点号
1
A
B
1
2
3
4
C
D
坐标
方位角
5
距离
m
6
2110753
1002711
125.36
107.31
64.81
107.27
64.83
98.76
144.63
17.92
30.88
97.12
97.10
141.29
17.89
30.92
= 4 + 180° −
′
= +6 × 180°
− 测
二、附合导线坐标计算
写成一般公式为:
式中
′
终
= 始 + × 180° − 测
始 ——起始边的坐标方位角
′
终
——终边的推算坐标方位角
若观测左角,则
′
终
= 始 + × 180° + 测
坐标值
点
m ∆x/m ∆y/m ∆x/m ∆y/m x/m y/m 号
6
7
8
9
10
11
12 13
125.36
98.76
144.63
116.44
156.25
603801
A
1536.86 837.54 B
附合导线测量的内业计算

第三节 导线测量的内业计算导线测量内业计算的目的就是计算各导线点的平面坐标x 、y 。
计算之前,应先全面检查导线测量外业记录、数据是否齐全,有无记错、算错,成果是否符合精度要求,起算数据是否准确。
然后绘制计算略图,将各项数据注在图上的相应位置,如图6-11所示。
一、坐标计算的基本公式 1.坐标正算根据直线起点的坐标、直线长度及其坐标方位角计算直线终点的坐标,称为坐标正算。
如图6-10所示,已知直线AB 起点A 的坐标为(x A ,y A ),AB 边的边长及坐标方位角分别为D AB 和αAB ,需计算直线终点B 的坐标。
直线两端点A 、B 的坐标值之差,称为坐标增量,用Δx AB 、Δy AB 表示。
由图6-10可看出坐标增量的计算公式为:y图6-10坐标增量计算⎭⎬⎫=-=∆=-=∆AB AB A B AB AB AB A B AB D y y y D x x x ααsin cos (6-1)根据式(6-1)计算坐标增量时,sin 和cos 函数值随着α角所在象限而有正负之分,因此算得的坐标增量同样具有正、负号。
坐标增量正、负号的规律如表6-5所示。
⎭⎬⎫+=∆+=+=∆+=AB AB A AB A B AB AB A AB A B D y y y y D x x x x ααsin cos (6-2)例6-1 已知AB 边的边长及坐标方位角为456380m 62.135'''︒==AB AB D α,,若A 点的坐标为m 82.658m 56.435==A A y x ,,试计算终点B 的坐标。
解 根据式(6-2)得m 62.792456380sin m 62.135m 82.658sin m 68.457456380cos m 62.135m 56.435cos ='''︒⨯+=+=='''︒⨯+=+=AB AB A B AB AB A B D y y D x x αα2.坐标反算根据直线起点和终点的坐标,计算直线的边长和坐标方位角,称为坐标反算。
附合导线(左角)坐标计算表(范本)
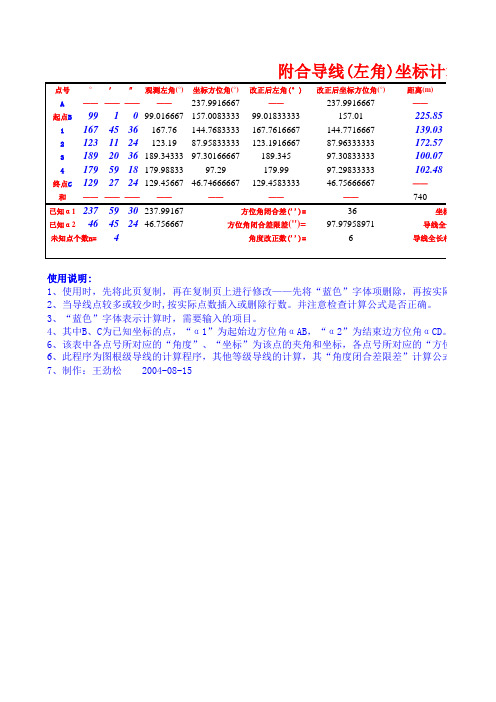
点号°′″观测左角(°)坐标方位角(°)改正后左角(°)改正后坐标方位角(°)距离(m)A ————————237.9916667——237.9916667——起点B 991099.016667157.008333399.01833333157.01225.8511674536167.76144.7683333167.7616667144.7716667139.0321231124123.1987.95833333123.191666787.96333333172.5731892036189.3433397.30166667189.34597.30833333100.0741795918179.9883397.29179.9997.29833333102.48终点C 1292724129.4566746.74666667129.458333346.75666667——和——————————————740已知α12375930237.99167-36已知α246452446.75666797.9795897146附合导线(左角)坐标计算表使用说明:1、使用时,先将此页复制,再在复制页上进行修改——先将“蓝色”字体项删除,再按实际数2、当导线点较多或较少时,按实际点数插入或删除行数。
并注意检查计算公式是否正确。
未知点个数n=方位角闭合差('')=坐标闭角度改正数('')=导线全长相对方位角闭合差限差('')=导线全长闭(m)=7、制作:王劲松 2004-08-154、其中B、C为已知坐标的点,“α1”为起始边方位角αAB,“α2”为结束边方位角αCD。
n为待定的3、“蓝色”字体表示计算时,需要输入的项目。
6、此程序为图根级导线的计算程序,其他等级导线的计算,其“角度闭合差限差”计算公式及“导线全6、该表中各点号所对应的“角度”、“坐标”为该点的夹角和坐标,各点号所对应的“方位角计算表(范本)实际数据进行填写。
附合导线计算方法

附合导线计算方法已知A (X=,Y=),B (X=,Y=),C (X=,Y=),D (X=,Y=)四点坐标,及a AB (起始边),a CD (终止边)计算得出。
ƒAB =tan -1(XA XB YA YB --)=tan -1(2507.6983.229963.12158.1303--)=-22。
59”’ =-22。
59”’+180=157000”52’(计算方位角为负,所以要加上180)同理求出ƒCD 方位角坐标为46045”23’1:用求出 ƒAB ±观测角(左正右负)±180,依次加减,得出最后的ƒ‘CD 方位角,用计算的方位角ƒ‘CD -ƒCD =闭合差值B1方位角=157000”52’-192。
14,24,,+180=144。
46,28,,12方位角=144。
46,28,,-236。
48,36,,+180=87。
57,52,,23方位角=87。
57,52,,-170。
39,36,,,+180=97。
38,16,, 34方位角=97。
38,16,,-180。
00,48,,+180=97。
17,28,,4C 方位角=97。
17,28,, -230。
32,36,,+180=46。
44,52,,ƒ‘CD -ƒCD =46。
44,52,,-46045”23’=-31” 将角度闭合差除与测边数分配到各观测角中即:-31÷5=”(角度闭合差调整中,观测角为左角时反符号平均分配到各观测角中,观测角为右角时,则按闭合差同符号分配到测角,如有小数,按长边少分,短边多分原则)即:B1观测角=192。
14,24,,-6”=192。
14,18,,12观测角=236。
48,36,,-6”=236。
48,30,,23观测角=170。
39,36,,-6”=170。
39,30,,34观测角=180。
00,48,,-7”=180。
00,41,,4C 观测角=230。
32,36,,-6”=230。
附和导线计算例题

附和导线计算例题{例题6.5]某一级附合导线外业结果如图氐9所示.各点坐标値如表氐4所示卜计算各点坐标并检验是否满足精度要求。
计算结果如表6.5所示。
(I)绘制导线草图,如图6-9所示◎« 6.4 « jft « 值A席巴•圭鮭Im)<«巳独佳坏(m)X>X yA 2 686.6BI J 744.191C2 882.59M 5 574.768B2 8OS.J33 4 229466D3 309 042 5 31X721a 65謝合导肢呈标计・A<<< ■加(• • •)(* • *)> ft H<■・-) 4 茕> # * «Cm)ft £ & « t(Hi 1< ffl >4Ar Ai2r y 123447t夕10n 扌1 2i 7M.H17J 5S X9-JIM 52 00|0« >1 S7 2 toa」33 4 229 16&t uis m no-4M.J69*M-42J.99O*»2 $4,3 JO42J.M3234.23117 ?0J OD J4103 00 2t9 U.3 Wlr2 3*4 571 4 ««) 404■亍riL |W jl・554 56?+ >1-32«.32t441.3*42* 1224 44 郭224 4« 23T * V «■ 'WV2 05・曲 4 9 JI T911» H264”加+ 28n,9M473.fe«07).01*j J J >214 1) SO21-1 2J 412 IJ] 090J 405,49*4* JJ )94U.2S9+ i»329 鼻n+ B3S1.W?3 29. M0JS 2.OO54-3250 l<09250 1*06 2 “0.TTO S 757.501316 )4 »"9 一砂*26 43btoi* •-112.74142I.12B-IB2-73J C-J tuoasa1M 02 $Smi)st二江型UZdJGtt n3』t»g mm Z)117^3-46-t 47OJ3517CU) 1 M53W74.263I MS.MI328*>1*20*aip z * n * IW* - V fi ti■*irt *i32r,3r2fr^i2ir,iri8*--ir・±JO V*-±KS/6 - ±i 屯少 > ir(^ 格 |-(*•ft*yfc)»-o.(Mj <«>♦ n,(■>—■―1<―L_工孑近孑“/ 16 «7 15000=arctan 4229166--?-744:191 2 808.333-2 686.681(3) 角度闭合差计算。
(整理)附合导线、闭合导线作业
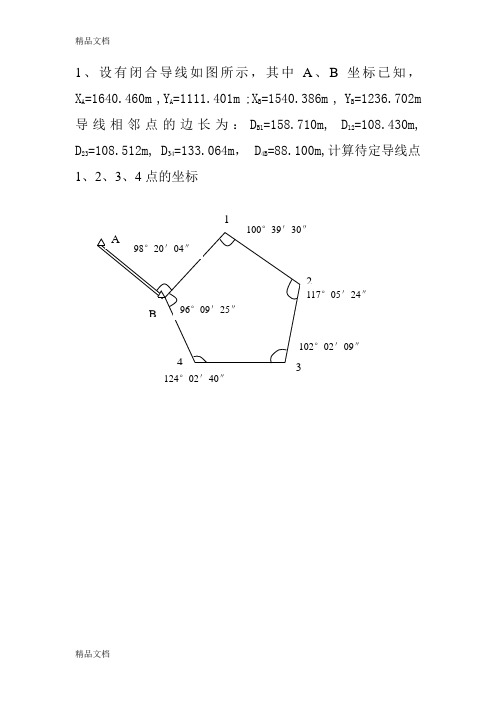
导线相邻点的边长为:DB1=158.710m,D12=108.430m,D23=108.512m,D34=133.064m,D4B=88.100m,计算待定导线点1、2、3、4点的坐标
2、设有如图所示附合导线,其中A、B、C、D坐标已知,XA=1708.117m ,YA=1355.584m ;XB=1864.222m ,YB=1413.350m
XC=1970.220m ,YC=1986.385m ;XD=2022.942m ,YD=1772.693m
导线相邻点的边长为:DB1=297.260m,D12=187.812m,D23=93.400m,D3C=150.642m,计算待定导线点1、2、3点的坐标
(6)环境影响评价结论的科学性。
(3)介绍评价对象的选址、总图布置、水文情况、地质条件、工业园区规划、生产规模、工艺流程、功能分布、主要设施、设备、装置、主要原材料、产品(中间产品)、经济技术指标、公用工程及辅助设施、人流、物流等概况。
每名环境影响评价工程师申请登记的类别不得超过2个。
在可行性研究时应进行安全预评价的建设项目有:
D.可能造成轻度环境影响、不需要进行环境影响评价的建设项目,应当填报环境影响登记表
市场价格在有些情况下(如对市场物品)可以近似地衡量物品的价值,但不能准确度量一个物品的价值。三者的关系为:
1)规划实施对环境Байду номын сангаас能造成影响的分析、预测和评估。主要包括资源环境承载能力分析、不良环境影响的分析和预测以及与相关规划的环境协调性分析。
附合导线严密平差算法总结
附合导线严密平差算法总结图1如图的单一附合导线,有4个已知点A、B、C、D,2个未知点TP1、TP2。
设观测边数为n, 则未知点数为n-1, 观测角数为n+1。
以上图为例,n = 3。
观测边为:S1 = B->TP1,S2 = TP1->TP2, S3 = TP2->C思路:由于A、B坐标已知,则可以算出起始方位角,再根据B点坐标和每个观测角(夹角,左角)推算出TP1、TP2、C点的近似坐标值。
如果是用全站仪进行测量,则用盘左盘右重复观测求平均的方式,直接测出TP1、TP2、C点的近似坐标值以及CD的方位角。
再根据c点的已知坐标与近似坐标求坐标闭合差,由CD的已知方位角和近似方位角求角度闭合差,两个闭合差联立求得边长和角度的改正数,最后求得未知点的坐标平差值。
条件平差过程:1.建立条件方程,求得条件系数2.求法方程系数3.求权阵4.计算出联系数K5.解算出观测值改正数V6.由观测值和改正数计算平差值详细步骤如下:1、建立条件方程在单一附合导线中,只需要三个条件方程即:方位角附合条件、纵坐标附合条件和横坐标附合条件方程。
(省略了条件方程的推导过程,详细过程请查看参考资料:《测量平差.pps》)(1)方位角附合条件[Vβi]n+11+ Wβ= 0式中,Wβ= - (T0– T CD+ [βi]n+11 - (n+1)*180°)(角度闭合差)βi ——角度观测值(夹角,左角)Vβi ——各观测角的改正数。
如果是用全站仪观测,则Wβ= - (T CD– T CD)式中,T CD ——CD的方位角观测值,T CD ——CD的已知方位角(2)纵坐标X附合条件方程[Cos TI * VSi]1n - (1/ ρ”)* [(Yn+1- Yi) * Vβi]1n - W x = 0;式中,TI——各方位角观测值(近似值)VSi——边长改正数Yn+1—— C点即终止点的横坐标Y的观测值(近似值)Yi——待定点的横坐标Y的观测值Wx = - (Xn+1- XC)XC—— C点即终止点的纵坐标X的已知值ρ” = 2062.65(3)横坐标Y附合条件方程[Sin TI * VSi]1n + (1/ ρ”)* [(Xn+1- Xi) * Vβi]1n– W Y = 0;式中,TI——各方位角观测值(近似值)VSi——边长改正数Xn+1—— C点即终止点的纵坐标X的观测值(近似值)Xi——待定点的纵坐标X的观测值WX = - (Yn+1- YC)YC—— C点即终止点的横坐标Y的已知值ρ” = 2062.652、求条件方程的系数矩阵联立3个方程得改正数条件方程组:[Vβi]n+11+ Wβ= 0[Cos TI * VSi]1n - 1/ ρ”* [(Yn+1- Yi) * Vβi]1n - W x = 0;[Sin TI * VSi]1n + 1/ ρ”* [(Xn+1- Xi) * Vβi]1n– W Y = 0;其系数矩阵arrA为:(即改正数V的系数,此处以图1为例, n = 3)3、联系数法方程(简称法方程)AP-1A T K – W = 0A——系数矩阵arrAK ——乘系数P ——权阵W ——闭合差矩阵由上得法方程的系数阵N:N = AP-1A T(权的推导见参考资料:《全站仪观测导线测量平差方法的研究.pdf》)角度权:P βi = 1;(因为角度的标称精度是固定的,各观测角权值相等) 边长权:P Si = (μ0 *μ0 ) / (M D * M D )(误差比例系数固定,边长的误差与距离有关,因此不一致)式中,μ0 ——先验测角中误差,以秒为单位 M D —— 距离观测中误差若 导线边长为S i (米),e1 为仪器的边长标称固定误差(mm ),e2为仪器的边长比例误差系数(无单位),则M D = ± (e1 + e2 * S i * 0.001)mm 需转化为厘米:M D = M D ** 0.1 (cm )由于此处是要P 的逆矩阵P -1,因此要求P 的各元素的倒数(P 是对角矩阵,对角矩阵的逆矩阵就是原矩阵元素的倒数) Psi = 1/ Psi ;由上可得,P -1 矩阵如下:4、求改正数由于N 已经在前面的步骤中求出,求N 的逆矩阵。
附合导线以及闭合导线方位角计算
例题:方位角的推算
2
2
已知:α 12=300,各观测角β
30 12
130
如图,求各边坐标方位角α23、 1 1 95
3
65
3
α 34、α 45、α 51。
解: α23= α 12-β 2±1800=800
122
5
128
4
5
α34= α23-β3±1800=1950
4
α45=2470
α51=3050
1
97 03 00
48 43 18A1
A
XA=536.27m
A
112
22
24
2
105 17
06 2
YA=328.74m
123 30 06
4 101 46 24
4
3
3
1
(1)计算坐标增量闭合差:
fx x测 x理 x测
1
97 03 00
fy y测 y理 y测
讲题:导线测量内业计算
内容提要:
四、导线的内业计算
四.导线的内业计算——计算各导线点的坐标
(一)几个基本公式 1、坐标方位角(grid bearing)的推算
前后左18 0
或: 前后右18 0
注意:若计算出的方位角>360°,则减去360°; 若为负值,则加上360°。
1
97 03 00
48 43 18A1
A
XA=536.27m
A
112
22
24
2
105 17
06 2
YA=328.74m
123 30 06
4 101 46 24
4
3
闭合、附合导线坐标计算作业
闭合、附合导线坐标计算作业1.闭合导线坐标计算闭合导线的起始数据、观测数据见表1和图1。
该作业的起始数据、连接角、连接边共36组,每位同学计算的题号要和本人的学号对应起来,不许选做或几个同学共做同一道题。
闭合导线观测数据:β1=104º04′40″,D 1=200.621m ;β2=114º09′30″,D 2=184.614m ;β3=48º30′14″,D 3=178.510m ;β4=216º15′20″,D 4=156.073m ;β5=57º01′06″,D 5=171.052m 。
计算1、2、3、4、5点的坐标。
计算要求(1)角度闭合差,其中n 为观测角个数,角度计算取至秒(2)导线全长相 , 其中 为导线全长;Df =1 闭合导线表1 闭合导线起始数据、观测数据D1β1D2D3β5β4D5β2β3βBD4BA54321βDnf 06''±≤β≤=k ∑D2.附合导线坐标计算附合导线的起始数据、观测数据见表2和图2。
该作业的数据共38组,每位同学计算的题号要和本人的学号对应起来,不许选做或几个同学共做同一道题。
附合导线观测数据。
β1=168º03′24″,D 12=160.321m;β2=145º20′48″,D 23=195.252m;β3=216º46′36″,D 34=140.813m ;β4=93º02′48″。
计算2、3点的坐标。
计算要求(1)角度闭合差,其中n 为观测角个数,角度计算取至秒图2 附合导线2AB(1)n f 06''±≤β≤表2 附合导线起始数据。
导线测量及计算
⊿y4n
3
B X终、y终 (n)
⊿x12
⊿xA1
X起、y起 0
⊿yAB
y
理论值:
x y
理 理
x终 x起 y终 y起
则闭合差为:
f x x测 x理
f y y测 y理
0 0
α
AB
β
α α
BA
AB
C
β左
AB 1800 左
α
B
BC
α
AB
A 若计算出的方位角超过360 0则应减去360 0。 若计算出的方位角小于0 0则应加上360 0 。
α
BA
C
(三)坐标增量的计算和坐标增量调整 1、坐标增量的计算: 坐标增量—相邻导线点坐标之差。 xB 坐标增量的计算方法: x B
导线测量的内业计算
要点: 1、角度闭合差的计算及闭合差的分配原则; 2、坐标增量闭合差的计算及闭合差的分配原则; 3、导线点的坐标计算; 4、利用表格计算方法;
一、闭合导线的计算 (一)、角度闭合差的计算和角度的调整 理论值: ∑β 理=(n-2)180⁰=540⁰00′00″ 实测内角和: ∑β 测=540⁰00′52″ 角度闭合差: fβ =∑β 测—∑β 理=+52″ 图根导线容许角度闭合差:
(四)、结点导线:从三个以上高级控制点开始的导线,在一个 或几个共同点汇合。如图,E、F点称为结点。 (五)、导线网:若干个闭合导线连接在一起,形成导线网。 二、各导线形式的使用条件: (一)闭合导线:适用于宽阔地区,无高级控制点的地区。 (二)附和导线:适用于狭长地带。例铁路、公路。 (三)支导线:无校核条件,适用 B A 于导线数目不足时的测图。在钢 尺量距时由于量距精度低一般不 D 超过两个点。 C (四)结点导线:增加校核条 A A D 件可以提高导线点的精度。 F D E (五)导线网:测区范围较大时, C B B' 首级控制可布成导线网。 C
