常微分方程第二章练习与答案

合集下载

常微分方程第一、二、三次作业参考答案

1、给定一阶微分方程2dyx dx=：（1）求出它的通解；解：由原式变形得：2dy xdx =.两边同时积分得2y x C =+.（2）求通过点（2，3）的特解；解：将点（2,3）代入题（1）所求的得通解可得：1C =-即通过点（2,3）的特解为：21y x =-.（3）求出与直线23y x =+相切的解；解：依题意联立方程组：223y x Cy x ⎧=+⎨=+⎩故有：2230x x C --+=。

由相切的条件可知：0∆=，即2(2)4(3)0C --⨯-+=解得4C =故24y x =+为所求。

（4）求出满足条件33ydx =⎰的解。

解：将 2y x C =+代入330dy =⎰，可得2C =-故22y x =-为所求。

2、求下列方程的解。

１）3x y dydx-= 2）233331dy x y dx x y -+=--解：依题意联立方程组：23303310x y x y -+=⎧⎨-+=⎩ 解得：2x =，73y =。

则令2X x =-，73Y y =-。

故原式可变成：2333dY x ydX x y-=-. 令Yu X =，则dy Xdu udx =+，即有 233263u dxdu u u x-=-+.两边同时积分，可得122(263)||u u C X --+= .将732y u x -=-，2X x =-代入上式可得： 12227()614323|2|2(2)y y C x x x -⎛⎫- ⎪--+=- ⎪-- ⎪⎝⎭.即上式为所求。

3、求解下列方程:1)24dyxy x dx+=. 解：由原式变形得：22dyxdx y=-. 两边同时积分得：12ln |2|y x C --=+. 即上式为原方程的解。

2)()x dyx y e dx-=. 解：先求其对应的齐次方程的通解： ()0dyx y dx -=. 进一步变形得：1dy dx y=.两边同时积分得：x y ce =.利用常数变异法，令()x y c x e =是原方程的通解。

常微分方程第三版习题答案

常微分方程第三版习题答案常微分方程是数学中的一个重要分支，它研究的是描述自然界中变化规律的方程。

在学习常微分方程的过程中，习题是非常重要的一部分，通过解习题可以加深对理论知识的理解和应用能力的培养。

本文将为大家提供《常微分方程第三版》习题的部分答案，希望能对大家的学习有所帮助。

1. 习题一1.1 解：首先，我们根据题意列出方程：$\frac{dy}{dt} = 2y + t^2$这是一个一阶线性常微分方程，我们可以使用常数变易法来求解。

令$y = u(t)e^{2t}$，则$\frac{dy}{dt} = \frac{du}{dt}e^{2t} + 2ue^{2t}$将上述结果代入原方程，得到：$\frac{du}{dt}e^{2t} + 2ue^{2t} = 2(u(t)e^{2t}) + t^2$化简得到：$\frac{du}{dt}e^{2t} = t^2$两边同时除以$e^{2t}$，得到：$\frac{du}{dt} = t^2e^{-2t}$对上式两边同时积分，得到：$u = -\frac{1}{4}t^2e^{-2t} + C$将$u$代入$y = u(t)e^{2t}$，得到最终的解：$y = (-\frac{1}{4}t^2e^{-2t} + C)e^{2t}$1.2 解：首先，我们根据题意列出方程：$\frac{dy}{dt} = \frac{t}{y}$这是一个一阶可分离变量的常微分方程，我们可以通过分离变量来求解。

将方程变形，得到：$ydy = tdt$对上式两边同时积分，得到：$\frac{1}{2}y^2 = \frac{1}{2}t^2 + C$解得：$y^2 = t^2 + C$由于题目中给出了初始条件$y(0) = 1$，将初始条件代入上式，得到：$1 = 0 + C$解得：$C = 1$将$C$代入$y^2 = t^2 + C$，得到最终的解：$y^2 = t^2 + 1$2. 习题二2.1 解：首先，我们根据题意列出方程：$\frac{dy}{dt} = 2ty + t^2$这是一个一阶线性常微分方程，我们可以使用常数变易法来求解。

常微分方程第二章练习与答案

1 / 16习题２-１判断下列方程是否为恰当方程,并且对恰当方程求解：１．0)12()13(2=++-dy x dx x解：13),(2-=x y x P , 12),(+=x y x Q ,则0=∂∂y P ,2=∂∂xQ, 所以 x Q y P ∂∂≠∂∂ 即原方程不是恰当方程．２．0)2()2(=+++dy y x dx y x 解：,2),(y x y x P +=,2),(y x y x Q -=则,2=∂∂y P ,2=∂∂xQ所以x Q y P ∂∂=∂∂,即原方程为恰当方程则,0)22(=-++ydy xdy ydx xdx两边积分得：.22222C y xy x =-+ 3．0)()(=+++dy cy bx dx by ax 〔a,b 和c 为常数〕．解：,),(by ax y x P +=,),(cy bx y x Q +=则,b y P =∂∂,b xQ =∂∂ 所以x Q y P ∂∂=∂∂,即原方程为恰当方程则,0=+++cydy bxdy bydx axdx两边积分得：.2222C cy bxy ax =++ 4．)0(0)()(≠=-+-b dy cy bx dx by ax解：,),(by ax y x P -=,),(cy bx y x Q -=则,b y P -=∂∂,b xQ=∂∂ 因为 0≠b , 所以x Q y P ∂∂≠∂∂,即原方程不为恰当方程５．0sin 2cos )1(2=++udt t udu t解：,cos )1(),(2u t u t P +=u t u t Q sin 2),(=则,cos 2u t t P =∂∂,cos 2u t xQ=∂∂ 所以x Q y P ∂∂=∂∂,即原方程为恰当方程则,0cos )sin 2cos (2=++udu udt t udu t2 / 16两边积分得：.sin )1(2C u t =+ ６．0)2()2(2=++++dy xy e dx y e ye xxx解： xy e y x Q y e ye y x P xxx2),(,2,(2+=++=,则,2y e y P x +=∂∂,2y e xQx +=∂∂ 所以x Q y P ∂∂=∂∂,即原方程为恰当方程则,0])2()[(22=++++dy xy e dx y ye dx e xxx两边积分得：.)2(2C xy e y x=++７．0)2(ln )(2=-++dy y x dx x xy解：,2ln ),(),(2y x y x Q x xy y x P -=+=则,1x y P =∂∂,1x x Q =∂∂ 所以xQy P ∂∂=∂∂,即原方程为恰当方程则02)ln (2=-++ydy dx x xdy dx x y两边积分得：23ln 3y x y x -+.C = ８．),(0)(22为常数和c b a cxydy dx by ax =++解：,),(,),(22cxy y x Q by ax y x P =+=则,2by y P =∂∂,cy xQ =∂∂ 所以当x Q y P ∂∂=∂∂,即 c b =2时, 原方程为恰当方程则0)(22=++cxydy dx by dx ax两边积分得：233bxy ax +.C = 而当c b ≠2时原方程不是恰当方程．９．01222=-+-dt ts s ds t s 解：,),(,12),(22ts s s t Q t s s t P -=-= 则,212t s t P -=∂∂,212tss Q -=∂∂ 所以x Q y P ∂∂=∂∂, 即原方程为恰当方程,两边积分得：C ts s =-2．3 / 1610．,0)()(2222=+++dy y x yf dx y x xf 其中)(⋅f 是连续的可微函数．解：),(),(),(),(2222y x yf y x Q y x xf y x P +=+=则,2f xy y P '=∂∂,2f xy xQ '=∂∂ 所以x Q y P ∂∂=∂∂, 即原方程为恰当方程,两边积分得：22()f xy dx C +=⎰,即原方程的解为C y x F =+)(22<其中F 为f 的原积分>．习题２-2. 1. 求解下列微分方程,并指出这些方程在平面上的有意义的区域:：〔１〕yx dx dy 2= 解：原方程即为：dx x ydy 2= 两边积分得：0,2332≠=-y C x y ．〔２〕)1(32x y x dx dy += 解：原方程即为：dx xx ydy 321+=4 / 16两边积分得：1,0,1ln 2332-≠≠=+-x y C x y ．〔３〕0sin 2=+x y dxdy解：当0≠y 时原方程为：0sin 2=+xdx y dy两边积分得：0)cos (1=++y x c ．又y=0也是方程的解,包含在通解中,则方程的通解为0)cos (1=++y x c ．〔４〕221xy y x dx dy +++=；解：原方程即为：2(1)1dyx dx y =++ 两边积分得：c x x arctgy ++=22, 即 )2(2c x x tg y ++=．〔５〕2)2cos (cos y x dxdy= 解：①当02cos ≠y 时原方程即为：dx x y dy 22)(cos )2(cos = 两边积分得：2222sin 2tg y x x c --=． ②y 2cos =0,即42ππ+=k y 也是方程的解. 〔N k ∈〕〔６〕21y dxdyx-= 解：①当1±≠y 时原方程即为：xdx y dy =-21 两边积分得：c x y =-ln arcsin ． ②1±=y 也是方程的解.〔７〕．yxe y e x dx dy +-=- 解．原方程即为：dx ex dy e y xy)()(--=+5 / 16两边积分得：c e x e y x y++=+-2222, 原方程的解为：c ee x y xy=-+--)(222.2. 解下列微分方程的初值问题．〔１〕,03cos 2sin =+ydy xdx 3)2(ππ=y ；解：两边积分得：c yx =+-33sin 22cos , 即c x y =-2cos 33sin 2因为 3)2(ππ=y , 所以 3=c .所以原方程满足初值问题的解为：32cos 33sin 2=-x y ．〔２〕．0=+-dy ye xdx x, 1)0(=y ；解：原方程即为：0=+ydy dx xe x,两边积分得：c dy y dx e x x=+-2)1(2, 因为1)0(=y , 所以21-=c , 所以原方程满足初值问题的解为：01)1(22=++-dy y dx e x x．〔３〕．r d dr=θ, 2)0(=r ；解：原方程即为：θd rdr=,两边积分得：c r =-θln ,因为2)0(=r , 所以2ln =c ,所以原方程满足初值问题的解为：2ln ln =-θr 即θe r 2=．〔４〕．,1ln 2yx dx dy+=0)1(=y ; 解：原方程即为：dx x dy y ln )1(2=+,两边积分得：3ln 3y y x x x c ++-=, 因为0)1(=y , 所以1=c ,所以原方程满足初值为：3ln 13y y x x x ++-=6 / 16〔５〕．321xy dxdyx=+, 1)0(=y ；解：原方程即为：dx xx y dy 231+=, 两边积分得：c x y ++=--22121, 因为1)0(=y , 所以23-=c ,所以原方程满足初值问题的解为：311222=++yx ．１．解下列微分方程,并作出相应积分曲线的简图．〔１〕．x dxdycos = 解：两边积分得：c x y +=sin ．积分曲线的简图如下：〔２〕．ay dxdy=, 〔常数0≠a 〕；解：①当0≠y 时,原方程即为：dx ay dy = 积分得：c x y a +=ln 1, 即 )0(>=c cey ax②0=y 也是方程的解．积分曲线的简图如下：7 / 16〔３〕．21y dxdy-=；解：①当1±≠y 时,原方程即为：dx y dy =-)1(2 积分得：c x yy+=-+211ln ,即 1122+-=x x ce ce y ．②1±=y 也是方程的解．积分曲线的简图如下：〔４〕．n y dx dy =, )2,1,31(=n ；解：①当0≠y 时, ⅰ〕2,31=n 时,原方程即为 dx y dy n =,积分得：c y n x n=-+-111．8 / 16ⅱ〕1=n 时,原方程即为dx ydy= 积分得：c x y +=ln ,即 )0(>=c ce y x．②0=y 也是方程的解．积分曲线的简图如下：4. 跟踪：设某A 从xoy 平面上的原点出发,沿x 轴正方向前进；同时某9 / 16B 从点开始跟踪A,即B 与A 永远保持等距b ．试求B 的光滑运动轨迹．解：设B 的运动轨迹为)(x y y =,由题意与导数的几何意义,则有22yb ydx dy --=,所以求B 的运动轨迹即是求此微分方程满足b y =)0(的解．解之得：222222ln21y b y b b y b b b x ----++=． 5. 设微分方程)(y f dxdy=〔2.27〕,其中f<y> 在a y =的某邻域〔例如,区间ε<-a y 〕内连续,而且a y y f =⇔=0)(,则在直线a y =上的每一点,方程〔2.27〕的解局部唯一,当且仅当瑕积分∞=⎰±εa ay f dy)(〔发散〕．证明：〔⇒〕首先经过域1R ：,+∞<<∞-x a y a <≤-ε 和域2R ：,+∞<<∞-x ε+≤<a y a内任一点〔00,y x 〕恰有方程〔2.13〕的一条积分曲线, 它由下式确定00)(x x y f dyyy-=⎰. 〔*〕这些积分曲线彼此不相交. 其次,域1R 〔2R 〕内的所有积分曲线c x y f dy +=⎰)(都可由其中一条,比如0)(c x y f dy+=⎰ 沿着 x 轴的方向平移而得到。

常微分方程标准答案-一二章

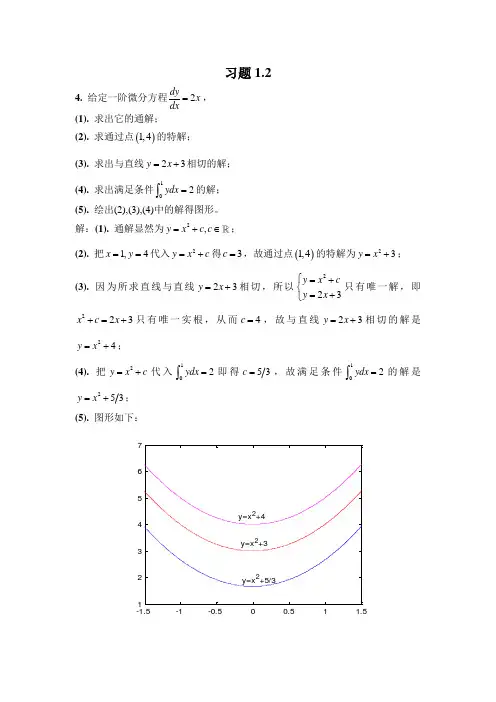
习题1.24. 给定一阶微分方程2dyx dx=， (1). 求出它的通解； (2). 求通过点()1,4的特解； (3). 求出与直线23y x =+相切的解； (4). 求出满足条件102ydx =⎰的解；(5). 绘出(2),(3),(4)中的解得图形。

解：(1). 通解显然为2,y x c c =+∈；(2). 把1,4x y ==代入2y x c =+得3c =，故通过点()1,4的特解为23y x =+；(3). 因为所求直线与直线23y x =+相切，所以223y x cy x ⎧=+⎨=+⎩只有唯一解，即223x c x +=+只有唯一实根，从而4c =，故与直线23y x =+相切的解是24y x =+；(4). 把2y x c =+代入12ydx =⎰即得5c =，故满足条件12ydx =⎰的解是253y x =+；(5). 图形如下：-1.5-1-0.500.51 1.512345675. 求下列两个微分方程的公共解：242422,2y y x x y x x x y y ''=+-=++--解：由2424222y x x x x x y y +-=++--可得()()222210y x xy -++=所以2y x =或212y x =--，2y x =代入原微分方程满足，而212y x =--代入原微分方程不满足，故所求公共解是代入原微分方程不满足。

6. 求微分方程20y xy y ''+-=的直线积分曲线。

解：设所求直线积分曲线是y kx b =+，则将其代入原微分方程可得2200010k b k xk kx b k b k b k k -=⎧+--=⇒⇒====⎨-=⎩或所以所求直线积分曲线是0y =或1y x =+。

8. 试建立分别具有下列性质的曲线所满足的微分方程：(2). 曲线上任一点的切线介于两坐标轴之间的部分等于定长l ； (5). 曲线上任一点的切线的纵截距等于切点横坐标的平方。

（完整版）常微分方程基本概念习题及解答

（完整版）常微分方程基本概念习题及解答§1.2 常微分方程基本概念习题及解答1．dxdy =2xy,并满足初始条件：x=0,y=1的特解。

解：ydy =2xdx 两边积分有：ln|y|=x 2+c y=e 2x +e c =cex 2另外y=0也是原方程的解，c=0时，y=0原方程的通解为y= cex 2,x=0 y=1时 c=1特解为y= e 2x .2. y 2dx+(x+1)dy=0 并求满足初始条件：x=0,y=1的特解。

解：y 2dx=-(x+1)dy 2y dy dy=-11+x dx 两边积分: -y1=-ln|x+1|+ln|c| y=|)1(|ln 1+x c 另外y=0,x=-1也是原方程的解x=0,y=1时 c=e特解：y=|)1(|ln 1+x c 3．dx dy =yx xy y 321++ 解：原方程为：dxdy =y y 21+31x x + y y 21+dy=31x x +dx 两边积分：x(1+x 2)(1+y 2)=cx 24. (1+x)ydx+(1-y)xdy=0解：原方程为： y y -1dy=-xx 1+dx 两边积分：ln|xy|+x-y=c另外 x=0,y=0也是原方程的解。

5．（y+x ）dy+(x-y)dx=0解：原方程为：dx dy =-yx y x +- 令xy =u 则dx dy =u+x dx du 代入有： -112++u u du=x 1dx ln(u2+1)x 2=c-2arctgu即 ln(y 2+x 2)=c-2arctg2x y . 6. x dxdy -y+22y x -=0 解：原方程为：dx dy =x y +x x ||-2)(1x y - 则令x y =u dx dy =u+ x dx du 211u - du=sgnx x1dx arcsin xy =sgnx ln|x|+c 7. tgydx-ctgxdy=0解:原方程为：tgy dy =ctgxdx 两边积分：ln|siny|=-ln|cosx|-ln|c| siny=x c cos 1=xc cos 另外y=0也是原方程的解，而c=0时，y=0. 所以原方程的通解为sinycosx=c. 8 dx dy +ye xy 32+=0 解：原方程为：dx dy =y e y 2e x 32 e x 3-3e 2y -=c.9.x(lnx-lny)dy-ydx=0解：原方程为：dx dy =x y ln xy 令xy =u ,则dx dy =u+ x dx du u+ x dxdu =ulnu ln(lnu-1)=-ln|cx| 1+lnx y =cy. 10. dxdy =e y x - 解：原方程为：dx dy =e x e y - e y =ce x 11 dxdy =(x+y)2 解：令x+y=u,则dx dy =dx du -1 dxdu -1=u 2 211u +du=dx arctgu=x+carctg(x+y)=x+c 12. dx dy =2)(1y x + 解：令x+y=u,则dx dy =dx du -1 dx du -1=21uu-arctgu=x+cy-arctg(x+y)=c. 13. dx dy =1212+-+-y x y x解: 原方程为：（x-2y+1）dy=(2x-y+1)dxxdy+ydx-(2y-1)dy-(2x+1)dx=0dxy-d(y 2-y)-dx 2+x=cxy-y 2+y-x 2-x=c 14: dx dy =25--+-y x y x 解：原方程为：（x-y-2）dy=(x-y+5)dxxdy+ydx-(y+2)dy-(x+5)dx=0dxy-d(21y 2+2y)-d(21x 2+5x)=0 y 2+4y+x 2+10x-2xy=c. 15:dxdy =(x+1) 2+(4y+1) 2+8xy 1+ 解：原方程为：dxdy =（x+4y ）2+3 令x+4y=u 则dx dy =41dx du -41 41dx du -41=u 2+3 dxdu =4 u 2+13 u=23tg(6x+c)-1 tg(6x+c)=32(x+4y+1). 16:证明方程y x dxdy =f(xy),经变换xy=u 可化为变量分离方程，并由此求下列方程：1）y(1+x 2y 2)dx=xdy2）y x dx dy =2222x -2 y x 2y+ 证明：令xy=u,则xdx dy +y=dxdu 则dx dy =x 1dx du -2x u ，有： u x dx du =f(u)+1)1)((1+u f u du=x1dx 所以原方程可化为变量分离方程。

常微分方程第二章

m
6：x
dy x− y =e dx 解：变量分离， e dy = e dx 两边积分得： e =e +c 11.
2 dy = ( x + y) dx y x y x
变量分离得：2
1 +1
12．解
令x + y = t，则变量分离
t2 dt = dx，两边积分t − arctgt = x + c，代回变量 t 2 +1 x + y − arctg ( x + y) = x + c dy 2 x − y − 1 = dx x − 2 y + 1
2
ww
w.
e
y x
解：变量分离，得
9 : x (ln x − ln y )dy − ydx = 0 y y 解：方程可变为： − ln • dy − dx = 0 x x y 1 ln u 令u = , 则有： dx = − d ln u x x 1 + ln u y 代回原变量得：cy = 1 + ln 。 x dy x− y 10： = e dx 解：变量分离 e dy = e dx 两边积分 e = e + c
w.
0
19. 已知 f(x) ∫ f ( x)dt = 1, x ≠ 0, 试求函数f ( x)的一般表达式 .
x
1 y = − 2 y' 1 y 解：设 f(x)=y, 则原方程化为 ∫ f (x)dt = 两边求导得 y 0 − y3 = dy 1 1 1 1 ; ; ; ; ; ; ; ; ; ; dx = − 3 ; ; ; ; ; ; ; ; ; ; ; ; 两边积分得x + c = ; ; ; ; ; 所以y = ± 2 dx 2y y dy 2x + c 1 代入

常微分方程第四版课后练习题含答案

常微分方程第四版课后练习题含答案第一章：常微分方程基本概念和初值问题1.2 课后练习题1.2.1（1）y′=2y+3，y(0)=1，求解y(t)；（2）y′+ty=1，y(0)=0，求解y(t)。

解答：（1）该微分方程为一阶线性常微分方程，其通解为$$y(t)=Ce^{2t}-\\frac{3}{2}$$代入初始条件y(0)=1，可得$$C=\\frac{5}{2}$$所以$$y(t)=\\frac{5}{2}e^{2t}-\\frac{3}{2}$$（2）首先设$u(t)=e^{\\frac{t^2}{2}}y(t)$，则$u'(t)=e^{\\frac{t^2}{2}}(y'+ty)$。

代入原方程可得$$u'(t)=e^{\\frac{t^2}{2}}$$对其积分得$$u(t)=\\int e^{\\frac{t^2}{2}} dt +C=\\frac{\\sqrt{2\\pi}}{2}erf\\frac{t}{\\sqrt{2}}+C$$其中$erf(x)=\\frac{2}{\\sqrt{\\pi}}\\int_0^x e^{-t^2} dt$称为误差函数。

进一步解得$$y(t)=e^{-\\frac{t^2}{2}}u(t)-ue^{-\\frac{t^2}{2}}=-\\frac{\\sqrt{2\\pi}}{2}erf\\frac{t}{\\sqrt{2}}e^{-\\frac{t^2}{2}}$$ 代入初始条件y(0)=0即可得到最终解答。

第二章：一阶线性微分方程2.2 课后练习题2.2.1求下列方程的通解：（1）(2x+1)y′+y=1；（2）(x−1)y′−y=2x；（3）$(2+\\cos x)y'-y=2-x\\cos x$。

解答：（1）该微分方程为一阶线性常微分方程，设方程的通解为$y=Ce^{-\\int \\frac{1}{2x+1} dx}+\\frac{1}{2x+1}$。

常微分方程与动力系统第二章课后题参考答案

常微分方程与动力系统第二章习题参考答案 1.证明：因为()t Φ是线性齐次系统（LH ）的一个基本解矩阵，由定理2.5知()t Φ在区间J 上满足矩阵微分系统()M LH ,即.()()()t A t t Φ=Φ，.1()()()A t t t -=ΦΦ所以由()A t 确定的线性齐次系统（LH ）必唯一。

2.证明：因为()t ϕ，()t ψ分别是.()x A t x=和.()T x A t x =-的解，所以111()()()nk k k nnk k k a d t A t t dt a ϕϕϕϕ==⎛⎫ ⎪ ⎪== ⎪ ⎪⎪ ⎪⎝⎭∑∑ ，11211111122222*121()()()nn k k k n n kn kn n n nnk a a a a a a a d t A t t dta a a a ψψψψψψ==⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪ ⎪⎪ ⎪=-ψ=-=- ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭∑∑ 因而1111112211(,)(,)(,),,nnk k k k k k nnkn k k nk k n n k a a d d d dt dt dt a a ψϕϕψψϕϕψϕψψϕψϕψϕ====⎡⎤⎛⎫⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥ ⎪-⎢⎥ ⎪⎪ ⎪⎢⎥ ⎪⎢⎥ ⎪ ⎪ ⎪⎢⎥=+= ⎪+⎢⎥ ⎪ ⎪ ⎪⎢⎥ ⎪-⎢⎥ ⎪⎪ ⎪⎢⎥⎪⎝⎭⎢⎥⎝⎭⎝⎭ ⎪⎣⎦⎢⎥⎝⎭⎣⎦∑∑∑∑ 11111111()0nnn n nnnnn n nnm m m m i ij j i ij j i mk k km k mk k km m m m m i j i j k k k k a a a a a a ϕψψϕϕψϕψϕψϕψ============-=+=-=-=∑∑∑∑∑∑∑∑∑∑∑∑所以(),()()()1nt t t t k kk ϕψϕψ≡≡∑=常数。

3.证明：设)t Φ(为系统.()x A t x=的一个基本解矩阵，则由定理2.11知[]1()Tt -Φ是系统.()Tx At x =-的基本解矩阵，由定理2.4知系统.()x A t x=满足初始条件00()x t x =的特解为100()))t t t x ϕ-=Φ(Φ(，[)0,0,t t ∈+∞由题可知)t Φ(与[]1()Tt -Φ在[)0,+∞上有界，从而由定理2.24知110()0k k t ∃=>和220()0k k t =>使得10120(),(),T t k t t t k t t -⎧Φ≤≤<+∞⎪⎨Φ≤≤<+∞⎪⎩,利用常数变易法公式（2.32），可知式.()()y A t y B t y=+的初始条件为00()y t y =的解满足1()()()()()()tt y t t t s B s y s ds ϕ-=+ΦΦ⎰因为1111()()(Ttttt---ΦΦ≤Φ所以12120()()(),tt y t k kx k k B s y s≤+≥⎰，利用格朗瓦尔不等式有12()120().tt k k B s dsy t k k x e⎰≤记12()12tt k k B s dsC k k e ⎰=设0()B t dt M +∞=<+∞⎰则()()tt B s ds B t dt M+∞≤=⎰⎰有1212k k MCk k e≤从而00(),y t C x t t ≤≥所以系统.()()y A t y B t y =+的一切解都在[)0,+∞上有界。

常微分课后答案第二章

第二章一阶微分方程的初等解法§2.1 变量分离方程与变量变换习题2.1求下列方程的解 1．xy dxdy2=，并求满足初始条件：1,0==y x 的特解．解分离变量，得到xdx ydy 2=，两边积分，即得C x y ~ln 2+=，因而，通解为 2x Ce y =，这里C 是任意常数．此外，方程还有解0=y ．由10==x y 得1=C ，特解2x e y =．2．0)1(2=++dy x dx y ，并求满足初始条件：1,0==y x 的特解．解分离变量，得到12+-=x dx y dy ，两边积分，即得C x y ~1ln 1++-=-，因而，通解为Cx y ++=1ln 1，这里C 是任意常数．此外，1-=x 和0=y 是两条积分曲线．由10==x y 得1=C ，特解11ln 1++=x y ．3．yx xy y dx dy 321++=．解分离变量，得到)1(122x x dx y ydy +=+，两边积分，即得C xx y ~1ln )1ln(222++=+，所以得通解222)1)(1(Cx y x =++，这里0>C 是任意正常数．4．0)1()1(=-++xdy y ydx x ．解分离变量，得到dx xx dy y y +=-11，两边积分，即得C x x y y ~ln ln ++=-，因此得通解C xy y x =+-ln ，这里C 是任意常数．另有特解0=x 和0=y ．5．0)()(=-++dx y x dy x y ．解变形得x y x y dx dy +-=，这是齐次方程，设x y u =，得dxdu x u dx dy +=，代入原方程得 11+-=+u u dx du xu ，分离变量得 x dx du u u -=++211，两边积分，即得 C x u u +-=++ln )1ln(21arctan 2，即C y x x y =++)ln(21arctan 22，这里C 是任意常数．6．22y x y dxdy x -+=．解变形得 21sgn ⎪⎭⎫ ⎝⎛-+=x y x x y dx dy ，这是齐次方程，设x y u =，得dx du x u dx dy +=，代入原方程得 21sgn u x dxdux-=，分离变量积分，即得 C x x u +=ln sgn arcsin ，即C x x xy+=ln sgn arcsin． C x u u +-=++ln )1ln(21arctan 2，即C y x x y =++)ln(21arctan 22，这里C 是任意常数． 7．0cot tan =-xdy ydx ．解分离变量，得到xdx ydy tan cot =，两边积分，即得C x y ~cos ln sin ln +-=，所以通解为C y x =sin cos ，这里0≠C 的任意常数．另有特解πk y =，Z k ∈及2ππ+=k x ，Z k ∈，这只须在通解表达式中允许0=C 即可，故通解为C y x =sin cos ，这里C 是任意常数．8．032=++ye dx dy x y ．解分离变量，得到dx e e ydy x y32-=，两边积分，即得C e e x y ~3232+-=--，得到通解C eey x=--2323，这里C 是任意常数．9．0)ln (ln =--ydx dy y x x ．解变形得y y x x dy dx )ln (ln -=，令u y x =，则dydu y u dy dx +=，代入方程并分离变量得，ydy u u du =-)1(ln ，两边积分，即得C y u ~ln 1ln ln +=-，或1ln +=Cy u ，回代原变量有，1ln+=Cy yx ，或1+=Cy ye x ，这里0≠C 的任意常数．另有特解满足01ln =-u ，即ey x =，这只须在通解表达式中允许0=C 即可，故通解为1+=Cy ye x ，这里C 是任意常数．10．y x e dxdy-=．解分离变量，得到dx e dy e xy=，积分得C e e xy +=，这里C 是任意常数．作适当的变量变换求解下列方程（11—17） 11．2)(y x dxdy+=．解设y x u +=，则dx dy dx du +=1，原方程化为C x u u dxdu+=⇒+=arctan 12，即通解为 C x y x +=+)a r c t a n(，这里C 是任意常数． 12．2)(1y x dx dy +=．解2)(y x dydx+=，由上题，注意到这里的x 和y 相当于上题的y 和x ，得到方程的通解为 C y y x +=+)a r c t a n(，这里C 是任意常数． 13．1212+-+-=y x y x dx dy ．解由⎩⎨⎧=+-=+-012,012y x y x 得⎪⎪⎩⎪⎪⎨⎧=-=31,31y x ，令⎪⎪⎩⎪⎪⎨⎧-=+=,31,31y Y x X 就有Y X Y X dX dY 22--=，这是齐次方程，令X Y u =，有u dXduX dX dY +=，代入方程后分离变量，X dX du u u u =+--)1(2212，得到C X u u ~ln 2)1ln(2+-=+-，回代变量得C y x y xy x =-++-22即为原方程的通解，这里C 是任意常数．14．25--+-=y x y x dx dy ．解令u y x =-，则dx du dx dy =-1，代入方程得 27--=u dx du ，分离变量并积分得，C x u u =+-1442，即C y x y xy x =+++-410222为方程的通解，这里C 是任意常数．15．18)14()1(22+++++=xy y x dxdy．解变形为2)14(2+++=y x dx dy ，令u y x =++14，则dxdydx du 41+=，代入原方程得942+=u dx du ，分离变量解之得，C x u +=632arctan ，回代原变量并变形化简，得到通解 )14(2)6t a n (3++=+y x C x ，这里C 是任意常数．16．2252622yx xy x y dx dy +-=．解变形为232632)2(3)(xxy x y dx y d +-=，令x y u 3=，则原方程化为 1262+--=u u u dx du x ，解之得537)2()3(Cx u u =+-，即153373)2()3(Cx x y x y =+-为方程的通解，这里C 是任意常数．17．yy y x xxy x dx dy -+++=32232332．解变形为123132)()(222222-+++=y x y x x d y d ，令⎪⎩⎪⎨⎧==22,yY x X ，原方程变为123132-+++=Y X Y X dX dY ，由⎩⎨⎧=-+=++0123,0132Y X Y X ，得到⎩⎨⎧-==1,1Y X ．设⎩⎨⎧+=-=1,1Y v X u ，则有v u v u dv du 2332++=，再令s v u =，得到dvds v s dv du +=，于是23)1(32+-=s s dv ds v ，解得C v s s =-+65)1)(1(，逐步回代变量，得原方程的通解为C y x y x =--+52222)2)((，这里C 是任意常数．18．证明方程)(xy f dxdyy x =经变换u xy =可化为变量分离方程，并由此求解下列方程：（1）xdy dx y x y =+)1(22；（2）222222y x y x dx dy y x -+=．证明令u xy =，则得dx dy x y dx du +=，代入原方程得]1)([+=u f u dxdu x 是变量分离方程．（1）中221)(y x xy f +=，所以)2(2+=u u dxdux，分离变量求解得 C u x u ++=)]2(ln[2arctan224，即得原告方程的通解C y x x xy ++=)]2(ln[2arctan2224．（2）中2222)(u u u f -+=，所以224udx du x -=，分离变量求解得 C x u u +=-ln 43123，即得原告方程的通解 C x y x xy +=-ln 431233． 19．已知0,1)()(0≠=⎰x dt t f x f x，试求函数)(x f 的一般表达式．解变形后等式两边对x 求导，有 ])(1[])(['='⎰x f dt t f x，即 )()()(2x f x f x f '-=，解得)(21)(C x x f +±=，由1)()1(1=⎰dt t f f ，得0=C ，所以xx f 21)(±=．20．求具有性质)()(1)()()(s x t x s x t x s t x -+=+的函数)(t x ，已知)0(x '存在．解因为)0(x '存在，故)(t x 在0=t 连续，即)0()(lim 0x t x x =→．由)()(1)()()(s x t x s x t x s t x -+=+，令0=s 就有)0()(1)0()()(x t x x t x t x -+=，得到0)0(=x ．ss x s x t x t x s t x s x t x s x t x s t x s t x )()()(1)(1)()()(1)()()()(2⋅-+=--+=-+，令0→s 取极限，由于右边的极限为)0()](1[2x t x '+，故左边的极限存在，从而得到函数)(t x 满足的方程， )0()](1[)(2x t x t x '+='，解之得 C t x t x +'=)0()(arctan ，或])0(t a n [)(C t x t x +'=．由0)0(=x ，推出Z k k C ∈=,π，所以])0(tan[)(πk t x t x +'=，Z k ∈．21．求一曲线，使它的切线介于两坐标轴之间的部分被切点分成相等的部分．解由习题 1.2—9（4），知曲线)(x f y =应满足的方程0=+'y y x ，即xy dx dy -=，分离变量解之得，C x y ~ln ln +-=，或C xy =为所求的曲线．22．在图（2.1）所示的C R -电路中，设10=E 伏，100=R 欧，01.0=C 法，而开始时电容C 上没有电荷，问：（1）当开关K 合上“1”后，经过多长时间电容C 上的电压5=C u 伏？（2）当开关K 合上“1”后，经过相当长的时间（如1分钟后）开关K 从“1”突然转至“2”，试求C u 的变化规律，并问经过多长时间5=C u 伏？解（1）由例7，)1(1t RCC eE u --=，将10=E ，100=R ，01.0=C 代入，有)1(10t C e u --=，由)1(105te --=，反解出)(6931.02ln s t ≈=，即经过约6931.0秒，电容C 上的电压5=C u 伏．（2）同样由例7，t RCC Eeu 1-=，代入具体数值有t C e u -=10，由te -=105，同样得到)(6931.02ln s t ≈=，即经过约6931.0秒，电容C 上的电压5=C u 伏．23．求出习题1.2第9题（1）所确定的曲线，其中4πα=．解由习题1.2—9（1），ααt a n t a n y x x y y -+='，代入4πα=得y x x y y -+='，这是齐次方程，令u x y =，则dx du x u dx dy +=，代入得2211u u dx du x -+=，解出C y x xy++=)ln(arctan 222即为所求曲线．24．证明满足习题1.2第9题（7）所给条件的曲线是抛物线族．证明由习题1.2—9（7），0(>='k kx y 常数)，解之得C kx y +=221，这是抛物线族，顶点在),0(C ，对称轴为y 轴．§2.2 线性方程与常数变易法习题2.2求下列方程的解： 1．x y dxdysin +=．解首先，求齐次线性方程y dxdy=的通解，从dx y dy =得到齐次方程通解x ce y =，令xe x c y )(=为方程的解，代入得x ex c xsin )(-='，即cx x e x c x ~)co s (si n 21)(++-=-，故原方程的通解为x e c x x y ~)cos (sin 21++-=，其中c ~为任意常数． 2．t e x dt dx 23=+．解由03=+x dtdx ，解出t ce x 3-=，设t e t c x 3)(-=是原方程的解，代入原方程得，t e t c 5)(='，故c e t c t ~51)(5+=，所以原方程的通解为t t e e c x 2351~+=-，其中c ~为任意常数．3．t t s dt ds 2sin 21cos +-=．解由t s dt ds cos -=，解得tce s sin -=，设t e t c s s i n )(-=是原方程的解，代入原方程得，t e t c t 2sin 21)(sin ='，得c t e t c t ~)1(sin )(sin +-=，所以通解为1sin ~sin -+=-t e c x t ，其中c ~为任意常数．4．n x e y x n dx dy n x ,=-为常数．解由0=-y xndx dy ，解得n cx y =，设n x x c y )(=是原方程的解，代入原方程得，x e x c =')(，即ce x c x ~)(+=，所以通解为n x x c e y )~(+=，这里c ~为任意常数． 5．01212=--+y x xdx dy ．解由0212=-+y xx dx dy ，解得x e cx y 12=，设xe x x c y 12)(=是原方程的解，代入原方程得，ce x c e xx c x x ~)(1)(112+=⇒='--，所以通解x e x c x y 122~+=，这里c ~为任意常数．6．234xyy x dx dy +=．解原方程即231y x y x dx dy +=，这是2-=n 的Bernoulli 方程，令3y z =，就有，233x z xdx dz +=，解这个一阶线性方程得通解为)ln 3(3c x x z +=，即)ln 3(33c x x y +=，这里c 为任意常数．7．3)1(12+++=x x y dx dy ．解由12+=x y dx dy ，得2)1(+=x c y ，令2)1)((+=x x c y 为原方程的解，代入原方程得，1)(+='x x c ，即c x x c ~)1(21)(2++=，所以原方程通解为24)1(~)1(21+++=x c x y ，其中c ~为任意常数．8．3y x ydx dy +=．解变形为21y x ydy dx +=，把x 看作未知函数，y 看作自变量，对于y 及dy dx 来说，这是一个线性方程．先解对应的齐线性方程x ydy dx 1=，得cy x =，其次把c 看作)(y c ，即设y y c x )(=为变形后方程的解，代入变形后的方程得y dy y dc =)(，得到c y y c ~21)(2+=，从而原方程的通解为y c y x ~213+=，其中c~为任意常数． 9．xx x ay dx dy 1++=．解先解xay dx dy =，得a cx y =，设ax x c y )(=为原方程的解，代入原方程得，11)(++='a x x x c ，即 ⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=+-≠≠+--=-0,~ln ,1,~1ln ,0,1,~)11()(a c x x a c x x a a c x a a xx c a ，所以原方程通解为⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=+-≠≠+--=0,~ln ,1,~1ln ,0,1,~11a c x x a x c x x a a x c a a x y a ，其中c ~为任意常数． 10．3x y dxdyx =+．解先解y dx dy x +，得xc y =，设x x c y )(=为原方程的解，代入原方程得，3)(x x c =' ，即c x x c ~41)(4+=，所以原方程通解为x c x y ~413+=，这里c~为任意常数． 11．33y x xy dxdy =+．解这是3=n 的Bernoulli 方程，令2-=y z 代入有322x xz dxdz -=，解这个一阶线性方程得通解为122++=x cez x ，即1)1(222=++x ce x y 为原方程的通解，这里c 为任意常数．另有特解0=y ．12．xdy ydx x y =-)2ln (．解变形为y xy x x dx dy 2ln 2-=，这是2=n 的Bernoulli 方程，令1-=y z 代入有 x xz x dx dz ln 2+-=，解这个一阶线性方程得通解为241ln 21cx x z ++=，即1)41ln 21(2=++cx x y 为原方程的通解，这里c 为任意常数．另有特解0=y ．13．dx x y xydy )2(22-=．解变形为yy x dx dy 211-=，这是1-=n 的Bernoulli 方程，令2y z =代入有 12-=z xdx dz ，解这个一阶线性方程得通解为2cx x z +=，即22cx x y +=，这里c 为任意常数．14．23x x e dx dy y +=．解设u e y=，则dx dy u dx dy e dx du y ==，代入原方程得2213u xu x dx du +=，这是2=n 的Bernoulli 方程，令1-=u z 代入有 213xz x dx dz --=，解这个关于z 的一阶线性方程得通解为3~21xcx z +-=，回代原变量得原方程的通解322)(x e x c y =-，其中c 为任意常数．15．331yx xy dx dy +=．解变形为33x y yx dydx +=，把x 看作未知函数，y 看作自变量，对于y 及dy dx 来说，这是一个3=n 的Bernoulli 方程．令2-=x u ，有322y yu dydu--=，解这个一阶线性方程得通解为122+-=-y ce u y ，即得原方程的通解1222+-=--y ce x y ，这里c 为任意常数．16．⎰+=xx dt t y e y 0)(．解两边求导得一阶线性方程x e y dxdy+=，解之得通解x e c x y )(+=，从原方程知道有初始条件10==x y ，代入通解表达式中得1=c ，故原积分方程的解为xe x y )1(+=．17．设函数)(t ϕ于+∞<<∞-t 上连续，)0(ϕ'存在且满足关系式)()()(s t s t ϕϕϕ=+，试求此函数．解由于ss t st s t st s t 1)()()()()()()(-⋅=-=-+ϕϕϕϕϕϕϕ，且)0(ϕ'存在，故在该式中令0→s 取极限就有，)0()()(ϕϕϕ'='t t ，解得t ce t )0()(ϕϕ'=．若0)(≡t ϕ，则是解；若)(t ϕ不恒为零，则由)0()()0()(ϕϕϕϕt t t =+=得1)0(=ϕ，由此得1=c ，所以t e t )0()(ϕϕ'=．18．如图所示的L R -电路，试求：（1）当开关1K 合上10秒后，电感L 上的电流；（2）1K 合上10秒后再将2K 合上，求2K 合上20秒后，电感L 上的电流．解（1）由Kirchhoff 第二定律得，E dtdIL I R =+1，把101=R ，2=L ，50=E 代入得到微分方程255=+I dtdI，初始条件0=t 时，0=I ．解之得t e I 555--=，当10=t 时，5055--=eI 约为5安培．（2）由Kirchhoff 第二定律得，E dt dILRI =+，其中320201020102121=+⨯=+=R R R R R ，2=L ，50=E 代入得25310=+I dt dI ，初始条件0=t 时，5=I ．解之得)3(25310t e I --=，当20=t 时，)3(253200--=eI 约为7.5安培．19．试求图示的L R -电路电感上电流)(t I 的变化规律，并解释其物理意义，设0=t 时，0=I ．解由Kirchhoff 第二定律得，E dtdILRI =+，即t L U I L R dt dI m ωsin =+，初始条件为00==t I，求出其通解为)sin(222ϕωω-++=-t L R U ce I m t LR，其中RL ωϕ=tan ，20πϕ<<．由初始条件得，ϕωsin 222L R U c m +=，所以，)]sin([sin 222ϕωϕω-++=-t e L R U I t LR m ．其物理意义是：当t 增大时，第一项逐渐衰减而趋于零（称为暂时电流），事实上很快就消失而不起作用．而第二项就起着重要作用（称为稳定电流）．稳定电流是一个周期函数，其周期与电动势的周期相同，而相角相差ϕ-．20．试证：（1）一阶非齐线性方程（2.28）的任两解之差必为相应的齐线性方程（2.3）之解；（2）若)(x y y =是（2.3）的非零解，而)(~x y y =是（2.28）的解，则方程（2.28）的通解可表为)(~)(x y x cy y +=，其中c 为任意常数；（3）方程（2.3）任一解的常数倍或任两解之和（或差）仍是（2.3）的解．证明（1）设)(1x y y =，)(2x y y =是方程（2.28）)()(x Q y x P dxdy+= 的任意两个解，即)()(11x Q y x P dx dy +=，)()(22x Q y x P dxdy+=，由此得到 ))(()]()([)]()([)(21212121y y x P x Q y x P x Q y x P dxdy dx dy dx y y d -=+-+=-=-，所以)()(21x y x y y -=是齐线性方程（2.3）：y x P dx dy)(=之解．（2）由于)(x y y =是（2.3）的非零解，故)()()(x y x P dxx dy =，而)(~x y y =是（2.28）的解，即)()(~)()(~x Q x y x P dx x y d +=，所以)]()(~)([)()()(~)())(~)((x Q x y x P x y x cP dxx y d dx x dy c dx x y x cy d ++=+=+)()](~)()[(x Q x y x cy x P ++=，所以)(~)(x y x cy y +=是（2.28）的解，其中含有一个任意常数c ，故是方程（2.28）的通解，其中c 为任意常数．（3）设)(1x y y =，)(2x y y =都是方程（2.3）的解，即)()()(11x y x P dx x dy =， )()()(22x y x P dxx dy =，因此有)]()[()()()())((1111x ky x P x y x kP dxx dy k dx x ky d ===，)]()()[()()()()()()()]()([21212121x y x y x P x y x P x y x P dxx dy dx x dy dx x y x y d ±=±=±=±，所以，方程（2.3）任一解的常数倍或任两解之和（或差）仍是（2.3）的解． 21．求解习题1.2第9题（5）和（6）．解（5）的方程为 2x y x y ='-，或变形为x y xy -='1，这是一阶线性方程．先解对应的齐次方程y xy 1='，得到cx y =，设原方程的解为)(x xc y =，代入原方程得1)(-='x c ，即c x x c +-=)(，故所求曲线方程为cx x y +-=2，其中c 为任意常数．（6）的方程为 x y x y ='-2，或变形为2121-='y x y ，这是一阶线性方程．同样先解对应的齐次方程y xy 21='，得到x c y =，设原方程的解为x x c y )(=，代入原方程得xx c 21)(-='，即c x x c +-=)(，故所求曲线方程为x c x y +-=，其中c 为任意常数．22．求解下列方程：（1）01)1(2=+-'-xy y x ；（2）0)12()1(322=+--'-x y x y x x ；（3）0sin cos sin 3=--'x y x x y ．解（1）先解xy y x ='-)1(2，得12-=x cy ，设方程的解为1)(2-=x x c y ，代入方程得)1sgn(1)(2232---='-x x x c ，推出1)(2-+=x c x x y 为原方程的通解（需分1>x ，1-<x 及1<x 三种情形分别求解后再统一），这里c 为任意常数．（2）先解y x y x x )12()1(22-='-，得到12-=x cxy ，设原方程的解为1)(2-=x x x c y ，代入原方程得 1)1()(22---='x x x x c ，即c x x c +-=11)(2，所以原方程的通解为12-+=x cxx y ，这里c 为任意常数．（3）先解0cos sin =-'y x x y ，得到x c y tan =，设原方程的通解为x x c y tan )(=，代入原方程得x x c sin )(='，即c x x c +=co s )(，所以通解x c x y tan sin +-=，这里c 为任意常数．§2.3 恰当方程与积分因子习题2.3验证下列方程是恰当方程，并求出方程的解： 1．0)2()(2=-++dy y x dx y x ．证明 y x N y x M 2,2-=+=，所以xNy M ∂∂==∂∂1，即所给方程是恰当方程．改写方程为02)(2=-++ydy xdy ydx dx x ，即0)31(23=-+y xy x d ，得原方程的解为c y xy x =-+2331，其中c 为任意常数． 2．0)4()3(2=---dy x y dx x y ．证明 )4(,32x y N x y M --=-=，所以xNy M ∂∂==∂∂1，即所给方程是恰当方程．改写方程为043)(2=--+ydy dx x xdy ydx ，即0)2(23=--y x xy d ，得原方程的解为c y x xy =--232，其中c 为任意常数．3．0])(1[]1)([2222=--+--dy y x x y dx x y x y ．证明 2222)(1,1)(y x x y N x y x y M --=--=，所以x N y x xy y M ∂∂=-=∂∂3)(2，即所给方程是恰当方程．改写方程为 0)(222=+---y dyx dx y x dy x dx y ，凑为0)()()()(2=-+----y dyx dx y x y x xyd xy d y x ，即0)ln ln (=-+-y x y x xy d ，得原方程的通解为c y x yx xy=-+-ln ln ，其中c 为任意常数．4．0)2(3)23(22232=+++dy y y x dx x xy ．证明 )2(3,)23(22232y y x N x xy M +=+=，所以xNxy y M ∂∂==∂∂12，即所给方程是恰当方程．改写方程为034)(623=+++dy y dx x xdy ydx xy ，即0)3(3422=++y x y x d ，得原方程的解为c y x y x =++34223，其中c 为任意常数．5．0)1sin cos 1()1cos sin1(222=+-++-dy yy x y x x y x dx x y x y y x y ．证明由于2221sin cos 1,1cos sin 1yy x y x x y x N xyx y y x y M +-=+-=，所以，x Ny x y x y x y x y x y x y xy M ∂∂=--+-=∂∂cos sin 1sin cos 13232，即所给方程是恰当方程．改写方程为01cos sin 222=++-+-dy ydx x y x ydx xdy y x y xdy ydx ，即0)1cos (sin=-+-y x y x x y d ，得原方程的解为c yx y x x y =-+-1cos sin ，其中c 为任意常数．求下列方程的解：6．0)1(222=+-dy e dx ye x x x ．解改写方程为02)2(22=-+⋅xdx dy e y dx xe x x ，即0)(22=-x ye d x ，所以得到原方程的通解c x ye x =-22，这里c 为任意常数．7．02)3(2=++xydy dx y e x．解由于xy N y e M x2,32=+=，故y xNy y M 2,6=∂∂=∂∂．因为xN xNy M 2=∂∂-∂∂只与x 有关，所以方程有只与x 有关的积分因子 2ln 22x eexdxx ==⎰=μ，以2x =μ乘方程两边得，0233222=++ydy x dx y x dx e x x，即0)()(223=+xe d x y x d ，故得原方程的通解为c e x x y x x=+-+)22(223，这里c 为任意常数．8．0)1(22=++dy x xydx ．解改写为0)2(2=++dy dy x xydx ，凑微分得0))((22=++dy dy x x yd ，得原方程的通解c y y x =+2，其中c 为任意常数．9．dx y x xdy ydx )(22+=-．解以22y x +除方程两边，有dx yx xdy ydx =+-22，即dx y xd =)(arctan ，得到原方程的通解为c x yx+=arctan，这里c 为任意常数． 10．0)(3=+-dy y x ydx ．解改写为dy y xdy ydx 3=-，得ydy yxdy ydx =-2，即)21()(2y d y x d =，所以得到原方程的通解c y y x +=221，或cy y x +=321，其中c 为任意常数． 11．0)1(=+--xdy dx xy y ．解由x N xy y M =--=,1，得1,1=∂∂-=∂∂x Nx y M ，由于1-=∂∂-∂∂Nx Ny M 与y无关，故方程有只与x 有关的积分因子x dxe e --=⎰=)1(μ，以x e -乘方程两边有，0)1(=+----xdy e dx xy y e x x ，分组得，0])([=--+---dx e dx xye xdy ydx ex x x，凑微分得0])1[(=+-x e xy d ，即得方程的通解为xce xy =+1，这里c 为任意常数．12．0)(2=--xdy dx x y ．解由x N x y M -=-=,2，得1,1-=∂∂=∂∂xN y M ，由于x N x Ny M 2-=∂∂-∂∂只与x 有关，故方程有积分因子2)2(1x edxx =⎰=-μ，以21x乘方程两边并组合变形有， dx xxdyydx =-2，即dx x y d =-)(，得到方程的通解为c x xy-=-，或)(x c x y -=，这里c 为任意常数．13．0)2(=++xdy dx y x ．解改写为02=++xdy ydx xdx ，显然有积分因子x ，故以x =μ乘方程两边有，0])([222=++dy x x yd dx x ，即0)()31(23=+y x d x d ，得到通解c y x x =+2331，其中c为任意常数．14．0)cos()]sin()cos([=+++++dy y x x dx y x y x x ．解改写为 0)sin())(cos(=++++dx y x dy dx y x x ，即 0)sin())(sin(=+++dx y x y x xd ，或0)]sin([=+y x x d ，所以原方程的通解为c y x x =+)sin(，其中c 为任意常数． 15．0)cos sin ()sin cos (=++-dy x x x y dx x x x y ．解 x x x y N x x x y M c o s s i n ,s i n c o s+=-=，则x x x x y xNsi n cos cos -+=∂∂，x yMcos =∂∂，由于1=-∂∂-∂∂M x Ny M 与x 无关，故方程有积分因子y dy e e =⎰=μ，以y e 乘方程两边并分项组合有，0sin cos )1()cos sin cos (=+-+⋅+-xdy ye xdx y e dy e x x xdx xe xdx e y y y y y ，或写为0)(sin )(sin )1()](cos ))(cos (cos [=+-+++y y y y e xd y x d y e e xd x x xd xdx e ，即0sin )](sin )(sin )[1()cos (=++-+xdy e e xd x d e y xe x d yyyy，也即0)1(sin )sin ()1()cos (=-+-+y xd e x e d y xe x d y y y ，故0)sin )1(cos (=-+x e y xe x d yy，得到方程的通解为c e x y x x y=-+]sin )1(cos [，这里c 为任意常数．16．0)53()24(3=+++xdy ydx y xdy ydx x ．解改写方程为 05324342=+++dy xy dx y dy x xydx ，可看出y x 2=μ是一个积分因子，用它乘方程两边有053244352423=+++dy y x dx y x ydy x dx y x ，分项组合就有，0)()(5324=+y x d y x d ，故方程的通解为c y x y x =+5324，其中c 为任意常数．17．试导出方程0),(),(=+dy y x N dx y x M 分别具有形为)(y x +μ和)(xy μ的积分因子的充要条件．解设)(y x +μ是0),(),(=+dy y x N dx y x M 的积分因子⇔0),()(),()(=+++dy y x N y x dx y x M y x μμ是恰当方程 ⇔xN y M ∂∂=∂∂)()(μμ ⇔NM y x xNy M y x d y x d -+∂∂-∂∂-=++)()()()(μμ ⇔NM y x xNy M -+∂∂-∂∂-)()(μ应为y x +的函数)(y x f +．又设)(xy μ是0),(),(=+dy y x N dx y x M 的积分因子⇔0),()(),()(=+dy y x N xy dx y x M xy μμ是恰当方程⇔xN y M ∂∂=∂∂)()(μμ ⇔xMyN xy xNy M xy d xy d -∂∂-∂∂=)()()()(μμ ⇔)()()(xy xMyN xy xNy M ϕμ=-∂∂-∂∂． 18．设),(y x f 及yf∂∂连续，试证方程0),(=-dx y x f dy 为线性方程的充要条件是它有仅依赖于x 的积分分子．证明 “⇒”即例4．“⇐” 若方程0),(=-dx y x f dy 有反依赖于x 的积分因子，则)()(x p yfx N y M -=∂∂-=∂∂-∂∂ 仅与x 有关，所以)()()(),(x Q y x p dy x p dy y fy x f +==∂∂=⎰⎰，其中)(x Q 是x 的任意连续函数．从而方程为0)]()([=+-dx x Q y x p dy ，即)()(x Q y x p dxdy+=是线性方程． 19．试证齐次方程0),(),(=+dy y x N dx y x M 当0≠+yN xM 时有积分因子yNxM +=1μ．证明将方程两端同乘以N 1，得0=+dy dx N M ，即0)(=+dy dx xy g ．设xyu =，则ux y =，从而0)(=++xdu udx dx u g ，或0])([=++xdu dx u u g ，这是可分离变量方程，取积分因子])([11u u g x +=μ，则有0])(1[ln =++⎰du uu g x d ，得到通解为c du u u g x =++⎰)(1ln ，其中c 为任意常数．积分因子为yN xM xy N M x Nu u g x N N +=+⋅=+⋅==1][11])([1111μμ，通解可写为c xyd yN xM N x =++⎰)(ln ，c 为任意常数．20．设函数)(u f ，)(u g 连续、可微且)()(u g u f ≠，试证方程0)()(=+dy xy xg dx xy yf有积分因子1)])()([(--=xy g xy f xy μ．证明以1)])()([(--=xy g xy f xy μ乘以方程两边，有0)]()([)()(=-+xy g xy f xy dyxy xg dx xy yf ，或0)]()([))((=--+y dy xy g xy f xy xdy ydx xy f ，即0)ln )]()([)((=--⎰y du u g u f u u f d )(xy u =，因而方程0)()(=+dy xy xg dx xy yf 有积分因子1)])()([(--=xy g xy f xy μ．21．假设方程（2.43）中的函数),(,),(y x N y x M 满足关系)()(y Mf x Nf xNy M -=∂∂-∂∂ 其中)(,)(y g x f 分别为x 和y 的连续函数，试证方程（2.43）有积分因子))()(exp(⎰⎰+=dy y g dx x f μ．证明因为yMy g M y M y M M y ∂∂+=∂∂+∂∂=∂∂μμμμμ)()(，xNx f N x N x N N x ∂∂+=∂∂+∂∂=∂∂μμμμμ)()(，所以0][)]()([)()(=∂∂-∂∂+-=∂∂-∂∂xNy M x Nf y Mg N x M y μμμμ，即)()(N xM y μμ∂∂=∂∂，从而方程0=+Ndy Mdx μμ是恰当方程，故方程（2.43）有积分因子))()(exp(⎰⎰+=dy y g dx x f μ．22．求出Bernoulli 方程的积分因子．解 Bernoulli 方程为n y x Q y x P dx dy )()(+= )1,0(≠n ，以ny n --)1(乘方程两边，并令u yu=-1，化为关于dx du u ,的一阶线性方程)()1()()1(x Q n u x P n dxdu-+-=，后者有积分因子⎰--dx x P n e )()1(，从而Bernoulli 方程的积分因子⎰-=--dxx P n ne yn )()1(1μ． 23．设),(y x μ是方程（2.43）的积分因子，从而求得可微函数),(y x U ，使得)(Ndy Mdx dU +=μ．试证),(~y x μ也是方程（2.43）的积分因子的充要条件是)(),(~U y x μϕμ=，其中)(t ϕ是t 的可微函数．证明 “⇐”若),(y x μ是方程（2.43）的积分因子，且)(Ndy Mdx dU +=μ，则))(()()()()(~0⎰==+=+=dU U d dU U U Ndy Mdx Ndy Mdx ϕϕϕμμ，所以c dU U =⎰)(ϕ为（2.43）的通解，故)(),(~U y x μϕμ=亦是方程（2.43）的积分因子，其中)(t ϕ是t 的可微函数．“⇒”设dV Ndy Mdx =+22μμ，则M xV2μ=∂∂，N y V 2μ=∂∂．由Ndy Mdx dU μμ+=，则M xUμ=∂∂，N y U μ=∂∂，得到yU x UN M y V x V ∂∂∂∂==∂∂∂∂，所以，0=∂∂∂∂∂∂∂∂yU x U yV x V，因而存在函数)(t Φ，使得)(U V Φ=，由此得 ))(())(()(Ndy Mdx U Ndy Mdx U dU U dV +Φ'=+Φ'=Φ'=μμμ )(2N d y M d x+=μ，得到)()(2U U μϕμμ=Φ'=．24．设),(,),(21y x y x μμ是方程（2.43）的两个积分因子，且21μμ不恒为常数，求证c =21μμ（任意常数）是方程（2.43）的通解．证明由于21,μμ是方程（2.43）的两个积分因子，由上题结论)(21U ϕμμ=，其中)(2Ndy Mdx dU +=μ，这里)(t ϕ是t 的可微函数．由于)(21U ϕμμ=不恒为常数，故有)(U ϕ'不恒为零，由此在c U =)(ϕ两边微分得0)()(2=+'Ndy Mdx U μϕ，因此得到，0)(2=+Ndy Mdx μ，所以c U =)(ϕ是方程（2.43）的解，又c U =)(ϕ中含有一个任意常数，故c U =)(ϕ即c =21μμ（任意常数）是方程（2.43）的通解．25．假设第19题中微分方程还是恰当的，试证它的通解可表为c y x yN y x xM =+),(),(（c 为任意常数）．证明由于方程是恰当的，故11=μ即是一个积分因子，而由第19题yNxM +=12μ也是积分因子，且yN xM +=21μμ不恒为常数，所以由第24题所证结论，就知道它的通解为c y x yN y x xM =+),(),(，c 为任意常数．§2.4 一阶隐方程与参数表示习题2.4求解下列方程： 1．y y x '+='13．解解出31y y x ''+=，设p y ='，方程为31ppx +=，两边对y 求导，有 dydpp p p )23(134+-=，即dp p p dy )23(23+-=，所以c p pp ++=2232，因此得原方程的通解为 ⎪⎪⎩⎪⎪⎨⎧++=+=c p py pp x 223,11223（p 为参数），c 为任意常数．2．0)1(33='--'y x y ．解设31t y ='-，则31t y -='，21t t x -=．由dt t tt dx y dy )21)(1(23---='=，得c t t t y ++-=52521，从而通解为 ⎪⎪⎩⎪⎪⎨⎧++-=-=c t t t y t tx 522521,1，（t 为参数），c 为任意常数． 3．y e y y ''=2．解设p y ='，则原方程为pe p y 2=，两边对x 求导有，dxdppep p p)2(+=，即dp e p dx p )2(+=，解得c e p x p ++=)1(，所以通解为⎪⎩⎪⎨⎧=++=ppep y c e p x 2,)1( （p 为参数），c 为任意常数． 4．a y y 2)1(2='+（a 为常数）．解解出212y a y '+=，p y ='，则原方程为212pay +=，两边对x 求导有， dx dpp p a p ⋅⋅+-=2)1(222，或dp p a dx 22)1(4+-=，解得c p a papx +-+-=arctan 2122，所以通解为 ⎪⎪⎩⎪⎪⎨⎧+=+-+-=2212,arctan 212p a y c p a p ap x （p 为参数），c 为任意常数． 5．122='+y x ．解设t x cos =，t y sin ='，则由tdt dx y dy 2sin -='=，得c t t y ++-=2s i n 4121，所以通解为⎪⎩⎪⎨⎧++-==c t t y t x 2sin 4121,cos （t 为参数），c 为任意常数． 6．22)2()1(y y y '-=-'．解令yt y ='-2，则有t t y -=1，所以21t y +='，dt ty dy dx 21-='=，由此解出c tx +=1，于是求得通解为⎪⎪⎩⎪⎪⎨⎧-=+=tt y c t x 1,1 （t 为参数），或消去参数t 得c x c x y +--=1，c 为任意常数．习题2.5求下列方程的解：1．1cos sin =+x dx dyx y ．解原方程为x y x dx dy sec tan +⋅-=，由y x dxdy⋅-=tan ，得到x c y cos =，设原方程的解是x x c y cos )(=，代入原方程得出x x c 2sec )(='，即c x x c +=tan )(，因此原方程的通解为x c x y cos sin +=，c 为任意常数．2．ydy x xdy ydx 2=-．解方程两边同乘以21x ，有ydy xxdy ydx =-2，凑微分得0)21(2=+x yy d ，故得通解c xyy =+221，这里c 为任意常数． 3．1sin 4-=-x e dxdy y ．解改写为0sin 4=-+xdx dx e dy e yy，两边乘以xe 并凑微分得0)sin 4(=-⎰xdx e e e d x y x ，所以c xdx e e e xy x +=⎰sin 4，即c x x e e e xy x +-=)cos (sin 2，其中c 为任意常数．4．xyx ydx dy -=．解这是齐次方程．设x y u =，则ux y =，dxdu x u dx dy +=，代入原方程化为 uuu dx du x-=1．分离变量求解得，c uux 22ln =+，即2)ln 21(y c y x -=，这里c 为任意常数．5．0)(22=-+dy e x dx y xye yx yx ．解变形为yxe x y x y dx dy -⎪⎭⎫ ⎝⎛+=2，这是齐次方程．设x y u =，则ux y =，dx du x u dx dy +=，代入化原方程为u e u dxdux 12-=，分离变量求解得x c e u ln 1=+-，即c e x y x=+ln ，其中c 为任意常数．6．0)1(=-+xdy ydx xy ．解变形为02=-=yxdy ydx xdx ，凑微分得0)21(2=+y xy d ，所以原方程的通解为c yxy =+221，其中c 为任意常数． 7．0)2()122(=-++-+dy y x dx y x ．解变形为2)(1)(2-+-+-=y x y x dx dy ，设u y x =+，则dxdudx dy =+1，代入原方程后得，21-+-=u u dx du ，解之得c x u u +-=+-1ln 3，即c y x y x +++=+1ln 2，这里c 为任意常数．8．32x y x y dx dy +=．解这是2=n 的Bernoulli 方程．令1-=y z ，有311xz x dx dz --=，解这个一阶线性方程，得x cxz +=21，即x c x y +=211，这里c 为任意常数． 9．23-+=x y dxdy．解先解y dxdy3=，得到x ce y 3=，设原方程的解是x e x c y 3)(=，代入原方程后得，x e x x c 3)2()(--='，所以c e x x c x +--=-3)53(91)(，得到x ce x y 3)53(91+--=是原方程的通解，这里c 为任意常数．10．21⎪⎭⎫ ⎝⎛+=dx dy dx dy x ．解设p dxdy=，则p p x +=1，两边对y 求导得dy dp p p )11(12+-=，从中就可解出c p p y +-=ln 212，所以通解为⎪⎪⎩⎪⎪⎨⎧+-=+=c p p y p px ln 21,12（p 为参数），c 为任意常数．11．312+++-=y x y x dx dy ．解改写并分项组合，有0)1()3()(2=+-+=+dx x dy y ydx xdy ，凑微分，得0)21331(22=--++x x y y xy d ，所以，c x x y y xy =--++2221331是方程的通解，这里c 为任意常数． 12．x y xe dxdy e =+-)1(．解原方程即y x xe dx dy +=+1，设u y x =+代入方程得u xe dxdu=，这是分离变量方程．解出c e x u =+-221，即得原方程的通解为c e x y x =++-)(221，这里c 为任意常数．13．02)(22=-+xydy dx y x ．解设xy N y x M 2,22-=+=，则y x N y y M 2,2-=∂∂=∂∂，x N x Ny M 2-=∂∂-∂∂仅与x 有关，故方程有积分因子2)2(1xedxx =⎰=-μ，用它乘方程两边并分项组合有， 0222=-+x xydy dx y dx ，即0)(2=-x y x d ，所以c xy x =-2，或cx y x =-22是原方程的通解，其中c 为任意常数． 14．1++=y x dx dy．解由y dxdy =，解得x ce y =，设原方程的解为x e x c y )(=，代入有xe x x c -+=')1()(，即c ex x c x++-=-)2()(，所以通解为)2(+-=x ce y x ，其中c 为任意常数．15．xy e dx dy x y+=．解设u x y =，则ux y =，dx du x u dx dy +=，代入化原方程为u e dxdu x =，分离变量解之得c e x u=+-ln ，即c ex xy=+-ln ，其中c 为任意常数．16．y e dxdyx -=++21)1(．解分离变量得112+=--x dx e dy y ，两边积分得通解12+=-x c e y，c 为任意常数． 17．0)1()(2=++-dy x y dx y x ．解改写为1111-+-+=y xxy x dx dy ，这是1-=n 的Bernoulli 方程．设2y z =，则原方程化为一阶线性方程xx z x dx dz +-+=1212，解之得2)1(12+++=x c x z ，因此得原方程的通解为22)1(12+++=x c x y ，这里c 为任意常数．18．0)1(24322=-+dy y x dx y x ．解 )1(2,4322-==y x N y x M ，则y x xN y x y M 226,8=∂∂=∂∂，y M x Ny M 21-=-∂∂-∂∂只与y 有关，故有积分因子yedyy 1)21(=⎰=-μ，用它乘以方程并分项组合有02)24(21213232=-+-dy y dy y x dx y x ，凑微分得，0)434(21233=-y y x d ，所以通解为c y y x =-212333，或c y y x =-)3(3，其中c 为任意常数．19．0422=+-⎪⎭⎫⎝⎛x dx dy y dx dy x ．解解出y y x y '+'=2)4(2，设p y ='，则原方程为pp x y 2)4(2+=，两边对x 求导有，dxdpp x p p p )221(2422-++=，或dp pxdx =，解得cp x =，所以通解为⎪⎩⎪⎨⎧+==)4(2,2p c y cp x （p 为参数），或消去参数p ，得2242c x cy +=，c 为任意常数．另外还有042=-p ，或x y 2±=也是解．20．1]1[22=⎪⎭⎫⎝⎛-dx dy y ．解令t dxdysin =，代入方程有1)sin 1(22=-t y ，即t y sec ±=．由于dt tdt t t t y dy dx 2cos 1sin tan sec ±=±='=，所以1tan c t x +±=，得到原方程的通解为⎩⎨⎧±=+±=ty c t x sec ,tan 1 （t 为参数），消去参数t 得1)(22++=c x y ，其中c 为任意常数．21．0)1()1(=-++dy yxe dx e yx yx ．解设u y x =，则yu x =，dy duy u dy dx +=，代入原方程化简得uu e u e dy du y ++-=1，分离变量求解得c y e u u=+)(，即c yex yx=+是原方程的通解，其中c 为任意常数．22．0324223=-+dy yx y dx y x ．解设42233,2y x y N y x M -==，则x N y x y M ∂∂=-=∂∂46，故为恰当方程．由于)()(2),(323y yx y dx y x y x u ϕϕ+=+=⎰，其中)(y ϕ是y 的待定可微函数，再由422423)(3y x y y y x y u -='+-=∂∂ϕ，得到21)(y y ='ϕ，即有y y 1)(-=ϕ，因此得到方程的通解为c y yx y x u =-=1),(32，即322cy y x =-，这里c 为任意常数．23．0)1(2=++-dy y x ydx ．解变形为dy y xdy ydx )1(2+=-，看出有积分因子21y =μ，用21y =μ乘以方程两边并凑微分得)1()(y y d y xd -=，即得方程的通解是c yy y x +-=1或cy y x =+-12，这里c 为任意常数．24．0)]([22=-+-xdy dx y x x y ．解变形为dx y x x xdy ydx )(22+=-，看出有积分因子221yx +=μ，用它乘以方程两边并凑微分得)2()(arctan 2x d y x d =，得方程的通解是c x y x +=2arctan 2，或其等价形式)2tan(2c x y x +=，其中c 为任意常数． 25．0=-+x e dxdydx dy．解设p dxdy=，则p e p x +=，两边对y 求导有dy dp e p p )1(1+=，即dp e p dy p )1(+=，由此得到c e p p y p +-+=)1(212，所以方程的通解为 ⎪⎩⎪⎨⎧+-+=+=ce p p y e p x pp )1(21,2 （p 为参数），c 为任意常数． 26．0)()32(2232=++++dy y x dx y y x xy ．解设2232,32y x N y y x xy M +=++=，则x x Ny x x y M 2,222=∂∂++=∂∂，1=∂∂-∂∂N xNy M 与y 无关，所以方程有积分因子x dx e e =⎰=1μ，以之乘方程的两边，分项组合得到0)3()2(2322=++++dy e y dx e y dy e x dx ye x dx xye x xxxx，即。

常微分方程第2章习题答案

习题２-4１．求解下列微分方程：（１）yx xy y --='22；解：令ux y =，则原方程化为uu u dx du x --=+212，即x dxdu u u =--122，积分得：c x u u u +=--+-ln 1ln 2111ln2 还原变量并化简得：3)()(y x c x y +=-（２）4252--+-='y x x y y ；解：由⎩⎨⎧=--=+-042052y x x y 得 ⎩⎨⎧-==21y x令2,1+=-=y v x u ，则有vu u v du dv --=22，由第一题的结果知此方程解为3)()(v u c u v +=-，还原变量并化简得：.)1(33++=+-y x c x y（３）14212-+++='y x y x y ；解：令y x v 2+=，则1212121-++=+=v v dx dy dx dv ，即1214-+=v v dx dv ，此方程为变量分离方程，分离变量并积分得：c x v v +=+-14ln 8321，还原变量并化简得：c y x x y =++--184ln 348．（４）xy y x y -='33．解：①当0≠y 时，方程两边同时乘以32--y ,则233222--+-='-xy x y y ，令2-=y z ，则322x xz dxdz-=, 此方程为一阶线性方程，由公式得：122++=x ce z x还原变量得：122)1(2-++=x ce y x . ②0=y 也是方程的解．2. 利用适当的变换，求解下列方程：（１）)cos(y x y -='；解：令y x u -=，则u dx dy dx du cos 11-=-=， ①当1cos ≠u 时，有dx udu =-cos 1，即 dx u du=2sin 22，两边积分得：c x uctg +=221还原变量化简得：2sin 2sin 22cos yx c y x x y x -+-=-． ②当1cos =u 时，即πk x y 2+=)(Z k ∈也是方程的解．（２）0)()3(22=+++dv uv u du v uv ；解：方程两边同时乘以u 则原方程化为：0)()3(2322=+++dv v u u du uv v u ，即 0)()3(2232=+++vdv u du uv dv u vdu u 此方程为全微分方程，则原方程的解为：c v u v u =+22321．（３）)2(2)3(222yx y x dx dy y x -=++；解：原方程即为324222222++-=y x x y xdx ydy ，令u y v x ==22,，则324++-=v u vu dv du ,由⎩⎨⎧=++=-03024v u v u 得⎩⎨⎧-=-=21v u ，令⎩⎨⎧+=+=21v n u m ，则有n m n m dn dm +-=24令z n m=，则zn m =， 124+-=+=z z z n dn dz dn dm ，则有1)2)(1(+--=z z z n dn dz ，此方程为变量分离方程，分离变量并积分得：n c zz ln 2)1(ln32+=--，还原变量并化简得：322222)32()1(-+-=+-y x c y x .（４）yy y x xxy x dx dy 8237323223-+-+=．解：原方程即为823732222222-+-+=y x y x xdx ydy ，令22,x v y u ==,则823732-+-+=u v u v dv du ，由⎩⎨⎧=++=-+08230732u v u v ⎩⎨⎧==⇒21v u ，令⎩⎨⎧-=-=21v n u m ，则m n m n dn dm 2332++=，令z n m=，可将方程化为变量分离形方程， n dn dz zz =-+)2223(2，两边积分得：c n z z z +=---+ln 1ln 2111ln 432，还原变量并化简得：)3()1(22522-+=--y x c y x ．3. 求解下列微分方程：（１）．2241xy y --='；解：令xy z =，则原方程可化为：)41(12-+-=z z x dx dz ， ①当21≠z 时，即21≠xy 时方程为x dxdz z =--2)21(1 ，此方程为变量分离方程，两边积分得：c x z +=-ln 211还原变量并化简得：cxx x x y ++=ln 121； ②当21=z 时，xy 21=是方程的特解．（２）．1222++='xy y x y x ；解：原方程即为：221x x y y y ++='，令xy z =，则2)1(1+=z xdx dz ，此方程为变量分离方程，分离变量积分得：c x z +=+-ln 11，还原变量并化简得：cxx x x y +--=ln 11． 4. 试把二阶微分方程0)()(=+'+''y x q y x p y 化为一个黎卡提方程．解：令⎰=udxe y ，则⎰='udxue y ，+⎰=''udxe u y 2⎰'udxe u ，代入原方程可得：=+'+''y x q y x p y )()(+⎰udxe u 2⎰'udxe u ＋)()(x q ue x p udx+⎰⎰udxe ＝０，即有：0)()(2=++'+x q u x p u u ，此方程为一个黎卡提方程．5. 求一曲线，使得过这一曲线上任一点的切线与该点向径的夹角等于45．解：设此曲线为)(x y y =，由题意得：1451==+-tg xy dx dy x y dx dy ，化简得：y x y x dx dy -+=，此方程为齐次方程，解之得：c y x x y arctg =+-)ln(2122．6. 探照灯的反光镜（旋转面）应具有何种形状，才能使点光源发射的光束反射成平行线束？解：取点光源所在处为坐标原点，而x 轴平行于光的反射方向，建立三维坐标系．设所求曲面由曲线⎩⎨⎧==0)(z x f y 绕x 轴旋转而成,则求反射镜面问题归结为求 xy 平面上的曲线y=f(x)的问题．由题意及光的反射定律，可得到函数)(x f y =所应满足的微分方程式：22yx x ydx dy ++=，此方程为齐次方程，解之得：)2(2x c c y +=，（其中c 为任意正常数）．)2(2x c c y +=就是所求的平面曲线，它是抛物线，因此反射镜面的形状为旋转抛物面)2(22x c c z y +=+．习题２-5１．求解下列微分方程：（１）．0)()23(2232=++++dy y x dx y xy y x ；解：方程两边同乘xe33，则)33()369(233323323=++++dy y e dx y e dy x e xydx e ydx x e x x x x x ，此方程为全微分方程，即 c y e y x e x x =+33233．（２）．0)2(2=-+-dy e xy ydx y ；解：方程两边同乘y e y 21，则 0)12(22=-+dy yxe dx e y y即01)2(22=-+dy ydy xe dx e yy 此方程为全微分方程，即有 c y xe y =-ln 2 ．（３）．0)3()63(2=+++dy xyy x dx y x ；解：方程两边同乘 xy ，则0)3()63(232=+++dy y x dx x y x即 0)36()3(232=+++dy y xdx dy x ydx x 此方程为全微分方程，即有c x y y x =++2333 ．（４）．22()0ydx x y x dy -++=; 解：方程两边同乘221y x +，则 022=-+-dy yx xdyydx ，此方程为全微分方程，即 c y yxarctg=- （5）．0)1(2223=-+dy y x dx xy ；解：方程两边同乘21y ，则0)1(222=-+dy y x xydx ，此方程为全微分方程，即c y x y=+21. （6）．0)1(=-+xd y dx xy y ；解：方程两边同乘21y ，则0)1(2=-+dy y xdx y xdx ，此方程为全微分方程，即c x y x =+221. （7）0)(2223=-+dy xy x dx y ；解：方程两边同乘y x 21，则 02)2(22=+-dy y dy x y dx x y ，此方程为全微分方程，即 c y xy =+-ln 22（8）．0)c o s2(=++dy y y ctgy e dx e xx解：方程两边同乘y sin ，则02sin )cos sin (=++ydy yc ydy e ydx e x x ，此方程为全微分方程，即 11cos cos 2sin 224xe y y y y c -+=. 2. 证明方程（5.1）有形如)),((y x φμμ=的积分因子的充要条件是)),((y x f yP P x Q Q xQy P φ=∂∂-∂∂∂∂-∂∂，并写出这个积分因子。

《常微分方程》王高雄高等教育出版社课后答案

习题1.21．dxdy=2xy,并满足初始条件：x=0,y=1的特解。

解：ydy =2xdx 两边积分有：ln|y|=x +c 2y=e +e =cex另外y=0也是原方程的解，c=0时，y=02x c 2原方程的通解为y= cex ,x=0 y=1时 c=1 2特解为y= e .2x2. y dx+(x+1)dy=0 并求满足初始条件：x=0,y=1的特解。

2解：y dx=-(x+1)dy22y dydy=-11+x dx 两边积分: -y 1=-ln|x+1|+ln|c| y=|)1(|ln 1+x c 另外y=0,x=-1也是原方程的解 x=0,y=1时 c=e 特解：y=|)1(|ln 1+x c3．dx dy =yx xy y 321++ 解：原方程为：dxdy =y y 21+31x x + y y 21+dy=31x x +dx 两边积分：x(1+x )(1+y )=cx2224. (1+x)ydx+(1-y)xdy=0 解：原方程为：y y −1dy=-xx 1+dx两边积分：ln|xy|+x-y=c另外 x=0,y=0也是原方程的解。

5．（y+x ）dy+(x-y)dx=0解：原方程为：dx dy =-yx y x +−令x y =u 则dx dy =u+x dxdu 代入有： -112++u u du=x 1dxln(u +1)x =c-2arctgu 22即 ln(y +x )=c-2arctg 222xy. 6. xdxdy-y+22y x −=0 解：原方程为：dx dy =x y +x x ||-2)(1xy − 则令x y =u dx dy =u+ x dxdu 211u − du=sgnxx1dx arcsinxy=sgnx ln|x|+c 7. tgydx-ctgxdy=0 解:原方程为：tgy dy =ctgxdx 两边积分：ln|siny|=-ln|cosx|-ln|c| siny=x c cos 1=xc cos 另外y=0也是原方程的解，而c=0时，y=0.所以原方程的通解为sinycosx=c.8 dx dy +ye xy 32+=0 解：原方程为：dx dy =ye y 2ex 32 e-3e=c.x32y −9.x(lnx-lny)dy-ydx=0 解：原方程为：dx dy =x y ln xy令x y =u ,则dx dy =u+ x dx duu+ xdx du=ulnu ln(lnu-1)=-ln|cx| 1+lnxy=cy. 10.dxdy =e yx − 解：原方程为：dxdy =e e x y−e =ceyx11dxdy =(x+y) 2解：令x+y=u,则dx dy =dxdu -1 dx du -1=u 2211u +du=dx arctgu=x+c arctg(x+y)=x+c12.dx dy =2)(1y x + 解：令x+y=u,则dx dy =dxdu -1dx du-1=21uu-arctgu=x+c y-arctg(x+y)=c. 13.dx dy =1212+−+−y x y x 解: 原方程为：（x-2y+1）dy=(2x-y+1)dx xdy+ydx-(2y-1)dy-(2x+1)dx=0 dxy-d(y 2-y)-dx +x=c2xy-y 2+y-x -x=c214:dx dy =25−−+−y x y x 解：原方程为：（x-y-2）dy=(x-y+5)dx xdy+ydx-(y+2)dy-(x+5)dx=0dxy-d(21y 2+2y)-d(21x +5x)=0 2y 2+4y+x +10x-2xy=c. 215:dxdy =(x+1) +(4y+1) +8xy 221+ 解：原方程为：dxdy =（x+4y ）+32令x+4y=u 则dx dy =41dx du -4141dx du -41=u +3 2dx du =4 u +13 2u=23tg(6x+c)-1 tg(6x+c)=32(x+4y+1).16:证明方程y x dxdy=f(xy),经变换xy=u 可化为变量分离方程，并由此求下列方程： 1） y(1+x y )dx=xdy222） y x dx dy =2222x -2y x 2y+ 证明：令xy=u,则xdx dy +y=dxdu 则dx dy =x 1dx du -2x u，有：u x dxdu=f(u)+1)1)((1+u f u du=x1dx所以原方程可化为变量分离方程。

常微分方程习题答案2章

u
2
) ln x c 。
2 dy 2 y y x dx y dy du 解：令 u , y ux , u x , 则原方程化为： x dx dx
6： x
du dx
x
2
(1 x
u
2
)
, 分离变量得：
1 1

u
2
du sgn x
1 dx x
两边积分得：
当 y 0时显然也是原方程的解 1 y 。 1 ln 1 x
。当 x 0 , y 1时，代入式子得
3
1 y dy dx xy x3 y
2
解：原式可化为：
dy dx 1 y
y
2

1 x
x
3
显然
1 y
y
2
0 , 故分离变量得 1 ln 1 2
2
y 1
e
y

e e
y x
dy c
e
x
dx
dy dx

e
x y
解：变量分离，两边积分得： dy dx
e
y
e

y
dy

x
e
e
x
dxΒιβλιοθήκη c11 .
(x y)
2
解：令
x y t,则 dt dx 1
dy dx dt
1
dt dx 1
1
原方程可变为：变量分离得：代回变量得：
arcsin
u sgn x ln x c arcsin
y sgn x ln x c x

[理学]常微分方程教程_丁同仁第二版_习题解答

∂y x ∂x x
∂y ∂x
则 ( y dx + ln xdy) + x2dx − 2 ydy = 0 x
两边积分得： x3 + y ln x − y 2 = C. 3
８． (ax2 + by 2 )dx + cxydy = 0 (a,b和c为常数)
解： P(x, y) = ax2 + by 2 , Q(x, y) = cxy,
两边积分得： (2 + y)e x + xy 2 = C.
７． ( y + x2 )dx + (ln x − 2 y)dy = 0 x
解： P(x, y) = y + x2 Q(x, y) = ln x − 2 y, x
则 ∂P = 1 , ∂Q = 1 , 所以 ∂P = ∂Q ，即原方程为恰当方程
常微分方程教程（第二版）-丁同仁等编-高等教育出版社-对恰当方程求解：
１． (3x2 −1)dx + (2x + 1)dy = 0
解： P(x, y) = 3x2 −1， Q(x, y) = 2x + 1 ，
则 ∂P = 0 ， ∂Q = 2 ，所以 ∂P ≠ ∂Q 即，原方程不是恰当方程．
则 ∂P = 2by, ∂Q = cy, 所以当 ∂P = ∂Q ，即 2b = c 时，原方程为恰当方程
∂y
∂x
∂y ∂x
-2-
常微分方程教程（第二版）-丁同仁等编-高等教育出版社-参考答案
则 ax2dx + (by 2dx + cxydy) = 0
两边积分得： ax3 + bxy 2 = C. 3
∂y
∂x

常微分方程2.2习题参考解答

习题2.2求下列方程的解1．dxdy =x y sin +解：y=e ⎰dx (⎰x sin e ⎰-dx c dx +)=e x [-21e x -(x x cos sin +)+c]=c e x -21(x x cos sin +)是原方程的解。

2．dt dx +3x=e t2解：原方程可化为：dt dx =-3x+e t 2所以：x=e ⎰-dt 3(⎰e t 2e -⎰-dt 3c dt +)=e t 3-(51e t 5+c)=c e t 3-+51e t 2是原方程的解。

3．dt ds =-s t cos +21t 2sin 解：s=e ⎰-tdt cos (t 2sin 21⎰e dt dt ⎰3c +)=e t sin -(⎰+c dt te t t sin cos sin )=e t sin -(c e te t t +-sin sin sin )=1sin sin -+-t ce t 是原方程的解。

4．dx dy nx x e y n x =-，n 为常数.解：原方程可化为：dx dy nx x e y nx +=)(c dx e x e e y dx x n n x x n +⎰⎰=⎰-)(c e x x n +=是原方程的解.5．dx dy +1212--y x x =0解：原方程可化为：dx dy =-1212+-y x x ⎰=-dx x x e y 212(c dx e x x+⎰-221))21(ln 2+=x e )(1ln 2⎰+--c dx ex x =)1(12x ce x +是原方程的解.6．dx dy 234xy x x +=解：dx dy 234xy x x +==23y x +x y 令x y u =则uxy =dx dy =u dx du x +因此：dx du x u +=2u x 21udx du =dxdu u =2c x u +=331c x x u +=-33（*）将x y u =带入（*）中得：3433cx x y =-是原方程的解.3332()21()227.(1)12(1)12(),()(1)1(1)(())1(1)dx P x dx x P x dx dy y x dx x dy y x dx x P x Q x x x e e x e Q x dx c x +--=++=+++==++⎰⎰==+⎰⎰++⎰⎰P(x)dx 232解：方程的通解为： y=e =(x+1)(*(x+1)dx+c) =(x+1)((x+23221(1)()211,()(())dy y x c dy y dx x y dx x y dy y yQ y y ye yQ y dy c -+++==+=⎰⎰==⎰⎰+⎰⎰2243P(y)dy P(y)dy P(y)dy 1)dx+c)=(x+1) 即：2y=c(x+1)+(x+1)为方程的通解。

常微分方程第三版课后答案

3t15t=e ( e +c)5=c e 3t +15e 2t 是原方程的解ds 13． =-s cost + sin2tdt 2cos tdt 13dt解：s=e ( sin2t e dt c )=esint( sin t coste sin t dt c) sin tsint sint= e( sin tee c )常微分方程习题 2.2求下列方程的解1． dy = y sin x dx解： y=e ( sinxe dx c)x1 x=e x [- e x (sinx cos x )+c]= ce sint sint 1 是原方程的解。

4．dy xy e x x n，n 为常数. dx n解：原方程可化为：dy xy e x x n dx n方程的解。

=c e(sinx cos x )是原yendxx x ( e x x e n n dx n xdx c)2．dx+3x=e 2tnxx (ec)dt 解：原方程可化为：dx=-3x+edt是原方程的解 .所以：3dtx=ee2te 3dt5．dy +1 22x y 1=0 dx x 2dt c)ds23P(x) ,Q(x) (x 1)3 x1P(x)dxee=(x+1) 2((x 21) c)即： 2y=c(x+21+)(x+14) 为方程的通解。

8.d dy x =x y y 33dx x+y 1 2 解： xy 2dy y yP(y)dy P(y)dy( e Q(y)dy c) =y( 1*y 2dy c)y3= y cy23即 x=y +cy 是方程的通解，且 y=0也是方程的解。

2解：原方程可化为：dy dx1x 22xy 1x7.dy 2y (x 1)3dx x 1 解：dy 2y(x 1)3 dx x 1 (x 1)2(ln x 2e方程的通解为：ln x 2 1( e x dx c)1= x 2(1 ce x )P(x)dx P(x)dxy=e ( e Q(x)dx c) =(x+1)(=(x+1)((x 11)2 *(x+1)3dx+c) (x+1)dx+c) 是原方程的解.x=edx c )2则P(y)=y 1,Q(y) y 2方程的通解9. dy ay x 1,a 为常数 dx x x解：(P x) a ,Q(x) x 1xP(x )dxeedx方程的通解为：y=(x)dx P (x)dx(e Q(x)dx=xa(1 x+1dx+c)x a时，x 方程的通解为11.dy xy x 3y 3 dx 解：dy xyx 3y 3dx 两边除以3y c)d 3y xy 2 x 3 ydxdy2( xy 2 x 3)y=x+ln/x/+c当 y=cx+xln/x/-1当 a 1时，方程的通解为a 0，1时，方程的通解为y=cxa x 1 +-1- a adx 令y 2 z dz 2( xz x 3) dx P(x) 2x,Q(x) 2x 3 epx dx e2xdxe x 2 方程的通解为：z= e dx( e dxQ(x)dx c)10.x d d x y y x 3解：d dy x 1x y x 3P(x) 1,Q(x) x =e =xx(e x (2x 3)dx c) 22ce x1故方程的通解为y ：2(x 2 ce x 1) 1,且y 0也是方程的解。

常微分方程习题2.doc

常微分方程习题2・11.— = 2xy，并求满足初始条件：x=O,y=l的特解.dx解：对原式进行变量分离得丄dy = 2衣仕，两边同时积分得：111卜|=兀2 +(?,即『=(?幺兀把x = 0, y = 1代入得c = 1,故它的特解为y =幺“。

22.y dx + (兀+ l)dy = 0,并求满足初始条件：x=0,y=l的特解.解：对原式进行变量分离得：dx =当y北0时，两边同时积分得;ln|x + l| = —+ c,即丁 = \x + 1 y y c + ln|x +1|r当y = 0时显然也是原方程的解。

当兀=0』=1时，代入式子得c = l,故特解是1歹 1 + ln|l + x|23 4 = Idx兀》+兀、解：原式可化为：2 2空=•丄显然工0,故分离变量得~^dy = —^dxdx y x+x y i+y~ x + x两边积分得*lnl+)/ =ln|x|-|ln|l + %2|+ ln|c|(c 0),即(1+才)(1 + %2) = c/ 故原方程的解为(1 +)/)(1+ +)= d4：(1 + x)ydx + (1- y)xdy = 0解：由y = 0或兀=0是方程的解，当xy ^0时，变量分离^-^-dx = -― dy = 0两边积分In卜| + 兀 + In卜| 一y = c,BPln|xy| + x - y = c.故原方程的解为ln|兀y| = x-y = c;y = 0;x = 0.解：^ — = u, y = ux, — = u + x —,则原方程化为：x dx dx du 二 sgn x^^-dx 兀 / 2 2、du_Jx(1~U\分离变量得 dx x /i2 两边积分得:arcsinu = sgnx • ln|x| + c 代回原来变量，得arcsin — = sgn x • ln|x| + c另外,y=x 也是方程的解。

7： tgydx - ctgxdy = 0 解：变量分离，得：ctgydy = tgxdx 两边积分得:ln|sin y\ = - ln|cos x| + c.dx y解：变量分离，得-=-扎％ + c y 3e9: x(ln x - In y)dy 一 ydx = 0解：方程可变为：-\n — 9dy-—dx = 0x x令u =—,贝U 有丄必 = dlnux x 1 + In w代回原变量得：cy = 1 +In —ox10：红厂dx解：变量分离$ dy = d dx5: (y + x)dy + (y - x)dx = 0解:史,令“ 坯空斗+二空 dx y + x x dx dx 贝I 拉+ x —= U +\变量分离，得:_弘?+1 du = — dxdx w +1 眈 +1 x两边积分得：arctgu + *ln(l + /) = —ln|T + c 。

常微分方程课后答案

1
解：设两个物体的质量分别为mc, ms，体积为Vc, Vs,则有：
mcg
−
λVc
=
mc
dVc dt
+ ρVcg
msg
−
λVs
=
ms
dVs dt
+ ρVsg
设 mcg − ρVcg = Mc msg − ρVsg = Ms
则
Mc Ms
=
4 3Biblioteka ，解得Vc(t) =
Mc mc λ
(1
−
e−
λ mc
y
=
0(其中c是任意常数);
(5)
y = ecx,
(
dy dx
)2
−
y
d2 y dx2
= 0(其中c是任意常数);
2
−
(x−C1 4
)2
,
−∞ < x < C1;
(6)
y =
0, C1 < x < C2,
(x−C1 4
)2
,
C2 < x < +∞,
dy dx
=
|y|.
答：将解代入验证就可得知是否为微分方程的解：
R
q(x)e− p(x) dxdx),
其中C
=
1 1 − eωp¯
ω
q(t)e−
Rt
0
p(s)
ds
dt
0
第二节习题
1.试求下列微分方程的通解或特解：
(1)
x
dy dx
−
4xy
=
x2√y;
(2)
dy dx
−
xy 2(x2 −1)

常微分方程教程+第二版+丁同仁+李承志+答案和练习第2章习题第二章答案

习题２-１判断下列方程是否为恰当方程，并且对恰当方程求解：１．0)12()13(2=++-dy x dx x解：13),(2-=x y x P ， 12),(+=x y x Q ，则0=∂∂y P ，2=∂∂x Q ，所以 xQy P ∂∂≠∂∂ 即原方程不是恰当方程．２．0)2()2(=+++dy y x dx y x解：,2),(y x y x P += ,2),(y x y x Q -=则,2=∂∂y P ,2=∂∂x Q 所以xQy P ∂∂=∂∂，即原方程为恰当方程则,0)22(=-++ydy xdy ydx xdx两边积分得：.22222C y xy x =-+ 3．0)()(=+++dy cy bx dx by ax （a,b 和c 为常数）．解：,),(by ax y x P += ,),(cy bx y x Q +=则,b y P =∂∂,b x Q =∂∂ 所以xQy P ∂∂=∂∂，即原方程为恰当方程则,0=+++cydy bxdy bydx axdx两边积分得：.2222C cy bxy ax =++ 4．)0(0)()(≠=-+-b dy cy bx dx by ax解：,),(by ax y x P -= ,),(cy bx y x Q -=则,b y P -=∂∂,b x Q =∂∂ 因为 0≠b , 所以xQ y P ∂∂≠∂∂，即原方程不为恰当方程５．0sin 2cos )1(2=++udt t udu t解：,cos )1(),(2u t u t P += u t u t Q sin 2),(=则,cos 2u t t P =∂∂,cos 2u t x Q =∂∂ 所以xQy P ∂∂=∂∂，即原方程为恰当方程则,0cos )sin 2cos (2=++udu udt t udu t两边积分得：.sin )1(2C u t =+ ６．0)2()2(2=++++dy xy e dx y e ye x x x解： xy e y x Q y e ye y x P x x x 2),(,2,(2+=++=，则,2y e y P x +=∂∂,2y e x Q x +=∂∂ 所以xQy P ∂∂=∂∂，即原方程为恰当方程则,0])2()[(22=++++dy xy e dx y ye dx e x x x 两边积分得：.)2(2C xy e y x =++７．0)2(ln )(2=-++dy y x dx x xy解：,2ln ),(),(2y x y x Q x xy y x P -=+=则,1x y P =∂∂,1x x Q =∂∂ 所以xQy P ∂∂=∂∂，即原方程为恰当方程则02)ln (2=-++ydy dx x xdy dx xy两边积分得：23ln 3y x y x -+.C = ８．),(0)(22为常数和c b a cxydy dx by ax =++解：,),(,),(22cxy y x Q by ax y x P =+=则,2by y P =∂∂,cy x Q =∂∂ 所以当xQy P ∂∂=∂∂，即 c b =2时，原方程为恰当方程则0)(22=++cxydy dx by dx ax两边积分得：233bxy ax +.C = 而当c b ≠2时原方程不是恰当方程．９．01222=-+-dt ts s ds t s 解：,),(,12),(22ts s s t Q t s s t P -=-= 则,212t s t P -=∂∂,212t s s Q -=∂∂ 所以xQ y P ∂∂=∂∂，即原方程为恰当方程,两边积分得：C ts s =-2．10．,0)()(2222=+++dy y x yf dx y x xf 其中)(⋅f 是连续的可微函数．解：),(),(),(),(2222y x yf y x Q y x xf y x P +=+=则,2f xy y P '=∂∂,2f xy x Q '=∂∂ 所以xQy P ∂∂=∂∂，即原方程为恰当方程,两边积分得：22()f xy dx C +=⎰,即原方程的解为C y x F =+)(22 (其中F 为f 的原积分)．习题２-2. 1. 求解下列微分方程，并指出这些方程在平面上的有意义的区域:：（１）yx dx dy 2=解：原方程即为：dx x ydy 2= 两边积分得：0,2332≠=-y C x y ．（２）)1(32x y x dx dy += 解：原方程即为：dx xx ydy 321+=两边积分得：1,0,1ln 2332-≠≠=+-x y C x y ．（３）0sin 2=+x y dxdy解：当0≠y 时原方程为：0sin 2=+xdx y dy两边积分得：0)cos (1=++y x c ．又y=0也是方程的解，包含在通解中，则方程的通解为0)cos (1=++y x c ．（４）221xy y x dxdy+++=；解：原方程即为：2(1)1dyx dx y=++ 两边积分得：c x x arctgy ++=22，即 )2(2c x x tg y ++=．（５）2)2cos (cos y x dxdy= 解：①当02cos ≠y 时原方程即为：dx x y dy 22)(cos )2(cos = 两边积分得：2222sin 2tg y x x c --=． ②y 2cos =0，即42ππ+=k y 也是方程的解. （N k ∈）（６）21y dxdyx-= 解：①当1±≠y 时原方程即为：xdx y dy =-21 两边积分得：c x y =-ln arcsin ． ② 1±=y 也是方程的解.（７）．yxe y e x dx dy +-=- 解．原方程即为：dx e x dy e y xy)()(--=+两边积分得：c e x e y x y ++=+-2222，原方程的解为：c e e x y x y =-+--)(222.2. 解下列微分方程的初值问题．（１）,03cos 2sin =+ydy xdx 3)2(ππ=y ；解：两边积分得：c yx =+-33sin 22cos ，即 c x y =-2cos 33sin 2因为 3)2(ππ=y , 所以 3=c .所以原方程满足初值问题的解为：32cos 33sin 2=-x y ．（２）．0=+-dy ye xdx x， 1)0(=y ；解：原方程即为：0=+ydy dx xe x，两边积分得：c dy y dx e x x=+-2)1(2，因为1)0(=y ，所以21-=c ，所以原方程满足初值问题的解为：01)1(22=++-dy y dx e x x ．（３）．r d dr=θ， 2)0(=r ；解：原方程即为：θd rdr=，两边积分得：c r =-θln ，因为2)0(=r ，所以2ln =c ，所以原方程满足初值问题的解为：2ln ln =-θr 即θe r 2=．（４）．,1ln 2yx dx dy+= 0)1(=y ; 解：原方程即为：dx x dy y ln )1(2=+,两边积分得：3ln 3y y x x x c ++-=, 因为0)1(=y ，所以1=c ，所以原方程满足初值为：3ln 13y y x x x ++-=（５）．321xy dxdyx=+， 1)0(=y ；解：原方程即为：dx xx y dy 231+=，两边积分得：c x y ++=--22121，因为1)0(=y ，所以23-=c ，所以原方程满足初值问题的解为：311222=++yx ．１．解下列微分方程，并作出相应积分曲线的简图．（１）．x dxdycos = 解：两边积分得：c x y +=sin ．积分曲线的简图如下：（２）．ay dxdy=，（常数0≠a ）；解：①当0≠y 时，原方程即为：dx aydy= 积分得：c x y a +=ln 1，即 )0(>=c ce y ax②0=y 也是方程的解．积分曲线的简图如下：y（３）．21y dxdy-=；解：①当1±≠y 时，原方程即为：dx y dy =-)1(2 积分得：c x yy+=-+211ln ，即 1122+-=x x ce ce y ．②1±=y 也是方程的解．积分曲线的简图如下：（４）．n y dx dy =， )2,1,31(=n ；解：①0≠y 时，ⅰ）2,31=n 时，原方程即为 dx ydyn =，积分得：c y n x n=-+-111．ⅱ）1=n 时，原方程即为dx ydy=积分得：c x y +=ln ，即)0(>=c ce y x．②0=y 也是方程的解．积分曲线的简图如下：4. 跟踪：设某A 从xoy 平面上的原点出发，沿x 轴正方向前进；同时某B 从点开始跟踪A ，即B 与A 永远保持等距b ．试求B 的光滑运动轨迹．解：设B 的运动轨迹为)(x y y =,由题意及导数的几何意义，则有22yb ydx dy --=，所以求B 的运动轨迹即是求此微分方程满足b y =)0(的解．解之得：222222ln 21y b y b b y b b b x ----++=．5. 设微分方程)(y f dxdy=（2.27），其中f(y) 在a y =的某邻域（例如，区间ε<-a y ）内连续，而且a y y f =⇔=0)(，则在直线a y =上的每一点，方程（2.27）的解局部唯一，当且仅当瑕积分∞=⎰±εa ay f dy)(（发散）．证明：（⇒）首先经过域1R ：,+∞<<∞-x a y a <≤-ε 和域2R ：,+∞<<∞-x ε+≤<a y a内任一点（00,y x ）恰有方程（2.13）的一条积分曲线，它由下式确定00)(x x y f dyyy-=⎰. （*）这些积分曲线彼此不相交. 其次，域1R （2R ）内的所有积分曲线c x y f dy +=⎰)(都可由其中一条，比如0)(c x y f dy+=⎰ 沿着 x 轴的方向平移而得到。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

习题２-１判断下列方程是否为恰当方程，并且对恰当方程求解：１．0)12()13(2=++-dy x dx x解：13),(2-=x y x P ， 12),(+=x y x Q ，则0=∂∂y P ，2=∂∂x Q ，所以 xQy P ∂∂≠∂∂ 即原方程不是恰当方程．２．0)2()2(=+++dy y x dx y x解：,2),(y x y x P += ,2),(y x y x Q -=则,2=∂∂y P ,2=∂∂x Q 所以xQy P ∂∂=∂∂，即原方程为恰当方程则,0)22(=-++ydy xdy ydx xdx两边积分得：.22222C y xy x =-+ 3．0)()(=+++dy cy bx dx by ax （a,b 和c 为常数）．解：,),(by ax y x P += ,),(cy bx y x Q +=则,b y P =∂∂,b x Q =∂∂ 所以xQy P ∂∂=∂∂，即原方程为恰当方程则,0=+++cydy bxdy bydx axdx两边积分得：.2222C cy bxy ax =++ 4．)0(0)()(≠=-+-b dy cy bx dx by ax解：,),(by ax y x P -= ,),(cy bx y x Q -=则,b y P -=∂∂,b x Q =∂∂ 因为 0≠b , 所以xQ y P ∂∂≠∂∂，即原方程不为恰当方程５．0sin 2cos )1(2=++udt t udu t解：,cos )1(),(2u t u t P += u t u t Q sin 2),(=则,cos 2u t t P =∂∂,cos 2u t x Q =∂∂ 所以xQy P ∂∂=∂∂，即原方程为恰当方程则,0cos )sin 2cos (2=++udu udt t udu t 两边积分得：.sin )1(2C u t =+ ６．0)2()2(2=++++dy xy e dx y e ye x x x解： xy e y x Q y e ye y x P x x x 2),(,2,(2+=++=，则,2y e yP x +=∂∂,2y e x Q x +=∂∂ 所以x Qy P ∂∂=∂∂，即原方程为恰当方程则,0])2()[(22=++++dy xy e dx y ye dx e x x x 两边积分得：.)2(2C xy e y x =++７．0)2(ln )(2=-++dy y x dx x xy解：,2ln ),(),(2y x y x Q x xy y x P -=+=则,1x y P =∂∂,1x x Q =∂∂ 所以xQy P ∂∂=∂∂，即原方程为恰当方程则02)ln (2=-++ydy dx x xdy dx xy两边积分得：23ln 3y x y x -+.C = ８．),(0)(22为常数和c b a cxydy dx by ax =++解：,),(,),(22cxy y x Q by ax y x P =+=则,2by y P =∂∂,cy x Q =∂∂ 所以当xQy P ∂∂=∂∂，即 c b =2时，原方程为恰当方程则0)(22=++cxydy dx by dx ax两边积分得：233bxy ax +.C = 而当c b ≠2时原方程不是恰当方程．９．01222=-+-dt ts s ds t s 解：,),(,12),(22ts s s t Q t s s t P -=-= 则,212t s t P -=∂∂,212t s s Q -=∂∂ 所以xQ y P ∂∂=∂∂，即原方程为恰当方程,两边积分得：C ts s =-2． 10．,0)()(2222=+++dy y x yf dx y x xf 其中)(⋅f 是连续的可微函数．解：),(),(),(),(2222y x yf y x Q y x xf y x P +=+=则,2f xy yP '=∂∂,2f xy x Q '=∂∂ 所以x Qy P ∂∂=∂∂，即原方程为恰当方程,两边积分得：22()f xy dx C +=⎰,即原方程的解为C y x F =+)(22 (其中F 为f 的原积分)．习题２-2. 1. 求解下列微分方程，并指出这些方程在平面上的有意义的区域:：（１）yx dx dy 2=解：原方程即为：dx x ydy 2= 两边积分得：0,2332≠=-y C x y ．（２）)1(32x y x dx dy += 解：原方程即为：dx xx ydy 321+= 两边积分得：1,0,1ln 2332-≠≠=+-x y C x y ．（３）0sin 2=+x y dxdy解：当0≠y 时原方程为：0sin 2=+xdx ydy两边积分得：0)cos (1=++y x c ．又y=0也是方程的解，包含在通解中，则方程的通解为0)cos (1=++y x c ．（４）221xy y x dxdy+++=；解：原方程即为：2(1)1dyx dx y =++ 两边积分得：c x x arctgy ++=22，即 )2(2c x x tg y ++=．（５）2)2cos (cos y x dxdy= 解：①当02cos ≠y 时原方程即为：dx x y dy 22)(cos )2(cos = 两边积分得：2222sin 2tg y x x c --=． ②y 2cos =0，即42ππ+=k y 也是方程的解. （N k ∈）（６）21y dxdyx-= 解：①当1±≠y 时原方程即为：xdx y dy =-21 两边积分得：c x y =-ln arcsin ．② 1±=y 也是方程的解.（７）．yxe y e x dx dy +-=- 解．原方程即为：dx e x dy e y x y )()(--=+两边积分得：c e x e y x y++=+-2222，原方程的解为：c e e x y x y =-+--)(222.2. 解下列微分方程的初值问题．（１）,03cos 2sin =+ydy xdx 3)2(ππ=y ；解：两边积分得：c yx =+-33sin 22cos ，即 c x y =-2cos 33sin 2因为 3)2(ππ=y , 所以 3=c .所以原方程满足初值问题的解为：32cos 33sin 2=-x y ．（２）．0=+-dy ye xdx x， 1)0(=y ；解：原方程即为：0=+ydy dx xe x ，两边积分得：c dy y dx e x x=+-2)1(2，因为1)0(=y ，所以21-=c ，所以原方程满足初值问题的解为：01)1(22=++-dy y dx e x x ．（３）．r d dr=θ， 2)0(=r ；解：原方程即为：θd rdr=，两边积分得：c r =-θln ，因为2)0(=r ，所以2ln =c ，所以原方程满足初值问题的解为：2ln ln =-θr 即θe r 2=．（４）．,1ln 2y x dx dy+= 0)1(=y ;解：原方程即为：dx x dy y ln )1(2=+,两边积分得：3ln 3y y x x x c ++-=,因为0)1(=y ，所以1=c ，所以原方程满足初值为：3ln 13y y x x x ++-= （５）．321xy dxdyx=+， 1)0(=y ；解：原方程即为：dx xx y dy 231+=，两边积分得：c x y ++=--22121，因为1)0(=y ，所以23-=c ，所以原方程满足初值问题的解为：311222=++y x ．１．解下列微分方程，并作出相应积分曲线的简图．（１）．x dxdycos = 解：两边积分得：c x y +=sin ．积分曲线的简图如下：（２）．ay dxdy=，（常数0≠a ）；解：①当0≠y 时，原方程即为：dx aydy= 积分得：c x y a +=ln 1，即 )0(>=c ce y ax②0=y 也是方程的解．积分曲线的简图如下：（３）．21y dxdy-=；解：①当1±≠y 时，原方程即为：dx y dy =-)1(2 积分得：c x y y+=-+211ln ，即 1122+-=x x ce ce y ．②1±=y 也是方程的解．积分曲线的简图如下：（４）．n y dx dy =， )2,1,31(=n ；解：①当0≠y 时， ⅰ）2,31=n 时，原方程即为 dx ydyn =，积分得：c y n x n=-+-111．ⅱ）1=n 时，原方程即为dx ydy=积分得：c x y +=ln ，即)0(>=c ce y x．②0=y 也是方程的解．积分曲线的简图如下：4. 跟踪：设某A 从xoy 平面上的原点出发，沿x 轴正方向前进；同时某B 从点开始跟踪A ，即B 与A 永远保持等距b ．试求B 的光滑运动轨迹．解：设B 的运动轨迹为)(x y y =,由题意及导数的几何意义，则有22yb ydx dy --=，所以求B 的运动轨迹即是求此微分方程满足b y =)0(的解．解之得：222222ln 21y b y b b y b b b x ----++=．5. 设微分方程)(y f dxdy=（2.27），其中f(y) 在a y =的某邻域（例如，区间ε<-a y ）内连续，而且a y y f =⇔=0)(，则在直线a y =上的每一点，方程（2.27）的解局部唯一，当且仅当瑕积分∞=⎰±εa ay f dy)(（发散）．证明：（⇒）首先经过域1R ：,+∞<<∞-x a y a <≤-ε 和域2R ：,+∞<<∞-x ε+≤<a y a内任一点（00,y x ）恰有方程（2.13）的一条积分曲线，它由下式确定00)(x x y f dyyy-=⎰. （*）这些积分曲线彼此不相交. 其次，域1R （2R ）内的所有积分曲线c x y f dy +=⎰)(都可由其中一条，比如0)(c x y f dy+=⎰ 沿着 x 轴的方向平移而得到。

因此只需详细考虑经过1R 内某一点),(0ε-a x 的积分曲线，它由（*）式确定.若⎰-aa y f dyε)(收敛，即存在 1x x = ，使得01)(x x y f dyaa -=⎰-ε, 即所讨论的积分曲线当 1x x = 时达到直线a y =上点（a x ,1）. 由（*）式易看出，所论积分曲线在（a x ,1）处与a y = 相切，在这种情形下，经过此直线上的一点就不只有一条积分曲线，与局部唯一矛盾，所以⎰-aa y f dyε)(发散.若积分⎰-aa y f dyε)(发散，此时由（*）式易看出，所论的经过),(0ε-a x 的积分曲线，不可能达到直线 a y =上，而以直线a y =为渐近线，又注意到a y =也是（２.13）的积分曲线，所以（2.13）过),(0ε-a x 的解是唯一的. 注：对于2R 内某点（ε+a x ,0）完全可类似地证明.6. 作出下列微分方程积分曲线族的大致图形．（１）．y dxdy =；（２）．⎩⎨⎧=≠=00ln y y yy dx dy()⇐习题２-3１．求解微分方程：（１）x xe y dxdy-=+2; 解：,2)(=x p xxe x q -=)(，由公式得：x x xx x x e xe cedx e xe c e y ------+=+=⎰222)(，原方程的解为：x x x e xe ce y ----+=2．（２）x ytgx dxdy2sin =+；解：,)(tgx x p = x x q 2sin )(=，c x dx xx d dx x x tgxdx dx x p +-=-===⎰⎰⎰⎰cos ln cos )(cos cos sin )(，则有xx c x c x dx xxc x dx ex c ey xx2cos ln cos ln cos 2cos )cos 2(cos )cos 2sin (cos )2sin (-=-=+=+=⎰⎰-原方程的解为：x x c y 2cos 2cos -=．（３）,sin 2x y dx dy x=+ ππ1)(=y ；解：原方程即为：x x y x dx dy sin 2=+，则x xx q x x p sin )(,2)(==，c x dx xdx x p +==⎰⎰2ln 2)(，则有)sin cos (1)sin (1)sin (22ln ln 22x x x c x xdx x c x e xx c e y x x +-=+=+=⎰⎰- 因为ππ1)(=y ，所以0=c ．原方程满足初值问题的解为：x xx x y sin 1cos 12+-= ．（４）x y x dx dy +=--1112，1)0(=y ；解：x x q x x p +=-=1)(,11)(2, 2111ln )(⎰+-=x x dx x p 则2111ln+-=x x ey ⎰++)1((x c )2111lndx ex x -+⎪⎪⎩⎪⎪⎨⎧<-+-+>-+-+=⎰⎰1)1(111)1(1122x dx x c xx x dx x c x x要求满足初值问题1)0(=y 的解只需求⎩⎨⎧<-+-+⎰1)1(112x dx x c xx)121a r c s i n 21(112x x x c x x -++-+=代入初值得1=c所以满足初值问题的解为)121a r c s i n 211(112x x x x x y -++-+=. 2. 将下列方程化为线性微分方程：（１）yy x dx dy 222+=；解：令z y =2，则原方程化为：2x z dxdz+=．（２）2yx ydx dy +=；解：由原方程得：，yy x dy dx 2+=, 即 y x y dy dx +=1 ．（３）03332=++x y dxdyxy；解：令z y =3，则原方程化为：21x z xdx dz --=．（４）xtgy ydx dy +=cos 1；解：原方程即为：yyx y dx dy cos sin cos 1+= 即y x dxydysin 1cos +=. 令y z sin =，则 1+=xz dxdz． 3. 设)(x y φ=满足微分不等式)0(,0)(≥≤+'x y x a y ．求证：,)0()(0)(⎰≤-xdss a e x φφ )0(≥x证明：将0)(≤+'y x a y 两边同乘0()xa s ds e⎰ 则有⎰xdss a e 0)(+'y ⎰xds s a e 0)(0)(≤y x a即0))((0)(≤⎰dxx e d xdss a φ 从０到x 积分得：⎰xds s a e0)()0()(φφ≤x ，得证．4. 用常数变易法求解非齐次线性方程)()(x q y x p dxdy=+．解：设方程有形如⎰=-dxx p e x c y )()(的解，将其代入方程则有解：设方程有形如⎰=-dx x p e x c y )()(的解，将其代入方程则有-⎰-dxx p e dxx dc )()(+⎰-dx x p e x p x c )()()()()()()(x q e x p x c dx x p =⎰- 即)()()(x q e dx x dc dxx p =⎰-，则c e x q x c dx x p +⎰=⎰)()()(，所以方程的解为⎰=-dx x p e y )())(()(c e x q dxx p +⎰⎰.5. 考虑方程)()(x q y x p dxdy=+，其中)(x p 和)(x q 都是以0>ω为周期的连续函数．试证：（１）若0)(=x q ，则方程的任一非零解以ω为周期⇔)(x p 的平均值⎰==ωω0)(1dx x p p ．（２）若0)(≠x q ，则方程的有唯一的ω周期解⇔0≠p ．试求出此解．证明：（１）设)(x y φ=是方程的任一非零解则,0)(⎰-=xx dxx p cey 且,0)(⎰++-=wx x dxw x p cey 也是解⇔⎰-xx dxx p e 0)(,0)(⎰++-=wx x dxw x p e⎰⎰+--=wx x dxx p xx dxx p ee)(0)( 10)(=⇔⎰ωdxx p e⎰=⇔ω00)(dx x p(2) 方程的通解为+=⎰-xdxx p cey 0)(⎰⎰-xdt t p xse s q 0)()( 选择常数c 使)(x y 成为 ω周期函数，即)()(x y w x y =+（*）我们先来证明，要使（*）对所有x 成立，其实只需对某一特定 x （例如0=x ）成立,即只需)0()(y y =ω.事实上，由于)(x y 是方程的解，且)()(x p w x p =+)()(x q w x q =+，所以)(w x y +也是解. 因此，函数)()()(x y w x y x u -+=是相应齐次方程0)(=+'y x p y 满足初始条件0)0(=y 的解。

常微分方程第二章练习与答案

常微分方程第一、二、三次作业参考答案

常微分方程第三版习题答案

常微分方程第二章练习与答案

常微分方程标准答案-一二章

（完整版）常微分方程基本概念习题及解答

常微分方程第二章

常微分方程第四版课后练习题含答案

常微分方程与动力系统第二章课后题参考答案

常微分课后答案第二章

常微分方程第2章习题答案

《常微分方程》王高雄高等教育出版社课后答案

常微分方程习题答案2章

[理学]常微分方程教程_丁同仁第二版_习题解答

常微分方程2.2习题参考解答

常微分方程第三版课后答案

常微分方程习题2.doc

常微分方程课后答案

常微分方程教程+第二版+丁同仁+李承志+答案和练习第2章习题 第二章答案

常微分方程教程+第二版+丁同仁+李承志+答案和练习第2章习题第二章答案