大学物理自感和互感PPT课件
合集下载
大学物理课件互感和自感

第九页,编辑于星期一:三点 二十一分。
第十页,编辑于星期一:三点 二十一分。
第十一页,编辑于星期一:三点 二十一分。
第十二页,编辑于星期一:三点 二十一分。
第十三页,编辑于星期一:三点 二十一分。
第十四页,编辑于星期一:三点 二十一分。
第十五页,编辑于星期一:三点 二十一分。
第一页,编辑于星期一:三点 二十一分。
第二页,编辑于星期一:三点 二十一分。
第三页,编辑于星期一:三点 二十一分。
第四页,编辑于星期一:三点 二十一分。
Hale Waihona Puke 第五页,编辑于星期一:三点 二十一分。
第六页,编辑于星期一:三点 二十一分。
第七页,编辑于星期一:三点 二十一分。
第八页,编辑于星期一:三点 二十一分。
人教版物理选修-互感与自感-ppt精品课件

自感电动势的方向
导体电流增加时,阻碍电流增加,此时自感电动势方 向与原电流方向相反;
导体电流减小时,阻碍电流小,此时自感电动势方 向与原电流方向相同.
增反减同
人教版物理选修3-2 4.6 互感与自感(共25张PPT)【PPT优秀课 件】- 精美版
人教版物理选修3-2 4.6 互感与自感(共25张PPT)【PPT优秀课 件】- 精美版
结论2:自感电动势的作用——
“ 阻碍”原电流的减少,但最终没有“阻止”其减
人教版物理选修3-2 4.6 互感与自感(共25张PPT)【PPT优秀课 件】- 精美版
人教版物理选修3-2 4.6 互感与自感(共25张PPT)【PPT优秀课 件】- 精美版
思考:灯泡一定会闪亮吗?
1.不能认为任何断电现象灯都会闪一下 当IL>IA时,会闪一下,再逐渐熄灭 当IL<IA或 IL=IA时,不会闪,逐渐熄灭 2.原来的IL和IA哪一个大,要由L的直流电阻RL与灯泡 的电阻RA的大小来决定。如果RL≥RA,则IL≤IA;如果 RL<RA,则IL>IA。
人教版物理选修3-2 4.6 互感与自感(共25张PPT)【PPT优秀课 件】- 精美版
人教版物理选修3-2 4.6 互感与自感(共25张PPT)【PPT优秀课 件】- 精美版
课堂例题
例2.在实验二中,若线圈L的电阻RL与灯泡 A的电阻RA相等,则电键断开前后通过线 圈的电流随时间的变化图像为_A__图,通过 灯泡的电流随时间的变化图像为_C__图;
3、互感现象不仅发生于绕在同一铁芯上的两个线圈之间, 且可发生于任何两个相互靠近的电路之间。
当线圈L1中电流发生变化时,线圈L1中是否 也会发生电磁感应象?
二、自感现象
《互感和自感》课件

互感和自感的相互作用
互感和自感的相互作用
当电流通过一个线圈时,会产生磁场,这个磁 场会影响到周围的线圈。当电流在这些线圈之 间变化时,就会引起它们之间的互感。
利用互感和自感构建电路
互感和自感的相互作用可以用来构建各种电路, 如共振电路、变压器、电感器等。
互感和自感的功率损耗
铜损
线圈中的电流会随着时间变化而导致磁场的变化, 这会在线圈中产生感应电动势,从而产生铜损。
互感和自感的衍生概念及应用
1
互感感应
利用互感关系来产生感应电动势。
高频晶振
2
利用线圈的自感和电容的容抗来构成高
精度的谐振电路。
3
超导体材料
超导体的电学特性很大程度上是由于其 自感的降低和互感的增加。
互感和自感的常见误区
1 互感和感应电动势等同
互感和感应电动势虽然有关联,但并不等同。
2 互感和自感不会相互影响
2 磁场的方向
磁场的方向与电流的方向和线圈的结构有关。
互感和自感的影响因素
1
线圈之间的距离
线圈之间的距离越近,互感系数就越大,自感系数就越小。
2
线圈的结构
线圈的结构和线圈的匝数、长度、直径等因素有关。
3
介质和材料
线圈周围的介质和材料对磁场的分布和影响有很大的影响。
互感和自感的实际应用示例
电力传输
互感和自感之间存在相互作用,互相影响。
互感和自感的未来发展方向
应用拓展
互感和自感技术还有很大的应用空间,尤其是 在新兴领域。
效率提升
提高互感和自感技术的效率,实现能源的更好 转换和利用,对于未来发展至关重要。
互感和自感PPT课件
本课件将为您介绍互感和自感的定义、区别、应用、公式、电路图示、相互 作用、功率损耗、频率响应、实际电路模型、磁场特性、影响因素、实际应 用示例、数据测量及分析、发展历程、发展趋势、应用前景、衍生概念及应 用、常见误区、未来发展方向。让你深入了解互感和自感这一有趣的话题。
大学物理13-3自感和互感
13. 3 自感和互感
解:条形磁铁运动导致通 过线圈的磁感应强度发生 变化(必需是短磁铁)。
通过线圈的磁通量发生变化。
第13章 电磁感应
在线圈中产生感应电动势和感应电流
由楞次定律可知,感应电流的磁场与原磁场方向反向, 阻碍原来的运动,所以振幅减小。
N N IS
l
L N2 S
I
l
n N l V lS
S
lE
(一般情况可用下式 测量自感)
L n2V
L
L
dI dt
4、自感的应用:稳流 , LC 谐振电路, 滤波电路, 感应圈等 。
13. 3 自感和互感
第13章 电磁感应
二、互感现象、互感电动势和互感系数
由于一个线圈中的
电流发生变化而在其 邻近线圈上引起感应
13. 3 自感和互感
第13章 电磁感应
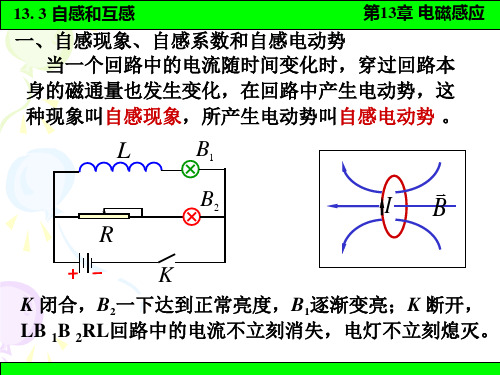
一、自感现象、自感系数和自感电动势
当一个回路中的电流随时间变化时,穿过回路本
身的磁通量也发生变化,在回路中产生电动势,这
种现象叫自感现象,所产生电动势叫自感电动势 。
L
B1
B 2
R
IB
K
K 闭合,B2一下达到正常亮度,B1逐渐变亮;K 断开, LB 1B 2RL回路中的电流不立刻消失,电灯不立刻熄灭。
M
棒向右运动
闭合回路 面积增加
N 穿过闭合回路的磁通量增加,
在回路中产生感应电动势和感应电流。
由楞次定律可判断回路感应电流方向如图所示
由右手定则可判断通过右边螺线管的磁感应线如图 (此磁感应线也穿过左边螺线管)
由楞次定律可 知左螺线管的 感应磁场的磁 感应线方向和 电流方向如图
M带有负电荷
新版《自感和互感》(共44张PPT)学习PPT

(2)自感电动势大小: E L I 4、自感系数L:与线圈的大小、形t 状、
圈数及有无铁心有关
5、磁场具有能量
电磁阻尼与电磁驱动的 区别和联系
电磁阻尼是导体相对于磁场 运动;电磁驱动是磁场相对于 导体运动。
安培力的作用都是阻碍它们 间的相对运动。
S R1 1.电路如图所示,当开关S闭合后,由传感器得到R中的电流随时间变化的图像。 1 应用: 在交流电路中、在各种用电设备和无线电技术中有着广泛的应用。 电流变化慢,穿过线圈的磁通量变化慢 一下,然后熄灭或正常发光。
A
B
C
D
3、利用互感现象,可以把能量从一个线圈传递到另一个线圈。
开关断开时,线圈作用相当于电源,把磁场中的能量转化成电能。
2、由于导体本身的电流发生变化而产生的电磁感应现象,叫自感现象。
析 什么情况下灯泡会闪亮一下再熄灭?
线圈L的磁通量逐渐增加,L中产生的感应电 然后断开电路,观察到什么现象?
2.传感器与L串联,当开关闭合后,由传感器得到L中的电流随时间变化的图像。
动势的方向与原来的电流方向相反,阻碍L A
B
C
D
1.电路如图所示,当开关S闭合后,由传感器得到R中的电流随时间变化的图像。
什么情况下灯泡会闪亮一下再熄灭?
原因: 在自感系数很大的情况下,灯泡会会闪亮
一下,然后熄灭或正常发光。 当自感系数很大时,在开关断开和闭合的瞬间,自 感线圈会产生瞬时的很高的自感电动势,该电动势 会补充A灯或A2灯中的电流,从而使A灯或A2灯中 电流突然变大,所以要闪亮一下。
实验1:(电路中电流传感器相当于电流表,因此用 A
灯泡A2立刻正常发光, 实验表明,线圈越长,越粗,匝数越多,自感系数越大。
圈数及有无铁心有关
5、磁场具有能量
电磁阻尼与电磁驱动的 区别和联系
电磁阻尼是导体相对于磁场 运动;电磁驱动是磁场相对于 导体运动。
安培力的作用都是阻碍它们 间的相对运动。
S R1 1.电路如图所示,当开关S闭合后,由传感器得到R中的电流随时间变化的图像。 1 应用: 在交流电路中、在各种用电设备和无线电技术中有着广泛的应用。 电流变化慢,穿过线圈的磁通量变化慢 一下,然后熄灭或正常发光。
A
B
C
D
3、利用互感现象,可以把能量从一个线圈传递到另一个线圈。
开关断开时,线圈作用相当于电源,把磁场中的能量转化成电能。
2、由于导体本身的电流发生变化而产生的电磁感应现象,叫自感现象。
析 什么情况下灯泡会闪亮一下再熄灭?
线圈L的磁通量逐渐增加,L中产生的感应电 然后断开电路,观察到什么现象?
2.传感器与L串联,当开关闭合后,由传感器得到L中的电流随时间变化的图像。
动势的方向与原来的电流方向相反,阻碍L A
B
C
D
1.电路如图所示,当开关S闭合后,由传感器得到R中的电流随时间变化的图像。
什么情况下灯泡会闪亮一下再熄灭?
原因: 在自感系数很大的情况下,灯泡会会闪亮
一下,然后熄灭或正常发光。 当自感系数很大时,在开关断开和闭合的瞬间,自 感线圈会产生瞬时的很高的自感电动势,该电动势 会补充A灯或A2灯中的电流,从而使A灯或A2灯中 电流突然变大,所以要闪亮一下。
实验1:(电路中电流传感器相当于电流表,因此用 A
灯泡A2立刻正常发光, 实验表明,线圈越长,越粗,匝数越多,自感系数越大。
大学物理自感和互感
~
~
变压器
收音机中的磁棒天线
19
10 - 4 自感和互感
第十章 电磁感应
互感的防止
电话串音(两路电话间的互感) 电路设计中互感的避免
20
10 - 4 自感1和0 -互5感磁场能量 第十章 电磁感应
一、自感磁能
L
考察在开关合上后的一段时
R
间内,电路中的电流滋长过程: 由全电路欧姆定律
BATTE
RY 电池
称为该线圈的自感系数,用L表示。
L的计算: LI
LI
注意:自感系数与电流无关,只决定于线圈本 身的性质--几何尺寸、匝数、介质。
3
10 - 4 自感和互感
第十章 电磁感应
4、自感电动势
根据法拉第电磁感应定律:
Ψ自 LI
L
d自 dt
d( LI ) dt
L dI I dL dt dt
若回路几何形状、 尺寸不变,周围介 质的磁导率不变
16
10 - 4 自感和互感
第十章 电磁感应
例. 如图,在磁导率为的均匀磁介质中,一长直导线与
矩形线圈一边相距为a,线圈共N匝,求互感系数.
解:设直导线中通有自下而上的电流I,它激发的磁场通过
矩形线圈的磁通链数为
N sB dS
ab I
NIl a b
N a
ldr ln
2r
2 a
互感为 M Nl ln a b
第十章 电磁感应
M12
I1
I2 M21
L1
L2
线圈中产 生焦耳热
反抗自感 电动势做功
反抗互感 电动势做功
互感磁能
W
1 2
L1I12
1 2
【大学物理】第二讲 自感和互感
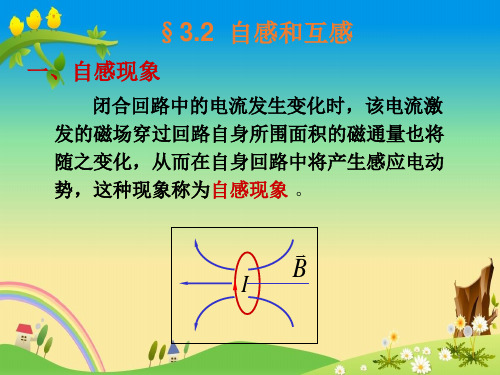
I1 在 I2电流回路中所产生的磁通量
Φ21 M 21I1
I2 在 I1 电流回路 中所产生的磁通量
Φ12 M12I2
9
(1)互感系数
M 21 Φ21 I1 M12 Φ12 I2
单位:亨利(H)
注意 互感仅与两个线圈形状、大小、匝数、
相对位置以及周围的磁介质有关。
M12
M 21
M
Φ21 I1
I2
0 n2 I 2
N112 N1B2 πR12 n1lB2 πR12 0n1n2l πR12 I2
M12 N112 I2
0n1n2l πR12
15
11
例题3-7 求两同轴长直密绕螺线管的互感。 有两个长度均为l,半径分别为R1和R2( R1<R2 ),匝数分别为N1和N2的 同轴长直密绕螺线管,如图所示, 试计算它们的互感 M 。
12
解 先设某一线圈中通以电流 I 求
出另一线圈的磁通量 Φ M
设半径为 R1 的线
圈中通有电流 I1,则
B1
6
解 两圆筒之间 B I
2πr 如图在两圆筒间取一长为 l 的面 PQRS,并
将其分成许多小面元。
则
dm
BdS
Bldr
Ildr
2πr
m
dm
R2 Ildr Il ln R2
R1 2πr 2π R1
L m ln R2
Il 2π R1
7
二 互感现象
假设有两个相邻的线圈,分别通有电流和当 其他条件不变,只要其中一个线圈的电流发生变 化,在另一线圈中也会有电动势产生,这种现象 称为互感现象。
Φ12 I2
10
(2)互感电动势
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12
d12
dt
M
dI2 dt
第十章 电磁感应
21
d 21
dt
M
dI1 dt
说明
•互感系数和两回路的几何形状、尺寸,它们 的相对位置,以及周围介质的磁导率有关。
•互感系数的大小反映了两个线圈磁场的相互 影响程度。
16
10 - 4 自感和互感
第十章 电磁感应
例. 如图,在磁导率为的均匀磁介质中,一长直导线与
在断路时,自感电动势可产生一个瞬时高
压,对有些场合(如日光灯的启动和感应圈 的升压)有用。
构成RC\RCL谐振电路,滤波器等
10
10 - 4 自感和互感
第十章 电磁感应
思考题1:自感系数的公式为
L
I
能否说明通过线圈中的电流强度越小,自
感系数越大?
答: 自感系数由线圈形状尺寸等有关,与 线圈中有无通电、电流强度多大等无关。
Ψ自 LI
L
d自 dt
d( LI ) dt
L dI I dL dt dt
若回路几何形状、 尺寸不变,周围介
dL 0
L
L
dI dt
质的磁导率不变
dt
负号表示自感电动势
自感系数描述线圈
总是要阻碍线圈回路
电磁惯性的大小
本身电流的变化。
单位:亨利,1H=1Wb/A
辅助单位: 1mH 103 H 1H 106 H 4
自感 L .
解 两圆筒之间 B I
2πr
如图在两圆筒间取一长
R1 Q R
为 l 的面 PQRS, 并将其分 I I r
成许多小面元.
l
则 dΦ B dS Bldr
Φ dΦ R2 I ldr
R1 2πr
P
S
R2
8
10 - 4 自感和互感
Il 2
6
10 - 4 自感和互感
第十章 电磁感应
L
I
N
l2
2
lS
n2V
提高 L 的途径
增大 V 提高 n
放入 值高的介质
实用
7
10 - 4 自感和互感
第十章 电磁感应
例 2 有两个同轴圆筒形导体 , 其半径分别为 R1
和 R2 , 通过它们的电流均为 I ,但电流的流向相反.
设在两圆筒间充满磁导率为 的均匀磁介质 , 求其
12 :互感磁链--由“2”产生穿过 “1”的磁链;
Ψ 21 N 2Φ21 M 21I1 Ψ12 N1Φ12 M12 I2
实验和理论都可以证明:
1
2
M12 M 21 M
Ψ21 M I1 Ψ12 M I2
I1
I2
Ψ 12
Ψ 21
15
10 - 4 自感和互感
2、互感电动势:
矩形线圈一边相距为a,线圈共N匝,求互感系数.
解:设直导线中通有自下而上的电流I,它激发的磁场通过
矩形线圈的磁通链数为
N sB dS
ab I
NIl a b
N a
ldr ln
2r
2 a
互感为
M
Nl ln a b
I
I 2
a
dr
l
互感系数的大小取决于两回路的 几何性质和介质性质.
10 - 4 自感和互感
5、自感的计算
LI
L
I
N N S B dS
计算步骤:
第十章 电磁感应
IB L
(1)假设导线中通电I,求出电流产生的磁场
(2)选取适当的面积计算磁通链
(3)代入公式 L I ,求L
5
10 - 4 自感和互感
第十章 电磁感应
例 试计算长直螺线管
自
磁通的和。用 自 表示。
自 自1 自2 自N
若:自1 自2 自N
自 N 2
10 - 4 自感和互感
第十章 电磁感应
3. 自感系数(self-inductance)
Ψ自 NΦ
N
B dS
s
B
由毕奥-沙伐尔定律与叠加原理: B I
ab
17
10 - 4 自感和互感
第十章 电磁感应
Il
b2 b2
若导线如左图放置, 则互感 系数为多少???
R2
R1
dr r
Il ln( R2 ) 2 R1
LΦ
l
ln(
R 2
)
I 2 R
1
单位长度的自感为:
Lo
L l
2
ln(
R2 R1
)
第十章 电磁感应
R1 Q R
I Ir l
P
S
R2
dr
9
10 - 4 自感和互感
第十章 电磁感应
自感的利用
在通路时,自感对电流的变化起抑制作用, 可稳定电路中的电流(扼流圈\镇流器等).
10 - 4 自感和互感
一、自感(self-induction)
1. 自感应现象
第十章 电磁感应
A
R, L
B R
K
IL
t o
1
10 - 4 自感和互感
第十章 电磁感应
2、自感磁通与自感磁链
自 自感磁通--由回路电流产生
穿过电流自身回路的磁通。
Ii
用 自表示。
自感磁链--由回路电流产生
穿过电流自身回路各匝线圈
L1
L2
磁棒
放 大 器
这种由磁链交连的电路称为互感电路 13
10 - 4 自感和互感
第十章 电磁感应
1.互感现象
一个回路中的电流变化在另一个邻近的回 路中产生感应电动势的现象。
互感现象遵循
法拉第电磁感应 定律和楞次定律
I2 21
回路2
I1
回路1
14
10 - 4 自感和互感
第十章 电磁感应
21 :互感磁链--由“1”产生穿过 “2”的磁链;
的自感. 已知:N, S, l ,
μ
S
自感的计算步骤:
l
Bdl
L
o B
I
N N S B dS
L
LI
B n I N I
l
S
B • dS
BS
NI
l
S
N N 2I S
l
L
I
N 2
l2
lS n2V
Ψ自 LI L — 自感系数
自 I
定义: 线圈的自感磁链与产生这磁链的电流之比,
称为该线圈的自感系数,用L表示。
L的计算: LI
LI
注意:自感系数与电流无关,只决定于线圈本 身的性质--几何尺寸、匝数、介质。
3
10 - 4 自感和互感
第十章 电磁感应
4、自感电动势
根据法拉第电磁感应定律:
11
10 - 4 自感和互感
第十章 电磁感应
思考题2:用金属线绕制的标准电阻要求无 自感,怎样绕制才能确保自感系数为零?
答: 如图,双线绕制,可确保自感系数为零
0 L 0
I
12
10 - 4 自感和互感
第十章 电磁感应
二、互感(mutual induction)
引:互感现象--当回路中电流变化时在邻近回路 中产生感应电动势的现象。
