数字电路习题集答案(CH3)
(完整版)数字电路与逻辑设计课后习题答案蔡良伟(第三版)
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
1 0 1 1
1 1 0 0
1 1 0 1
1 1 1 0
1 1 1 1
0 0 0 0
0 0 0 1
0 0 1 0
0 0 1 1
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
1 0 1 0
3-6
3-7
3-8
3-9
3-10
求减数的补码，然后与被减数相加即可。电路图如下：
3-11
3-12
（1）
（2）
（3）
（4）
（5）
（6）
（7）
（8）
3-13
(1)真值表：
（2）电路图
3-14
3-15
第四章习题
4-1
4-2
4-3
4-4
4-5
4-6
4-7
4-8
4-9
4-10
RSDRSJK RST
4-11
(1)转换真值表
1 1 0 1
1 1 1 0
1 1 1 1
1 0 1 0
0 0 0 0
0 0 0 1
0 0 1 0
00 11
0 1 0 0
0 1 0 1
0 1 1 0
0 1 1 1
1 0 0 0
1 0 0 1
××××
××××
××××
××××
××××
1×0×1×0×
0×0×0××1
0×0××1 1×
0×0××0×1
0××1 1×1×
数字电路第三章习题答案
数字电路第三章习题答案
3-10
F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B F F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B
数字电路第三章习题答案
3-11
试用六个与非门设计一个水箱控制电路。图为水箱示意图。A、B、C是三个电极。 当 电极被水浸没时，会有信号输出。水面在A，B间为正常状态，点亮绿灯G；水面在B、 C间或在A以上为异常状态，点亮黄灯Y；水面在C以下为危险状态．点亮红灯R。
3531736半加器的设计1半加器真值表2输出函数3逻辑图输入输出被加数a加数b4逻辑符号31837ab改为用与非门实现函数表达式变换形式
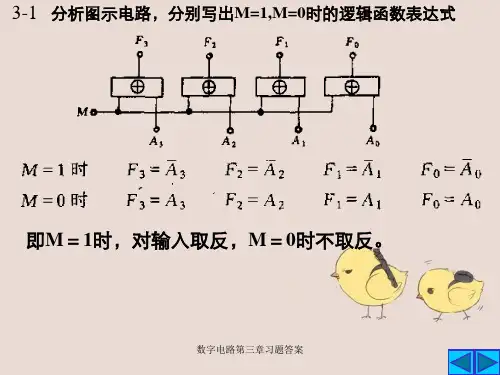
3-1 分析图示电路，分别写出M=1,M=0时的逻辑函数表达式
即M＝1时，对输入取反，M＝0时不取反。
数字电路第三章习题答案
3-2 分析图示补码电路，要求写出逻辑函数表达式，列出真值表。
3-10 试用与非门设计一个逻辑选择电路。
S1、S0为选择端，A、B为数据输入端。 选择电路的功能见下表。选择电路可 以有反变量输入。
数字电路第三章习题答案
3-10
F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B F F S 1 A S 0 B A S 0 B A B S 0 A B S 1 S 0 A B FS 1 S 0A B S 1 S 0(A B )S 1 S 0(A BA)B
数字电路第三章习题答案
3-5
Ai 0 0 0 0 1 1 1 1
Si Ai BiCi Ai BiCi Ai BiCi Ai BiCi
数字电子技术基础(第3版)练习答案
第1章 数字电路基础1.1 (1001010)2=1×26+1×23+1×21=(74)10(111001)2=1×25+1×24+1×23+1×20=(57)10 1.2 (54)10=(110110)2 (47)10=(101111)2 5427 13 6 3 1 01……MSB 10 1 1 0……LSB2 4723 11 5 2 1 01……MSB 01 1 1 1……LSB1.3 (58A)16 =(0101 1000 1010)2=1×210+1×28+1×27+1×23+1×21=1024+256+128+10=(1418)10或(58A)16=5×162+8×161+10×160=(1418)10 (CE)16 =(1100 1110)2=27+26+14=128+64+14=(206)10 =(0010 0000 0110)8421BCD 1.4 a 1.5 c 1.6 c 1.7 (×) 1.8 (×) 1.9 (√)1.10 ① 数字信号：在幅值上，时间上离散的（间断的、不连续的脉冲）信号． ② 数字电路：产生、处理、传输、变换数字信号的电路称为数字电路．③ 数字电路的特点：a ）电路处于开关状态. 与二进制信号要求相一致，这两个状态分别用0和1两个数码表示；b ）数字电路的精度要求不高，只要能区分出两种状态就可以；c ）数字电路研究的问题是逻辑问题，一为逻辑分析，是确认给定逻辑电路的功能，二为逻辑设计，是找到满足功能要求的逻辑电路；d ）研究数字电路的方法是逻辑分析方法，其主要工具是逻辑代数．有代数法和卡诺图法等；e ）数字电路能进行逻辑运算、推理、判断，也能进行算术运算．算术运算也是通过逻辑运算实现的．1.11 ① 位置计数法：将表示数值的数码从左到右按顺序排列起来．它有三个要素a ）基数R ，是指相邻位的进位关系，十进制R =10，即逢十进一，二进制R =2，即逢二进一．b ）数码：表示数字的符号，十进制k i 从0~9共十个．二进制k i 是0和1，十六进制k i 从0~9~A~F 共十六个．c ）位权：数码处于不同位置代表不同的位权，用R i表示．以小数点前从右到左为i 的位号分别为0、1、2、3…，小数点后从左到右i 的位号从–1，–2，–3…来确定R i．② 按权展开式是将任何进制数表示为十进制数值公式，是系数乘位权的集合，即(N )10=i i i k R ∞=-∞⨯∑． 1.12 ① (3027)10=3×103+2×101+7×100② (827)=8×102+2×101+7×100③ (1001)2=1×23+1×20④ (11101)2=1×24+1×23+1×22+1×20⑤ (273)16=2×162+7×161+3×160⑥ (4B5)16=4×162+11×161+5×1601.13 ① (6)10=(110)2② (13)=(1101)2 ③ (39)10=(100111)2 ④ (47)10=(101111)2 1.14 ① (1011)2=(11)10② (110101)2=(53)10③ (4A)16=4×161+10×160=(74)10④ (37)16 =3×161+7×160=(55)101.15 ① (1010 1101)2=(010 101 101)2=(255)8=(1010 1101)2=(AD)16② (100101011)2=(100 101 011)2=(453)8 =(0001 0010 1011)2=(12B)16 ③ ()2=(010 110 001 010)2=(2612)8 =(0101 1000 1010)2=(58A)16 1.16 ① (78)16=(0111 1000)2=(1111000)2 ② (EC)16=(1110 1100)2=(1110 1100)2 ③ (274)16=(0010 0111 0100)2=(1001110100)2注：从1.15~1.16均用分组方法，即二进制3位一组可表示1位八进制数；二进制4位一组可表示1位十六进制数．1.17 A =(1011010)2；B =(101111)2； C =(1010100)2；D =(110)2 （1）① A +B =(10001001)2② A –B =(101011)2 1011010 + 101111 100010011011010 – 101111 101011 ③ C ×D =(111111000)2④ C ÷D =(1110)2 1010100× 110 0000000 1010100 + 1010100 1111110001110 110 1010100 110 1001 110 0110110 0（2）A=(1011010)2=(90)10B=(101111)2=(47)10①A+B=(137)10=(10001001)2②A–B=(43)10=(101011)2C=(1010100)2=(84)10D=(110)2=(6)10③C×D=(504)10=(111111000)2这说明十进制四则运算的法则在二进制四则运算中也完全适用，对其它进制也一样．1.18 ① [0]8421BCD=(238)10② [10001]8421BCD=(7951)10③ [0]8421BCD=(640)101.19 ①逻辑函数：反映因果关系的二值逻辑表达式．原因（条件）为逻辑自变量，结果为逻辑因变量，它们都只有两种状态0和1，用以反映存在不存在，成立不成立，所以它们之间的关系称为（二值）逻辑函数．②与逻辑：表明所有的条件都具备结果才会发生这样的基本逻辑关系为“与”逻辑（逻辑乘）．用式Y=A·B·C…表示．如学生成绩合格及不犯罪与能否毕业的关系即为与逻辑．③或逻辑关系：表明诸多条件中只要有1个以上具备结果就会发生，用Y=A+B+…表示．如去银行办理业务（储蓄），持存款证或持银行卡都可以办理．④非逻辑：是否定的因果关系，即条件具备结果就不能发生，用Y=A表示．如：征兵体检“有病”和“入伍”的关系就是非逻辑．“有病”存在，“入伍”就被否定了，有病不能入伍．1.21 由真值表可以写出最小项与或表达式．方法是将使函数Z为1的几种情况下输入变量的取值组合写成乘积项（变量取值为0写反变量因子，变量取值为1写原变量因子），然后将各乘积项相加，得Z=A B C+A B C+A BC+A B C+A B C1.23Z a=AB AB=A B+A B(摩根定理) =A⊕BZ b=B C AB+= (B⊕C)·AB=(BC+B C)AB=ABC1 1 1 0 1 1 1 1 1 11.24 见教材原文1.5节 1.25 a ）Z a =m (0, 2, 3, 5, 6) =A B C +A B C +A BC +A B C +AB C =A C +B C +A B +A B Cb ）Z b =m (0, 2, 7, 13, 15, 8, 10)=A B C D +A B C D +A BCD +A B C D +A B C D +AB C D +ABCD=B D +BCD +ABD1.26 （1）Z =A B +B +A B =A B +B =A +B （2）Z =A B C +A +B +C =A B C +A B C ++ =A B C +A B C =1（3）Z =AB ABC AB AB C +=++ =11AB AB C C +=+= （4）Z =A B CD +ABD +A C D=AD (B C +B +C ) =AD (C +B +C ) =AD ·1 =AD（5）Z =(A +B )(A CD +AD BC +)A B=(A +B )·A B ·(A CD +AD BC +) =0注：(A +B )A B =A A B +A B ·B =0（6）Z =AC (C D +A B )+BC (B AD CE ++)=0+BC ·(B +AD )·CE =BC (C +E )(B +AD ) =(BC E )(B +AD ) =BC E +BC E AD =BC E （7）Z =ABC +AC D +A C +CD=C (AB +A D +D )+A C =C (D +A )+A C =AC +CD +A C =A +CD（8）Z =A +B C +·(A +B +C )(A +B +C )=A +B C (A +B +C )(A +B +C ) ←展开=A +(A B C +B C )(A +B +C )←展开、吸收=A +B C（9）Z =B (A D +A D )+B (AD AD ABCE BC +++)=B (A D +A D )+B (A D +A D ) =A D +A D =A ⊕D（10）Z =AC +A C D +A B E F +B (D ⊕E )+BD E +B D E +BF=A (C +C D )+A B E F +BD E +B D E +BF =AC +AD +F (A B E +B )+B D E +BD E=AC +AD +A E F +BF +BD E +B D E1.27 求反函数Z 和对偶函数Z' （1）Z =AB +C （2）Z =(A +BC )C D Z =(A +B )·C Z =A ·(B +C )+C +DZ'=(A +B )·C Z' =A ·(B +C )+C +D（3）Z =()(+)A C A B AC BC ++ Z =(AC AB A C +++)·(B +C ) Z'=(AC AB A C +++)·(B +C )（4）Z =A D +AC +BCD +CZ =(A +D )·A C +·(B C D ++)·C Z'=(A +D )·A C +·(B C ++D )·C （5）Z =(AC +BD )ABC CD +Z =(A +C )·(B +D )+()()A B C C D +++ Z'=(A +C )·(B +D )+()()A B C C D +++ 1.28 用填卡诺图方法写最小项表达式 （1）F 1=A BC +AC +B C =m (1, 3, 5, 7)=ABC +A BC +A B C +ABC（2）F 2=A +B +CD =m (3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15)=ABCD ABCD ABCD ABCD ABCD ABCD ++++++ABCD ABCD ABCD +++ABCD ABCD ABCD ABCD +++题1.28（1）F1卡诺图题1.28（2）F2卡诺图1.29 证明异或关系的正确性（1）A⊕0=A·0+A·0=A得证（2）A⊕1=A·1+A·1=A得证（3）A⊕A=A·A+A·A=0 得证（4）A⊕A=A·A+A·A=1 得证=A+A=1（5）(A⊕B)⊕C =(A⊕B)C+A B C⊕=ABC ABC ABC ABC+++=m(1, 2, 4, 7)A⊕(B⊕C) =A()⊕+⊕B C A B C=A(BC+BC)+A(B C+B C)=ABC ABC ABC ABC+++=m(1, 2, 4, 7)左式=右式，得证（6）右式AB⊕AC=AB·()()+=+++=+AC ABAC AB A C A B AC ABC ABC左式A(B⊕C)=A(B C+B C)=ABC ABC+得证（7）左式A⊕B=A B+AB=AB+AB=中式右式A⊕B⊕1=A⊕(B⊕1)=A⊕B=AB AB AB AB+=+=中式得证．1.30 用卡诺图法将函数化简为与或式．（1）Z ABC ABC ABC ABC=+++（2）1Z A B AB ABC BC=++++=题1.30（1）的卡诺图题1.30（2）的卡诺图（3）Z ABC AB AD C BD=++++填图后，可圈“0”得到Z=Z BCD再对Z取反，得到ZZ Z BCD B C D===++（4）Z(A、B、C)=m(0, 1, 2, 5, 6, 7)Z=AB AC BC++题1.30（3）的卡诺图题1.30（4）的卡诺图（5）Z(A、B、C、D)=m(0, 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 14)Z=B AC AD CD+++（6）Z(A、B、C、D)=m(0, 1, 2, 5, 8, 9, 10, 12, 14)Z=BC+BD+AD ACD+题1.30（5）的卡诺图题1.30（6）的卡诺图（7）Z=A C D ABCD ABCD++++，给定的约束条件为ABCD ABCD ABCD ABCD++++ 0ABCD ABCD+=Z=ACD ABCD ABCD++=ACD BCD AD++（8）Z=()CD A B ABC ACD⊕++给定的约束条件为AB+AC=0AC ACDZ=ABCD ABCD ABC ACD +++=BD ACD +题图1.30（7）的卡诺图题图1.30（8）的卡诺图（9）Z =m (0, 1, 2, 4)+d (3, 5, 6, 7)=1（10）Z =m (2, 3, 7, 8, 11, 14)+d (0, 5, 10, 15) Z =BD CD AC ++题图1.30（9）的卡诺图题图1.30（10）的卡诺图1.31 试用卡诺图法化简下列逻辑图 ① Z a =ABC ABC BC=ABC ABC BC ++ =ABC AC BC ++② Z b ：按逻辑图逐级写函数式，最后得出Z b =A ⊕C +(A +B )()BC AC BD AD +=A ⊕C +(A +B )()()B C AC BD A D +++=A ⊕C +(A +B )ABCD ↓展开为与或式 =A ⊕C +(A +B )(A +B +C +D )=A ⊕C +AB +A C +AD +AB +B +BC +BD=A C +A C +AD +B 填入卡诺图 由卡诺图判断：Z b=AC+AC+AD+B该式已为最简与或式．题图1.31（a）的卡诺图题图1.31（b）的卡诺图1.32 化函数式为与非-与非式，并画出对应的逻辑图．（1）Z1 =AB+BC+AC=AB BC AC+++（2）Z2 =ABC AB BC AB=()++ABC AB BC AB=()++++ABC A B BC A BABC=1=ABC题图1.32（1）题图1.32（2）1.33 用最小项性质证明两个逻辑函数的与、或、异或运算可用卡诺图中对应的最小项分别进行与、或、异或运算来实现．解：命题所给出的结论是正确的．因为当输入变量的取值组合使某一最小项为1时，其他最小项均为0，若两函数相“与”，即Y=Y1·Y2，在对应最小项位置上Y1、Y2均为1时必然使Y为1；Y1Y2在该位置上有0，则0·0或1·0，Y必然为0，将所有对应最小项作乘运算就实现了Y=Y1·Y2运算．其他运算（或和异或）也是同样的道理．或运算是对应最小项相加；异或运算是对应最小项相异或．。
数字电路ch3补充：最大项、最小项、无关项
四.最简或与表达式
F ( A B)( A B)
__ __
__
__
五.最简或-与非表达式 F ( A B)( A B)
【例1】: 将逻辑函数
Y AB C BC BD 化成与非-与非形式。
解： 首先将Y化成标准的与-或式
Y ABC BC BD
再利用德-摩根定律即得到
可写成：
ABC ABC ABC ABC ABC 0
约束项：恒等于0的最小项
2)、 任意项
有时还会遇到另外一种情况，就是 在输入变量的某些取值下函数值是1还 是0皆可，并不影响电路的功能。
任意项：在这些变量取值下，其值等于1的那 些最小项称为任意项。
3)、无关项
约束项和任意项统称为无关项 。
强化： 逻辑函数的公式化简法
1 逻辑函数的最简形式
乘积项最少；每个乘积项里的因子也最少 一. 最简与-或式 二. 最简与非-与非式等
_ _
F AB A B
F AB A B
__________ ______ ____ __ __
三.最简与或非表达式
F AB AB
__________ ___ __ __
( ABD ABD) ( ACD ACD) AD AD
【例3】 化简具有约束的逻辑函数
Y ABCD ABCD ABCD
给定约束条件为
ABCD ABCD ABCD ABCD ABCD ABCD ABCD 0
解：采用卡诺图化简法
AD
Y AD AD
变量的各组取值 对应的最大项及其编号 最大项 编 号 A B C
0 0 0 0 1 1 1 1
数电课后习题答案
思考题与习题思考题与习题第一章【1-1】（1）（1101）2= （13）10（2）（10111）2=（23）10 （3）（110011）2=（51）10 （4）（11.011）2=（3.375）10【1-2】（1）（35）10=（100011）2 （2）（168）10 =（10101000）2 （3）（19.85）10=（10011.11011）2（4）（199）10=（11000111）2【1-3】（1）(1011011682)()55()AD ==（2）(1110011011682)1()715()CD == （3）(11000111011682)36()1435()D == （4）(1010101111682)157()527()==【1-4】答：数字逻辑变量能取“1”，“0”值。
它们不代表数量关系，而是代表两种状态，高低电平.【1-5】答：数字逻辑系统中有“与”，“或”，“非”三种基本运算，“与”指只有决定事件发生的所有的条件都成立，结果才会发生，只要其中有一个条件不成立，结果都不会发生. “与“指只要所有的条件中有一个条件成立，结果就会发生，除非所有的条件都不成立，结果才不会发生. ”非“指条件成立，结果不成立。
条件不成立，结果反而成立。
【1-6】答：逻辑函数：指用与，或，非，等运算符号表示函数中各个变量之间逻辑关系的代数式子。
将由真值表写出逻辑函数表达式的方法： 1.在真值表中挑选出所有使函数值为1的变量的取值组合。
2.将每一个选出的变量取值组合对应写成一个由各变量相与的乘积项，在此过程中，如果某变量取值为1，该变量以原变量的形式出现在乘积项中，如果某变量取值为0，则该变量以反变量的形式出现在乘积项中。
3.将所有写出的乘积项相或，即可得到该函数的表达式。
【1-7】答：在n 输入量的逻辑函数中，若m 为包含n 个因式的乘积项，而且这n 个输入变量均以原变量或反变量的形式在m 中出现且仅出现一次，这m 称为该n 变量的一个最小项。
数字电路练习题及答案
数字电路练习题及答案选择题：1．下列四个数中，与十进制数10不相等的是A、16B、2C、8421BCDD、82．N个变量可以构成多少个最小项A、NB、2NC、2ND、2N-13．下列功能不是二极管的常用功能的是A、检波B、开关C、放大D、整流4．.将十进制数10转换成八进制数是A、20B、22C、21D、235．译码器的输入地址线为4根，那么输出线为多少根A、B、12C、16D、206．能把正弦信号转换成矩形脉冲信号的电路是A、多谐振荡器B、D/A转换器C、JK触发器D、施密特触发器7．三变量函数F?A,B,C??A?BC的最小项表示中不含下列哪项A、m2B、 m5C、m3D、 m78．用PROM来实现组合逻辑电路，他的可编程阵列是 A、与阵列 B、或阵列C、与阵列和或阵列都可以D、以上说法都不对9．A/D转换器中，转换速度最高的为转换A、并联比较型B、逐次逼近型C、双积分型D、计数型10．关于PAL器件与或阵列说法正确的是A、只有与阵列可编程B、都是可编程的C、只有或阵列可编程D、都是不可编程的11. 当三态门输出高阻状态时，输出电阻为A、无穷大B、约100欧姆C、无穷小D、约10欧姆12为使采样输出信号不失真地代表输入模拟信号，采样频率fs和输入模拟信号的最高频率A、fs≥C、fs≥2fImax fImax fImax的关系是 fImaxB、fs≤D、fs≤2fImax13. 下列说法不正确的是A．集电极开路的门称为OC门B．三态门输出端有可能出现三种状态C．OC门输出端直接连接可以实现正逻辑的线或运算D.利用三态门电路可实现双向传输14. 以下错误的是A．数字比较器可以比较数字大小B．实现两个一位二进制数相加的电路叫全加器C．实现两个一位二进制数和来自低位的进位相加的电路叫全加器D．编码器可分为普通全加器和优先编码器15. 下列描述不正确的是A．触发器具有两种状态，当Q=1时触发器处于1态 B．时序电路必然存在状态循环C．异步时序电路的响应速度要比同步时序电路的响应速度慢D．边沿触发器具有前沿触发和后沿触发两种方式，能有效克服同步触发器的空翻现象16．离散的，不连续的信号，称为。
数字电路与逻辑设计习题及参考答案全套
数字电路与逻辑设计习题及参考答案一、选择题1. 以下表达式中符合逻辑运算法则的是 D 。
A.C ·C=C 2B.1+1=10C.0<1D.A+1=12. 一位十六进制数可以用 C 位二进制数来表示。
A . １B . ２C . ４D . 163. 当逻辑函数有n 个变量时，共有 D 个变量取值组合？A. nB. 2nC. n 2D. 2n4. 逻辑函数的表示方法中具有唯一性的是 A 。
A .真值表 B.表达式 C.逻辑图 D.状态图5. 在一个8位的存储单元中，能够存储的最大无符号整数是 D 。
A .（256）10B .（127）10C .（128）10D .（255）106.逻辑函数F=B A A ⊕⊕)( = A 。
A.BB.AC.B A ⊕D. B A ⊕7．求一个逻辑函数F 的对偶式，不可将F 中的 B 。
A .“·”换成“+”，“+”换成“·”B.原变量换成反变量，反变量换成原变量C.变量不变D.常数中“0”换成“1”，“1”换成“0”8．A+BC= C 。
A .A+B B.A+C C.（A+B ）（A+C ） D.B+C9．在何种输入情况下，“与非”运算的结果是逻辑0。
DA ．全部输入是0 B.任一输入是0 C.仅一输入是0 D.全部输入是110．在何种输入情况下，“或非”运算的结果是逻辑1。
AA ．全部输入是0 B.全部输入是1 C.任一输入为0，其他输入为1 D.任一输入为111．十进制数25用8421BCD 码表示为 B 。
A .10 101B .0010 0101C .100101D .1010112．不与十进制数（53.5）10等值的数或代码为 C 。
A .(0101 0011.0101)8421BCDB .(35.8)16C .(110101.11)2D .(65.4)813．以下参数不是矩形脉冲信号的参数 D 。
A.周期B.占空比C.脉宽D.扫描期14．与八进制数(47.3)8等值的数为： BA. (100111.0101)2B.(27.6)16C.(27.3 )16D. (100111.101)215. 常用的BCD码有 D 。
数电课后习题及答案
第1章 数字电路基础知识1 电子电路主要分为两类：一类是电子电路主要分为两类：一类是 模拟电路 ，另一类是，另一类是 数字电路 。
2 模拟电路处理的是模拟电路处理的是 模拟信号 ，而数字电路处理的是，而数字电路处理的是 数字信号 。
3 晶体管（即半导体三极管）的工作状态有三种：晶体管（即半导体三极管）的工作状态有三种：截止截止、 放大和 饱和。
在模拟电路中，晶体管主要工作在体管主要工作在 放大状态 。
4 在数字电路中，晶体管工作在在数字电路中，晶体管工作在 截止与 饱和状态，也称为状态，也称为 “开关”状态。
状态。
5 模拟信号是一种模拟信号是一种大小随时间连续变化大小随时间连续变化的电压或电流，数字信号是一种的电压或电流，数字信号是一种突变突变的电压和电流。
6 模拟信号的电压或电流的大小是模拟信号的电压或电流的大小是随时间连续缓慢变化的随时间连续缓慢变化的，而数字信号的特点是“保持”（一段时间内维持低电压或高电压）和“段时间内维持低电压或高电压）和“突变突变”（低电压与高电压的转换瞬间完成）。
7 在数字电路中常将0~1v 范围的电压称为范围的电压称为低电平低电平，用，用““0”来表示；将3~5v 范围的电压称为高电平，用，用““1”来表示。
来表示。
介绍了数字电路的发展状况和数字电路的一些应用领域，并将数字电路和模拟电路进行了比较，让读者了解两者的区别，以利于后面数字电路的学习。
以利于后面数字电路的学习。
第2章 门电路1 基本门电路有基本门电路有与门与门、或门、非门三种。
三种。
2 与门电路的特点是：只有输入端都为只有输入端都为 高电平 时，输出端才会输出高电平；只要有一个输入端为“0”，输出端就会输出输出端就会输出 低电平 。
与门的逻辑表达式是与门的逻辑表达式是 Y A B =· 。
3 或门电路的特点是：只要有一个输入端为只要有一个输入端为 高电平 ，输出端就会输出高电平。
只有输入端都为 低电平 时，输出端才会输出低电平。
数电习题及答案
数电习题及答案(总32页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一、时序逻辑电路与组合逻辑电路不同，其电路由组合逻辑电路和存储电路（触发器）两部分组成。
二、描述同步时序电路有三组方程，分别是驱动方程、状态方程和输出方程。
三、时序逻辑电路根据触发器的动作特点不同可分为同步时序逻辑电路和异步时序逻辑电路两大类。
四、试分析图时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图和时序图。
解：驱动方程：001101J KJ K Q====状态方程：100111010nnQ QQ Q Q Q Q++==+输出方程：10Y Q Q=状态图：功能：同步三进制计数器五、试用触发器和门电路设计一个同步五进制计数器。
解：采用3个D触发器，用状态000到100构成五进制计数器。
（1）状态转换图（2）状态真值表（3）求状态方程（4）驱动方程（5）逻辑图（略）[题] 分析图所示的时序电路的逻辑功能，写出电路驱动方程、状态转移方程和输出方程，画出状态转换图，并说明时序电路是否具有自启动性。
解：触发器的驱动方程2001021010211J Q K J Q J QQ K Q K ====⎧⎧⎧⎨⎨⎨==⎩⎩⎩ 触发器的状态方程120011010112210n n n Q Q Q Q Q Q Q Q Q Q Q Q +++==+=⎧⎪⎪⎨⎪⎪⎩输出方程 2Y Q = 状态转换图如图所示所以该电路的功能是：能自启动的五进制加法计数器。
[题] 试分析图时序电路的逻辑功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，并检查电路能否自启动。
解：驱动方程输出方程 状态方程状态转换图如图 所示功能：所以该电路是一个可控的3进制计数器。
[题] 分析图时序电路的功能，写出电路的驱动方程、状态方程和输出方程，画出电路的状态转换图，并检查电路能否自启动。
数字电子技术基础-第3章课后习题答案
第3章集成逻辑门电路3-1 如图3-1a）～d）所示4个TTL门电路，A、B端输入的波形如图e）所示，试分别画出F1、F2、F3和F4的波形图。
A1A234a)b)c)d)F1F2F3F4BAe）图3-1 题3-1图解：从图3-1a）～d）可知，11F=，2F A B=+，3F A B=⊕，4F A B= ，输出波形图如图3-2所示。
F1F2F3F4AB图3-2题3-1输出波形图3-2 电路如图3-3a ）所示，输入A 、B 的电压波形如图3-3b ）所示，试画出各个门电路输出端的电压波形。
1A 23b)a)AB图3-3 题3-2图解：从图3-3a ）可知，1F AB =，2F A B =+，3F A B =⊕，输出波形如图3-4所示。
F 1F 2F 3AB图3-4 题3-2输出波形3-3在图3-5a ）所示的正逻辑与门和图b ）所示的正逻辑或门电路中，若改用负逻辑，试列出它们的逻辑真值表，并说明F 和A 、B 之间是什么逻辑关系。
b)a)图3-5 题3-3图解：（1）图3-5a ）负逻辑真值表如表3-1所示。
表3-1 与门负逻辑真值表F 与A 、B 之间相当于正逻辑的“或”操作。
（2）图3-5b ）负逻辑真值表如表3-2所示。
表3-2 或门负逻辑真值表F 与A 、B 之间相当于正逻辑的“与”操作。
3-4试说明能否将与非门、或非门和异或门当做反相器使用？如果可以，各输入端应如何连接？解：与非门、或非门和异或门经过处理以后均可以实现反相器功能。
1）与非门：将多余输入端接至高电平或与另一端并联； 2）或非门：将多余输入端接至低电平或与另一端并联；3） 异或门：将另一个输入端接高电平。
3-5为了实现图3-6所示的各TTL 门电路输出端所示的逻辑关系，请合理地将多余的输入端进行处理。
b)a)AB=A B=+A BC DABC D图3-6 题3-5图解：a ）多余输入端可以悬空，但建议接高电平或与另两个输入端的一端相连；b ）多余输入端接低电平或与另两个输入端的一端相连；c) 未用与门的两个输入端至少一端接低电平，另一端可以悬空、接高电平或接低电平；d ）未用或门的两个输入端悬空或都接高电平。
数字电路试题及答案
数字电路试题及答案一、选择题（每题2分，共20分）1. 在数字电路中，最基本的逻辑关系是：A. 与逻辑B. 或逻辑C. 非逻辑D. 异或逻辑答案：A2. 一个3输入的与门，当所有输入都为高电平时，输出为：A. 低电平B. 高电平C. 浮空D. 不确定答案：B3. 触发器的两个稳定状态是：A. 0和1B. 正和负C. 高和低D. 真和假答案：A4. 下列哪个不是数字电路的优点？A. 高速度B. 高稳定性C. 低功耗D. 易于集成答案：C5. 以下哪个是组合逻辑电路的特点？A. 输出状态只与当前输入有关B. 具有记忆功能C. 输出状态与过去输入有关D. 以上都不是答案：A6. 一个D触发器的Q端在时钟信号上升沿触发时，其输出将：A. 保持不变B. 变为0C. 变为1D. 翻转答案：D7. 以下哪个逻辑门不是基本逻辑门？A. 与门B. 或门C. 非门D. 异或门答案：D8. 以下哪个是数字电路设计中的同步设计？A. 所有信号在同一个时钟信号下操作B. 信号在不同的时钟信号下操作C. 信号没有时钟信号D. 以上都不是答案：A9. 一个4位二进制计数器，其计数范围是：A. 0到3B. 0到7C. 0到15D. 1到4答案：C10. 在数字电路中，布尔代数的基本原理不包括：A. 幂等律B. 互补律C. 反演律D. 欧拉定律答案：D二、简答题（每题10分，共30分）1. 简述数字电路与模拟电路的主要区别。
答：数字电路主要处理离散的数字信号，使用二进制数字表示信息，具有较高的抗干扰能力，易于实现大规模集成。
而模拟电路处理连续变化的模拟信号，使用电压或电流的连续变化来表示信息，通常需要较高的精度和稳定性。
2. 解释什么是时序逻辑电路，并给出一个例子。
答：时序逻辑电路是一种数字电路，其输出不仅依赖于当前的输入，还依赖于电路的历史状态。
这种电路通常包含存储元件，如触发器或寄存器。
一个常见的例子是计数器，它可以按照时钟信号的上升或下降沿进行计数。
数字电路课后题参考答案
习题参考答案注：参考答案，并不是唯一答案或不一定是最好答案。
仅供大家参考。
第一章习题2. C B A D B A C B A F ⋅⋅+⋅⋅+⋅⋅=3. 设：逻辑变量A 、B 、C 、D 分别表示占有40%、30%、20%、10%股份的四个股东，各变量取值为1表示该股东投赞成票；F 表示表决结果，F =1表示表决通过。
F =AB +AC +BCD4. 设：A 、B 开关接至上方为1，接至下方为0；F 灯亮为1，灯灭为0。
F =A ⊙B5. 设：10kW 、15kW 、25kW 三台用电设备分别为A 、B 、C ，设15kW 和25kW 两台发电机组分别为Y 和Z ，且均用“0”表示不工作，用“1”表示工作。
C AB Z BA B A Y ⋅=⋅=6.输入为余3码，用A 、B 、C 、D 表示，输出为8421BCD 码，用Y 0、Y 1、Y 2、Y 3表示。
D C A B A Y CB DC BD B Y DC Y DY ⋅⋅+⋅=⋅+⋅⋅+⋅=⊕==32107. 设：红、绿、黄灯分别用A 、B 、C 表示，灯亮时为1，灯灭时为0；输出用F 表示，灯正常工作时为0，灯出现故障时为1。
C A B A C B A F ⋅+⋅+⋅⋅=8. D C B D A H DC B AD C B A D C B A D C B A G DC B AD C A B A F DC B A E ⋅⋅+⋅=⋅⋅⋅+⋅⋅⋅+⋅⋅⋅+⋅⋅⋅=⋅⋅⋅+⋅⋅+⋅=⋅⋅⋅=第二章习题1. 设：红、绿、黄灯分别用A 、B 、C 表示，灯亮时其值为1，灯灭时其值为0；输出报警信号用Y 表示，灯正常工作时其值为0，灯出现故障时其值为1。
AC AB C B A Y ⋅⋅=2. 设：烟、温度和有害气体三种不同类型的探测器的输出信号用A 、B 、C 表示，作为报警信号电路的输入，有火灾探测信号时用1表示，没有时用0表示。
报警信号电路的书躇用Y 表示，有报警信号时用1表示，没有时用0表示。
数字电路ch3补充：最大项、最小项、无关项
性质
互补性
对于任意一个最大项Mi，都存在 一个对应的最大项Mi'，它们的输 出值互为相反数。
唯一性
对于任意一个最大项Mi，其输出 值在所有输入变量的取值组合中 是唯一的。
无关性
对于任意一个最大项Mi，当其中 任意一个输入变量取值为0时，其 输出值与该输入变量取值无关。
应用场景
组合逻辑电路设计
在组合逻辑电路设计中，可以使用最 大项来表示和实现复杂的逻辑函数， 简化电路结构。
在逻辑函数中，最大项是包含 所有变量的项，即当所有变量
取值为1时得到的项。
最小项
在逻辑函数中，最小项是包含 一个变量的项，即当只有一个
变量取值为1时得到的项。
无关项
在逻辑函数中，无关项是指对 逻辑函数的输出结果没有影响
的项。
关系证明
最大项和最小项的关系
最大项可以表示为若干个最小项的或运算， 反之，最小项也可以表示为若干个最大项的 与运算。
完备性
所有最小项合起来能够覆盖所有可能的输入变量取值 组合，即所有最小项之和等于全部输出变量。
独立性
每个最小项与其他最小项之间是独立的，即一个最小 项的取值不会影响其他最小项的取值。
应用场景
逻辑函数化简
通过最小项可以将复杂的逻辑函数化简为简单的形式，便于分析 和设计。
真值表生成
根据最小项可以生成逻辑函数的真值表，用于描述逻辑函数的输入 输出关系。
符号表示
用mi(i=0,1,2,...)表示，其中i表示该 最小项包含的变量个数。
无关项
无关项
在逻辑函数中，与输出变量 无关的项。
特点
无关项的取值不影响输出变 量的值，因此在逻辑函数化 简时可以忽略。
数字电路与逻辑设计课后习题答案蔡良伟(第三版)
数字电路答案
00011100 0011 11111001
111000011.111110012 = 111000011.111110010= 703.7628
703
76 2
703.762 8 = 7*8 2 + 0*8 1 + 3*8 0 + 7*8 - 1 + 6*8 - 2 + 2*8 - 3 = 451.972610
00 0 0 1 0 01 0 0 1 1 11 1 1 1 1 10 1 1 1 1
8
数字电路答案
A B C DF A B C DF 0 0 0 00 1 0 0 00 0 0 0 10 1 0 0 11 0 0 1 01 1 0 1 01 0 0 1 11 1 0 1 11 0 1 0 01 1 1 0 00 0 1 0 11 1 1 0 10 0 1 1 01 1 1 1 00 0 1 1 11 1 1 1 10
1
1
1
1
0
1
1
1
1
1
3
数字电路答案
（3） A B A B
A 0 0 1 1 左式＝右式，得证。
（4） AB A B
A 0 0 1 1 左式＝右式，得证。
（5） A BC A BC 1
A 0 0 0 0 1 1 1 1 左式＝右式，得证。
（6） AB AB AB A B
数字电路课后题参考答案
习题参考答案注：参考答案，并不是唯一答案或不一定是最好答案。
仅供大家参考。
第一章习题2. C B A D B A C B A F ⋅⋅+⋅⋅+⋅⋅=3. 设：逻辑变量A 、B 、C 、D 分别表示占有40%、30%、20%、10%股份的四个股东，各变量取值为1表示该股东投赞成票；F 表示表决结果，F =1表示表决通过。
F =AB +AC +BCD4. 设：A 、B 开关接至上方为1，接至下方为0；F 灯亮为1，灯灭为0。
F =A ⊙B5. 设：10kW 、15kW 、25kW 三台用电设备分别为A 、B 、C ，设15kW 和25kW 两台发电机组分别为Y 和Z ，且均用“0”表示不工作，用“1”表示工作。
C AB Z BA B A Y ⋅=⋅=6.输入为余3码，用A 、B 、C 、D 表示，输出为8421BCD 码，用Y 0、Y 1、Y 2、Y 3表示。
D C A B A Y CB DC BD B Y DC Y DY ⋅⋅+⋅=⋅+⋅⋅+⋅=⊕==32107. 设：红、绿、黄灯分别用A 、B 、C 表示，灯亮时为1，灯灭时为0；输出用F 表示，灯正常工作时为0，灯出现故障时为1。
C A B A C B A F ⋅+⋅+⋅⋅=8. D C B D A H DC B AD C B A D C B A D C B A G DC B AD C A B A F DC B A E ⋅⋅+⋅=⋅⋅⋅+⋅⋅⋅+⋅⋅⋅+⋅⋅⋅=⋅⋅⋅+⋅⋅+⋅=⋅⋅⋅=第二章习题1. 设：红、绿、黄灯分别用A 、B 、C 表示，灯亮时其值为1，灯灭时其值为0；输出报警信号用Y 表示，灯正常工作时其值为0，灯出现故障时其值为1。
AC AB C B A Y ⋅⋅=2. 设：烟、温度和有害气体三种不同类型的探测器的输出信号用A 、B 、C 表示，作为报警信号电路的输入，有火灾探测信号时用1表示，没有时用0表示。
报警信号电路的书躇用Y 表示，有报警信号时用1表示，没有时用0表示。
数字电路逻辑设计课后习题答案第三章
3-1 分析题图3-1所示电路，写出电路输出Y 1和Y 2的逻辑函数表达式，列出真值表，说明它的逻辑功能。
解：由题图3-1从输入信号出发，写出输出Y 1和Y 2的逻辑函数表达式为1Y A B C =⊕⊕ ； 2()()Y A B C AB A B C A =⊕⋅⋅=⊕⋅+B将上式中的A 、 B 、C 取值000～111，分别求出Y 1和Y 2，可得出真值表如题解 表3-1所示。
题解 表3-1ABCA B ⊕()A B C ⊕⋅AB1Y2Y0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 1 1 0 0 1 1 0 0 1 0 0 1 0 1 0 1 1 1 0 0 1 1 1 0 0 0 1 0 1 111111综上，由题解 表3-1可以看出，该电路实现了一位全加器的功能。
其中，A 和B 分别是被加数及加数，C 为相邻低位来的进位数；Y1为本位和数，Y 2为相邻高位的进位数。
3-2 分析题图3-2所示电路，要求：写出输出逻辑函数表达式，列出真值表，画出卡诺图，并总结电路功能。
解：由题图3-2从输入信号出发，写出输出F 的逻辑函数表达式为()()F A B C D =:::将上式中的A 、 B 、C 、D 取值0000～1111，求出F ，可得真值表和卡诺图分别如题解 表3-2和题解 图3-1所示。
题解 表3-2A B C DA B : C D :F0 0 0 0 1 1 1 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 1 0 0 1 0 1 0 0 1 0 1 1 0 0 0 1 0 1 1 1 0 1 0 1 0 0 0 0 1 0 1 0 0 1 0 0 11 0 1 0 0 0 1 1 0 1 1 0 1 0 1 1 0 0 1 1 1 1 1 0 1 1 0 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1综上，由题解 表3-2可以看出，当输入A 、 B 、C 、D 中含有偶数个“1”时，输出；否则，当输入A 、 B 、C 、D 中含有奇数个“1”时，输出。
数字电路习题参考答案详解
第27页，共29页。
4.24 判断用下列函数构成的电路是否存在冒险？冒险的类型？
(1)F=AB+ABC
AC
F
00
0
01
0
10
B
1 1 B+B
0型冒险
(4)F=AB+AB
11 0 0 1 1
10 1 0 0 1
D1 D3 D7 D5
10
D
第25页，共29页。
（3）三变量多数表决电路。
AB
D0 D2 D6 D4
C 00 01 11
0 100 0 1 0
1 0 1 01 1
D1 D3 D7 D5
10
第26页，共29页。
4.23 用数据选择器组成的电路如图所示，求输出Y 的表达式。
又Si m1 m2 m4 m7 Ai BiCi1 Ai BiCi1 Ai BiCi1 Ai BiCi1
比较得： D0=D3= Ci-1 D1=D2= Ci-1
且 Ci m3 m5 Ai Bi Ai BiCi1 Ai BiCi1 Ai Bi
Y m0 D0 m1D1 m2 D2 m3D3
D0 B 0 0 1 1 0 1 1111
D1 1
D2 B D3 1
A C
B1
第22页，共29页。
(4)二变量异或表达式。
A
B
0
00
1 AB
1
11 0
D0=0
AB
D3=0
数字电路试题及答案
数字电路试题及答案一、单项选择题（每题2分，共10分）1. 在数字电路中，最基本的逻辑门是：A. 与门B. 或门C. 非门D. 异或门答案：C2. 以下哪个不是数字电路的特点？A. 离散性B. 线性C. 确定性D. 可预测性答案：B3. 一个D触发器的输入端是：A. SB. RC. DD. Q答案：C4. 在TTL逻辑门中，高电平的最小值是：A. 0.8VB. 2.0VC. 3.5VD. 5.0V答案：A5. 以下哪个是组合逻辑电路？A. 计数器B. 寄存器C. 译码器D. 触发器答案：C二、填空题（每题2分，共10分）1. 一个标准的二进制数由______和______组成。
答案：0，12. 一个完整的触发器可以存储______位二进制信息。
答案：13. 一个4位二进制计数器可以计数到______。
答案：154. 一个8x3的译码器可以产生______个输出。
答案：85. 在数字电路中，______是最小的可识别信号单位。
答案：位三、简答题（每题5分，共20分）1. 简述数字电路与模拟电路的主要区别。
答案：数字电路处理的是离散信号，具有确定性，而模拟电路处理的是连续信号，具有不确定性。
2. 解释什么是上升沿触发。
答案：上升沿触发是指在时钟信号的上升沿（从低电平变为高电平）时，触发器会根据输入信号更新其状态。
3. 什么是同步电路和异步电路？答案：同步电路是指电路中的各个部分都由同一个时钟信号控制，而异步电路则没有统一的时钟信号，各个部分可以独立工作。
4. 描述一个典型的数字电路设计流程。
答案：数字电路设计流程通常包括需求分析、逻辑设计、电路设计、仿真测试、PCB布局布线、调试和验证。
四、计算题（每题10分，共20分）1. 给定一个逻辑表达式：Y = AB + A'C，请计算当A=0, B=1, C=0时，Y的值。
答案：Y = 0*1 + 0'*0 = 0 + 1 = 12. 一个4位二进制计数器，初始状态为0000，每次计数加1，求经过5次计数后的状态。
数字电路答案大全(DOC)
数字电路试卷答案大全试卷A一、选择题（从每小题的四个备选答案中，选出一个正确答案，并将其号码填在括号内，每小题2分，共20分）1.将十进制数（18）10转换成八进制数是 [ ]① 20 ② 22 ③ 21 ④ 23 2. 三变量函数()BC A C B A F+=,,的最小项表示中不含下列哪项 [ ]① m2 ② m5 ③ m3 ④ m7 3.一片64k ×8存储容量的只读存储器（ROM ），有 [ ]①64条地址线和8条数据线 ②64条地址线和16条数据线 ③16条地址线和8条数据线 ④16条地址线和16条数据线4.下列关于TTL 与非门的输出电阻描述中，正确的是 [ ] ①门开态时输出电阻比关态时大 ②两种状态都是无穷大输出电阻 ③门关态时输出电阻比开态时大 ④两种状态都没有输出电阻5.以下各种ADC 中，转换速度最慢的是 [ ]① 并联比较型 ② 逐次逼进型 ③ 双积分型 ④ 以上各型速度相同6. 关于PAL 器件与或阵列说法正确的是 [ ]① 只有与阵列可编程 ② 都是可编程的③ 只有或阵列可编程 ④ 都是不可编程的7. 当三态门输出高阻状态时，输出电阻为 [ ]① 无穷大 ② 约100欧姆 ③ 无穷小 ④ 约10欧姆8.通常DAC 中的输出端运算放大器作用是 [ ]① 倒相 ② 放大③ 积分 ④ 求和 9. 16个触发器构成计数器，该计数器可能的最大计数模值是 [ ]① 16 ② 32 ③ 162 ④ 216 10.一个64选1的数据选择器有（ ）个选择控制信号输入端。
[ ]① 6 ② 16 ③ 32 ④ 64 二、填空题（把正确的内容填在题后的括号内。
每空1分，共15分。
）1．已知一个四变量的逻辑函数的标准最小项表示为()()13,11,9,8,6,4,3,2,0,,,m d c b a F ∑=，那么用最小项标准表示=*F ，以及=F ，使用最大项标准表示F。
F，以及==2．具有典型实用意义的可编程逻辑器件包括，，，。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
CD
AB
00
00 0
01 11 10
00
1
ACD
01 0 1 1 1
BC
11 1 1 1 1
F = AB⋅ C + AB（⋅ C ⊕ D）+ AB ⋅ 0 + AB⋅D = ABC + AB（CD + CD）+ ABD = ABC + ABCD + ABCD + ABD = ABC + (AC＋A)BD + ABCD = ABC + (C＋A)BD + ABCD = ABC + CBD + ABD + ABCD
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
F A A+B A+B 1 AB B AB
A+B AB A⊕B B
AB 0
AB
AB
A
3-12 试分析图 3-7 电路的逻辑功能。
BIN/OCT
A1
0
B2
1
C4
2
3
4
1
&
5
EN 6
7
& F1
MUX
B A
0 1
G
0 3
C D
=1 0
0
Y
1
2
F
&
D
3
F2
(a)
(b)
解：（a）逻辑表达式
3-2 某集成电路具有如下电气特性：VOL ＝0.4V，VOH ＝2.4V，VIL ＝0.8V，VIH ＝1.8V， IOL=10mA，IOH=800μA，试问该电路的扇出系数为多少?并分别计算VNH及VNL。
（注：题目中漏了条件：IIL=1.2mA，IIH=100μA）
解： 扇出系数=Min（10mA/1.2mA，800µA/100µA）=8 VNH= VOH- VIH=2.4V-1.8V=0.6V VNL= VIL- VOL=0.8V-0.4V=0.4V
解：① 适用于与门和与非门。 ② 适用于或门和或非门。 ③ 适用于与门、与非门、或门、或非门。
3-19 用 3 线-8 线译码器 74138 和与非门实现下列多输出函数：
⎧ ⎪ ⎨
F1(A, B, C) = AB + BC + AC F2 (A, B, C) = Σm(2,3,4,5,7)
⎪⎩ F3(A, B, C) = ΠM(0,3,5,7)
图 3-7 题 3.12 逻辑图
F1(C,B,A) = Y1 ⋅ Y2 ⋅ Y4 ⋅ Y7 =m1 ⋅ m2 ⋅ m4 ⋅ m7 =m1+m2 +m4 +m7
F2 (C,B,A) = Y3 ⋅ Y5 ⋅ Y6 ⋅ Y7 =m3 ⋅ m5 ⋅ m6 ⋅ m7 =m3 +m5 +m6 +m7
真值表：
逻辑功能：一位全加器。 （b）
01 1 1 0
11 0 1 1
F5
BC A 00 01 11 10
01 1 1 0
11
01
1 F6
①、②、③、④有逻辑险象，⑤、⑥无逻辑险象。
3-34 用无逻辑险象的两级与非门电路实现下列函数： ② F(A,B,C,D)＝Σm (0～3,5,8,10,12～14)；
解： F = AB + BD + AD + BCD + ACD + ABC
Z = (FE) ⋅ (DX) + (FE) ⋅ (DX) + (FE) ⋅ (DX) + (FE) ⋅ (DX) = (FE) ⋅ (D + X) + (FE) ⋅ (D + X) + (FE) ⋅ (D + X) + (FE) ⋅ (D + X) = FED + FEX + FED + FEX + FED + FEX + FED + FEX
BIN/OCT
B1
1
0
B2
2
1
A
B3
4
2
B
3
C
B7
&
4
D
5
E
B5
B6 1
B4
EN 6
F
7
G
3-9 图 3-4 是一个多功能逻辑运算电路，图中S3、S2、S1、S0为控制输入端。试列功能表说明 该电路在S3、S2、S1、S0的各种取值组合下F与A、B的逻辑关系。
S2 S3
&1
A
B
1
=1 F
&1
S1 S0
第 3 章 组合逻辑电路
3-1 参阅图 3-1-2，列出AHC、TTL、AHCT、3.3V ALVT、2.5V ALVT的VOH、VOL、VIH、VIL， 计算它们的VNH及VNL。
解： AHC： VOH=4.44V，VOL=0.5V，VIH=3.5V，VIL=1.5V VNH= VOH- VIH=0.94V，VNL= VIL- VOL=1V TTL、AHCT、3.3V ALVT： VOH=2.4V，VOL=0.4V，VIH=2.0V，VIL=0.8V VNH= VOH- VIH=0.4V，VNL= VIL- VOL=0.4V 2.5V ALVT： VOH=2.3V，VOL=0.2V，VIH=1.7V，VIL=0.7V VNH= VOH- VIH=0.6V，VNL= VIL- VOL=0.5V
BCD ABC
ACD AB AD
BD
A& B
B& D A& D B C& D
A C& D A B& C
&
F
3-36 已知函数 F(A,B,C,D)=Σm（2，6～9，12～15），试判断当输入变量按自然二进制码的顺 序变化时，是否存在功能险象。若存在，请用选通脉冲法消除之，并画出用与非门实现它的逻辑 电路图。
10 1 1 0 0
AC
F
逻辑表达式 逻辑图
F(A, B, C, D) = AC + BC + ACD = AC ⋅ BC ⋅ ACD
A
&
1
B
&
1
C
&
D1
&F
选通脉冲
解：列出真值表
图 3-10 题 3.21 的波形图
逻辑图
MUX
0
EN
C
0
B
G
0 7
A
2
1
0
1
1
Y
F
0
2
0
3
W
1
4
0
5
1
6
0
7
3-22 用 4 选 1 MUX 实现下列函数：
③ F(A,B,C,D)＝Σm (0,l,3,5,6,8,9,11～13)；
解：③
AB CD 00
00 1
01 11 10
110
3-13 写出图 3-8 所示电路的逻辑方程。
MUX
MUX
A B
0 1
G
0 3
E X/Y F
0 1
G
0 3
0
0
Y X1 0
0
YZ
C
1
D 21
1
C
2
2
2
1
3
3
3
解：
图 3-8 题 3.13 逻辑图
X = BA ⋅ 0 + BA ⋅ C + BA ⋅ C + BA ⋅1
= AC + AB + BC
= AC + BC
3-5 试构成一个字符识别电路，它可以识别 A、B、C、D、E、F、G 7 个字符的 ASCII 码，并 指出为何字符。
解：查教材P19 表 1.5 知，A～G的ASCII码B7B6B5B4B3B2B1为 1000 001～1000 111，显然高 4 位相同，可将此用于译码器的使能控制，低 3 位连接到译码器的数据端进行译码输出，如下图所 示。
0 D1 D2 D3
1
D0 1
MUX
EN
0 2
G
0 7
0
Y
1
2
W
3
4
5
6
7
0
1 F3
MUX
EN
0 2
G
0 7
0
Y
1
2
W
3
4
5
6
7
F2
=1 F1 F0
解：
图 3-9 题 3.14 逻辑图
F0 = D0 F1 = D1 ⊕ D0
D0
D0
D0
F2 = D2 ⊕ (D1 + D0 ) F3 = D3 ⊕ (D2 + D1 + D0 )
DX FE 00
00 0
01 11 10
111
01 1 0 1 111 1 1 0 1源自10 1 1 1 0Z
Z = DF + DF + XE + XE = DF + DF + ACE + BCE + ACE + BCE
3-14 试分析图P3-9 所示逻辑电路，说明输出F3F2F1F0和输入D3D2D1D0的逻辑关系。