大学物理专业《电磁学》恒定磁场例题分析
大学物理专业《电磁学》恒定磁场例题分析

B 2 r 0
B 0
H I 2 r
R1 r R 2
H 2 r I
B 0rH
0rI
2 r
r R2
B 2 r 0 ( I I )
B 0
例11 一无限长的圆柱体,半径为R ,沿轴线方向的电流 I 在横截面上均匀分布,整个柱体浸没在无限大的各向同性 的均匀线性磁介质中,介质的相对磁导率为 r ,如图所 示,求导体内和介质中的磁感强度。
4 r
(cos 1 cos 2 )
(1 2 2 )
B1
0I
4 R 1
方向向外
B3
2
B2
3 0 I 16 R 1
0I
8R2
3 2
方向向里
方向向里
R1 R2
B B1 B 2 B 3
0I 2
( 8 R1
) 向外为正
例10 一无限长同轴电缆,内外分别是半径为 R 1和R 2 ( R 2 R 1 ) 的导体圆筒(其厚度均忽略不计),内外筒上的电流等值 反向,内外筒面之间充满相对磁导率为 r 的均匀、不导 电磁介质,其它均为真空。求各空间磁感强度的分布。
3
3
(D)
20M 3
另外如磁化电流、总的磁矩!!
例7 解答: 磁化电流面密度
M sin
P
把整个球面分成许多球带,通过每个球带的 的电流为 d I Rd MR sin d 设点坐标为 x 积分得
B
,因此半径为 r 的球带在 P 点产生的磁场
dB
期 末 复 习
恒定磁场例题分析
例题分析
恒定磁场部分例题及思考题

ω
3.长直圆柱形铜导线半径为 R1 , 外面一层相 对磁导率为 µr的圆桶形磁介质外半径R2 , 设导线内有均匀分布电流I 通过,铜的相对 磁导率 = 1 ,求导线和磁介质内外的磁场 强度和磁感应强度的分布
r oR
R2
1
µ 0 = 4π ×10 N ⋅ A
−7
−2
例:R,I的半圆形闭合线圈,绕直径为轴旋转, 均匀磁场,求线圈受的磁力矩。 a. Ⅰ法 均匀场 M = m × B
M = I(
πR 2
2
)B
y
方向:沿oy轴正方向
b. Ⅱ法 一般方法 (对非均匀场也适用)
en
x
Idl → dF → dM → M = ∫ dM
µ 0 I1 B1 = 2πr
d F2 µ 0 I1 I 2 d F1 = = d l2 2πr d l1
I1 d l1
B2
B1
d F1 d F2
I 2 d l2
国际单位制中电流单位安培的定义
I1
I2
r
在真空中两平行长直导线相距 1 m ,通有大小 相等、方向相同的电流,当两导线每单位长度上的 吸引力为 2 × 10 −7 N ⋅ m −1 时,规定这时的电流为 1 A 可得
I 2πr
r = 0.4 mm
I m = 2πrH c = 0.4A
思考题: 1. 宽度为b的长金属薄板,电流为I,求 (1)在薄板平面上,距板的一边为r的P点 的磁感强度; (2)板的中心线正上方Q点的磁感强度
I p
b
r
2. 有一长为 b,电荷线密度为 λ 的带电线 段 AB ,绕垂直轴 OO′ 在水平面内匀角速 转动,设 A 点距轴为a ,角速度 ω , 求带电 线段在O点产生的磁感强度和磁矩
大学物理马文蔚版-第七章恒定磁场习题课选讲例题

解: F F F bc bo oc
Fbc Foc aIB
第十一章 恒定磁场
Fbo 0
c a I o a b
B
恒定磁场习题课选讲例题
物理学教程 (第二版)
例 有一根流有电流 I 的导线,被折成长度分别 为 a 、b ,夹角为 120 的两段,并置于均匀磁场 B 中, 若导线的长度为 b 的一段与 B 平行,则 a 、 b 两段载 流导线所受的合磁力的大小为多少?
3. 运动电荷的磁场
第十一章 恒定磁场
恒定磁场习题课选讲例题 三 反映磁场性质的两条基本定理
物理学教程 (第二版)
磁场的高斯定理 Φm S B dS 0
安培环路定理
无源场
有旋场
l B dl 0 I i
i
磁场的高斯定理和安培环路定理反映了磁场是无源 有旋(非保守)场.
L
B0 B0 B0
B 常量
I
I
L
第十一章 恒定磁场
恒定磁场习题课选讲例题
物理学教程 (第二版)
例 取一闭合积分回路 L ,使三根载流导线穿过 它所围成的面,现改变三根导线之间的相互间隔,但 不越出积分回路,则: ()
(1) 回路 L 内的 I (2) 回路 L 内的 I (3) 回路 L 内的 I (4) 回路 L 内的 I
物理学教程 (第二版)
例 求无限大均匀通电平面的磁场,已知电流密度如图. 解:1)对称性分析磁场分布
j
L
I
dI dI
2)取正方形回路 L 如图, 边长为 l .
B
B dl 0 jl
L
I
B
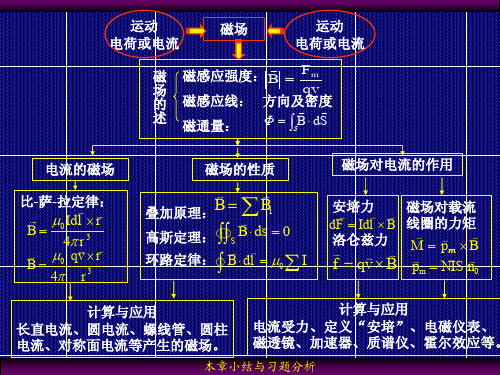
恒定磁场 小结与习题分析
dB
P
x
0 I 0 I 2 Bx 2 sin d 2 R R 0
0 I 2 0 I By 2 cos d 2 R 0 R
本章小结与习题分析
y dl
dB
0 I 0 I 2 Bx 2 sin d 2 R R 0
B
通电细螺绕环外:
本章小结与习题分析
B0
(5) 限长通电圆柱导体内、外
无限长通电圆柱面内、外
I R
0 Ir r R: B 2 R 2
I
r R: B 0
B
r
r
0 I r R: B 2 r
0 I r R: B 2 r
o
B
B2
L2
I1
P d
r2
o
I2
x
0 j 0 r2 j 0 j k d k ( r1 r2 ) k r2 k r1 2 2 2 2 0 Id 空腔内为垂直于 d 的均匀磁场:B 2 ( R 2 r 2 )
本章小结与习题分析
μ 0I C B dl 2 ( cos θ1 cos θ2 ) μ0 I
3.一无限长任意导线中通以电流I,有人运 用安培环路定律计算空间P点的磁感应强度. L 由: B dl I
I I 0 得到: B 2 a 与无限长载流直导线的磁场一样。这样处理对吗?
分析:这样处理显然是错误的。使用安培环路定律计算磁感应 强度时,是有一定条件的, 即B可以从积分式中作为常量提出 来,因为 LB dl LB cos dl ,所以在积分路径L或各个分段路 径上,应保证B为常量,而且 为已知。本题中给出的电流形 状是任意的,积分路径L上各处的B及θ都无法确定,故不能用 安培环路定律求得。一般只是具有一定对称性的或分段均匀的 磁场分布,才能应用安培环路定律求其磁感应强度。
大学物理第06章 恒定磁场习题解答之欧阳史创编

第6章 恒定磁场习题解答1. 空间某点的磁感应强度B的方向,一般可以用下列几种办法来判断,其中哪个是错误的? ( C )(A )小磁针北(N )极在该点的指向;(B )运动正电荷在该点所受最大的力与其速度的矢积的方向;(C )电流元在该点不受力的方向;(D )载流线圈稳定平衡时,磁矩在该点的指向。
2. 下列关于磁感应线的描述,哪个是正确的? ( D )(A )条形磁铁的磁感应线是从N 极到S 极的; (B )条形磁铁的磁感应线是从S 极到N 极的; (C )磁感应线是从N 极出发终止于S 极的曲线; (D )磁感应线是无头无尾的闭合曲线。
3. 磁场的高斯定理⎰⎰=⋅0S d B 说明了下面的哪些叙述是正确的? ( A )a 穿入闭合曲面的磁感应线条数必然等于穿出的磁感应线条数;b 穿入闭合曲面的磁感应线条数不等于穿出的磁感应线条数;c 一根磁感应线可以终止在闭合曲面内;d 一根磁感应线可以完全处于闭合曲面内。
(A )ad ; (B )ac ; (C )cd ; (D )ab 。
4. 如图所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量Φ和面上各点的磁感应强度B 将如何变化? ( D )(A )Φ增大,B也增大; (B )Φ不变,B 也不变;I(C )Φ增大,B 不变; (D )Φ不变,B 增大。
5. 两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置,一个处于竖直位置,两个线圈的圆心重合,则在圆心o 处的磁感应强度大小为多少? ( C )(A )0; (B )R I 2/0μ; (C )R I 2/20μ; (D )R I /0μ。
6、有一无限长直流导线在空间产生磁场,在此磁场中作一个以截流导线为轴线的同轴的圆柱形闭合高斯面,则通过此闭合面的磁感应通量( A )A 、等于零B 、不一定等于零C 、为μ0ID 、为i ni q 11=∑ε7、一带电粒子垂直射入磁场B后,作周期为T 的匀速率圆周运动,若要使运动周期变为T/2,磁感应强度应变为(B )A 、B/2 B 、2BC 、BD 、–B8 竖直向下的匀强磁场中,用细线悬挂一条水平导线。
第七章 恒定磁场-习题解答

解 (1)r<a B dl 0 应用安培环路定理 L i 在r<a柱体内绕轴作环形回路L,其中
于是有
I
i
r2 Ii a 2 I
πr 2 B1 2πr 0 I 2 πa
B1
0 Ir
2πa 2
第七章、稳恒磁场
0 I (2)a r b : B 2r 0 I , B 2r
霍尔电势差有多大?(铜的电子浓度n=8.41028 l/m3)。 解 (1)根据洛伦兹力
F qv B
可判断铜片内载流子(电子)在磁场中 的受力方向向右,因此右侧积聚了电子 带负电,左侧因缺少电子而带等量的正 电。所以左侧电势高
(2)霍耳电势差
1 IB 5 UH 2.2 10 V ne a
方向沿oo’竖直向下。
第七章、稳恒磁场
习题7-19 如图所示,一闭合回路由半径 为a和b的两个同心半圆连成,载有电流I。 试求(1)圆心P点处磁感应强度B的大小 和方向;(2)回路的磁矩。 解: (1)由磁场叠加原理
方向垂直纸面向里。 (2)由磁矩定义
方向垂直纸面向里。
第七章、稳恒磁场
7-20 质谱仪的构造原理如图所示。离子源S提供质量为M、 电荷为q的离子。离子初速很小,可以看作是静止的,然后经 过电压U的加速,进入磁感应强度为B的均匀磁场,沿着半圆 周运动,最后到达记录底片P上。测得离子在P上的位置到入 qB 2 x 2 。 口处A的距离为x。试证明该离子的质量为:M
S
B dS 0
三、安培环路定理——求解磁感应强度B
B dl 0 I i
L i
四、磁场对载流导线的作用——安培力
dF Idl B
大学物理10-1恒定磁场解读
(1
3) 2
圆弧bc段:
B2
0I
2R
1 3
0I
6R
向里
B B1 B2 B3
I
0 (1
R
3 I
) 0 2 6R
向里
例2 在一个半径为R的无限长半圆筒形金属片中,沿轴 向方向均匀通有电流 I,求半圆筒轴线上的磁感应强度。
解: dI I dl R
dl Rd
R
dB
0dI 2 R
0 I 2 2R2
整个物体的磁效应就是所有分子电流对外界磁效 应的总和;磁性物质的本质在于其分子电流的有序排 列。
分子电流
S
N
二、磁感应强度 B
用磁场对电流的作用力来定义磁感强度。
I
在闭合回路中取电流元 Idl
(1) 不同场点, 电流元受力不同;同一场
Idl
点, 电流元在磁场中的方向不同, 受力也不同;
总存在一个方向使 dF 0
设电流元截面积为S ,电荷定 向运动的速度为v,电流元每单 位体积的运动电荷数为n,则单 位时间内通过电流元截面的电荷
量为 I nqvS
Sv
I
dl
dB
0 4
I dl er r2
dN
dB
0 (nqvS ) dl er 0
4 B
dB
r2
0
4
q v er
q nSdl v er r2
dN 4 r 2
dl
0 Id 2 2R
I
由对称性有:By dBy 0
B
Bx
dBx
d Bco s (
2
)
B 0I
2 2R
sin d
0 I
大学物理第06章恒定磁场习题解答
第6章 恒定磁场习题解答1. 空间某点的磁感应强度B的方向,一般可以用下列几种办法来判断,其中哪个是错误的 ( C )(A )小磁针北(N )极在该点的指向;(B )运动正电荷在该点所受最大的力与其速度的矢积的方向; (C )电流元在该点不受力的方向;(D )载流线圈稳定平衡时,磁矩在该点的指向。
2. 下列关于磁感应线的描述,哪个是正确的 ( D )(A )条形磁铁的磁感应线是从N 极到S 极的; (B )条形磁铁的磁感应线是从S 极到N 极的; (C )磁感应线是从N 极出发终止于S 极的曲线; (D )磁感应线是无头无尾的闭合曲线。
3. 磁场的高斯定理 0S d B说明了下面的哪些叙述是正确的 ( A )a 穿入闭合曲面的磁感应线条数必然等于穿出的磁感应线条数;b 穿入闭合曲面的磁感应线条数不等于穿出的磁感应线条数;c 一根磁感应线可以终止在闭合曲面内;d 一根磁感应线可以完全处于闭合曲面内。
(A )ad ; (B )ac ; (C )cd ; (D )ab 。
4. 如图所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量 和面上各点的磁感应强度B 将如何变化 ( D )(A ) 增大,B 也增大;(B ) 不变,B 也不变; (C ) 增大,B 不变; (D ) 不变,B 增大。
5. 两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置,一个处于竖直位置,两个线圈的圆心重合,则在圆心o 处的磁感应强度大小为多少 ( C )(A )0; (B )R I 2/0 ;(C )R I 2/20 ; (D )R I /0 。
6、有一无限长直流导线在空间产生磁场,在此磁场中作一个以截流导线为轴线的同轴的圆柱形闭合高斯面,则通过此闭合面的磁感应通量( A )A 、等于零B 、不一定等于零C 、为μ0ID 、为i ni q 117、一带电粒子垂直射入磁场B后,作周期为T 的匀速率圆周运动,若要使运动周期变为T/2,磁感应强度应变为(B )A 、B /2 B 、2BC 、BD 、–BI8 竖直向下的匀强磁场中,用细线悬挂一条水平导线。
大学物理第06章 恒定磁场习题解答解读
第6章 恒定磁场习题解答1. 空间某点的磁感应强度B的方向,一般可以用下列几种办法来判断,其中哪个是错误的? ( C )(A )小磁针北(N )极在该点的指向;(B )运动正电荷在该点所受最大的力与其速度的矢积的方向; (C )电流元在该点不受力的方向;(D )载流线圈稳定平衡时,磁矩在该点的指向。
2. 下列关于磁感应线的描述,哪个是正确的? ( D )(A )条形磁铁的磁感应线是从N 极到S 极的; (B )条形磁铁的磁感应线是从S 极到N 极的; (C )磁感应线是从N 极出发终止于S 极的曲线; (D )磁感应线是无头无尾的闭合曲线。
3. 磁场的高斯定理⎰⎰=⋅0S d B说明了下面的哪些叙述是正确的? ( A )a 穿入闭合曲面的磁感应线条数必然等于穿出的磁感应线条数;b 穿入闭合曲面的磁感应线条数不等于穿出的磁感应线条数;c 一根磁感应线可以终止在闭合曲面内;d 一根磁感应线可以完全处于闭合曲面内。
(A )ad ; (B )ac ; (C )cd ; (D )ab 。
4. 如图所示,在无限长载流直导线附近作一球形闭合曲面S ,当曲面S 向长直导线靠近时,穿过曲面S 的磁通量Φ和面上各点的磁感应强度B 将如何变化? ( D )(A )Φ增大,B 也增大;(B )Φ不变,B 也不变; (C )Φ增大,B 不变; (D )Φ不变,B 增大。
5. 两个载有相等电流I 的半径为R 的圆线圈一个处于水平位置,一个处于竖直位置,两个线圈的圆心重合,则在圆心o 处的磁感应强度大小为多少? ( C )(A )0; (B )R I 2/0μ;(C )R I 2/20μ; (D )R I /0μ。
6、有一无限长直流导线在空间产生磁场,在此磁场中作一个以截流导线为轴线的同轴的圆柱形闭合高斯面,则通过此闭合面的磁感应通量( A )A 、等于零B 、不一定等于零C 、为μ0ID 、为i ni q 11=∑ε7、一带电粒子垂直射入磁场B后,作周期为T 的匀速率圆周运动,若要使运动周期变为T/2,磁感应强度应变为(B )A 、B /2 B 、2BC 、BD 、–BIS IIo8 竖直向下的匀强磁场中,用细线悬挂一条水平导线。
恒定磁场题解
恒定磁场题解第四章恒定磁场(注意:以下各题中凡是未标明磁媒质的空间,按真空考虑)4-1 如题4-1图所示,两条通以电流的半无穷长直导线垂直交于O 点。
在两导线所在平面,以O 点为圆心作半径为的圆。
求圆周上A 、B 、C 、D 、E 、F 各点的磁感应强度。
解参考教材71页的例4-1,可知,图4-2所示通有电流I 的直导线在P 点产生的磁感应强度为()αθθπμe B 120cos cos 4--=rI因此,可得(设参考正方向为指出纸面)R IR R I B A πμπμ422135cos 180cos 220cos 135cos 400=----= ()RIR I B B πμπμ410cos 90cos 400=--=用类似的方法可得 RI B C πμ40=,I R B C 0212μπ-=,RI B D πμ40=,R I B E πμ20=,I R B F 0212μπ+-= 4-2平面上有一正边形导线回路。
回路的中心在原点,边形顶点到原点的距离为。
导线中电流为。
1)求此载流回路在原点产生的磁感应强度;2)证明当趋近于无穷大时,所得磁感应强度与半径为的圆形载流导线回路产生的磁感应强度相同; 3)计算等于3时原点的磁感应强度。
解如图4-3中所示为正边形导线回路的一个边长,则所对应的圆心角为nπ2,各边在圆心产生的磁感应强度为()()()()()αααααααππμππμθπμθπμθπμθθπμθθπμe e e e e e e B ??=??? ??====---=--=n R I n r I r I r I rIr I r I tan 2sin 2cos 2cos 2cos 24cos cos 4cos cos 40010101011012011)n 条边在圆心产生的磁感应强度为αππμe B ??=n R I n tan 20 2)当n ∞→时,圆心处的磁感应强度为ααμππμe e B R I n R I n n 2tan 2lim 00=??=∞→3)当等于3时圆心处的磁感应强度为ααπμππμe e B R I R I 2333tan 2300=??=4-3 设矢量磁位的参考点为无穷远处,计算半径为的圆形导线回路通以电流时,在其轴线上产生的矢量磁位。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
合力和磁力矩的大小分别为( )
(A) 2BIR, BIR2 sin
(B) 4BIR, BIR2 sin
(C) 0, BIR2
(D) 0, BIR2 sin
M pm B
例6 一根半径为 R 长直导线载有电流 I ,I 均匀分布在
(B) 1 2
(C) l1 l2
j E
(D) l2 l1
1E1 2 E2
例3 如图所示,一段长为L的直导线载有电流为 I ,那么
r 在离直导线距离为 处(其中 1和2为已知)P点的磁
感强度的大小为( )
(A) 0 I 2r
(B) 0 I 4r
(C)
0I 2r
(cos1
cos
2
)
(
D)
0I 4r
0 I1 2r
A
FCE E
它的横截面上,那么这导线内部单位长度的磁场能量为 ()
(A) 0 I 2 32
(B)
0I 2 16
(C) 0 见P317习题7.6.3
例7 如图所示,有一半径为 R的均匀磁介质球,沿直径方
向被均匀磁化,磁化强度 M 为恒量,那么该介质球体内
的磁感强度为( )
(A) 0 Ma
3x3
在球外 x R
xR xR
B
2 0 MR 3
3x3
0 4
2
pm x3
式中
pm
4 R3M
3
为介质球内分子磁矩的总和.
这等效表于明一一磁个矩均为匀磁化pm球的上圆的电磁流化的电磁流场在. 球外轴线上的磁场
总的磁化电流:
0
I MR sind 2MR
例8 螺绕环的平均半径为R,线圈总匝数为N,环内充满 均匀磁介质,当通以电流I后,磁介质的磁化强度为M, 则螺绕环内的磁感强度B的大小为( )
cos2 )
B1
0I 4R1
(1
2) 2
方向向外
B2
30 I
16R1
方向向里
B3
0I
8R2
方向向里
B
B1
B2
B3
0I
8R1
(2
2 3 R1 ) 2 R2
向外为正
例10 一无限长同轴电缆,内外分别是半径为 R1和R2(R2 R1) 的导体圆筒(其厚度均忽略不计),内外筒上的电流等值
反向,内外筒面之间充满相对磁导率为 r 的均匀、不导
电流垂直方向单位长度上的电流密度 ;(2)无限大截
流平面上单位面积所受磁场力的大小。
(1) L B dl 0 I
B0
1 2
0
B1
B0
0
2
B2
B0
0
2
B0
(2)
dF
B2 B1 2
Idl
B
B2 B1 0
Idl dx dz dS
B B0 , 900
f dF B22 B12
的均匀线性磁介质中,介质的相对磁导率为 r ,如图所
示,求导体内和介质中的磁感强度。
B dl 0 I 或者 H dl Ic
c
c
rR
B
2r
0
I
R 2
r 2
B
0I 2R 2
r
rR
H 2r I H I 2r
B
0r H
0r I 2r
例12 一电流均匀分布的无限大截流平面放入均匀磁场B0 中,已知无限大截流平面两侧的磁感应强度分别为B1与B2, 如图所示,求:(1)均匀磁场B0及无限大截流平面沿与
dS 20
见P218习题5.6.7
例13 如图所示,无限长直导线 AB通有电流 I1,与其共面
的有一三角形导线框 CDE ,通有电流 I 2,CD长为 a ,DE
b 长 ,AB与 C 间距为 d 。试求:导线框 CDE 所受的磁场
力的合力大小 和方向。
dF Idl B
B
ED边受力
FED
0 I1I 2b 2 (d a)
电磁介质,其它均为真空。求各空间磁感强度的分布。
r R1 B 2r 0 B 0
R1 r R2
H 2r I H I 2r
B
0r H
0r I 2r
r R2 B 2r 0 (I I ) B 0
例11 一无限长的圆柱体,半径为R ,沿轴线方向的电流I
在横截面上均匀分布,整个柱体浸没在无限大的各向同性
期末复习
恒定磁场例题分析
例题分析
例1 且
(R两b 个 R同a )心,的其导间体充薄满球电壳阻,率内为外半 径的分均别匀为介质Ra和,若Rb两,球而
壳之间的电压是 U ,则任意点的电流密度为( )
(A) Ra RbU
(Rb Ra )r 2
(B)
Ra RbU
(Rb Ra )r 2
U
(C) r 2 ln Ra
3z
(B) 0Ma2
3z 2
(C)
2 0 Ma
3z3
3
(D) 20M
3
另外如磁化电流、总的磁矩!!
例7 解答:
P
磁化电流面密度
M sin
把整个球面分成许多球带,通过每个球带的
的电流为 dI Rd MR sind
设点坐标为 x ,因此半径为 r 的球带在 P 点产生的磁场
积分得
dB
0 MR 3
Rb
U
(D) r 2 ln Rb
Ra
dR dr I U j I
4r 2
R
4r 2
例2 如图所示,截面积相同的二段均匀导体串联组成的电
路,其电导率分别为 1和 2,长度分别为 l1 和 l2 ,当
导体中通过电流强度为I时,则二段导体中电场强度之比
E1 E2 为 ( )
I 1
l1
2
l2
(A) 2 1
(A)
0
NI
2R
M
(B)
0
(
NI
2R
M)
(C)
0
NI
2R
rM
(D)
0
NI
2R
H dl I
(L)
( L内) 0
NI
H
H
B
2R
M
0
B 0(H M )
例9 一条无限长的直导线,弯成如图所示形状,已知电 流为I,半径为R1、R2,则圆心O点的磁感应强度B的大 小和方向如何.
B
0I 4r
(cos1
(cos1
cos 2
)
例4 如图所示,在真空中,有一半径为 R 载流导线,通 过的电流为 I 。通过圆心并垂直于圆形导线平面的轴线
上任意点P处的磁感强度大小为( )
(A)
0I
2R
(B)
0I
4R
(C)
0
2
R2I (z 2 R 2 )1 2
(D)
0
2
(z2
R2I R2 )3 2
例5 一通有电流 I ,半径为 R 的圆电流放在磁感强度
2
(x2
sin3 d R2 2xR cos )3
2
B 0M {(x2 R 2 )( x R x R ) xR( x R x R )}
3x3
在球内 x R
xR Rx
B
2 3
0M
例7 解答:
P
积分得
B 0M {(x2 R 2 )( x R x R ) xR( x R x R )}
