小学五年级奥数PPT课件
合集下载
小学五年级奥数教学ppt课件

abc=a×100+b×10+c×1
• 例题1: (1)9999×7777+3333×6666= (2)2010×2011-2009×2012=
• 例题2: 算式:201×891/111+201 ×73/37=
原式=201×(891/111+ 73/37) =201×(891/37/3+73/37) =201×(297/37+ 73/37) =201×370/37 =2010
和一定 差小积大
23×10101=232323
723×1001001=7237 23723
12×100101=120121 2
期中考试过后,李玲同学语文、数学的平均成绩为91分, 语文、英语的平均成绩为88分,数学、英语的平均成绩 为93分,李玲三门功课各得多少分?
1,语+数=91*2=182(分) 2,语+英=88*2=176(分) 3,数+英=93*2=186(分) 有1,2可知,数学成绩比英语成绩高182-176=6(分), 再根据3可以算出数学:(186+6)/ 2=96(分) 英语:96-6=90(分) 语文:182-96=86(分) (91*2+88*2+93*2)/2=272(分)语数英之和 272-91*2=90(分)..........英语 272-88*2=96(分)..........数学 272-93*2=86(分)...........语文
等差数列: 万位 5,6,7,8,9=7×5=35000 0 千位 5,6,7,8,9=7×5=35000 百位 5,6,7,8,9=7×5=3500 十位,个位都是35
和+:3位(5值30原5+理03050)0/+73=55050505+53500
• 位值原理:将一个数拆开,重新按位进行计 算。例如:
• 例题1: (1)9999×7777+3333×6666= (2)2010×2011-2009×2012=
• 例题2: 算式:201×891/111+201 ×73/37=
原式=201×(891/111+ 73/37) =201×(891/37/3+73/37) =201×(297/37+ 73/37) =201×370/37 =2010
和一定 差小积大
23×10101=232323
723×1001001=7237 23723
12×100101=120121 2
期中考试过后,李玲同学语文、数学的平均成绩为91分, 语文、英语的平均成绩为88分,数学、英语的平均成绩 为93分,李玲三门功课各得多少分?
1,语+数=91*2=182(分) 2,语+英=88*2=176(分) 3,数+英=93*2=186(分) 有1,2可知,数学成绩比英语成绩高182-176=6(分), 再根据3可以算出数学:(186+6)/ 2=96(分) 英语:96-6=90(分) 语文:182-96=86(分) (91*2+88*2+93*2)/2=272(分)语数英之和 272-91*2=90(分)..........英语 272-88*2=96(分)..........数学 272-93*2=86(分)...........语文
等差数列: 万位 5,6,7,8,9=7×5=35000 0 千位 5,6,7,8,9=7×5=35000 百位 5,6,7,8,9=7×5=3500 十位,个位都是35
和+:3位(5值30原5+理03050)0/+73=55050505+53500
• 位值原理:将一个数拆开,重新按位进行计 算。例如:
五年级上册数学课件-奥数 最大和最小 通用版(共8张PPT)
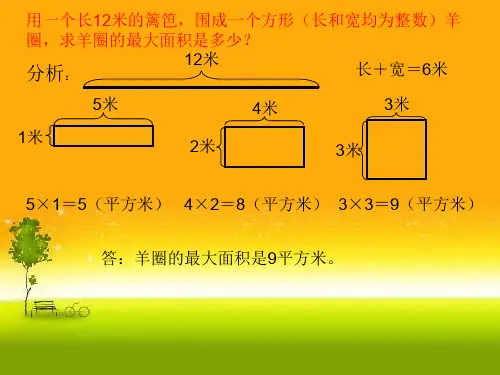
用一个长12米的篱笆,围成一个方形(长和宽均为整数)羊
圈,求羊圈的最大面积是多少?
分析:
12米
长+宽=6米
5米
4米
3米
1米
2米
3米
5×1=5(平方米) 4×2=8(平方米) 3×3=9(平方米)
答:羊圈的最大面积是9平方米。
最大和最小
例1 和是10的两个自然数,这两个数的乘积最大是多
少?最小是多少?
如果三个自然
分析: 10
数它们的乘积
最大是?
0 10
0×10=0ຫໍສະໝຸດ 191×9=928
2×8=16
37
3×7=21
46
4×6=24
55
5×5=25
答:这两个数的乘积最大是25,最小是0。
例2 用30米长的围栏围成一个长方形(长和宽均为整数
米)的花园,要使花园的面积最大,花园的长和宽应该
分别是多少米?花园的最大面积是多少平方米?
• 解:最大:81×72=5832
最小:17×28=476
• 最大与最小问题的解题策略:
• 1 如果两个数的和一定,那么这两个数的差越小,它们的 积越大。
• 2 如果两个数的乘积一定,那么这两个数的差越小,它 们的和也越小。
• 3 把一个自然数拆分成若干个自然数之和,如果要使这若 干个自然数的乘积最大,那么这些自然数应全是2或3,且 2的个数不能超过2个。
分析:如果把4拆成若干个数的和,那么积最大:2×2=4
如果把5拆成若干个数的和,那么积最大:3×2=6 如果把6拆成若干个数的和,那么积最大:3×3=9 如果把7拆成若干个数的和,那么积最大:3×2×2=12 如果把8拆成若干个数的和,那么积最大:3×3×2=18 如果把9拆成若干个数的和,那么积最大:3×3×3=27
圈,求羊圈的最大面积是多少?
分析:
12米
长+宽=6米
5米
4米
3米
1米
2米
3米
5×1=5(平方米) 4×2=8(平方米) 3×3=9(平方米)
答:羊圈的最大面积是9平方米。
最大和最小
例1 和是10的两个自然数,这两个数的乘积最大是多
少?最小是多少?
如果三个自然
分析: 10
数它们的乘积
最大是?
0 10
0×10=0ຫໍສະໝຸດ 191×9=928
2×8=16
37
3×7=21
46
4×6=24
55
5×5=25
答:这两个数的乘积最大是25,最小是0。
例2 用30米长的围栏围成一个长方形(长和宽均为整数
米)的花园,要使花园的面积最大,花园的长和宽应该
分别是多少米?花园的最大面积是多少平方米?
• 解:最大:81×72=5832
最小:17×28=476
• 最大与最小问题的解题策略:
• 1 如果两个数的和一定,那么这两个数的差越小,它们的 积越大。
• 2 如果两个数的乘积一定,那么这两个数的差越小,它 们的和也越小。
• 3 把一个自然数拆分成若干个自然数之和,如果要使这若 干个自然数的乘积最大,那么这些自然数应全是2或3,且 2的个数不能超过2个。
分析:如果把4拆成若干个数的和,那么积最大:2×2=4
如果把5拆成若干个数的和,那么积最大:3×2=6 如果把6拆成若干个数的和,那么积最大:3×3=9 如果把7拆成若干个数的和,那么积最大:3×2×2=12 如果把8拆成若干个数的和,那么积最大:3×3×2=18 如果把9拆成若干个数的和,那么积最大:3×3×3=27
五年级小学奥数数学课件PPT(共488页)

【思路导航】
(1)1箱苹果+1箱梨+1箱橘子=42×3=136(个); (2)1箱桃+1箱梨+1箱橘子=36×3=108(个) (3)1箱苹果+1箱桃=37×2=72(个) 由(1)(2)两个等式可知: 1箱苹果比1箱桃多126-108=18(个),再根据等式(3)就可以算出:1箱桃有(74-18)÷2=28(个),1箱苹果有28 +18=46(个)。 1箱苹果和1箱桃共有多少个:37×2=74(个) 1箱苹果比1箱桃多多少个:42×3-36=18(个) 1箱苹果有多少个:28+18=46(个)
2020/7/26
把几个不相等的数,在总数不变的条件下,通过移多补少, 使它们完全相等,求得的相等的数就是平均数。 如何灵活运用平均数的数量关系解答一些稍复杂的问题呢? 下面的数量关系必须牢记:
平均数=总数量÷总份数 总数量=平均数×总份数 总份数=总数量÷平均数
2020/7/26
【例题1】 有4箱水果,已知苹果、梨、橘子平均每箱42个, 梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。一箱 苹果多少个?
【思路导航】 98分比89分多9分。多算9分就能使全班平均每人的成绩上升91.7-
91.5=0.2(分)。9里面包含有几个0.2,五一班就有几名同学
2020/7/26
【练习4】
1,五(1)班有40人,期中数学考试,有2名同学去参加体育比赛而缺考, 全班平均分为92分。缺考的两位同学补考均为100分,这次五(1)班同 学期中考试的平均分是多少分?
平均数=总数量÷总份数 总数量=平均数×总份数 总份数=总数量÷平均数
2020/7/26
【例题1】 小明前几次数学测验的平均成绩是84分,这次要考100分, 才能把平均成绩提高到86分。问这是他第几次测验?
(1)1箱苹果+1箱梨+1箱橘子=42×3=136(个); (2)1箱桃+1箱梨+1箱橘子=36×3=108(个) (3)1箱苹果+1箱桃=37×2=72(个) 由(1)(2)两个等式可知: 1箱苹果比1箱桃多126-108=18(个),再根据等式(3)就可以算出:1箱桃有(74-18)÷2=28(个),1箱苹果有28 +18=46(个)。 1箱苹果和1箱桃共有多少个:37×2=74(个) 1箱苹果比1箱桃多多少个:42×3-36=18(个) 1箱苹果有多少个:28+18=46(个)
2020/7/26
把几个不相等的数,在总数不变的条件下,通过移多补少, 使它们完全相等,求得的相等的数就是平均数。 如何灵活运用平均数的数量关系解答一些稍复杂的问题呢? 下面的数量关系必须牢记:
平均数=总数量÷总份数 总数量=平均数×总份数 总份数=总数量÷平均数
2020/7/26
【例题1】 有4箱水果,已知苹果、梨、橘子平均每箱42个, 梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。一箱 苹果多少个?
【思路导航】 98分比89分多9分。多算9分就能使全班平均每人的成绩上升91.7-
91.5=0.2(分)。9里面包含有几个0.2,五一班就有几名同学
2020/7/26
【练习4】
1,五(1)班有40人,期中数学考试,有2名同学去参加体育比赛而缺考, 全班平均分为92分。缺考的两位同学补考均为100分,这次五(1)班同 学期中考试的平均分是多少分?
平均数=总数量÷总份数 总数量=平均数×总份数 总份数=总数量÷平均数
2020/7/26
【例题1】 小明前几次数学测验的平均成绩是84分,这次要考100分, 才能把平均成绩提高到86分。问这是他第几次测验?
五年级《盈亏问题》奥数课件

卡尔 用完所有信封 每封2张信纸 多20张信纸 米德 用完所有信封 每封3张信纸 少30张信纸
信封:(30+20)÷(3-2)=50(个) 信纸:50×2+20=120(张) 答:他们每人各买了120张信纸。
五年级三班向希望小学某班送铅笔若干支,如果有2人拿4支,
少2支 其余人各拿5支,还余12支;如果每人拿6支,就有2人拿不到,
那么五年级三班共送铅笔多少支?
如果每人都拿5支 如果每人都拿6支
多12-2=10(支) 少2×6=12(支)
人数:(10+12)÷(6-5)=22(人) 支数:22×6-12=120(支) 答:五年级三班共送铅笔120支。
博士将一筐香蕉分给小朋友,如果分给四年级的小朋友每 人4根,则余11根;如果分给五年级的小朋友每人6根,则缺3根, 并且四年级与五年级的人数不一样,四年级的人数比五年级多4 人。求这筐香蕉共有多少根?
1、五年级要进行跳绳比赛,于是学校体育组给各班分跳绳。 若每班分4根,则余7根;若每班分5根,则正好分完。那么 学校共有跳绳多少根?此年级共有多少个班?
每班分4根 每班分5根
余7根 刚好分完
班级:7÷(5-4)=7(个)
跳绳:7×4+7=35(根) 答:共有跳绳35根,此年级共有7个班。
2、博士去早市买肉,发现自己带的钱如果买10千克牛肉则还差 6元;如果买12千克猪肉则还剩4元。已知每千克牛肉比猪肉贵3 元,博士带了多少钱去买肉?
五(1)班 五(2)班
每人5个 每人8个
剩10个 缺3×8+2=26(个)
五(1)班人数:(26+10)÷(8-5)=12(人)
个数:12×5+10=70(个) 答:这一筐苹果有70个。
信封:(30+20)÷(3-2)=50(个) 信纸:50×2+20=120(张) 答:他们每人各买了120张信纸。
五年级三班向希望小学某班送铅笔若干支,如果有2人拿4支,
少2支 其余人各拿5支,还余12支;如果每人拿6支,就有2人拿不到,
那么五年级三班共送铅笔多少支?
如果每人都拿5支 如果每人都拿6支
多12-2=10(支) 少2×6=12(支)
人数:(10+12)÷(6-5)=22(人) 支数:22×6-12=120(支) 答:五年级三班共送铅笔120支。
博士将一筐香蕉分给小朋友,如果分给四年级的小朋友每 人4根,则余11根;如果分给五年级的小朋友每人6根,则缺3根, 并且四年级与五年级的人数不一样,四年级的人数比五年级多4 人。求这筐香蕉共有多少根?
1、五年级要进行跳绳比赛,于是学校体育组给各班分跳绳。 若每班分4根,则余7根;若每班分5根,则正好分完。那么 学校共有跳绳多少根?此年级共有多少个班?
每班分4根 每班分5根
余7根 刚好分完
班级:7÷(5-4)=7(个)
跳绳:7×4+7=35(根) 答:共有跳绳35根,此年级共有7个班。
2、博士去早市买肉,发现自己带的钱如果买10千克牛肉则还差 6元;如果买12千克猪肉则还剩4元。已知每千克牛肉比猪肉贵3 元,博士带了多少钱去买肉?
五(1)班 五(2)班
每人5个 每人8个
剩10个 缺3×8+2=26(个)
五(1)班人数:(26+10)÷(8-5)=12(人)
个数:12×5+10=70(个) 答:这一筐苹果有70个。
五年级奥数 ppt课件

换成
少2只脚
• 提问:那是把几只兔换成了鸡呢?
– 简单!10÷2=5(只)
• 解答:兔,(70-30×2)÷2=5(只)
– 鸡:30-5=25(只)
• 第二,还是假设法: 4×30-70=50, 50÷2=25,30-25=5。4×30是求的30 只兔子一共有120只脚,120-70是求的鸡 多出50只脚,每只鸡比兔少2只脚,所以用 50÷2=25,求出了鸡的只数,用总数减去 鸡的只数就得到了兔的只数。
• 我们问有没有更简单点的解法。大家思考了 一会儿,发现第三种解法:70÷2=35,35 -30=5。原来,70÷2=35是把每只鸡和 兔的一半脚的的。
•方案二:倒序相加 •比较1+2+3+……+100 •和100+99+98+……+1
• 计算2+4+6+8+……+296+298+ 300=?
五年级奥数
• 鸡兔同笼,上有30头,下有70足。鸡兔各多少?
• 提问:假设这30个头全部是鸡,会怎样? – 那应该只有30×2=60(只)脚
• 提问:那怎么就少了70-60=10(只)脚呢? – 因为咱们把兔子也看成了是鸡,
五年级奥数
什么是奥数?
• 有难度的数学 • 用好方法—解决的数学 • 用来选拔、用来竞赛的数学
如何学好奥数呢?
• 善于观察 • 善于分析 • 善于总结
实战演练1
• 计算:1+2+3+……+100
• 观察发现:这是求100个连续自然数的和 • 提出解决方案:
•方案一:配对相加 •1+99,2+98,3+97,……, 49+51,50,100
五年级奥数
五年级奥数
问题:数学是什么?
五年级奥数第5周数数图形ppt课件
例2 数一数下面图形中有多少个正方形?(每个小方格为 边长为1个长度单位的小正方形)
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
例2 数一数下面图形中有多少个正方形?(每个小方格为 边长为1个长度单位的小正方形)
A
B
D
C
长边AB上一共有1+2=3条线段
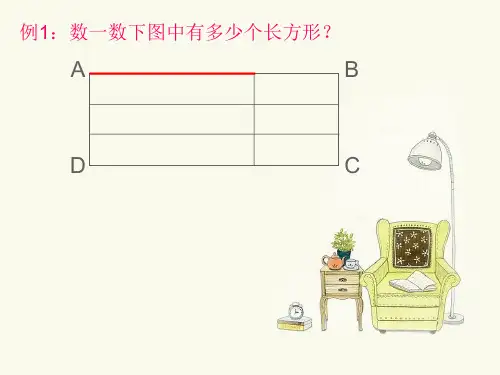
数一数下图中有多少个长方形?
A
B
D
C
长边AB上一共有1+2=3条线段
数一数下图中有多少个长方形?
A
B
D
C
长边AB上一共有1+2=3条线段
数一数下图中有多少个长方形?
A
B
D
C
长边AB上一共有1+2=3条线段
宽边AD上一共有1+2+3=6条 线段
因此,这个图中共有长方形 3×6=18个
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
数长方形的个数可以用公式:
长边上的线段数×宽边上的线段数=长方形的个 数
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
例2 数一数下面图形中有多少个正方形?(每个小方格为 边长为1个长度单位的小正方形)
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
例2 数一数下面图形中有多少个正方形?(每个小方格为 边长为1个长度单位的小正方形)
A
B
D
C
长边AB上一共有1+2=3条线段
数一数下图中有多少个长方形?
A
B
D
C
长边AB上一共有1+2=3条线段
数一数下图中有多少个长方形?
A
B
D
C
长边AB上一共有1+2=3条线段
数一数下图中有多少个长方形?
A
B
D
C
长边AB上一共有1+2=3条线段
宽边AD上一共有1+2+3=6条 线段
因此,这个图中共有长方形 3×6=18个
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
数长方形的个数可以用公式:
长边上的线段数×宽边上的线段数=长方形的个 数
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
例2 数一数下面图形中有多少个正方形?(每个小方格为 边长为1个长度单位的小正方形)
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
五年级上册奥数(课件)第11讲:梯形的面积
108×2÷8-12 = 216÷8-12 = 27-12 = 15(分米)
答:这个梯形的下底是15分米。
练习四
两个完全一样的梯形拼成一个平行四边形,这个平行四 边形的面积是80平方厘米,高是5厘米,梯形的上底是7厘米, 梯形的下底是多少厘米?
这两个梯形的面积相等,都是 80÷2=40(平方厘米)
梯形的面积=(上底+下底)×高÷2
(15+28)×14÷2 = 43×14÷2 = 301(平方米)
301×36= 10836(元)
答:这块菜地的总收入是10836元。
练习二
有一块梯形花地,上底是8米,下底是10米,高是 4.8米。已知每株花占地0.06平方米,这块地能种花多 少株?
梯形的面积=(上底+下底)×高÷2
梯形
梯形的面积=(上底+下底)×高÷2
下底
上底
上底+下底= 22-8 = 14(米)
高
14×8÷2 = 56(平方米)
答:养鸡场的面积等于56平方米。
例题四
一个梯形的上底是12分米,高是8分米,面积是108 平方分米。这个梯形的下底是多少分米?
梯形的面积=(上底+下底)×高÷2
下底 = 梯形的面积×2÷高-上底
上底 高
下底
梯形的面积 =(上底+下底)×高÷2
上底
高 下底
平行四边形的面积=底×高 =(上底+下底)×高
梯形的面积
例题一
一条新挖的水渠,横截面是梯形(如图),渠口宽 2.8米,渠底宽1.4米,渠深1.2米。它的横截面的面积是 多少平方米?
梯形的面积=(上底+下底)×高÷2
(1.4+2.8)×1.2÷2 = 4.2×1.2÷2 = 2.52(平方米)
(8+10)×4.8÷2 = 18×4.8÷2 = 43.2(平方米) 43.2÷0.06=720(株)
答:这个梯形的下底是15分米。
练习四
两个完全一样的梯形拼成一个平行四边形,这个平行四 边形的面积是80平方厘米,高是5厘米,梯形的上底是7厘米, 梯形的下底是多少厘米?
这两个梯形的面积相等,都是 80÷2=40(平方厘米)
梯形的面积=(上底+下底)×高÷2
(15+28)×14÷2 = 43×14÷2 = 301(平方米)
301×36= 10836(元)
答:这块菜地的总收入是10836元。
练习二
有一块梯形花地,上底是8米,下底是10米,高是 4.8米。已知每株花占地0.06平方米,这块地能种花多 少株?
梯形的面积=(上底+下底)×高÷2
梯形
梯形的面积=(上底+下底)×高÷2
下底
上底
上底+下底= 22-8 = 14(米)
高
14×8÷2 = 56(平方米)
答:养鸡场的面积等于56平方米。
例题四
一个梯形的上底是12分米,高是8分米,面积是108 平方分米。这个梯形的下底是多少分米?
梯形的面积=(上底+下底)×高÷2
下底 = 梯形的面积×2÷高-上底
上底 高
下底
梯形的面积 =(上底+下底)×高÷2
上底
高 下底
平行四边形的面积=底×高 =(上底+下底)×高
梯形的面积
例题一
一条新挖的水渠,横截面是梯形(如图),渠口宽 2.8米,渠底宽1.4米,渠深1.2米。它的横截面的面积是 多少平方米?
梯形的面积=(上底+下底)×高÷2
(1.4+2.8)×1.2÷2 = 4.2×1.2÷2 = 2.52(平方米)
(8+10)×4.8÷2 = 18×4.8÷2 = 43.2(平方米) 43.2÷0.06=720(株)
五年级奥数第3讲:行程问题(四)流水(2)-课件
192÷8=24(千米/小时)
逆水速度=静水速度-水流速度 静水速度=顺水速度-水流速度
24-2×4=16(千米/小时)
逆水速度=顺水速度-2×水流速度 192÷16=12(小时)
答:逆水行完全程要12小时。
练习二
甲、乙两码头相距560千米,一只船从甲码头顺水航行20小时 到达乙码头,已知船在静水中每小时航行24千米,问船返回甲码头 要几小时?
75÷5=15(千米/小时) 15×15=225(千米)
答:A、B两地相距225千米。
总结
顺水速度=静水速度+水流速度 逆水速度=静水速度-水流速度 静水速度(船速)=(顺水速度+逆水速度)÷2 水速=(顺水速度-逆水速度)÷2
天每
开个
放孩
;子
有的
的花
孩期
子不
是一
菊样
花,
,有
选的
择孩
在子
秋是
天牡
逆水速度=顺水速度-2×水流速度 逆水速度=2×静水速度-顺水速度
例题三
某船在静水中每小时行18千米,水流速度是每小时2千米。此船 从甲地逆水航行到乙地需要15小时。求甲、乙两地的路程是多少千 米?此船从乙地回到甲地需要多少小时?
逆水速度=静水速度-水流速度
18-2=16(千米/小时) 16×15=240(千米)
顺水速度=静水速度+水流速度
18+2=20(千米/小时) 240÷20=12(小时)
答:甲、乙两地的路程是240千米。 此船从乙地回到甲地需要12小时。
练习三
已知一条河的水流速度是每小时6千米,一艘船在静水中3小时 航行48千米。这艘船从甲地顺水航行到乙地需要10小时。求甲、乙 两地的路程是多少千米?此船从乙地回到甲地需要几小时?
五年级上册奥数(课件)第12讲:组合图形的面积
答:阴影部分的面积为140平方厘米。
米德思考
总结
(一)组合图形面积的计算方法: 1.分割法:把一个复杂的组合图形分割成我们学过的几 个简单的基本图形,通过求这几个简单的基本图形的面积来 得到组合图形的面积。 2.添补法:充分利用已知的数据,恰当地使用辅助线, 用添补的方法,把复杂的组合图形转化为简单的图形,从而 计算出组合图形的面积。
3.挖空法:就是把多边形看成是一个完整的规则图 形,计算它的面积以后,再减去空缺部分的面积。
天每
开个
放孩
;子
有的
的花
孩期
子不
是一
菊样
花,
,有
选的
择孩
在子
秋是
天牡
开丹
放花
;,
而选
有择
的在
孩春
➢ He who falls today may rise tomorrow.
子天
是开
梅放
花;
,有
选的
择孩
在子
例题三
求下面图形的面积(单位:m)
把它看成一个 三角形和梯形 的面积组合
三角形面积:11×8÷2=44(平方米) 梯形的面积:(11+22)×10÷2=165(平方米) 图形的面积:165+44=209(平方米)
答:这个图形的面积是209平方米。
练习三
求下面图形的面积。(单位:m)
8.5 4
13
答:图形的面积为525平方米。
练习一
求下面图形的面积。(单位:m)
22
52
20
31
48
上面为三角形, 下面为梯形。
三角形的面积:52×22÷2=572(平方米) 梯形的面积:(31+20)×48÷2=1224(平方米) 图形的面积:1224+572=1796(平方米)
小学五年级奥数-数的整除特征课件
反过来,如果b︱a , c︱a 那么bc︱a一定正确吗?
数的整除性质3
我们看下面的例子: 4能够整除36,6也能整除36,4与6的积能整除36吗? 4能够整除80,5也能整除80,4与5的积能整除80吗? 5能够整除80,8也能整除80,5与8的积能整除80吗? 这说明这两个数需要满足一定的条件!
数的整除性质1
性质1: 如果a、b都能被c整除,那么他们的和或差也能被c整除。 即:如果c︱a , c︱b 那么 c︱(a±b) 你能再举出一个例子吗?
数的整除性质2
我们再来看一组例子:
添加标题
01
3×7=21,21能整除84,3和7都能整除84吗?
添加标题
03
上面的3个例子有什么共同点?
添加标题
∣
01
02
应用举例(二)根据规律填空
例2、⑴ 已知45︱ 求所有满足条件的六位数。
5
9
519930
李老师为学校一共买了28支价格相同的钢笔,共付人民币9□.2□元,已知□处数字相同,请问:每支钢笔多少元?
分析:由28支钢笔的价格相同可知,总钱数9□.2□是28 的倍数,同上面的解题思路类似,可以用数的整除性质和数的整除特征结合起来解答。
分别能被2 3、5、11整除,这个七位数最小值是多少?
6、在1992后面补上三个数字,组成一个七位数,使它们
02
能被11整除, 方格内应填_____。
5、“25□79这个数的□内填上一个数字,使这个数
01
∣
∣
33333333468375能不能被125整除 回忆:能被125整除的数的特征: 末三位数字能被125整除。 解: 因为这个数的末三位数字375能被125整除,所以33333333468375能被125整除。
数的整除性质3
我们看下面的例子: 4能够整除36,6也能整除36,4与6的积能整除36吗? 4能够整除80,5也能整除80,4与5的积能整除80吗? 5能够整除80,8也能整除80,5与8的积能整除80吗? 这说明这两个数需要满足一定的条件!
数的整除性质1
性质1: 如果a、b都能被c整除,那么他们的和或差也能被c整除。 即:如果c︱a , c︱b 那么 c︱(a±b) 你能再举出一个例子吗?
数的整除性质2
我们再来看一组例子:
添加标题
01
3×7=21,21能整除84,3和7都能整除84吗?
添加标题
03
上面的3个例子有什么共同点?
添加标题
∣
01
02
应用举例(二)根据规律填空
例2、⑴ 已知45︱ 求所有满足条件的六位数。
5
9
519930
李老师为学校一共买了28支价格相同的钢笔,共付人民币9□.2□元,已知□处数字相同,请问:每支钢笔多少元?
分析:由28支钢笔的价格相同可知,总钱数9□.2□是28 的倍数,同上面的解题思路类似,可以用数的整除性质和数的整除特征结合起来解答。
分别能被2 3、5、11整除,这个七位数最小值是多少?
6、在1992后面补上三个数字,组成一个七位数,使它们
02
能被11整除, 方格内应填_____。
5、“25□79这个数的□内填上一个数字,使这个数
01
∣
∣
33333333468375能不能被125整除 回忆:能被125整除的数的特征: 末三位数字能被125整除。 解: 因为这个数的末三位数字375能被125整除,所以33333333468375能被125整除。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
14
将100个小朋友从左往右排成一排并依次编成1~100 号。然后从左往右“一、二”报数,报“一”的退下; 再从左往右“一、二”报数,报“一”的退下;……; 这样循环到剩下最后一个人为止。那么最后留下的这 个小朋友是多少号?
.
15
实战演练5
鸡兔同笼,上有29头,下有92足。鸡兔各多少?
提问:假设这29个头全部是鸡,会怎样? 那应该只有29×2=58(只)脚
(5÷13-7)×(17+9)。
当“÷”在第二或第四个○内时,运算结果不可能是
整数。当“÷”在第三个○内时,可得下面的填法:
(5+13×7)÷(17-9)=12。
.
10
在下面的算式中,不同的字母代表不同的数字,相同 的字母代表相
分析与解:这道题可以从个位开始,比较等式两边 的数,逐个确定各个
(100000+x)×3=10x+1,
.
4
实战演练1
计算:1+2+3+……+100
观察发现:这是求100个连续自然数的和 提出解决方案:
方案一:配对相加 1+99,2+98,3+97,……,49+51,50,100
方案二:倒序相加 比较1+2+3+……+100 和10+0+9+9++98+……+1+
=
= = =
101 101 101
.
18
定义新运算 (一)
我们学习过加、减、乘、除运算,这些运算, 即四则运算,也是数学中最基本的运算,它们的 意义、符号及运算律已被我们熟知。除此之外, 还会有什么别的运算吗?接下来我们就来研究 这个问题。这些新的运算及其符号,在中、小 学课本中没有统一的定义及运算符号,但学习 讨论这些新运算,对于开拓思路及今后的学习 都大有益处。
提问:那怎么就少了92-58=34(只)脚呢? 因为咱们把兔子也看成了是鸡,
.
16
1
换成
少2只脚
提问:那是把几只兔换成了鸡呢?
简单!34÷2=17(只)
解答:兔,(92-29×2)÷2=17(只)
鸡:29-17=12(只)
.
17
(古代算题)大小100和尚吃100个馒头,大和尚1人 吃4个,小和尚4人吃1个。大小和尚各几人?
.
21
.
22
.
23
练习
1.对于任意的两个数a和b,规定a*b=3×a-b÷3。求8*9的值。
2.已知a b表示a除以3的余数再乘以b,求13 4的值。
3.已知a b表示(a-b)÷(a+b),试计算:(5 3) (10 6)。
4.规定a◎b表示a与b的积与a除以b所得的商的和,求8◎2的值。
300000+3x=10x+1,
7x=299999,
x=42857。
ห้องสมุดไป่ตู้
这种代数方法干净利落,比用传统方法解简洁。
.
11
下列竖式中,相同字母代表同一数字、不同字母代表
不同数字。
ABC
-B C A
A B A=? B=? C=?
.
12
实战演练4
在个月内,有3个星期天的日期为双数。那么这个月的1号是星期 几?
5.假定m◇n表示m的3倍减去n的2倍,即 m◇n=3m-2n。
(2)已知x◇(4◇1)=7,求x的值。
7.对于任意的两个数P, Q,规定 P☆Q=(P×Q)÷4。例如:2☆8=(2×8)÷4。已知
x☆(8☆5)=10,求x的值。
8.定义: a△b=ab-3b,ab=4a-b/a。计算:(4△3)△(2b)。
等式的○内,使等式成立(每个运算符号只准使用一
次):(5○13○7)○(17○9)=12。
分析与解:因为运算结果是整数,在四则运算中
只有除法运算可能出现分数,所以应首先确定“÷”的
位置。
当“÷”在第一个○内时,因为除数是13,要想得
到整数,只有第二个括号内是13的倍数,此时只有下
面一种填法,不合题意。
101
.
5
计算2+4+6+8+……+296+298+ 300=?
.
6
实战演练2
今年妈妈的年龄是小明的7倍,但是4年后妈妈的年龄 就只是小明的4倍了。你知道今年小明多少岁吗?
今年
小明: 妈妈:
4年后
小明: 妈妈:
.
7
小华的故事书本数是小青的3倍,如果再各买10本,小 华的故事书本数就只是小青的2倍了。那么小华原有多 少本故事书?
.
9
这种题型我们叫做数字谜。在平时的作业练习中都见过 或者做过,有的老师也讲过,有不少解题方法。例如 用猜想、拼凑、排除、枚举等方法解题。数字谜涉及 的知识多,思考性强,所以很能锻炼我们的思维。
在今后的学习中,除了复习巩固学过的知识外,
还要讲述数字谜的代数解法及小数的除法竖式问题。
例1 把+,-,×,÷四个运算符号,分别填入下面
成为一名优秀学生很简单
心理上: 坚持不懈、积极向上
行动上: 按时上课,认真完成作业
.
1
.
2
什么是奥数?
有难度的数学 有好方法解决的数学 用来选拔、用来竞赛的数学
.
3
如何学好奥数呢?
善于观察 善于分析 善于总结 充分发展学生的数学才能,可以提高能力的培养,着
重培养学生的运算能力、逻辑思维能力和空间想象能 力,要使学生逐步学会分析、综合、归纳、演绎、概 括、抽象、类比等重要的思想方法。培养学生的独立 思考和自学的能力。
提问:一个月内顶多有几个星期日?
5个。
提问:5个星期日至少包含多少天?
29天
提问:第一个星期日可能是哪几天?
1号、2号、或者3号
.
13
解答:
(1)当第一个星期日是1号时,1号便是星期日;
(2)当第一个星期日是2号时,1号便是星期六;
(3)当第一个星期日是3号时,1号便是星期五;
.
8
实战演练3
在5个5之间添运算符号(+、-、×、÷或括号),使之组成一 个结果是24的等式。
分析:一般地,
24=25-1, 24=4 ×6,24=20+4 开拓思维:24=120 ÷5,24=5 ×4.8
所以:
(5 × 5×5 -5) ÷5=24 或者(5 -5 ÷5 ÷ 5) × 5=24
例1 对于任意数a,b,定义运算“*”:
a*b=a×b-a-b。
求12*4的值。
.
19
根据以上的规定,求10△6的值。 3,x>=2,求x的值。
.
20
例6 对于任意自然数,定义:n!=1×2×… ×n。 例如 4!=1×2×3×4。那么1!+2!+3!+…+100!的个位数字是几?
例7 如果m,n表示两个数,那么规定:m¤n=4n-(m+n)÷2。 求3¤(4¤6)¤12的值。
