薄透镜的成像公式和放大率
薄透镜焦距的测定物理实验报告

薄透镜焦距的测定物理实验报告一、实验目的1、加深对薄透镜成像原理的理解。
2、学习几种测量薄透镜焦距的方法。
3、掌握光学实验中的基本测量技术和数据处理方法。
二、实验原理1、薄透镜成像公式当光线通过薄透镜时,遵循薄透镜成像公式:$\frac{1}{u} +\frac{1}{v} =\frac{1}{f}$,其中$u$ 为物距,$v$ 为像距,$f$ 为焦距。
2、自准直法当物屏上的物点发出的光线经透镜折射后,变成平行光,若在透镜后面垂直于光轴放置一个平面反射镜,此平行光将沿原路返回,再次通过透镜后仍成像于物屏上的物点处。
此时,物屏与透镜之间的距离即为透镜的焦距。
3、物距像距法当物距和像距分别为$u$ 和$v$ 时,通过测量物距和像距,代入薄透镜成像公式可求得焦距$f$ 。
4、共轭法移动透镜,在物屏和像屏之间分别得到放大和缩小的清晰像。
根据光路可逆原理,两次成像时物距和像距互换,利用公式$\frac{u + v}{4}$可计算出焦距。
三、实验仪器光具座、凸透镜、凹透镜、物屏、像屏、平面反射镜、光源等。
四、实验内容与步骤1、自准直法测凸透镜焦距(1)将凸透镜固定在光具座的一端,在凸透镜的另一侧放置物屏,使物屏上的十字叉丝清晰可见。
(2)在凸透镜后面垂直于光轴放置平面反射镜。
(3)沿光具座移动物屏,直到在物屏上再次看到清晰的十字叉丝与原物大小相等、方向相反。
(4)记录此时物屏与凸透镜的位置,两者之间的距离即为凸透镜的焦距。
(5)重复测量三次,计算焦距的平均值。
2、物距像距法测凸透镜焦距(1)将凸透镜固定在光具座的中间位置。
(2)在凸透镜的一侧放置物屏,另一侧放置像屏。
(3)移动物屏和像屏,直到在像屏上得到清晰的像。
(4)记录物屏和像屏的位置,分别得到物距$u$ 和像距$v$ 。
(5)代入薄透镜成像公式计算焦距,并重复测量三次,计算平均值。
3、共轭法测凸透镜焦距(1)将物屏固定在光具座的一端,凸透镜放在光具座中间附近。
透镜角放大率计算公式

透镜角放大率计算公式
一、透镜角放大率的概念与意义
透镜角放大率,简称放大率,是指透镜成像时,像与物的角度之比。
它是一个重要的光学参数,可以用来评估透镜对光线的折射和聚焦效果。
在光学、摄影、显微镜等领域具有广泛的应用。
二、透镜角放大率的计算公式
1.薄透镜公式
对于薄透镜,其角放大率的计算公式为:
M = -1 / (f * tan(α"))
其中,M 为角放大率,f 为透镜焦距,α" 为像的角度。
2.厚透镜公式
对于厚透镜,其角放大率的计算公式为:
M = -1 / (f * (1 - (n - 1) * tan^2(α"))
其中,M 为角放大率,f 为透镜焦距,n 为透镜折射率,α" 为像的角度。
三、透镜角放大率的应用领域
透镜角放大率在以下领域具有重要的应用:
1.光学仪器设计:如望远镜、显微镜等,通过调整透镜的角放大率,可以实现对光线的聚焦和成像效果的优化。
2.摄影:在摄影镜头设计中,合理选择透镜的角放大率,可以提高成像质量和画面效果。
3.光学薄膜:在光学薄膜中,透镜角放大率可用于调整薄膜的折射率和厚度,实现对光的控制和调控。
四、提高透镜角放大率的方法
1.增加透镜的折射率:通过选用高折射率的材料制作透镜,可以提高角放大率。
2.调整透镜的焦距:缩短或延长透镜的焦距,可以改变角放大率。
3.优化透镜结构:如采用多透镜组合、反射镜等结构,可以提高角放大率。
五、总结
透镜角放大率是评估透镜成像性能的重要指标,通过计算和调整透镜的角放大率,可以实现光学系统的高效成像和光线控制。
35薄透镜

n’ n’
n
a 8/10/2020
n’ n n’
b 第3章
n’
n n’
c 几何光学
n’
n n’
d
空气中的透镜 n’=1
焦距
1
1
11
(n 1)( )
f' f
r1 r2
高斯物像公式
f ' f 1 s' s
牛顿物像公式
xx' ff '
1 1 1 s' s f '
8/10/2020
第3章 几何光学
P3’
O3
分析:
P经L1直接成像P1’(实像); P像经PL4’2(成实像像P)2’(虚L1像)成像L3是P成5’像(虚P像3’()实。像)L2 成
求解系统成像P1’、 P5’的位置:
P经L1所成的像P1’(实像);
s1' 4cm
s1 5 1 4cm f1' f1 2cm 8/1像0/20L210 物
s5 (5 4) 1cm f1' f1 2cm
f ' f 1 s' s
2 s5'
2 1
1
s5' 2cm
可见,通过光学系统可到叉丝P的2个像P1’(实像)和 P5’(虚像)。
分析:
由上讨论可见,叉丝P位置不当时,将观察到2个 “像”,要想观察到一个清晰的叉丝像,在L1与L2间 距不变的情况下,可通过调节L3与L2之间的距离来实 现。
8/10/2020
第3章 几何光学
高斯公式和牛顿公式是球面反射、球面折射和薄透镜成 像最基本、最普遍的物像公式。
对以上三种情况的区别仅在于焦距f和f’不同;
§3.5 薄透镜
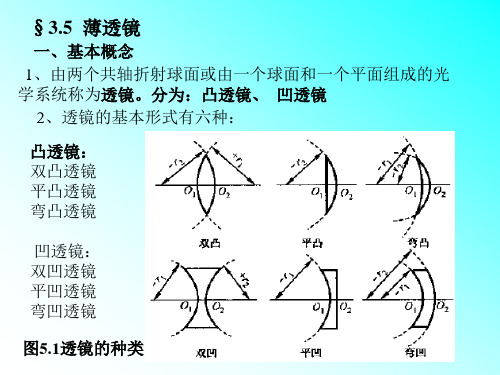
透镜是会聚透镜,凸透镜是发散透镜,二者刚好相反。
4、几何光学物象公式小结
图5.2 焦面及光轴(a, b)
而物方焦平面上任一点P发出的光,经透镜折射后,将成为 一束平行于过P点的副光轴的平行光束[如图5.2,c d]。
图5.2 焦面及光轴 (c d)
3、作图法
(1)对于近轴物点可以利用下述三条特殊光线中的任意两条, 确定像的位置见图5.3(a) (b) (a) 过物方焦点的光线,经透镜折射后与主光轴平行。 (b) 平行于主光轴的入射光线,经透镜折射后通过像方焦点。 (c) 过透镜光心的光线经透镜后方向不变。
l (s OM )2 h2
在近轴条件下,由于
l (s ON )2 h2
r12 h2 (r1 OM )2 2OM r1 OM 2 h2
h2 h2 OM 任意光线PA/AP/的光程就可表示为: ON 2(r2 ) 2r1
( PAAP) n1l n(t OM ON ) n2l
f ( f x) f xx f x x f x (10) x f xx fx x f ( f x) f
f x x f ff
f x x f
(普适式)
图5.2 透镜
二、轴上物点通过薄透镜的成像公式
1、薄透镜的成像公式的推导。图5.2 方法一:利用逐次成像法推导
物点P经第一球面 O折射后将成像于 p//故有:
2019年薄透镜成像公式及作图法

薄透镜成像公式及作图法薄透镜成像公式及作图法薄透镜成像公式及作图法 2011年04月01日本节向您讲述透镜成像的各种有效的作图法,以及薄透镜成像公式应用,您一定会在这里找到许多有用的方法。
[内容综述]如果一个透明物体的两个界面都是球面,或者一个界面是球面,另一个界面是平面,这就是透镜,中央部分比边缘厚的,叫凸透镜,它具有会聚光线的性能,所以也叫做会聚透镜。
透镜中央部分比边缘薄的,叫凹透镜,它具有发散光线的性能,也以也叫做发散透镜。
如果透镜的厚度比两球面的曲率半径小得多,叫做薄透镜。
本讲主要的重点、难点是薄透镜成像公式的应用及透镜成像的作图法。
[要点讲解]1、单球面折射成像公式如图15-28所示,设单球面左、右方的折射率分别为1和n,S’是S的像,因为是近轴光线,所以i与r均很小,所以有(R为球面曲率半径),代入?及,?式即为单球面成像公式,当时的v就是焦距f,所以2、薄透镜成像公式透镜实质上是两个单折射球面组成,它的成像过程就是连续两次的单球面成像过程。
下面讨论薄透镜成像。
如图15-29所示,设左球面的半径为,右球面半径为,透镜材料的折射率为n。
点光源S发出的近轴光经左球面折射后设成像于S’’,由于透镜很薄,两球面顶点可视为一点,设为O,设SO=u,OS’’=V’,由单球面折射成像公式可得原应成像于S"的光束在尚未会聚前又被第二个球面折射,第二次成像。
S’’成为物,是虚物,折射后成像于S’。
现在的物距是-v’,像距为v,则 ?+?可得,这就是薄透镜成像公式。
这里,u,v, , 均有正、负,规则同前面所规定的。
对图15-29,u,v, 均为正,为负,当时,当时,当透镜两边处于同一介质中时f=f ’。
当f和f’>0的透镜称为会聚透镜(凸透镜)。
当f 和f’<0的透镜称为发散透镜(凹透镜)。
用焦距表示,可将?式透镜的成像公式写成 (当f=f ’时)上式称为高斯公式。
3(透镜成像作图法(1)基本光线作图法如图15-30所示,从物方焦点发出的任意光线径透镜折射后必成为平行于主轴的光;平行于主轴射向透镜的任意光线径透镜折射后必经过像方焦点;过光心的光线径透镜后方向不变。
九年级物理上册知识点公式

九年级物理上册知识点公式一、力学知识点公式1.速度公式:速度(v)= 距离(s)/ 时间(t)2.加速度公式:加速度(a)= 变化的速度(Δv)/ 时间(t)3.匀变速直线运动公式:位移(s)= 初速度(v₀) ×时间(t) + ½ ×加速度(a) ×时间(t)²末速度²(v²)= 初速度²(v₀²)+ 2 ×加速度(a) ×位移(s)4.牛顿第二定律(力学基本定律):力(F)= 质量(m)×加速度(a)5.功公式:功(W)= 力(F) ×位移(s) ×cosθ二、声学知识点公式1.声速公式:声速(v)= 频率(f)×波长(λ)2.声音强度公式:声音强度(I)= 功率(P)/ 面积(A)3.频率与周期关系公式:频率(f)= 1 / 周期(T)4.共振频率公式:共振频率(f₀)= 1 / 2π × √(弹性系数(k)/ 质量(m))5.光的折射公式:折射率(n)= 光速在真空中的速度(c₀)/ 光速在介质中的速度(c)三、光学知识点公式1.焦距公式:物距(d₀) ×物的折射率(n₀) =像距(d)×像的折射率(n)2.透镜公式:1 / 物距(d₀)+ 1 / 像距(d)= 1 / 焦距(f)3.放大率公式:放大率(β)= 像的高度(h)/ 物的高度(h₀)4.光的反射公式:入射角(i)= 反射角(r)5.薄透镜成像公式:1 / 物距(d₀)+ 1 / 像距(d)= 1 / 焦距(f)四、电学知识点公式1.电流公式:电流(I)= 电量(Q)/ 时间(t)2.欧姆定律:电流(I)= 电压(U)/ 电阻(R)3.电功公式:电功(W)= 电压(U)×电量(Q)4.电阻与电导公式:电阻(R)= 电电阻率(ρ) ×长度(L)/ 面积(A)电导(G)= 1 / 电阻(R)5.串联电阻公式:总电阻(R₁+ R₂+ ...+ Rₙ)= R₁ + R₂ + ...+ Rₙ以上是九年级物理上册的常见知识点及相应的公式。
11-2 薄透镜成像

•球面反射成像的物像公式 球面反射成像的物像公式: 球面反射成像的物像公式
1 1 2 + = p p′ R
或
B
1 1 1 + = p p′ f
R i′
i
α
P
C
ϕ
β
h
O
P′
y′ p′ •横向放大率: 横向放大率: 横向放大率 m= = − y p 符号法则: 符号法则:
p
p′
1.物点 P 在镜前时,物距为正;物点 P 在镜后时, 1.物点 在镜前时,物距为正; 在镜后时, 物距为负。 物距为负。 2.像点在镜前时,像距为正;像点在镜后时,像距为 2.像点在镜前时 像距为正;像点在镜后时, 像点在镜前时, 负。 3.凹面镜的曲率半径 R 取正,凸面镜的曲率半径 R 3.凹面镜的曲率半径 取正, 取负。 取负。
n1
P
O 1
C2
n2
n1
O 2 C1 ′ p2
P′
P′ 1
p1
t
′ p1
p2
P′为入射于右侧球面光线的一个虚物点 1 为入射于右侧球面光线的一个虚
′ ∴−p2 = p1 − t ≈ p′ 1
n1 n2 n2 n1 n2 − n1 n1 − n2 + + + = + p1 p′ p2 p′ R1 R2 1 2
′ p1
p2
n1 n2 n2 − n1 + = 光线在透镜的左侧面折射: 光线在透镜的左侧面折射: p1 p′ R1 1 n2 n1 n1 − n2 光线在透镜内右侧面入射: 光线在透镜内右侧面入射: + = p2 p′ R2 2 n1 n2 n2 n1 n2 − n1 n1 − n2 两式相加: 两式相加: + + + = + p1 p′ p2 p′ R1 R2 1 2
高一物理公式大全及知识点汇总

高一物理公式大全及知识点汇总物理是一门研究物质的运动、能量与相互作用的科学,是自然科学中一门较为基础的学科之一。
在高中物理学习中,物理公式的掌握和理解起着至关重要的作用。
下面将为大家整理高一物理公式大全及相关知识点,希望对同学们的学习有所帮助。
一、运动学公式1.平均速度:v = Δs/Δt2.加速度:a = Δv/Δt3.加速度与速度之间的关系:v = u + at4.加速度与位移之间的关系:s = ut + 1/2at²5.力的定义:F = ma6.牛顿第二定律:F = dp/dt7.重力:F = mg8.万有引力定律:F = G * (m₁m₂)/r²二、热学公式1.热传导:Q = k * A * ΔT / x2.热容量:Q = mcΔT3.热平衡:mcΔT = mcΔT4.理想气体状态方程:PV = nRT5.焦耳定律:P = IV = I²R三、光学公式1.光的传播速度:v = c2.折射定律:n₁sinθ₁ = n₂sinθ₂3.薄透镜成像公式:1/f = 1/v - 1/u4.放大率:β = v/u5.光的反射:θ₁ = θ₂四、电学公式1.欧姆定律:I = V/R2.电功率:P = IV3.等效电阻:1/R = 1/R₁ + 1/R₂ + ...4.串联电阻:R = R₁ + R₂ + ...5.并联电阻:1/R = 1/R₁ + 1/R₂ + ...五、原子物理公式1.波长与频率之间的关系:c = λν2.能量与频率之间的关系:E = hν3.相对论质能关系:E = mc²以上仅是高一物理学习中的一部分公式和知识点,但它们在物理学的基础中占据着重要的地位。
同学们在学习物理的过程中,要努力理解并熟练运用这些公式,在解题时灵活运用,掌握其适用范围和注意事项。
在学习物理时,除了掌握公式外,还需要关注一些重要的知识点。
例如,在运动学中,要了解匀速直线运动、匀变速直线运动、自由落体等基本概念;在热学中,要理解热能传递、热平衡和理想气体等知识点;在光学中,要掌握反射、折射、成像等基本原理;在电学中,要了解电流、电压、电阻等基本概念和电路的基本组成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
′ h2 = h3
垂轴放大率为 β = h ′ / h 1
′ ′ ′ ′ hk h1′h 2 h3 hk β = = L = β 1β 2 β 3 L βk h 1 h 1h 2 h 3 hk
系统总的垂轴放大率为各单球面的垂 轴放大率之乘积。 轴放大率之乘积。
′ h′h2h3 ′ ′ ′ hk hk 1 β= = L = β1β 2β 3Lβk h1 h1h2h3 hk
P2′ =
P2 f ′ f1′
f2′P 2 P′ = 2 P − f2 2
f ′ = f1′ ( P′ = 2
P f′ P′ = 2 2 f1′
′ ′ f2 f1′f2 )= P − f2 −∆ 2
′ P f1′f2 P (∆ − f2 ) 2 2 ′= ′ × =− f2 f2 f1′ − ∆ ∆ ∆
S
− P /(− f ) = (h − h′) /(−h′)
f′ f + =1 P′ P
P′ / f ′ = (h − h′) / h
xx′ = ff ′
共轴系统的高斯公式和牛顿公式与薄透 镜和单球面中的公式在形式上完全相同。 镜和单球面中的公式在形式上完全相同。 共轴系统的一对焦点, 共轴系统的一对焦点,一对主点和一对 节点,统称为系统的基点( 节点,统称为系统的基点(cardinal points) ) 对于给定的光学系统, 对于给定的光学系统,其基点之位置可 通过光线追迹逐步成像,作图或计算求得。 通过光线追迹逐步成像,作图或计算求得。 2、计算法求组合共轴球面系统的基点 、
3a −3a + =1 得 P′ − a 1
−3 P′ = a = −1.5a 1 2
同理对于第二个透镜, 同理对于第二个透镜,有
a −a + =1 P′ (−3/ 2)a − 2a 2
P′ = 7a / 5 =1.4a 2
例题:凸透镜焦距为 厘米 厘米, 例题:凸透镜焦距为10厘米,凹透镜焦距 厘米, 厘米。 为4厘米,两个透镜相距 厘米。已知物在凸 厘米 两个透镜相距12厘米 透镜左方20厘米处 厘米处, 透镜左方 厘米处,计算像的位置和横向放大 率并作图。 率并作图。
§1-4
薄透镜的成像公式和放大率
一、薄透镜(thin lens)成像 薄透镜( ) 薄透镜是最简单的共轴球面系统, 薄透镜是最简单的共轴球面系统,它由 两个单球面组成。 两个单球面组成。两球面之间的间距 d 比 小很多。 两折射球面的曲率半径 r1、 r2 小很多。 当 d 0时,两球面顶点重合为一点, 时 两球面顶点重合为一点, 称为光心 光心( 称为光心(optical center) ) 薄透镜分为凸透镜和凹透镜。 薄透镜分为凸透镜和凹透镜。 凸透镜的中央厚度大于边缘部分, 凸透镜的中央厚度大于边缘部分,有 双凸、平凸、弯凸; 双凸、平凸、弯凸;凹透镜的边缘厚度大 于中央部分,有双凹、平凹、弯凹。 于中央部分,有双凹、平凹、弯凹。
P = 20−12 = 8cm 虚 ) 2 = −4cm ( 物 , f′ 2
1 1 1 − = ′ P′ P2 f2 2
P′ β2 = 2 = −1 P 2
得 P′ = −8cm(虚 ) 象 2
∴β = β1β2 =1
二、共轴系统的基点和基面 1841年高斯提出共轴系统的一般理论: 年高斯提出共轴系统的一般理论: 年高斯提出共轴系统的一般理论 在理想共轴系统中, 在理想共轴系统中,物方的任一点都和像方的 一点共轭。同样, 一点共轭。同样,相应于物方的每一条直线或 每一个平面,在像方都应有一条共轭直线或一 每一个平面, 个共轭平面。 个共轭平面。 这样共轴系统就成了点与点、 这样共轴系统就成了点与点、直线与直 线以及平面与平面之间的共轭关系的纯几何理 利用基点与基面, 论。利用基点与基面,可描述共轴系统的基本 光学特性。 光学特性。
f1d −3a⋅ 2a xH = H1H = = = 3a ∆ − 2a f2′d a⋅ 2a ′ x′ = H2H′ = = = −a H ∆ − 2a f1 f2 (−3a)(−a) f = HF = = = −a ∆ − 2a
F´
F
例题: 例题:已知入射光线求出射光线
S M F O F´ Q´ M´ N F´ M N Q O F
已知物点求像点
N M O S F F´ S´ S F´ M S´ N O
§1-5
共轴球面系统
一、共轴球面系统的逐次成像
个折射球面组成一共轴球面系统, 由 k 个折射球面组成一共轴球面系统, 物体 SQ 经过这个光学系统所成的像为 SKQK
拉格朗日—亥姆霍兹恒等式 拉格朗日 亥姆霍兹恒等式
′ ′ ′ ′ ′ n1h1µ1 = n1h1′µ1 = n2 h2 µ 2 = L = nk hk µ k
例:惠更斯目镜 组成, 由两个凸透镜 L1 L2组成,用逐次成像 法求像位置。 法求像位置。
已知: 已知: f1′ = 3a, f2′ = a, d = 2a 物点 Q 位于L1前a处 处 解: - P1= a ,代入第一个透镜的高斯公式
Φ = (nL −1)(1/ r1 −1/ r2)
透镜制造者公式( 透镜制造者公式(lens-maker,s formula) )
1 f ′ =−f = (nL −1)(1/ r1 −1/ r2)
1 1 1 1 (nL −1 d ) = − = (nL −1 )[ − + ] f′ f r1 r2 nr1r2
QM = − P FH = − f MN = h − h′ NH = − h′ − P /( − f ) = ( h − h′) /( − h′)
S
N ′Q ′ = P ′ H ′F ′ = f ′ M ′N ′ = h − h ′ M ′H ′ = h P ′ / f ′ = ( h − h ′) / h
各种薄透镜
对第一折射面
′ ′ n1 n1 n1 − n1 − = = Φ1 P′ P1 r1 1
对第二折射面
′ ′ n2 n2 n2 − n2 − = = Φ2 P2′ P 2 r2
P1′ = P2
′ n1 = n 2
n′ n − =Φ P′ P
薄透镜成像公式
′ n2 n1 − = Φ1 + Φ2 = Φ P′ P1 2
µ′ n 1 γ= = ⋅ µ n′ β
若薄透镜处于空气中, 若薄透镜处于空气中,则 n = n´= 1,设薄 透镜材料的折射率为 nL,两球面的曲率半径 为 r1 、r2,则可得
′ n1 − n1 nL − n = = Φ1 r1 r1 ′ n2 − n2 n′ − nL = = Φ2 r2 r2
n′ n − =Φ P′ P
n′ 当 →−∞时 P′ = f ′ = P , f´为薄透镜的像方焦距 为薄透镜的像方焦距 Φ −n 当 ′ →∞时 P = f = P , Φ f 为薄透镜的物方焦距
薄透镜的高斯公式: 薄透镜的高斯公式:
f′ f + =1 P P
薄透镜的垂轴放大率和角放大率
h′ nP′ β= = h n′P
(3)物方焦距与像方焦距 ) 物方主焦点到物方主点的距离为物方焦 距,记为 f 。像方主焦点到像方主点的距 离为像方焦距,记为 f´。 离为像方焦距, 。 单球面的主点与其顶点重合, 单球面的主点与其顶点重合,而薄透 镜的主点与其光心重合。 镜的主点与其光心重合。 (4)节点(nodal points) )节点( ) 从薄透镜作图法成像可知, 从薄透镜作图法成像可知,置于空气中 的薄透镜有一条特殊光线, 的薄透镜有一条特殊光线,它通过光心不 发生偏折。 发生偏折。
对于两边是同一介质的任意组合的理想 光学系统来说, 光学系统来说,一个离轴物点发出的许多光 线中,总有一条入射光与其对应的出射光平 线中,总有一条入射光与其对应的出射光平 行。 这对共轭光线与光轴的交点为一对共轭点 称为节点。 称为节点。物方节点记为 k;像方节点记为 ; k´。 。
k´ k
1、计算法求物像关系: 、计算法求物像关系:
定义: ⑴ 定义:
′ F1′F 2 = ∆ , H 1′ H 2 = d , H 2 H ′ = x ′ , H ′F ′ = f ′ H
有物像关系: ⑵ F1´与F´有物像关系: 与 有物像关系
f 2′ f 2 + =1 P2′ P2
S
f 2′P2 P2′ = P2 − f 2
S
⑶
f1′ − f ′ = P2′ − P2
个球面, 对应 k 个球面,可得 k 个物像距公式
′ ′ n1 n1 n1 − n1 − = P′ P1 r1 1
LL
L
′ n′ nk nk − nk k − = Pk′ Pk rk
两相邻球面顶点的距离为
d 12 = P′ − P 2 1
d 23 = P2′ − P 3
k
dk − 1, k = Pk′−1 − Pk
基点与基面:主焦点与焦平面; 基点与基面:主焦点与焦平面;主点与主平面 (1)主焦点与焦平面 ) 与无穷远处的像平面共轭的物平面为物 方焦平面。 方焦平面。物方焦平面与主光轴的交点为物 方主焦点, 方主焦点,记为 F。 与无穷远处的物平面共轭的像平面为像 方焦平面。 方焦平面。像方焦平面与主光轴的交点为像 方主焦点, 方主焦点,记为 F´。 (2)主点(principal point)与主平面 )主点( ) 共轴系统中存在一对共轭面, 共轴系统中存在一对共轭面,面上任一 对共轭点到主光轴的距离相等。( 。(β=1) 对共轭点到主光轴的距离相等。( )
(∆ − f2 ) f2′ f1′f2′ (∆ − f2 + f1′) f2′ f2′d x′ = P′ − f ′ = + = = H 2 ∆ ∆ ∆ ∆
同理, 同理,定义
xH = H1H, f = H F
