自控实验典型环节频率特性的测试

合集下载

实验三典型环节的频率特性测量

姓名，班级学号；姓名，班级学号姓名，班级学号；姓名，班级学号姓名，班级学号；姓名，班级学号实验三典型环节（系统）的频率特性测量一．实验目的1．学习和掌握测量典型环节（或系统）频率特性曲线的方法和技能。

2．学习根据所测得频率特性，作出伯德图。

二．实验内容1．用实验方法完成一阶惯性环节的频率特性曲线测试。

2．用实验方法完成比例环节、积分环节、惯性环节及二阶系统的频率特性曲线测试。

三．实验步骤1．熟悉实验设备上的信号源，掌握改变正弦波信号幅值和频率的方法。

2．利用实验设备完成比例环节、积分环节、惯性环节和二阶系统开环频率特性曲线的测试。

3．根据测得的频率特性曲线（或数据）求取各自的传递函数。

4．分析实验结果，完成实验报告。

四．实验线路及原理(一)实验原理对于稳定的线性定常系统或环节，当输入端加入一正弦信号时，它的稳态输出时一与输入信号同频率的正弦信号，但其幅值和相位将随输入信号频率的改变而改变，即：即相频特性即幅频特性,)()()(,)()()(sin )(])(sin[)()(ωωωωωφωωωωωωωj G t j G t j G Aj G A A tA t r j G t j G A t c ∠=-∠+====∠+=只要改变输入信号的频率，就可以测出输出信号与输入信号的幅值比)(ωj G 和它的相位差)(ωφ，不断改变输入信号的频率，就可测得被测环节的幅频特性和相频特性。

（二）实验线路1．比例(P)环节的模拟电路比例环节的传递函数为：K s U s U i O =)()(，取ωj s =代入，得G(jw)=k, A(w)=k, Φ(w)=0°其模拟电路和阶跃响应，分别如图1.1.2，实验参数取R 0＝100k ，R 1＝200k ，R=10k 。

2．积分(I)环节的模拟电路积分环节的传递函数为：Tss U s U i O 1)()(=其模拟电路，如图1.2.2所示，实验参数取R 0＝100k ，C ＝1uF ，R=10k 。

自动控制频率特性测试实验报告

自动控制频率特性测试实验报告1. 引言在现代自动控制系统中，频率特性是一个重要的参数，对于系统的稳定性和性能起着决定性的作用。

频率特性测试实验旨在评估自动控制系统的频率响应，并分析系统在不同频率下的性能。

本实验报告将介绍自动控制频率特性测试实验的目的、实验器材、实验步骤和实验结果分析。

2. 实验目的本实验的主要目的是通过频率响应测试，评估自动控制系统的频率特性以及系统在不同频率下的性能。

具体目标包括：1.测试系统的幅频特性，即系统的增益与频率之间的关系；2.测试系统的相频特性，即系统的相移与频率之间的关系；3.分析系统的频率特性对系统的稳定性和性能的影响。

3. 实验器材本实验所需的器材包括：•信号发生器：用于产生不同频率的输入信号；•可变增益放大器：用于控制输入信号的幅度；•相位巡迥器：用于调节输入信号的相位；•示波器：用于观测输入信号和输出信号；•自动控制系统：接受输入信号并提供相应的控制输出。

4. 实验步骤4.1 准备工作1.确保实验器材连接正确，信号发生器连接到自动控制系统的输入端，示波器连接到自动控制系统的输出端。

2.将可变增益放大器和相位巡迥器分别接入信号发生器的输出端，用于调节输入信号的幅度和相位。

4.2 测试幅频特性1.设置信号发生器的频率为起始频率，将幅度设置为合适的值。

2.将相位巡迥器的相位设置为零，确保输入信号的相位与输出信号相位一致。

3.记录输入信号和输出信号的幅度，并计算增益。

4.逐渐增加信号发生器的频率，重复步骤3，直到达到结束频率。

4.3 测试相频特性1.设置信号发生器的频率为起始频率，将幅度和相位设置为合适的值。

2.记录输入信号和输出信号的相位差，并计算相移。

3.逐渐增加信号发生器的频率，重复步骤2，直到达到结束频率。

4.4 结果记录与分析1.将实验得到的数据记录下来，包括输入信号频率、幅度、输出信号频率、幅度、相位差等。

2.绘制幅频特性曲线图，分析系统的增益随频率变化的规律。

实验五典型环节和系统频率特性的测量

实验五典型环节和系统频率特性的测量一、实验目的1. 了解典型环节和系统的频率特性曲线的测试方法；2. 根据实验求得的频率特性曲线求取传递函数。

二、实验设备同实验一。

三、实验内容1. 惯性环节的频率特性测试；2. 二阶系统频率特性测试；3. 无源滞后—超前校正网络的频率特性测试；4. 由实验测得的频率特性曲线，求取相应的传递函数；5. 用软件仿真的方法，求取惯性环节和二阶系统的频率特性。

四、实验原理1. 系统（环节）的频率特性设G(S)为一最小相位系统（环节）的传递函数。

如在它的输入端施加一幅值为Xm 、频率为ω的正弦信号，则系统的稳态输出为)sin()()sin(ϕωωϕω+=+=t j G Xm t Y y m由式①得出系统输出，输入信号的幅值比相位差)()(ωωj G Xmj G Xm Xm Ym == (幅频特性) )()(ωωφj G ∠= (相频特性)式中)(ωj G 和)(ωφ都是输入信号ω的函数。

2. 频率特性的测试方法 2.1 李沙育图形法测试 2.1.1幅频特性的测试由于 mmm m X Y X Y j G 22)(==ω 改变输入信号的频率，即可测出相应的幅值比，并计算 mmX Y A L 22log 20)(log 20)(==ωω （dB ）其测试框图如下所示：图5-1 幅频特性的测试图(李沙育图形法)注：示波器同一时刻只输入一个通道，即系统（环节）的输入或输出。

2.1.2相频特性的测试图5-2 幅频特性的测试图(李沙育图形法)令系统（环节）的输入信号为：t X t X m ωsin )(= (5-1) 则其输出为 )sin()(φω+=t Y t Y m (5-2)对应的李沙育图形如图5-2所示。

若以t 为参变量,则)(t X 与)(t Y 所确定点的轨迹将在示波器的屏幕上形成一条封闭的曲线(通常为椭圆)，当t=0时，0)0(=X 由式(5-2)得 )sin()0(φm Y Y = 于是有 mm Y Y Y Y 2)0(2sin )0(sin )(11--==ωφ (5-3) 同理可得mX X 2)0(2sin )(1-=ωφ (5-4) 其中)0(2Y 为椭圆与Y 轴相交点间的长度； )0(2X 为椭圆与X 轴相交点间的长度。

实验七典型环节频率特性的测试

实验七典型环节频率特性的测试一、实验目的(1)掌握用李沙育图形法，测量各典型环节的频率特性。

(2)根据所测得频率特性，做出伯德图，据此求得环节的传递函数。

二、实验设备序号型号备注1 DJK01 电源控制屏该控制屏包含“三相电源输出”等几个模块。

2 DJK15控制理论实验挂箱或DJK16控制理论实验挂箱3 双踪慢扫描示波器4 万用表三、实验线路及原理对于稳定的线性定常系统或环节，当其输入端加入一正弦信号X(t)=XmSinωt，它的稳态输出是一与输入信号同频率的正弦信号，但其幅值和相位将随着输入信号频率ω的变化而变化。

即输出信号为Υ（t）=ΥmSin（ωt+ϕ）=Χm⏐G（jω）⏐Sin（ωt+ϕ）其中 ⏐G（jω）⏐= Υm /Xm ，ϕ(ω)=argG（jω）只要改变输入信号x（t）的频率ω，就可测得输出信号与输入信号的幅值比⏐G（jω）⏐和它们的相位差ϕ（ω）=argG（jω）。

不断改变x（t）的频率，就可测得被测环节（系统）的幅频特性⏐G （jω）⏐和相频特性ϕ（ω）。

本实验采用李沙育图形法，图7-1为测试的方框图。

图7-1 典型环节的测试方框图在表（1）中列出了超前与滞后时相位的计算公式和光点的转向。

表中2Y0为椭圆与Y轴交点之间的长度，2X0为椭圆与X轴交点之间距离，Xm 和Ym 分别为X（t）和Y（t）的幅值。

四、实验方法(1)惯性环节的频率特性的测试令G （S）=1/（0.5S+1）,则其相应的模拟电路如图7-2所示。

测量时示波器的X 轴停止扫描，把扫频电源的正弦信号同时送到被测环节的输入端和示波器的X 轴，被测环节的输出送到示波器的Y 轴，如图7-3所示。

(R1=R2=510K，C=1uF) 图7-2 惯性环节的模拟电路图图7-3 相频特性测试的接线图当扫频电源输出一个正弦信号，则在示波器的屏幕上呈现一个李沙育图形------椭圆。

据此，可测得在该输入信号频率下的相位值：mY Y Sin2201−=ϕ不断改变扫频电源输出信号的频率，就可得到一系列相应的相位值，列表记下不同ω值时的Y 0和Ym。

实验四系统频率特性测量

实验四系统频率特性测量一、实验目的1、加深了解系统及元件频率特性的物理概念。

2、掌握系统及元件频率特性的测量方法。

二、实验设备1、D1CE-AT-∏型自动控制系统实验箱一台2、带串口计算机一台3、RS232串口线三、实验原理及电路1、被测系统的方块图及原理:系统(或环节)的频率特性G(jω)是一个复变量，可以表示成以角频率3为参数的幅值和相角:G(M=IG(%)I∕G(网本实验应用频率特性测试仪测量系统或环节的频率特牲。

图4-1所示系统的开环频率特性为:B(jω)B(ιω)B(jω)G3)GR3)H(j3)=叼舟I/追采用对数幅频特牲和相频特性表示，则式(4-2)表示为:(4—1) (4-2)图4-1被测系统方块图2。

IgGG3)G∕)Hg)H。

啕需I=2(Hg1BG3-2(Hg1EG3)I (4—3) C⅛Gω)G<jω)HGω)=/*线=∕BQω)-EGω)(4-4)E(j3)将频率特性测试仪内信号发生器产生的超低频正弦信号的频率从低到高变化，并施加于被测系统的输人端Et)］,然后分别测量相应的反馈信号［b⑴］和误差信号［e(t)］的对数幅值和相位。

频率特性测试仪测试数据经相关运算器后在显示器中显示。

根据式(4—3)和式(4—4)分别计算出各个频率下的开环对数幅值和相位，在半对数座标纸上作出实验曲线：开环对数幅频曲线和相频曲线。

根据实验开环对数幅频曲线画出开环对数幅频曲线的渐近线，再根据渐近线的斜率和转角频确定频率特性(或传递函数)。

所确定的频率特性(或传递函数)的正确性可以由测量的相频曲线来检验，对最小相位系统而言，实际测量所得的相频曲线必须与由确定的频率特性(或传递函数)所画出的理论相频曲线在一定程度上相符，如果测量所得的相位在高频(相对于转角频率)时不等于一900(q—p)［式中P和q分别表示传递函数分子和分母的阶次］，那么，频率特性(或传递函数)必定是一个非最小相位系统的频率特性。

自动控制原理系统频率特性的测定

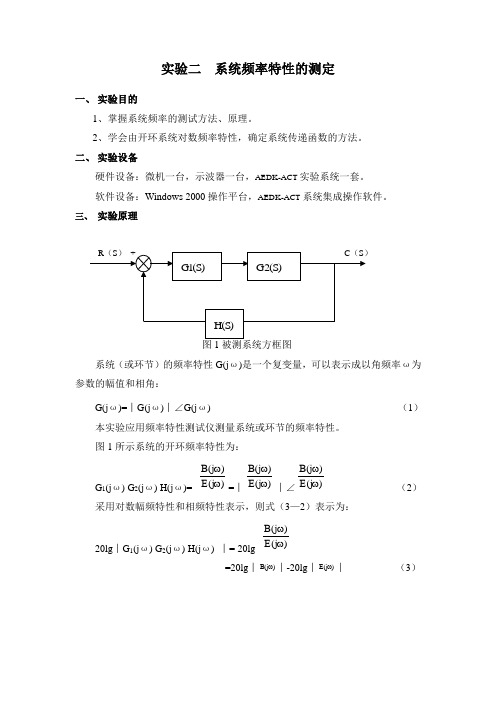
实验二系统频率特性的测定一、实验目的1、掌握系统频率的测试方法、原理。

2、学会由开环系统对数频率特性，确定系统传递函数的方法。

二、实验设备硬件设备：微机一台，示波器一台，AEDK-ACT 实验系统一套。

软件设备：Windows 2000操作平台，AEDK-ACT 系统集成操作软件。

三、实验原理图1被测系统方框图系统（或环节）的频率特性G(j ω)是一个复变量，可以表示成以角频率ω为参数的幅值和相角：G(j ω)=︱G(j ω)︱∠G(j ω)（1）本实验应用频率特性测试仪测量系统或环节的频率特性。

图1所示系统的开环频率特性为：G 1(j ω) G 2(j ω) H(j ω)= )E(j )B(j ωω=︱)E(j )B(j ωω︱∠)E(j )B(j ωω （2）采用对数幅频特性和相频特性表示，则式（3—2）表示为：20lg ︱G 1(j ω) G 2(j ω) H(j ω) ︱= 20lg )E(j )B(j ωω=20lg ︱)B(j ω︱-20lg ︱)E (j ω︱（3）G 1(j ω) G 2(j ω) H(j ω) = ∠)E(j )B(j ωω=∠)B(j ω- ∠)E (j ω （4）将频率特性测试仪内信号发生器产生的超低频正弦信号的频率从低到高变化，并施加于被测系统的输入端[r （t ）]，然后分别测量相应的反馈信号[b （t ）]和误差信号[e （t ）]的对数幅值和相位。

频率特性测试仪测试数据经相关运算后在显示器中显示。

根据式（3）和式（4）分别计算出各个频率下的开环对数幅值和相位，在半对数坐标纸上做出实验曲线：开环对数幅频曲线和相频曲线。

根据实验开环对数幅频曲线画出开环对数幅频曲线的渐近线，再根据渐近线的斜率和转角确定频率特性（或传递函数）。

所确定的频率特性（或传递函数）的正确性可以由测量的相频曲线来检验，对最小相位系统而言，实际测量所得的相频曲线必须与确定的频率特性（或传递函数）所画出的理论相频曲线在一定程度上相符。

自动控制理论3-频率特性的测量

自动控制理论试验之三频率特性的测量一、实验目的学习测量系统或环节的频率特性二、实验设备1、超低频信号发生器2、示波器3、电子模拟装置及导线三、实验内容，数据记录1、测量微分积分环节的频率特性(1)相频特性相频特性的测试线路如图1所示。

信号发生器的输出信号送入X轴，系统的输出送入Y1轴。

得李萨如图形，以示波器的光标测量椭圆X上的投影长2X0和椭圆中间的长度2Xm，得θ=arcsin(2X0/2Xm)。

变化输入频率w，得到一组θ，即可绘制系统的相频特性，并可以与理论计算θ得到的图形比较。

w=30(1/s)李萨如图 w＝ 80（1/s）李萨如图数据记录如下。

相频特性表格f(Hz)w(rad/s) T(s)2Xm(v) 2Xo(v) 实测θ0(w)计算θ0(w)光点转动方向0.16 1 6.28E+00 6.063 2.719 -26.645 -25.3 逆 0.32 2 3.14E+00 6.063 3.813 -38.969 -38.2 逆 0.80 5 1.26E+00 6.063 4.031 -41.671 -42.6 逆 1.27 8 7.85E-01 6.063 3.438 -34.544 -35.8 逆 1.59 10 6.28E-01 6.063 3.063 -30.344 -30.6 逆 4.77 30 2.09E-01 6.063 0.000 0.000 -1.2 直线 7.96 50 1.26E-01 6.063 1.500 14.324 12.3 顺 12.73 80 7.85E-02 6.063 2.766 27.143 25.2 顺 15.92 100 6.28E-02 6.063 3.281 32.762 30.7 顺 31.83 200 3.14E-02 6.063 4.156 43.272 42.6 顺 47.75 300 2.09E-02 6.063 4.125 42.871 43.5 顺 95.50 600 1.05E-02 6.063 3.313 33.122 35.1 顺 127.33 800 7.85E-03 6.063 2.718 26.634 29.6 顺 159.1610006.28E-036.0632.43823.71025.2 顺根据电路图得出系统的传递函数为：G(s)=2211010006101000s s s s ++++根据所测的数据画出相频特性曲线如下图所示100101102103一阶系统的相频特性曲线w <G (w )(2)幅频特性信号发生器的正弦信号送入Y2，被测系统的输出仍然送入Y1。

实验四典型系统的频率特性测试

自动控制原理实验报告实验名称：典型系统的频率特性测试班级：姓名：学号：实验四典型系统的频率特性测试一、实验目的1、加深理解系统及元件频率特性的物理概念2、掌握测量典型一阶系统和二阶系统频率特性曲线的方法3、掌握软件仿真求取一阶和二阶系统开环频率特性的方法4、了解从频率特性求系统传递函数及参数的方法二、实验容1、搭建一阶惯性环节，绘制其频率特性曲线2、搭建典型二阶环节，绘制其频率特性曲线3、用软件仿真求取一阶和二阶系统频率特性曲线，跟实验结果比较三、实验步骤1、一阶惯性环节的频率特性（1）用Matlab函数绘制系统的幅相曲线和对数频率特性曲线，记录理想幅频曲线和相频曲线。

程序如下:sys=tf(1,[0.005,1]);nyquist(sys);title('系统的奈氏图');figurebode(sys);title('系统的波特图');（2）在simulink下创建惯性环节的幅相曲线和对数频率特性曲线仿真系统。

改变正弦输入函数的频率，测试并记录输出与输入幅值之比，相位之差，保存仿真结果（3）在实验箱中搭建模拟电路，输入正弦波信号，观测输入输出正弦波曲线。

调节正弦波频率和幅值，绘制该一阶惯性环节的幅频曲线和相频曲线，与软件仿真对比2、二阶系统的频率特性曲线（1）用Matlab 函数绘制二阶系统的幅相曲线和对数频率特性曲线，记录理想幅频曲线和相频曲线。

程序仿真：sys=tf(200,[1,10,200]);nyquist(sys);title('系统的奈氏图'); figure bode(sys);title('系统的波特图');（2）在simulink 下创建二阶环节的幅相曲线和对数频率特性曲线仿真系统。

实验四系统频率特性测量(模拟实验)

实验四系统频率特性测量一、实验目的1．加深了解系统及元件频率特性的物理概念。

2．掌握系统及元件频率特性的测量方法。

二、实验仪器1．EL-AT-II 型自动控制系统实验箱一台 2．计算机一台三、实验原理 1．模拟电路图若输入信号U1（t ）=U1sin ωt,则在稳态时，其输出信号为U2（t ）=U2sin （ωt+ψ），改变输入信号角频率ω值，便可测得二组U2/U1和ψ随ω变化的数值，这个变化规律就是系统的幅频特性和相频特性。

图4-1为二阶系统的模拟电路图，它是由惯性环节、积分环节和比例环节组成。

图4-2为图4-1的方框原理图，图中23212112,,C R T C R T R R K ===。

图4-1 二阶系统的模拟电路图4-2 二阶系统原理图由图4-1求得二阶系统的闭环传递函数为：211221222112)()()(T T K T ss T T K Ks T s T T Ks U s U s ++=++==φ典型二阶系统的闭环传递函数为：2222)(nn ns s s ωζωωφ++= 对比可得：21T T K n =ω，K T T 124=ζ若令s T 2.01=，s T 5.01=，则K n 10=ω，K 625.0=ζ由上式可知，调节开环增益K 的值，就能同时改变系统阻尼比ζ和无阻尼自然频率n ω的值，我们可以改变k 的值，令系统处于稳定状态下。

当625.0>K ，10<<ζ，系统处于欠阻尼状态，当625.0=K ，1=ζ，系统处于临界阻尼状态，当625.0<K ，1>ζ，系统处于过阻尼状态。

四、实验步骤1．连接被测量典型环节的模拟电路。

电路的输入U1接A/D 、D/A 卡的DA1输出，电路的输出U2接A/D 、D/A 卡的AD1输入。

检查无误后接通电源。

2．启动计算机，在桌面双击图标 [自动控制实验系统] 运行软件。

3．测试计算机与实验箱的通信是否正常,通信正常继续。

自动控制原理实验-系统频率特性的测量与分析-推荐下载

试用MATLAB 绘制出不同ζ和ωn 的伯德图。实验3. 已知系统的开环传递函数为
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电通，力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置，机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2，荷试而下卷且高总可中体保资配障料置2试时32卷，3各调需类控要管试在路验最习；大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试，况卷要下安加与全强过，看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资；中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整，高核或中对者资定对料值某试，些卷审异弯核常扁与高度校中固对资定图料盒纸试位，卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置，地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中，案资要，料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气，设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术，技槽以来术、及避管系免架统不等启必多动要项方高方案中式；资，对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资，件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调，并试合且技理进术利行，用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活：。。在对对分于于线调差盒试动处过保，程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试，题技应，术采作是用为指金调发属试电隔人机板员一进，变行需压隔要器开在组处事在理前发；掌生同握内一图部线纸故槽资障内料时，、，强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试，卷卷线试切缆验除敷报从设告而完与采毕相用，关高要技中进术资行资料检料试查，卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

自动控制原理实验：典型环节及其阶跃响应,二阶系统阶跃响应,统频率特性测量

自动控制原理实验：典型环节及其阶跃响应,二阶系统阶跃响应,统频率特性测量实验一、典型环节及其阶跃响应实验目的1、学习构成典型环节的模拟电路,了解电路参数对环节特性的影响。

2、学习典型环节阶跃响应的测量方法,并学会由阶跃响应曲线计算典型环节的传递函数。

实验内容构成下述典型环节的模拟电路,并测量其阶跃响应。

比例环节的模拟电路及其传递函数示图2-1。

G(S)=-R2/R1惯性环节的模拟电路及其传递函数示图2-2。

G(S)=-K/TS+1 K=R2/R1 ,T=R2*C 积分环节的模拟电路及其传递函数示图2-3。

G(S)=1/TS T=RC 微分环节的模拟电路及其传递函数示图2-4。

G(S)=-RCS 比例加微分环节的模拟电路及其传递函数示图2-5。

G(S)=-K(TS+1) K=R2/R1 T=R2C 比例加积分环节的模拟电路及其传递函数示图2-6。

G(S)=K(1+1/TS) K=R2/R1,T=R2C软件使用1、打开实验课题菜单,选中实验课题。

2、在课题参数窗口中,填写相应AD,DA或其它参数。

3、选确认键执行实验操作,选取消键重新设置参数。

实验步骤1、连接被测量典型环节的模拟电路及D/A、A/D连接,检查无误后接通电源。

2、启动应用程序,设置T和N。

参考值,T=0.05秒,N=200。

3、观测计算机屏幕示出的响应曲线及数据记录波形及数据(由实验报告确定)。

实验报告1、画出惯性环节、积分环节、比例加微分环节的模拟电路图,用坐标纸画出所有记录的惯性环节、积分环节、比例加微分环节的响应曲线。

2、由阶跃响应曲线计算出惯性环节、积分环节的传递函数,并与由电路计算的结果相比较。

实验二二阶系统阶跃响应一、实验目的1、研究二阶系统的特征参数,阻尼比ζ 和无阻尼自然频ωn 对系统动态性能的影响,定量分析ζ和ωn与最大超调量Mp和调节时间 ts 之间的关系。

2、进一步学习实验仪器的使用方法。

3、学会根据系统阶跃响应曲线确定传递函数。

自动控制原理实验报告 (频率特性测试)

自动控制原理实验报告（三）
频率特性测试
一．实验目的
1．了解线性系统频率特性的基本概念。

2．了解和掌握对数幅频曲线和相频曲线（波德图）的构造及绘制方法。

二．实验内容及步骤
被测系统是一阶惯性的模拟电路图见图3-2-1，观测被测系统的幅频特性和相频特性，填入实验报告。

本实验将正弦波发生器（B4）单元的正弦波加于被测系统的输入端，用虚拟示波器观测被测系统的幅频特性和相频特性，了解各种正弦波输入频率的被测系统的幅频特性和相频特性。

图3-2-1 被测系统的模拟电路图
实验步骤：
（1）将函数发生器（B5）单元的正弦波输出作为系统输入。

（2）构造模拟电路。

三．实验记录：
ω
ω=1
ω=1.6
ω=3.2
ω=4.5
ω=6.4
ω=8
ω=9.6
ω=16
实验分析：
实验中，一阶惯性环节的幅频特性)(ωL ，相频特性)(ωϕ随着输入频率的变化而变化。

惯性环节的时间常数T 是表征响应特性的唯一参数，系统时间常数越小，输出相应上升的越快，同时系统的调节时间越小。

【自控原理实验】实验三典型环节

实验三典型环节（或系统）的频率特性测量一．实验目的1．学习和掌握测量典型环节（或系统）频率特性曲线的方法和技能。

2．学习根据实验所得频率特性曲线求取传递函数的方法。

二．实验内容1．用实验方法完成一阶惯性环节的频率特性曲线测试。

2．用实验方法完成典型二阶系统开环频率特性曲线的测试。

3．根据测得的频率特性曲线求取各自的传递函数。

4．用软件仿真方法求取一阶惯性环节频率特性和典型二阶系统开环频率特性，并与实验所得结果比较。

三．实验步骤1．熟悉频率测试软件的使用方法，了解实验的线路的连接。

利用实验箱上的模拟电路单元，参考本实验附录设计并连接“一阶惯性环节”模拟电路或“两个一阶惯性环节串联”的二阶系统模拟电路。

2．利用实验设备完成一阶惯性环节的频率特性曲线测试。

（1）无上位机时，利用用户自配的信号源输出的正弦波信号作为环节输入，即连接信号源的“正弦波”与环节的输入端（例如对一阶惯性环节即图1.5.2的Ui）。

然后用示波器观测该环节的输入与输出（例如对一阶惯性环节即测试图1.5.2的Ui和Uo）。

注意调节正弦波信号的“频率”电位器RP与“幅值”电位器RP，测取不同频率时环节输出的增益和相移（测相移可用“李沙育”图形），从而画出环节的频率特性。

（2）有上位机时，必须在熟悉上位机界面操作的基础上，充分利用上位机提供的虚拟示波器与信号发生器功能。

一阶惯性环节接线方式如下：接线完成，经检查无误，再给实验箱上电后，启动上位机程序，进入主界面。

软件界面上的操作步骤如下：1、打开已经准备好的实验项目后，点击，使系统进入运行装态。

2、程序界面中的参数安照如下图所示设置（下图一般为默认设置无需修改参数）：3、测试信号为正弦波，请勿设置成其他波形，否则会造成程序运行的错误。

①选择D/A输出通道，如“O1”，将其作为环节输入，接到环节输入Ui 端, 将环节的输出端Uo 接到A/D 输入通道I1，再将其作为原始测试信号接到A/D 输入的I2（便于观看虚拟示波器发出的原始信号）。

典型环节的频率特性实验

实验报告
实验名称：
典型环节的频率特性实验
实验目的：
加深理解系统频率特性的物理概念；掌握系统频率特性的实验方法；
掌握频率特性的Bode 图Nquist图的绘制。

实验原理：
实验方法与步骤：
1. 在实验项目下拉框中选中[系统频率特性]实验并设置相应的实验参数。

2. 选择时间-电压图、信号发生器的频率：频率2、周期5（参考值），选《自动》采样。

数据采集过程如图所示：
3、待数据采样结束后点击按钮，即可显示出所测量的波特图。

4、在完成步骤3后，在显示区单击鼠标右键，即出现奈氏图。

实验内容：
1、做一阶系统的频率特性实验，画出该系统的Bode 图与Nquist图。

2、二阶系统的频率特性实验，画出该系统的Bode 图与Nquist图。

3、改变二阶系统的阻尼比ζ，观察欠阻尼与临界阻尼情况下的频率特性。

3、确定系统的转角频率、幅值穿越频率、截至频率的实测值。

●实验报告
1、图示一阶系统频率特性实验的Bode 图与Nquist图。

2、二阶振荡系统（欠阻尼）频率特性实验的Bode 图与Nquist图。

3、确定系统的转角频率、谐振频率、截至频率的实测值。

4、填写实验数据与响应曲线。

自动控制原理实验-系统频率特性的测量与分析

测奈氏图
7．在测量波特图的过程中首先应选择[实验课题→系统频率特性测量→测奈氏图→数据采样]采集信息。
8．待数据采样结束后点击[实验课题→系统频率特性测量→测奈氏图→图形观测]即可以在显示区内显示出所测量的波特图。
9．实验2、实验3涉及的主要命令有：Bode（）、rlocus()、rlocfind（）、margin()、nyquist()。
格式1：margin（sys）
格式2：margin（mag,phase,w）
格式3：[Gm,Pm, Wcg, Wcp]=margin（sys）
[Gm,Pm, Wcg , Wcp]=margin（mag,phase,w）
说明：margin函数可从频率响应数据中计算出幅值裕度(不是db)、相角裕度和剪切频率。
格式1：nyquist(sys) [re,im,w]=nyquist(sys)
格式2：nyquist(sys,w) [re,im,w]=nyquist(sys,w)
格式3：nyquist(sys,iu,w) [re,im,w]=nyquist(sys,iu w)
说明：sys为tf(),zpk(),ss()中任一种模型。
说明：nicholsh函数的输入变量定义与nyquist相同
3．bode求连续系统的Bode（伯德）频率响应
格式1：bode(sys) [mag,phase,w]= bode(sys)
格式2：bode(sys,w) [mag,phase,w]= bode(sys,w)
格式3：bode(sys,iu,w) [mag,phase,w]= bode(sys,iu w)
为便于比较，可用hold on指令将多条曲线放在一个图中。进一步，为清楚起见，用legend指令在图中加注释。用rlocus()画出根轨迹后，需要时用rlocfind（）找出临界稳定点。

自动控制原理实验-控制系统频率特性的测试..

实验四控制系统频率特性的测试1、实验目的认识线性定常系统的频率特性，掌握用频率特性法测试被控过程模型的原理和方法，根据开环系统的对数频率特性，确定系统组成环节的参数。

2、实验装置（1）PC586微型计算机。

（2）自动控制实验教学系统软件。

3、实验步骤及数据处理（1）首先确定被测对象模型的传递函数G （S ），根据具体情况，先自拟三阶系统的传递函数，)12)(1()(22221+++=s T s T s T K s G ξ，设置好参数K T T ,,,21ξ。

要求：1T 和2T 之间相差10倍左右，1T <2T 或2T <1T 均可，数值可在0.01秒和10秒之间选择，ξ取0.5左右，K ≤10。

设置T1=0.1，T2=1，ξ =0.5，K=5。

（3）设置好各项参数后，开始作仿真分析，首先作幅频特性测试。

①根据所设置的1T ，2T 的大小，确定出所需频率范围（低端低于转折频率小者10倍左右，高端高于转折频率高者10倍左右）。

所需频率范围是：0.1rad/s 到100rad/s 。

②参考实验模型窗口图，设置输入信号模块正弦信号的参数，首先设置正弦信号幅度Amplitude,例如设置Amplitude=1，然后设置正弦频率Frequency ，单位为rads/sec 。

再设置好X 偏移模块的参数，调节Y 示波器上Y 轴增益，使在所取信号幅度下，使图象达到满刻度。

③利用Y 示波器上的刻度（最好用XY 示波器上的刻度更清楚地观察），测试输入信号的幅值（用2m X 表示），也可以参考输入模块中设置的幅度，记录于表7--2中。

此后，应不再改变输入信号的幅度。

④依次改变输入信号的频率（按所得频率范围由低到高即ω由小到大慢慢改变，特别是在转折频率处更应多测试几点，注意：每次改变频率后要重新启动Simulation|Start 选项，观察“李沙育图形” 读出数据），利用Y 示波器上的刻度（也可以用XY 示波器上的刻度更清楚地观察，把示波器窗口最大化，此时格数增多更加便于观察），测试输出信号的幅值（用2m Y 表示），并记录于表7--2（本表格不够，可以增加）。

实验四典型环节和系统频率特性的测量

一、实验目的1、了解典型环节系和统的频率特性曲线的测量方法2、根据实验求得的频率特性曲线求取传递函数二实验设备1、THBDC-1型控制理论·计算机控制技术实验平台2、PC 机一台（含“THBDC-1”软件）、USB 数据采集卡、37针通信线1根、16芯数据排线、USB 接口线三实验内容（1）惯性环节的频率特性测试R1=R2=100K C=1uF R0=200K闭环传递函数为=)()(0S U S U i 1+TS K =实验记录Bode 图理论计算数据（2）二阶系统OP1，惯性环节，10.2S+1 ；OP2，积分环节，1S 10.1S ；OP3，反相，（-1）；25100:()52552X R K G S S S ==+⨯⨯+ ωn=2.236 ζ=1.118250R 10:()502505020X K G S S ==+⨯⨯+ ωn=7.071 ζ=0.3536实验记录波特图 Rx=100K实验记录波特图 Rx=10K仿真波特图 Rx=100K 仿真波特图 Rx=10K校正前观察响应曲线为校正后串联一个惯性装置波特图校正前后对比思考题：1、根据上位机测得的Bode图的幅频特性，就能确定系统（或环节）的相频特性，试问这在什么系统时才能实现？必须在开环二阶系统中，而且只能确定最小相位系统。

2、实验时所获得的性能指标为何与设计时确定的性能指标有偏差？因为在设计时，很多计算采用的近似计算，同时实验时用的电阻元件参数与设计不完全一致。

3.什么是超前校正装置和滞后校正装置，他们各利用矫正装置的什么特性对系统进行校正？答：超前校正装置用于改善系统的动态性能，实现在系统静态性能不受损的前提下，提高系统的动态性能。

通过加入超前校正环节，利用其相位超前特性来增大系统的相位裕度，改变系统的开环频率特性。

一般使校正环节的最大相位超前角出现在系统新的穿越频率点。

而滞后校正装置则通过加入滞后校正环节，使系统的开环增益有较大幅度增加，同时又使校正后的系统动态指标保持原系统的良好状态。

实验四控制系统频率特性的测试(实验报告)

实验四控制系统频率特性的测试一．实验目的认识线性定常系统的频率特性，掌握用频率特性法测试被控过程模型的原理和方法，根据开环系统的对数频率特性，确定系统组成环节的参数。

二．实验装置（1）微型计算机。

（2）自动控制实验教学系统软件。

三．实验原理及方法（1）基本概念一个稳定的线性定常系统，在正弦信号的作用下，输出稳态与输入信号关系如下：幅频特性相频特性（2）实验方法设有两个正弦信号：若以)(t x ω为横轴，以)(y t ω为纵轴，而以t ω作为参变量，则随t ω的变化，)(t x ω和)(y t ω所确定的点的轨迹，将在 x--y 平面上描绘出一条封闭的曲线（通常是一个椭圆）。

这就是所谓“李沙育图形”。

由李沙育图形可求出Xm ，Ym ，φ，四．实验步骤（1）根据前面的实验步骤点击实验七、控制系统频率特性测试菜单。

（2）首先确定被测对象模型的传递函数, 预先设置好参数 T1、T2、ξ、K（3）设置好各项参数后，开始仿真分析，首先做幅频测试，按所得的频率范围由低到高，及ω由小到大慢慢改变，特别是在转折频率处更应该多取几个点五.数据处理（一）第一种处理方法：（1）得表格如下：（2）作图如下：（二）第二种方法：由实验模型即，由实验设置模型根据理论计算结果绘制bode 图，绘制Bode 图。

（三）误差分析两图形的大体趋势一直，从而验证了理论的正确性。

在拐点处有一定的差距，在某些点处也存在较大的误差。

分析：（1）在读取数据上存在较大的误差，而使得理论结果和实验结果之间存在。

（2）在数值应选取上太合适，而使得所画出的bode图形之间存在较大的差距。

（3）在实验计算相角和幅值方面本来就存在着近似，从而使得误差存在，而使得两个图形之间有差异六.思考讨论（1）是否可以用“李沙育”图形同时测量幅频特性和想频特性答：可以。

在实验过程中一个频率可同时记录2Xm，2Ym，2y0。

（2）讨论用“李沙育图形”测量频率特性的精度，即误差分析（说明误差的主要来源）答：用“李沙育图形”测量频率特性的精度从上面的分析处理上也可以看出是比较高的，但是在实验结果和理论的结果之间还是存在一定的差距，这些误差主要来自于从“李沙育图形”上读取数据的时候存在的误差，也可能是计算机精度方面的误差。