数学实验习题解答
Matlab与数学实验(第二版)(张志刚 刘丽梅 版) 习题答案

Matlab与数学实验(第二版)(张志刚刘丽梅版)习题答案(1,3,4,5章)第一章d1zxt1用format的不同格式显示2*Pi,并分析格式之间的异同。
a=2*pi ;disp('***(1) 5位定点表示2*pi:')format short , a % 5位定点表disp('***(2) 15位定点表示2*pi:')format long , a % 15位定点表disp('***(3) 5位浮点表示2*pi:')format short e , a % 5位浮点表示disp('***(4) 15位浮点表示2*pi:')format long e , a % 15位浮点表示disp('***(5) 系统选择5位定点和5位浮点中更好的表示2*pi:')format short g , a % 系统选择5位定点和5位浮点中更好的表示disp('***(6) 系统选择15位定点和15位浮点中更好的表示2*pi:')format long g , a % 系统选择15位定点和15位浮点中更好的表disp('***(7) 近似的有理数的表示2*pi:')format rat , a % 近似的有理数的表disp('***(8) 十六进制的表示:')format hex , a % 十六进制的表disp('***(9) 用圆角分(美制)定点表示2*pi:')format bank , a % 用圆角分(美制)定点表示d1zxt2利用公式求Pi的值。
sum=0 ;n=21;for i = 1:4:n % 循环条件sum= sum+(1/i) ; % 循环体enddiff=0 ;for j = 3:4:(n-2) % 循环条件diff= diff+(1/j) ; % 循环体endpai=4*(sum-diff)d1zxt3 编程计算1!+3!+...+25!的阶乘。
数学实验(MATLAB)课后习题答案
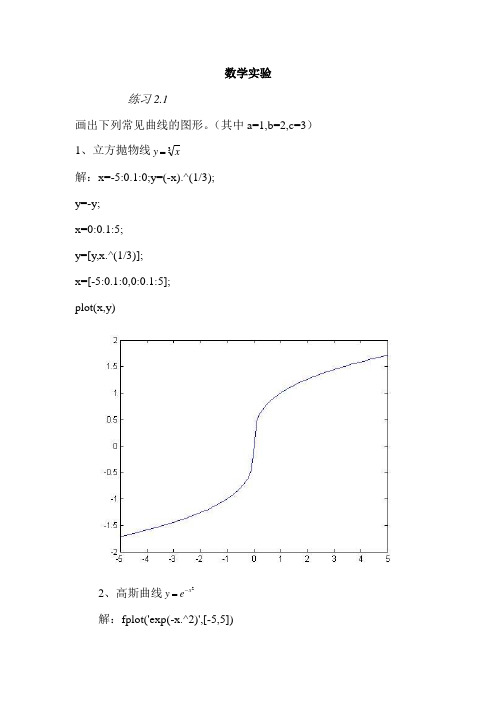
数学实验练习2.1画出下列常见曲线的图形。
(其中a=1,b=2,c=3)1、立方抛物线3xy=解:x=-5:0.1:0;y=(-x).^(1/3);y=-y;x=0:0.1:5;y=[y,x.^(1/3)];x=[-5:0.1:0,0:0.1:5];plot(x,y)2、高斯曲线2x e=y-解:fplot('exp(-x.^2)',[-5,5])3、笛卡儿曲线)3(13,1333222axy y x t at y t at x =++=+=解:ezplot('x.^3+y.^3-3*x*y',[-5,5])xyx.3+y.3-3 x y = 0或t=-5:0.1:5; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)4、蔓叶线)(1,1322322xa x y t at y t at x -=+=+=解:ezplot('y.^2-x.^3/(1-x)',[-5,5])xyy.2-x.3/(1-x) = 0或t=-5:0.1:5; x=t.^2./(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)5、摆线)cos 1(),sin (t b y t t a x -=-= 解:t=0:0.1:2*pi;x=t-sin(t); y=2*(1-cos(t)); plot(x,y)6、星形线)(sin ,cos 32323233a y x t a y t a x =+== 解:t=0:0.1:2*pi; x=cos(t).^3; y=sin(t).^3;plot(x,y)或ezplot('x.^(2/3)+y.^(2/3)-1',[-1,1])xyx.2/3+y.2/3-1 = 07、螺旋线ct z t b y t a x ===,sin ,cos 解:t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z) grid on8、阿基米德螺线θa r = 解:x =0:0.1:2*pi; r=x; polar(x,r)902701809、对数螺线θa e r = 解:x =0:0.1:2*pi; r=exp(x); polar(x,r)90270180010、双纽线))()((2cos 22222222y x a y x a r -=+=θ 解:x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-(x.^2-y.^2)',[-1,1]) grid onxy(x.2+y.2).2-(x.2-y.2) = 011、双纽线)2)((2sin 222222xy a y x a r =+=θ 解:x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-2*x*y',[-1,1]) grid onxy(x.2+y.2).2-2 x y = 012、心形线)cos 1(θ+=a r 解:x =0:0.1:2*pi; r=1+cos(x); polar(x,r)90270练习2.21、求出下列极限值。
华东师范大学第二附属中学(实验班用)数学习题详解-20

第十九章 导数及其应用19.1 函数的极限 基础练习1.判断下列函数的极限是否存在,并说明理由:(1)1lim πxx →+∞⎛⎫⎪⎝⎭. (2)lim 2x x →-∞.(3)31lim x x →∞.解:(1)()1lim 0.2πxx →+∞⎛⎫= ⎪⎝⎭()lim 20.3x x →-∞=(3)31lim0x x →∞=(理由说明略). 2.根据函数极限的εδ-定义,求下列函数的极限: (1)132lim1x x x →-+. (2)2lim 21x x →-.解:(1)1321lim12x x x →-=+.(2)2lim 213x x →-=. 3.求下列函数的极限: (1)()22lim 33x x x →--. (2)22123lim 1x x x x →--+-. (3)2224lim 321x x x x x →-∞-+-+.(4)232306lim 253x x x x x x x →----. (5)()*11lim 1m n x x m n x →-∈-N ,. (6)30lim x x x x →-. (7)[]()1lim x x x →---. (8)21211lim 21x x x x x →+⎛⎫- ⎪+--⎝⎭. 解:()22lim 331x x x →--=.(2)不存在.(3)2222142242lim lim 2132133x x x x x x x x x x→-∞→-∞-+-+==-+-+. (4)232232006161lim lim 2532532x x x x x x x x x x x x →→----==----. (5)()()()()121212*********lim lim lim 1111m m m m m n n n n n x x x x x x x x x m x x x n x x x --------→→→-+++-+++===-+++-+++ . (6)332001limlimlim 11x x x x x x x x x x →→→-===----. (7)[]()()11lim lim 21x x x x x →--→---=+=.(8)22111121121211lim lim lim 212223x x x x x x x x x x x x x x →→→+++⎛⎫⎛⎫-=-== ⎪ ⎪+--+-+-+⎝⎭⎝⎭. 能力提高4.设正数a b ,满足()22lim 4x x ax b →+-=,求111lim 2n n n nx a ab a b +--→∞++.解:()22lim 42x x ax b a b →+-=⇒=1211111lim lim 2242n n n n n nn n a a aa ab a b a b b a b b -+---→∞→∞⎛⎫+ ⎪+⎝⎭===+⎛⎫+ ⎪⎝⎭. 5.把()()()21111nx x x +++++++ 展开成关于x 的多项式,其各项系数和为n a ,求21lim 1n n na a →∞-+.解:令1x =,得到各项系数和:21122221n n n a +=++++=- . 则212123limlim 212n n n n n na a ++→∞→∞--==+. 6.若241lim 01n x axb x →∞⎛⎫+-+= ⎪+⎝⎭,求a b ,的值.解:()()22414111a xb a x b x ax b x x -+-+++-+=++, ()()224141lim lim 011x x a x b a x b x ax b x x →∞→∞⎛⎫-+-++⎛⎫+-+== ⎪ ⎪ ⎪++⎝⎭⎝⎭. 则40a -=,0b a -=,得出4a =,4b =.7.设()f x 为多项式,且()()34limlim 1x n f x x f x x x→∞→∞-==,求()f x 的表达式. 解:()()334lim14x f x x f x x x m x →∞--=⇒=++,()m ∈R , ()200lim1lim 4110x x f x m x m xx →→⎛⎫=⇒++=⇒= ⎪⎝⎭,则()f x 的表达式为()34f x x x =+.8.已知函数()231121x x f x x a x ⎧-⎪=⎨+>⎪⎩,,≤,试确定常数a ,使()1lim x f x →存在.解:()()11lim lim 02x x f x f x a -+→→=⇒=+,则2a =-. 9.设函数()2210x x f x x b x ⎧+>=⎨+⎩,,≤,当b 取什么值时,()0lim x f x →存在?解:()()0lim lim 1x x f x f x b -+→→=⇒=,当1b =时,()0lim x f x →存在. 19.2 两个重要极限 1.求下列函数的极限: (1)0tan limx x x →. (2)0tan lim x kxx→.(3)01sin cos lim 1sin cos x x x tx tx →+-+-. (4)212lim 1x x x -→∞⎛⎫+⎪⎝⎭.解:(1)0000tan sin 1sin 1lim lim lim lim 1cos cos x x x x x x x x x x x x→→→→=⋅=⋅=.(2)000sin sin limlim lim cos cos x x x kx k kx kk kx kx kx kx→→→=⋅=.(3)200022sin sin cos sin 2sin 1sin cos 2222lim lim lim 1sin cos sin 2sin 2sin sin cos 2222x x x x x x x x x x tx tx tx tx tx tx tx →→→⎛⎫++ ⎪+-⎝⎭==+-⎛⎫++ ⎪⎝⎭00sinsin cos 1222lim lim sin sin cos222x x x x xtx tx tx t →→+=⋅=+. (4)212221421lim 1lim 12x xxx x x e x x --→∞→∞⎡⎤⎛⎫⎢⎥ ⎪⎛⎫⎢⎥+=+= ⎪ ⎪⎢⎥⎝⎭ ⎪⎢⎥⎝⎭⎢⎥⎣⎦.2.证明()0ln 1lim1x x x →+=.证明:()()()110ln 1limlim ln 1ln lim 1ln 1xxx x x x x x e x→→→+=+=+==,3.证明01lim 1x x e x→-=.证明:令1xt e =-,则()ln 1x t =+,当0x →时,0t →,()001limlim 1ln 1x x x e txt →→-==+. 19.3 函数的连续性1.试判断下列函数在给定点处是连续?并说明理由. (1)()112121xx f x -=+,在00x =处.(2)()2ln 00x x f x x x >⎧=⎨⎩,,≤,在00x =处;(3)10sgn 00x y x x ≠⎧==⎨=⎩,点0x =.解:(1)左、右极限都存在,1121lim 121xx x-→-=-+,1121lim 121xx x+→-=+,但不相等,在0x =处不连续.(2)左极限都存在,右极限不存在,在0x =处不连续.(3)()()0lim 1lim x x f x f x -+→→==,()()0lim 100x f x f →=≠=,所以函数sgn y x =在0x =处不连续. 2.求下列函数的极限: (1)π4limlg tan x x →.(2)()sec cot 0lim 1tan x xx x →+.(3)()lim sin 1sin x x x →+∞+-.(4)()2lim arccosx x x x →+∞+-.解:(1)π4limlg tan lg10x x →==.(2)()sec cot sec cot 001lim 1tan lim 1cot xxx xx x x e x →→⎛⎫⎛⎫+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭.(3)()11sin 1sin 2sin cos 221x x x x x x ⎛⎫⎛⎫++ ⎪+-= ⎪ ⎪ ⎪++⎝⎭⎝⎭,1lim cos 021x x x →+∞⎛⎫= ⎪++⎝⎭,则()lim sin 1sin 0x x x →+∞+-=. (4)()2211lim lim lim 2111x x x x x x x x x x x →+∞→+∞→+∞⎛⎫⎪⎛⎫ ⎪+-=== ⎪ ⎪++⎝⎭++ ⎪⎝⎭, 则()2πlim arccos 3x x x x →+∞+-=. 3.求函数在0x =处的极限:(1)()2200010x x f x x x x ⎧>⎪==⎨⎪+<⎩.(2)()ln cos5f x x =.(3)()()20a x af x a x +-=>, (4)()arctan 2x f x x=.(5)()sin 211x f x x =+-.(6)()()211cos 1cos xa x f x x+-=-.解:(1)()()0lim lim 1x x f x f x -+→→==,则极限为()0lim 0x f x →=. (2)极限为()()0lim lim lncos50x x f x x →→==.(3)极限为()2200011lim lim lim 2x x x a x a f x x a a x a→→→+-===++. (4)极限为()00arctan122lim limlim 2x x x x xf x x x →→→===.(5)极限为()()()000sin 2sin 2sin 2lim limlim 11limlim1122411x x x x x x x xf x x x xxx →→→→→==++=⋅++=⋅=+-.(6)()()()()0021sin sin lim lim2lim 2lim cot 1cos 22sin 2xx x x x a x x xf x xx----→→→→+⋅--===--不存在,则极限不存在. 4.求下列函数的极限:(1)1123lim2x x x →+--.(2)()2π2lim2sin cos x x x x →--.(3)()222sin lim 1x x x xe x →++.(4)()11lim 1x x x -→+.(5)()2lim arcsinx x x x →+∞+-. (6)22sin sin limx a x ax a→--. 解:(1)44412328224limlim2lim 432123123x x x x x x x x x x x →→→+--++=⋅==--++++.(2)()222π2ππlim2sin cos 21244x x x x →⎛⎫--=-=- ⎪⎝⎭.(3)22222sin 4sin 2limlim51xx x x x e ex→→++=+.(4)()111100011lim 1lim 1lim 111xx x x x x e x x --→→→⎛⎫⎛⎫⎪ ⎪+=+⋅+= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭.(5)()2211lim lim lim 2111x x x x x x x x x x x →+∞→+∞→+∞⎛⎫⎪⎛⎫ ⎪+-=== ⎪ ⎪++⎝⎭++ ⎪⎝⎭, 则()2πlim arcsin 6x x x x →+∞+-=. (6)()()22sin sin sin sin sin sin lim lim x a x a x a x a x ax a x a→→+--=--()cossin sin sin 22limlim sin sin 2sin lim2sin cos sin 22x a x a x a x a x ax ax a a a a a x a x a→→→+--=+===--. 能力提高5.求20lim lim cos cos cos cos 222n x n x x x x →→∞⎡⎤⎛⎫ ⎪⎢⎥⎝⎭⎣⎦ 的值.解:22cos cos cos cos sin 2222cos cos cos cos 222sin 2n n n n x x x x x x x x x x = 1sin 221sin 2n n x x +=, 11211sin 2sin 2sin 222lim cos cos cos cos lim lim 2222sin 22n n n x x x nnx x x x x x x x x x ++→∞→∞→∞⎛⎫===⎪⎝⎭ ,2200sin 2lim lim cos cos cos cos lim cos cos cos cos lim 12222222n n x n n x x x x x x x x x x x →→∞→∞→⎡⎤⎛⎫⎛⎫=== ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ . 6.研究函数()221lim 1n nn x f x x x →+∞-=⋅+的连续性.解:当1x >时,()2222111lim lim 111nnn n n x x x f x x x x x x →+∞→+∞⎛⎫- ⎪-⎝⎭=⋅=⋅=-+⎛⎫+ ⎪⎝⎭; 当1x <时,()221lim 1nnx x f x x x x →+∞-=⋅=+;当1x =时,()0f x =,则()1011x x f x x x x ⎧<⎪==⎨⎪->⎩,,,,由于()()11lim lim 1x x f x x --→-→-=-=,()11lim lim 1x x f x x ++→-→-==-,则()1lim x f x →-不存在;又()11lim lim 1x x f x x --→→==,()()11lim lim 1x x f x x ++→→=-=-则()1lim x f x →不存在. 则()f x 在1x =±处不连续,()f x 在定义域内的其余点都连续,即在区间()1-∞-,、(-1,1)和(1,+∞)上分别连续.7.讨论[]01,上黎曼函数()()()*11101p x p q p q p p qq R x x x ⎧==∈⎪=⎨⎪=⎩N ,,其中,,,,,,,理≤≤无数的连续性. 证明:设()01ξ∈,为无理数,任给0ε>(不妨设12ε<), 满足1qε≥正数显然只有有限个q (但至少有一个,如2q =),从而使()R x ε≥的有理数()01x ∈,只有有限个(至少有一个,如12),设为1n x x ,,,取 ()1min 1n x x δξξξξ=--- ,,,,,(显然0δ>) 则对任何()()()01x U ξδ∈⊂,,,当x 为有理数时有()R x ε<,当x 为无理数时()0R x =.于是,对任何()x U ξε∈,,总有()()()R x R R x ξε-=<, 这就证明了()R x 在无理点ξ处连续. 现设p q为(0,1)内任一有理数,取012q ε=,对任何正数δ(无论多少小),在p U q δ⎛⎫ ⎪⎝⎭,内总可取无理数()()001x ∈,,使得()001p R x R q qε⎛⎫-=> ⎪⎝⎭,所以()R x 在任何有理点处都不连续. 19.4 导数的概念与运算 1.求下列函数的导数: (1)42356y x x x =--+.(2)tan y x x =⋅. (3)()()()123y x x x =+++.(4)11x y x -=+. 解:(1)3465y x x =--′.(2)2tan cos x y x x =+′.(3)231211y x x =++′.(4)()221y x =+′. 2.求下列函数的导数: (1)579x x x y x++=. (2)44sin cos 44x xy =+. (3)1111x x y xx+-=+-+.(4)2sin 12cos 24x x y ⎛⎫=-- ⎪⎝⎭. 解:(1)32432y x x x =++′,(2)1sin 4y x =-′.(3)()241y x =-′,(4)1cos 2y x =′. 3.求下列函数的导数: (1)21y x x =+. (2)()2223x y x x e =-+⋅. (3)3223x y x -=+.(4)31xy x=-. 解:(1)22211x y x +=+′.(2)()22224x y x x e =-+⋅′.(3)()21323y x =+′.(4)()23211311x y x x -⎛⎫= ⎪-⎝⎭-′.能力提高4.如图19-5,函数()f x 的图像是折线段ABC ,其中A B C ,,的坐标分别为(0,4),(2,0),(6,4),则()()0f f =__________;函数()f x 在1x =处的导数()1f =′__________.图 19-5y OxABC4321564321解:()()042f f f ==⎡⎤⎣⎦,()041220f -==--′. 5.若()02f x =′,求()()000lim2k f x k f x k→--.解:()()()()0000001limlim 122k k f x k f x f x k f x kk→→----=-=--.6.求下列函数的导数:(1)()()21231y x x x =-+-.(2)3231x x x y x x -++=.(3)()2cos y ax b =+.(4)1sin 21sin 2xy x-=+.(5)()1ln 11x y x x -=>+.(6)42ln1x y x =+.解:(1)6102y x x =++′.(2)135222233322y x x x x ---=+-+′. (3)()sin 2y a ax b =-⋅+⎡⎤⎣⎦′. (4)()2cos 2cos 21sin 2x y x x -=+′. (5)211y x =-′.(6)241xy x x =-+′. 7.已知函数()y f x =是可导的周期函数,试救证其导函数()y f x =′也为周期函数. 证明:()()()()()()0limlimr r f x x f x f x x T f x T f x f x T xxδδδδδδ→→+-++-+===+′′.8.若可导函数()f x 是奇函数,求证:其导函数()f x ′是偶函数. 证明:函数()f x 是奇函数,所以()()f x f x -=-,()()()()()()d d d d f x f x f x f x f x f x x x--⎡⎤⎡⎤⎣⎦⎣⎦=⇒-=--⇒=-′′′′所以导函数()f x ′是偶函数,显然得证.19.5 导数的应用 基础练习1.(1)曲线3231y x x =-+在点(1,-1)处的切线方程为__________.(2)过曲线11y x =+上点112P ⎛⎫⎪⎝⎭,且与过P 点的切线夹角最大的直线的方程为__________. (3)曲线sin 3y x =在点π03P ⎛⎫⎪⎝⎭,处切线的斜率为__________.(4)函数2y x =的曲线上点A 处的切线与直线310x y -+=的夹角为45︒,则点A 的坐标为__________.(5)曲线2122y x =-与3124y x =-在交点处的切线夹角是__________.解:(1)2363y x x y =-⇒=-′′,则切线方程为32y x =-+. (2)()21141y y x =-⇒=-+′′,则夹角最大为π2,所以过曲线11y x =+上点112P ⎛⎫ ⎪⎝⎭,且与过P 点的切线夹角最大的直线的斜率为4,则直线方程为:2870y x -+=. (3)3cos33y x y =⇒=′′. (4)设切线的斜率为k ,231232013k k k k -=⇒+-=+,2k =-,12, 因为22y x ==-′,112x ⇒=-,14,所以点A 的坐标为11416⎛⎫⎪⎝⎭,或()11-,. (5)23122124y x y x ⎧=-⎪⎪⎨⎪=-⎪⎩()()322216024802x x x x x x ⇒+-=⇒-++=⇒=.21222y x y x y =-⇒=-⇒=-′′,32132344y x y x y =-⇒=⇒=′′.则夹角是()()32πarctan1324--=+⋅-. 2.(1)设函数32y ax bx cx d =+++的图像与y 轴交点为P 点,且曲线在P 点处的切线方程为1240x y --=.若函数在2x =处取得极值0,试确定函数的解析式.(2)若函数()f x 在区间[]a b ,内恒有()0f x <′,则求函数的[]a b ,上的最小值. (3)求曲线4321111432y x x x x =+--+的极值点. 解:(1)令()32y f x ax bx cx d ==+++,则()232f x ax bx c =++′, 则()21240f a b c =++=′,()012f c ==′ ()28420f a b c d =+++=,12040d ⋅--=解得:29124a b c d =⎧⎪=-⎪⎨=⎪⎪=-⎩,则函数的解析式为3229124y x x x =-+-.(2)函数()f x 在区间[]a b ,内恒有()0f x <′,所以()f x 在区间[]a b ,单调递减,因此函数在[]a b ,上的最小值为()f b .(3)()()3222111y x x x x x =+--=-+′,因此在1x =时有极小值. 3.求下列函数的单调区间: (1)()()212y x x =++. (2)21xy x=+. (3)x y xe =.(4)lg y x x =.解:(1)()()135y x x =++′,单调递增区间为53⎛⎤-∞- ⎥⎝⎦,和[)1-+∞,,单调递减区间为513⎛⎫-- ⎪⎝⎭,.(2)()22211x y x -+′=,单调递增区间为(-1,1),单调递减区间为(]1-∞-,.(3)()1x y e x =+′,单调递增区间为[)1-+∞,,单调递减区间为(]1-∞-,. (4)ln 1ln10x y +=′,单调递增区间为1e ⎛⎫+∞ ⎪⎝⎭,,单调递减区间为10e ⎛⎫ ⎪⎝⎭,.4.求下列函数的极值或最值:(1)[]3239544y x x x x =--+∈-,,. (2)2sin y x x =+,[]02πx ∈,. (3)()231y x x =-.(4)2ln x y x=. 解:(1)2369y x x =--′,单调递增区间为(]1-∞-,和[)3+∞,,单调递减区间为(-1,3), 当1x =-时取到极大值10y =,当3x =时取到极小值22y =-.(2)12cos y x =+′,单调递增区间为2π03⎡⎤⎢⎥⎣⎦,和4π2π3⎡⎤⎢⎥⎣⎦,,单调递减区间为2π4π33⎛⎫⎪⎝⎭,, 当2π3x =时取到极大值2π33y =+,当2π3x =时取到极小值4π33y =-. 当0x =时取到最小值0y =,当2πx =时取到最大值2πy =; (3)()13523x y x -=-′,单调递增区间为25⎛⎫+∞ ⎪⎝⎭,,单调递减区间为205⎛⎫ ⎪⎝⎭,, 当25x =时取到极小值332025y =-.(4)2ln 12ln x y x-=′,单调递增区间为()e +∞,,单调递减区间为()0e ,, 当e x =时取到极小值2e y =. 5.当0x >时,证明下列不等式成立:(1)()2ln 12x x x +>-.(2)24cos 1224x x x <-+.证明:(1)令()()2ln 12x f x x x ⎛⎫=+-- ⎪⎝⎭,()211011x f x x x x =+-=>++′, 所以()f x 在区间()0+∞,上单调递增,则()()()2ln 1002x f x x x f ⎛⎫=+-->= ⎪⎝⎭,则()2ln 12x x x +>-,显然得证.(2)令()241cos 224x x f x x =-+-,()()3sin 6x g x f x x x ==-++′,()()2cos 12x h x g x x ==+-′,()()sin x h x x x ϕ==-′,()1cos 0x x ϕ=+′≥, 则()sin x x x ϕ=-在区间()0+∞,上单调递减,所以()()sin 00x x x ϕϕ=->=,则()2cos 12x h x x =+-在区间()0+∞,上单调递增,所以()()2cos 1002x h x x h =+->=,则()3sin 6x g x x x =-++在区间()0+∞,上单调递增,所以()()3sin 006x g x x x g =-++>=,则()241cos 224x x f x x =-+-在区间()0+∞,上单调递增,所以()()241cos 00224x x f x x f =-+->=,即24cos 1224x x x <-+得证.6.设()()21e x f x ax x -=+-⋅(e 为自然对数的底,a 为常数且0a <,x ∈R ),则()f x 何时取得极小值?解:()()()21212e 2e x xf x ax a x a x x a --⎛⎫⎡⎤=-+-+=-+- ⎪⎣⎦⎝⎭′, 当102a -<<时,1x a =-时,()f x 取得极小值;当12a <-时,2x =时,()f x 取得极小值.7.求抛物线212y x =上与点()60A ,距离最近的点. 解:任取抛物线上一点212x x ⎛⎫ ⎪⎝⎭,,则()22442116123644z d x x x x x ==-+=+-+.()()32212226z x x x x x =+-=-++′,则在()2-∞,单调递减,()2+∞,单调递增,则抛物线212y x =上与点()60A ,距离最近的点是(2,2). 能力提高8.已知函数()323f x ax bx x =+-在1x =±处取得极值.(1)讨论()1f 和()1-是函数()f x 的极大值还是极小值. (2)过点()016A ,作曲线()y f x =的切线,求此切线方程. 解:(1)函数()323f x ax bx x =+-在1x =±处取得极值()0f x ⇔=′的解为32313230a b x a b +-=⎧=±⇔⎨--=⎩1a b =⎧⇒⎨=⎩,则()33f x x x =-, 则()12f -=是极大值,()12f =-是极小值.(2)设切点为()33M m m m -,,则切线方程为()()23333y m x m m m =--+-. 过点()016A ,,则()()23316330382m m m m m m =--+-⇔=-⇒=-, 则切点为()22M --,,则切线方程为9160x y -+=.9.设函数()()20f x ax bx k k =++>在0x =处取得极值,且曲线()y f x =在点()()11f ,处的切线垂直于直线210x y ++=.(1)求a b ,的值.(2)若函数()()xe g xf x =,讨论()g x 的单调性.解:(1)因()()20f x ax bx k k =++>,故()2f x ax b =+′; 又()f x 在0x =处取得极限值,故()0f x =′,从而0b =.由曲线()y f x =在()()11f ,处的切线与直线210x y -+=相互垂直可知: 该切线斜率为2,即()12f =′,有22a =,从而1a =.(2)由(1)知,()()20x e g x k x k =>+,()()()()22220x e x x k g x k x k -+=>+′. 令()0g x =′,有220x x k -+=.①当440k ∆=-<,即当1k >时,()0g x >′在R 上恒成立,故函数()g x 在R 上为增函数. ②当440k ∆=-=,即当1k =时,()()()()222100x e x g x x xk -=>≠+′,1k =时,()g x 在R 上为增函数.③440k ∆=->,即当01k <<时,方程220x x k -+=有两个不相等实根,111x k =--,211x k =+-.当()11x k ∈-∞--,是()0g x >′,故()g x 在()11k -∞--,上为增函数,当()1111x k k ∈--+-,时,()0g x <′,故()g x 在()1111k k --+-,,上为减函数,10.已知函数()3213f x x ax bx =++,且()10f -=′.(1)试用含a 的代数式表示b .(2)求()f x 的单调区间.(3)令1a =-,设函数()f x 在()1212x x x x <,处取得极值,记点()()11M x f x ,,()()22N x f x ,,证明:线段MN 与曲线()f x 存在异于M N 、的公共点.解:(1)依题意,得()22f x x ax b =++′,由()1120f a b -=-+=′得21b a =-. (2)由(1)得()()321213f x x ax a x =++-,故()()()2221121f x x ax a x x a =++-=++-′,令()*0f x =′,则1x =-或12x a =-.①当1a >时,121a -<-当x 变化时,()f x ′与()f x 的变化情况如下表:x()12a -∞-,()21a --, ()1-+∞, ()f x ′ + - + ()f x单调递增单调递减单调递增由此得,函数()f x 的单调增区间为()12a -∞-,和()1-+∞,,单调减区间为()121a --,. ②由1a =时,121a -=-,此时,()0f x ′≥恒成立,且仅在1x =-处()0f x =′,故函数()f x 的单调区间为R .③当1a <时,121a ->-,同理可得函数()f x 的单调增区间为()1-∞-,和()12a -+∞,,单调减区间为()112a --,. 综上:当1a >时,函数()f x 的单调增区间为()12a -∞-,和()1-+∞,,单调减区间为()121a --,; 当1a =时,函数()f x 的单调增区间为R ;当1a <时,函数()f x 的单调增区间为()1-∞-,和()12a -+∞,,单调减区间为()112a --,. (3)当1a =-时,得()32133f x x x x =--,由()3230f x x x =--=′,得11x =-,23x =.由(2)得()f x 的单调增区间为()1-∞-,和()3+∞,,单调减区间为(-1,3), 所以函数()f x 在11x =-,23x =处取得极值.故513M ⎛⎫- ⎪⎝⎭,,()39N -,.所以直线MN 的方程为813y x =--.由32133813y x x x y x ⎧=--⎪⎪⎨⎪=--⎪⎩,得32330x x x --+=. 令()3233F x x x x =--+,易得()030F =>,()230F =-<,而()F x 的图像在(0,2)内是一条连续不断的曲线, 故()F x 在(0,2)内存在零点0x ,这表明线段MN 与曲线()f x 有异于M ,N 的公共点. 11.设定义在R 上的函数()()43201230123i f x a x a x a x a x a i =+++∈=R ,,,,,当22x =-时,()f x 取得极大值23,并且函数()y f x =′的图像关于y 轴对称. (1)求()f x 的表达式.(2)试在函数()f x 的图像上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在区间[-1,1]上.(3)求证:()()()22sin cos 3f x f x x -∈R ≤. 解:(1)由于()320123432f x a x a x a x a =+++′为偶函数,则()()f x f x -=′′, 则323201230123432432a x a x a x a a x a x a x a -+-+=+++, 则302420a x a x +=对一切x ∈R 恒成立, 则020a a ==,则()313f x a x a x =+, 又当22x =-时,()f x 取得极大值23, 则2223202f f ⎧⎛⎫-=⎪ ⎪ ⎪⎪⎝⎭⎨⎛⎫⎪-= ⎪⎪ ⎪⎝⎭⎩′,解得13231a a ⎧=⎪⎨⎪=-⎩,则()3233f x x =-,()221f x x =-′.(2)设所求两点的横坐标为1x ,()212x x x <,则()()221221211x x -⋅-=-, 又由于1x ,[]211x ∈-,,则2121x -,[]222111x -∈-,,则2121x -,2221x -中有一个为1,一个为-1,则1201x x =⎧⎨=⎩或1210x x =-⎧⎨=⎩,则所求的两点为(0,0)与113⎛⎫- ⎪⎝⎭,或(0,0)与113⎛⎫- ⎪⎝⎭,.(3)证明:易知sin x ,[]cos 11x ∈-,.当202x ⎡⎤∈⎢⎥⎣⎦,时,()0f x <′;当212x ⎡⎤∈⎢⎥⎣⎦,时,()0f x >′. 则()f x 在202⎡⎤⎢⎥⎣⎦,为减函数,在212⎡⎤⎢⎥⎣⎦,上为增函数,又()00f =,2223f ⎛⎫=- ⎪ ⎪⎝⎭,()113f =-,而()f x 在[]11-,上为奇函数, 则()f x 在[]11-,上最大值为23,最小值为23-,即()23f x ≤,则()2sin 3f x ≤,()2cos 3f x ≤,则()()()()22sin cos sin cos 3f x f x f x f x -+≤≤. 12.已知函数()sin f x x x =-,(1)若[]0πx ∈,,试求函数()f x 的值域. (2)若[]0πx ∈,,()0πθ∈,,求证:()()2233f f x x f θθ++⎛⎫ ⎪⎝⎭≥.(3)若()π1πx k k ∈+⎡⎤⎣⎦,,()π1πk k θ∈+⎡⎤⎣⎦,,∈Z ,猜想()()23f f x θ+与23x f θ+⎛⎫⎪⎝⎭的大小关系(不必写出比较过程).解:(1)当()0πx ∈,时,()1cos 0f x x =->′,则()f x 为增函数.又()f x 在区间[]0π,上连续,所以()()()0πf f x f ≤≤,求得()0πf x ≤≤,即()f x 的值域为[]0π,. (2)设()()()2233f f x x g x f θθ++⎛⎫=-- ⎪⎝⎭.即()()2sin 2sin33f xx g x θθ++=-+,()12cos cos 33x g x x θ+⎛⎫=-+ ⎪⎝⎭′, 由于[]0πx ∈,,()0πθ∈,,则()20π3xθ+∈,,由()0g x =′,得x θ=,则当()0x θ∈,时,()0g x <′,()g x 为减函数,当()πx θ∈,时,()0g x >′,()g x 为增函数. 由于()g x 在区间[]0π,上连续,则()g θ为()g x 的最小值 对[]0πx ∈,有()()0g x g θ=≥,因而()()2233f f x x f θθ++⎛⎫⎪⎝⎭≥.(3)在题设条件下,当k 为偶数时,()()2233f f x x f θθ++⎛⎫ ⎪⎝⎭≥,当k 为奇数时,()()2233f f x x f θθ++⎛⎫ ⎪⎝⎭≤.。
浙江省瑞安市实验小学六年级数学下册解决问题解答应用题练习题60带答案解析

浙江省瑞安市实验小学六年级数学下册解决问题解答应用题练习题60带答案解析一、人教六年级下册数学应用题1.为了测量一个空瓶子的容积,一个学习小组进行了如下实验。
①测量出整个瓶子的高度是22厘米;②测量出瓶子圆柱形部分的内直径是6厘米;③给瓶子里注入一些水,把瓶子正放时,测量出水的高度是5厘米;④把瓶盖拧紧,将瓶子倒置放平,无水部分是圆柱形,测量出无水部分圆柱的高度是12厘米。
(1)要求这个瓶子的容积,上面记录中的哪些信息是必须有的?________(填实验序号)(2)请根据选出的信息,求出这个瓶子的容积。
2.水果店里西瓜个数与哈密瓜个数的比为7:5,如果每天卖哈密瓜40个,西瓜50个,若干天后,哈密瓜正好卖完,西瓜还剩36个。
水果店里原来有西瓜多少个?3.以小强家为观测点,量一量,填一填,画一画。
(1)新城大桥在小强家________方向上________m处。
(2)火车站在小强家________偏________(________)°方向上________m处。
(3)电影院在小强家正南方向上1500m处。
请在图中标出电影院的位置。
(4)商店在小强家北偏西45°方向上2000m处。
请在图中标出商店的位置。
4.厦门某大型儿童乐园的门票零售每张20元。
六(1)班有46人,请你根据乐园管理处规定(如图),设计两种或三种购票方式,并指出哪种购票方式最便宜。
购买25张(含25张)以上的可以购买集体票,每张票价为原价的80%.方式二:方式三:最便宜的购票方式是:5.民航部门规定:乘坐飞机的旅客,携带行李超过20千克的部分,每千克要按飞机票原价的1.5%另行支付行李逾重费。
李青青从上海乘飞机,购买了七折机票,付钱707元,他携带了30千克的行李,应付行李逾重费多少元?6.—个棱长是6分米的正方体。
(1)它的表面积是多少?(2)如果把它削成一个最大的圆柱体,圆柱体的体积是多少?(3)如果把它削成一个最大的圆锥体,削去的体积是多少立方分米?7.一个圆锥形沙堆,底面积是28.26m²,高是2.5m。
数学实验1-3章习题答案
ans =
18.3287
函数的单调区间为:
(1)单调递增区间:-2<x<-1.5326 -0.7315<x<0以及1.5951<x<2;
(2)单调递减区间:-1.5326<x<-0.7315以及0<x<1.5951.
(2)
函数的图形为:
clear
>> fplot('3*x^5-20*x^3+10',[-3,3])
ans =
-3
最值2:
x=1:0.1:3;
>> y=3.*x.^5-20.*x.^3+10;
>> [m k]=max(y)
m =
199
k =
21
>> x(k)
ans =
3
驻点1及相应的二阶导数值:
clear
>> syms x y
>> y=3*x^5-20*x^3+10;
>> yxx=diff(y,x,2);
>> grid on
f=inline('100*acos(1-1/200*(r^2))+r^2*acos(1/20*r)-10*sqrt(r^2-1/400*r^4)-50*pi','r');
>> y=fzero(f,12)
y =
11.5873
3.求解下列非线性方程组在远点附近的根:
clear
>> syms x y z
>> [x y z]=solve('9*x^2+36*y^2+4*z^2-36','x^2-2*y^2-20*z','16*x-x^3-2*y^2-16*z^2',x,y,z)
数学建模与数学实验课后习题答案

P594•学校共1002名学生,237人住在A 宿舍,333人住在B 宿舍,432 人住在C 宿舍。
学生要组织一个10人的委员会,使用Q 值法分配各 宿舍的委员数。
解:设P 表示人数,N 表示要分配的总席位数。
i 表示各个宿舍(分别取 A,B,C ), p i 表 示i 宿舍现有住宿人数, n i 表示i 宿舍分配到的委员席位。
首先,我们先按比例分配委员席位。
23710 A 宿舍为:n A ==2.365 1002 333"0 B 宿舍为:n B =3.323 1002 432X0 C 宿舍为:n C =4.3111002现已分完9人,剩1人用Q 值法分配。
经比较可得,最后一席位应分给 A 宿舍。
所以,总的席位分配应为: A 宿舍3个席位,B 宿舍3个席位,C 宿舍4个席位。
QA23722 3= 9361.5 Q B33323 4 = 9240.7 Q C4322 4 5=9331.2商人们怎样安全过河傻麴删舫紬削< I 11山名畝臥蹄峨颂禮训鋤嫌邂 韻靖甘讹岸讎鞍輯毗匍趾曲展 縣確牡GH 錚俩軸飙奸比臥鋪謎 smm 彌鯉械即第紘麵觎岸締熾 x^M 曲颁M 删牘HX …佛讪卜过樹蘇 卜允棘髒合 岡仇卅毘冋如;冋冋1卯;砰=口 於广歎煙船上觸人敦% V O J U;xMmm朗“…他1曲策D 咿川| thPl,2卜允隸策集合 刼為和啊母紳轉 多步贱 就匚叫=1入“山使曲并按 腿翻律由汩3』和騒側),模型求解 -穷举法〜编程上机 ■图解法S={(x ?jOI x=o, j-0,1,2,3;X =3? J =0,1,2,3; X =»*=1,2}J规格化方法,易于推广考虑4名商人各带一随从的情况状态$=(xy¥)~ 16个格点 允许状态〜U )个。
点 , 允许决策〜移动1或2格; k 奇)左下移;&偶,右上移. 右,…,必I 给出安全渡河方案评注和思考[廿rfn片,rfl12 3xmm賤縣臓由上题可求:4个商人,4个随从安全过河的方案。
MATLAB实验练习题计算机南邮MATLAB数学实验大作业答案
“M A T L A B ”练习题 要求:抄题、写出操作命令、运行结果,并根据要求,贴上运行图。
1、求230x e x -=的所有根。
(先画图后求解)(要求贴图)>>solve('exp(x)-3*x^2',0)ans=-2*lambertw(-1/6*3^(1/2))-2*lambertw(-1,-1/6*3^(1/2))-2*lambertw(1/6*3^(1/2))2、求下列方程的根。
1)5510x x ++=a=solve('x^5+5*x+1',0);a=vpa(a,6)a=1.10447+1.05983*i-1.00450+1.06095*i-.-1.00450-1.06095*i1.10447-1.05983*i2)1sin 02x x -=至少三个根 >>fzero('x*sin(x)-1/2',3)ans=2.9726>>fzero('x*sin(x)-1/2',-3)ans=-2.9726>>fzero('x*sin(x)-1/2',0)ans=-0.74083)2sin cos 0x x x -=所有根>>fzero('sin(x)*cos(x)-x^2',0)ans=>>fzero('sin(x)*cos(x)-x^2',0.6)ans=0.70223、求解下列各题:1)30sin lim x x x x ->- >>symx;ans=1/62)(10)cos ,x y e x y =求 >>symx;>>diff(exp(x)*cos(x),10)ans=(-32)*exp(x)*sin(x)3)21/20(17x e dx ⎰精确到位有效数字)>>symx;>>vpa((int(exp(x^2),x,0,1/2)),17)ans=0.4)42254x dx x +⎰ >>symx;>>int(x^4/(25+x^2),x)ans=125*atan(x/5)-25*x+x^3/35)求由参数方程arctan x y t⎧⎪=⎨=⎪⎩所确定的函数的一阶导数dy dx 与二阶导数22d y dx 。
南邮数学实验习题选及答案
第一次练习教学要求:熟练掌握Matlab 软件的基本命令和操作,会作二维、三维几何图形,能够用Matlab 软件解决微积分、线性代数与解析几何中的计算问题。
补充命令vpa(x,n) 显示x 的n 位有效数字,教材102页fplot(‘f(x)’,[a,b]) 函数作图命令,画出f(x)在区间[a,b]上的图形在下面的题目中m 为你的学号的后3位(1-9班)或4位(10班以上) 1.1 计算30sin limx mx mx x →-与3sin lim x mx mxx→∞- 程序:syms xlimit((627*x-sin(627*x))/x^3,x,0) 结果:1003003001/6程序: syms xlimit((627*x-sin(627*x))/x^3,x,inf) 结果: 01.2 cos1000xmxy e =,求''y 程序: syms xdiff(exp(x)*cos(627*x/1000),2) 结果:-2001/1000000*exp(x)*cos(1001/1000*x)-1001/500*exp(x)*sin(1001/1000*x)1.3 计算221100xy e dxdy +⎰⎰程序:dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1) 结果:2.139350195142281.4 计算4224x dx m x+⎰ 程序: syms xint(x^4/(627^2+4*x^2)) 结果:1/12*x^3-1002001/16*x+1003003001/32*atan(2/627*x)1.5 (10)cos ,x y e mx y =求程序: syms xdiff(exp(x)*cos(627*x),10) 结果: - 9389137388146839380380277888*cos(627*x)*exp(x) -149759579095532896918284384*sin(627*x)*exp(x)1.6 0x =的泰勒展式(最高次幂为4).程序:syms xtaylor(sqrt(627/1000+x),4) 结果:(62500*627^(1/2)*1000^(1/2)*x^3)/246491883 - (125*627^(1/2)*1000^(1/2)*x^2)/393129 +(627^(1/2)*1000^(1/2)*x)/1254 + (627^(1/2)*1000^(1/2))/10001.7 Fibonacci 数列{}n x 的定义是121,1x x ==,12,(3,4,)n n n x x x n --=+=用循环语句编程给出该数列的前20项(要求将结果用向量的形式给出)。
北京市师大实验八年级数学上册第十二章《全等三角形》经典习题(含答案解析)
一、选择题1.如图,在ABC 中,ABC 的面积为10,4AB =,BD 平分ABC ∠,E 、F 分别为BC 、BD 上的动点,则CF EF +的最小值是( )A .2B .3C .4D .52.芜湖长江三桥是集客运专线、市域轨道交通、城市主干道路于一体的公铁合建桥梁,2020年9月29日公路段投入运营,其侧面示意图如图所示,其中AB CD ⊥,现添加以下条件,不能判定ABC ABD △≌△的是( )A .ACB ADB ∠=∠B .AB BD =C .AC AD = D .CAB DAB ∠=∠3.MAB ∠为锐角,AB a ,点C 在射线AM 上,点B 到射线AM 的距离为d ,BC x =,若△ABC 的形状、大小是唯一确定的,则x 的取值范围是( )A .x d =或x a ≥B .x a ≥C .x d =D .x d =或x a > 4.如图,若DEF ABC ≅,点B 、E 、C 、F 在同一条直线上,9BF =,5EC =,则CF 的长为( )A .1B .2C .2.5D .35.如图,OP 平分AOB ∠,PC OA ⊥于点C ,PD OB ⊥于点D ,延长CP ,DP 交OB , OA 于点E ,F ,下列结论错误的是( )A .PC PD =B .OC OD = C .CPO DPO ∠=∠ D .PC PE =6.如图,点O 在ABC 内,且到三边的距离相等.若110BOC ∠=°,则A ∠的度数为( )A .40︒B .45︒C .50︒D .55︒7.如图,给出下列四组条件:①AB=DE ,BC=EF ,AC=DF ;②AB=DE ,∠B=∠E ,BC=EF ;③∠B=∠E ,BC=EF ,∠C=∠F ;④AB=DE ,AC=DF ,∠B=∠E .其中,能使△ABC ≌△DEF 的条件共有( )A .1组B .2组C .3组D .4组8.用三角尺画角平分线:如图,先在AOB ∠的两边分别取OM ON =,再分别过点M ,N 作OA ,OB 的垂线,交点为P .得到OP 平分AOB ∠的依据是( )A .HLB .SSSC .SASD .ASA 9.已知如图,AC ⊥BC ,DE ⊥AB ,AD 平分∠BAC ,下面结论错误的是( )A .BD +ED =BCB .DE 平分∠ADBC .AD 平分∠EDC D .ED +AC >AD 10.如图,在Rt ABC △中,90C ∠=︒,CAB ∠的平分线交BC 于点D ,且DE 所在直线是AB 的垂直平分线,垂足为E .若3DE =,则BC 的长为( ).A .6B .7C .8D .911.如图,已知△ABC 的周长是20,OB ,OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于,且OD=2,△ABC 的面积是( )A .20B .24C .32D .4012.如图,点D 在线段BC 上,若1802ACE ABC x ∠=︒-∠-︒,且BC DE =,AC DC =,AB EC =,则下列角中,大小为x ︒的角是( )A .EFC ∠B .ABC ∠ C .FDC ∠D .DFC ∠ 13.如图,点C ,D 在线段AB 上,AC DB =,AE //BF ,添加以下哪一个条件仍不能判定△AED ≌△BFC ( )A .ED CF =B .AE BF =C .E F ∠=∠D .ED //CF14.如图,C 是∠AOB 的平分线上一点,添加下列条件不能判定△AOC ≌△BOC 的是( )A .OA =OB B .AC =BC C .∠A =∠BD .∠1=∠2 15.如图,已知,CAB DAE ∠=∠,AC AD =.下列五个选项:①AB AE =,②BC ED =,③C D ∠=∠,④B E ∠=∠,⑤12∠=∠,从中任选一个作为已知条件,其中能使ABC AED ≌△△的条件有( )A .2个B .3个C .4个D .5个二、填空题16.如图,△ABE ≌△ADC ≌△ABC ,若∠1=130°,则∠α的度数为________.17.已知在△ABC 中,AB =9,中线AD =4,那么AC 的取值范围是____18.如图所示,在ABC 中,AB AC =,AD 是ABC 的角平分线,DE AB ⊥,DF AC ⊥,垂足分别是E ,F .则下面结论中(1)DA 平分EDF ∠;(2)AE AF =,DE DF =;(3)AD 上的点到B ,C 两点的距离相等;(4)图中共有3对全等三角形.正确的有________ .19.在ABC 中,48ABC ︒∠=,点D 在BC 边上,且满足18,BAD DC AB ︒∠==,则CAD ∠=________度. 20.如图,在ABC 中,90C ∠=︒,AD 平分BAC ∠,交BC 边于点D ,若12AB =,4CD =,则ABD △ 的面积为__________.21.如图,90,,,ACB AC BC AD CE BE CE ∠=︒=⊥⊥,垂足分别为,D E ,若9,6AD DE ==,则BE 的长为________________________.22.如图,9cm AB =,3cm AC =,点P 在线段AB 上以1cm/s 的速度由点B 向点A 运动,同时点Q 在射线BD 上以x cm/s 的速度由点B 沿射线BD 的方向运动,它们运动的时间为t (s )(1)如图①,若AC AB ⊥,BD AB ⊥,当ACP BPQ △≌△,x =________;CPQ ∠=________.(2)如图②,CAB DBA ∠=∠,当ACP △与BPQ 全等,x =________; 23.如图,AB =8cm ,AC =5cm ,∠A =∠B ,点P 在线段AB 上以2cm/s 的速度由点A 向B 运动,同时,点Q 以x cm/s 的速度从点B 出发在射线BD 上运动,则△ACP 与△BPQ 全等时,x 的值为_____________24.如图,OM 平分∠POQ ,MA ⊥OP ,MB ⊥OQ ,垂足为A ,B ,S △AOM =8cm 2,OA=4cm ,则MB=___.25.如图,已知AB AC =,D 为BAC ∠的角平分线上面一点,连接BD ,CD ;如图,已知AB AC =,D 、E 为BAC ∠的角平分线上面两点,连接BD ,CD ,BE ,CE ;如图,已知AB AC =,D 、E 、F 为BAC ∠的角平分线上面三点,连接BD ,CD ,BE ,CE ,BF ,CF ;…,依此规律,第n 个图形中有全等三角形的对数是______.26.如图,AD 是ABC 中BAC ∠的平分线,DE AB ⊥交AB 于点E ,DF AC ⊥交AC 于点F .若28ABC S =,4DE =,8AB =,则AC =_________.三、解答题27.如图,△ABC 中,AB=AC ,∠BAC=90°,CD 平分∠ACB ,BE ⊥CD ,垂足E 在CD 的延长线上.求证:CD=2BE .28.如图,A 、D 、F 、B 在同一直线上,EF ∥CD ,AE ∥BC ,且AD =BF . 求证:AE =BC29.如图,在平面直角坐标系中,已知点()1,A a a b -+,(),0B a ,且()2320a b a b +-+-=,C 为x 轴上点B 右侧的动点,以AC 为腰作等腰三角形ACD ,使AD AC =,CAD OAB ∠=∠,直线DB 交y 轴于点P . (1)求证:AO AB =;(2)求证:AOC ABD ∆∆≌;(3)当点C 运动时,点P 在y 轴上的位置是否发生改变,为什么?30.已知:如图,AOB ∠.求作: A O B '''∠,使A O B AOB '''∠=∠.作法:①以点O 为圆心,任意长为半径画弧,分别交OA ,OB 于点C ,D ; ②画一条射线O A '',以点O '为圆心,OC 长为半径画弧,交O A ''于点C '; ③以点C '为圆心,CD 长为半径画弧,与②中所画的弧相交于点D ; ④过点D 画射线O B '',则A O B AOB '''∠=∠;A OB '''∠就是所求作的角.(1)使用直尺和圆规,依作法补全图形(保留作图痕迹);(2)完成下面的证明证明:连接C D ''.由作法可知OC O C ''=,,,∴COD C O D '''≅.( )(填推理依据).∴A O B AOB '''∠=∠.∴A O B '''∠就是所求作的角.。
数学实验课习题总结(带答案)
第二次实验内容
1、求下列方程的根 1)ex-3x=0, 在[-1,1]上的近似解,使用 fzero,fsolve 分 别进行求解 2 )判定方程 x7+2x5+3x3+5x+7=0 有几个实根,并使用 roots,fzero,fsolve 分别进行求解,也使用牛顿法编程计算 问题的近似解。 2、求解线性方程组:
答案:
1. 程序设计: (1) fzero('exp(x)-3*x',[-1,1]) fsolve('exp(x)-3*x',[-1,1]) (2)函数 fun1: function ff=fun1(x) ff=(x^7+2*x^5+3*x^3+5*x+7)/(7*x^6+10*x^4+9*x^2+5); 程序: x=-1:0.01:1; y=x.^7+2*x.^5+3*x.^3+5*x+7; plot(x,y,'r-') gtext('零点') grid on 数 p=[1,0,2,0,3,0,5,7]; roots(p) fzero('x^7+2*x^5+3*x^3+5*x+7',0) fsolve('x^7+2*x^5+3*x^3+5*x+7',0) x0=1; x1=x0-fun1(x0); while abs(x1-x0)>=0.0001 x0=x1; x1=x0-fun1(x0); end x0 结果: (1) ans = 0.6191 0.6191 (2)有 1 个实根,如右图 ans = 1.0633 + 0.8552i 1.0633 - 0.8552i 0.1980 + 1.4799i 0.1980 - 1.4799i -0.8442 + 1.1442i -0.8442 - 1.1442i -0.8341 ans = -0.8341 %画图法判断实根个
