30、反函数与对数运算(含答案)
对数及其运算的练习题(附答案)

姓名_______ §2.2.1 对数与对数运算一、课前准备 1,。
对数:定义:如果a N a a b=>≠()01且,那么数b 就叫做以a 为底的对数,记作b Na =l o g (a 是底数,N 是真数,lo g a N 是对数式。
) 由于N a b=>0故lo g a N 中N 必须大于0。
2.对数的运算性质及换底公式.如果 a > 0,a ≠ 1,b>0,M > 0, N > 0 ,则:(1)log ()a MN = ; (2)nm mn b a =log (3)log aMN= ;(4) log n a M = . (5) b a b a =log 换底公式log a b = . (6) b aba=log (7)ba b a nn log 1log =考点一: 对数定义的应用例1:求下列各式中的x 的值; (1)23log27=x; (2)32log 2-=x ; (3)9127log =x (4)1621log =x例2:求下列各式中x 的取值范围; (1))10(2log-x (2)22)x )1(log +-(x (3)21)-x )1(log (+x例3:将下列对数式化为指数式(或把指数式化为对数式) (1)3log3=x (2)6log 64-=x (3)9132-= (4)1641=x )(考点二 对数的运算性质1.定义在R 上的函数f(x )满足f(x)=⎩⎨⎧>---≤-)0(),2()1(log )0(),4(2x x f x f x x ,则f(3)的值为__________2.计算下列各式的值: (1)245lg 8lg 344932lg 21+- (2)8.1lg 10lg 3lg 2lg -+3.已知)lg(y x ++)32lg(y x +-lg3=lg4+lgx+lgy,求x:y 的值4.计算: (1))log log log 582541252++()log log log 812542525++( (2)3473159725log log log log ∙∙+)5353(2log --+(3)求0.3252log 4⎛⎫ ⎪ ⎪⎝⎭的值 (4):已知 2log 3 = a , 3log 7 = b ,用 a ,b 表示42log 56.随堂练习:1.9312-=⎪⎭⎫⎝⎛写成对数式,正确的是( ) 2log .319-=A 2log .931-=B 9log .2-31=)(C 31log .2-9=)(D 2.=34349log( )A.7B.2C.32D.23 3.成立的条件yx xy 33)(3log log log +=( ) A.x>0,y>0 B.x>0,y<0 C.x<0.y>0 D.R y R x ∈∈, 4.,0,0,1,0>>≠>y x a a 若下列式子中正确的个数有( )①)(log log log y x a y a x a +=∙ ②)-(log log -log y x a y a x a = ③y ax a y x alog log log ÷= ④y a x a xy a log log log ∙= A.0 B.1 C.2 D.35.已知0log)2(log 3log 7=⎥⎦⎤⎢⎣⎡x ,那么21-x =( )A.31 B.321 C.221 D.3316已知x f x =)10(,则f(5)=( )A.510B.105C.105logD.lg57.若16488443log log log log =∙∙m ,则m=( ) A.21 B.9 C.18 D.278.设638323log 2log ,log -=则a ,用a 表示的形式是( )A.a-2B.2)1(3a +-C.5a-2D.132-+-a a 9.设a 、b 、c 均为正实数,且c b a 643==,则有( )A.b a c 111+=B.b a c 112+=C.b a c 2111+=D.ba c 212+=10若方程05lg 7lg lg )5lg 7(lg )lg 2=∙+++x x (的两根为βα,,则βα∙=( ) A.5lg lg7∙ B.35lg C.35 D.351 二.填空题11.若4123log =x ,则x=________ 12.已知______)21(,)lo (2==f x g f x 则13.已知lg2=0.3010,lg3=0.4771,lgx=-2+0.7781,则x=_________ 三.选做题(三题中任选两道)14.已知lgx+lgy=2lg(x-2y),求yx2log 的值15.已知2014log 4)3(32-=x f x ,求f(2)+f(4)+f(8)+.....+)2(1007f 的值 16.设a 、b 、c 均为不等于1的正数,且0111,=++==zyxc b a z y x ,求abc 的值附答案: 考点一:例1:1,x=9 2,223=x 3,32-=x 4,x=-4例2:1,x>0; 2,21≠>x x 且 3,101-≠≠>x x x 且且例3:1,33)(=x , 2,646=-x 3,2log 913-= 4,x =1641log 考点二:1,-2 2,(1)21 (2)213,x:y=1:2或x:y=3:1(x>0,y>0) 4, (1)13, (2)-1 (3)-21 (4)12+++a ab aab 随堂练习:一选择题:1B;2D;3A;4A;5C;6D;7B;8A;9C;10D(注意原方程的根为x,不是lgx,别弄错了) 二.三.填空题:11,91 12,2 13, 0.06三选做题:14, 4 15,2014 16,1。
对数函数运算公式大全

对数函数运算公式大全1. 对数函数的定义:y = loga x,其中a为正数且a ≠ 1,x为正数。
则y表示以a为底,x的对数。
2. 对数函数与指数函数互为反函数:loga a^x = x,a^loga x = x。
3. 对数函数的性质:① loga (xy) = loga x + loga y。
② loga (x/y) = loga x - loga y。
③ loga x^n = n loga x。
④ logb x = loga x / loga b。
⑤ loga √x = 1/2 loga x。
⑥ loga (1/x) = -loga x。
4. 常用对数函数值:① log10 1 = 0。
② log10 10 = 1。
③ log10 100 = 2。
④ log10 1000 = 3。
⑤ loge 1 = 0。
⑥ loge e = 1。
5. 解对数方程的方法:①转化为指数形式,即a^x = b。
②化简为一般形式,即loga (mx + n) = p。
将等式两边化为指数形式。
③变形为倒数形式,即loga x - loga (x - 1) = b。
将等式两边化为分数形式。
6. 求解对数函数性质的方法:①分解对数式。
②合并同类项。
③平方移项。
④如有必要,将对数式转化为指数式。
⑤根据指数函数的性质求解。
7. 对数函数的图像特征:①定义域为正实数集。
②值域为全体实数集。
③函数图像关于直线y = x对称。
④在x轴上有一个特殊点:x = 1,此时对数值为0。
⑤在函数图像上任意两点的连线与x轴所成的角度相等,且这个角度叫做该点的倾角。
反函数练习附答案

13.已知函数f(x)的定义域为[-1,1],值域为[-3,3],其反函数为1(x),则1(32)的定义域为,值域为.
解析:由于函数f(x)的定义域为[-1,1],值域为[-3,3],所以其反函数1(x)的定义域为[-3,3],值域为[-1,1].所以由-3≤32≤3,解得 ≤x≤ .
3.若函数y=f(1)的图象与函数 的图象关于直线y=x对称,则f(x)等于()
212x2122
解析:由函数y=f(1)的图象与函数 的图象关于直线y=x对称,可知y=f(1)与 互为反函数,有 x=e22,所以y=e22 y=f(1)=e22.故f(x)=e2x.答案
4.已知函数f(x)=231(x)是f(x)的反函数,若=16(∈),则1(m)1(n)的值为( )
又y=f(x)与y=1(x)关于y=x对称=x沿向量(-1,2)平移得到y=3,
∴y=f(1)+2与y=1(1)+2关于y=3对称.答案=3
三、解答题
15.已知函数 (x)=1(),求g(x).
解:由 ,得=1,∴ ,即 ,∴g(x)=1()= .
16.已知函数f(x)=2( )(a>0且a≠1).
8.设0<a<1,函数 ,则函数1(x)<1的x的取值范围是( )
A.(0,2) B.(2∞) C.(0∞) D.((2)∞)
解析(x)在(0,2)上是减函数,所以x>f(1)=0.故选C.
9.设函数为y=f(x)的反函数为y=1(x),将y=f(23)的图象向左平移2个单位,再作关于x轴的对称图形所对应的函数的反函数是( )
反函数基础练习含答案

反函数根底练习(一)选择题1.函数y =-x 2(x ≤0)的反函数是[ ]A y (x 0)B y (x 0)C y (x 0)D y |x|.=-≥.=≤.=-≤.=-x x x --2.函数y =-x(2+x)(x ≥0)的反函数的定义域是 [ ]A .[0,+∞)B .[-∞,1]C .(0,1]D .(-∞,0]3y 1(x 2).函数=+≥的反函数是x -2[ ]A .y =2-(x -1)2(x ≥2)B .y =2+(x -1)2(x ≥2)C .y =2-(x -1)2(x ≥1)D .y =2+(x -1)2(x ≥1)4.以下各组函数中互为反函数的是[ ]A y y xB y y 2.=和=.=和=x x x11C y y (x 1)D y x (x 1)y (x 0)2.=和=≠.=≥和=≥3131311x x x x x +-+-5.如果y =f(x)的反函数是y =f -1(x),那么以下命题中一定正确的选项是[ ]A .假设y =f(x)在[1,2]上是增函数,那么y =f -1(x)在[1,2]上也是增函数B.假设y=f(x)是奇函数,那么y=f-1(x)也是奇函数C.假设y=f(x)是偶函数,那么y=f-1(x)也是偶函数D.假设f(x)的图像与y轴有交点,那么f-1(x)的图像与y轴也有交点6.如果两个函数的图像关于直线y=x对称,而其中一个函数是x 1y=-,那么另一个函数是[ ] A.y=x2+1(x≤0)B.y=x2+1(x≥1)C.y=x2-1(x≤0)D.y=x2-1(x≥1)7.设点(a,b)在函数y=f(x)的图像上,那么y=f-1(x)的图像上一定有点[ ] A.(a,f-1(a))B.(f-1(b),b)C.(f-1(a),a) D.(b,f-1(b))8.设函数y=f(x)的反函数是y=g(x),那么函数y=f(-x)的反函数是[ ] A.y=g(-x) B.y=-g(x)C.y=-g(-x) D.y=-g-1(x)9.假设f(x-1)=x2-2x+3(x≤1),那么函数f-1(x)的草图是[ ]10y g(x).函数=的反函数是,则13x[ ]A .g(2)>g(-1)>g(-3)B .g(2)>g(-3)>g(-1)C .g(-1)>g(-3)>g(2)D .g(-3)>g(-1)>g(2) (二)填空题1y 32y (x 0)y f(x)y x .函数=+的反函数是..函数=>与函数=的图像关于直线=对称,x x ++2121 解f(x)=________.3.如果一次函数y =ax +3与y =4x -b 的图像关于直线y =x 对称,那a =________,b =________.4y (1x 0).函数=-<<的反函数是,反函数的定92-x义域是________.5.函数y =f(x)存在反函数,a 是它的定义域内的任意一个值,那么f -1(f(a))=________.6y 7y (x 1)(x 1)8f(x)(x 1)f ()1.函数=的反函数的值域是..函数=≥-<的反函数是:..函数=<-,则-=.121121232x x x x ---⎧⎨⎪⎩⎪--(三)解答题1y 12f(x).求函数=+的反函数,并作出反函数的图像..已知函数=.x ax x +++252(1)求函数y =f(x)的反函数y =f -1(x)的值域;(2)假设点P(1,2)是y =f -1(x)的图像上一点,求函数y =f(x)的值域.3.函数y =f(x)在其定义域内是增函数,且存在反函数,求证y =f(x)的反函数y =f -1(x)在它的定义域内也是增函数.4f(x)y g(x)y f (x 1).设函数=,函数=的图像是=+的图像2311x x +-- 关于y =x 对称,求g(2)的值.参考答案(一)选择题1.(C).解:函数y=-x 2(x ≤0)的值域是y ≤0,由y=-x 2得x=--,∴反函数--≤.y x f (x)=(x 0)1-2.(D).解:∵y=-x 2-2x=-(x +1)2,x ≥0,∴函数值域y ≤0,即其反函数的定义域为x ≤0.3(D)y =x 21x 2y 1y =x 2..解:∵-+,≥,∴函数值域≥,由-+1,得反函数f -1(x)=(x -1)2+1,(x ≥1).4.(B).解:(A)错.∵y=x 2没有反函数.(B)中如两个函数互为反函数.中函数+-≠的反函数是+-≠而不是+-.中函数≥的值域为≥.应是其反函数的定义域≥.但中的定义域≥,故中两函数不是互为反函数.(C)y =3x 1x (x 1)y =x 1x 3(x 3)y =3x 13x 1(D)y =x (x 1)y 1x 1y =x x 0(D)21 5.(B).解:(A)中.∵y=f(x)在[1,2]上是增函数.∴其反函数y=f -1(x)在[f(1),f(2)]上是增函数,∴(A)错.(B)对.(C)中如y=f(x)=x 2是偶函数但没有反函数.∴(C)错.(D)中如函数f(x)=x 2+1(x ≥0)的图像与y 轴有交点,但其反函数-≥的图像与轴没有交点.∴错.f -(x)=x 1(x 1)y (D)1 6(A)y =y 0f (x)=x 12..解:∵函数--的值域≤;其反函数+x 1-+1(x ≤0).选(A).7.(D).解:∵点(a ,b)在函数y=f(x)的图像上,∴点(b ,a)必在其反函数y=f -1(x)的图像上,而a=f -1(b),故点(b ,f -1(b))在y=f -1(x)的图像上.选(D).8.(B).解:∵y=f(x)的反函数是y=f -1(x)即g(x)=f -1(x),而y=f(-x)的反函数是y=-f -1(x)=-g(x),∴选(B).9.(C).解:令t=x -1.∵x ≤1,∴t ≤0,f(t)=t 2+2(t ≤0),即f(x)=x 2+2(x ≤0),值域为f(x)≥2,∴反函数f -1(x)的定义域是x ≥2,值域y ≤0,应选(C).10(B)g(x)=1x (0)33..解:∵在-∞,上是减函数,又-<-<1 00g(3)g(1)g(2)=120g(2)g(3)g(1)3,∴>->-而>,∴>->-.故选 (B).(二)填空题1y =3y 3y =x 6x 2.解:∵函数++的值域≥,其反函数-+x 27(x ≥3)2y =12x 1(x 0)y 1f(x)=1x2x(x 1).解:+>的值域<,其反函数-<. 3y =4x b y =14x x =ax .解:函数-的反函数是+,则++,b b41443比较两边对应项系数得,.a =14b =12 4y =9x (1x 0)y (223)2.解:函数--<<的值域∈,,反函数f -1 (x)=(223)--.反函数的定义为,.92x5.a6.[0,2)∪(2,+∞)7f (x)=x 1(x 1)1x(x 0)122.+≥-<-⎧⎨⎪⎩⎪8.-2(三)解答题1x 2y 1y =x 21=.解:∵≥-,得值域为≥.由++得反函数f x -1()(x -1)2-2,(x ≥1),其图像如右图.2.解(1):∵y=f(x)的定义域是{x|x ≠1,x ∈R ,∴y=f -1(x)的值域是{y|y ≠1,y ∈R}.解(2):∵点P(1,2)在,y=f -1(x)的图像上,点P(1,2)关于直线y=x的对称点为′,一定在的图像上,即由++得-,∴-+,其反函数-+.∵的定义域为≠-,∈,∴的值域为≠-,∈.P (21)y =f(x)=1a =f(x)=10x 2x 4f -(x)=104x 2x 1f -(x){x|x x R}y =f(x){y|y y R}112522121212a3.证明略.4f(x)=2x 3x 1f -(x)=x 3f (x 1)=11.略解;+-的反函数是+-,∴+x 2x 4x 1x 4x 1=2x =6g(2)=6+-,由+-得即.。
指数函数与对数函数图像性质讲义练习题含答案-反函数

指数函数与对数函数知识点一:对数函数与指数函数的图像与性质 表1 指数函数()0,1x y a a a =>≠对数数函数()log 0,1a y x a a =>≠定义域 x R ∈ ()0,x ∈+∞值域()0,y ∈+∞y R ∈图象性质过定点(0,1)过定点(1,0)减函数增函数减函数增函数a b <a b >a b <a b >知识点二:对数函数与指数函数的基本运算 指数函数:(1)_______(0,,)r s a a a r s R ⋅=>∈ (2)_______(0,,)r s a a a r s R ÷=>∈()(3)_______(0,,)sr aa r s R =>∈ ()(4)________(,0,)rab a b r R =>∈对数函数: 恒等式:N aNa =log ;b a b a =log )1,0(≠>a a①M a (log ·=)N ____________________;②=N Ma log __________________________; ③log na M =_________________________)(R n ∈.换底公式abb c c a log log log =(0>a ,且1≠a ;0>c ,且1≠c ;0>b ).(4)几个小结论:①log _____n n a b =;②log ______naM =;③log _______n m a b =;④log log ____a b b a ⋅=log 1____;log _____a a a ==.例:1、230.5207103720.12392748π--⎛⎫⎛⎫++-+ ⎪ ⎪⎝⎭⎝⎭; 2、1244839(log 3log 3)(log 2log 2)log 32++-3.化简()1142332243(0,0)a b ab a b b a b a⋅>>⋅的结果是__________. 4.方程lg lg(3)1x x ++=的解x =_______. 5.3128xy==,则11______x y-=. 6.若103x =,104y=,则210x y-=________.知识点三:反函数1.当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数的自变量,而把这个函数的自变量作为新的函数的因变量,我们称这两个函数互为反函数。
函数反函数对数及对数函数

函数一、函数:1.函数的概念(1)函数的定义:设B A 、是两个非空的数集,如果按照某种对应法则f ,对于集合A 中的每一个数x ,在集合B 中都有唯一确定的数和它对应,那么这样的对应叫做从A 到B 的一个函数,通常记为A x x f y ∈=),( (2)函数的定义域、值域在函数A x x f y ∈=),(中,x 叫做自变量,x 的取值范围A 叫做)(x f y =的定义域;与x 的值相对应的y 值叫做函数值,函数值的集合{}A x x f ∈)(称为函数)(x f y =的值域。
(2)函数的三要素:定义域、值域和对应法则 2.映射的概念设B A 、是两个集合,如果按照某种对应法则f ,对于集合A 中的任意元素,在集合B 中都有唯一确定的元素与之对应,那么这样的单值对应叫做从A 到B 的映射,通常记为B A f →:重、难点突破重点:掌握映射的概念、函数的概念,会求函数的定义域、值域 难点:求函数的值域和求抽象函数的定义域 重难点:1.关于抽象函数的定义域求抽象函数的定义域,如果没有弄清所给函数之间的关系,求解容易出错误 问题1:已知函数)(x f y =的定义域为][b a ,,求)2(+=x f y 的定义域 问题2:已知)2(+=x f y 的定义域是][b a ,,求函数)(x f y =的定义1. 求值域的几种常用方法〔1〕配方法:对于〔可化为〕“二次函数型”的函数常用配方法,如求函数4cos 2sin 2+--=x x y ,可变为2)1(cos 4cos 2sin 22+-=+--=x x x y 解决〔2〕基本函数法:一些由基本函数复合而成的函数可以利用基本函数的值域来求,如函数)32(log 221++-=x x y 就是利用函数u y 21log =和322++-=x x u 的值域来求。
〔3〕判别式法:通过对二次方程的实根的判别求值域。
如求函数22122+-+=x x x y 的值域 由22122+-+=x x x y 得012)1(22=-++-y x y yx ,假设0=y ,则得21-=x ,所以0=y 是函数值域中的一个值;假设0≠y ,则由0)12(4)]1(2[2≥--+-=∆y y y 得021332133≠+≤≤-y y 且,故所求值域是]2133,2133[+- 〔4〕别离常数法:常用来求“分式型”函数的值域。
反函数练习附答案
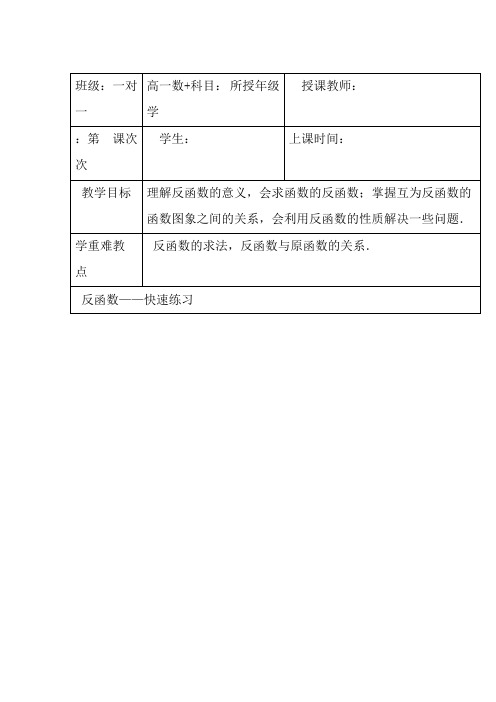
:∵f(x)=(1)+2,∴解析151xf2(x)41ax.=,则若函数a的图象关于直线y=x对称12.)(ay55x41ax4的图象上取在f(x),:∵,∴且存在反函数.不是常函数解析ya545x11a,可解得也在函数,0)f(x)的图象上的对称点一点(0,它关于),y=x(55-5.
=1(x),,值域为[-3,3]其反函数为,-1,1f(x)13.已知函数的定义域为[]1.
教案审核:6 / 6
=yx对称g(x)的图象与函数y=(1)的图象关于直线解析:∵函数y=1.
(1)互为反函数y=g(x)与函数y=∴函数71即x=f(11)+1.∵,∴得由g(11)(1)=11,∴1=f(11),f(11)512答案.(11)g5二、填空题13254. (x)==x-5x+10x-10x+51,则f(x)的反函数为11.设f(x)5.
C.4 B.1 2
D.10
13于是则有3=y,可得(x)=3.2解析:设y=,2211答案6=-2.(m)(n)=m6=22211( )
2023年高考数学一轮复习讲义——对数与对数函数

§2.7 对数与对数函数考试要求 1.理解对数的概念及运算性质,能用换底公式将一般对数转化成自然对数或常用对数.2.通过实例,了解对数函数的概念,会画对数函数的图象,理解对数函数的单调性与特殊点.3.了解指数函数y =a x 与对数函数y =log a x (a >0,且a ≠1)互为反函数.知识梳理 1.对数的概念一般地,如果a x =N (a >0,且a ≠1),那么数x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫做对数的底数,N 叫做真数. 以10为底的对数叫做常用对数,记作lg N . 以e 为底的对数叫做自然对数,记作ln N . 2.对数的性质与运算性质(1)对数的性质:log a 1=0,log a a =1,log a Na =N (a >0,且a ≠1,N >0).(2)对数的运算性质如果a >0,且a ≠1,M >0,N >0,那么: ①log a (MN )=log a M +log a N ; ②log a MN =log a M -log a N ;③log a M n =n log a M (n ∈R ).(3)换底公式:log a b =log c blog c a (a >0,且a ≠1,b >0,c >0,且c ≠1).3.对数函数的图象与性质y =log a xa >10<a <1图象定义域 (0,+∞)值域R性质过定点(1,0),即x =1时,y =0当x >1时,y >0; 当0<x <1时,当x >1时,y <0; 当0<x <1时,y <0y >0在(0,+∞)上是增函数在(0,+∞)上是减函数4.反函数指数函数y =a x (a >0且a ≠1)与对数函数y =log a x (a >0且a ≠1)互为反函数,它们的图象关于直线y =x 对称. 常用结论1.log a b ·log b a =1,log nm b a =n m log a b .2.如图给出4个对数函数的图象则b >a >1>d >c >0,即在第一象限,不同的对数函数图象从左到右底数逐渐增大. 3.对数函数y =log a x (a >0且a ≠1)的图象恒过点(1,0),(a,1),⎝⎛⎭⎫1a ,-1. 思考辨析判断下列结论是否正确(请在括号中打“√”或“×”) (1)若MN >0,则log a (MN )=log a M +log a N .( × )(2)对数函数y =log a x (a >0,且a ≠1)在(0,+∞)上是增函数.( × ) (3)函数y =log a 1+x1-x 与函数y =ln(1+x )-ln(1-x )是同一个函数.( × )(4)函数y =log 2x 与y =121log x的图象重合.( √ ) 教材改编题1.函数y =log a (x -2)+2(a >0且a ≠1)的图象恒过定点 . 答案 (3,2) 解析 ∵log a 1=0, 令x -2=1,∴x =3, ∴y =log a 1+2=2,∴原函数的图象恒过定点(3,2). 2.计算:(log 29)·(log 34)= .答案 4解析 (log 29)·(log 34)=lg 9lg 2×lg 4lg 3=2lg 3lg 2×2lg 2lg 3=4.3.若函数y =log a x (a >0,a ≠1)在[2,4]上的最大值与最小值的差是1,则a = . 答案 12或2解析 当a >1时,log a 4-log a 2=log a 2=1, ∴a =2;当0<a <1时,log a 2-log a 4=-log a 2=1, ∴a =12,综上有a =12或2.题型一 对数式的运算例1 (1)设2a =5b =m ,且1a +1b =2,则m 等于( )A.10 B .10 C .20 D .100 答案 A解析 2a =5b =m , ∴log 2m =a ,log 5m =b ,∴1a +1b =1log 2m +1log 5m =log m 2+log m 5 =log m 10=2, ∴m 2=10,∴m =10(舍m =-10). (2)计算:log 535+122log 2log 5150-log 514= .答案 2解析 原式=log 535-log 5150-log 514+212log 2=log 535150×14+12log 2 =log 5125-1=log 553-1=3-1=2.教师备选计算:(1-log 63)2+log 62·log 618log 64= .答案 1 解析 原式=1-2log 63+(log 63)2+log 663·log 6(6×3)log 64=1-2log 63+(log 63)2+1-(log 63)2log 64=2(1-log 63)2log 62=log 66-log 63log 62=log 62log 62=1.思维升华 解决对数运算问题的常用方法 (1)将真数化为底数的指数幂的形式进行化简. (2)将同底对数的和、差、倍合并.(3)利用换底公式将不同底的对数式转化成同底的对数式,要注意换底公式的正用、逆用及变形应用.跟踪训练1 (1)已知a >b >1,若log a b +log b a =52,a b =b a ,则a +b = .答案 6解析 设log b a =t ,则t >1,因为t +1t =52,所以t =2,则a =b 2.又a b =b a , 所以b 2b =2b b ,即2b =b 2,又a >b >1,解得b =2,a =4. 所以a +b =6.(2)计算:lg 25+lg 50+lg 2·lg 500+(lg 2)2= . 答案 4解析 原式=2lg 5+lg(5×10)+lg 2·lg(5×102)+(lg 2)2 =2lg 5+lg 5+1+lg 2·(lg 5+2)+(lg 2)2 =3lg 5+1+lg 2·lg 5+2lg 2+(lg 2)2=3lg 5+2lg 2+1+lg 2(lg 5+lg 2) =3lg 5+2lg 2+1+lg 2 =3(lg 5+lg 2)+1 =4.题型二 对数函数的图象及应用例2 (1)已知函数f (x )=log a (2x +b -1)(a >0,且a ≠1)的图象如图所示,则a ,b 满足的关系是( )A .0<a -1<b <1 B .0<b <a -1<1 C .0<b -1<a <1 D .0<a -1<b -1<1答案 A解析 由函数图象可知,f (x )为增函数,故a >1.函数图象与y 轴的交点坐标为(0,log a b ),由函数图象可知-1<log a b <0,解得1a <b <1.综上有0<1a<b <1.(2)若方程4x =log a x 在⎝⎛⎦⎤0,12上有解,则实数a 的取值范围为 . 答案 ⎝⎛⎦⎤0,22解析若方程4x =log a x 在⎝⎛⎦⎤0,12上有解,则函数y =4x 和函数y =log a x 在⎝⎛⎦⎤0,12上有交点, 由图象知⎩⎪⎨⎪⎧0<a <1,log a 12≤2,解得0<a ≤22. 教师备选已知x 1,x 2分别是函数f (x )=e x +x -2,g (x )=ln x +x -2的零点,则1e x +ln x 2的值为( ) A .e 2+ln 2 B .e +ln 2 C .2D .4答案 C解析根据题意,已知x1,x2分别是函数f(x)=e x+x-2,g(x)=ln x+x-2的零点,函数f(x)=e x+x-2的零点为函数y=e x的图象与y=2-x的图象的交点的横坐标,则两个函数图象的交点为(x1,1e x),函数g(x)=ln x+x-2的零点为函数y=ln x的图象与y=2-x的图象的交点的横坐标,则两个函数图象的交点为(x2,ln x2),又由函数y=e x与函数y=ln x互为反函数,其图象关于直线y=x对称,而直线y=2-x也关于直线y=x对称,则点(x1,1e x)和(x2,ln x2)也关于直线y=x对称,则有x1=ln x2,则有1e x+ln x2=1e x+x1=2.思维升华对数函数图象的识别及应用方法(1)在识别函数图象时,要善于利用已知函数的性质、函数图象上的特殊点(与坐标轴的交点、最高点、最低点等)排除不符合要求的选项.(2)一些对数型方程、不等式问题常转化为相应的函数图象问题,利用数形结合法求解.跟踪训练2(1)已知函数f(x)=log a x+b的图象如图所示,那么函数g(x)=a x+b的图象可能为()答案 D解析 结合已知函数的图象可知, f (1)=b <-1,a >1,则g (x )单调递增,且g (0)=b +1<0,故D 符合题意.(2)(2022·广州调研)设x 1,x 2,x 3均为实数,且1e x -=ln x 1,2e x -=ln(x 2+1),3e x -=lg x 3,则( ) A .x 1<x 2<x 3 B .x 1<x 3<x 2 C .x 2<x 3<x 1 D .x 2<x 1<x 3答案 D解析 画出函数y =⎝⎛⎭⎫1e x ,y =ln x ,y =ln(x +1),y =lg x 的图象,如图所示.数形结合,知x 2<x 1<x 3.题型三 对数函数的性质及应用 命题点1 比较指数式、对数式大小 例3 (1)设a =log 3e ,b =e 1.5,c =131log 4,则( ) A .b <a <c B .c <a <b C .c <b <a D .a <c <b答案 D 解析 c =131log 4=log 34>log 3e =a . 又c =log 34<log 39=2,b =e 1.5>2, ∴a <c <b .(2)(2022·昆明一中月考)设a =log 63,b =log 126,c =log 2412,则( )A .b <c <aB .a <c <bC .a <b <cD .c <b <a答案 C解析 因为a ,b ,c 都是正数, 所以1a =log 36=1+log 32,1b=log 612=1+log 62, 1c=log 1224=1+log 122, 因为log 32=lg 2lg 3,log 62=lg 2lg 6,log 122=lg 2lg 12,且lg 3<lg 6<lg 12,所以log 32>log 62>log 122, 即1a >1b >1c , 所以a <b <c .命题点2 解对数方程不等式例4 若log a (a +1)<log a (2a )<0(a >0,a ≠1),则实数a 的取值范围是 . 答案 ⎝⎛⎭⎫14,1解析 依题意log a (a +1)<log a (2a )<log a 1,∴⎩⎪⎨⎪⎧ a >1,a +1<2a <1或⎩⎪⎨⎪⎧0<a <1,a +1>2a >1,解得14<a <1.命题点3 对数性质的应用例5 (2020·全国Ⅱ)设函数f (x )=ln|2x +1|-ln|2x -1|,则f (x )( ) A .是偶函数,且在⎝⎛⎭⎫12,+∞上单调递增 B .是奇函数,且在⎝⎛⎭⎫-12,12上单调递减C .是偶函数,且在⎝⎛⎭⎫-∞,-12上单调递增 D .是奇函数,且在⎝⎛⎭⎫-∞,-12上单调递减 答案 D解析 f (x )=ln|2x +1|-ln|2x -1|的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≠±12. 又f (-x )=ln|-2x +1|-ln|-2x -1| =ln|2x -1|-ln|2x +1|=-f (x ), ∴f (x )为奇函数,故排除A ,C. 当x ∈⎝⎛⎭⎫-∞,-12时, f (x )=ln(-2x -1)-ln(1-2x )=ln -2x -11-2x=ln 2x +12x -1=ln ⎝ ⎛⎭⎪⎫1+22x -1,∵y =1+22x -1在⎝⎛⎭⎫-∞,-12上单调递减, ∴由复合函数的单调性可得f (x )在⎝⎛⎭⎫-∞,-12上单调递减. 教师备选1.(2022·安徽十校联盟联考)已知a =log 23,b =2log 53,c =13log 2,则a ,b ,c 的大小关系为( ) A .a >c >b B .a >b >c C .b >a >c D .c >b >a答案 B解析 ∵a =log 23>1,b =2log 53=log 59>1, c =13log 2<0,∴a b =log 23log 59=lg 3lg 2×lg 5lg 9=lg 3lg 2×lg 52lg 3 =lg 52lg 2=lg 5lg 4=log 45>1, ∴a >b ,∴a >b >c .2.若f (x )=lg(x 2-2ax +1+a )在区间(-∞,1]上单调递减,则a 的取值范围为( ) A .[1,2) B .[1,2] C .[1,+∞) D .[2,+∞)答案 A解析 令函数g (x )=x 2-2ax +1+a =(x -a )2+1+a -a 2,对称轴为x =a ,要使函数f (x )在(-∞,1]上单调递减,则有⎩⎪⎨⎪⎧ g (1)>0,a ≥1,即⎩⎪⎨⎪⎧2-a >0,a ≥1,解得1≤a <2,即a ∈[1,2).思维升华 求与对数函数有关的函数值域和复合函数的单调性问题,必须弄清三个问题:一是定义域;二是底数与1的大小关系;三是复合函数的构成.跟踪训练3 (1)若实数a ,b ,c 满足log a 2<log b 2<log c 2<0,则下列关系中正确的是( ) A .a <b <c B .b <a <c C .c <b <a D .a <c <b答案 C解析 根据不等式的性质和对数的换底公式可得1log 2a <1log 2b <1log 2c <0,即log 2c <log 2b <log 2a <0, 可得c <b <a <1.(2)若函数f (x )=⎩⎪⎨⎪⎧log a x ,x ≥2,-log ax -4,0<x <2存在最大值,则实数a 的取值范围是 .答案 ⎝⎛⎦⎤0,22解析 当a >1时,函数f (x )=log a x 在[2,+∞)上单调递增,无最值,不满足题意, 故0<a <1.当x ≥2时,函数f (x )=log a x 在[2,+∞)上单调递减,f (x )≤f (2)=log a 2; 当0<x <2时,f (x )=-log a x -4在(0,2)上单调递增,f (x )<f (2)=-log a 2-4, 则log a 2≥-log a 2-4,即log a 2≥-2=log a a -2, 即1a 2≥2,0<a ≤22, 故实数a 的取值范围是⎝⎛⎦⎤0,22. (3)(2022·潍坊模拟)已知f (x )=1+log 3x (1≤x ≤9),设函数g (x )=f 2(x )+f (x 2),则g (x )max -g (x )min= .答案 5解析 由题意得⎩⎪⎨⎪⎧ 1≤x ≤9,1≤x 2≤9,∴1≤x ≤3,∴g (x )的定义域为[1,3],g (x )=f 2(x )+f (x 2)=(1+log 3x )2+1+log 3x 2=(log 3x )2+4log 3x +2,设t =log 3x ,则0≤t ≤1,则y =t 2+4t +2=(t +2)2-2,在[0,1]上单调递增,∴当t =0即x =1时,g (x )min =2,当t =1即x =3时,g (x )max =7,∴g (x )max -g (x )min =5.课时精练1.(2022·重庆巴蜀中学月考)设a =12,b =log 75,c =log 87,则( )A .a >b >cB .a >c >bC .c >b >aD .c >a >b答案 D解析 a =12=log 77>b =log 75,c =log 87>log 88=12=a ,所以c >a >b .2.若函数y =f (x )是函数y =a x (a >0,且a ≠1)的反函数且f (2)=1,则f (x )等于() A .log 2x B.12x C .12log x D .2x -2答案 A解析 函数y =a x (a >0,且a ≠1)的反函数是f (x )=log a x ,又f (2)=1,即log a 2=1,所以a =2.故f (x )=log 2x .3.(2022·昆明模拟)我们知道:人们对声音有不同的感觉,这与它的强度有关系.一般地,声音的强度用(W/m 2)表示,但在实际测量时,声音的强度水平常用L 1=10 lg I I 0(单位:分贝,L 1≥0,其中I 0=1×10-12是人们平均能听到的最小强度,是听觉的开端).某新建的小区规定:小区内公共场所的声音的强度水平必须保持在50分贝以下,则声音强度I 的取值范围是( )A .(-∞,10-7)B .[10-12,10-5)C .[10-12,10-7)D .(-∞,10-5)答案 C解析 由题意可得,0≤10·lg I I 0<50, 即0≤lg I -lg(1×10-12)<5,所以-12≤lg I <-7,解得10-12≤I <10-7,所以声音强度I 的取值范围是[10-12,10-7).4.设函数f (x )=()212log ,0,log ,0.x x x x >⎧⎪⎨-<⎪⎩若f (a )>f (-a ),则实数a 的取值范围是( ) A .(-1,0)∪(0,1)B .(-∞,-1)∪(1,+∞)C .(-1,0)∪(1,+∞)D .(-∞,-1)∪(0,1)答案 C解析 由题意得2120,log log a a a >⎧⎪⎨>⎪⎩ 或()()1220,log log a a a <⎧⎪⎨->-⎪⎩ 解得a >1或-1<a <0.5. (多选)函数y =log a (x +c )(a ,c 为常数,其中a >0,a ≠1)的图象如图所示,则下列结论成立的是( )A .a >1B .0<c <1C .0<a <1D .c >1答案 BC解析 由图象可知函数为减函数,∴0<a <1,令y =0得log a (x +c )=0,x +c =1,x =1-c ,由图象知0<1-c <1,∴0<c <1.6.(多选)已知函数f (x )=ln(e 2x +1)-x ,则( )A .f (ln 2)=ln 52B .f (x )是奇函数C .f (x )在(0,+∞)上单调递增D .f (x )的最小值为ln 2答案 ACD解析 f (ln 2)=ln(e 2ln 2+1)-ln 2=ln 52, 故A 项正确;f (x )=ln(e 2x +1)-x =ln(e 2x +1)-ln e x=ln e 2x +1e x =ln(e x +e -x ), 所以f (-x )=ln(e x +e -x ),所以f (-x )=f (x ),所以f (x )为偶函数,故B 项错误;当x >0时,y =e x +e -x 在(0,+∞)上单调递增,因此y =ln(e x +e -x )在(0,+∞)上单调递增,故C 项正确;由于f (x )在(0,+∞)上单调递增,又f (x )为偶函数,所以f (x )在(-∞,0]上单调递减,所以f (x )的最小值为f (0)=ln 2,故D 项正确.7.(2022·海口模拟)log 327+lg 25+lg 4+27log 7+138的值等于 . 答案 152 解析 原式=323log 3+lg 52+lg 22+2+1332⨯ =32+2lg 5+2lg 2+2+2 =32+2(lg 5+lg 2)+2+2 =32+2+2+2 =152. 8.函数f (x )=log 2x ·()2x 的最小值为 .答案 -14 解析 依题意得f (x )=12log 2x ·(2+2log 2x )=(log 2x )2+log 2x =⎝⎛⎭⎫log 2x +122-14≥-14,当log 2x =-12,即x =22时等号成立,所以函数f (x )的最小值为-14. 9.设f (x )=log 2(a x -b x ),且f (1)=1,f (2)=log 212.(1)求a ,b 的值;(2)当x ∈[1,2]时,求f (x )的最大值.解 (1)因为f (x )=log 2(a x -b x ),且f (1)=1,f (2)=log 212,所以⎩⎪⎨⎪⎧ log 2(a -b )=1,log 2(a 2-b 2)=log 212,即⎩⎪⎨⎪⎧a -b =2,a 2-b 2=12,解得a =4,b =2.(2)由(1)得f (x )=log 2(4x -2x ),令t =4x -2x ,则t =4x -2x =⎝⎛⎭⎫2x -122-14, 因为1≤x ≤2,所以2≤2x ≤4,所以94≤⎝⎛⎭⎫2x -122≤494,即2≤t ≤12, 因为y =log 2t 在[2,12]上单调递增,所以y max =log 212=2+log 23,即函数f (x )的最大值为2+log 23.10.(2022·枣庄模拟)已知函数f (x )=log a (x +1)-log a (1-x ),a >0且a ≠1.(1)判断f (x )的奇偶性并予以证明;(2)当a >1时,求使f (x )>0的x 的解集.解 (1)f (x )是奇函数,证明如下:因为f (x )=log a (x +1)-log a (1-x ),所以⎩⎪⎨⎪⎧x +1>0,1-x >0,解得-1<x <1,f (x )的定义域为(-1,1).f (-x )=log a (-x +1)-log a (1+x )=-[log a (1+x )-log a (-x +1)]=-f (x ),故f (x )是奇函数.(2)因为当a >1时,y =log a (x +1)是增函数,y =log a (1-x )是减函数,所以当a >1时,f (x )在定义域(-1,1)内是增函数,f (x )>0即log a (x +1)-log a (1-x )>0,log a x +11-x >0,x +11-x >1,2x 1-x >0,2x (1-x )>0,解得0<x <1,故使f (x )>0的x 的解集为(0,1).11.设a =log 0.20.3,b =log 20.3,则( )A .a +b <ab <0B .ab <a +b <0C .a +b <0<abD .ab <0<a +b答案 B解析 ∵a =log 0.20.3>log 0.21=0,b =log 20.3<log 21=0,∴ab <0. ∵a +b ab =1a +1b=log 0.30.2+log 0.32=log 0.30.4, ∴1=log 0.30.3>log 0.30.4>log 0.31=0,∴0<a +b ab<1,∴ab <a +b <0. 12.若实数x ,y ,z 互不相等,且满足2x =3y =log 4z ,则( )A .z >x >yB .z >y >xC .x >y ,x >zD .z >x ,z >y 答案 D解析 设2x =3y =log 4z =k >0,则x =log 2k ,y =log 3k ,z =4k ,根据指数、对数函数图象易得4k >log 2k ,4k >log 3k ,即z >x ,z >y .13.(2022·沈阳模拟)函数f (x )=|log 3x |,若正实数m ,n (m <n )满足f (m )=f (n ),且f (x )在区间[m 2,n ]上的最大值为2,则n -m 等于( ) A.83 B.809 C.154 D.25516答案 A解析 ∵f (x )=|log 3x |,正实数m ,n (m <n )满足f (m )=f (n ),∴0<m <1<n ,且|log 3m |=|log 3n |,∴log 3m =-log 3n ,∴log 3m +log 3n =0,解得mn =1,又∵f (x )在区间[m 2,n ]上的最大值为2,易知f (m 2)=-log 3m 2=2,此时⎩⎪⎨⎪⎧m =13,n =3,∴n -m =83. 14.(2022·惠州模拟)若函数f (x )=log a ⎝⎛⎭⎫x 2-ax +12有最小值,则实数a 的取值范围是 . 答案 (1,2)解析 令u =x 2-ax +12=⎝⎛⎭⎫x -a 22+12-a 24, 则u 有最小值12-a 24, 欲使函数f (x )=log a ⎝⎛⎭⎫x 2-ax +12有最小值, 则有⎩⎪⎨⎪⎧a >1,12-a 24>0,解得1<a <2,即实数a 的取值范围为(1,2).15.(2022·丽水模拟)已知log a (a +1)<log (a +1)a (a >0且a ≠1),则a 的取值范围是 . 答案 ⎝ ⎛⎭⎪⎫-1+52,1 解析 ∵log a (a +1)-log (a +1)a=lg (a +1)lg a -lg a lg (a +1)=lg 2(a +1)-lg 2a lg a lg (a +1)=[lg (a +1)-lg a ][lg (a +1)+lg a ]lg a lg (a +1)当a >1时,lg(a +1)>lg a >0,∴log a (a +1)>log (a +1)a ,不符合题意;当0<a <1时,lg a <0,lg(a +1)>0, lg(a +1)-lg a =lg a +1a>lg 1=0, lg(a +1)+lg a =lg [a (a +1)]=lg ⎣⎡⎦⎤⎝⎛⎭⎫a +122-14, ∴log a (a +1)<log (a +1)a (0<a <1)即为lg ⎣⎡⎦⎤⎝⎛⎭⎫a +122-14>0, 由于y =lg x (x >0)单调递增,∴⎝⎛⎭⎫a +122-14>1. 又0<a <1,解得-1+52<a <1, 综上有a 的取值范围是⎝ ⎛⎭⎪⎫-1+52,1. 16.已知函数f (x )=log 2(2x +k )(k ∈R ).(1)当k =-4时,解不等式f (x )>2;(2)若函数f (x )的图象过点P (0,1),且关于x 的方程f (x )=x -2m 有实根,求实数m 的取值范围. 解 (1)当k =-4时,f (x )=log 2(2x -4).由f (x )>2,得log 2(2x -4)>2,得2x -4>4,得2x >8,解得x >3.故不等式f (x )>2的解集是(3,+∞).(2)因为函数f (x )=log 2(2x +k )(k ∈R )的图象过点P (0,1), 所以f (0)=1,即log 2(1+k )=1,解得k =1.所以f (x )=log 2(2x +1).因为关于x 的方程f (x )=x -2m 有实根, 即log 2(2x +1)=x -2m 有实根. 所以方程-2m =log 2(2x +1)-x 有实根. 令g (x )=log 2(2x +1)-x ,则g (x )=log 2(2x +1)-x=log 2(2x +1)-log 22x=log 22x +12x =log 2⎝⎛⎭⎫1+12x . 因为1+12x >1,log 2⎝⎛⎭⎫1+12x >0, 所以g (x )的值域为(0,+∞). 所以-2m >0,解得m <0.所以实数m 的取值范围是(-∞,0).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
对数运算及反函数
一、知识与方法
1、对数的运算法则(将高一级运算向低级运算转化)
(1)N M MN a a a log log log += (2)N M N
M
a a a log log log -= (3)M n M a n a log log = (4)M n
M a n a log 1
log =
2、一个正数的对数是由首数加尾数组成的
3、几个常用的对数结论
01log =a 1log =a a n a n a =log b a b a =log
m n a n a m =
log b m
n b a n
a
m l o g l o g = 1l o g l o g =⋅a b b a 4、换底公式:a
b
a b b c c a lg lg log log log =
=
5、常用对数与自然对数
6、对数的运算:以同底为基本要求,注意质因数分解,未知数在指数位置即为求对数
7、研究反函数是否存在:从函数的单调性出发
8、反函数的定义域:与原函数的值域相同,必须研究原函数值域求得 9、求反函数的基本步骤,分段函数的反函数分段求得 10、原函数与反函数的图像关于x y =对称 11、()[
]x x f
f =-1
()f R x ∈
()[]x x f f =-1()D x ∈
12、反函数具有保奇性,并且保持单调性不变 13、函数()a x f y +=与()a x f
y +=-1
不是互为反函数关系
14、互为反函数的公共点不一定在x y =上 二、练习
1、若2log (2)log log a a a M N M N -=+,则N
M
的值为__________ 2、计算:① =8log 2
2
_______ ② 2
log 293+=________ ③ 1
3log 22-=____________
④ =-2lg 20lg _____ ⑤=+⋅+5lg 5lg 2lg 22lg 2
2
________
⑥=+++2
1
lg 20lg 1000lg 01.0lg ______
⑦(
1
3___________+=⑧_____)
2(lg 50lg 2lg 25lg 2
=++
3、已知732log [log (log )]0x =,那么12
x -等于__________
4、计算:11
log log a
a
b b
-之值为__________ 5、若3log 41x =,则332222x x
x x
--++的值是_______________
6、已知32a
=,那么33log 82log 6-用a 表示是__________ 7、若2log 2,log 3,m n a a m n a +=== 8、已知35a
b
m ==,且
11
2a b
+=,则m 之值为 __________ 9、如果方程()07lg 5lg lg 7lg 5lg lg 2=⋅+++x x 的两根是,αβ,则βα⋅的值是________ 10、求下列函数的反函数
(1)≤0) (2))3(42-<--=x x
x y
(3))21
,(2121-≠∈+-=x R x x x y 且 (4)()
()
⎩⎨⎧>-≤=0302
x x
x x y
11、若函数()1
y f x -=的图象经过点(-2,0)
,则函数(5)y f x =+的图象经过点_______
12、已知函数12y x m =
+与1
3
y nx =-互为反函数,则__________,________m n == 13、已知函数5
()2x f x x m
-=+的图象关于直线y x =对称,则_________m =
14、若点(4,3)既在函数1y =数的解析式为___________
15、已知()1f x =的反函数为1
()f x -,则1(2)f --的值为___________
16、已知x
x x x x f ---+=
2222)((1)求1
()f
x -;
(2)求()f x 值域;(3)判断1
()f x -的奇偶性 17、函数()x f 的定义域为R ,对任意R a ∈,()a x f
y +=-1
的反函数为()a x f y +=,
(1)若()21=f ,求()2f 的值;(2)判断函数()x f 单调性,并加以证明
30、反函数与对数运算
1、4
2、(1)2(2)29(3)
2
6
(4)21(5)1(6)2(7)2-(8)2
3、
4
2
4、0
5、37
6、2-a
7、12
8、15
9、351
10(1)()02≥-=x x y (2)()342<---=x x y (3)()12
21-≠+-=
x x x
y (4)
()()
⎪⎩⎪⎨⎧<-≥-=03
0x x
x x y
11、()2,5-- 12、2,6
1
==
n m 13、1-=m 14、x y 5241-+= 15、8
16、(1)1()f x -()111
1
log 2>-<-+=orx x x x (2)()()∞+⋃-∞-.11,(3)奇函数 17、(1)()a x f
y +=-1
的反函数为()a x f y -=,则()()a x f a x f -=+,令1==a x ,
则()()1112=-=f f
(2)任取21x x <,可得:()()02112<-=-x x x f x f ,则()x f 为减函数。
