第四章电路基础
电路分析基础第四章(李瀚荪)

一、陈述 对任意含源单口网络N,都可以用一个电压源 与一个电阻相串联来等效。 R0 i i + + 即 + 等效 u N u u oc _ _ _
电压源的电压等于该网络的开路电压uoc, 这个电阻等于从此单口网络两端看进去,当网 络内部所有独立源均置零(No)时的等效电阻R0 i =0
+
4.6 戴维南定理
7Ω
10Ω
例(2) a 44 b
20 60 60
20
20 60
22
结论 只含电阻单口网络 等效为一个电阻
只含 电阻
R
2.含独立源电路 1V 例(1)
+
_
2
3
0.5A
0.2A 5
0.5A
5
5 0.3A
+ 1.5V _
结论 含独立源单口网络 等效为实际电压源 或实际电流源 含独立 源和电 阻电路
试用电压源与电流源等效变换的方 法计算2电阻中的电流。
1 2A
解:
I
1 3 2A 2A 6
1
3 + 6V –
6 + – 12V (a)
1 2
(b)
– 2V 2
I + +
由图(d)可得
82 I A 1A 2 2 2
2 2 +
2 2 4A
–
8V (d)
(c)
+
– 2V 2
第四章
分解方法及单口网络
——用等效化简的方法分析电路
本章的主要内容: 1、分解、等效的概念; 2、二端网络的等效化简,实际电源 的等效变换 ; 3、置换、戴维南、诺顿定理, 最大功率传递定理; 4、三端网络T形和形的等效变换。
第4章 三极管及放大电路基础1

与 的关系
IC IC ICBO I E ICBO IC I B ICBO
(1 ) IC I B ICBO
I CBO IC IB 1 1
IE
N
P
N
I'C ICBO IC
IC I B (1 ) ICBO
共射直流电流放大倍数: IC I B 1.7 42.5 0.04 共射交流电流放大倍数: IC I B 2.5 1.7 40 0.06 0.04 说明: 例:UCE=6V时: 曲线的疏密反映了 的大小; IC(mA ) 160mA 电流放大倍数与工作点的位置有关; I 5 140mA CM 120mA 交、直流的电流放大倍数差别不大, 4 100mA 今后不再区别;
3 80mA
___
4. 集电极最大电流ICM 当值下降到正常值的三分之二时的 集电极电流即为ICM。
IC
2.5 2 1.7
1 0 2 4 6 8
IB 40mA
IB=60mA 20mA IB=0 10 UCE(V)
六、主要参数
5. 集-射极反向击穿电压U(BR)CEO 手册上给出的数值是25C、基极开路时的击穿电压U(BR)CEO。 6. 集电极最大允许功耗PCM 集电极电流IC 流过三极管, 所发出的焦耳热为: PC =ICUCE 导致结温 上升,PC 有限制, PCPCM 7. 频率参数
扩散 I C 复合 I B
IC
C
N
IB
P N
EC
或者 IC≈IB
I E IC I B (1 ) I B
EB
E
IE
二、电流放大原理
电路分析基础第5版第4章 分解方法及单、双口网络

9V
4Ω 3
I1
应用举例
例1:求图示电路中各支路电流。
解: 将3Ω电阻用电流源置换
I3 = 2.7
I1
9 4
1 2
0.9
2.7
A
I2
9 4
1 2
0.9
1.8
A
I4
I5
1 2
I3
0.45
A
I1
2
+
9V
I3 3
2
2
I2
I4
4- 3
2 I5
I1
0.9A I3
2
+
9V
2
I2
2 2
I4
I5
结论:置换后对其他支路没有任何影响。
电压u =α和端口电流i =β,则N2 (或N1)可用一个电压为 α 的电
压源或用一个电流为 β 的电流源置换 ,置换后对 N1 (或N2 ) 内各支路电压、电流没有影响。
i=β
N1
+
u=α
N2
i=β
+
N1
α
N1
+ u=α
β
置换定理适用于线性和非线性电路。
二. 置换的实质
置换:如果一个网络N由两个单口网络组成,且已
联立(1)、(2),解得 u=12V, i=-1A
用12V电压源置换N1,可求得 i1
用-1A电流源置换N2,可求得 u2=12V
[例]求上一例题中N1和N2的等效电路
0.5i1
6Ω
i
5Ω i1
+
+ 10Ω 1A
12V u
- -2
+
九年级物理第四章 电路人教版知识精讲

九年级物理第四章电路人教版【同步教育信息】一. 本周教学内容:第四章电路3. 电流的形成4. 导体和绝缘体5. 电路和电路图6. 串联电路和并联电路二. 重、难点:1. 电流概念的建立和电流方向的规定是重点又是难点,怎样判断电流的存在是疑点。
2. 导体和绝缘体的微观解释是重难点,疑点是怎样判别一个物体是导体还是绝缘体。
3. 电路的组成,电路中各元件的作用,按要求画电路图。
4. 串、并联电路的识别,按要求画电路图及根据电路图连接电路。
三. 知识点分析:(一)电流的形成(二)做课本(电流的形成)图4—5实验1. 用毛皮摩擦过的橡胶棒给验电器A带电,验电器B不带电。
2. 用金属棒把A和B连接起来,观察两验电器箔片的变化。
可以看到A的金属箔张开的角度减小,B的金属箔张开,最后两验电器金属箔张开的角度相同。
这实验表明验电器B也带了电。
有电荷通过金属棒从A流到B,即金属棒中有了电荷的定向移动,这就形成了电流。
1. 电荷的定向移动形成电流与水流相似,水在水管中沿一定方向流动,水管中就有了水流。
当两验电器张角相同不再变化时,金属棒中不再有电流,所以这是瞬间电流,瞬间电流在实际中用处不大,那么如何得到持续电流呢?将小灯泡与干电池,开关连接电路。
合上开关,小灯泡发光,打开开关,小灯泡不发光。
小灯泡持续发光,表示有持续电流通过小灯泡的灯丝。
这个持续电流存在的条件是什么?2. 维持持续电流的条件①有电池②合上开关3. 能够持续供电的装置叫电源电源的作用是在电源内部不断地使正极聚集正电荷,负极聚集负电荷,以持续对外供电。
你了解到的电源有哪些?1. 干电池有两个极,一个正极、一个负极,碳棒是正极,锌筒是负极。
2. 蓄电池正、负极通常用“+”“-”号标在电池的上部。
干电池、蓄电池是将化学能转化为电能的。
3. 发电机发电时机械能转化为电能,我们将在第十二章学习。
从能量转化的角度看,电源是把其他形式的能量转化为电能的装置。
水流有方向,就是水流动的方向,电流的方向是怎样的呢?电荷有两种,电路中有电流时,发生定向移动的电荷可能是正电荷、也可能是负电荷,还有可能是正负电荷同时向相反方向移动。
电气基础知识:第四章 线性电路基本定理

i 52 2.6A 12 8
+
- UocRo
16
例4:图示电路,用戴维南定理求电流I。
+ Uoc -
解:移去待求支路求:Uoc 40V
Ro
除去独立电源求: Ro =7
I 40 10 A 75 3
画出戴维南等效电路,并接入待求支路求响应。 17
3、含受控源电路分析
例5:图示电路,用戴维南定理求电流I2。
Us
I0
Us R1
Is
R0
R1R2 R1 R2
R1 R2
Is Isc
Ro Io
Uo
Ro
Us R1
U0
Io Ro
(U s
/ R1 ( R1
I s )R1R2 R2 )
(Ro :除源输入电阻)
+
R1
Uoc
-
(Io : 短路电流Isc )
(Uo : 开路电压Uoc )
10
二、定理:
1、线性含源单口网络对外电路作用可等效为一
30
三、定理应用: 例1:求图示电路中电流I。
I
I4
I0
解:I0 =1A I4 = -0.25A
I1
I3
I2
I1 =0.5A
I2 =0.5A
I= -Io -I4 = -0.75A
31
例2:已知条件如图所示,求图(b)的电压源电压us。
4A
us
(a)
10A ++
U2o0cV --
4A
us
(b)
Ro = 2 Uoc = 20V us = 100V
Ro
u i
=6
画出等效电路,有 R=Ro =6
第四章 电路分析基础分解(1)分解步骤

R
由元件的VCR得: u=Us u=Ri 联立后解得: u=Us i =Us /R
(4-1) (4-2)
(4-3) (4-4)
求解目标
从这个例子不难得到启发:如果在端钮11‘处相连接的是两 个内部结构复杂或是内部情况不明的单口网络,也可按此 思路求得这两个网络的端口电压和端口电流。所不同者, 需要的是这两个单口网络的VCR而不是元件的VCR。 求解策略
图解法求两个网络的端口电压和端口电流
u
Us Q 2 1
绘出这两元件的伏安特性曲 线后,用曲线相交法求得解 答,求交点Q。
坐标为: u=Us i =Us /R (4-3) (4-4)
O
Us/R 图4-2 (b)
i
(b)伏安特性曲线相交法求解图
单口网络及其VCR
重要概念
单口网络:只有两个端钮与其它电路相连接的网络,称为二 端网络。当强调二端网络的端口特性,而不关心网络内部的情况 时,称二端网络为单口网络,简称为单口(One-port)。 电阻单口网络的特性由端口电压电流关系(简称为VCR)来表 征(它是u-i平面上的一条曲线)。
一个元件的电压电流关系是由这个元件本身所确定的,与 外接的电路无关,例如,电阻元件的VCR总是u=Ri (在u、i为 关联参考方向的前提下),这一关系不会因外接电路不同而不 同。 同样,一个单口网络的VCR也是由这个单口网络本身所确 定,与外接电路无关,只要这个单口网络除了通过它的两个端 钮与外界相连外,别无其他联系。
分解的一般规则:
下列情况,划分就不是随意的。 ⑴当N1是N2的负载,而我们只对负载所得到的电压、 电流、功率感兴趣时; ⑵或当N2(N1)内部情况不明(黑箱)或是一个不可 分割的整体(如某种器件的模型),而我们只需了解它的外 部性能时;性质不同网络相连处的电压、电流易于首先求解 时; ⑶或电路中有非线性电路时。
电路理论基础第四章习题解答西安电子科技大学出版社
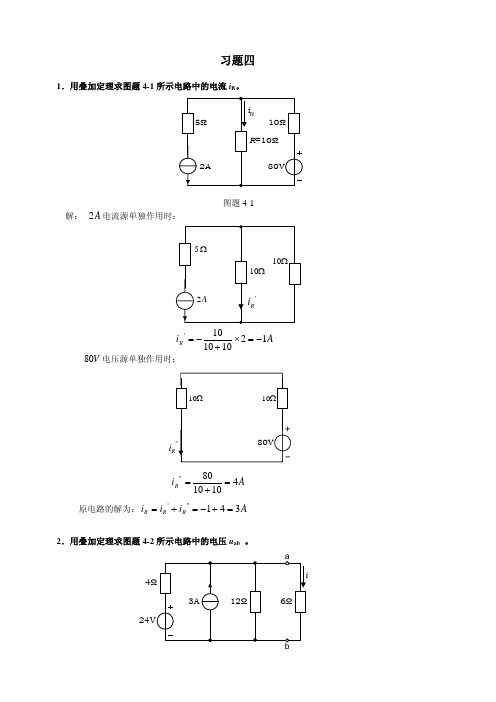
习题四1.用叠加定理求图题4-1所示电路中的电流i R 。
图题4-1解: A 2电流源单独作用时:A i R 12101010'−=×+−=V 80电压源单独作用时:i A i R 4101080''=+=原电路的解为:A i i i R R R 341'''=+−=+=2.用叠加定理求图题4-2所示电路中的电压u ab 。
4图题4-2解:V 24电压源单独作用时:Ω6Ω=+×==46126126//121RV R R u ab 1224411'=×+=A 3电流源单独作用时:Ω4Ω6''A i 13623611214161''=×=×++=V i u ab 6616''''=×=×= 原电路的解为:V u u u ab ab ab 18612'''=+=+=3.用叠加定理求图题4-3所示电路中的电流i 。
6A图题4-3解: A 6电流源单独作用时:ΩΩ6A i 4612612'−=×+−= V 36电压源单独作用时:Ω6Ω6ΩΩA i 261236''−=+−=原电路的解为:()()A i i i 624'''−=−+−=+=4.图题4-4所示电路中,R =6Ω,求R 消耗的功率。
图题4-4解: 将R 支路以外的部分看作一个二端电路。
可采用叠加原理求oc u :12⎟⎠⎞⎜⎝⎛++××+×+=26363212636oc u V 1688=+=求其等效电阻:eqRΩ=++×=426363eq R 原电路简化为:Ri=eq R u oc =RA R R u i eq oc R 6.14616=+=+=W R i P R R 36.1566.122=×=×=5.图题4-5所示电路中, R 1=1.5Ω R 2=2Ω,求(a )从a、b 端看进去的等效电阻;(b )i 1与i s 的函数关系。
电子电工学——模拟电子技术 第四章 双极结型三极管及发达电路基础

4.1 双极结型三极管BJT
(Bipolar Junction Transistor)
又称半导体三极管、晶 体管,或简称为三极管。
分类: 按材料分:硅管、锗管 按结构分:NPN型、PNP型 按频率分:高频管、低频管 按功率分:小功率、大功率
半导体三极管的型号
国家标准对半导体三极管的命名如下:
3 D G 110 B
c
e V VCE
VCC
V
VBE
也是一组特性曲线
实验电路
1.共射极电路的特性曲线
输入特性 :iB=f(vBE)|vCE=const
(1)VCE=0V时,发射结和集电结均正偏,输入特性相当于两个PN结并联
(2)VCE=1V时,发射结正偏,集电结反偏,收集电子能力增强,发射极发
射到基区的电子大部分被集电极收集,从而使得同样的VBE时iB减小。
ICEO (1 )ICBO 值愈大,则该管的 ICEO 也愈大。
3.极限参数
(1) 集电极最大允许电流 ICM
过流区
当IC过大时,三极管的值要 iC
减小。在IC=ICM时,值下降 ICM
到额定值的三分之二。
PCM = iCvCE
(2) 集电极最大允许耗散功率 PCM
将 iC 与 vCE 乘 积 等 于 规 定 的 PCM 值各点连接起来,可得 一条双曲线。
利用IE的变化去控制IC,而表征三极管电流控制作用的参 数就是电流放大系数 。
共射极组态连接方式
IE UBE
+ Uo
-
49 IC 0.98(mA)
IB
20( A)
共射极接法应用我们得到的结论:
1、从三极管的输入电流控制输出电流这一点看来,这两 种电路的基本区别是共射极电路以基极电流作为输入控制 电流。 2、共基极电路是以发射极电流作为输入控制电流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Us'= -10I1'+4= -10×1+4= -6V 10×
共同作用: 共同作用: Us= Us'
Us"= -10I1"+(6//4)×4 +(6//4
=-10×(-1.6)+9.6=25.6V 10× )+9 25. +Us"= -6+25.6=19.6V
如图, (a)中 (b)中 6A, 如图,N为线性含源电阻网络 (a)中I1=4A (b)中I2= –6A, 6A 例:求 (c)中I =? (c)中 3 R2 R2 R2 N I1 (a) R1 N I2 (b) I1=4A I2= –6A 6 R1 + 4V N I3 (c) + R1 6V
解: (a)中仅由N内独立源单独作用时 (a)中仅由 中仅由N
(b)中由N内独立源和4V电源共同作用时 (b)中由N内独立源和4V电源共同作用时 中由 4V
4V电源单独作用时 电源单独作用时R 故仅由 4V电源单独作用时R1支路电流 I2′= –6-4= –10A 6 10A
′
若仅由(c)中6V电源单独作用时R 若仅由(c)中6V电源单独作用时R1支路电流 (c) 电源单独作用时
+ x(t) -
电路
+ y(t) -
+ Kx(t) -
+ 电路 Ky(t) -
2、叠加性superposition 、叠加性superposition
若输入x (t)(单独作用 单独作用) 若输入x1(t) → y1(t)(单独作用) , x2(t) → y2(t) … xn(t) → yn(t) 则x1(t) 、x2(t) … xn(t) 同时作用时响 应y(t)= y1(t)+ y2(t)+ … +yn(t)
+ -
+ -
-
求各支路电流和电阻R 例2:电路如图,已知UR=20v,求各支路电流和电阻R 电路如图,已知U =20v,求各支路电流和电阻 I1 a I1 a I2 I2 I3 3Ω 5Ω 3Ω + 5Ω + R UR + + + 35V 30V 35V 30V – – – – – b b =20V的电压源替代 解:将电阻R用Us=20V的电压源替代 将电阻R 30 − 20 35 − 20 I2 = = 2A I1 = = 5A 5 3
I3 + 20V –
I3=I1+I2=5+2=7A
U R 20 R= = Ω I3 7
例3、电路如图,已知I=0.2A,求支路电流I1 电路如图,已知I=0.2A,求支路电流I I=0.2A 6Ω Ω 3Ω Ω
I1
I 1Ω Ω
+ 3V –
3V
+ – –
6Ω Ω I 3Ω Ω
I1
解:(1)用Is=0.2A的电流 =0.2A的电流 源替代电阻 3 (2)列所选回路的 Ω KVL方程 KVL方程 6Ω Ω 0.2)3I1+6(I1-0.2)-3=0 得: I1=4.2/9=0.466A 3Ω Ω 6Ω Ω
–
2Ω Ω
4Ω Ω
2V
+
I1
1Ω Ω
Ω
U – b
2 3
Ω
N
2
N
1
–
10Ω Ω
0.5A
I2
2Ω Ω
14 3
V
2 3
V
+
+
1V –
a
I
a +
+ 10Ω 10Ω I1 2Ω
1V 0.5A 4Ω N1
a I1 2Ω 1/3A b 图(c) 4Ω 1/6A
图(d)
1/3A电流源替代 电流源替代( (d)) 为求I1,将N2用1/3A电流源替代(图(c) 、(d))
8
3Ω Ω + 10V – I
1Ω Ω 0.5Ω Ω
Rx – U
Ix +
0.5Ω Ω 0.5Ω Ω
试求Rx 试求R
解:用替代
1 Ω –
1 I 8
1
u b a u
2 3
Ω
i N
1
1/3A b
-
a
2 3
V
+
N2 被 等 效
N2 被 替 代
-
注:替代是特定条件下的一种等效(即只在一点等效) 替代是特定条件下的一种等效(即只在一点等效) 替代后电路具有唯一解: 替代后电路具有唯一解 应用替代定理是有条件的,那便是替代后电路应具有唯 应用替代定理是有条件的,那便是替代后电路应具有唯 一解。 一解。 1 例: 如果要使 I x = I ,
1 4 1 I1 = × = A 6 4+2 9
为求I 电压源替代( (4) 为求I2,将N1用 8/9V 电压源替代(图(e) )
a + 8/9V b 图(e) i2 1Ω 2Ω + 2V N2 -
8 8 得 I2 = 1 = A 9 9
等效与替代的区别 如前例中,N2可用2/3V电压源串联2/3Ω电阻来等效它, 如前例中,N2可用2/3V电压源串联2/3Ω电阻来等效它,也 可用2/3V电压源串联2/3 可用1/3A电流源来替代它。 1/3A电流源来替代它 可用1/3A电流源来替代它。这时电路中其他部分电压电 流分布都不变。但替代只针对特定的外电路N1时才成立, N1时才成立 流分布都不变。但替代只针对特定的外电路N1时才成立, 外电路改变,替代的电流源大小也改变。 外电路改变,替代的电流源大小也改变。而等效是端口 伏安关系相同,是指对任意外电路都成立。 伏安关系相同,是指对任意外电路都成立。 i a 2Ω Ω 2V b N2 + N1 1Ω Ω N
4.2
替代定理 (Superposition Theorem)
替代(置换)定理: 替代(置换)定理: 含独立源的任意网络中,若已知其中某一单口网络(或某一支路) 含独立源的任意网络中,若已知其中某一单口网络(或某一支路) 的电压和电流分别为u 则可将此单口网络(或支路) 的电压和电流分别为uK和iK,则可将此单口网络(或支路)用uK 电压源或i 电流源替代。若替代后网络仍有唯一解, 电压源或iK电流源替代。若替代后网络仍有唯一解,则原网络中 其它部分电压电流分配不变。 其它部分电压电流分配不变。 i=iK + + N uK N N u=uK M iK (a) 原网络 M被 (b) M被uK电压 源替代 (c) M被iK电流 c) M被 源替代
+ x2(t) + x1(t) + y(t) -
电 路 + xn(t) -
注: x1(t) … xn(t) 可以是不同位置上的激励信号
3、线性=齐次性+叠加性 线性=齐次性+ 若输入x (t)(单独作用 单独作用) 若输入x1(t) → y1(t)(单独作用) x2(t) → y2(t) … xn(t) → yn(t) 则: +…+K K1 x1(t) +K2 x2(t) + +Kn xn(t) → K1 y1(t)+ K2 y2(t)+ … + Kn yn(t)
u'=4V
(2) 4A电流源单独作用,10V电压源短路(图b) 电流源单独作用, 电压源短路( u"= -4×(6//4)= -9.6V 6//4) (3)共同作用:u=u'+u"= 4+(- 9.6)= - 5.6V 共同作用: 4+(6Ω 6Ω + + + 10V 4Ω u'' 4Ω u' – – – (图a) ) (图b) )
注意: 一个独立源单独作用,其余独立源需置零。 注意: 一个独立源单独作用,其余独立源需置零。 电压源置零—视为短路。 电压源置零 视为短路。 视为短路 电流源置零—视为开路。 电流源置零 视为开路。 视为开路
6Ω 求图中电压u 例1 求图中电压u + 10V – + 4Ω u – 4A
解: (1) 10V电压源单独作用,4A电流源开路(图a) 电压源单独作用, 电流源开路(
iK + uK N
+ uK -
+ uK -
iK N
+ uK -
+ uK (d)
Hale Waihona Puke (a) iK N + uK iK N
(b)
电流为零 可以断开
(c) iK N
与理想电 流源串联
iK iK i (c)
K
(a)
(b)
(d)
0.5A, 例1:如图(a)电路,运用节点法可以求得I1= -0.5A, 如图(a)电路,运用节点法可以求得I (a)电路 =0.75A, =0.75A, =15V。运用替代定理将I I2=0.75A,I3=0.75A,U1=15V。运用替代定理将I3支路用 0.75A电流源替代如图(b),试验证其余各支路电流、 电流源替代如图(b) 0.75A电流源替代如图(b),试验证其余各支路电流、电压不 变。 10Ω I1 Ω 10Ω I1 Ω + + I3 I2 I2 I3 2A 2A U1 10V 20Ω Ω 20Ω 20Ω U 10V Ω Ω
第四章 线性电路的若干定理
4. 1 4. 2 4. 3 4.4 叠加定理 (Superposition Theorem) 替代定理 (Substitution Theorem) 互易定理 (Reciprocity Theorem) 戴维南定理和诺顿定理 Thevenin(Thevenin-Norton Theorem) *特勒根定理 (Tellegen’s
