大学热学期末总复习资料
大学热学期末总复习
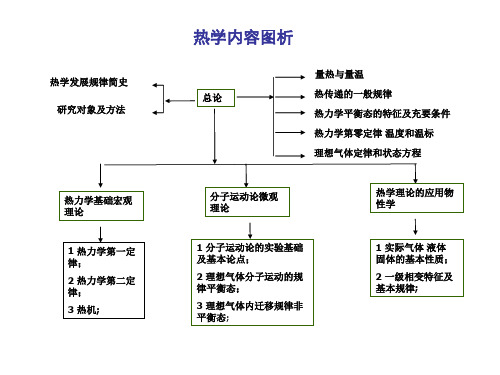
理想气体状态方程 pV M RT RT
非理想气体状态方程范德瓦耳斯方程
1m ol气 体 : (pa2)(b)R T
任意质量气体: (pM 2V 2a2)(VM b)M RT
第二章 气体分子动理论的基本概念
物质的微观模型
一 物质是由大量的原子或分子组成
N A6.0 2 12 0 个 3 /mol
平均自由程 :
气体分子在相邻两次碰 撞间飞行的平均路程;
kT 2 d 2 p
v z
二 分子按自由程的分布
N0个分子中自由程大于x的分子数:
NN0ex
自由程介于区间 x xdx内的分子数:
dN1Ndx1N0exdx
N 0 个 分 子 中 自 由 程 大 于 的 分 子 数 : NN0e10.37N0 N 0 个 分 子 中 自 由 程 小 于 的 分 子 数 : N N 0N0.63N 0
U 0
Q AvRTlnV2 V1
4 绝热过程
方程:
pV
常数TV1 常数p 1
T
常数
Q 0
U A 1 1 [P 2 V 2 P 1 V 1 ] = R 1 (T 2 T 1 )
5 多方过程
方程: pVn C
TVn1 C p1nTn C
n=γ
n=∞
n=0; 等压过程
p
n=1; 等温过程
绝热 n=1
等 体
n=γ; 绝热过程
等温
n=∞; 等体过程
n=0
0
等压
V
Cn,m
CV,m
n
1n
A n 1 1 [P 2 V 2 P 1 V 1 ]或 n R 1 (T 2 T 1 )
UvCV,m(T2T1) QvCn,m(T2T1)
热学期末考试题库及答案

热学期末考试题库及答案一、选择题1. 热力学第一定律的数学表达式是:A. ΔU = Q - WB. ΔH = Q + WC. ΔS = Q/TD. ΔG = H - TS答案:A2. 在理想气体的等压过程中,温度与体积的关系是:A. T ∝ VB. T ∝ 1/VC. T ∝ V^2D. T ∝ 1/V^2答案:A二、填空题3. 理想气体的内能只与______有关。
答案:温度4. 根据热力学第二定律,不可能制造一种循环动作的热机,从单一热源吸热全部用来做功而不引起其他变化。
这种热机被称为______。
答案:永动机三、简答题5. 解释什么是熵,并简述熵增原理。
答案:熵是热力学中表征系统无序程度的物理量。
熵增原理表明,在孤立系统中,自发过程总是向着熵增加的方向进行,直到达到平衡状态。
6. 描述什么是热机效率,并给出其表达式。
答案:热机效率是指热机在将热能转化为机械能的过程中,输出的机械功与输入的热能之比。
其表达式为:η = W/Q_in。
四、计算题7. 一个理想气体从状态A(P1, V1, T1)经历一个等容过程到达状态B(P2, V2, T2)。
已知P1 = 2 atm,V1 = 2 L,T1 = 300 K,求状态B 的体积V2。
答案:首先,根据理想气体状态方程 PV = nRT,可以得到P1V1/T1 = P2V2/T2。
由于是等容过程,体积V不变,所以V2 = V1 = 2 L。
8. 一个绝热容器内装有理想气体,初始温度为T0,经过一个绝热膨胀过程,气体温度变为T。
求气体的最终体积Vf,已知初始体积V0 = 1 m³,初始温度T0 = 300 K,最终温度T = 600 K。
答案:绝热过程中,根据热力学第一定律,Q = 0,W = ΔU。
对于理想气体,ΔU = nCvΔT。
由于是绝热过程,W = -PdV = nCv(T -T0)。
根据理想气体状态方程,PV/T = constant,可以得到Vf/V0 = T/T0。
南华大学热学复习资料

南华⼤学热学复习资料⼀、煤油燃烧后所产⽣的混合⽓体按质量计,各成分的百分⽐为:%8.71的氮,%4.21的⼆氧化碳和%8.6的⽔。
(1)求该混合⽓体的平均摩尔质量;(2)双原⼦分⼦的⾃由度取5,三原⼦分⼦的⾃由度取6,混合⽓体视为理想⽓体,求mol 1该混合⽓体在标准状态下的内能。
⼆、设温度为T 、分⼦质量为m 、总分⼦数为N 的某理想⽓体服从麦克斯韦分布律。
求:(1)分⼦速率处在1v 到12v v >区间内的分⼦数;(2)该区间内分⼦的平均速率。
五、选温度T 及体积V 作为系统的状态参量。
已知p T p T V U VT -=???,求mol 1理想⽓体经可逆过程从状态),(11V T 到达状态),(22V T 时熵的增量。
设理想⽓体的定体摩尔热容量molV C 为常量。
地球⼤⽓温度的垂直分布⽤准静态绝热模型来处理更符合实际。
试证明温度梯度为pgT dz dT ργγ1--= 式中的p 、ρ、T 分别是所考虑⾼度地点的压强、质量密度及温度,γ是⼤⽓的⽐热容⽐。
⼋、假定⽓体中分⼦之间的作⽤⼒是⼀种有⼼⼒f ,它与分⼦间距r 之间的关系为s cr f -=其中s 为某⼀整数,c 为常量。
(1)试⽤量纲分析法找出分⼦碰撞截⾯⾯积σ与分⼦之间平均相对速率u 、摩尔质量molM 以及常量c 之间的关系;(2)这种⽓体的粘滞系数η (λρηv 31=)与温度T 之间的关系是怎样的?⼗、理想⽓体从状态A 出发,经等温膨胀到达状态B ,从状态B 经等容降温到达状态C ,最后从状态C 经绝热压缩回到状态A 。
设过程均为准静态过程,且A T 、C T 已知。
求循环效率。
⼗、选温度T 及压强p 作为系统的状态参量。
已知V T V T p H p T+-= ,求mol 1理想⽓体经可逆过程从状态),(11p T 到达状态),(22p T 时熵的增量。
设理想⽓体的定压摩尔热容量molp C 为常量。
⼋、假定⽓体中分⼦之间的作⽤⼒是⼀种有⼼⼒f ,它与分⼦间距r 之间的关系为s cr f -=其中s 为某⼀整数,c 为常量。
期末复习之热学

期末复习之热学1.只要知道下列哪一组物理量,就可以估算出气体中分子的平均距离()A.阿伏加德罗常数、该气体的摩尔质量和质量B.阿伏加德罗常数、该气体的摩尔质量和密度C.阿伏加德罗常数、该气体的摩尔质量和体积D.该气体的密度、体积和摩尔质量2.关于物体的内能和热量,下列说法中正确的是()A.热水的内能比冷水的内能多B.温度高的物体其热量必定多,内能必定大C.在热传递的过程中,内能大的物体其内能将减小,内能小的物体其内能将增大,直到两物体的内能相等D.热量是热传递过程中内能转移量的量度3.关于永动机不能制成的下列说法中正确的是()A.第一类永动机和第二类永动机都违背了能量守恒定律,所以都不可能制成B.第一类永动机违背了能量守恒定律,第二类永动机没有违背能量守恒定律,因此,随着科学技术的迅猛发展,第二类永动机是可以制成的。
C.第一类永动机违反了热力学第一定律第二类永动机违反了热力学第二定律,这两类永动机都不可能制成。
D.第二类永动机不能制成,说明自然界中进行的涉及热现象的宏观过程都具有方向性4.根据热力学定律和分子动理论,下列说法正确的是()A.布朗运动就是液体分子的运动,它说明了分子在永不停息地做无规则运动B.密封在容积不变的容器内的气体,若温度升高,则气体分子对器壁单位面积上的平均作用力增大C.第二类永动机违反了能量守恒定律,所以不可能制成D.根据热力学第二定律可知,热量能够从高温物体传到低温物体,但不可能从低温物体传到高温物体5.下列叙述正确的是 ( )A.用手捏面包,面包体积会缩小,说明分子之间有间隙B.温度相同的氢气和氧气,氢气分子和氧气分子的平均速率相同C.夏天荷叶上小水珠呈球状,是由于液体表面张力使其表面积具有收缩到到最小趋势的缘故D.自然界中进行的一切与热现象有关的宏观过程都具有方向性6.如图是观察布朗运动时每隔30,记录1次的微粒位置连线图,开始时微粒在位置1,以后的位置依次是2、3、4、……,由此图得到的下列结论中正确的是()A.此图反映了观察时间内微粒的运动轨迹B.此图只是间接地反映了液体分子运动是无规则运动C.若在第75 s再观察一次,微粒应处于位置3和位置4连线的中点D.微粒在从位置7到位置8的这30 s,内运动得最快7.根据分子动理论,物质分子之间的距离为r0时,分子所受的斥力和引力相等,以下关于分子力和分子势能的说法正确的是()A.当分子间距离为r0时,分子具有最大势能B.当分子间距离为r0时,分子具有最小势能C.当分子间距离为r0时,引力和斥力都是最大值D.当分子间距离为r0时,引力和斥力都是最小值8.如图所示,设有一分子位于图中的坐标原点O处不动,另一分子可位于x轴上不同位置处,图中纵坐标表示这两个分子间分子力的大小,两条曲线分别表示斥力和吸引力的大小随两分子间距离变化的关系,e为两曲线的交点,则()A .ab 表示吸引力,cd 表示斥力,e 点的横坐标可能为10-15mB .ab 表示斥力,c d 表示吸引力,e 点的横坐标可能为10-10mC .ab 表示斥力,cd 表示吸引力,e 点的横坐标可能为10-15 mD .ab 表示吸引力,cd 表示斥力,e 点的横坐标可能为10-10 m9.一定质量的气体处于平衡态I,现设法使其温度降低而压强增大,达到平衡态II,则:( )A.状态I 时气体的密度比状态II 时气体的密度大B.状态I 时分子的平均动能比状态II 时分子的平均动能大C.从状态I 到状态II 过程中气体要向外放热D.从状态I 到状态II 过程中气体要对外做功10.用密闭活塞封闭在汽缸内一定质量的某种理想气体,如果与外界没有热交换,下列说法正确的是( )A .若气体分子的平均动能增大,则气体的压强一定增大B .若气体分子的平均动能增大,则气体的压强一定减小C .若气体分子的平均距离增大,则气体分子的平均动能一定增大D .若气体分子的平均距离增大,则气体分子的平均动能一定减小11.一定质量的理想气体,保持体积不变。
《热学》期末复习用 各章习题+参考答案

(
29 × 10 3
)
485������
(4) 空气分子的碰撞频率为
√2������ ������
√2
6 02 × 10 × 22 4 × 10
3 3
×
(3
7 × 10−10)
× 485
(5) 空气分子的平均自由程为
7 9 × 109
������
485 7 9 × 109
6 1 × 10 8������
(������ + ������ )������������ ������ ������������ + ������ ������������
(4)
联立方程(1)(2)(3)(4)解得
������ + ������
������
2
������ ������ ������ (������ ������ + ������ ������ ) (������ + ������ )
������ (������ + ∆������) ������
������
������
(������ + ∆������) ������
������
ln
������������ ������
ln ������
������ + ∆������
ln
Hale Waihona Puke 133 101000ln
2
2
+
20 400
269
因此经过 69 × 60 40 后才能使容器内的压强由 0.101MPa 降为 133Pa.
1-7 (秦允豪 1.3.6) 一抽气机转速������ 400������ ∙ ������������������ ,抽气机每分钟能抽出气体20������.设 容器的容积������ 2 0������,问经过多长时间后才能使容器内的压强由 0.101MPa 降为 133Pa.设抽 气过程中温度始终不变.
热统期末知识点总结

热统期末知识点总结一、热力学基础知识1. 热力学系统:封闭系统、开放系统、孤立系统2. 热力学过程:等容过程、等压过程、等温过程、绝热过程3. 热力学第一定律:能量守恒定律4. 热力学第二定律:热力学不可逆定律5. 热力学第三定律:绝对零度不可达定律二、热力学状态方程1. 理想气体状态方程:PV=nRT2. 绝热方程:PV^γ=常数3. van der Waals方程:(P+a/V^2)(V-b)=RT三、热力学过程1. 等容过程:ΔU=Q,W=02. 等压过程:ΔU=Q-PΔV,W=PΔV3. 等温过程:Q=W,ΔU=04. 绝热过程:Q=0,ΔU=−W四、热力学循环1. 卡诺循环:由等温膨胀、绝热膨胀、等温压缩、绝热压缩四个过程组成的热力学循环2. 卡诺循环效率:η=1- T2/T13. 高效率循环:例如布雷顿循环、热力循环等五、熵和熵增原理1. 熵:系统的无序程度的度量2. 熵增原理:孤立系统的熵不会减少六、热力学定值1. 等温线:PV=常数2. 等容线:P/T=常数3. 等熵线:PV^(γ-1)=常数4. 绝热线:P*V^γ=常数七、不可逆循环1. 单级制冷机和热泵2. 制冷系数和制冷效率3. 制冷系统和热泵系统的效率八、传热1. 传热方式:导热、对流、辐射2. 热传导方程:Q=κAΔT/Δx3. 对流换热方程:Q=mcΔT4. 辐射换热:∈AσT^4九、热力学关系1. 准静态过程:在系统进行状态变化的过程中,系统每一瞬间的参数都可以近似看作平衡的过程2. 等压过程、等容过程、绝热过程的特点及实际应用3. 内能、焓、熵等热力学量的物理意义和计算公式十、热力学定律1. 卡诺定理:卡诺热机效率只与工作物质两个温度有关2. 克劳修斯不等式:任何两个热机无法达到或超过Carnot热机效率3. 热力学循环ΔS=0:卡诺循环4. 有用工作和抽取热5. 充分条件为ΔU=0十一、工程应用1. 蒸汽发动机2. 内燃机3. 空气压缩机总结:热态学是描述热力学性质以及热力学基本定律的一门学科,它研究热力学定态下物质的性质及其变化。
大学物理总复习——热学

3 R 2
气体定体摩尔热容 :____________________ , 气体定压摩尔热容 :________________
(3)
5 R 2
P128二、19. 用绝热材料制成的一个容器,体积为2V0, 被绝热板隔成A、B 两部分,A 内储有1 mol单原子分子 理想气体,B 内储有2 mol 刚性双原子分子理想气体,A、 B 两部分压强相等均为p0,两部分体积均为V0,则 3p0V0/2 ;EB= (1)两种气体各自的内能分别为EA=________ 5p0V0/2 ________; (2) 抽去绝热板,两种气体混合后处于平衡时的温度为T =______。 8p0V0/13R
式中A为常数.则该电子气电子的平均速率为
A 2 (A) v m 3
(B)
A 4 vm 4
(C) v
m
A 2 (D) v m 3
答:[ B ]
P127二、7. 质量为 6.2×10−14 g 的某种粒子悬浮于 27℃的气体中,观察到它们的方均根速率为 1.4cm/s, 则该种粒子的平均速率为_________________。(设 粒子遵守麦克斯韦速率分布律)
P56 6. 用公式 E CV、m T 式中CV为定体摩尔热容 、m
量,视为常量,ν 为气体摩尔数)计算理想气体内能 增量时,此式 (A) 只适用于准静态的等体过程. (B) 只适用于一切等体过程. (C) 只适用于一切准静态过程. (D) 适用于一切始末态为平衡态的过程. 答:[ D ]
200
(C)
10 R
(B)
400
10 R
答:[ c ]
10 R 10 R 200 + 2 (D) 400 10 R + 10 R 2
大学物理热学部分复习资料
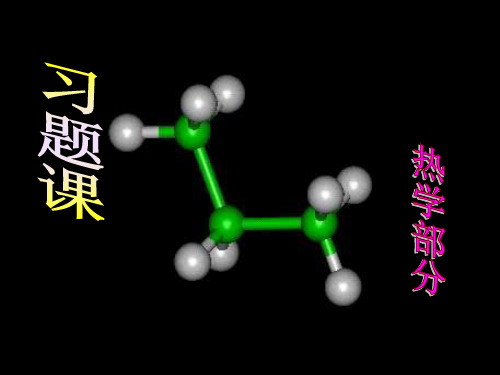
v
dS f vdv
表示速率 v 附近单位 速率区间的分子数占分子 总数的百分比 .
v v dv 区间
内的分子数占总分子数
的百分比
2020/10/10
7
热学习题课
f (v)
2.速率分布曲线
(1)f v v 曲线
S
o
v1 v2 v
S
f v2
v1
v
dv
N N
表示速率在 v1 v2
区间的分子数占总分子数的百
分比 .
归一化条件
0
f
v dv
1
f (v)
dS
o v v dv
v
dS f vdv
v v dv 区间
内的分子数占总分子数
的百分比
2020/10/10
8
热学习题课
f (v)
S
o
v1 v2 v
S
f v2
v1
v
dv
N N
表示速率在 v1 v2
区间的分子数占总分子数的百
分比 .
归一化条件
2
2
分子的 平均动能
3 kT 2
5 kT 2
3kT
理想气体 内能E
3 RT 2
5 RT 2
3RT
2020/10/10
例1、2
5
热学习题课
四、麦克斯韦速率分布律
dN:v v dv区间内的分子数 dN :v v dv区间内的分子 N 数占总分子数的百分比
dN f v dv
N
1.速率分布函数:
分子质量 相同,试比较
温度的关系 T1和T2的大小
f (v) T1
T2
0 v p1 vp2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
气体压强随高度变化的规律:
p p0e
mgh kT
p0e
gh RT
利用气压公式可近似估算爬山或航空 中上升的高度:
p0 RT h ln g p
能量均分定理:在温度 T的平衡状态 下,物质分子的每一个自由 度都具有相同的平均动能,其大小都等于kT/2。 分子平动自由度 t ,转动自由度 r,振动自由度 s,平均总能 量:
dU m 1 (t r 2s ) R dT 2
3 R 3cal mol 1 K 1 2 7 R 7cal mol 1 K 1 2
单原子分子气体 t r 2s 3, CV,m 双原子分子气体 t r 2s 7, CV,m
1、实际气体、液 体、固体的基本性 质; 2、一级相变特征 及基本规律。
第一章 温度
平衡态:在不受外界影响的条件下,也即与外界无任何形式 的物质与能量交换的条件下,系统的宏观性质不随时间变化 的状态称平衡态。 热平衡:假设有两个热力学系统各自处在平衡态,当它们热 接触后,两个系统间要发生热交换(传热),它们原来的平衡态 都被破坏,状态要发生变化。但经过一定时间后,它们都将 达到一个新的平衡态。这种平衡是两个系统在热接触时通过 热交换实现的,所以称为热平衡。 然后,再将它们分开,它们仍各自保持此平衡状态不变。 热力学第零定律:在不受外界影响的情况下,两个物体同时 和第三个物体热平衡时,这两个物体彼此之间也处于热平衡 状态。
dU CV dT vCV ,m dT
U 2 U1 vCV ,m dT
T1 T2
3、理想气体定压热容及焓
H U pV U (T ) vRT
dH m dH Cp , C p ,m , C p vC p ,m dT dT
dH vC p,m dT ;
4、迈雅(Mayer)公式
方程:p C(常量)
A pdV p(V2 V1 )
v x v y vz 0 ; v 2 x
v2 y
2 vz
1 2 v 3
理想气体压强公式
2 p n 3
气体分子的平均平动动能只与温度 有关,并与热力学温度成正比。 T是大量分子热运动平均平动动能 的量度。
温度的统计意义
3 kT 2
方均根速率:
1 m v2 2
第五章
热力学第一定律
改变系统热力学状态的方法:1.作功 2.传热
热力学第一定律:在任一过程中,系统从外界吸收的热
量等于系统自身内能的增加加上系统对外所做的功之和。
数学表达式:
Q U A
dQ dU dA
符号规定: Q > 0 系统吸热 U > 0 系统内能增加 A > 0 系统对外界作正功
理想气体状态方程
pV
M
RT RT
非理想气体状态方程(范德瓦耳斯方程)
1mol气体: (p
任意质量气体:
a
2
)( b) RT
M 2a M M ( p 2 2 )(V b) RT V
第二章 气体分子动理论的基本概念
物质的微观模型
一、物质是由大量的原子或分子组成
dN 4 3 f (v ) vp e Ndv
m 12 f (v x ) ( ) e 2 kT
mvx 2
v2 v2 p
v2
气体分子按速度的分布律:
2 kT
m 3 2 mv2 2 kT f (v ) ( ) e 2 kT
最概然速率:
vp =
2kT m
=
2RT
1 (t r 2s ) kT 2
3 单原子分子 kT 2
5 刚性双原子分子 kT 2
7 非刚性双原子分子 kT 2
理想气体内能: U N (t r 2 s ) m k
N v kT (t r 2s ) RT 2 2
气体定容摩尔热容: CV , m
kT 1.414 m
平均速率:
v= 8kT
m
=
8RT
kT 1.596 m
方均根速率:
v2 =
kT 3kT 3RT 1.732 = m m
f(v) f(vp1) T1 T2 T3
T3 T2 T1
f(vp2) f(vp3)
vp 温度越高,速率大的分子数越多
v
气体分子按势能的分布律:
理想气体的热力学过程
dQ dU dA vCV ,mdT pdV
满足pV=νRT关系;
1、理想气体宏观性质: 满足道尔顿分压定律;
满足阿伏加德罗定律; 满足焦耳定律U=U(T)。 焦耳定律:理想气体内能仅是温度的函数,与体积无关。
U U (T )
2、理想气体定体热容及内能
dU CV dT
3 kT 2
v
2
3kT 3RT m
称为方均根速率
v
2
压强公式应用
1、阿伏伽德罗定律: 在相同的温度和压强下,各种气体在
相同的体积内所含的分子数相等。
p nkT
标准状态下: p 1atm 1.013105 N m2 , T 273.15K
任何气体在1m3中含有的分子数都等于:
p 1.013 105 n m3 2.6868 1025 m3 kT 1.380 1023 273.15
--------洛施密特常量
2、道尔顿分压定律:
一个温度为T 的容器中贮有n种气体。
1 = 2 == n
n n1 n2 nn
代入压强公式,有:
C p ,m CV ,m
H 2 H1 vC p,mdT
T 1T2ຫໍສະໝຸດ dH m dU m d (U m RT ) dU m R dT dT dT dT
1、等体过程
方程:V C(常量) A 0, Q U vCV ,m (T2 T1 )
2、等压过程
测温属性-液体(水银或酒精)体积随温度 变化;
固定点-冰点为零度,汽点为100度; 函数关系-液体体积随温度作线性变化。
• 华氏温标 tF :
9 t F ( 32 t ) F 5
t F 100 F t 37.8 C
t 水 的 冰 点F 32 F t 水 的 沸 点F 212 F
N A 6.021023 个 / m ol
二、分子热运动 1、分子或原子不停的运动 2、分子或原子的运动是无规则的
f
分 斥 子 力 力 引
3、分子或原子的运动剧烈程度与温度有关
三、分子间的吸引力与排斥力
o
r
力
理想气体的微观模型
1. 分子个体的运动模型 (1)大小 — 分子线度<<分子间平均距离; (2)分子力 — 除碰撞的瞬间,在分子之间、 分子与器壁之间无作用力; (3)碰撞性质 — 弹性碰撞; (4)服从规律 — 牛顿力学。 2. 分子的集体运动模型(平衡态) (1)无外场时,分子在各处出现的概率相同。 dN N 分子数密度: n con st. dV V (2)由于碰撞,分子可以有各种不同的速度,速度取向各 方向等概率,速度取向各方向等概率,即:
二、分子间互作用势能
dEp (r ) F (r )dr或F E p (r ) F (r )dr
r
dEp dr
Ep0
r0
r
分子互作用势能曲线
第三章 气体分子热运动速率和能量的统计分布率
气体分子的速率分布函数:
设总分子数N,速率区间 v ~ v+dv,该速率区间内分子数 dNv 速率分布函数
V T lim T (V) 273.16 K lim (定压) p 0 p 0 V tr
•
热力学温标T:不依赖测温物质及其测温属性。
单位:K (Kelvin),规定: T0=273.16K
在理想气体温标有效范围内二者一致。
• 摄氏温标 t : t =(T - 273.15) C t0 = 0.01 C
结论: 1、T一定时, 、 与p或n无关,D与p或n成反比。 2、p一定时, 、、D 都随T的升高而加大; 、 与
T 1 2 成正比,D与 T 3 2 成正比。
四、低压下的热传导和粘滞现象
设有两块平行板间距为 l ,温度分别 保持在 T 和T2,且T>T2。 1 1 当两板间的气压很低,分子的自由程大于l 时,当任一分子与板1相碰时将获得与温 度T1对应的平均热运动能量 1 ,然后这 个分子将无碰撞地冲向板2,与板2相碰, 能量变为与温度T2对应的平均能量 2 , 即将一部分能量传递给板2。分子不断无 碰撞地往返于两板之间,将能量由板1输 运到板2。 继续降低压强,分子数密度减小,即参与输运的 分子数减少,而分子自由程仍为 l ,故气体的导 热性能将减弱。即低压下气体的导热系数随压强 降低而减小,即导热系数与压强成正比。
热学内容图析
热学发展规律简史 总论 研究对象及方法 量热与量温 热传递的一般规律 热力学平衡态的特征及充要条件 热力学第零定律、温度和温标 理想气体定律和状态方程
热力学基础(宏 观理论)
分子运动论(微 观理论)
热学理论的应用 (物性学)
1、热力学第一 定律; 2、热力学第二 定律; 3、热机。
1、分子运动论的实验基 础及基本论点; 2、理想气体分子运动的 规律(平衡态); 3、理想气体内迁移规律 (非平衡态)。
2 2 2 2 p n n1 1 n2 2 nn n 3 3 3 3 p1 p2 pn
