勾股定理的逆定理4PPT课件
合集下载
勾股定理数学优秀ppt课件
实际应用
在建筑、工程等领域，经常需要利用勾股定理求解直角三角形的边长问题，如计算梯子抵墙 时的长度等。
判断三角形类型问题
判断是否为直角三角形
01
若三角形三边满足勾股定理公式，则该三角形为直角三角形。
判断直角三角形的直角边和斜边
02
在直角三角形中，斜边是最长的一边，通过勾股定理可以判断
哪条边是斜边，哪条边是直角边。
06
总结回顾与展望未来
关键知识点总结回顾
勾股定理的定义和表达式
在直角三角形中，直角边的平方和等于斜边的平方，即a²+b²=c²。
勾股定理的证明方法
通过多种几何图形（如正方形、梯形等）的面积关系来证明勾股定 理。
勾股定理的应用场景
在几何、三角学、物理学等领域中广泛应用，如求解三角形边长、 角度、面积等问题。
勾股定理与其他数学定理关系探讨
与三角函数关系
勾股定理是三角函数的基础，通 过勾股定理可以推导出正弦、余 弦、正切等三角函数的基本关系。
与向量关系
在向量空间中，勾股定理可以表示 为两个向量的点积等于它们模长的 平方和，这进一步揭示了勾股定理 与向量的紧密联系。
与几何图形关系
勾股定理在几何图形中有着广泛的 应用，如求解直角三角形、矩形、 菱形等图形的边长、面积等问题。
勾股定理是数学中的基本定理之一， 也是几何学中的基础概念，对于理 解三角形、圆等几何形状的性质具 有重要意义。
历史发展及应用
历史发展
勾股定理最早可以追溯到古埃及时期，但最为著名的证明是由 古希腊数学家毕达哥拉斯学派给出的。在中国，商高在周朝时 期就提出了“勾三股四弦五”的勾股定理的特例。
应用
勾股定理在几何、三角、代数、物理等多个领域都有广泛应用， 如求解三角形边长、角度、面积等问题，以及力学、光学等领 域的计算。
在建筑、工程等领域，经常需要利用勾股定理求解直角三角形的边长问题，如计算梯子抵墙 时的长度等。
判断三角形类型问题
判断是否为直角三角形
01
若三角形三边满足勾股定理公式，则该三角形为直角三角形。
判断直角三角形的直角边和斜边
02
在直角三角形中，斜边是最长的一边，通过勾股定理可以判断
哪条边是斜边，哪条边是直角边。
06
总结回顾与展望未来
关键知识点总结回顾
勾股定理的定义和表达式
在直角三角形中，直角边的平方和等于斜边的平方，即a²+b²=c²。
勾股定理的证明方法
通过多种几何图形（如正方形、梯形等）的面积关系来证明勾股定 理。
勾股定理的应用场景
在几何、三角学、物理学等领域中广泛应用，如求解三角形边长、 角度、面积等问题。
勾股定理与其他数学定理关系探讨
与三角函数关系
勾股定理是三角函数的基础，通 过勾股定理可以推导出正弦、余 弦、正切等三角函数的基本关系。
与向量关系
在向量空间中，勾股定理可以表示 为两个向量的点积等于它们模长的 平方和，这进一步揭示了勾股定理 与向量的紧密联系。
与几何图形关系
勾股定理在几何图形中有着广泛的 应用，如求解直角三角形、矩形、 菱形等图形的边长、面积等问题。
勾股定理是数学中的基本定理之一， 也是几何学中的基础概念，对于理 解三角形、圆等几何形状的性质具 有重要意义。
历史发展及应用
历史发展
勾股定理最早可以追溯到古埃及时期，但最为著名的证明是由 古希腊数学家毕达哥拉斯学派给出的。在中国，商高在周朝时 期就提出了“勾三股四弦五”的勾股定理的特例。
应用
勾股定理在几何、三角、代数、物理等多个领域都有广泛应用， 如求解三角形边长、角度、面积等问题，以及力学、光学等领 域的计算。
勾股定理的逆定理-完整版课件
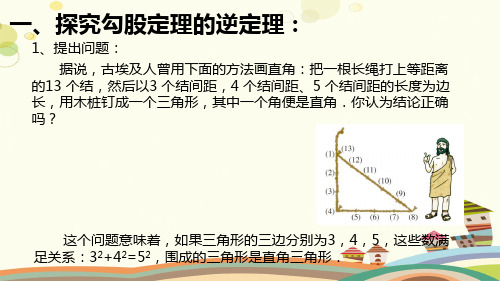
一、探究勾股定理的逆定理：
2、实验探究： （1）画一画：下列各组数中的两数平方和等于第三数的平方，分别以这些数 为边长画出三角形（单位：cm），它们是直角三角形吗？ ① 2.5，6，6.5； ② 6，8，10． （2）量一量：用量角器分别测量上述各三角形的最大角的度数． （3）想一想：请判断这些三角形的形状，并提出猜想．
PQ=16×1.5=24，PR=12×1.5=18，QR=30. ∵24²+18²=30²， 即PQ²+PR²=QR²， ∴△PQR为直角三角形，即∠QPR=90°. ∵∠1=45°， ∴∠2=45°，即“海天”号沿西北方向航行.
练习4、如图，如图，南北向MN为我国领域，即MN以西为我国领海，以东 为公海.上午9时50分，我反走私A艇发现正东方向有一走私艇C以13海里/时的 速度偷偷向我领海开来，便立即通知正在MN线上巡逻的我国反走私艇B.已知 A、C两艇的距离是13海里，A、B两艇的距离是5海里；反走私艇B测得离C艇 的距离是12海里.若走私艇C的速度不变，最早会在什么时间进入我国领海？
2
2
∴BE= AB•BC60.
B
AC 13
.
在Rt△BCE中，由勾股定理得，
N
∴CE= BC 2BE 2 12 2(60 )2144
13 13
∴最早进入时间≈0.85小时=51分钟.
.
9时50分+51分=10时41分.
答：走私艇最早在10时41分进入我国领海.
五、课堂小结：
1、利用勾股定理的逆定理判定是否为直角三角形的一般步骤： ①确定最大边长c； ②计算a2+b2和c2的值, 若a2+b2=c2，则此三角形是直角三角形； 若a2+b2<c2，则此三角形是钝角三角形； 若a2+b2>c2，则此三角形是锐角三角形. 2、互逆命题表明两个命题在形式上的关系，将一个命题的题设和结论互换 即可得到它的逆命题，当原命题成立时，它的逆命题不一定成立，即互逆 的两个命题不一定同真或同假. 3、已知一三角形的三边的长度时，首先应对该三角形进行判断，判断最长 边的平方是否等于其余两边的平方和，如何满足这一条件则此三角形为直 角三角形.
勾股定理的逆定理ppt课件
数学 八年级上册 SK
第
勾股定理
3
章
3.2 勾股定理的逆定理
-
3.2 勾股定理的逆定理
探究与应用
探 活动1 探索并应用勾股定理的逆定理,体会“数”与
究
“形”的内在联系
与
应 [思考探究]
用 1.写出“直角三角形两条直角边的平方和等于斜边的平方”
的逆命题.
解:如果一个三角形的两条边的平方和等于第三边的平方,那么
是钝角三角形;如果a2+b2>c2,那么这个三角形是锐角三角形.
探 究
[概括新知]
与 勾股定理的逆定理:如果三角形的三边长分别为a,b,c,且a2+
应
用 b2=c2,那么这个三角形是直角三角形.
探 归纳 勾股定理与勾股定理的逆定理的联系与区别
究
与
勾股定理
勾股定理的逆定理
应 用
在Rt△ABC中,∠C=90°, 在△ABC中,BC=a,AC=b, 条件
例2 C [解析] A项,82+52≠172,不能构成直角三角形,故不 是勾股数,不符合题意; B项,1.5,2,2.5不都是正整数,故不是勾股数,不符合题意; C项,52+122=132,且5,12,13都是正整数,故是勾股数,符合题 意; D项,32+42≠62,不能构成直角三角形,故不是勾股数,不符合 题意. 故选C.
根据勾股定理,可得A'B'2=a2+b2.
因为AB2=a2+b2,
所以A'B'2=AB2,所以A'B'=AB.
根据“SSS”,可证△ABC≌△A'B'C'.
于是,∠C=∠C'=90°,
第
勾股定理
3
章
3.2 勾股定理的逆定理
-
3.2 勾股定理的逆定理
探究与应用
探 活动1 探索并应用勾股定理的逆定理,体会“数”与
究
“形”的内在联系
与
应 [思考探究]
用 1.写出“直角三角形两条直角边的平方和等于斜边的平方”
的逆命题.
解:如果一个三角形的两条边的平方和等于第三边的平方,那么
是钝角三角形;如果a2+b2>c2,那么这个三角形是锐角三角形.
探 究
[概括新知]
与 勾股定理的逆定理:如果三角形的三边长分别为a,b,c,且a2+
应
用 b2=c2,那么这个三角形是直角三角形.
探 归纳 勾股定理与勾股定理的逆定理的联系与区别
究
与
勾股定理
勾股定理的逆定理
应 用
在Rt△ABC中,∠C=90°, 在△ABC中,BC=a,AC=b, 条件
例2 C [解析] A项,82+52≠172,不能构成直角三角形,故不 是勾股数,不符合题意; B项,1.5,2,2.5不都是正整数,故不是勾股数,不符合题意; C项,52+122=132,且5,12,13都是正整数,故是勾股数,符合题 意; D项,32+42≠62,不能构成直角三角形,故不是勾股数,不符合 题意. 故选C.
根据勾股定理,可得A'B'2=a2+b2.
因为AB2=a2+b2,
所以A'B'2=AB2,所以A'B'=AB.
根据“SSS”,可证△ABC≌△A'B'C'.
于是,∠C=∠C'=90°,
《勾股定理的逆定理》勾股定理PPT精品课件
问题3 古埃及人用来画直角的三边满足这个等式吗？
∵32+42=52，∴满足.
猜想：
命题2：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直
角三角形。
这个命题和前面学的命题1（勾股定理）之间有什么关系吗？
1.题设和结论正好相反的两个命题，叫做互逆命题。
2.如果把其中一个命题叫做原命题，那么另一个命题叫做它的逆命题。
勾股定理的逆定理
1、理解勾股定理的逆定理。
2、了解逆命题的概念，知道原命题为真命题，它的逆命题不一
定为真命题。
3、应用勾股定理的逆定理解决实际问题。
学习目标
学习目标
1.理解勾股定理的逆定理及证明过程。
2.能简单的运用勾股定理的逆定理判定直角三角形。
3.利用勾股定理逆定理解决实际问题
重点
运用勾股定理的逆定理判定直角三角形。
命题2是正确的吗？你能试着证明吗？
利用勾股定理逆定理判断直角三角形
下面以a,b,c为边长的三角形是不是直角三角形？
1）a=15 ，b=8 ，c=17
2）a=13 ，b=14 ，c=15
解：∵152+82=289，172=289，
∴152+82=172，
根据勾股定理的逆定理，这个三角形是直角三角形。
∴∠QPR=90°。
P
由“远航”号沿东北方向航行可知，∠QPS=45°。 ∴∠RPS=45°，
即“海天”号沿西北方向航行。
E
利用勾股定理逆定理判断直角三角形
满足下列条件的△ABC不是直角三角形的是（
A．BC＝1，AC＝2，AB＝
C．BC：AC：AB＝3：4：5
）
B．BC＝1，AC＝2，AB＝
∵32+42=52，∴满足.
猜想：
命题2：如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直
角三角形。
这个命题和前面学的命题1（勾股定理）之间有什么关系吗？
1.题设和结论正好相反的两个命题，叫做互逆命题。
2.如果把其中一个命题叫做原命题，那么另一个命题叫做它的逆命题。
勾股定理的逆定理
1、理解勾股定理的逆定理。
2、了解逆命题的概念，知道原命题为真命题，它的逆命题不一
定为真命题。
3、应用勾股定理的逆定理解决实际问题。
学习目标
学习目标
1.理解勾股定理的逆定理及证明过程。
2.能简单的运用勾股定理的逆定理判定直角三角形。
3.利用勾股定理逆定理解决实际问题
重点
运用勾股定理的逆定理判定直角三角形。
命题2是正确的吗？你能试着证明吗？
利用勾股定理逆定理判断直角三角形
下面以a,b,c为边长的三角形是不是直角三角形？
1）a=15 ，b=8 ，c=17
2）a=13 ，b=14 ，c=15
解：∵152+82=289，172=289，
∴152+82=172，
根据勾股定理的逆定理，这个三角形是直角三角形。
∴∠QPR=90°。
P
由“远航”号沿东北方向航行可知，∠QPS=45°。 ∴∠RPS=45°，
即“海天”号沿西北方向航行。
E
利用勾股定理逆定理判断直角三角形
满足下列条件的△ABC不是直角三角形的是（
A．BC＝1，AC＝2，AB＝
C．BC：AC：AB＝3：4：5
）
B．BC＝1，AC＝2，AB＝
人教版八年级下册数学课件 勾股定理的逆定理
B' a C' B a C
A
cb
B
a
C A'
b B' a C'
证明:画一个△A'B'C'，使∠ C'=90°， B'C'=a，C'A'=b. ∵ ∠ C'=90°，∴ A'B'2= a2+b2=c2， ∴ A'B' =c. 在△ABC和△A'B'C'中 BC=a=B'C'，CA=b=C'A'，AB=c=A'B'.
∴△BCD为直角三角形，∠DBC=90°.
S四边形ABCD
S Rt ABD
S Rt BCD
1 ·AD·AB 2
1 ·BD·BC 2
1 4 3 1 512 36 dm2 .
2
2
课堂小结
勾股定理 的逆定理
逆命题和逆定理 勾股定理的逆定理 勾股数
提问 用量角器量一量，它们是什么三角形？ 直角三角形 由前面几个例子，我们可以作出什么猜想？ 如果三角形ABC的三边长a，b，c满足a2+b2 =c2，那么这个三角形是直角三角形．
题设
命题1 如果直角三角形两直角边长分别为a， b，斜边长为c，那么a2+b2=c2．结论
命题2 如果三角形ABC的三边长a，b，c满足
拓展练习
6.一个零件的形状如图所示，工人 师傅量得这个零件各边尺寸如下 (单位：dm)：AB=3，AD=4， BC=12，CD=13.且∠DAB=90°.你 能求出这个零件的面积吗？
解：如图，连接BD.在Rt△ABD中，
第十七章05节 勾股定理勾股定理的逆定理
learn about different formats and writing methods of
s a m pl e e s s a ys , pl e a s e s t a y t une d!
目录
01
学习目标
LEARNING OBJECTIVES
1.理解勾股定理的逆定理及证明过程。
2.能简单的运用勾股定理的逆定理判定直角三角形。
1、a=15 ，b=8 ，c=17
2、a=13 ，b=14 ，c=15
解：∵152+82=289，172=289，
∴152+82=172，
根据勾股定理的逆定理，这个三角形是直角三角形。
∵132+142=365，152=225，
∴132+142≠152，不符合勾股定理的逆定理，
∴这个三角形不是直角三角形.
第十七章05节 勾股定理
本编为大家提供各种类型的PPT课件，如数学课件、语文课件、英语
课件、地理课件、历史课件、政治课件、化学课件、物理课件等等，
想了解不同课件格式和写法，敬请下载!
M o r e o v e r, o u r s t o r e p r o v i d e s v a r i o u s t y p e s o f c l a s s i c
3
2.5
1
BC
4
6
1
AC
5
6.25
2
45°
∠A
约36.5°
∠B
∠C
90°
约22.5°
90°
90°
约53.5°
约67.5°
45°
A
如果三角形的三边长a,b,c满足a2+b2=c2,
s a m pl e e s s a ys , pl e a s e s t a y t une d!
目录
01
学习目标
LEARNING OBJECTIVES
1.理解勾股定理的逆定理及证明过程。
2.能简单的运用勾股定理的逆定理判定直角三角形。
1、a=15 ，b=8 ，c=17
2、a=13 ，b=14 ，c=15
解：∵152+82=289，172=289，
∴152+82=172，
根据勾股定理的逆定理，这个三角形是直角三角形。
∵132+142=365，152=225，
∴132+142≠152，不符合勾股定理的逆定理，
∴这个三角形不是直角三角形.
第十七章05节 勾股定理
本编为大家提供各种类型的PPT课件，如数学课件、语文课件、英语
课件、地理课件、历史课件、政治课件、化学课件、物理课件等等，
想了解不同课件格式和写法，敬请下载!
M o r e o v e r, o u r s t o r e p r o v i d e s v a r i o u s t y p e s o f c l a s s i c
3
2.5
1
BC
4
6
1
AC
5
6.25
2
45°
∠A
约36.5°
∠B
∠C
90°
约22.5°
90°
90°
约53.5°
约67.5°
45°
A
如果三角形的三边长a,b,c满足a2+b2=c2,
《勾股定理的逆定理》PPT课件(第1课时)
的逆定理，这个三角形是直角三角形，且∠C是直角. (2)∵132+142=365，152=225，∴132+142≠152，不符合勾股定
理的逆定理，∴这个三角形不是直角三角形.
总结：根据勾股定理的逆定理，判断一个三角形是不是直角三 角形，只要看两条较小边长的平方和是否等于最大边长的平方.
巩固练习
D
在Rt△CEF中，得EF2＝CE2＋CF2＝a2＋4a2＝5a2.
在Rt△ADF中，得AF2＝AD2＋DF2＝16a2＋4a2＝20a2.
在△AEF中，AE2＝EF2＋AF2，∴△AEF为直角三角形，且AE为
斜边．∴∠AFE＝90°，即AF⊥EF.
课堂小结
勾股定理 的逆定理
内容 作用 注意
如果三角形的三边长a 、b 、c满
下列各组线段中，能够组成直角三角形的一组是( D )
A. 1,2,3
B. 2,3,4
C. 4,5,6
D. 1, 2, 3 C
满足下列条件的三角形中，不是直角三角形的是( C )
A.三个内角比为1：2：1
C.三边之比为 3 : 2 : 5
B. 三边之比为1：2： 5 D. 三个内角比为1：2：3
探究新知 考 点 2 勾股定理的逆定理和乘法公式判断三角形
b
根据勾股定理，则有 A1B1 2=B1C1 2+C1A1 2=a2+b2. B
B
∵a2+b2=c2, ∴A1B1 =c， ∴AB=A1B1.
A1
在△ABC和△A1B1C 1中，
aC
BC=B1C1,
b
CA=C1A1, AB=A1B1.
B1 a C1
∴∆ABC ≌ ∆A1B1C1. ∠C=∠ C1 =90°.
理的逆定理，∴这个三角形不是直角三角形.
总结：根据勾股定理的逆定理，判断一个三角形是不是直角三 角形，只要看两条较小边长的平方和是否等于最大边长的平方.
巩固练习
D
在Rt△CEF中，得EF2＝CE2＋CF2＝a2＋4a2＝5a2.
在Rt△ADF中，得AF2＝AD2＋DF2＝16a2＋4a2＝20a2.
在△AEF中，AE2＝EF2＋AF2，∴△AEF为直角三角形，且AE为
斜边．∴∠AFE＝90°，即AF⊥EF.
课堂小结
勾股定理 的逆定理
内容 作用 注意
如果三角形的三边长a 、b 、c满
下列各组线段中，能够组成直角三角形的一组是( D )
A. 1,2,3
B. 2,3,4
C. 4,5,6
D. 1, 2, 3 C
满足下列条件的三角形中，不是直角三角形的是( C )
A.三个内角比为1：2：1
C.三边之比为 3 : 2 : 5
B. 三边之比为1：2： 5 D. 三个内角比为1：2：3
探究新知 考 点 2 勾股定理的逆定理和乘法公式判断三角形
b
根据勾股定理，则有 A1B1 2=B1C1 2+C1A1 2=a2+b2. B
B
∵a2+b2=c2, ∴A1B1 =c， ∴AB=A1B1.
A1
在△ABC和△A1B1C 1中，
aC
BC=B1C1,
b
CA=C1A1, AB=A1B1.
B1 a C1
∴∆ABC ≌ ∆A1B1C1. ∠C=∠ C1 =90°.
《勾股定理的逆定理》数学教学PPT课件(5篇)
求证:△ ABC是直角三角形
证明:画一个△A′B′C′,
使∠
C′=900,
B′C′= a,
A'
A
B
b
b
a
C
B'
a
C'
在△ ABC和△ A′B′C′中
BC = a = B′C′,
CA = b = C′A′，
AB = c = A ′B′
C′A′=b
∵ ∠ C′=900
∴ A′B′ 2= a2+b2
∵ a2+b2=c2
c
b
C
作用：已知三角形的三边长，判断
这个三角形是否为直角三角形。
a
B
，
自主学习
例1：注意归纳例题的解题步骤和解题技巧！
已知三角形三条边的长度分别是：（1）1，
,
（2）2，3，4；
（3）3n，4n，5n（n > 0）， 它们是否分别构成直角三角形？
解
（1）在 1， ，,
中，
）2 ，所以，边长为1，
（
∴S四边形ABCD=S△ABD+S△BCD
B
1
= -AB×AD+
2
1
= -×3×4+
2
1
-BD×CD
2
1
-×5×12
2
= 36
所以四边形ABCD的面积
为36.
C
知识升华
满足
a b的三个正整数，
c
2
称为勾股数组.
2
2
自主检测
1、满足________
勾股数组。
的三个____
__
正整数
如:
证明:画一个△A′B′C′,
使∠
C′=900,
B′C′= a,
A'
A
B
b
b
a
C
B'
a
C'
在△ ABC和△ A′B′C′中
BC = a = B′C′,
CA = b = C′A′，
AB = c = A ′B′
C′A′=b
∵ ∠ C′=900
∴ A′B′ 2= a2+b2
∵ a2+b2=c2
c
b
C
作用：已知三角形的三边长，判断
这个三角形是否为直角三角形。
a
B
，
自主学习
例1：注意归纳例题的解题步骤和解题技巧！
已知三角形三条边的长度分别是：（1）1，
,
（2）2，3，4；
（3）3n，4n，5n（n > 0）， 它们是否分别构成直角三角形？
解
（1）在 1， ，,
中，
）2 ，所以，边长为1，
（
∴S四边形ABCD=S△ABD+S△BCD
B
1
= -AB×AD+
2
1
= -×3×4+
2
1
-BD×CD
2
1
-×5×12
2
= 36
所以四边形ABCD的面积
为36.
C
知识升华
满足
a b的三个正整数，
c
2
称为勾股数组.
2
2
自主检测
1、满足________
勾股数组。
的三个____
__
正整数
如:
初二数学《勾股定理》课件
18世纪，欧拉证明了任意三角形的三 条边长都可以用三种不同的实数来表 示，这三种实数之和等于另外三种实 数的平方和。
勾股定理的重要性
勾股定理是几何学中的重要定理 之一，它揭示了直角三角形三边 之间的关系，是解决几何问题的
重要工具。
勾股定理在数学、物理、工程等 领域都有广泛的应用，如物理中 的力学、光学、声学等都涉及到
06
思考题
总结词：拓展思维
你能举出一些生活中应用 勾股定理的实际例子吗？
你认为勾股定理在现代科 技中有哪些应用？
列举
如何理解勾股定理在数学 中的地位和意义？
如何通过勾股定理来探索 和研究更复杂的几何问题
？
THANKS.
勾股定理在复数域的应用
勾股定理在复数域的应用
勾股定理可以在复数域中找到应用，例如在量子力学和信号处理等领域。
应用实例
在量子力学中，勾股定理可以用于描述粒子在三维空间中的运动状态；在信号处理中，勾股定理可以 用于计算信号的能量或功率等。
练习与思考
05
基础练习题
总结词：巩固基础
01
02
列举
勾股定理的基本形式是什么？
总结词
利用相似三角形证明勾股定理
详细描述
欧几里得通过构造两个相似三角形，利用相似三角形的性质，推导出直角三角 形两条直角边的平方和等于斜边的平方，从而证明了勾股定理。
赵爽的证法
总结词
利用面积证明勾股定理
详细描述
赵爽通过将直角三角形转化为矩形，利用面积关系，推导出直角三角形两条直角 边的平方和等于斜边的平方，从而证明了勾股定理。
勾股定理在解决与自然界的规律、现象等相关的问题时也 有着广泛的应用。例如，在解决与地球的自转、公转、太 阳系行星运动等相关的问题时，勾股定理可以提供重要的 思路和方法。
勾股定理的重要性
勾股定理是几何学中的重要定理 之一，它揭示了直角三角形三边 之间的关系，是解决几何问题的
重要工具。
勾股定理在数学、物理、工程等 领域都有广泛的应用，如物理中 的力学、光学、声学等都涉及到
06
思考题
总结词：拓展思维
你能举出一些生活中应用 勾股定理的实际例子吗？
你认为勾股定理在现代科 技中有哪些应用？
列举
如何理解勾股定理在数学 中的地位和意义？
如何通过勾股定理来探索 和研究更复杂的几何问题
？
THANKS.
勾股定理在复数域的应用
勾股定理在复数域的应用
勾股定理可以在复数域中找到应用，例如在量子力学和信号处理等领域。
应用实例
在量子力学中，勾股定理可以用于描述粒子在三维空间中的运动状态；在信号处理中，勾股定理可以 用于计算信号的能量或功率等。
练习与思考
05
基础练习题
总结词：巩固基础
01
02
列举
勾股定理的基本形式是什么？
总结词
利用相似三角形证明勾股定理
详细描述
欧几里得通过构造两个相似三角形，利用相似三角形的性质，推导出直角三角 形两条直角边的平方和等于斜边的平方，从而证明了勾股定理。
赵爽的证法
总结词
利用面积证明勾股定理
详细描述
赵爽通过将直角三角形转化为矩形，利用面积关系，推导出直角三角形两条直角 边的平方和等于斜边的平方，从而证明了勾股定理。
勾股定理在解决与自然界的规律、现象等相关的问题时也 有着广泛的应用。例如，在解决与地球的自转、公转、太 阳系行星运动等相关的问题时，勾股定理可以提供重要的 思路和方法。
人教版八年级下册数学：17.2.2-勾股定理的逆定理课件
过了2秒后行驶了50米，此时测得小汽车与车速检测仪
间的距离为40米. 问：2秒后小汽车在车速检测仪的哪
个方向?这辆小汽车超速了吗?
小汽车在车 速检测仪的2秒后
你觉的此题解对了吗?
50米
小汽车
北偏西60° 方向 25米/秒=90千米/时 40米 >70千米/时∴小汽车超速了
30米 北 30°
60°
车速检测仪
∠B=90°
B
答：C在B地的正北方向．
13cm
A 12cm
2、有一电子跳蚤从坐标原点O出发向正东方向跳1cm，
又向南跳2cm，再向西跳3cm，然后又跳回原点，问电
子跳蚤跳回原点的运动方向是怎样的？所跳距离是多
少厘米？
y
电子跳蚤跳回原点 的运动方向是
东北方向；
所跳距离是 2 2 厘
米．
O1 x
22 2 2 2
（1）类似这样的关系6，8，10；9，12，15是否 也是勾股数？如何验证？
（2）通过对以上勾股数的研究，你有什么样的 猜想？
结论：若a，b，c是一组勾股数，那么ak，bk，ck （k为正整数)也是一组勾股数．
北
Q
30
R S 东 12×1.5=1485° 16×1.5=24 P
港口
解:根据题意画图,如图所示:
N
PQ=16×1.5=24
Q
PR=12×1.5=18
30
S
QR=30 ∵242+182=302,
R
16×1.5=24
12×1.5=18 45°45°
即 PQ2+PR2=QR2 ∴∠QPR=900
P
E
3
3、小明向东走80m后，又向某一方向走60m后，再沿
勾股定理的证明(比较全的证明方法)课件
欧几里得证明：逻辑严密，易于理解，但需要一定的数学基础
海伦证明：简洁明了，易于理解，但需要一定的数学基础
卡尔丹证明：简洁明了，易于理解，但需要一定的数学基础
费马证明：简洁明了，易于理解，但需要一定的数学基础
牛顿证明：简洁明了，易于理解，但需要一定的数学基础
欧拉证明：简洁明了，易于理解，但需要一定的数学基础
诺特证明：简洁明了，易于理解，但需要一定的数学基础
冯 ·诺 伊 曼 证 明 ： 简 洁 明 了 ， 易 于 理 解 ， 但 需 要 一 定 的 数 学 基 础
希尔伯特证明：简洁明了，易于理解，但需要一定的数学基础
罗素证明：简洁明了，易于理解，但需要一定的数学基础
哥德尔证明：简洁明了，易于理解，但需要一定的数学基础
弦图：由两个直角三角形组成的图形 证明过程：通过比较两个直角三角形的面积，得出勾股定理 应用：适用于解决勾股定理相关的问题 优点：直观易懂，易于理解
添加标题
折弦证明法的原理：通过将直角三角形的斜边和直角边分别折成两个直角三角形，从而证明 勾股定理。
添加标题
折弦证明法的步骤：首先，将直角三角形的斜边和直角边分别折成两个直角三角形；然后， 比较这两个直角三角形的斜边和直角边的长度，发现它们满足勾股定理。
未来展望：随着科技的发展，勾股定理的证明方法将更加多样化、智能化，为人类探索未知世 界提供更多可能。
汇报人：PPT
添加标题
折弦证明法的优点：直观易懂，易于理解。
添加标题
折弦证明法的局限性：只适用于直角三角形，对于其他类型的三角形不适用。
原理：将直角三角 形的两个直角边分 别延长，形成两个 全等三角形
步骤：将两个全等 三角形的斜边分别 延长，形成两个全 等矩形
八年级数学勾股定理的逆定理4(PPT)5-4
段的垂直平分线上． （ ） • 4．原命题：角平分线上的点，到这个角的两
边距离相等．（ ） • 逆命题：到角两边距离相等的点，在这个角的
平分线上．（ ）
几款新～。 【菜圃】名菜园。 【菜谱】名①菜单?。②介绍菜肴制作方法的书（多用于书名）：《大众～》。 【菜畦】名有土埂围着的一块块排列整齐的种 蔬菜的田。 【菜青】ī形绿中略带灰黑的颜色。 【菜色】名指人因靠吃菜充饥而营养不良的脸色：面带～。 【菜市】名集中出售蔬菜和肉类等副食品的场所。 【菜式】名菜肴的品种样式。也指不同地区的菜肴。 【菜蔬】名①蔬菜。②家常饭食或宴备的各种菜。 【菜薹】名①某些1．原命题：猫有四只脚．（ ） • 逆命题：有四只脚的是猫．（ ） • 2．原命题：对顶角相等．（ ） • 逆命题：相等的角是对顶角．（ ） • 3．原命题：线段垂直平分线上的点，到这条
线段两端距离相等．（ ） • 逆命题：到线段两端距离相等的点，在这条线
【菜】①名能做副食品的植物；蔬菜：种～｜野～。②专指油菜?：～油。③名经过烹调供下饭下酒的蔬菜、蛋品、鱼、肉等：荤～｜川～｜四～一汤。④（） 名姓。 【菜案】’名炊事分工上指做菜的工作；红案。 【菜霸】名欺行霸市，垄断蔬菜市场的人。 【菜场】名菜市。 【菜单】（～儿）名①开列各种菜肴
名称的单子。②选单的俗称。 【菜刀】名切菜切肉用的刀。 【菜点】名菜肴和点心：风味～｜宫廷～｜西式～。 【菜豆】名①一年生草本植物，茎蔓生，
你知道吗？
• 据说古埃及人用下图的方法画直角：把一 根长绳打上等距离的13个结，然后以3个结、 4个结、5个结的长度为边长，用木桩钉成 一个三角形，其中一个角便是直角．你知 道为什么吗？
【彩纸】名①彩色的纸张。②彩色印相纸。 【寀】古代指官。 【睬】（倸）动答理；理会：理～｜不要～他｜人家对你说话，你怎么能～也不～？ 【踩】 （跴）动脚底接触地面或物体：当心～坏了庄稼｜妹妹～在凳子上贴窗花。 【踩道】∥（～儿）动盗贼作案前察看地形。 【踩点】∥（～儿）动①踩道。② 泛指事先到某；316ti不锈钢管 / 316ti不锈钢管；一地点了解情况。 【踩咕】?〈方〉动贬低：别～人。 【踩水】动一种游泳方法，人直立深 水中，两腿交替上抬下踩，身体保持不沉，并能前进。 【采】（埰）［采地］（）名古代诸侯分封给卿大夫的田地（包括耕种土地的奴隶）。也叫采邑。
边距离相等．（ ） • 逆命题：到角两边距离相等的点，在这个角的
平分线上．（ ）
几款新～。 【菜圃】名菜园。 【菜谱】名①菜单?。②介绍菜肴制作方法的书（多用于书名）：《大众～》。 【菜畦】名有土埂围着的一块块排列整齐的种 蔬菜的田。 【菜青】ī形绿中略带灰黑的颜色。 【菜色】名指人因靠吃菜充饥而营养不良的脸色：面带～。 【菜市】名集中出售蔬菜和肉类等副食品的场所。 【菜式】名菜肴的品种样式。也指不同地区的菜肴。 【菜蔬】名①蔬菜。②家常饭食或宴备的各种菜。 【菜薹】名①某些1．原命题：猫有四只脚．（ ） • 逆命题：有四只脚的是猫．（ ） • 2．原命题：对顶角相等．（ ） • 逆命题：相等的角是对顶角．（ ） • 3．原命题：线段垂直平分线上的点，到这条
线段两端距离相等．（ ） • 逆命题：到线段两端距离相等的点，在这条线
【菜】①名能做副食品的植物；蔬菜：种～｜野～。②专指油菜?：～油。③名经过烹调供下饭下酒的蔬菜、蛋品、鱼、肉等：荤～｜川～｜四～一汤。④（） 名姓。 【菜案】’名炊事分工上指做菜的工作；红案。 【菜霸】名欺行霸市，垄断蔬菜市场的人。 【菜场】名菜市。 【菜单】（～儿）名①开列各种菜肴
名称的单子。②选单的俗称。 【菜刀】名切菜切肉用的刀。 【菜点】名菜肴和点心：风味～｜宫廷～｜西式～。 【菜豆】名①一年生草本植物，茎蔓生，
你知道吗？
• 据说古埃及人用下图的方法画直角：把一 根长绳打上等距离的13个结，然后以3个结、 4个结、5个结的长度为边长，用木桩钉成 一个三角形，其中一个角便是直角．你知 道为什么吗？
【彩纸】名①彩色的纸张。②彩色印相纸。 【寀】古代指官。 【睬】（倸）动答理；理会：理～｜不要～他｜人家对你说话，你怎么能～也不～？ 【踩】 （跴）动脚底接触地面或物体：当心～坏了庄稼｜妹妹～在凳子上贴窗花。 【踩道】∥（～儿）动盗贼作案前察看地形。 【踩点】∥（～儿）动①踩道。② 泛指事先到某；316ti不锈钢管 / 316ti不锈钢管；一地点了解情况。 【踩咕】?〈方〉动贬低：别～人。 【踩水】动一种游泳方法，人直立深 水中，两腿交替上抬下踩，身体保持不沉，并能前进。 【采】（埰）［采地］（）名古代诸侯分封给卿大夫的田地（包括耕种土地的奴隶）。也叫采邑。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
能知道“海天”号沿哪个方向航行吗？
海天 R
N Q 远航
E P
2020年10月2日
6
例3 如果△ABC的三边长分别为 a,b,c,且 a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数） 则△ABC是直角三角形
解：∵ a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数）
2020年10月2日
2
1. 说出下列命题的逆命题, 它们都是真命题吗? (1). 两条直线平行, 同位角相等. (2). 对顶角相等. (3). 全等三角形的对应角相等.
从上述命题的逆命题的编制中, 我们知道凡是命题, 都可以写出它的逆命题, 也就是说每个命题都有逆命题. 同时我们也发现一个真命题的逆命题不一定是真命题. 如(2). (3).
汇报人：XXX 汇报日期：20XX年10月10日
8
2020年10月2日
1
互逆命题:
两个命题中, 如果第一个命题的题设是第二个命题的 结论, 而第一个命题的结论又是第二个命题的题设,那么 这两个命题叫做互逆命题.
如果把其中一个叫做原命题, 那么另一个叫做它的逆 命题.
互逆定理:
如果一个定理的逆命题经过证明是真命题, 那么它也是 一个定理, 这两个定理叫做互逆定理, 其中一个叫做另一 个的逆定理.
∴a2+b2=(m2-n2)2+(2mn)2
=m4-2m2n2+n4+4m2n2
=m4+2m2n2+n4 =(m2+n2)2
பைடு நூலகம்
=c2 ∴△ABC是直角三角形。
2020年10月2日
7
演讲完毕，谢谢观看！
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
(2)a=5,b=7,c=8
(3)a= 7 ,b= 3 ,c=2
2020(年410月)a2日:b:c=2:3:4
5
例2 .“远航”号、“海天”号轮船同时离开
港口，各自沿一固定方向航行，“远航”号 每小时航行16海里，“海天”号每小时航行 12海里。它们离开港口一个半小时后相距30 海里。如果知道“远航”号沿东北方向航行，
题的逆命题不一定也是真命题, 所以并不是所有的定 理都有逆定理. 4.是非题： 一个定理的题设与结论互换，就得到它的逆定理（ ）
2020年10月2日
4
例1.根据下列条件,分别判断以a,b,c 为边的三角形是不是直角三角形?
(1)a=7,b=24,c=25;
2
(2)a=
3
2 ， b=1,c= 3
.
练一练：根 三 （1据 角）下形a列是=2条不0,件是b=， 直21判 角,c断 三=2下 角9 面 形以 ？a,b,c为边的
2020年10月2日
3
1. 你能举一个互逆的定理吗?
2. 把命题“ 等腰三角形的底角相等” 的逆命题叙述为 “底角相等的三角形是等腰三角形” 是否恰当? 如 果不当, 应怎样叙述?
3. “ 每一个定理不一定都有逆定理, 因为逆定理不一定 正确” 这句话对吗? 如果不对, 应如何改正?
注: 虽然每个命题都有逆命题, 但要注意, 因为一个真命
海天 R
N Q 远航
E P
2020年10月2日
6
例3 如果△ABC的三边长分别为 a,b,c,且 a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数） 则△ABC是直角三角形
解：∵ a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数）
2020年10月2日
2
1. 说出下列命题的逆命题, 它们都是真命题吗? (1). 两条直线平行, 同位角相等. (2). 对顶角相等. (3). 全等三角形的对应角相等.
从上述命题的逆命题的编制中, 我们知道凡是命题, 都可以写出它的逆命题, 也就是说每个命题都有逆命题. 同时我们也发现一个真命题的逆命题不一定是真命题. 如(2). (3).
汇报人：XXX 汇报日期：20XX年10月10日
8
2020年10月2日
1
互逆命题:
两个命题中, 如果第一个命题的题设是第二个命题的 结论, 而第一个命题的结论又是第二个命题的题设,那么 这两个命题叫做互逆命题.
如果把其中一个叫做原命题, 那么另一个叫做它的逆 命题.
互逆定理:
如果一个定理的逆命题经过证明是真命题, 那么它也是 一个定理, 这两个定理叫做互逆定理, 其中一个叫做另一 个的逆定理.
∴a2+b2=(m2-n2)2+(2mn)2
=m4-2m2n2+n4+4m2n2
=m4+2m2n2+n4 =(m2+n2)2
பைடு நூலகம்
=c2 ∴△ABC是直角三角形。
2020年10月2日
7
演讲完毕，谢谢观看！
Thank you for reading! In order to facilitate learning and use, the content of this document can be modified, adjusted and printed at will after downloading. Welcome to download!
(2)a=5,b=7,c=8
(3)a= 7 ,b= 3 ,c=2
2020(年410月)a2日:b:c=2:3:4
5
例2 .“远航”号、“海天”号轮船同时离开
港口，各自沿一固定方向航行，“远航”号 每小时航行16海里，“海天”号每小时航行 12海里。它们离开港口一个半小时后相距30 海里。如果知道“远航”号沿东北方向航行，
题的逆命题不一定也是真命题, 所以并不是所有的定 理都有逆定理. 4.是非题： 一个定理的题设与结论互换，就得到它的逆定理（ ）
2020年10月2日
4
例1.根据下列条件,分别判断以a,b,c 为边的三角形是不是直角三角形?
(1)a=7,b=24,c=25;
2
(2)a=
3
2 ， b=1,c= 3
.
练一练：根 三 （1据 角）下形a列是=2条不0,件是b=， 直21判 角,c断 三=2下 角9 面 形以 ？a,b,c为边的
2020年10月2日
3
1. 你能举一个互逆的定理吗?
2. 把命题“ 等腰三角形的底角相等” 的逆命题叙述为 “底角相等的三角形是等腰三角形” 是否恰当? 如 果不当, 应怎样叙述?
3. “ 每一个定理不一定都有逆定理, 因为逆定理不一定 正确” 这句话对吗? 如果不对, 应如何改正?
注: 虽然每个命题都有逆命题, 但要注意, 因为一个真命