锐角三角函数题型分类总结
锐角三角函数知识点总结大全
锐角三角函数知识点总结大全
1.解直角三角形必备条件：（除直角外）至少知道两条边的
长度或一条边的长度和一个角的度数。
2.近似计算不能用勾股定理求边长，否则误差会很大。
3.解直角三角形解题思路总结：（除直角外）
（1）知一角求另一角题型：已知一个角的度数，用直角三角形中两锐角互余，求出另一角的度数。
（2）知两边求另一边题型：已知两边的边长，用勾股定理求出第三边的长。
（3）锐角三角函数：适用于“知角求边”或“知边求角”
的题型中。
（用sin，cos，tan，cot求出）。
4.仰角和俯角
（1）仰角：视线在水平线上方，与水平线形成的夹角。
（2）俯角：是现在水平线下方，与水平线形成的夹角。
5.锐角三角函数的性质（a为锐角）
（1）正弦的性质：
①取值范围：0＜sina＜1 ②增减性：a越大，sina越大（2）余弦的性质：
①取值范围：0＜cosa＜1 ②增减性：a越大，cosa越小联系：sina和cosa互为反函数
（3）正切的性质：
①取值范围：tana可取全体正数②a越大，tana越大
③当a无限接近90度时，tana无穷大。
（4）余切的性质
①取值范围：cota可取全体正数②当a无限接近0度时，cota无穷大③a越大，cota越小
6.锐角三角函数间的关系
（1）平方关系：sina2+cosa2=1
（2）倒数关系：tana=1
cota
（3）比值关系：①tana=sina
cosa ②cota=cosa
sina。
专题01 锐角三角函数和特殊角的三角函数(六大类型)(题型专练)(解析版)
专题01 锐角三角函数和特殊角的三角函数（六大类型）【题型1锐角三角函数的概念】【题型2 锐角三角函数的增减性】【题型3特殊角三角函数值】【题型4 同角三角函数的关系】【题型5 互余两角三角函数的关系】【题型6 三角函数的计算】【题型1锐角三角函数的概念】1．（2022秋•道县期末）在Rt△ABC中，∠C＝90°，AC＝5，BC＝12，则tan A 的值为（ ）A．B．C．D．【答案】B【解答】解：在Rt△ABC中，∠C＝90°，AC＝5，BC＝12，∴tan A＝．故选：B．2．（2023•南岗区校级开学）在Rt△ABC中，∠C＝90°，AB＝2BC，则tan B 等于（ ）A．B．C．D．【答案】D【解答】解：∵∠C＝90°，AB＝2BC，∴AC＝＝＝BC，∴tan B＝＝＝．故选：D．3．（2022秋•路北区校级期末）在Rt△ABC中，∠C＝90°，AB＝10，AC＝8，则cos B的值等于（ ）A．B．C．D．【答案】A【解答】解：∵∠C＝90°，AB＝10，AC＝8，∴BC＝＝6，∴cos B＝＝＝．故选：A．4．（2023•新华区校级模拟）在Rt△ABC中，∠C＝90°，若c为斜边，a、b 为直角边，且a＝5，b＝12，则sin A的值为（ ）A．B．C．D．【答案】B【解答】解：在Rt△ABC中，c＝＝＝13，sin A＝．故选：B．5．（2023•陈仓区模拟）如图，在Rt△ABC中，∠A＝90°，AB＝8，BC＝10，则sin B的值是（ ）A．B．C．D．【答案】C【解答】解：∵在Rt△ABC中，∠A＝90°，AB＝8，BC＝10，∴AC＝，∴sin B＝＝＝，故选：C ．6．（2023•虹口区一模）如图，在Rt △ABC 中，∠C ＝90°，AC ＝1，BC ＝2，那么cos A 的值为（ ）A ．B ．2C ．D ．【答案】C【解答】解：在Rt △ABC 中，∠C ＝90°，AC ＝1，BC ＝2，由勾股定理，得AB ＝＝．由锐角的余弦，得cos A ＝＝＝．故选：C ．7．（2023•金山区一模）在Rt △ABC 中，∠ACB ＝90°，AC ＝4，BC ＝3，则∠B 的正切值等于（ ）A ．B ．C ．D ．【答案】A【解答】解：∵∠ACB ＝90°，AC ＝4，BC ＝3，∴tan B ＝＝．故选：A ．8．（2023•长宁区一模）在△ABC 中，∠C ＝90°，已知AC ＝3，AB ＝5，那么∠A 的余弦值为（ ）A ．B ．C ．D ．【答案】C【解答】解：在Rt △ABC 中，AC ＝3，AB ＝5，故选：C．【题型2 锐角三角函数的增减性】9．（2023•未央区校级三模）若tan A＝2，则∠A的度数估计在（ ）A．在0°和30°之间B．在30°和45°之间C．在45°和60°之间D．在60°和90°之间【答案】D【解答】解：∵tan45°＝1，tan60°＝，而tan A＝2，∴tan A＞tan60°，∴60°＜∠A＜90°．故选：D．10．（2022秋•惠山区校级期中）已知∠A为锐角，且tan A＝3，则∠A的取值范围是（ ）A．0°＜∠A＜30°B．30°＜∠A＜45°C．45°＜∠A＜60°D．60°＜∠A＜90°【答案】D【解答】解：tan30°＝，tan45°＝1，tan60°＝，∵tan A＝3，∴3，又∵一个锐角的正切值随锐角度数的增大而增大，∴60°＜∠A＜90°，故选：D．11．（2021秋•淮北月考）已知角α为△ABC的内角，且cosα＝，则α的取值范围是（ ）A．0°＜α＜30°B．30°＜α＜45°C．45°＜α＜60°D．60°＜α＜90°【答案】C【解答】解：∵cos60°＝，cos45°＝，∴cos60°＜cosα＜cos45°，∴45°＜α＜60°，故选：C．【题型3特殊角三角函数值】12．（2022秋•嵊州市期末）已知tan A＝，∠A是锐角，则∠A的度数为（ ）A．30°B．45°C．60°D．90°【答案】A【解答】解：∵，且∠A是锐角，∴∠A＝30°，故选：A．13．（2023•河西区模拟）计算2cos30°的结果为（ ）A．B．1C．D．【答案】C【解答】解：∵cos30°＝，∴2cos30°＝2×＝．故选：C．14．（2023•肃州区三模）sin60°的相反数（ ）A．B．C．D．【答案】C【解答】解：∵sin60°＝，∴sin60°的相反数是﹣．故选：C．15．（2023•高州市一模）在Rt△ABC中，∠C＝90°，若cos A＝，则∠A的大小是（ ）A．30°B．45°C．60°D．75°【答案】C【解答】解：∵在Rt△ABC中，∠C＝90°，∴∠A为锐角，∵cos A＝，∴∠A＝60°，故选：C．16．（2023•南开区二模）下列三角函数中，结果为的是（ ）A．cos30°B．tan30°C．sin60°D．cos60°【答案】D【解答】解：A．cos30°＝，不符合题意；B．tan30°＝，不符合题意；C．sin60°＝，不符合题意；D．cos60°＝sin30°＝，符合题意．故选：D．17．（2023•河西区一模）cos60°的值等于（ ）A．B．C．D．【答案】D【解答】解：cos60°＝，故选：D．18．（2023•东莞市校级一模）已知∠A为锐角且tan A＝，则∠A＝（ ）A．30°B．45°C．60°D．不能确定【答案】C【解答】解：∵∠A为锐角，tan A＝，∴∠A＝60°．故选：C．19．（2023•迎泽区校级二模）在Rt△ABC中，∠C＝90°，BC＝1，AC＝，那么∠B的度数是（ ）A．15°B．45°C．30°D．60°【答案】D【解答】解：在Rt△ABC中，∠C＝90°，∵tan B＝＝＝，∴∠B＝60°，故选：D．【题型4 同角三角函数的关系】20．（2023•泉港区模拟）已知∠A是锐角△ABC的内角，，则cos A的值是（ ）A．B．C．D．【答案】C【解答】解：由勾股定理可得sin2A+cos2A＝1，∵，∴（）2+cos2A＝1，∴cos2A＝，∴cos A＝或cos A＝﹣（舍去），故选：C．21．（2022秋•日照期末）若α为锐角，且sinα＝，则tanα为（ ）A．B．C．D．【答案】D【解答】解：由α为锐角，且sinα＝，得cosα＝＝＝，tanα＝＝＝，故选：D．22．（2022秋•桐柏县期末）已知在Rt△ABC中，∠C＝90°．若sin A＝，则cos A等于（ ）A．B．C．D．1【答案】A【解答】解：∵sin2A+cos2A＝1，sin A＝，∴+cos2A＝1，∵∠A为锐角，∴cos A＝．故选：A．23．（2022秋•滦州市期中）在Rt△ABC中，∠C＝90°，，则cos A＝（ ）A．B．C．D．【答案】C【解答】解：在Rt△ABC中，∠C＝90°，＝，可设BC＝4k，则AB＝5k，由勾股定理得，AC＝＝3k，∴cos A＝＝，故选：C．24．（2023•钟楼区校级模拟）在Rt△ABC中，∠C＝90°，tan A＝，则cos A 等于（ ）A．B．C．D．【答案】D【解答】解：如图：设BC＝5x，∵tan A＝，∴AC＝12x，AB＝＝13x，∴cos A＝＝＝．故选：D．25．（2023秋•二道区校级月考）在Rt△ABC中，∠C＝90°，若cos A＝，则sin A的值为 ．【答案】．【解答】解：∵sin2A+cos2A＝1，又∵，∴，∴sin A＝或（舍去），故答案为：．【题型5 互余两角三角函数的关系】26．（2023秋•肇源县校级月考）已知在Rt△ABC中，∠C＝90°，sin A＝，则tan B的值为（ ）A．B．C．D．【答案】D【解答】解：在Rt△ABC中，∵∠C＝90°，，∴，设BC＝12x，则AB＝13x，，∴，故选：D．27．（2023•二道区校级模拟）在Rt△ABC中，AC≠BC，∠C＝90°，则下列式子成立的是（ ）A．sin A＝sin B B．sin A＝cos B C．tan A＝tan B D．cos A＝tan B 【答案】B【解答】解：A、sin A＝，sin B＝，sin A≠sin B，故不符合题意；B、sin A＝，cos B＝，sin A＝cos B，故B符合题意；C、tan A＝，tan B＝，tan A≠tan B，故不符合题意；D、cos A＝，tan B＝，则cos A≠tan B，故不符合题意；故选：B．28．（2023秋•东阿县校级月考）在Rt△ABC中，∠C＝90°，sin A＝，则cos B 的值为（ ）A．B．C．D．【答案】B【解答】解：∵cos B＝，sin A＝＝，∴cos B＝．故选：B．29．（2022秋•双牌县期末）已知在Rt△ABC中，∠C＝90°，sin A＝，则tan B 的值为（ ）A．B．C．D．【答案】D【解答】解：在Rt△ABC中，∠C＝90°，sin A＝，∴sin A＝＝，∴设BC＝4a，AB＝5a，∴AC＝＝＝3a，∴tan B＝＝，故选：D．30．（2023•新邵县校级一模）已知△ABC中，∠A＝90°，tan B＝，则sin C＝ ．【答案】．【解答】解：如图．∵∠A＝90°，tan B＝，∴设AC＝x，则AB＝2x．∴BC＝＝．∴sin C＝．故答案为：．31．（2023•未央区校级二模）在Rt△ABC中，∠C＝90°，sin A＝，则tan B 的值为 ．【答案】．【解答】解：在Rt△ABC中，∠C＝90°，sin A＝，∴sin A＝＝，∴设BC＝3a，AB＝5a，∴AC＝＝＝4a，∴tan B＝＝＝．故答案为：．【题型6 三角函数的计算】32．（2023春•江岸区校级月考）计算：．【答案】1．【解答】解：＝＝2﹣1＝1．33．（2022秋•蜀山区校级期末）计算：sin245°+tan60°•cos30°．【答案】2．【解答】解：原式＝（）2+×＝+＝2．34．（2023春•朝阳区校级期末）计算：．【答案】见试题解答内容【解答】解：＝2×﹣+1﹣×＝﹣+1﹣＝．35．（2022秋•武功县期末）计算：sin45°+2cos30°﹣tan60°．【答案】见试题解答内容【解答】解：原式＝+2×﹣＝+﹣＝．36．（2022秋•南通期末）计算：tan45°﹣2sin30°+4cos230°．【答案】3．【解答】解：原式＝＝1﹣1+3＝3．37．（2022秋•辛集市期末）计算：sin60°•tan30°+．【答案】1．【解答】解：原式＝＝+＝1．。
(完整)锐角三角函数题型分类总结,推荐文档
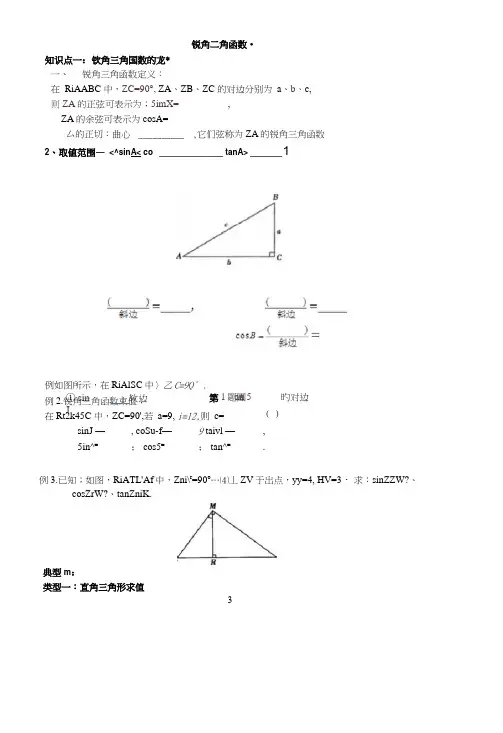
锐角二角函数•知识点一：钦角三角国数的龙* 一、 锐角三角函数定义：在 RiAABC 中，ZC=90°, ZA 、ZB 、ZC 的对边分别为 a 、b 、c, 则ZA 的正弦可表示为；5imX= _________ ,ZA 的余弦可表示为cosA= __________厶的正切：曲心 __________ ,它们弦称为ZA 的锐角三角函数2、取値范围— <^sinA< co ______________ tanA> _______ 1例如图所示，在RiAlSC 中〉乙C=9Q° .例2.锐角三角函数束值；在Rt2k45C 中，ZC=90',若 a=9, i=l2,则 c= _______________sinJ — ____ , coSu-f — ____ 9 taivl — ____ , 5in^= _____ ； cos5= ______ ； tan^= _____ .例3.已知；如图，RiATL'Af 中，Zni\r =90o …⑷丄ZV 于出点，yy=4, HV=3・ 求：sinZZW?、cosZrW?、tanZniK.典型m ：类型一：直角三角形求值3第1题團 ① sin J ( ) 软边 an 5 旳对边( )1 .已知中丿ZC = 90°: tanJ= .5C-12,求・4C\ 和uo£・2. 如朗 0O 的半径OA = 16cm, OC 丄貝B 于C 点，an ^AOC =-.求肋及OC 的长.3・已知：0。
中，OC 丄朋于C 点；16cm ； dnZAOC (1) 求OQ 的半径0A 的长及弦心距 (2) 求 cos/JOC 及 tan^AOC.g4.已知是锐角，sin 」』=一；求cosA tan J 的值17对应ill 练二1. 在 RtA^C 中 7 ZC=90C 7 若BCf A£=应，则 tanJ 的值为5B.巫5C.丄 2D. 22.在t^ABC 中，ZC=90°, 52)I A=- ＞那么tanA 的值等于().53c 4 小 3 c 4 A.-5 B.— 5 C.- 4 D. 一3类型二利用角度转化求值,2. 如團，直径为10的CU 经过点C(Q ・5)和点O(QO)；与轴的正半釉交于点D, $是》轴右侧圆弧上一点〉则代乙OBC 的值为〈)1.已知；如图，C.-3. 如图，角a 的顶点为0,它的一边在工轴的正半轴上，另一边0』上有一点P0 4）,则丄如5.如國06＞AC =1,则sin5的7\c.£ 知/£=卩 BC=10,A.- C.-57.如图7,在等腰直角三角形43C 中'ZC=90° , JC = 6, Z ＞为AC ±—点，若 tanZDA.l = -,则的长为（）5求Z5的度数B.边BC. AB 的长.类型三 化斜三角形为直角三角形 例 1 如图，在△ABC 中，ZA=30c, ZB=45% AC=2\/3 、求 AB 的长.例2.已知：如團，在AABC 中，ZA4C= 120 °，肿=10,/C=5・对应岷1.如图，在RIA.ABC 中,ZBAC=90=，点D 在BC 边上，且A.4BD 是等边三甬形.若.43=2, 求A.ABC 的周长.〈结果保留根号）2. 已知：如虱 AABC 中「3=9, 3C=6,厶皿？的面枳尊于9丿求血^3. ABC 中,乙4=60 ° , .4-5=6 cm …404 cm,则44BC 的面积是类型四；利用构造直角三角形对应练习：1. ________________________________________________ 如图，4ABC 的顶点都在方格纸的格点上，则sinA= _____________ .2・如團八4、B. C 三点在正方形网络线的交点处，若将\A£C 绕着D. 1.4 羽 cm*D.L2cm ：例1如图所示，AABC 的顶点杲正方形网格的格点，则sinA 的值为＜10D.3.正方形网格中, 如團放乱则t^ZAOB 的值是（R求:sin 厶3C 的值.点厘逆吋针旋转得到AC8,则tanF 的值为I特殊角的三角函数值锐角a30s45°60。
锐角三角函数单元总结
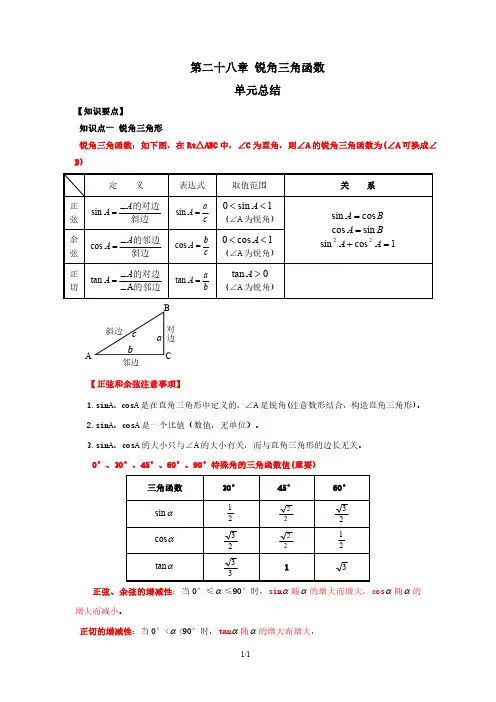
第二十八章锐角三角函数单元总结【知识要点】知识点一锐角三角形锐角三角函数：如下图，在Rt△ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B)定义表达式取值范围关系正弦斜边的对边A A ∠=sin c a A =sin1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A 余弦斜边的邻边A A ∠=cos c b A =cos1cos 0<<A (∠A 为锐角)正切的邻边的对边A tan ∠∠=A A ba A =tan 0tan >A (∠A 为锐角)对边邻边斜边ACBba c 【正弦和余弦注意事项】1.sinA、cosA 是在直角三角形中定义的，∠A 是锐角(注意数形结合，构造直角三角形)。
2.sinA、cosA 是一个比值（数值，无单位）。
3.sinA、cosA 的大小只与∠A 的大小有关，而与直角三角形的边长无关。
0°、30°、45°、60°、90°特殊角的三角函数值(重要)三角函数30°45°60°αsin 212223αcos 232221αtan 3313正弦、余弦的增减性：当0°≤α≤90°时，sin α随α的增大而增大，cos α随α的增大而减小。
正切的增减性：当0°<α<90°时，tan α随α的增大而增大，知识点二解直角三角形一般地，直角三角形中，除直角外，共有五个元素，即三条边和两个锐角．由直角三角形中的已知元素，求出其余未知元素的过程，叫做解直角三角形．直角三角形五元素之间的关系： 1.勾股定理（）2.∠A+∠B=90°3.sin A==4.cos A==5.tan A==【考查题型】考查题型一正弦典例1．（2020·陕西西安市·西北工业大学附属中学九年级期中）如图，在54⨯的正方形网格中，每个小正方形的边长都是1，ABC ∆的顶点都在这些小正方形的顶点上，则sin BAC ∠的值为（）A ．43B ．34C ．35D ．45变式1-1．（2018·西城区·北京四中九年级期中）如图，在Rt ABC ∆中，90C = ∠，10AB =，8AC =，则sin A 等于（）A ．35B ．45C ．34D ．43变式1-2．（2019·山东淄博市·九年级期中）如图，在Rt △ABC 中，∠C ＝90°，sin A ＝45，AC ＝6cm ，则BC 的长度为()A ．6cmB ．7cmC ．8cmD ．9cm考查题型二余弦典例2．（2020·福建省泉州市培元中学九年级期中）如图，△ABC 的顶点都是正方形网格中的格点，则cos ∠ABC 等于（）A ．55B ．255C 5D ．23变式2-1．（2016·辽宁铁岭市·九年级期末）在ABC 中，C 90∠= ，AB 6=，1cosA 3=，则AC 等于（）A ．18B ．2C ．12D ．118变式2-2．（2019·山东滨州市·九年级期末）如图，在平面直角坐标系中，点M 的坐标为M 52），那么cosα的值是（）A B ．23C ．252D ．53考查题型三正切典例3．（2020·广东深圳市·深圳中学八年级期中）如图，A 、B 、C 是小正方形的顶点，且每个小正方形的边长为1，则tan ∠BAC 的值为（）A ．12B ．1C ．33D 变式3-1．（2018·江苏苏州市·九年级期末）如图，在等腰Rt ABC ∆中，90C ∠=︒，6AC =，D 是AC 上一点，若1tan 5DBA ∠=，则AD 的长为（）.A ．2B C D ．1变式3-2．（2020·河北唐山市·九年级期末）如图，有一斜坡AB ，坡顶B 离地面的高度BC 为30m ，斜坡的倾斜角是∠BAC ，若2tan 5BAC ∠=，则此斜坡的水平距离AC 为（）A ．75mB ．50mC ．30mD ．12m考查题型四特殊角的三角函数值典例4．（2018·南昌市期末）点M(－sin 60°，cos 60°)关于x 轴对称的点的坐标是()A ．(32，12)B ．(－32，－12)C ．(－32，12)D ．(－12，－32)变式4-1．（2019·山东淄博市·九年级期中）下列式子错误的是（）A ．cos40°=sin50°B ．tan15°•tan75°=1C ．sin 225°+cos 225°=1D ．sin60°=2sin30°变式4-2．（2018·河北唐山市·九年级期末）如果△ABC 中，sin A =cos B =22，则下列最确切的结论是（）A ．△ABC 是直角三角形B ．△ABC 是等腰三角形C ．△ABC 是等腰直角三角形D ．△ABC 是锐角三角形考查题型五同角的三角函数典例5．（2018·山东潍坊市·九年级期末）在Rt △ABC 中，∠C =90°，sinA=45，则cosB 的值等于()A ．35B ．45C ．34D ．55变式5-1．（2018·浙江台州市·九年级期末）在Rt △ABC 中，cosA=12，那么sinA 的值是（）A ．22B ．32C ．33D ．12变式5-2．（2018·湖南岳阳市·九年级期末）在Rt ABC 中，C 90∠= ，如果4cosA 5=，那么tanA 的值是（）A ．35B ．53C ．34D ．43考查题型六解直角三角形典例6．（2020·东北师大附中明珠学校九年级期中）如图，两根竹竿AB 和AD 斜靠在墙CE 上，量得∠ABC=α，∠ADC=β，则竹竿AB 与AD 的长度之比为()A ．tan tan αβB ．sin sin βαC ．sin sin αβD ．cos cos βα变式6-1．（2020·山东枣庄市·九年级期末）如图，在ABC ∆中，144CA CB cosC ＝＝，＝，则sinB 的值为（）A ．102B ．3C ．4D ．104变式6-2．（2019·辽宁沈阳市·九年级期末）如图，甲乙两楼相距30米，乙楼高度为36米，自甲楼顶A 处看乙楼楼顶B 处仰角为30°，则甲楼高度为（）A ．11米B ．（36﹣）米C ．D ．（36﹣考查题型七利用解直角三角形相关知识解决实际问题典例7．（2019·河南许昌市·九年级期末）如图，某消防队在一居民楼前进行演习，消防员利用云梯成功救出点B 处的求救者后，又发现点B 正上方点C 处还有一名求救者.在消防车上点A 处测得点B 和点C 的仰角分别是45°和65°，点A 距地面2.5米，点B 距地面10.5米.为救出点C 处的求救者，云梯需要继续上升的高度BC 约为多少米？（结果保留整数.参考数据：≈1.4）变式7-1．（2018·江苏无锡市·九年级期末）如图，为了测量出楼房AC的高度，从距离楼底C 处603D（点D与楼底C在同一水平面上）出发，沿斜面坡度为3的斜坡DB前进30米到达点B，在点B处测得楼顶A的仰角为53°，求楼房AC的高度（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈43，计算结果用根号表示，不取近似值）．变式7-2．（2018·山西晋中市期末）“高低杠”是女子体操特有的一个竞技项目，其比赛器材由高、低两根平行杠及若干支架组成，运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离．某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题，请你解答．如图所示，底座上A，B两点间的距离为90cm．低杠上点C到直线AB的距离CE的长为155cm，高杠上点D到直线AB的距离DF的长为234cm，已知低杠的支架AC与直线AB 的夹角∠CAE为82.4°，高杠的支架BD与直线AB的夹角∠DBF为80.3°．求高、低杠间的水平距离CH的长．（结果精确到1cm，参考数据sin82.4°≈0.991，cos82.4°≈0.132，tan82.4°≈7.500，sin80.3°≈0.983，cos80.3°≈0.168，tan80.3°≈5.850）。
第7章锐角三角函数(题型分类全解)
第7章锐角三角函数一、知识点梳理--------锐角三角函数【考点1】如图，在Rt △ABC 中，∠C ＝90°， a 、b 分别是∠A 的对边和邻边，c 是斜边。
1、正切将∠A 的对边a 与邻边b 的比叫做∠A 的正切，记作：tanA . 即：baA A A =∠∠=的邻边的对边tan2、正弦将∠A 的对边a 与斜边c 的比叫做∠A 的正弦，记作：sinA 即：c aA A =∠=斜边的对边sin3、将∠A 的邻边b 与斜边c 的比叫做∠A 的余弦，记作：cosA 即cbA A =∠=斜边的邻边cos【考点2】特殊角三角函数值【考点3】解直角三角形---------构造直角三角形 1、解直角三角形-------已知元素至少有一个是边在直角三角形中，除直角外，由直角三角形中的已知元素，求出其余未知元素的过程，叫做解直角三角形。
2、方法点拨（1）涉“斜”选“弦”的策略 （ 2） 无“斜”选“切”的策略3、方位角方位角：首先确定好基准点，然后在基准点做好坐标，规定以南北方向为始边，左右旋转即可得到方位角.4、仰角和俯角5、坡度或破比通常把坡面的铅直高度h和水平宽度l的比hl叫做坡面的坡度或坡比，坡面与水平面的夹角叫做坡角，通常用α表示，即tanα＝hl.显然，坡度越大，坡角越大，坡面就越陡.6、利用解直角三角形的知识解决实际问题的过程：.(1)将实际问题抽象为数学问题(画出平面图形，转化为解直角三角形的问题)；(2)根据问题中的条件，适当选用锐角三角函数等解直角三角形；(3)得到数学问题的答案；(4)得到实际问题的答案.二、题型分类全解1、在Rt△ABC中，∠C＝90°，AB＝10，sin A＝35，cos A＝45，tan A＝34，则BC的长为( )A.6B．7.5C．8D．12.52、在Rt△ABC中，∠C＝90°，若∠A＝60°，AC＝20 m，则BC是3、如图，在Rt △ABC 中，∠C ＝90°，AC ＝2，BC ＝6，解这个直角三角形.3、如图，在锐角△ABC 中，AB=10,AC=32,53sin B ,求（1）C tan （2）BC 长4.在△ABC 中，若∠C ＝90°，sin A ＝12，AB ＝2，则△ABC 的周长为__ __.5.在Rt △ABC 中，∠C ＝90°，有两边长分别为3和4，则sin A 的值为__ _.6.如图28－2－8，在△ABC 中，BD ⊥AC ，AB ＝6，AC ＝5 3，∠A ＝30°. (1)求BD 和AD 的长； (2)求tan C 的值.7、如图，在边长为1的小正方形网格中，点A 、B 、C 、D 都在这些小正方形的顶点上，连结CD 与AB 相交于点P ，则tan∠APD 的值是( ) A ．2 B ．C ．D ．8、如图，A 、B 、C 是小正方形的顶点，且每个小正方形的边长为1，则tan ∠BAC 的值为（ ）A ．12B ．1CD9、若a ，β是一个三角形的两个锐角，且满足2sin tan 0αβ⎫-+-=⎪⎪⎝⎭，则此三角形是________.10、如图，若直线y ＝－3x ＋3与x 轴所形成的锐角为α，求α的正切值．11、如图, 在Rt △ABC 中, ∠A=90°,AB=AC,D 为AC 上的一点,AD=13AC,求tan ∠DBC 的值12、如图，将矩形ABCD沿CE 折叠，点B 恰好落在边AD 上的点F 处，如果AB BC ＝23.求tan ∠DCF 的值．13、如图，在半径为3的⊙O 中，直径AB 与弦CD 相交于点E ，连接AC 、BD ，若AC ＝2，则cosD ＝ .14、如图，⊙O 是△ABC 的外接圆，AB 为直径，OD ∥BC 交⊙O 于点D ，交AC 于点E ，连接AD 、BD 、CD.(1)求证：AD ＝CD ；(2)若AB ＝10，cos ∠ABC ＝35，求tan ∠DBC 的值．15．如图，AB 是⊙O 的直径，CD 与⊙O 相切于点C ，与AB 的延长线交于点D ，DE ⊥AD 且与AC 的延长线交于点E. (1)求证：DC ＝DE ；(2)若tan ∠CAB ＝12，AB ＝3，求BD 的长．16、热气球的探测器显示，从热气球看一栋楼顶部的仰角为30°，看这栋楼底部的俯角为60°，热气球与楼的水平距离为120 m．这栋楼有多高？17、如图，小明想测量河对岸的一幢高楼AB的高度，在河边C处测得楼顶A的仰角是60°，在距C处60米的E处有幢楼房，小明从该楼房距离地面20米的D处测得高楼顶端A的仰角是30°(点B，C，E在同一直线上，且AB，DE均与地面BE垂直)，求楼AB的高度.18、如图一水库大坝的横断面为梯形ABCD，坝顶BC宽6米，坝高20米，斜坡AB的坡度i＝1∶2.5，斜坡CD的坡角为30°，求坝底AD的长度(精确到0.1米，参考数据：2≈1.414，3≈1.732).19、如图，某建筑物BC上有一旗杆AB，小明在与BC相距12 m的F处，观测到旗杆顶部A的仰角为60°，底部B的仰角为45°，小明的眼睛E与地面的距离EF为1.6 m．(1)求建筑物BC的高度；(2)求旗杆AB的高度.(结果精确到0.1 m，参考数据：2≈1.41，3≈1.73)三、才华展示1、（8分）如图，1号楼在2号楼的南侧，两楼高度均为90m，楼间距为AB．冬至日正午，太阳光线与水平面所成的角为32.3°，1号楼在2号楼墙面上的影高为CA；春分日正午，太阳光线与水平面所成的角为55.7°，1号楼在2号楼墙面上的影高为DA．已知CD=42m．（1）求楼间距AB；（2）若2号楼共30层，层高均为3m，则点C位于第几层？（参考数据：sin32.3°≈0.53，cos32.3°≈0.85，tan32.3°≈0.63，sin55.7°≈0.83，cos55.7°≈0.56，tan55.7°≈1.47）2、（3分）如图，无人机于空中A 处测得某建筑顶部B 处的仰角为45°，测得该建筑底部C 处的俯角为17°．若无人机的飞行高度AD 为62m ，则该建筑的高度BC 为 m ．（参考数据：sin17°≈0.29，cos17°≈0.96，tan17°≈0.31）4、如图，梯子斜靠在与地面垂直（垂足为O ）的墙上，当梯子位于AB 位置时， 它与地面所成的角∠ ABO = 60°；当梯子底端向右滑动1 m （即BD = 1m ）到达CD 位置时，它与地面所成的角∠ CDO = 51°18′，求梯子的长． （参考数据：sin 51°18′ ≈ 0.780，cos 51°18′ ≈ 0.625，tan51°18′ ≈ 1.248）。
锐角三角函数分类总结 经典 含答案
锐角三角函数锐角三角函数锐角三角函数值的变化情况锐角三角函数关系互余两角的三角函数关系同角三角函数关系特殊角的三角函数值锐角三角函数的定义一、锐角三角函数的定义锐角∠A 的正弦、余弦、正切、余切，统称为锐角∠A 的三角函数。
题型1 锐角三角函数的定义例1 在R ABC t ∆中,∠C=090,AC=15,BC=8,分别求∠A 、∠B 的四个三角函数值。
解：815 A B C例2 已知 在R ABC t ∆中，CD 是斜边AB 上的高，AD=8，BD=4，求A tan 的值。
22 8A BC D 4例3 用正弦函数、余弦函数的定义说明：1cos sin 22=+A A例4、P 是∠α的边OA 上一点，且P 点的坐标为()4,3，求ααtan ,sin 的值。
题型二、锐角三角函数之间的关系例5 设α为锐角，1、已知53sin =α，求αααcot ,tan ,cos 的值。
2、已知43tan =α，求αααcot ,cos ,sin 的值 例6、已知α为锐角，2tan =α，求ααααsin 5cos 4cos sin 3-+的值67-题型三、利用三角函数的变化情况化简例7、已知：在⊿ABC 中，∠C=090，化简A A cos sin 21题型四 锐角三角函数的综合应用例8、已知：在⊿ABC 中，AB=AC ，∠BAC=1200，D 是BC 中点，DE ⊥AB 于E ，试说明EB=3EA AB C D E例9、⊿ABC 中，D 是AB 中点，DC ⊥AC ，且∠BCD=300，求∠CDA 的正弦、余弦、和正切的值。
A BC D E。
锐角三角函数的题型及解题技巧
锐角三角函数的题型及解题技巧锐角三角函数是三角函数的基础，它应用广泛，解题技巧性强，下面归纳出锐角三角函数的常见题型，并结合例题介绍一些解题技巧。
一、 化简或求值例1 （1）已知tan 2cot 1αα-=，且α的值。
（2）化简()()22sin cos cos sin a b a b αααα++-。
分析 （1）由已知可以求出tan α可用1tan cot αα=⋅；（2）先把平方展开，再利用22sin cos 1αα+=化简。
解 （1）由tan 2cot 1αα-=得2tan 2tan αα-=，解关于tan α的方程得tan 2α=或tan 1α=-。
又α是锐角，∴tan 2α=。
＝＝tan cot αα-。
由tan 2α=，得1cot 2α=＝tan cot αα-＝13222-=。
（2）()()22sin cos cos sin a b a b αααα++-＝2222sin 2sin cos cos a ab b αααα+⋅⋅+＋2222cos 2cos sin sin a ab b αααα-⋅⋅+＝()()222222sin cos sin cos a b αααα+++＝22a b +。
说明 在化简或求值问题中，经常用到“1”的代换，即22sin cos 1αα+=，tan cot 1αα⋅=等。
二、已知三角函数值，求角例2 在△ABC 中，若223cos sin 022A B ⎛⎫-+-= ⎪ ⎪⎝⎭(),A B ∠∠均为锐角，求C ∠的度数。
分析 几个非负数的和为0，则这几个数均为0。
由此可得cos A 和sin B 的值，进而求出,A B ∠∠的值，然后就可求出C ∠的值。
解 由题意得2cos 0,23sin 0.2A B ⎧-=⎪⎪⎨⎪-=⎪⎩解得2cos ,23sin .3A B ⎧=⎪⎪⎨⎪=⎪⎩又∵,A B ∠∠均为锐角，∴45A ∠=,60B ∠=。
∴18075C A B ∠=-∠-∠=.说明 解这类问题首先要熟记特殊角的三角函数值，还要掌握一些化简的技巧。
锐角三角函数全章复习
B
D
C
专题二、锐角三角函数的性质
1.锐角三角函数的增减性： (1)当角度在00～900之间变化时， 正弦和正切值随角度的增大而增大； 余弦随角度的增大而减小。 (2)当∠A为锐角时， 0<sinA<1;0<cosA<1; tanA>0 2.互余两角的三角函数之间关系 ∠A为锐角时，sinA=cos(900-∠A) cosA=sin(900-∠A)
• 例4.若∠A为锐角，且 cosA≤0.5,则∠A的范围是（ ） A.00<∠A≤600 B.600≤∠A<900 C.00<∠A≤300 D.300≤∠A<900
• 例5.当锐角A>450时，下列不等式 中不成立的是 （ ）
2 A. sin A 2 2 B. cos A 2 C. t an A 1 D. t an A 1
• 例6.下列不正确的是（
A. sin 48 37 cos 41 21
0 / 0 / 2
）
B.RtABC中，C＝90 ，则sin A sin B 1
0 2
C.RtABC中，C＝90 ，则AB＝ACsinB
0
1 D.RtABC中，C＝90 ，则 sinB cosB tanB
0
专题三、解直角三角形及其应用
1.定义； 2.直角三角形边角关系； 3.解直角三角形的应用 (1)在测量距离方面的应用； (2)在工程建筑、航空、航海等 方面的应用.
• 例7.在△ABC中，
BC 1 3, B 60 ,
0
∠C＝450，求AB的长
A
B
C
• 例8.A、B之间有条河，原来从A到B需 过桥CD：A→D→C→B。 A 现建桥EF，可沿直线AB 从A到B.已知 D ∠A＝450， C ∠B＝300，BC＝ E 11km，CD∥AB， F 则现在从A到B比 原来少走多少路程？
锐角三角函数、概率、圆总结
锐角三角函数 一、锐角三角函数 1、正弦：在△ABC 中，∠C=90°，我们把锐角A 的对边与斜边的叫做∠A 的正弦，记做sinA 。
2、余弦：在△ABC 中，∠C=90°，我们把锐角A 的邻边与斜边的叫做∠A 的余弦，记做cosA 。
3、正切：在△ABC 中，∠C=90°，我们把锐角A 的对边与邻边的叫做∠A 的正切，记做tanA 。
4、余切：在△ABC 中，∠C=90°，我们把锐角A 的邻边与对边的叫做∠A 的余切，记做cotA 。
[注]：0°、30°、45°、60°、90°特殊角的三角函数值二、解直角三角形1、定义：已知边和角（两个，其中必有一边）→所有未知的边和角。
2、依据：①边的关系：222c b a =+；②角的关系：A+B=90°；③边角关系：三角函数的定义。
(注意：尽量避免使用中间数据和除法) [注]：（1）三角形面积公式：111sin sin sin 222S ab C bc A ca B ===. （2）正弦定理 ：2sin sin sin a b cR A B C ===. （3）余弦定理：2222cos a b c bc A =+-;2222cos b c a ca B =+-;2222cos c a b ab C =+-三、实际应用1、仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。
(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示，即hi l=。
把坡面与水平面的夹角记作α(叫做坡角)，那么tan hi lα==。
概率一、随机事件和概率 1、 事件的分类：（1）不可能事件：事件一定不会发生 （2）必然事件：事件一定会发生（2）随机事件：事件有可能发生，也有可能不发生2、概率：对于一个事件A ，我们把刻画其发生可能性的大小的数值叫做事件A 的概率，记做：P(A)特点：每次试验结果只有有限个；各种结果出现的可能性相等。
三角函数题型分类总结(18篇)
三角函数题型分类总结第1篇sin(-α) = -sinαcos(-α) = cosαtan (—a)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍：奇变偶不变，符号看象限万能公式sinα=2tan(α/2)/[1+tan^(α/2)]cosα=[1-tan^(α/2)]/1+tan^(α/2)]tanα=2tan(α/2)/[1-tan^(α/2)]三角函数题型分类总结第2篇诱导公式sin(-α)=-sinαcos(-α)=cosαtan(—a)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαsin(π/2+α)=cosαcos(π/2+α)=-sinαsin(π-α)=sinαcos(π-α)=-cosαsin(π+α)=-sinαcos(π+α)=-cosαtanA=sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA); cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA。
sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a)) 三角函数题型分类总结第3篇倒数关系：tanα ·cotα=1sinα ·cscα=1cosα ·secα=1商的关系：sinα/cosα=tanα=secα/cscαcosα/sinα=cotα=cscα/secα平方关系：sin^2(α)+cos^2(α)=11+tan^2(α)=sec^2(α)1+cot^2(α)=csc^2(α)平常针对不同条件的常用的两个公式sin^2(α)+cos^2(α)=1tan α _cot α=1一个特殊公式(sina+sinθ)_(sina-sinθ)=sin(a+θ)_sin(a-θ)证明：(sina+sinθ)_(sina-sinθ)=2 sin[(θ+a)/2] cos[(a-θ)/2] _2 cos[(θ+a)/2] sin[(a-θ)/2] =sin(a+θ)_sin(a-θ)坡度公式我们通常半坡面的铅直高度h与水平高度l的比叫做坡度(也叫坡比), 用字母i表示, 即 i=h / l, 坡度的一般形式写成 l : m 形式,如i=1:5.如果把坡面与水平面的夹角记作a(叫做坡角),那么 i=h/l=tan a.锐角三角函数公式正弦： sin α=∠α的对边/∠α 的斜边余弦：cos α=∠α的邻边/∠α的斜边正切：tan α=∠α的对边/∠α的邻边余切：cot α=∠α的邻边/∠α的对边二倍角公式sin2A=2sinA·cosA(a)-Sin^2(a)(a)(a)-1即Cos2a=Cos^2(a)-Sin^2(a)=2Cos^2(a)-1=1-2Sin^2(a) tan2A=(2tanA)/(1-tan^2(A))三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a = tan a · tan(π/3+a)· tan(π/3-a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 两角和公式tan(α+β)=(tanα+tanβ)/(1-tanαtanβ)tan(α-β)=(tanα-tanβ)/(1+tanαtanβ)cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin(α+β)=sinαcosβ+cosαsinβsin(α-β)=sinαcosβ -cosαsinβ积化和差sinαsinβ =-[cos(α+β)-cos(α-β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/2公式一：设α为任意角,终边相同的角的同一三角函数的值相等：sin(2kπ+α)= sinαcos(2kπ+α)= cosαtan(2kπ+α)= tanαcot(2kπ+α)= cotα公式二：设α为任意角,π+α的三角函数值与α的三角函数值之间的关系：sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα公式三：任意角α与 -α的三角函数值之间的关系：sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五：利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα公式六：π/2±α及3π/2±α与α的三角函数值之间的关系：sin(π/2+α)= cosαcos(π/2+α)= -sinαtan(π/2+α)= -cotαcot(π/2+α)= -tanαsin(π/2-α)= cosαcos(π/2-α)=sinαtan(π/2-α)= cotαcot(π/2-α)= tanαsin(3π/2+α)= -cosαcos(3π/2+α)= sinαtan(3π/2+α)= -cotαcot(3π/2+α)= -tanαsin(3π/2-α)= -cosαcos(3π/2-α)= -sinαtan(3π/2-α)= cotαcot(3π/2-α)= tanα(以上k∈Z)三角函数题型分类总结第4篇下文《雅思听力考试题型》由出国雅思频道为您整理，供您参考，了解更多考试信息，请收藏本章。
锐角三角函数知识点总结与复习
锐角三角函数知识点总结与复习1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方;2、如下图,在Rt △ABC 中,∠C 为直角, 则∠A 的锐角三角函数为∠A 可换成∠B ：3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值;4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余角的正切值;5、0°、30°、45°、60°、90°特殊角的三角函数值重要A 90B 90∠-︒=∠︒=∠+∠得由B A邻边A90B 90∠-︒=∠︒=∠+∠得由B A直角三角形中 的边角关系解直角三角形当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小; 7、正切、余切的增减性：当0°<α<90°时,tan α随α的增大而增大,cot α随α的增大而减小;一、知识性专题专题1：锐角三角函数的定义例 1 在Rt △ABC 中,∠ACB ＝90°,BC ＝1,AB ＝2,则下列结论正确的是 A ．sin A B ．tan A ＝12C ．cos BD ．tan B 分析 sin A ＝BC AB ＝12,tan A ＝BC AC ,cos B ＝BCAB ＝12．故选D.例2 在△ABC 中,∠C ＝90°,cos A ＝35,则tan A 等于 ； 分析 在Rt △ABC 中,设AC ＝3k ,AB ＝5k ,则BC ＝4k ,由定义可知tan A ＝4433BC k AC k ==． 分析 在Rt △ABC 中,BC =3,∴sin A ＝35BC AB =．故填35．例312·哈尔滨在Rt △ABC 中,∠C=900,AC=4,AB=5,则sinB 的值是 ； 解析本题考查了锐角三角函数的意义．解题思路：在直角三角形中,锐角的正弦等于对边比邻边,故sinB=54. 例42012内江如图4所示,△ABC 的顶点是正方形网格的格点,则sinA 的值为 ；解析欲求sinA,需先寻找∠A 所在的直角三角形,而图形中∠A 所在的△ABC 并不是直角三角形,所以需要作高．观察格点图形发现连接CD 如下图所示,恰好可证得CD ⊥AB,于是有图4图4sinA ＝CD AC ＝210＝55．例5 2012宁波,Rt △ABC,∠C=900,AB=6,cosB=错误!,则BC 的长为 ；解析cosB=错误!=错误!,又∵AB=6∴BC=4例62012贵州铜仁如图,定义：在直角三角形ABC 中,锐角α的邻边与对边的比叫做角α的余切,记作ctan α, 即ctan α=BCAC=的对边角的邻边角αα,根据上述角的余切定义,解下列问题：1ctan30◦= ；2如图,已知tanA=43,其中∠A 为锐角,试求ctanA 的值．分析1可先设最小边长为一个特殊数这样做是为了计算方便,然后在计算出其它边长,根据余切定义进而求出ctan30◦;2由tanA=43,为了计算方便,可以设BC=3 AC=4根据余切定义就可以求出ctanA 的值．解析1设BC=1, ∵α=30◦∴AB=2∴由勾股定理得：AC=3ctan30◦=BCAC=32 ∵tanA=43∴设BC=3 AC=4∴ctanA =BC AC =34例72012山东滨州把△ABC 三边的长度都扩大为原来的3倍,则锐角A 的正弦函数值 A ．不变B ．缩小为原来的13C ．扩大为原来的3倍D ．不能确定 解析因为△ABC 三边的长度都扩大为原来的3倍所得的三角形与原三角形相似,所以锐角A 的大小没改变,所以锐角A 的正弦函数值也不变．答案选A ．例82012湖南观察下列等式 ①sin30°= cos60°=②sin45°=cos=45°=③sin60°= cos30°=根据上述规律,计算sin 2a+sin 290°﹣a= ．解析：根据①②③可得出规律,即sin 2a+sin 290°﹣a=1,继而可得出答案． 答案：解：由题意得,sin 230°+sin 290°﹣30°=1；sin 245°+sin 290°﹣45°=1； sin 260°+sin 290°﹣60°=1；故可得sin 2a+sin 290°﹣a=1．故答案为：1．点评：此题考查了互余两角的三角函数的关系,属于规律型题目,注意根据题意总结,另外sin 2a+sin 290°﹣a=1是个恒等式,同学们可以记住并直接运用．例9 2012山东德州为了测量被池塘隔开的A ,B 两点之间的距离,根据实际情况,作出如下图形,其中AB BE ⊥,EF BE ⊥,AF 交BE 于D ,C 在BD 上．有四位同学分别测量出以下四组数据：22题图①BC ,∠ACB ； ②CD ,∠ACB ,∠ADB ；③EF ,DE ,BD ；④DE ,DC ,BC ．能根据所测数据,求出A ,B 间距离的有哪 组解析对于①,可由公式AB=BC ×tan ∠ACB 求出A 、B 两点间的距离；对于②,可设AB 的长为x,则BC=x tan ACB ∠,BD=xtan ADB ∠,BD-BC=CD,可解出AB ．对于③,易知△DEF ∽△DBA,则DE BDEF AB=,可求出AB 的长；对于④无法求得,故有①、②、③三组点评此题考查解直角三角形和三角形相似的性质与判定．在直角三角形中至少要有已知一边和一角才能求出其他未知元素；判定两三角形相似的方法有：AA,SAS,SSS,两直角三角形相似的判定还有HL ． 例102012江苏泰州18如图,在边长相同的小正方形组成的网格中,点A 、B 、C 、D 都在这些小正方形的顶点上,AB 、CD 相交于点P,则tan ∠APD 的值是 ．解析 要求tan ∠APD 的值,只要将∠APD 放在直角三角形中,故过B 作CD 的垂线,然后利用勾股定理计算出线段的长度,最后利用正切的定义计算出结果即可． 答案作BM ⊥CD,DN ⊥AB 垂足分别为M 、N,则2,易得：10,设PM=x,则PD=22-x,由△DNP ∽△BMP,得：PN DN PM BM =,即10102PN x =,∴PN=55x,由DN 2+PN 2=PD 2,得：110+15x 2=22-x 2,解得：x 1=24,x 2=2舍去,∴tan ∠APD=2224BM PM ==2．例11. 2011江苏苏州如图,在四边形ABCD 中,E 、F 分別是AB 、AD 的中点,若EF=2,BC=5,CD=3,则tanC 等ABCDEFF于 ．分析：根据三角形的中位线定理即可求得BD 的长,然后根据勾股定理的逆定理即可证得△BCD 是直角三角形,然后根据正切函数的定义即可求解．解答：解：连接BD ．∵E 、F 分別是AB 、AD 的中点．∴BD=2EF=4∵BC=5,CD=3∴△BCD是直角三角形．∴tanC= 43例122011山东日照在Rt△ABC 中,∠C=90°,把∠A 的邻边与对边的比叫做∠A 的余切,记作cotA=ab．则下列关系式中不成立的是A ．tanA•cotA=1B ．sinA=tanA•cosAC ．cosA=cotA•sinAD ．tan 2A+cot 2A=1解答：解：根据锐角三角函数的定义,得 A 、tanA•c otA=a b b a ⋅=1,关系式成立；B 、sinA=c a ,tanA•cosA=cac b b a =⋅,关系式成立； C 、cosA=,cotA•sinA=c b a b c a =⋅,关系式成立；D 、tan 2A+cot 2A=b a 2+ab 2≠1,关系式不成立．故选D ．点评：本题考查了同角三角函数的关系．1平方关系：sin 2A+cos 2A=1 2正余弦与正切之间的关系积的关系：一个角的正切值等于这个角的正弦与余弦的比,即tanA=BAcos sin 或sinA=tanA•cosA．3正切之间的关系：tanA•tanB=1． 例132011•贵港如图所示,在△ABC 中,∠C=90°,AD 是BC 边上的中线,BD=4,AD=2,则tan∠CAD 的值是 ．解答：解：∵AD 是BC边上的中线,BD=4,∴CD=BD=4,在Rt△ACD中,AC===2,∴tan∠CAD===2．故选A ．例142011烟台如果△ABC 中,sin A =cos B 2,则下列最确切的结论是 A. △ABC 是直角三角形 B. △ABC 是等腰三角形C. △ABC 是等腰直角三角形D. △ABC 是锐角三角形 解：∵sinA=cosB=22,∴∠A =∠B =45°,∴△ABC 是等腰直角三角形．故选C ． 例152011四川如图所示,在数轴上点A 所表示的数x 的范围是A 、330sin 602sin x ︒︒<< B 、3cos302x ︒︒<<cos45C 、3tan 302x ︒︒<<tan45D 、3cot 4502x ︒︒<<cot3 解答：故选D ．同步练习12011甘肃如图,A 、B 、C 三点在正方形网格线的交点处,若将△ACB 绕着点A 逆时针旋转得到△AC ’B ’,则tanB ’的值为 ．解答：解：过C 点作CD ⊥AB ,垂足为D ．根据旋转性质可知,∠B′=∠B ．在Rt△BCD 中,tanB= CD ：BD =13,∴tan B′=tan B = 13． 2 2011甘肃兰州点M －sin60°,cos60°关于x 轴对称的点的坐标是 ． 解：∵sin60°=32,cos60°= 12,∴点M －32,12．∵点P m ,n 关于x 轴对称点的坐标P′m ,-n ,∴M 关于x 轴的对称点的坐标是－32,－12．故选B ． 32011广东已知：45°＜A ＜90°,则下列各式成立的是A 、sinA =cosAB 、sinA ＞cosAC 、sinA ＞tanAD 、sinA ＜cosA解答：解：∵45°＜A ＜90°,∴根据sin 45°=cos 45°,sinA 随角度的增大而增大,cosA 随角度的增大而减小,当∠A ＞45°时,sinA ＞cosA ,故选：B ．4、2011•宜昌教学用直角三角板,边AC=30cm,∠C=90°,tan∠BAC=33,则边BC 的长为 ．cm解：在直角三角形ABC 中,根据三角函数定义可知：tan ∠BAC=BCAC,又AC=30cm,tan ∠3则BC=ACtan 33cm ．故选C ． 5、 2011福建莆田如图,在矩形ABCD 中,点E 在AB 边上,沿CE 折叠矩形ABCD ,使点B 落在AD 边上的点F 处,若AB =4,BC=5,则tan ∠AFE 的值为 ．ABCC ’ B ’解答：解：∵四边形ABCD 是矩形,∴∠A =∠B =∠D =90°,CD =AB =4,AD =BC =5,由题意得：∠EFC =∠B =90°,CF =BC =5,∴∠AFE +∠DFC =90°,∠DFC +∠FCD =90°, ∴∠DCF =∠AFE ,∵在Rt △DCF 中,CF =5,CD =4,∴DF =3,∴tan ∠AFE =tan ∠DCF =DFDC =34 ．6、2012连云港小明在学习“锐角三角函数”中发现,将如图所示的矩形纸片ABCD 沿过点B的直线折叠,使点A 落在BC 上的点E 处,还原后,再沿过点E 的直线折叠,使点A 落在BC 上的点F 处,这样就可以求出°的角的正切值是 ．EC DA BF答案设AB=x,则BE=x,在直角三角形ABE 中,用勾股定理求出AE=EF=2x,于是2在直角三角形ABF 中,tan ∠FAB=21)BF xAB x=2°.选B; 7、2012福州如图15,已知△ABC,AB=AC=1,∠A=36°,∠ABC 的平分线BD 交AC 于点D,则AD 的长是 ,cosA 的值是 .结果保留根号解析：由已知条件,可知△BDC 、△ADB 是等腰三角形,且DA=DB=BC,可证△BDC ∽△ABC,则有BC DC AC BC =,设BC=x,则DC=1-x,因此21,101x xx x x -=+-=即,解方程得, 125151x x ---==,舍去,即AD=512；又cosA=512451512AB AD===--⨯答案：5151,24 8、2012南京如图,将45°的∠AOB 按下面的方式放置在一把刻度尺上：顶点O 与尺下沿的端点重合,OA 与尺下沿重合.OB 与尺上沿的交点B 在尺上的读书恰为2厘米,若按相同的方式将37°的∠AOC 放置在该刻度尺上,则OC 与尺上沿的交点C 在尺上的读数为 厘米.结果精确到厘米,参考数据sin370≈,cos370≈,tan370≈C B AO4321解析：由于∠AOB=45°,B 点读书为2厘米,则直尺的宽为2厘米,解直角三角形得点C 的读数为2÷tan370≈2÷≈厘米.答案：9、2012·湖南张家界黄岩岛是我国南海上的一个岛屿,其平面图如图甲所示,小明据此构造出该岛的一个数学模型如图乙所示,其中∠A=∠D=90°,AB=BC=15千米,CD=23千米,请据此解答如下问题：1 求该岛的周长和面积结果保留整数,参考数据2≈ 73.13≈45.26≈ 2 求∠ACD 的余弦值.解答1结AC,∵AB=BC=15千米,∠B=90°,∴∠BAC=∠ACB=45°,AC=152千米. 又∵∠D=90°, ∴AD=2222)23()215(-=-CD AC =123千米∴周长=AB+BC+CD+DA=30+32+123=30++≈55千米. 面积=S △ABC +S △ADC =21×15×15+21×123×32=2225+186≈157平方千米. 2cos ∠ACD=5121523==AC CD . 10、2012甘肃兰州在建筑楼梯时,设计者要考虑楼梯的安全程度;如图1,虚线为楼梯的倾斜度,斜度线与地面的夹角为倾角θ,一般情况下,倾角越小,楼梯的安全程度越高；如图2,设计者为了提高楼梯的安全程度,要把楼梯的倾角1θ减至2θ,这样楼梯占用地板的长度由d 1增加到d 2 ,已知d 1=4米,140θ∠=,236θ∠=,楼梯占用地板的长度增加了多少米 计算结果精确到米;参考数据：tan40°=,tan36°=AC解析：根据在Rt△ACB中,AB=d1tanθ1=4tan40°,在Rt△ADB中,AB=d2tanθ2=d2tan36°,即可得出d2的值,进而求出楼梯占用地板增加的长度．解：由题意可知可得,∠ACB=∠θ1,∠ADB=∠θ2在Rt△ACB中,AB=d1tanθ1=4tan40°,在Rt△ADB中,AB=d2tanθ2=d2tan36°,得4tan40°=d2tan36°,∴d2=4tan40tan36≈,∴d2-d1==≈,答：楼梯占用地板的长度增加了米．11、2012贵州为促进我市经济的快速发展,加快道路建设,某高速公路建设工程中需修隧道AB,如图,在山外一点C测得BC距离为200m,∠CAB=54°,∠CBA=30°,求隧道AB的长．参考数据：sin54°≈,cos54°≈,tan54°≈,≈,精确到个位解析：首先过点C作CD⊥AB于D,然后在Rt△BCD中,利用三角函数的知识,求得BD,CD的长,继而在Rt△ACD 利用∠CAB的正切求得AD的长,继而求得答案．答案：解：过点C作CD⊥AB于D∵BC=200m,∠CBA=30°,∴在Rt△BCD中,CD=BC=100m,BD=BC•cos30°=200×=100≈173m,∵∠CAB=54°,在Rt△ACD中,AD=≈≈74m,∴AB=AD+BD=173+74=247m．答：隧道AB的长为247m．12、2011新疆建设兵团如图,在△ABC中,∠A＝90°．1用尺规作图的方法,作出△ABC绕点A逆时针旋转45°后的图形△AB1C1保留作图痕迹；2若AB＝3,BC＝5,求tan∠AB1C1．第22题图d2解答：解：1作∠CAB 的平分线,在平分线上截取AB 1＝AB ,作C 1A ⊥AB 1,在AC 1上截取AC 1＝AC ,如图所示即是所求．2∵AB ＝3,BC ＝5,∴AC ＝4,∴AB 1＝3,AC 1＝4,tan∠AB 1C 1＝错误!＝错误!． 专题2 特殊角的三角函数值例12012,湖北孝感计算：cos 245°+tan30°·sin60°=________．答案1例22012陕西计算：(02cos 45-38+1-2=︒ ．解析原式2=2-322+1=-52+12⨯⨯答案-52+1 例32012广安计算：---)32(218cos45o +13- ； 解析：1182()cos 4533---︒+=322212323+-+21 例4 计算|－3|＋2cos 45310． 解：原式＝3＋22－122． 例5 计算－12⎛⎫- ⎪⎝⎭9＋－12007－cos 60°．解：原式＝12＋3＋－1－12＝3－1＝2． 例6 计算|2＋cos 60°－tan 30°08 21十＋221． 例7 计算312-⎛⎫ ⎪⎝⎭－π－0－|1－tan 60°|32-.解：原式＝8－13132＝10. 例82012呼和浩特计算：11|122sin 45--+︒解析三角函数、绝对值、乘方答案11|12sin 45--+︒11)2211232=-+=+=例92011天水计算：si n 230°+tan 44°tan 46°+si n 260°= ． 分析：根据特殊角的三角函数值计算．tanA •tan 90°﹣A =1． 解答：解：原式=14+1+34=2．故答案为2． 例102011•莱芜若a=3﹣tan60°,则196)121(2-+-÷--a a a a = ;33-解答：解：a=3﹣tan60°=3﹣3,∴原式=23-a 1-a 121）（⨯---a a =31-a =33313331-=-=--故答案为：33-． 练习1、2011浙江计算：|－1|5－π0+4cos45°. 解原式=1－122练习2、2011浙江衢州1计算：|﹣2|﹣3﹣π0+2c os45°；解答：解：1原式=2122-+⨯,=1 练习3、计算：20110＋8－2sin45°；原式＝1＋22－2＝1＋2；练习3、观察下列各式：①sin 59°＞sin 28°；②0＜cos α＜1α是锐角；③tan 30°＋tan 60°＝tan 90°；④tan 44°＜1．其中成立的有A ．1个B ．2个C ．3个D ．4个 练习3、C 提示：sin 59°＞sin 28°成立,0＜cos α＜1α是锐角成立,tan 30°＋tan 60tan 90°,tan 44°＜tan 45°,即tan 44°＜1．练习4、计算2sin 30°－tan 60°＋tan 45°＝ ．练习5、如图28－146所示,在△ABC 中,∠A ＝30°,tan B ＝13,BC 10则AB 的长为 ． 练习6、当x ＝sin 60°时,代数式2242x x x -+·22244x x x x +-+＋42xx-的值是 ．练习7、已知cos 59°24′≈,则sin 30°36′≈ ．练习8、若∠A ,∠B 互余,且tan A －tan B ＝2,则tan 2A ＋tan 2B ＝ ．练习9、如图28－147所示,在菱形ABCD 中,AE ⊥BC 于E ,EC ＝1,cos B＝513,则这个菱形的面积是 . 10．已知正方形ABCD 的边长为1,若将线段BD 绕着点B 旋转后,点D落在DC 延长线上的点D ′处,则∠BAD ′的正弦值为 . 11．如图28－148所示,若将四根木条钉成的矩形木框变为平行四边形ABCD 的形状,并使其面积为矩形面积的一半,则这个平行四边形的一个最小内角等于 ．12．在△ABC 中,∠B ＝30°,tan C ＝2,AB ＝2,则BC ＝ ．13．设θ为锐角,且x 2＋3x ＋2sin θ＝05．则θ＝ ． 14．如图28－149所示,在△ABC 中,∠C ＝90°,点D 在BC 边上,BD ＝4,AD ＝BC ,cos ∠ADC ＝35． 1求DC 的长；2求sin B 的值．练习4、23 提示：2sin 30°－tan 60°＋tan 45°＝2×1231＝23 练习5、33提示：过点C 作CD ⊥AB ,垂足为D ,在Rt △BDC 中,tan B ＝13．∴13CD BD =,∴BD ＝3CD ,∵BC 10∴CD 2＋3CD 210,∴CD ＝1,BD ＝3．在Rt △ADC 中,tan A ＝CDAD,∴AD 3∴AB ＝AD ＋BD ＝33 练习632242x x x -+·22244x x x x +-+＋42xx-＝2x ,∴原式＝2sin 603练习7、提示：sin 30°36′＝cos 59°24′．练习8、6提示：∵∠A ,∠B 互余,∴tan A ·tan B ＝1,tan 2A ＋tan 2B ＝tan A －tan B 2＋2tan A ·tan B ＝22＋2＝6． 练习9、3916提示：∵cos B ＝513,设BE ＝5x ,则AB ＝13x ,∴AE 22AB BE -12x ．∵AB ＝BC ＝BE ＋CE ,∴13x ＝5x ＋1,∴x ＝18,则AE ＝12x ＝12×18＝32,BC ＝5x ＋1＝5×18＋1＝138,∴S ＝32×138＝3916．10．5提示:如图28－155所示,根据题意得DD ′＝2DC ,设正方形的边长为x ,则AD ＝x ,DD ′＝2x ．∵∠ADD ′＝90°,根据勾股定理得AD 22AD DD '+5x ．∵AD ＝x ,∴sin ∠AD ′D ＝ADAD '＝555x x=.∵AB ∥DD ′,∴∠BAD ′＝∠AD ′D ,∴sin ∠BAD ′＝55．11．30°提示：如图28＝156所示,∵S ABCD＝12S 矩形BEFC ,且BC ＝BC 底相同, ∴GC ＝12FC ．∵CF ＝DC ,∴GC ＝12DC ,12CG DC =．∵∠DGC ＝90°,sin 30°＝12,∴∠CDG ＝30°,即这个平行四边形的一个最小内角为30°． 12．12＋3 13．30°提示：x 1·x 2＝2sin θ,x 1＋x 2＝－3,则x 1－x 22＝x 1＋x 22－4x 1x 2＝9－8sin θ＝52,∴sin θ＝12,∴θ＝30°． 14．解：1∵cos ∠ADC ＝35,∴设CD ＝3x ,则AD ＝5x ,AC ＝4x ,∴BC ＝AD ＝5x ．∵BD ＝BC－CD ,∴5x －3x ＝4,∴x ＝2,∴CD ＝3x ＝6． 2∵AC ＝4x ＝8,BC ＝5x ＝10,∴AB ＝2222810241AC BC +=+=,∴sin B ＝844141241AC AB ==． ★ 专题三：题型一俯角与仰角仰角：视线在水平线上方的角；★ 俯角：视线在水平线下方的角;仰角铅垂线水平线视线视线俯角例1、2012湖北襄阳在一次数学活动中,李明利用一根拴有小锤的细线和一个半圆形量角器制作了一个测角仪,去测量学校内一座假山的高度CD ．如图5,已知李明距假山的水平距离BD 为12m,他的眼睛距地面的高度为,李明的视线经过量角器零刻度线OA 和假山的最高点C,此时,铅垂线OE 经过量角器的60°刻度线,则假山的高度为 m ．解析如下图,过点A 作AF⊥CD 于F,则AF ＝BD ＝12m,FD ＝AB ＝．再由OE∥CF 可知∠C＝∠AOE＝60°．所以,在Rt△ACF 中,CF ＝tan 60AF＝43,那么CD ＝CF ＋FD ＝43＋m ．例2、2012珠海如图,水渠边有一棵大木瓜树,树干DO 不计粗细上有两个木瓜A 、B 不计大A O BE D CF图5 CDA BO E小,树干垂直于地面,量得AB=2米,在水渠的对面与O 处于同一水平面的C 处测得木瓜A 的仰角为45°、木瓜B 的仰角为30°.求C 处到树干DO 的距离CO.结果精确到1米参考数据：41.12,73.13≈≈第16题图D BA OC解析如图,根据题意,得∠COD ＝90°, ∠ACO ＝45°, ∠BCO ＝30°, AB ＝2,求CO.设CO 为x 米, 根据AO ＝CO,列方程,解得即可.答案解:设CO 为x 米在Rt △BCO 中,tan30°＝BO CO ,则BO ＝33x 在Rt △ACO 中,AO ＝CO,得方程33x ＋2＝x 解得x ≈5.答: CO 长大约是5米. 例3、2012江苏盐城如图所示,当小华站立在镜子EF 前A 处时,他看自己的脚在镜中的像的俯角为450 ：如果小华向后退米到B 处,这时他看自己的脚在镜中的像的俯角为300.求小华的眼睛到地面的距离;结果精确到米,参考数据：3≈.答案设AC=BD=x,在Rt △ACA 1中,∠AA 1C=450,∴AA 1=x,在Rt △DBB 1中,BB 1=tan30x=3x ,又∵12BB 1-12AA 1=12,即12×3x -12x=12,解得：x=312+≈米． 例4、2012山西如图,为了开发利用海洋资源,某勘测飞机预测量一岛屿两端A ．B 的距离,飞机在距海平面垂直高度为100米的点C 处测得端点A 的俯角为60°,然后沿着平行于AB 的方向水平飞行了500米,在点D 测得端点B 的俯角为45°,求岛屿两端A ．B 的距离结果精确到米,参考数据：解析解：过点A 作AE⊥CD 于点E,过点B 作BF⊥CD 于点F,∵AB∥CD,∴∠AEF=∠EFB=∠ABF=90°,∴四边形ABFE 为矩形．第24题图∴AB=EF,AE=BF．由题意可知：AE=BF=100米,CD=500米．…2分 在Rt△AEC 中,∠C=60°,AE=100米．∴CE===米． …4分在Rt△BFD中,∠BDF=45°,BF=100． ∴DF===100米．…6分∴AB=EF=CD+DF﹣CE=500+100﹣≈600﹣×≈600﹣≈米． …8分答：岛屿两端A ．B 的距离为米．例5、2012呼和浩特22如图,线段AB 、DC 分别表示甲、乙两建筑物的高;某初三课外兴趣活动小组为了测量两建筑物的高,用自制测角仪在B 处测得D 点的仰角为α,在A 处测得D 点的仰角为β;已知甲、乙两建筑物之间的距离BC 为m ;请你通过计算用含α、β、m 的式子分别表示出甲、乙两建筑物的高度;答案解：过点A 作AM ⊥CD 于M在Rt △BCD 中,tan α=CD BC ∴CD =BC ·tan α=m tan α在Rt △AMD 中,tan β=DMAM∴DM =AM ·tan β=m tan β∴AB =CD –DM =mtan α–tan β例6、2012湖北随州,20在一次暑假旅游中,小亮在仙岛湖的游船上A 处,测得湖西岸的山峰太婆尖C 处和湖东岸的山峰老君岭D 处的仰角都是45°,游船向东航行100米后B 处,测得太婆尖、老君岭的高度为多少米3 1.732 ,结果精确到米;解析：设太婆尖高h 1米,老君岭高h 2米;可分别在直角三角形中利用正切值表示出水平线段的长度,再利用移动距离为AB=100米,可建立关于h 1、h 2的方程组,解这个方程组求得两山峰高度;答案：设太婆尖高h 1米,老君岭高h 2米,依题意,有FE第20题图60304545D (老君岭)C （太婆尖）BAβα乙甲ADB M C⇒⎪⎪⎩⎪⎪⎨⎧=-=-10060tan 45tan 10045tan 30tan 2211h h h h 1376.136)1732.1(50)13(5045tan 60tan 1001≈=+=+=-=h 米33110030tan 45tan 1002-=-=h 2376.236)732.13(50)33(50)13(350≈=+=+=+=米答：太婆尖高度为137米,老君岭高度为237米;题型二方位角问题1、从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角;如图3,OA 、OB 、OC 、OD 的方向角分别是：45°、135°、225°;2、指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角;如图4：OA 、OB 、OC 、OD 的方向角分别是：北偏东30°东北方向,南偏东45°东南方向,南偏西60°西南方向,北偏西60°西北方向;例1、2011山东省潍坊轮船从B 处以每小时海里的速度沿男偏东30°方向匀速航行,在B 处观测灯塔A 位于南偏东75°方向上,轮船航行半小时到达C 处,在观测灯塔A 北偏东60°方向上,则C 处与灯塔A 的距离是 ．海里解答： BC=50×=25海里；根据方位角知识得,∠BCD=30°,=75°－30°；CB=∠BCD+∠ACD=30°+60°=90°；∠A=∠CBD=45°所以CA=CB 所以CB=25海里例2、2012年四川德阳某时刻海上点P 处有一客轮,测得灯塔A 位于客轮P 的北偏东30°方向,且相距20海里.客轮以60海里/小时的速度沿北偏西60°方向航行32小时到达B 处,那么tan ∠ABP=A.21 C.55 D.552解析如图6所示,根据题意可知∠APB=90°．且AP=20, PB=60×23=40. 所以tan ∠ABP=201402PA PB ==例3、2012连云港已知B 港口位于A 观测点北偏东°方向,且其到A 观测点正北方向的距离BD 的长为16km;一艘货轮从B 港口以40km/h 的速度沿如图所示的BC 方向航行,15min 后到达C 处;现测得C 处位于Ａ观测点北偏东°方向;求此时货轮与A 观测点之间的距离AC 的长精确到.25东北CBDCBH解析过点B 作AC 的垂线,把所求线段AC 换为两线段的差;利用Rt △ABH 和Rt △BCH 求线段AH 、CH 的长,利用AH －CH 确定AC 的长; 答案BC=40×1560=10.在Rt△ADB 中,sin ∠DAB=DB AB , °≈;所以AB=DAB DB ∠sin ≈1.60.8=20.如图,过点B 作BH⊥AC,交AC 的延长线于H;在Rt△AHB 中,∠BAH=∠DAC －∠DAB=°―37°=°,tan∠BAH=BH AH ,=BH AH,AH =＋CH 2=AB 2,BH 2+2BH 2=2025所以AH=85,在Rt△AHB 中, BH 2＋CH 2=BC 2,CH=2108025-=所以第22题图APCB °°AC=AH―CH=85―25＝65≈.例4、2012四川攀枝花如图6,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场．若渔政310船航向不变,航行半小时后到达B 处,此时观测到我渔船C在北偏东30°方向上．问渔政310船再航行多久,离我渔船C的距离最近假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值．答案作CD⊥AB于D,设BD=x,∵∠BCD=30°,∴CD=3x,因为∠CAD=45°,∴AD=CD3,AB3–x,依据题意3x–x=,x 31+,31+小时,离渔船C的距离最近;例5、2012山东东营如图某天上午9时,向阳号轮船位于A处,观测到某港口城市P位于轮船的北偏西°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到城市P位于该船的南偏西°方向,求此时轮船所处位置B 与城市P的距离参考数据：°≈35,°≈34,°≈1213,°≈125解析过点P作PC⊥AB,构造直角三角形,设PC=x海里,用含有x的式子表示AC,BC的值,从而求出x的值,再根据三角函数值求出BP的值即可解答．答案过点P作PC⊥AB,垂足为C,设PC=x海里．在Rt△APC中,∵tan∠A=PCAC,∴AC=5tan67.512PC x=︒．在Rt△PCB中,∵tan∠B=PCBC,∴BC=4tan36.93x x=︒．∵AC＋BC=AB=21×5,∴54215123x x+=⨯,解得60x=.∵sinPCBPB∠=,∴60560100sin sin36.93PCPBB===⨯=∠︒海里．∴向阳号轮船所处位置B与城市P的距离为100海里．例6、2012山东省青岛如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE ；而当光线与地面夹角是45°时,教学楼顶A 在地面上的影子F 与墙角C 有13米的距离B 、F 、C 在一条直线上 ⑴求教学楼AB 的高度；⑵学校要在A 、E 之间挂一些彩旗,请你求出A 、E 之间的距离结果保留整数.参考数据：sin22°≈错误!,cos22°≈错误!,tan22°≈错误! 答案解：⑴过点E 作EM ⊥AB,垂足为M.设AB 为x.Rt △ABF 中,∠AFB=45°,∴BF=AB=x,∴BC=BF+FC=x+13在Rt △AEM 中,∠AEM=22°,AM=AB-BM=AB-CE=x-2,∴tan22°= 错误!, 错误!=错误!,x=12.即教学楼的高12m.⑵由1可得ME=BC=x+13=12+13=25.在Rt △AME 中,cos22°= 错误!, ∴ＡＥ＝ 错误!≈ 错误!≈２７．即ＡＥ之间的距离约为２７ｍ．题型三、坡比是垂直高度与水平距离的比值,即是坡角的正切值应用举例： 坡面的铅直高度h 和水平宽度l 的比叫做坡度坡比;用字母i 表示,即hi l=;坡度一般写成1:m 的形式,如1:5i =等;把坡面与水平面的夹角记作α叫做坡角,那么tan hi lα==;例1、2012广安如图2,某水库堤坝横断面迎水坡AB 的坡比是1：3,堤坝高BC=50m,则迎水坡面AB 的长度是 ．m解：tan∠BAC=13,∠BAC=30°,sin∠BAC=12, sin∠BAC=BC AB ,AB=2BC=100m例2、小强在教学楼的点P 处观察对面的办公大楼．为了测量点P 到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A 的仰角为45°,测得办公大楼底部点B 的俯角为60°,已知办公大楼高46米,CD ＝10米．求点P 到AD 的距离用含根号的式子表示．图2:i h l=hlαABCDPN M解析连结PA 、PB ,过点P 作PM ⊥AD 于点M ；延长BC ,交PM 于点N则∠APM =45°,∠BPM =60°,NM =10米………1分设PM =x 米 在Rt △PMA 中,AM =PM ×tan ∠APM =x tan 45°＝x 米…3分在Rt △PNB 中,BN =PN ×tan ∠BPM =x －10tan 60°＝x －103米…5分 由AM +BN =46米,得x +x －103 ＝46……6分解得,4610313x +=+ ,∴点P 到AD 的距离为4610313++米．结果分母有理化为()1838-米也可……8分答案4610313++结果分母有理化为()1838-米也可例3、2012湖北如图,某公园入口处原有三级台阶,每级台阶高为18cm,深为30cm,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A ,斜坡的起始点为C ,现设计斜坡BC 的坡度1:5i =,则AC 的长度是 cm ．解析如图,过点B 作BD ⊥AC 于D,依题意可求得AD ＝60cm,BD ＝54cm ；由斜坡 BC 的坡度i ＝1：5,求得CD ＝270cm,故AC ＝CD －AD ＝270－60＝210cm ．例4、2012浙江省绍兴,19如图1,某超市从一楼到二楼的电梯AB 的长为米,按坡角∠BAC 为32°.1求一楼与二楼之间的高度BC 精确到米；2电梯每级的水平级宽均是米,如图2.小明跨上电梯时,该电梯以每少上升2级的高度运行,10秒后他上升了多少米精确到米 备用数据：sin 32°=,cos 32°=,tan 32°=.解析1在Rt△ABC 中,已知∠B AC=32°,斜边AB 的长为米,根据锐角三角函数的定义即可求得第20题图MPDCBA第12题A BC3018一楼与二楼之间的高度BC ．2先计算1级电梯的高,再根据10秒钟电梯上升了20级可计算10秒后他上升的高度．答案解：1∵sin ∠BAC =ABBC ,∴BC =AB ×sin32°=×≈米. 2∵tan32°= 级高级宽,∴级高=级宽×tan32°=×=,∵10秒钟电梯上升了20级,∴小明上升的高度为：20×米. 例5、2012浙江丽水,19学校校园内有一小山坡,经测量,坡角∠ABC=30°,斜坡AB 长为12米.为方便学生行走,决定开挖小山坡,使斜坡BD 的坡比是1:3即为CD 与BC 的长度之比,A,D 两点处于同一铅垂线上,求开挖后小山坡下降的高度AD.解析：∴AD=AC-CD=6-23.答：开挖后小山坡下降的高度AD 为6-23米.例6、2012深圳小明想测一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图3,此时测得地面上的影长为8米,坡面上的影长为4米,已知斜坡的坡角为30,同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为 ．米解答：如图3—1,根据坡角易求树的下半部分的高为2米,树的上半部分所在直角三角形的水平距离为(+823米,由两个直接三角形相似易求树的上半部分高度为(43米,知树的高度为()63米,选择A例72012江苏泰州24如图,一居民楼底部B 与山脚P 位于同一水平线上,小李在P 处测得居民楼顶A 的仰角为60°,然后他从P 处沿坡角为45°的山坡上走到C 处,这时,PC=30m,点C 与点A 在同一水平线上,A 、B 、P 、C 在同一平面内．1求居民楼AB 的高度；2求C 、A 之间的距离．精确到,参考数据：2≈,3≈,6≈60° CA B 45°图330°21图3-1第24题图解析过C作BP的垂线,垂足为G,利用特殊Rt△PCG和Rt△ABP中的边角关系,我们容易计算出CG即AB的长,最后用AC=BP+PG,就是C、A之间的距离．答案1过C作BP的垂线,垂足为G,在Rt△PCG中,CG=PCsin450=30×2所以=m2PG= PCcos450=30×2=所以C、A之间的距离例82012四川水务部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD．如图9所示,已知迎水坡面AB的长为16米,∠B＝60°,背水坡面CD的长为,加固后大坝的横截面为梯形ABED,CE的长为8米．1已知需加固的大坝长为150米,求需要填土石方多少立方米2求加固后大坝背水坡面DE的坡度．解析1求出横截面△DCE的面积,然后乘以坝堤长度即可得出体积．可以分别过点A,D 作BC边上的高将问题转化为解直角三角形问题．2求大坝背水坡面DE的坡度就是求坡面DE上一点到BE的铅直高度与它到点E的水平宽度的比,这一点通常取梯形的顶点．答案解：1过点A作AG⊥BC于G,过点D作DH⊥BC于H,∴AG＝DH．在Rt△ABG中,AG＝sin60°·AB×16＝∴DH＝S△DCE＝12·DH·CE＝12×8＝∴需要填土石方150＝3．2在Rt△DHC中,HC24,∴HE＝HC＋CE＝24＋8＝32．∴加固后大坝背水坡面DE的坡度＝DHHE．AB CD图9E例9 2012江苏苏州如图,已知斜坡AB 长60米,坡角即∠BAC 为30°,BC⊥AC,现计划在斜坡中点D 处挖去部分坡体用阴影表示修建一个平行于水平线CA 的平台DE 和一条新的斜坡BE ．请讲下面2小题的结果都精确到米,参考数据：≈．1若修建的斜坡BE 的坡角即∠BEF 不大于45°,则平台DE 的长最多为 米；2一座建筑物GH 距离坡角A 点27米远即AG=27米,小明在D 点测得建筑物顶部H 的仰角即∠HDM 为30°．点B 、C 、A 、G 、H 在同一个平面内,点C 、A 、G 在同一条直线上,且HG⊥CG,问建筑物GH 高为多少米解答： 解：1∵修建的斜坡BE 的坡角即∠BEF 不大于45°,∴∠BEF 最大为45°当∠BEF=45°时,EF 最短,此时ED 最长,∵∠DAC=∠BDF=30°,AD=BD=30,∴BF=EF=BD=15,DF=15,故：DE=DF ﹣EF=15﹣1≈；2过点D 作DP⊥AC,垂足为P ．在Rt△DPA中,DP=AD=×30=15,PA=AD•cos30°=×30=15． 在矩形DPGM 中,MG=DP=15,DM=PG=15+27,在Rt△DMH 中,HM=DM•tan30°=×15+27=15+9． GH=HM+MG=15+15+9≈．答：建筑物GH 高为米．A B C DE GH。
专题01 锐角的三角函数重难点题型专训(7大题型)(原卷版)
【题型目录】题型一题型二【经典例题一1．（22·235．（2021秋·河北石家庄5AB=，3AC=．(1)求AD的长；(2)求sin DABÐ的值．【经典例题二求角的正弦值1．（22·23下·沈阳·开学考试）如图，6BD=，则sin ACDÐ的值是（A．34B．32．（22·23上·青岛·期末）如图，值为（ ）A．5B．3．（21·22下·哈尔滨·阶段练习）在5．（2023·浙江温州<），连接（AE EC(1)求证：四边形DEBF为菱形．(2)记菱形ABCD的面积为1S，菱形长．【经典例题三1．（22·23D，若A．22．（22·23下·深圳·阶段练习）如图，的距离是（ ）A．556B．6553．（22·23下·绵阳·阶段练习）如图，在上，1BAE ABCÐ=Ð，点F4．（22·23下·合肥·三模）在Rt上，将BDE△沿直线DE翻折，使得点(1)求证：CE是Oe的切线；(2)若2sin,53E AC==，求DF 【经典例题四求角的余弦值A．11 152．（2022春·福建福州格点．已知菱形的一个角为A．13B．123．（2023秋·全国·九年级专题练习）如图，在AC于点D、E，且13AB AC==，4．（2023·黑龙江齐齐哈尔的两边长分别是2和3，则5．（2022秋·黑龙江大庆·八年级校考期末）沿着过点B的某条直线折叠，使点(1)求点A、B、C、D的坐标；(2)求ABCÐ的余弦值．【经典例题五已知余弦值求边长】1．（2023·广西北海·统考模拟预测）如图，在直角梯形3 BD=，2cos3CDBÐ=，则下底AB的长是（A．212B．92．（2023春·四川南充·九年级校考阶段练习）如图，A．94B．1253．（2023·山东聊城·统考三模）在Rt ABC△5．（2023秋·山东聊城·九年级校考阶段练习）于点E ．(1)求证；BEA ADC V V ∽(2)求证：··CD AD AC BE =(3)若2AD =5，cos ABE Ð【经典例题六1．（2023点F 在边A ．272．（2023秋·重庆沙坪坝90BAC EAD Ð=Ð=°的值为（ ）A ．13B 3．（2023秋·江苏常州·九年级统考期末）如图，连接BD ，将BCD △沿BD4．（2022春·湖北武汉AB AC =，CD AB ^的值是．5．（2022春·黑龙江绥化等腰Rt CEF △的直角顶点与正方形线FE 与AD 交于点P ，与(1)求证：CDE CBF △△≌；(2)求CF 的长；【经典例题七1．（2022落在边A ．53B ．22．（2023·广东深圳·深圳市高级中学校考二模）如图，平行四边形4tan 3BAD Ð=，点O 为对角线A ．4033B ．33403．（2023秋·全国·九年级专题练习）如图，在1tan 3ABG Ð=，那么BC 的长等于4．（2022秋·黑龙江哈尔滨5OP =，点M ，(1)求证：四边形BCEF^于点G，连结(2)BG CE①求CG的长．②求平行四边形BCEF【重难点训练】1．（21·22A．42．（23·24上·长春上，且90Ð=°AEFA．273．（22·23下·江门·期中）在A．247B．4．（22·23下·株洲·自主招生）的值为（）A．3 35．（21·22下·深圳·模拟预测）如图，已知平行四边形A．12B．136．（23·24上·黄浦·期中）如图已知在7．（21·22·武汉·模拟预测）如图，E为AB边上一动点，DEFV为等边三角形，则线段8．（22·23下·深圳·模拟预测）如图，在1tan 2A =，8BC =，CF AB ∥9．（21·22·武汉·模拟预测）如图，在矩形GBE V ，BG 的延长线交则cos DEC Ð的值为10．（23·24上·专题练习）如图，在四边形点M 、N 分别在AB11．（21·22·哈尔滨·模拟预测）如图，在小正方形的边长均为方形的顶点上．(1)在图1中画一个以线段AB 为一边的平行四边形ABCD 的面积为8；(2)在图2中画一个钝角三角形ABE ，点E 在小正方形顶点上，直接写出AE 的长．13．（21·22下·宜昌·模拟预测）如图，已知平行四边形(1)如图当点E 在边AD 上时．①求证AEF BGF V V ∽．②当4DCE BFG S S =V V 时，求:AE ED 的值．(2)当点E 在边AD 的延长线上时，是否存在这样的点E 使AEF △与五、作图题14．（23·24上·哈尔滨·期中）如图，在边长为1的小正方形网格中，ABC V 的三个顶点均在格点上，坐标分别为()2,4A ，()1,2B ，()5,3C ． 请解答下列问题：(1)画出ABC V 关于y 轴的对称图形111A B C △．(2)将ABC V 绕点O 顺时针旋转90°得到222A B C △，画出222A B C △．(3)连接1B B 、12B C ，写出12BB C Ð的正切值．六、证明题15．（23·24上·齐齐哈尔·期中）已知，四边形ABCD 是正方形，DEF V 绕点D 旋转()DE AB <，90,EDF DE DF Ð=°=，连接AE ，CF ；直线AE 与CF 相交于点G 、交CD 于点P ．(1)如图1，猜想AE 与CF 的关系，并证明：(2)如图2，BM AG ^于点M ，^BN CF 于点N ，则四边形BMGN 是________形；(3)如图3，连接BG ，若4,2AB DE ==，直接写出在DEF V 旋转的过程中，①当点E 在正方形ABCD 的内部，且EF CD ^时BG =_________；②线段BG 长度的最小值__________；。
锐角三角函数的题型及解题技巧
锐角三角函数的题型及解题技巧锐角三角函数是三角函数的基础，它应用广泛，解题技巧性强，下面归纳出锐角三角函数的常见题型，并结合例题介绍一些解题技巧。
一、 化简或求值例1 （1）已知tan 2cot 1αα-=，且α是锐角，的值。
（2）化简()()22sin cos cos sin a b a b αααα++-。
分析 （1）由已知可以求出tan α1tan cot αα=⋅；（2）先把平方展开，再利用22sin cos 1αα+=化简。
解 （1）由tan 2cot 1αα-=得2tan 2tan αα-=，解关于tan α的方程得tan 2α=或tan 1α=-。
又α是锐角，∴tan 2α=＝tan cot αα-。
由tan 2α=，得1cot 2α=＝tan cot αα-＝13222-=。
（2）()()22sin cos cos sin a b a b αααα++-＝2222sin 2sin cos cos a ab b αααα+⋅⋅+＋2222cos 2cos sin sin a ab b αααα-⋅⋅+＝()()222222sin cos sin cos a b αααα+++＝22a b +。
说明 在化简或求值问题中，经常用到“1”的代换，即22sin cos 1αα+=，tan cot 1αα⋅=等。
二、已知三角函数值，求角例2 在△ABC 中，若2cos sin 02A B ⎛--= ⎝⎭(),A B ∠∠均为锐角，求C ∠的度数。
分析 几个非负数的和为0，则这几个数均为0。
由此可得cos A 和sin B 的值，进而求出,A B ∠∠的值，然后就可求出C ∠的值。
解由题意得cos 0,2sin 0.A B ⎧-=⎪⎪-=解得cos 2sin 3A B ⎧=⎪⎪⎨⎪=⎪⎩又∵,A B ∠∠均为锐角，∴45A ∠=,60B ∠=。
∴18075C A B ∠=-∠-∠=.说明 解这类问题首先要熟记特殊角的三角函数值，还要掌握一些化简的技巧。
(完整版)求锐角三角函数值的经典题型+方法归纳(超级经典好用)
求锐角三角函数值的几种常用方法一、定义法当已知直角三角形的两条边，可直接运用锐角三角函数的定义求锐角三角函数的值． 例1 如图1，在△ABC 中，∠C =90°，AB =13，BC =5，则sin A 的值是( )(A )513 (B )1213 (C )512 (D )135 对应训练：1．在Rt △ABC 中，∠ C ＝90°，若BC ＝1，AB =5，则tan A 的值为( )A ．5 B ．25 C ．12D ．2 二、参数（方程思想）法锐角三角函数值实质是直角三角形两边的比值，所以解题中有时需将三角函数转化为线段比，通过设定一个参数，并用含该参数的代数式表示出直角三角形各边的长，然后结合相关条件解决问题． 例2 在△ABC 中，∠C =90°，如果tan A =512，那么sin B 的值是 ． 对应训练：1．在△ABC 中，∠C =90°，sin A=53，那么tan A 的值等于（ ）. A ．35 B . 45 C . 34 D . 432．已知△ABC 中，ο90=∠C ，3cosB=2， AC=52 ，则AB= ．3．已知Rt △ABC 中，,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B ．4．已知：如图，⊙O 的半径OA ＝16cm ，OC ⊥AB 于C 点，⋅=∠43sin AOC求：AB 及OC 的长．D C B A Oyx第8题图AD ECBF三、等角代换法当一个锐角的三角函数不能直接求解或锐角不在直角三角形中时，可将此角通过等 角转换到能够求出三角函数值的直角三角形中，利用“两锐角相等，则三角函数值也相等” 来解决．例3 在Rt △ABC 中，∠BCA =90°，CD 是AB 边上的中线，BC =5，CD =4，则cos ∠ACD 的值为 ． 对应训练1.如图，O ⊙是ABC △的外接圆，AD 是O ⊙的直径，若O ⊙的半径为32，2AC =，则sin B 的值是（ ）A ．23 B ．32 C ．34 D ．432. 如图4，沿AE 折叠矩形纸片ABCD ，使点D 落在BC 边的点F 处．已知8AB =，10BC =，AB=8,则tan EFC ∠的值为 ( )Ａ．34 Ｂ．43 Ｃ．35 Ｄ．453. 如图6，在等腰直角三角形ABC ∆中，90C ∠=︒，6AC =，D 为AC 上一点，若1tan 5DBA ∠= ，则AD 的长为( )A ．2B ．2C ．1D ．224． 如图，直径为10的⊙A 经过点(05)C ，和点(00)O ，，与x 轴的正半轴交于点D ，B 是y 轴右侧圆弧上一点，则cos ∠OBC 的值为（ ）A ．12 B ．32 C ．35D ．455.如图，角α的顶点为O ，它的一边在x 轴的正半轴上，另一边OA 上有一点P （3，4），则sin α= ．6.（庆阳中考）如图，菱形ABCD 的边长为10cm ，DE ⊥AB ，3sin 5A =，则这个菱形的面积= cm 2．7. 如图6，在Rt △ABC 中，∠C =90°，AC =8，∠A 的平分线AD =3316求 ∠B 的度数及边BC 、AB 的长.DABCCBA四、构造（直接三角形）法直角三角形是求解或运用三角函数的前提条件，故当题目中已知条件并非直角三角 形时，需通过添加辅助线构造直角三角形，然后求解，即化斜三角形为直角三角形． （1）化斜三角形为直角三角形例4 在△ABC 中，∠A =120°，AB =4，AC =2，则sinB 的值是( )(A )5714 (B )35 (C )217 (D )2114对应训练：1．已知：如图，△ABC 中，AB ＝9，BC ＝6，△ABC 的面积等于9，求sin B ．2．（重庆）如图，在Rt △ABC 中，∠BAC=90°，点D 在BC 边上，且△ABD 是等边三角形．若AB=2，求△ABC 的周长．（结果保留根号）（2）利用网格构造直角三角形例5 如图所示，△ABC 的顶点是正方形网格的格点，则sinA 的值为（ ）A ．12 B ．55 C ．1010D ．255 1．如图，△ABC 的顶点都在方格纸的格点上，则sin A =_______. 2．如图，A 、B 、C 三点在正方形网络线的交点处，若将ABC ∆绕着点A 逆时针旋转得到''B AC ∆，则'tan B 的值为（ ）A.41B.31C.21D.13．正方形网格中，AOB∠如图放置，则tan AOB∠的值是（）Ａ．5Ｂ．25Ｃ．12Ｄ．24. 如图，在边长为1的小正方形组成的网格中，ABC△的三个顶点在格点上，请按要求完成下列各题：（1）用签字笔．．．画AD∥BC（D为格点），连接CD；（2）线段CD的长为；（3）请你在ACD△的三个内角中任选一个锐角．．，若你所选的锐角是，则它所对应的正弦函数值是．（4）若E为BC中点，则tan∠CAE的值是 .三角函数与四边形：1．如图，四边形ABCD中，∠BAD=135°，∠BCD=90°，AB=BC=2，tan∠BDC=63．(1) 求BD的长；(2) 求AD的长．2．如图，在平行四边形ABCD中，过点A分别作AE⊥BC于点E，AF⊥CD于点F．（1）求证：∠BAE=∠DAF；（2）若AE=4，AF=245，3sin5BAE∠=，求CF的长．三角函数与圆：3.如图，DE是⊙O的直径，CE与⊙O相切，E为切点.连接CD交⊙O于点B，在EC上取一个点F，使EF=BF. （1）求证:BF是⊙O的切线;（2）若54Ccos=, DE=9，求BF的长．ABO。
(完整)锐角三角函数题型分类总结,推荐文档
锐角=角函数∙知识点一：钦角三角国数的≡x≡ 一、 锐角三角函数定义：在 RiAABC 中，ZC=9O 0, ZAS ZBX ZC 的对边分别为 a 、b 、c, 则ZA 的正弦可表示为；S ilLX= _________ JZA 的余弦可表示为CoSA= _________厶的正切:Tan-A= ________ ,它们弦称为ZA 的锐角三角函数2、取値范围—<¾inA< Co i⅛< __________ tanA>______1例如图所示，在RlA^C 中〉乙C=9Q° .例2.锐角三角函数束值；在 RtΔ,45C 中，ZC= 90° ,若 σ=9, B= 12,则 C= ___________SilL a l — _______ , COSU I f- __________ 9 taiL -l — __________ SSin^= _____ ； CQ ∖B= ____ ； tan.例3∙已知；如图，RI0∙∖M r 中，Z∏I ∖r =90o …⑷丄ZV 于出点，Zy=4, Hv=3• 求：SinZ732KxCOSZrVC?、tanZ∏IK .典型m ：类型一：直角三角形求值31 .已知 RtQUBC 中丿 ZC≡90Q 5 taπJ= ,5C≡1⅞ 求.4C ∖∙3 和 8田・② CoSJ = ® tan.4∙=第1题團① sin J( ) 软边 an 5【an 方=ZB 旳对边( )2. 如朗 OO 的半径θA = 16cm, OC 丄貝B 于C 点，an ΛAOC =-.求肋及OC 的长•3. 已知：0。
中，OC 丄朋于 C 点；J5= 16cm ； dnZA0C (1) 求OQ 的半径OA 的长及弦心距& (2) 求 COSz4 OC 及 ta∏ZJθC∙g4. 已知ZJ 是锐角，SitIW=—；求COSA > tan J 的值17对应ill 练二1. 在RtA^C 中7 ZC=90C 7 若5C=1, .15-√5 ；则Ianj 的值为5B.巫5C.丄 2D. 22.在ABC 中，ZC=90o ,S inA=- >那么tanA 的值等于( ).53G 4 C 3 c 4 A.-5 B.— 5 C. 一4D. 一 3类型二利用角度转化求值,2. 如團，直径为10的CU 经过点C(Oo)和点O(Qo)；与X 轴的正半釉交于点D, B 是》轴右侧圆弧上一点〉则C O SZ^C 的值为〈)C.-D-I1.已知；如图，RtZUBC 中，ZC= 90o ∙ Q 是Je 边上一点'DE 丄曲于E 点.^≡s⅛E3.如图，角α的顶点为0,它的一边在工轴的正半轴上J另一边Od上有一点Pd 4）,则3丄如團，菱形九5CD的边长为IQCm,DE1AB, SinJ =-,则遗个菱形的面积二.5.如國06＞是^iBC的外接圆,AD杲©O的直径，AC = I,则sin5的值是（7 \A. -B.-3 26.如图6,沿川E折蠡矩形纸片曲CQ ,c.£⅞□-4B=8, BC =10, AB=⅛ 则tan NEFC 的值为（A.- C.-57.如图7,在等腰直角三角形C中'ZC =90o , JC = 6, Z）为AC±—点，若tan ZDA.! = -,则-Q 的长为（）5A・近B・2 C・1 D・2√21 ^rIS.如图S,在RtA-LffC 中，Z090°,AOS, Ad的平分线/D=」一求ZB的度数及边BC. AB的长.类型三化斜三角形为直角三角形例1 如图，在A ABC中，Z A=30C,Z B=45% AC=2√3、求AB 的长.Cn T •353.正方形网格中, ZHoB 如團放乱则tanZJ （95的值是（√L例 2∙已知：如團，在 AABC 中，ZBAC=I 20° , ∠S=10, AC=5 .对应岷1.如图，在RlAABC 中,ZBAC=90=,点D 在BC 边上，且AABD 是等边三甬形.若.43=2, 求AABC 的周长•〈结果保留根号）2. 已知：如虱 AABC 中「3=9, BC=G,厶4恥的面枳尊于9丿求血^3. ABC 中,乙4=60° …4方=6 Cm , AC=4 Clrb 则A-45C 的面积是求:siik^ABC 的值..4 羽 CnrDllcm 2类型四；利用 构造直角三角形例1如图所示，AABC 的顶点杲正方形网格的格点，则SinA 的值为＜对应练习：1. ________________________________________________ 如图，AABC 的顶点都在方格纸的格点上，则Sir I A= ____________ .点厘逆吋针旋转得到AC8,则tanF 的值为D∙ 110D.IR特殊角的三角函数值锐角C30s45060。
初中三角函数知识点+题型总结+课后练习
锐角三角函数知识点1、勾股定理：直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如以下图，在Rt △ABC 中，∠C 为直角，则∠A 的锐角三角函数为(∠A 可换成∠B)：定义表达式取值围关系正弦 斜边的对边A A ∠=sin caA =sin1sin 0<<A(∠A 为锐角)B A cos sin = B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A(∠A 为锐角)正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A(∠A 为锐角)B A cot tan = B A tan cot =AA cot 1tan =(倒数) 1cot tan =⋅A A余切的对边的邻边A A A ∠∠=cot abA =cot0cot >A(∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值；任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值；任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan 0 33 1 3 不存在 αcot不存在3133 0对边邻边 斜边 B锐角三角函数题型训练类型一：直角三角形求值1．Rt △ABC 中，,12,43tan ,90==︒=∠BC A C 求AC 、AB 和cos B ．2．：如图，⊙O 的半径OA ＝16cm ，OC ⊥AB 于C 点，⋅=∠43sin AOC 求：AB 及OC 的长．3．：⊙O 中，OC ⊥AB 于C 点，AB ＝16cm ，⋅=∠53sin AOC(1)求⊙O 的半径OA 的长及弦心距OC ； (2)求cos ∠AOC 及tan ∠AOC ． 4.A ∠是锐角，178sin =A ，求A cos ，A tan 的值 类型二. 利用角度转化求值：1．：如图，Rt △ABC 中，∠C ＝90°．D 是AC 边上一点，DE ⊥AB 于E 点．DE ∶AE ＝1∶2．求：sin B 、cos B 、tan B ．2. 如图4，沿AE 折叠矩形纸片ABCD ，使点D 落在BC 边的点F 处．8AB =，10BC =,则tan EFC ∠的值为 ( ) Ａ．34 Ｂ．43Ｃ．35Ｄ．453. 如图6，在等腰直角三角形ABC ∆中，90C ∠=︒，6AC =，D 为AC 上一点，假设1tan 5DBA ∠=，则AD 的长为( )A ．2 B ．2 C ．1 D ．224. 如图6，在Rt △ABC 中，∠C =90°，AC =8，∠A 的平分线AD =3316求∠B 的度数及边BC 、AB 的长. 类型三. 化斜三角形为直角三角形例1〔2021•〕如图，在△ABC 中，∠A=30°，∠B=45°，AC=23，求AB 的长．例2．：如图，△ABC 中，AC ＝12cm ，AB ＝16cm ，⋅=31sin A(1)求AB 边上的高CD ； (2)求△ABC 的面积S ； (3)求tan B ．例3．：如图，在△ABC 中，∠BAC ＝120°，AB ＝10，AC ＝5．求：sin ∠ABC 的值．对应训练 1．〔2021•〕如图，在Rt△ABC 中，∠BAC=90°，点D 在BC 边上，且△ABD 是等边三角形．假设AB=2，求△ABC 的周长．〔结果保存根号〕2．：如图，△ABC 中，AB ＝9，BC ＝6，△ABC 的面积等于9，求sin B ． 类型四：利用网格构造直角三角形例1 〔2021•江〕如下图，△ABC 的顶点是正方形网格的格点，则sinA 的值为〔 〕 A ．12 B ．55 C ．1010 D ．255DABC对应练习：1．如图，△ABC 的顶点都在方格纸的格点上，则sin A =_______.特殊角的三角函数值例1．求以下各式的值︒-︒+︒30cos 245sin 60tan 2=. 计算：3－1+(2π－1)0－33tan30°－tan45°= 030tan 2345sin 60cos 221⎪⎪⎭⎫ ⎝⎛︒-︒+︒+= ︒-︒+︒60tan 45sin 230cos 2tan 45sin 301cos 60︒+︒-︒=在ABC ∆中，假设0)22(sin 21cos 2=-+-B A ，B A ∠∠，都是锐角，求C ∠的度数 例2．求适合以下条件的锐角．(1)21cos =α (2)33tan =α (3)222sin =α(4)33)16cos(6=- α〔5〕为锐角，且3)30tan(0=+α，求αtan 的值〔〕在ABC ∆中，假设0)22(sin 21cos 2=-+-B A ，B A ∠∠，都是锐角，求C ∠的度数 例3. 三角函数的增减性 1．∠A 为锐角，且sin A <21，则∠A 的取值围是 A. 0°< A < 30° B. 30°< A ＜60° C. 60°< A < 90° D. 30°< A < 90° 2. A 为锐角，且030sin cos <A ，则 〔 〕A. 0°< A < 60°B. 30°< A < 60°C. 60°< A < 90°D. 30°< A < 90° 例4. 三角函数在几何中的应用1．：如图，在菱形ABCD 中，DE ⊥AB 于E ，BE ＝16cm ，⋅=1312sin A 求此菱形的周长．2．：如图，Rt △ABC 中，∠C ＝90°，3==BC AC ，作∠DAC ＝30°，AD 交CB 于D 点，求：(1)∠BAD ；(2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD ．3. ：如图△ABC 中，D 为BC 中点，且∠BAD ＝90°，31tan =∠B ，求：sin ∠CAD 、cos ∠CAD 、tan ∠CAD ． 解直角三角形：1．在解直角三角形的过程中，一般要用的主要关系如下(如下图)： 在Rt △ABC 中，∠C ＝90°，AC ＝b ，BC ＝a ，AB ＝c ， ①三边之间的等量关系：________________________________．②两锐角之间的关系：__________________________________． ③边与角之间的关系：==B A cos sin ______；==B A sin cos _______；==BA tan 1tan _____；==B A tan tan 1______．④直角三角形中成比例的线段(如下图)．在Rt △ABC 中，∠C ＝90°，CD ⊥AB 于D ．CD 2＝_________；AC 2＝_________； BC 2＝_________；AC ·BC ＝_________．类型一例1．在Rt △ABC 中，∠C ＝90°．(1)：a ＝35，235=c ，求∠A 、∠B ，b ；(2)：32=a ，2=b ，求∠A 、∠B ，c ； (3)：32sin =A ，6=c ，求a 、b ；(4)：,9,23tan ==b B 求a 、c ； (5)：∠A ＝60°，△ABC 的面积,312=S 求a 、b 、c 及∠B ．例2．：如图，△ABC 中，∠A ＝30°，∠B ＝60°，AC ＝10cm ．求AB 及BC 的长．例3．：如图，Rt △ABC 中，∠D ＝90°，∠B ＝45°，∠ACD ＝60°．BC ＝10cm ．求AD 的长． 例4．：如图，△ABC 中，∠A ＝30°，∠B ＝135°，AC ＝10cm ．求AB 及BC 的长． 类型二：解直角三角形的实际应用 仰角与俯角：例1．〔2021•〕如图，从热气球C 处测得地面A 、B 两点的俯角分别是30°、45°，如果此时热气球C 处的高度CD 为100米，点A 、D 、B 在同一直线上，则AB 两点的距离是〔 〕 A ． 200米 B ． 200米 C ． 220米 D ． 100〔〕米例2．：如图，在两面墙之间有一个底端在A 点的梯子，当它靠在一侧墙上时，梯子的顶端在B 点；当它靠在另一侧墙上时，梯子的顶端在D 点．∠BAC ＝60°，∠DAE ＝45°．点D 到地面的垂直距离m 23=DE ，求点B 到地面的垂直距离BC ．例3〔昌平〕19.如图，一风力发电装置竖立在小山顶上，小山的高BD =30m ． 从水平面上一点C 测得风力发电装置的顶端A 的仰角∠DCA =60°， 测得山顶B 的仰角∠DCB =30°，求风力发电装置的高AB 的长．例4.如图，小聪用一块有一个锐角为30︒的直角三角板测量树高，小聪和树都与地面垂直，且相距33米，小聪身高AB 为1.7米，求这棵树的高度.例5．：如图，河旁有一座小山，从山顶A 处测得河对岸点C 的俯角为30°，测得岸边点D 的俯角为45°，又知河宽CD 为50m ．现需从山顶A 到河对岸点C 拉一条笔直的缆绳AC ，求山的高度及缆绳AC 的长(答案可带根号)． 例5．〔2021•〕如图，为测量*物体AB 的高度，在D 点测得A 点的仰角为30°，朝物体AB 方向前进20米，到达点C ，再次测得点A 的仰角为60°，则物体AB 的高度为〔 〕 A ． 10米 B ． 10米 C ． 20米 D ．米 例6．〔2021•〕超速行驶是引发交通事故的主要原因之一．上周末，小明和三位同学尝试用自己所学的知识检测车速．如图，观测点设在A 处，离大道的距离〔AC 〕为30米．这时，一辆小轿车由西向东匀速行驶，测得此车从B 处行驶到C 处所用的时间为8秒，∠BAC=75°． 〔1〕求B 、C 两点的距离；〔2〕请判断此车是否超过了大道60千米/小时的限制速度.〔计算时距离准确到1米，参考数据：sin75°≈0.9659，cos75°≈0.2588，tan75°≈3.732，3≈1.732，60千米/小时≈16.7米/秒〕 类型四. 坡度与坡角A B CD EA例．〔2021•〕如图，*水库堤坝横断面迎水坡AB 的坡比是1：3，堤坝高BC=50m ，则应水坡面AB 的长度是〔 〕A ．100mB ．1003mC ．150mD ．503m类型五. 方位角1．：如图，一艘货轮向正北方向航行，在点A 处测得灯塔M 在北偏西30°，货轮以每小时20海里的速度航行，1小时后到达B 处，测得灯塔M 在北偏西45°，问该货轮继续向北航行时，与灯塔M 之间的最短距离是多少"(准确到0.1海里，732.13≈) 综合题：三角函数与四边形：〔西城二模〕1．如图，四边形ABCD 中，∠BAD=135°，∠BCD=90°，AB=BC=2， tan∠BDC=63． (1)求BD 的长； (2)求AD 的长．〔2021东一〕2．如图，在平行四边形ABCD 中，过点A 分别作AE BC E AF ⊥CD 于点F ． 〔1〕求证：∠BAE =∠DAF ； 〔2〕假设AE =4，AF =245，3sin 5BAE ∠=，求CF 的长．三角函数与圆：1． 如图，直径为10的⊙A 经过点(05)C ，和点(00)O ，，与*轴的正半轴交于点D ，B 是y 轴右侧圆弧上一点，则cos∠OBC 的值为〔 〕 A ．12 B ．32C ．35D ．45〔延庆〕19.：在⊙O 中,AB 是直径，CB 是⊙O 的切线，连接AC 与⊙O 交于点D,(1) 求证：∠AOD=2∠C(2) 假设AD=8，tanC=34，求⊙O 的半径。