绳球模型与杆球模型
绳模型和杆模型
（二）轻杆模型 A）特点： 小球在竖直平面内做圆周运动时，物体能被支持 B）临界条件 （1）能否到达最高点的临界条件: V=0
(2)拉力还是支持力的临界条件： C）讨论： F
1）当 V＞ rg 时，杆对小 球施加拉力，且速度越大， 拉力越大（此时杆子相当于 绳子） 2）当 0＜V＜ rg 时，杆对球施加支 持力，速度越大，支持里越小
表演“水流星” ，需要保证杯 子在圆周运动最高点的线速度不 得小于 gr v gr 即：
V rg
K
E G
例1．如图所示，质量为m的小球置于正方
体的光滑盒子中，盒子的边长略大于球的直径。 某同学拿着该盒子在竖直平面内做半径为R的 匀速圆周运动，已知重力加速度为g，问： 图5－7－6
要使盒子在最高点时盒子与小球之间恰好无作用力，
则该盒子做匀速圆周运动的周期为多少？
[思路点拨] 解答本题时应注意： 1小球在最高点的合力等于向心力。 2通过最高点的临界
[解析 ] 设此时盒子的运动周期为 T 0，因为在最高点时
盒子与小球之间恰好无作用力，因此小球仅受重力作用。 根据牛顿第二定律得
4 2 mg m 2 r T0
，
得
T0 2
r g
1）质量为m的小球在竖直平面内的圆轨道的内则运动， 经过最高点而不脱离轨道的临界速度为V，当小球以2V 的速度经过最高点时，对轨道的压力是多大？ 解析: v m 由临界速度得：mg= r ， 当小球的速度为2v时，
（2）当V2=4m/s时，杆受到的力大小，是拉力还 是压力？
A
B
3)如图：在A与B点，杆对球 的力是（ AD ） A）A处可能为拉力，B处为拉力 B）A处可能为拉力，B处为压力 C）A处可能为支持力，B处为压力 D）A处可能为支持力，B处为拉力
竖直面圆周运动的绳球,杆球模型
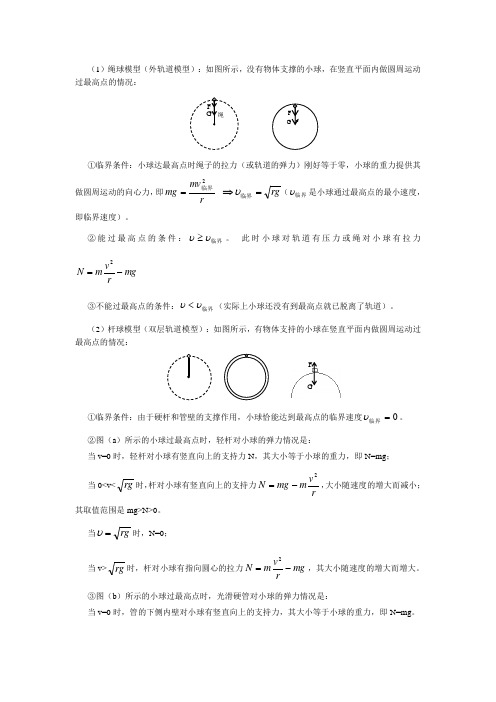
（1）绳球模型（外轨道模型）：如图所示，没有物体支撑的小球，在竖直平面内做圆周运动过最高点的情况：①临界条件：小球达最高点时绳子的拉力（或轨道的弹力）刚好等于零，小球的重力提供其做圆周运动的向心力，即rmvmg2临界=⇒rg=临界υ（临界υ是小球通过最高点的最小速度，即临界速度）。
②能过最高点的条件：临界υυ≥。
此时小球对轨道有压力或绳对小球有拉力mgrvmN-=2③不能过最高点的条件：临界υυ<（实际上小球还没有到最高点就已脱离了轨道）。
（2）杆球模型（双层轨道模型）：如图所示，有物体支持的小球在竖直平面内做圆周运动过最高点的情况：①临界条件：由于硬杆和管壁的支撑作用，小球恰能达到最高点的临界速度0=临界υ。
②图（a）所示的小球过最高点时，轻杆对小球的弹力情况是：当v=0时，轻杆对小球有竖直向上的支持力N，其大小等于小球的重力，即N=mg；当0<v<rg时，杆对小球有竖直向上的支持力rvmmgN2-=，大小随速度的增大而减小；其取值范围是mg>N>0。
当rg=υ时，N=0；当v>rg时，杆对小球有指向圆心的拉力mgrvmN-=2，其大小随速度的增大而增大。
③图（b）所示的小球过最高点时，光滑硬管对小球的弹力情况是：当v=0时，管的下侧内壁对小球有竖直向上的支持力，其大小等于小球的重力，即N=mg。
GF当0<v<rg 时，管的下侧内壁对小球有竖直向上的支持力rv m mg N 2-=，大小随速度的增大而减小，其取值范围是mg>N>0。
当v=gr 时，N=0。
当v>gr 时，管的上侧内壁对小球有竖直向下指向圆心的压力mg rv m N -=2，其大小随速度的增大而增大。
④图(c)的球沿球面运动，轨道对小球只能支撑，而不能产生拉力。
在最高点的v 临界=gr 。
当v=gr 时，小球将脱离轨道做平抛运动。
绳球杆球模型2
2 2
思考：小球过最高点的最小速度是多少?
T2 0, v临 gR
模型1：绳球模型
v2 mg
T2
2 v1 最低点： Fn T1 m g m R
o
T1
v 最高点： F n T2 m g m R
v1
2 2
mg
当 v gR ，小球能过最高点
【随堂练习1】长为L的轻绳一端固定着一质量为 m的小球，使小球在竖直平面内做圆周运动，下 列说法正确的是（ D ）。 B A、小球在圆周最高点时受到 的向心力一定是重力。
拓展：物体在管型轨道内的运动
有一内壁光滑、竖直放置的管 型轨道，其半径为R，管内有 一小球做圆周运动，小球的直 径刚好略小于管的内径。问： 小球运动到最高点时，速度与受力的关系如何？ 小球运动到最低点时，速度与受力的关系如何？
F3
V2
G F2
;
F1
V1
G
小球在竖直双层轨道内的运动情况和小球 随杆子的竖直运动情况相同
A. P球的速度一定大于Q球的速度 B.P球的动能一定小于Q球的动能 C.P球所受绳的拉力一定大于Q球所受绳的拉力 D.P球的向心加速度一定小于Q球的向心加速度
课堂练习： 绳系着装水的桶，在竖直平面 内做圆周运动，水的质量 m=0.5kg ，绳长 =90cm.求 （1）桶在最高点水不流出的最小速率？ （2）水在最高点速率=6m/s时水对桶底的 压力？(g取10m/s2)
F3
v2
mg
v2很小时，
支持力
2
o
v1
v2 FN m g F3 m R
A
杆球模型： 最高点分析： B
mg
v2
v 既不太大又不太小时， 小球既不受支持力，也不受拉力
高中物理人教版必修第二册教学课件《专题2：绳关联模型和杆关联模型》
v2cos α＝v1
绳模型举例：
(1)实际速度：绳的速度v，小木块的速度物
(2)连接物：绳（沿绳方向速度一样）
(3)分解速度：沿绳v∥
(4)结论：v＝v∥＝v物cos θ
(1)实际速度：圆环绳（沿绳方向速度一样）
(3)分解速度：沿绳v∥
(4)结论：v物′＝v∥＝v物cos θ
(4)结论：v物cos θ＝v物′cos α
例题：
1.如图所示，有两条位于同一竖直平面内的水平轨道，轨道上有两个物
体A和B，它们通过一根绕过光滑轻质定滑轮O的不可伸长的轻绳相连接，
物体A以速率vA＝10 m/s匀速运动，在绳与轨道成30°角时，物体B的速度
大小vB为
A.5 m/s
C.20 m/s
5 3
1∶2，故C错误；
P从开始运动到到达最低点的过程中，先向下做加速运动，加速度向下，处于
失重状态，然后又减速向下运动，加速度向上，处于超重状态，故D错误.
感谢聆听
(1)实际速度：小车B的速度物 ，小车A的速度物‘
(2)连接物：绳（沿绳方向速度一样）
(3)分解速度：沿绳v∥、v∥′
(4)结论：v物cos α＝v物′cos β
杆模型举例：
(1)实际速度：杆上端的速度物 ，下端的速度物‘
(2)连接物：杆（沿杆方向速度一样）
(3)分解沿杆速度：沿绳v∥、v∥′
角为θ时(图中未标出)，关于两球速度vA和vB的关系，下列说法正确的是
A.若θ＝30°，则A、B两球的速度大小相等
B.若θ＝60°，则A、B两球的速度大小相等
C.vA＝vBtan θ
√
D.vA＝vBsin θ
当杆与竖直方向的夹角为θ时，根据运动的分解可知(如图所示)，沿
绳模型和杆模型ppt课件
病原体侵入机体，消弱机体防御机能 ，破坏 机体内 环境的 相对稳 定性， 且在一 定部位 生长繁 殖，引 起不同 程度的 病理生 理过程
[思路点拨] 解答本题时应注意： 1小球在最高点的合力等于向心力。 2通过最高点的临界
病原体侵入机体，消弱机体防御机能 ，破坏 机体内 环境的 相对稳 定性， 且在一 定部位 生长繁 殖，引 起不同 程度的 病理生 理过程
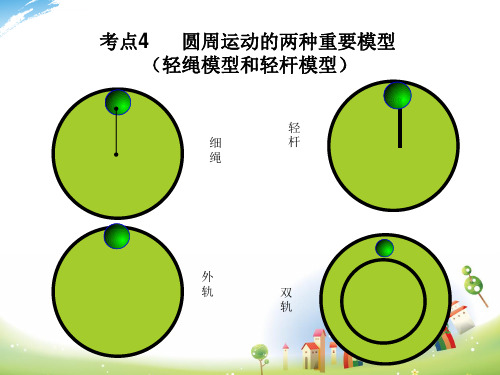
考点4 圆周运动的两种重要模型 （轻绳模型和轻杆模型）
轻
细杆绳外来自轨双轨
病原体侵入机体，消弱机体防御机能 ，破坏 机体内 环境的 相对稳 定性， 且在一 定部位 生长繁 殖，引 起不同 程度的 病理生 理过程
B
病原体侵入机体，消弱机体防御机能 ，破坏 机体内 环境的 相对稳 定性， 且在一 定部位 生长繁 殖，引 起不同 程度的 病理生 理过程
4. 在“水流星”表演中，杯子在竖直平面做
圆周运动，在最高点时，杯口朝下，但杯中水
却不会流下来，为什么？
对杯中水：mg
FN
v2 m
r
FN
当v gr 时，FN = 0
（一）轻绳模型
A）特点：小球在竖直平面内做圆周运 v 动时，物体不能被支持就， 即不受竖直向上的支持力
思考：小球过最高点的最小速度是多少
?
v2
最高点： T mg m
r
临界状态：T=0 mg mV02
r
B）能否通过最高点的临界条件
V0 rg
mg
T
o
病原体侵入机体，消弱机体防御机能 ，破坏 机体内 环境的 相对稳 定性， 且在一 定部位 生长繁 殖，引 起不同 程度的 病理生 理过程
022竖直面内圆周运动之绳”模型和“杆”模型及其临界问题
一.竖直面内的圆周运动——“绳”模型和“杆”模型1.在竖直平面内做圆周运动的物体，按运动到轨道最高点时的受力情况可分为两类：一是无支撑(如球与绳连接、沿内轨道运动的物体等)，称为“绳(环)约束模型”；二是有支撑(如球与杆连接、在弯管内的运动等)，称为“杆(管)约束模型”。
2．绳、杆模型涉及的临界问题绳模型杆模型常见类型均是没有支撑的小球均是有支撑的小球受力特征除重力外，物体受到的弹力向下或等于零除重力外，物体受到的弹力向下、等于零或向上受力示意图过最高点的临界条件由mg＝mv2r得v临＝gr由小球恰能做圆周运动得v临＝0讨论分析(1)过最高点时，v≥gr，F N＋mg＝mv2r，绳、圆轨道对球产生弹力F N(2)不能过最高点时，v<gr，在到达最高点前小球已经脱离了圆轨道(1)当v＝0时，F N＝mg，F N为支持力，沿半径背离圆心(2)当0<v<gr时，mg－F N＝mv2r，F N背离圆心，随v的增大而减小(3)当v＝gr时，F N＝0(4)当v>gr时，F N＋mg＝mv2r，F N指向圆心，并随v的增大而增大3.竖直面内圆周运动问题的解题思路二. 杆—球模型经典例题讲解与对点演练（一）例题例1：一轻杆一端固定质量为m 的小球，以另一端O 为圆心，使小球在竖直面内做半径为R 的圆周运动，如图所示，重力加速度为g ，则下列说法正确的是( ) A ．小球过最高点时，杆所受到的弹力可以等于零 B ．小球过最高点的最小速度是gRC ．小球过最高点时，杆对球的作用力一定随速度增大而增大D ．小球过最高点时，杆对球的作用力一定随速度增大而减小 答案 A解析 当小球在最高点所受的弹力为零时，有mg ＝m v 2R ，解得v ＝gR ，即当速度v ＝gR时，轻杆所受的弹力为零，所以A 正确．小球通过最高点的最小速度为零，所以B 错误．小球在最高点，若v <gR ，则有：mg －F ＝m v 2R ，轻杆的作用力随着速度的增大先减小后反向增大，若v >gR ，则有：mg ＋F ＝m v 2R ，轻杆的作用力随着速度增大而增大，所以C 、D 错误．（二）杆—球模型对点演练：1.如图所示，轻杆长3L ，在杆两端分别固定质量均为m 的球A 和B ，光滑水平转轴穿过杆上距球A 为L 处的O 点，外界给系统一定能量后，杆和球在竖直平面内转动，球B 运动到最高点时，杆对球B 恰好无作用力．忽略空气阻力，重力加速度为g ，则球B 在最高点时( ) A ．球B 的速度为零 B ．球A 的速度大小为2gL C ．水平转轴对杆的作用力为1.5mg D ．水平转轴对杆的作用力为2.5mg 答案 C解析 球B 运动到最高点时，杆对球B 恰好无作用力，即重力恰好提供向心力，则有mg ＝m v B 22L ，解得v B ＝2gL ，故A 错误；由于A 、B 两球的角速度相等，则球A 的速度大小v A ＝122gL ，故B 错误；B 球在最高点时，对杆无弹力，此时A 球受到的重力和拉力的合力提供向心力，有F －mg ＝m v A 2L ，解得：F ＝1.5mg ，根据牛顿第三定律可知，C 正确，D 错误．2.(2020·全国卷Ⅰ)如图，一同学表演荡秋千。
高中物理【绳球模型和杆球模型】
绳球模型和杆球模型
竖直平面内的圆周运动与临界问题
基本思路和方法：
以匀速圆周运动规律为基础，建立模型，根据物体做 匀速圆周运动时合力提供向心力，通过受力分析得到提供 的向心力，利用向心力公式得到需要的向心力，联立求解。
基本思路和方法：
合外力
受力分析
F提供
向心力公式
F需要
F提供 = F需要
关于两个模型需要注意两点：
v
绳球模型(最低点）
延伸 若细绳所能承受的最大张力为Fmax，试求小球通过最低点时，允许的最大速度 vmax。
绳球模型(最高点）
例 如图，长为l的细绳拉质量为m的小球在竖直面内做圆周运动，当小球以速度v通 过圆周最高点时，试求绳中张力F的大小。试求小球通过圆周最高点时所允许的最小速度vmin。
绳球模型 —— 圆环轨道、水流星
杆球模型(最低点）
例 如图，长为l的轻杆拉质量为m的小球在竖直面内做圆周运动，当小球以速度v通 过圆周最低点时，试求轻杆中弹力F的大小。
v
杆球模型(最高点）
例 如图，长为l的轻杆拉质量为m的小球在竖直面内做圆周运动，当小球以速度v通 过圆周最高点时，试求轻杆中拉力F的大小。
练习
例2 （多选）如图所示，质量可以不计的细杆的一端固定着一个质量为 m的小球，另一端能绕光滑的水平轴O转动.让小球在竖直平面内绕轴O做 半径为l的圆周运动，小球通过最高点时的线速度大小为v.下列说法中正确 的是( ) A. v不能小于 gl B. v＝ gl 时，小球与细杆之间无弹力作用 C. v大于 gl 时，小球与细杆之间的弹力随v增大而增大 D. v小于 gl 时，小球与细杆之间的弹力随v减小而增大
➢ 因为重力影响，模型中小球无法做匀速圆周运动， 但在最低点和最高点，受力符合匀速圆周运动的特点， 所以，我们只研究最低点和最高点。 ➢ 绳只能产生沿绳方向的拉力，杆可以产生任意方向 的弹力。
圆周运动——绳球杆球模型 ppt课件
在最高点时速 度应不小于
gr
在最高点时速 度应不小于
gr
在最高点速度 应大于0
在最高点速度 应大于0
ppt课件
18
临界问题：由于物体在竖直平面内做圆周运动 的依托物（绳、轨道、轻杆、管道等）不同， 所以物体恰好能通过最高点的临界条件也不同。
N
N
球在竖直平面内做圆周运动。
B
试分析：
（1）当小球在最低点A的速度
为v2时，杆的受力与速度的关
系怎样？
（2）当小球在最高点B的速度
为v1时，杆的受力与速度的关
A
系怎样？
ppt课件
10
问题2：杆球模型：
B
F3
v2
最低点：F1
mg
m
v12 L
mg
F2
o
最高点：F2
mg
m
v22 L
拉力
F1
v1 A mg
当v<v0，小球偏离原运动轨迹，不能通过最高点； 当v>v0，小球能够通过最高点。
ppt课件
5
实例一：水流星
在“水流星”表演中，杯子在竖直平面做圆周
运动，在最高点时，杯口朝下，但杯中水却不
会流下来，为什么？
对杯中水：mg FN
当v gr 时，FN =
0
m
v2 r
FN G
水恰好不流出
表演“水流星” ，需要保证杯 子在圆周运动最高点的线速度不
关系如何？
L
（2）当小球在最高点B 的速
A
v1 度为v2 时，绳的拉力与速度的
高考物理大一轮复习 物理模型4 竖直平面内圆周运动的绳、杆模型
确；由FN1＝m4Tπ212·R，T1＝π Rg 得：FN1＝4mg，由牛顿第三定律 可知，小球对盒子右侧面的力为4mg，B错误；由FN2＋mg＝
mω2R得小球以ω＝2
g R
做匀速圆周运动时，在最高点小球对盒
子上面的压力为3mg，C错误；盒子由最低点向最高点运动的过
程中，小球的加速度先斜向上，后斜向下，故小球先超重后失
4mg
C．若盒子以角速度2 Rg 做匀速圆周运动，则当盒子运动到 最高点时，小球对盒子下面的力为3mg
D．盒子从最低点向最高点做匀速圆周运动的过程中，球处 于超重状态；当盒子从最高点向最低点做匀速圆周运动的过程 中，球处于失重状态
解析
由mg＝m
4π2 T2
·R可得：盒子运动周期T＝2π
R g
，A正
对小球没有作用力，选项A错误；小球只受重力，重力竖直向下
提供向心力，根据牛顿第二定律得小球的向心加速度大小为a＝
mg m
＝g，再根据圆周运动规律得a＝
v2 R
＝g，解得v＝
gR ，选项B
错误，C、D正确．
2．(多选)如图所示，质量为m的小球在竖直放置的半径为R 的光滑圆形管道内做圆周运动(小球半径不计)，下列说法正确的 是( )
物理模型4 竖直平面内圆周运动的绳、杆模型
[模型概述] 在竖直平面内做圆周运动的物体，运动至轨道 最高点时的受力情况可分为两类．一是无支撑(如球与绳连接， 沿内轨道的“过山车”等)，称为“轻绳模型”；二是有支撑(如 球与杆连接，小球在弯管内运动等)，称为“轻杆模型”．
[模型特点]
轻绳模型
轻杆模型
解析：选CD.小球在最高点时刚好不脱离圆环，则圆环刚好
对小球没有作用力，选项A错误；小球只受重力，重力竖直向下
绳球模型+杆球模型导学案原创
圆周运动模型之——绳球模型+杆球模型导学案【学习目标】1.从生活实例出发，掌握竖直平面内两种圆周运动模型，绳球模型和杆球模型2.自主探究，小组协作，能够分析两种模型最高点和最低点受力及最高点速度临界问题。
3.学以致用，能用自己探究得到的模型知识解决绳球及杆球相关习题【课前自学】绳球模型一、填空题1.绳子和杆相比，绳子（是硬的，是软的），可以（拉伸，支持）物体，可以产生（支持，拉）力2.杆和绳子对比，杆（是硬的，是软的），可以（拉伸，支持）物体，可以产生（支持，拉）力二、讨论题在那某年某月的某一天，天气晴朗，微风拂面，风和日丽，时光美好。
于是，心情爽朗的你去感受过山车的速度与激情。
但是，在搭乘过山车到最高点时你的安全带脱落了！！问，在过山车运行到此最高点时，你会不会出事？此过山车是正圆环形状。
参考答案：一定会出事；不一定会出事。
【课中互学】三、绳球模型速度分析（一）在最高点1.用绳子连一物体做圆周运动，问，当物体在最高点速度等于0时，能不能使物体继续做圆周运动？（能，不能）2.用绳子连一物体做圆周运动，问，在最高点绳子能产生支持力么？（能，不能）3. 用绳子连一物体做圆周运动，问，在最高点绳子能产生拉力么？（能，不能）4. 用绳子连一物体做圆周运动，问，在最高点若重力刚好提供向心力，此时绳子对物体有拉力么？（有，没有）5. 用绳子连一物体做圆周运动，若在最高点物体仅受重力，由，求出此时物体的速度？（）6.用绳子连一物体做圆周运动，若在最高点物体不只受重力还受到绳子拉力作用，问，此时物体的速度情况如何？（等于，小于，大于）（二）在最低点根据物体在最低点的受力情况，选出求解向心力的表达式。
（，），此时物体处于（超重，失重）状态，绳子（容易，不容易）断四、方法总结1. 绳球模型中，在最高点，当速度小于时，物体（能，不能）继续做圆周运动2.绳球模型中，在最高点，当速度等于时，物体（能，不能）继续做圆周运动,物体此时仅受（重力，拉力）作用3.绳球模型中，在最高点，当速度等于0时，物体（能，不能）继续做圆周运动4.绳球模型中，在最高点，当速度大于时，物体（能，不能）继续做圆周运动,物体此时受（重力，拉力）作用,此时向心力公式为（，）5.绳球模型中，物体恰能上到最高点的临界速度是，物体此时仅受（重力，拉力）作用6.绳球模型中，在最低点，物体向心力的求解公式为【模型延伸】拓展：单轨模型有一竖直放置、内壁光滑的圆环，其半径为r，质量为m 的小球沿着它的内表面做圆周运动。
绳球模型与杆球模型
绳球模型与杆球模型摘要：绳球模型与杆球模型作为竖直面内圆周运动的典型，在高中物理分析综合能力考查中属于重点内容，也是难点内容。
本文就带大家一起来从根本上认识它们。
关键词：高中物理；绳球模型；杆球模型绳球模型与杆球模型作为竖直面内圆周运动的典型，在高中物理分析综合能力考查中属于重点内容，也是难点内容。
它常常与能量观点综合运用，用于解决实际生活中的诸如过山车、水流星等运动。
因此正确认识、区分、理解这两种模型十分重要，本文就带大家一起来从根本上认识它们。
首先来看看它们的相似之处。
两种模型“外貌相似”：如下图（1）轻绳L一端栓结可视为质点的小球m，另一端绕水平转轴O在竖直面内转动即为绳球模型；将轻绳换作轻杆即为杆球模型图（2）。
“向心力的来源相似”。
讨论小球向心力的来源，都是轻绳（或轻杆）的作用力与小球重力的合力沿半径方向的分量来提供。
绳球模型与杆球模型如此相似，难道就是一个字的差别？它们究竟有哪些区别呢？首先从根本上讲，轻绳与轻杆提供的力不一样：轻绳只能给小球提供沿着绳并指向绳收缩方向的拉力，而轻杆既可以给小球提供向圆周内的拉力，也可以提供向圆周外的推力，甚至它提供的力可以不沿着轻杆自身。
其次约束情况不一样：轻绳对球产生了单面约束，即小球不能跑到半径为L的圆周以外，但可以跑到半径为L的圆周之内，轻杆对球产生了双面约束，小球既不能跑到半径为L的圆周以外，也不能跑到半径为L的圆周之内，只能在半径为L的圆周上运动。
其三小球运动情况不一样：绳球模型中小球不能实现竖直面内匀速圆周运动，只能是一般圆周运动，杆球模型中小球能够实现在竖直面内匀速圆周运动。
第四做功情况不一样：轻绳对小球不做功，小球机械能守恒，而轻杆可以对小球做功改变其机械能。
最后，小球在最高点的临界条件不同，这点是常考点。
（默认向下为正方向）绳球模型小球在最高点时：mg+T=mv2L，其中T≥0，因此mg≤mv2L，即有v≥gL，故绳球模型中小球过最高点时的最小速度为gL。
人教版高中物理必修二绳球(内轨道)模型.docx
高中物理学习材料（灿若寒星**整理制作）绳球（内轨道）模型1、细绳一端固定，另一端系一小球在竖直平面内做完整的圆周运动，设绳长为L ，重力加速度为g ，则（ ）2、如图所示，杂技演员在表演“水流星”， 用长为1.6m 轻绳的一端，系一个总质量为0.5kg 的盛水容器，以绳的另一端为圆心，在竖直平面内圆周运动，若“水流星”通过最高点的速度为4m/s ，g 取10m/s 2，则下列说法正确的是（ ）A. “水流星”通过最高点时，有水从容器中流出B. “水流星”通过最高点时，绳的张力及容器的底部受到的压力均为零C. “水流星”通过最高点时，处于完全失重状态，不受力的作用D. “水流星”通过最高点时，绳子的拉力大小为5N3、一根长L=60cm 的绳子系着一个小球，小球在竖直平面内做圆周运动。
已知球的质量，求：（1）试确定到达最高点时向心力的最小值；（2）小球能够到达最高点继续做圆周运动的最小速度；kg m 5.0（3）当小球在最高点时的速度为时，绳对小球的拉力。
（g=10m/s 2）4、杂技演员在做“水流星”表演时，用一根细绳系着盛水的杯子，抡起绳子，让杯子在竖直面内做圆周运动．如图所示，杯内水的质量m ＝0.5 kg ，绳长l ＝0.6m 求：（g=10m/s 2）(1)在最高点水不流出的最小速率．(2)水在最高点速率v ＝3 m/s 时，水对杯底的压力．5、如图所示，是马戏团中上演的飞车节目，在竖直平面内有半径为R=5m 的圆轨道．表演者骑着摩托车在圆轨道内做圆周运动．已知人和摩托车的总质量为100kg ，人以v 1=10m/s 的速度过轨道最高点B ，并以v 2=20m/s 的速度过最低点A ．求：（1）在B 点轨道对摩托车的压力大小为多少？（2）在A 点摩托车对轨道的压力大小为多少？（3）能过B 点最小速度多大？杆球（管道）模型1、质量为1kg 的重球用长为0.4m 的轻质杆连接，杆的另一端为圆心，使重球在竖直平面内做圆周运动，重球运动到最高点时的速度大小为1m/s 时，杆对球作用力方向____，大小等于_____；若到达最高点时的速度大小为2m/s 时，杆对球作用力大小等于____．s m /32、如图2所示，长度为0.5m 的轻质细杆OA ，A 端有一质量为3kg 的小球，正在以O 点为圆心在竖直平面内做圆周运动，已知小球通过最高点时的速度为2m/s ，取 g =10m/s 2。
圆周运动专题(绳球模型、杆球模型、轨道和管道模型、圆锥摆、斜面上的圆周运动、转盘上的圆周运动)解析版
圆周运动专题（绳球模型、杆球模型、轨道和管道模型、圆锥摆、斜面上的圆周运动、转盘上的圆周运动）60分钟考点序号考点 考向 题型分布考点1圆周运动专题（绳球模型、杆球模型、轨道和管道模型、圆锥摆、斜面上的圆周运动、转盘上的圆周运动）考向1：绳球模型模型考向2：杆球模型模型考向3：轨道和管道模型考向4：圆锥摆模型 考向5：斜面上的圆周运动 考向6：转盘上的圆周运动12单选+3多选+2计算圆周运动专题（绳球模型、杆球模型、轨道和管道模型、圆锥摆、斜面上的圆周运动、转盘上的圆周运动）（13单选+2多选） 1．（2024·浙江宁波·模拟预测）如图半径为L 的细圆管轨道竖直放置，管内壁光滑，管内有一个质量为m 的小球做完整的圆周运动，圆管内径远小于轨道半径，小球直径略小于圆管内径，下列说法不正确的是（ ）A．经过最低点时小球可能处于失重状态B．经过最高点Z时小球可能处于完全失重状态C．若小球能在圆管轨道做完整圆周运动，最高点Z的速度v最小值为0D．若经过最高点Z的速度v增大，小球在Z点对管壁压力可能减小A．小车在BD下方运动时处于失重状态B．小车在B点不受摩擦力作用C．小车在C点时对轨道的压力恰好为零D．小车在A点时对轨道的压力比在C点时大10N【答案】D【详解】A．小球在BD下方运动时，向心加速度指向圆心，均有竖直向上的分量，故处于超重状态，故A 错误；A．从B运动到C过程中机器人的向心加速度2a=0.5m/sB．为防止餐盘与水平托盘之间发生相对滑动，机器人在BC段运动的最大速率为4m/s C．从A点运动到B点过程中机器人的加速度20.125m/sa=且餐盘和水平托盘不会发生相对滑动t=秒D．餐盘和水平托盘不发生相对滑动的情况下，机器人从C点到D点的最短时间12A．在角速度缓慢增大的过程中两绳的拉力始终不变B．当小球运动半径为6L、4A．2gB．L【答案】A则用更长的绳做实验，得到的图线与横轴交点的位置距离原点的的距离变大，选项D 错误。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
绳球模型与杆球模型
摘要：绳球模型与杆球模型作为竖直面内圆周运动的典型，在高中物理分析综合能力考查中属于重点内容，也是难点内容。
本文就带大家一起来从根本上认识它们。
关键词：高中物理；绳球模型；杆球模型
绳球模型与杆球模型作为竖直面内圆周运动的典型，在高中物理分析综合能力考查中属于重点内容，也是难点内容。
它常常与能量观点综合运用，用于解决实际生活中的诸如过山车、水流星等运动。
因此正确认识、区分、理解这两种模型十分重要，本文就带大家一起来从根本上认识它们。
首先来看看它们的相似之处。
两种模型“外貌相似”：如下图（1）轻绳L一端栓结可视为质点的小球m，另一端绕水平转轴O在竖直面内转动即为绳球模型；将轻绳换作轻杆即为杆球模型图（2）。
“向心力的来源相似”。
讨论小球向心力的来源，都是轻绳（或轻杆）的作用力与小球重力的合力沿半径方向的分量来提供。
绳球模型与杆球模型如此相似，难道就是一个字
的差别？它们究竟有哪些区别呢？
首先从根本上讲，轻绳与轻杆提供的力不一样：轻绳只能给小球提供沿着绳并指向绳收缩方向的拉力，而轻杆既可以给小球提供向圆周内的拉力，也可以提供向圆周外的推力，甚至它提供的力可以不沿着轻杆自身。
其次约束情况不一样：轻绳对球产生了单面约束，即小球不能跑到半径为L的圆周以外，但可以跑到半径为L的圆周之内，轻杆对球产生了双面约束，小球既不能跑到半径为L的圆周以外，也不能跑到半径为L的圆周之内，只能在半径为L的圆周上运动。
其三小球运动情况不一样：绳球模型中小球不能实现竖直面内匀速圆周运动，只能是一般圆周运动，杆球模型中小球能够实现在竖直面内匀速圆周运动。
第四做功情况不一样：轻绳对小球不做功，小球机械能守恒，而轻杆可以对小球做功改变其机械能。
最后，小球在最高点的临界条件不同，这点是常考点。
（默认向下为正方向）绳球模型小球在最高点时：mg+T=mv2L，其中T≥0，因此mg≤mv2L，即有v
≥gL，故绳球模型中小球过最高点时的最小速度为gL。
而对于杆球模型小球在最高点时：mg+F=mv2L，其中F>0，F=0，F0（即轻杆提供向下拉力）时有mggL；当F=0（即轻杆恰不提供力）时有mg=mv2L，即有
v=gL；当Fmv2L，即有v<gL。
由上分析可知杆球模型中小球过最高点时的最小速度为0。
下面我们通过一典型例题加以理解：如图所示，质量为m小球从斜面AB上的A点由静止下滑，通过水平轨道BC后进入半径为R的半圆轨道CD，恰好通过圆弧最高点D，斜面AB?c水平轨道BC在B处通过一小段光滑圆弧轨道连接。
一切摩擦不计。
求：（1）小球从静止开始下落时的高度h。
（2）小球经过半圆轨道的最低点C时对轨道的压力。
（3）其他条件不变，仅将CD段改成粗糙圆管道。
小球从高度h=52R 静止释放恰好通过最高点D。
求粗糙圆管道对小球做的功。
分析与解答：竖直面内圆弧对小球的作用力只能是沿着半径指向圆心的，因此属于绳球模型，故（1）在D点，设小球的速度为vD，则有
mg=mvD2L∴vD=gL
小球由A运动到D点的过程，由机械能守恒得：mg（h-2R）=12mv2D∴h=52R
（2）小球由A运动到C点的过程，由机械能守恒得：mgh=12mv2C
通过C点时，有N-mg=mv2CR联立上两式解得，N=6 mg
则根据牛顿第三定律得：小球经过半圆轨道的最低点C时对轨道的压力大小为6 mg，方向竖直向下.
竖直面内圆管道对小球的弹力既可以指向圆心也可以背向圆心，因此属于杆球模型，故
（3）在D点，小球的速度为0。
小球由A运动到D点的过程，由动能定理得：
mg（h-2R）+Wf=0-0∴Wf=-12mgR
即粗糙圆管道对小球做了12mgR的负功。
通过题例我们可以看到，处理绳球模型和杆球模型的切入点是认真对小球进行受力分析，然后分清属于哪一个模型，找准小球向心力的来源，列出牛顿第二定律式，注意结合能量观点解决问题。
作者简介：
叶巧英，江苏省南京市，江苏省六合高级中学。