第4章习题答案.
第4章 习题解答

第4章 习题与答案4-1作简谐振动的物体,每次通过同一位置时,不一定相同的量是 [ ] (A) 位移 ; (B) 速度 ; (C) 加速度; (D) 能量。
[答案:B ]4-2 把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相为 [ ](A) π; (B) π/2; (C) 0; (D) θ [答案:C ]4-3 谐振动的振动曲线如题4-3图所示,则有[ ] (A )A 超前π/2; (B )A 落后π/2; (C )A 超前π; (D )A 落后π。
[答案:A ]4-4 一个质点作简谐振动,振辐为A ,在起始时刻质点的位移为A /2,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为题4-4图 中哪一个? [ ][答案:B ]4-5 两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点恰在最大负位移处。
则第二个质点的振动方程为 [ ] (A) )π21cos(2++=αωt A x ; (B) )π21cos(2-+=αωt A x ; (C) )π23cos(2-+=αωt A x ; (D) )cos(2π++=αωt A x 。
[答案:A ]4-6 已知某简谐振动的振动曲线如题4-6图所示。
则此简谐振动的振动方程(SI )为 [ ](A) 题4-4图题4-3图(A )220.02cos()33x t =π+π;(B )220.02cos()33x t =π-π;(C )420.02cos()33x t =π+π;(D )420.02cos()33x t =π-π。
[答案:C ]4-7 弹簧振子作简谐振动,先后以相同的速度依次通过A 、B 两点,历时1秒,质点通过B 点后再经过1秒又第二次通过B 点,在这2秒内质点通过的总路程为12cm ,则质点的振动周期和振幅分别为 [ ](A )3s 、12cm ; (B )4s 、6cm ; (C )4s 、9cm ; (D )2s 、8cm 。
(完整版)线性代数练习册第四章习题及答案

第四章 线性方程组§4-1 克拉默法则一、选择题1.下列说法正确的是( C )A.n 元齐次线性方程组必有n 组解;B.n 元齐次线性方程组必有1n -组解;C.n 元齐次线性方程组至少有一组解,即零解;D.n 元齐次线性方程组除了零解外,再也没有其他解. 2.下列说法错误的是( B )A 。
当0D ≠时,非齐次线性方程组只有唯一解;B 。
当0D ≠时,非齐次线性方程组有无穷多解;C 。
若非齐次线性方程组至少有两个不同的解,则0D =; D.若非齐次线性方程组有无解,则0D =. 二、填空题1.已知齐次线性方程组1231231230020x x x x x x x x x λμμ++=⎧⎪++=⎨⎪++=⎩有非零解,则λ= 1 ,μ= 0 。
2.由克拉默法则可知,如果非齐次线性方程组的系数行列式0D ≠,则方程组有唯一解i x =iD D. 三、用克拉默法则求解下列方程组 1.832623x y x y +=⎧⎨+=⎩解:832062D ==-≠123532D ==-,2821263D ==-所以,125,62D Dx y D D====- 2.123123123222310x x x x x x x x x -+=-⎧⎪+-=⎨⎪-+-=⎩解:213112112122130355011101r r D r r ---=--=-≠+---11222100511321135011011D r r ---=-+-=---,212121505213221310101101D r r --=-+-=-----, 3121225002112211511110D r r --=+=---所以, 3121231,2,1D D Dx x x D D D ======3.21241832x z x y z x y z -=⎧⎪+-=⎨⎪-++=⎩解:132010012412041200183583D c c --=-+-=≠-13110110014114020283285D c c -=-+=,2322112102112100123125D c c -=-+=--, 31320101241204120182582D c c =-=--所以, 3121,0,1D D Dx y z D D D ====== 4.12341234123412345242235232110x x x x x x x x x x x x x x x x +++=⎧⎪+-+=-⎪⎨---=-⎪⎪+++=⎩解:2131412131111111111214012322315053733121102181231235537013814222180514r r D r r r r r r r r ---=------------+=----=-+---3214212325111511102221422518231523528110121101005110010525182733214210252823522c c D c c c c c c --------=----------+=-----=----212314113231511151112140723222150123733021101518723230132123733031284315181518r r D r r r r r r r r -----=--------------=----=------12342213111512151031224522182325111132283101101002510200251521852974265211228115127c c D c c c c c c -------=---------+=-----=----12432322111152115312125252223121135231200100215215552502714251152604c c D c c r r r r --------=----------+=----=---所以, 312412341,2,3,1D D D Dx x x x D D D D========-§4-2 齐次线性方程组一、选择题1.已知m n ⨯矩阵A 的秩为1n -,12,αα是齐次线性方程组0AX =的两个不同的解,k 为任意常数,则方程组0AX =的通解为( D )。
自动控制原理课后习题第四章答案

G(s)H(s)=
Kr s(s+1)(s+3)
σ根 s=3-K+ω轨r4-3-迹+p4s132ω1-3的+~3ω32分p===s2-离+001K点.p-3r=3:KK~0θrr===012+ωω6021,o=3,=0+±1810.7o
8
jω
1.7
s1
A(s)B'系(s)统=根A'轨(s迹)B(s)
s3 p3
s=sK2±r没=j24有.8.6位×于2K.r根6=×4轨80.迹6=上7,. 舍去。
2
第四章习题课 (4-9)
4-9 已知系统的开环传递函数,(1) 试绘制出
根轨迹图。
G(s)H与(s虚)=轴s交(0点.01s+1K)(系0.统02根s+轨1迹)
jω
70.7
解: GKK(rr=s=)10H5(0s)=ωω2s1,(3=s=0+±17000K.7)r(s+50)
s1
A(s)B'(系s)统=A根'(轨s)迹B(s)
s3 p3
p2
p1
-4
-2
0
((24))ζ阻=尼03.振5s2荡+1响2应s+s的81==K-r0值0.7范+围j1.2
s=s-s10=3=.-80-56.8+50K.7r×=20=s.82-=54×-.631..1155×3.15=3.1
-2.8
450
1080
360
0σ
0σ
第四章习题课 (4-2)
4-2 已知开环传递函数,试用解析法绘制出系
统的根轨迹,并判断点(-2+j0),(0+j1),
习题参考答案(第4章)
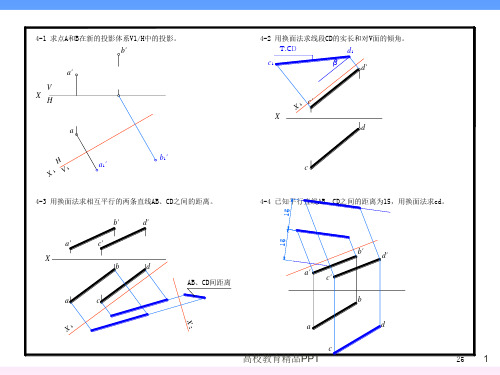
a' V XH
a
4-2 用换面法求线段CD的实长和对V面的倾角。
T.CD
d1
c1 d'
X 1 c' X
d
H X1 V1
a1'
b1'
c
4-3 用换面法求相互平行的两条直线AB、CD之间的距离。
b'
d'
a'
c'
X
b
d
a
c
AB、CD间距离
4-4 已知平行直线AB、CD之间的距离为15,用换面法求cd。
15
15
a' c'
b'
d'
b
X2
பைடு நூலகம்X1
a
d
c
高校教育精品PPT
25 1
4-5 已知直线AB与CD垂直相交,用换面法求c'd'。 b'
a'
c a
b d
4-6 用换面法求点到直线BC距离,并求垂足。
a'
c'
b'
c a
A到BC距离 b
O2
4-7 已知点A到直线BC的距离为15,求a。 a1
R15
b1
c1
O1
a b
c a'1
c'1 c2
a2
b1' b2
高校教育精品PPT
27 3
4-11 已知直线AB与 CDE的距离为10,用换面法求ab。
c' e'
b'
a' X
第四章 习题答案

第四章的习题及答案4-1 设有一台锅炉,水流入锅炉是之焓为62.7kJ ·kg -1,蒸汽流出时的焓为2717 kJ ·kg -1,锅炉的效率为70%,每千克煤可发生29260kJ 的热量,锅炉蒸发量为4.5t ·h -1,试计算每小时的煤消耗量。
解:锅炉中的水处于稳态流动过程,可由稳态流动体系能量衡算方程:Q W Z g u H s +=∆+∆+∆221体系与环境间没有功的交换:0=s W ,并忽 动能和位能的变化, 所以: Q H =∆设需要煤mkg ,则有:%7029260)7.622717(105.43⨯=-⨯m解得:kg m 2.583=4-2 一发明者称他设计了一台热机,热机消耗热值为42000kJ ·kg -1的油料0.5kg ·min -1,其产生的输出功率为170kW ,规定这热机的高温与低温分别为670K 与330K ,试判断此设计是否合理?解:可逆热机效率最大,可逆热机效率:507.06703301112max =-=-=T T η 热机吸收的热量:1m in210005.042000-⋅=⨯=kJ Q热机所做功为:1m in 102000m in)/(60)/(170-⋅-=⨯-=kJ s s kJ W该热机效率为:486.02100010200==-=Q W η 该热机效率小于可逆热机效率,所以有一定合理性。
4-3 1 kg 的水在1×105 Pa 的恒压下可逆加热到沸点,并在沸点下完全蒸发。
试问加给水的热量有多少可能转变为功?环境温度为293 K 。
解:查水蒸气表可得始态1对应的焓和熵为:H 1=83.93kJ/kg, S 1=0.2962kJ/kg.K 末态2对应的焓和熵为:H 2=2675.9kJ/kg, S 2=7.3609kJ/kg.K)/(0.259293.839.267512kg kJ H H Q =-=-=)/(0.522)2962.03609.7(15.2930.25920kg kJ S T H W sys id =-⨯-=∆-∆=4-4如果上题中所需热量来自温度为533 K 的炉子,此加热过程的总熵变为多少?由于过程的不可逆性损失了多少功? 解:此时系统的熵变不变)./(0647.7K kg kJ S sys =∆炉子的熵变为)./(86.45330.2592K kg kJ T H T Q S sur -=-=∆-==∆ )./(205.286.40647.7K kg kJ S t =-=∆ )/(0.646205.215.2930kg kJ S T W t l =⨯=∆=4-5 1mol 理想气体,400K 下在气缸内进行恒温不可逆压缩,由0.1013MPa 压缩到1.013MPa 。
第4章 习题及答案
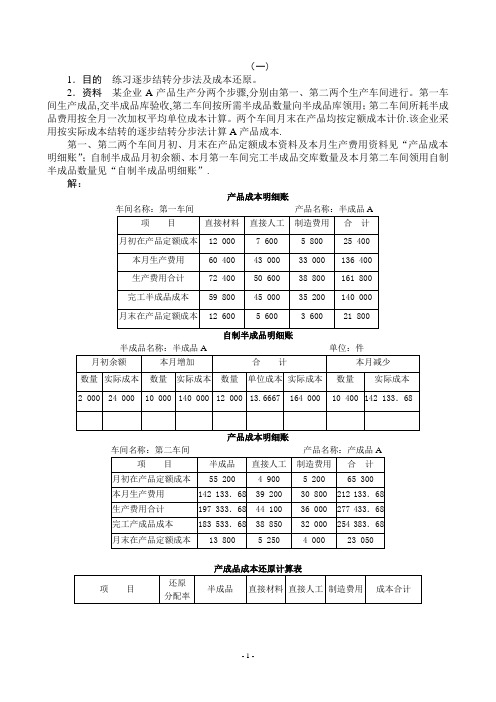
(一)1.目的练习逐步结转分步法及成本还原。
2.资料某企业A产品生产分两个步骤,分别由第一、第二两个生产车间进行。
第一车间生产成品,交半成品库验收,第二车间按所需半成品数量向半成品库领用;第二车间所耗半成品费用按全月一次加权平均单位成本计算。
两个车间月末在产品均按定额成本计价.该企业采用按实际成本结转的逐步结转分步法计算A产品成本.第一、第二两个车间月初、月末在产品定额成本资料及本月生产费用资料见“产品成本明细账”;自制半成品月初余额、本月第一车间完工半成品交库数量及本月第二车间领用自制半成品数量见“自制半成品明细账”.解:产品成本明细账车间名称:第一车间产品名称:半成品A自制半成品明细账半成品名称:半成品A 单位:件产品成本明细账产成品成本还原计算表(二)1.目的练习产品成本计算的综合结转分步法.2.资料某企业生产甲产品,分三个生产步骤进行生产。
该企业设有第一、第二、第三三个基本生产车间,甲产品由这三个车间顺序加工而成。
成本计算采用综合结转法。
原材料在第一车间开始加工时一次投入,半成品不通过中间仓库收发,上一步骤完工后全部交由下一步骤继续加工。
月末在产品按约当产量法计算,各车间月末在产品完工程度均为50%。
该企业本年5月份有关成本计算资料如表1、表2所示。
表1产量记录表2月初在产品成本和本月发生费用表3产品成本计算单135070÷(88+16)=1298。
75 24960÷(88+16×50%)=260 19200÷(88+16×50%)=200表4产品成本计算单173890÷(8050%)=326。
6表5产品成本计算单244450÷(96+4)=2444.5 34300÷(96+4×50%)=350 23520÷(96+4×50%)=240表6(三)1.目的练习产品成本计算的平行结转分步法.2.资料某厂设有三个基本生产车间,第一车间生产甲半成品,交第二车间继续加工,第二车间生产乙半成品,交第三车间生产丙产成品。
第4章形状和位置公差的检测 习题参考答案
第4章形状和位置公差的检测习题参考答案1、在图4-1所示销轴的三种形位公差标注中,它们的公差带有何不同?图4-1 销轴答:a)公差带是距离为0.02mm的两平行平面之间的区域;b)公差带是直径为0.02mm的圆柱面内的区域;c)公差带是距离为0.02mm且平行于基准A的平行平面之间的区域。
2、图4-2所示零件标注的位置公差不同,它们所要控制的位置误差区别何在?图4-2 零件图答:a)为垂直度公差,公差带与基准轴线相垂直。
它的公差带相对于基准有确定的方向,并且公差带的位置可以浮动。
它的公差带具有综合控制被测要素的方向和形状的职能。
b)为圆跳动公差,控制与基准同轴的任一半径位置的圆柱面上的位置误差。
c)为全跳动公差,控制与基准同轴的所有半径位置的圆柱面上的位置误差;跳动公差带相对于基准轴线有确定的位置,它可以综合控制被测要素的位置、方向和形状的。
3、图4-3所示的两种零件,标注敢不同的位置公差,它们的要求有何不同?答:a)要求斜端面对φ基准轴线成60°的理想方向,又要求斜端面中点在φ轴方向距离B面有公差要求。
b)要求斜端面对φ基准轴线成60°的理想方向,则公差带是距离为公差值0.05mm,且与基准轴线成60°角的两平行平面之间的区域。
图4-3 零件图4、在底边的边角上有一孔,要求位置度公差为φ0.1mm,图4-4所示的三种标注方法,哪种标注方法正确?为什么另一些标注方法不正确?图4-4 零件图答:a)尺寸无公差而且也不是理论正确尺寸,无基准;b)基准符号标注位置不对;c)正确。
5、图4-5所示零件的技术要求是:⑴ 2×φd轴线对其公共轴线的同轴度公差为φ0.02mm;⑵φD轴线对2×φd公共轴线的垂直度公差为100:0.02;⑶φD轴线对2×φd公共轴线的偏离量不大于±10μm。
试用形位公差代号标出这些要求。
图4-5 零件图解:参考答案如图所示:图4-5 零件图参考答案6、图4-6所示零件的技术要求是:⑴法兰盘端面A对φ18H8孔的轴线的垂直度公差为0.015mm;⑵φ35圆周上均匀分布的4×φ8H8孔,要求以φ18H8孔的轴线和法兰盘端面A为基准以互换装配,位置度公差为φ0.05mm;⑶ 4×φ8H8四孔组中,有一个孔的轴线与φ4H8孔的轴线应在同一平面内,它的偏离量不大于±10μm。
第4章 控制结构习题(含答案及解析)
第4章控制结构习题一、选择题。
1.关于程序设计所要求的基本结构,以下选项中描述错误的是( )A)循环结构B)分支结构C)goto 跳转D)顺序结构正确答案: C解析:为了表示更复杂的处理逻辑,在Python程序中存在三种基本结构,它们分别是:顺序结构;分支结构;循环结构。
2.下面代码的输出结果是for s in “HelloWorld”:if s==“W”:continueprint(s,end="")A)HelloB)WorldC)HelloWorldD)Helloorld正确答案: D解析:Python通过保留字for实现“遍历循环”,for语句的循环执行次数是由遍历结构体中元素的个数确定的。
遍历循环可以理解为从要遍历的结构中逐一提取元素,并赋值给循环变量,对于所提取的每个元素执行一次循环体。
Python 提供了两个保留字:break和continue,用来辅助控制循环执行。
continue语句只结束本次循环,而不终止整个循环的执行。
3.关于Python循环结构,以下选项中描述错误的是()A)遍历循环中的遍历结构可以是字符串、文件、组合数据类型和range()函数等。
B)break用来跳出最内层for或者while循环,脱离该循环后程序从循环代码后继续执行C)每个continue语句只有能力跳出当前层次的循环D)Python通过for、while等保留字提供遍历循环和无限循环结构正确答案: C解析:continue用来结束当前当次循环,但不跳出当前循环;每个break语句只有能力跳出当前层次的循环。
4.以下程序的输出结果是:()for i in "CHINA":for k in range(2):print(i, end="")if i == 'N':breakA)CCHHIINNAAB)CCHHIIAAC)CCHHIAAD)CCHHIINAA正确答案: D解析:每个break语句只有能力跳出当前层次的循环。
第四章 习题答案
习题4.1选择填空1、选用差分放大电路的原因是 A 。
A 、克服温漂B 、 提高输入电阻C 、稳定放入倍数2、用恒流源取代长尾式差分放大电路中的发射极电阻Re ,将使电路的 B 。
A 、差模放大倍数数值增大B 、抑制共模信号能力增强C 、差模输入电阻增大 3、差动放大器中的差模输入是指两输入端各加大小___相等_____、相位___相反____的信号。
4、设差放电路的两个输入端对地的电压分别为v i1和v i2,差模输入电压为v id ,共模输入电压为v ic ,则当v i1=50mV ,v i2=50mV 时,v id =_0mV __,v ic =_50mV __;当v i1=50mV ,v i2=-50mV 时,v id =_100mA __,v ic =_0mA__;当v i1=50mV ,v i2=0V 时,v id =_50mV __,v ic =_25mA __。
5、电流源常用于放大电路,作为_A ___(A.有源负载,B.电源,C.信号源),使得放大倍数__A __(A.提高,B.稳定)。
6、电压放大电路主要研究的指标是 a 、 b 、 c ;功率放大电路主要研究的指标是 d 、 e 、 f 、 g 、(a 电压放大倍数 b 输入电阻 c 输出电阻 d 输出功率 e 电源提供的功率 f 效率 g 管耗)7、功率放大电路中,___甲类____功率放大电路导通角最大;_____乙类___功率放大电路效率较高。
(甲类、乙类、甲乙类) 8、甲类功放效率低是因为 B 。
A 、只有一个功放管B 、 静态电流过大C 、管压降过大4.1对称差动放大电路如题图 4.1所示。
已知晶体管1T 和2T 的50=β,并设U BE (on )=0.7V,r bb ’=0,r ce =∞。
(1)求V 1和V 2的静态集电极电流I CQ 、U CQ 和晶体管的输入电阻r b’e 。
(2)求双端输出时的差模电压增益A ud ,差模输入电阻R id 和差模输出电阻R od 。
(完整word版)第四章 习题答案
第四章的习题及答案4-1 设有一台锅炉,水流入锅炉是之焓为62.7kJ ·kg -1,蒸汽流出时的焓为2717 kJ ·kg -1,锅炉的效率为70%,每千克煤可发生29260kJ 的热量,锅炉蒸发量为4.5t ·h -1,试计算每小时的煤消耗量。
解:锅炉中的水处于稳态流动过程,可由稳态流动体系能量衡算方程:Q W Z g u H s +=∆+∆+∆221体系与环境间没有功的交换:0=s W ,并忽 动能和位能的变化, 所以: Q H =∆设需要煤mkg ,则有:%7029260)7.622717(105.43⨯=-⨯m解得:kg m 2.583=4-2 一发明者称他设计了一台热机,热机消耗热值为42000kJ ·kg -1的油料0.5kg ·min -1,其产生的输出功率为170kW ,规定这热机的高温与低温分别为670K 与330K ,试判断此设计是否合理?解:可逆热机效率最大,可逆热机效率:507.06703301112max =-=-=T T η 热机吸收的热量:1m in210005.042000-⋅=⨯=kJ Q热机所做功为:1m in 102000m in)/(60)/(170-⋅-=⨯-=kJ s s kJ W该热机效率为:486.02100010200==-=Q W η 该热机效率小于可逆热机效率,所以有一定合理性。
4-3 1 kg 的水在1×105 Pa 的恒压下可逆加热到沸点,并在沸点下完全蒸发。
试问加给水的热量有多少可能转变为功?环境温度为293 K 。
解:查水蒸气表可得始态1对应的焓和熵为:H 1=83.93kJ/kg, S 1=0.2962kJ/kg.K 末态2对应的焓和熵为:H 2=2675.9kJ/kg, S 2=7.3609kJ/kg.K)/(0.259293.839.267512kg kJ H H Q =-=-=)/(0.522)2962.03609.7(15.2930.25920kg kJ S T H W sys id =-⨯-=∆-∆=4-4如果上题中所需热量来自温度为533 K 的炉子,此加热过程的总熵变为多少?由于过程的不可逆性损失了多少功? 解:此时系统的熵变不变)./(0647.7K kg kJ S sys =∆炉子的熵变为)./(86.45330.2592K kg kJ T H T Q S sur -=-=∆-==∆ )./(205.286.40647.7K kg kJ S t =-=∆ )/(0.646205.215.2930kg kJ S T W t l =⨯=∆=4-5 1mol 理想气体,400K 下在气缸内进行恒温不可逆压缩,由0.1013MPa 压缩到1.013MPa 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
绳与滑轮间无滑动,滑轮轴光滑)
习题答案
第四章刚体的转动
解 T1 m1g sin m1g sin m1a
求两物体的加速度和绳的张力.
r
FTA
FTB
R
A aA
B
aB
r
PA
PB
R
B A
FTB
FTA
习题答案
解
m1g FTA m1aA FTB m2 g m2aB
RFTA rFTB ( J1 J2 )
aA R
aB r
aA
R
J1
m1R m2r J2 m1R2
gR
aB
r
J1
m1R m2r J2 m1R2
m2r 2
gr
B A
习题答案
aA
R
J1
m1R m2r J2 m1R2
m2r 2
gR
aB
r
J1
m1R m2r J2 m1R2
m2r 2
gr
m1g FTA m1aA
FTB m2 g m2aB
m2r 2
gr
FTA
J1 J2 J1 J2
m2r 2 m2Rr m1R2 m2r 2
m1 g
FTB
J1 J2 m1R2 m1Rr J1 J2 m1R2 m2r 2
m2 g
FTA
A aA
PA
FTB
B
aB
PB
r R
FTB
FTA
习题答案
第四章刚体的转动
习题答案
第四章刚体的转动
P144 4-14
已知两物体A、B质量分别为m1和m2,两轮半径分别
为R和r,转动惯量分别为J1和J2.
求两物体的加速度和绳的张力.
r
J1
m1 gR m2 gr J2 m1R2 m2r 2
R
aA
R
J1
m1R m2r J2 m1R2
m2r 2
(1)其角速度减少为初角速度的一半时所需的时间;
(2) 在此时间内转过的圈数.
解: 转动定律 M J
c J d
dt
0 /2 1 d
tc dt
0
0J
ln 2 ct J
t J ln 2 c
习题答案
第四章刚体的转动
P145 4-18 一转动惯量为J的通风机的转动部分绕其轴转动,起初 角速度为w0.设它所受阻力矩与转动角速度成正比, 比例系数c为一常量.求: (1)其角速度减少为初角速度的一半时所需的时间; (2) 在此时间内转过的圈数.
习题答案
第四章刚体的转动
解 (1)系统对z轴的转动惯量
J 2m(l sin )2
系统在t时刻对z轴的角动量
L J 2m(l sin )20 (1 et )
ωz m α 2l
0
方向:铅直向上(或Z轴正向)
(2) 转动的角加速度为
d
dt
0et
在t=0时刻的角加速度为
方向:铅直向上(或Z轴正向)
习题答案
第四章刚体的转动
P147 4-21
在光滑的水平桌面上有一木杆,质量为m1=1.0kg、长 l=40cm,可绕通过其中点且与之垂直的轴转动.一质量为
m2=10g的子弹,以v = 2.0×102 m·s-1的速度射入杆端,方 向与杆及轴正交.若子弹陷入杆中,试求所得到的角速度.
P144 4-14
已知两物体A、B质量分别为m1和m2,两轮半径分别
为R和r,转动惯量分别为J1和J2.
求两物体的加速度和绳的张力.
解 以物体及滑轮所组成的系统
r
为研究对象,运用转动定律.
R
m1gR m2 gr J
J J1 J2 m1R2 m2r 2
B A
J1
m1 gR m2 gr J2 m1R2 m2r 2
O m1,l
m2 v
解
m2 v
l 2
J
[ 1 12
m1l 2
m
2
(
l 2
)2
]
6m 2 v 29.1rad / s
(m1 3m 2 )l
习题答案
第四章刚体的转动
P147 4-22
半径分别为r1和r2的两个薄伞形轮,它们各自对通过盘 心且垂直盘面转轴的转动惯量为J1和J2,开始时轮Ⅰ 以角速度ω0转动,问与轮Ⅱ成正交啮合后,两轮的角速 度分别为多大?
FTA
J1 J1
J2 J2
m2r 2 m2Rr m1R2 m2r 2
m1 g
FTB
J1 J2 m1R2 m1Rr J1 J2 m1R2 m2r 2
m2 g
第四章刚体的转动
r
R
B
FTA
A aA
PA
A
FTB
B
aB
PB
习题答案
第四章刚体的转动
P144 4-15 如图,定滑轮的半径为r,绕轴的转动惯量为J,滑
质量m,半径R的匀质圆盘,以0为中心,挖去半径R 2
一小圆盘.求剩余部分对00轴和0'0'轴的转动惯量.
解:大圆盘对00轴的转动惯量为
0'
0
J 01
1 2
mR2
小圆盘对00轴转动惯量为
R Om 0' 0
J 02
1 2
m2r 2
1 2
m
R2
( R)2(
2
R )2 2
1 32
mR2
剩余部分对00轴的转动惯量
J0
J01
J 02
15 32
mR2
习题答案
P144 4-10
第四章刚体的转动
质量m,半径R的匀质圆盘,以0为中心,挖去半径R 2
一小圆盘.求剩余部分对00轴和0'0'轴的转动惯量.
剩余部分对00轴的转动惯量
J0
J01
J 02
15 32
mR2
0' 0 R Om
0' 0
剩余部分对0'0'轴的转动惯量
解 设相互作用力为F,由角动量定理 ω0
t
t
r1
Fdt
0
0 Fr1dt
J1(1 0 )
t
t
r2
Fdt
0
0 Fr2dt J22
Ⅰ Ⅱ
r11 r22
1
J10r22
J1r22 J2r12
2
J10r1 r2
J1r22 J2r12
习题答案
第四章刚体的转动
解 (1)由刚体的角动量定理
L J0 Mdt Flt 2.0kg.m2.s1
0
(2)棒在转动的过程中,机械能守恒.
θ
1 2
(1 3
ml 2
)02
mg
l 2
(1
cos
)
arccos(1
3F 2t 2 m2 gl )
88038
F ml
习题答案
第四章刚体的转动
c J d J d d J d
dt
dt d
d
d J 0 /2d
0
c 0
J 0
c2
N J0 2 π 4 c
习题答案
第四章刚体的转动
P145 4-19
一长为2l、质量可以忽略的细棒AB,两端分别固定有 质量均为m的小球,棒在外力作用下绕z轴(正向为铅
P147 4-28
我国1970年4月24日发射的第一颗人造卫星沿椭圆
轨道运动,地球的中心O为该椭圆的一个焦点.其近地
点为4.39×105m,远地点为2.38×106m.试计算卫星
J1 mR2
1
0
v R
0
0
mR2 J0 mR2
v R
9.52102 rad
/s
习题答案
第四章刚体的转动
P147 4-27 一质量为1.12kg,长为1.0m的均匀细棒,支点在棒的上 端点,开始时棒自由悬挂.当以100N的力打击它的下端 点,打击时间为0.02s时,(1)若打击前棒是静止的,求 打击时其角动量的变化;(2)棒的最大偏转角.
P147 4-23
一质量为20.0kg的小孩,站在一半径为3.00m、转动
惯量为 450kg·m2的静止水平转台的边缘上,此转台
可绕通过转台中心的竖直轴转动,转台与轴间的摩擦
不计.如果此小孩相对转台以1.00m·s-1的速率沿转台
边缘行走,问转台的角速率有多大?
解:角动量守恒 J00 J11 0
m2r 2
gR
aB
r
J1
m1R m2r J2 m1R2
m2r 2
gr
