非完整移动机器人的有限时间跟踪控制算法研究
基于滑模变结构的移动机器人轨迹跟踪控制

不确定非完整轮式移动机器人的运动控制研究

不确定非完整轮式移动机器人的运动控制研究非完整轮式移动机器人(wheeled mobile robot,WMR)是典型的多输入多输出耦合欠驱动非线性系统, 其运动控制问题极具挑战性。
轮式移动机器人大多工作在复杂未知环境之下, 容易受到多种不确定性和扰动的综合影响, 因此, 解决复杂不确定下非完整轮式移动机器人的运动控制问题意义深刻且现实需求迫切。
本文研究了轮式机器人包含定位不确定性、参数和非参数不确定性、侧滑和打滑干扰等情形下的运动控制策略, 探讨了非完整单链系统的有限时间控制以及力矩受限下轮式移动机器人的动力学控制。
主要的研究成果包括: (1)研究了定位不确定的轮式移动机器人路径跟随问题, 提出一种基于改进遗传算法优化自适应扩展卡尔曼滤波的全局一致渐进稳定控制器。
(2)提出了一类n维不确定非完整单链系统的鲁棒有限时间镇定控制律。
通过不连续变换将原系统分解为1阶和n-1阶两个解耦的独立子系统, 对1阶子系统采用分段控制策略解决不连续变换引起n-1阶子系统奇异问题, 保证控制律的全局性, 对n-1阶子系统采用反演(backstepping)设计方法, 降低设计复杂度, 设计过程基于有限时间Lyapunov理论, 保证系统的有限时间稳定。
(3)研究了本体动力学模型包含参数和非参数不确定性的轮式移动机器人轨迹跟踪问题, 提出基于自适应反演滑模控制的全局渐进稳定饱和控制方案。
通过运动学输入-输出非线性反馈和动力学输入变换, 建立包含系统总体不确定性项的线性模型, 采用一种动态调整机制实现控制输入饱和约束, 基于幂次趋近律提高了滑模控制的平滑性和快速性, 自适应估计总体不确定性的上界有效削弱了滑模控制的抖振现象。
(4)提出了执行器动力学模型包含参数和非参数不确定性的轮式移动机器人轨迹跟踪与镇定统一控制方法。
通过backstepping分别设计系统的运动学、本体动力学和执行器动力学控制器, 运动学控制器引入了时变控制量, 使跟踪误差模型用于镇定控制时不存在奇异, 本体和执行器动力学控制器分别采用带鲁棒项的强化学习自适应模糊控制补偿系统的复杂不确定性, 采用非线性跟踪-微分器避免了backstepping过程的“计算膨胀”, 闭环系统为最终一致有界收敛。
《不确定非完整动力学系统控制研究》

《不确定非完整动力学系统控制研究》作者简介:董文杰,男,1970年12月出生,xx年09月师从于北京航空航天大学霍伟教授,于xx年12月获博士学位。
摘要非完整约束是指含有系统广义坐标导数且不可积的约束。
典型的受非完整约束系统(简称非完整系统)包括车辆、移动机器人、某些空间机器人、水下机器人、欠驱动机器人和运动受限机器人等。
因此,非完整系统的控制研究具有广泛应用背景和重要应用价值。
19世纪末20世纪初在经典力学中已对非完整系统做了基础性研究。
自1960年代以来,科技发展和生产实际的需要促使非完整系统的基础和应用研究都有了进一步发展。
从xx年代末起,由于机器人及车辆控制的需要,使得国外开始对非完整系统的控制问题进行深入研究。
由于非完整约束是对系统广义坐标导数的约束,它不减少系统的位形自由度,这使得系统的独立控制个数少于系统的位形自由度,给其控制设计带来很大困难。
另外,利用非线性控制系统理论的微分几何方法已证明:非完整系统不能用连续的状态反馈镇定。
因此以研究连续状态反馈为主的现代控制理论中大量成熟的结果无法直接用于非完整系统的镇定控制研究,使得非完整控制系统研究成为当今控制领域最具挑战性的难题之一。
国际上xx年代至xx年代中期对非完整系统的控制研究主要是针对由非完整约束方程导出的非完整运动学系统进行的,提出的反馈镇定控制方法主要有时变反馈控制策略、不连续控制策略及以各种方式将二者结合的混合控制策略。
在非完整运动学系统的轨迹跟踪控制研究中,基于不同的分析工具和方法也提出了多种控制方案。
由于实际系统是动力学系统,在对系统性能要求较高的情况下通常不能忽略系统的动力学部分,故基于运动学模型设计出的以广义速度为控制量的控制律不能直接用于以广义力为控制量的实际动力学系统。
因此自xx年代后期起国际上更加注重非完整动力学系统的控制研究,通常采用速度跟踪的思想将对非完整运动学系统设计的控制律推广到非完整动力学系统,这种研究一般依赖于非完整系统的准确动力学模型。
基于解耦控制的非完整移动机器人实时轨迹跟踪

始阶段的误差较大 但能较快地逼近参考轨线 达到
良好的跟踪效果
机器人
年月
图 位置跟踪曲线
ƒ
°
∏√
图 电机 的控制输入
ƒ
≤
∏
5 结论 Χονχλυσιον
本文介绍的非完整移动机器人的实验平台 为 进行各种实时跟踪控制实验 特别是智能控制算法 的研究打下了坚实的基础 在该实验平台上实现的 基于解耦控制算法的实时轨迹跟踪实验的结果表明 了算法和实验平台的可行性 利用该实验平台 可以 进行学习算法! 人工神经网络方法! 遗传算法! 模糊 控制和变结构控制方法等各种高级智能算法的实验 研究
可知 采用如下的解耦算法可达到控制目的
υ υ
ρ
Η
δ Ηβ
≈ζαρεφ
Κε
Η δ Ηβ
3 移 动 机 器 人 的 实 验 平 台 Ε ξπεριμ ενταλ
πλατφορμ οφ μ οβιλε ροβοτ
3 1 总体结构及其驱动 根据实验的需要 我们自行设计和组装了一套
两轮独立驱动! 三轮结构的移动机器人控制实验平 台 如图 两个后轮为驱动轮 分别由两套直流伺服 系统驱动 提供需要的转速或者力矩 前轮为一万向 轮 可以任意移动而不会对机器人产生阻力和约束 作用 这样 只要分别控制两个驱动轮的不同的速度 或者力矩 就可以使机器人按照所要求的方向和速 度移动 从而实现运动规划!稳定以及跟踪等控制任 务
2 男 博士生导师!教授 研究领域 非线性
控制系统理论 机器人控制系统 模式识别与检测
第 卷第 期 年月
机器人 ΡΟΒΟΤ
∂
文章编号
2
22
基于解耦控制的非完整移动机器人实时轨迹跟踪α
池瑞楠 胡跃明 胡终须
不确定非完整轮式移动机器人的运动控制

2023-11-06contents •引言•不确定非完整轮式移动机器人的描述•基于控制策略的设计•实验和结果分析•结论和未来工作目录01引言研究背景不确定非完整轮式移动机器人在许多应用中具有重要意义,如无人驾驶车辆、自主机器人和无人驾驶飞机等。
这些机器人系统通常需要在复杂的动态环境中进行自主导航和操作,因此对它们的运动控制进行研究具有重要意义。
研究意义对于不确定非完整轮式移动机器人,研究其运动控制方法有助于提高机器人的自主性、适应性和鲁棒性,从而使其在各种应用中表现出更好的性能。
研究背景和意义相关工作一在不确定非完整轮式移动机器人的运动控制方面,一些研究者提出了基于模型的控制器设计方法。
这些方法利用机器人的动力学模型进行控制,并考虑了不确定性和非完整性对控制系统性能的影响。
相关工作概述相关工作二另外,一些研究工作致力于开发基于学习的控制方法。
这些方法利用机器学习技术对机器人行为进行学习和预测,并设计相应的控制器以实现稳定和准确的运动控制。
相关工作三还有一些相关工作涉及基于优化方法的运动控制研究。
这些方法通常利用优化算法来优化机器人的运动轨迹和控制信号,以实现最优的运动控制效果。
研究目的和方法研究目的本研究旨在开发一种鲁棒且自适应的运动控制方法,以处理不确定性和非完整性对不确定非完整轮式移动机器人运动控制的影响。
研究方法为了实现这一目标,本研究将采用基于学习的控制方法。
首先,利用机器学习技术对机器人的动力学行为进行学习和建模。
然后,基于学习到的模型设计相应的控制器以实现稳定和准确的运动控制。
02不确定非完整轮式移动机器人的描述非完整轮式移动机器人通常由刚体组成,具有确定的质量和惯性特性。
刚体系统非完整性轮式移动该机器人不具备全方位移动能力,只能在部分方向上实现移动。
该机器人通过轮子进行移动,可以实现在平面上的平移和旋转。
030201非完整轮式移动机器人的动力学特性包括重力、摩擦力、驱动力等。
动力学特性该机器人的运动特性包括速度、加速度、位姿等。
【国家自然科学基金】_避障规划_基金支持热词逐年推荐_【万方软件创新助手】_20140729
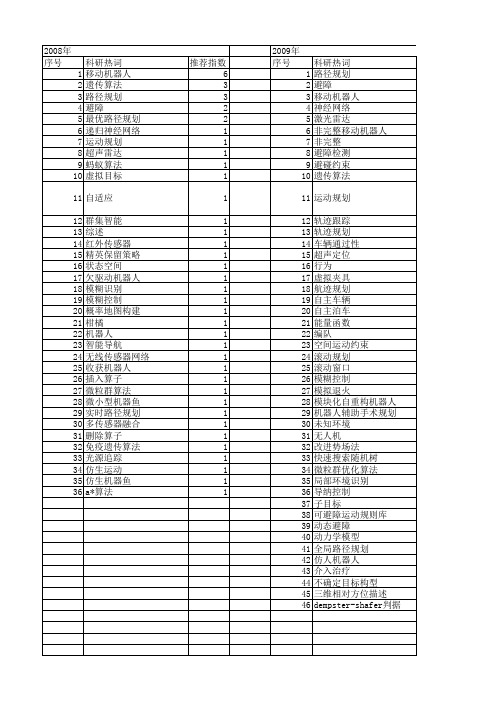
推荐指数 6 3 3 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 机器人 非完整约束 隐性基因 针挠曲 遗传算法 运动规划 运动估计 路径预测 路径规划 视觉检测 视线导航 行走控制 自动泊车 自主导航 立体视觉 目标跟踪 环境二次划分 特征地图 滚装船 模糊控制 机器人辅助针穿刺 机器人视觉 机器人行为 智能车 显性基因 改进camshift算法 悬臂梁 弹道成型制导律 定位 安保机器人 多机器人协同 复杂环境 地形拼接 地图创建 启发式搜索算法 可视化路标 双目光束法平差(bba) 保险矩阵 仿真软件 仿真技术 仿生机器鱼 仿人机器人 人工协调场 surf sift ransac dsmt算法 at89s52 推荐指数 3 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 10 5 3 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80
非完整轮式移动机器人轨迹跟踪控制研究

考虑到机器人运动过程的动力学特性, 如果系统误差比较大, 控制律所产生的控制量
( c , c ) 有可能超出系统的最大速度( max, max ) 或系统的加速度超出系统允许范围( max ,
第3期
非完整轮式移动机器人轨迹跟踪控制 研究
37 9
max ) , 并且系统的速度或加速度太大将会引起机器人运动打滑, 为此, 在控制律中引入如下 控制策略, 从而保证机器人运动平滑.
a1 f ( k c ) ye , e 0. 取 Lyapunov 函数
V=
1 2
x
2 e
+
1 2
y
2 e
+
2 ay
1-
cos
e
2
( 5)
由于 ay > 0, 很明显 V ! 0, 当且仅当( x e , y e , e ) T = 0, V = 0( e ∀ [ - !, !) ) .
由( 4) 式和( 3) 式得:
c
otherw ise
3 实验分析
为了验证算法的有效性, 基于 MATLAB 对算法进行了仿真研究, 仿真过程中, 控制律的 参数选择十分重要, 参数 k 将影响双曲正切函数的平滑程度, 如果 k 值越大则f ∃( k c ) 更快 趋于零, f ( k c) 趋近于 % 1, 从控制律式( 7) 可以发现控制器的调节将变得非常简单. a1, ax 一般改变x 方向误差, ay 改变y 方向误差, a 改变角度误差, 虽然原理上只要 a1 、ax 、ay 、a 均为大于零, 都能保证系统收敛稳定, 但是, 太大的系数会使系统运动振荡较大, 系数太小会 使系统误差收敛速度变慢, 误差调节过程中参数间又是互相影响的. 试验中系统控制参数 ( a1, ax , ay , a , k ) 取为( 1, 2, 0. 2, 2, 5) . 为了保证机器人运动平滑, 我们选取
《2024年非完整移动机器人路径规划与轨迹跟踪控制的研究》范文

《非完整移动机器人路径规划与轨迹跟踪控制的研究》篇一一、引言随着现代机器人技术的快速发展,非完整移动机器人在生产制造、服务型机器人等领域得到了广泛应用。
其高效、精准的路径规划和轨迹跟踪控制技术,成为当前研究的热点。
本篇论文主要研究非完整移动机器人的路径规划方法和轨迹跟踪控制技术,以提高机器人的工作效能和灵活性。
二、非完整移动机器人的特性非完整移动机器人指无法实现任意运动的移动机器人。
这种机器人在结构和功能上往往具备更多的灵活性和可操作空间,但在路径规划和轨迹跟踪方面存在一定限制。
因此,对非完整移动机器人的路径规划和轨迹跟踪控制技术的研究显得尤为重要。
三、路径规划方法研究(一)全局路径规划全局路径规划主要依赖于环境地图信息,通过算法搜索出从起点到终点的最优或次优路径。
常见的全局路径规划算法包括基于图搜索的算法、基于采样的算法等。
这些算法在处理静态环境时效果较好,但在动态环境下需要实时更新地图信息,对计算资源和时间有较高要求。
(二)局部路径规划局部路径规划主要根据机器人当前的感知信息,在局部范围内进行路径规划。
常见的局部路径规划算法包括基于势场的方法、基于学习的方法等。
这些方法能够根据环境变化实时调整路径,但需要机器人具备较高的感知和决策能力。
四、轨迹跟踪控制技术研究轨迹跟踪控制技术是实现机器人精准运动的关键。
常用的轨迹跟踪控制方法包括PID控制、模糊控制、神经网络控制等。
这些方法可以结合机器人的动力学模型和运动学模型,实现对机器人运动的精确控制。
在非完整移动机器人的轨迹跟踪控制中,需要考虑到机器人的运动约束和动力学特性,选择合适的控制方法以实现精准的轨迹跟踪。
五、非完整移动机器人路径规划和轨迹跟踪的融合在实现非完整移动机器人的路径规划和轨迹跟踪时,需要考虑到两者之间的协同作用。
一方面,路径规划为机器人的运动提供全局指导;另一方面,轨迹跟踪控制确保机器人能够按照规划的路径精确运动。
因此,需要将两者融合起来,实现机器人的高效、精准运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
此基础上一些研究者提出了全局的跟踪控制算法. 其中一种是采用一维动态跟踪控制器的方法[4], 由 此得到的闭环系统无奇异点且为全局跟踪, 该方法 要求参考模型角速度不趋于零; 还有利用L yap unov 直接方法和积分 back stepp ing 的方法[5], 该方法对 非完整移动机器人的局部及全局跟踪问题分别进行 了研究, 全局跟踪的前提是参考模型平移速度不趋 于零或参考模型平移速度趋于零时, 参考模型角速 度不趋于零; 文献[ 6 ]对非完整移动机器人的全局跟 踪问题进行了研究, 对满足一定条件的参考模型可
收稿日期: 2004208224; 修回日期: 2004210222. 基金项目: 东南大学优秀青年教师教学科研资助项目. 作者简介: 李世华 (1975—) , 男, 江西萍乡人, 博士, 副教授, 从事机器人控制、混沌控制等研究; 田玉平 (1964—) , 男,
安徽马鞍山人, 教授, 博士生导师, 从事复杂系统控制理论及应用、鲁棒控制等研究.
2 移动机器人问题及模型描述
本文研究对象为轮式移动机器人. 其动力学特
性由下列微分方程描述:
xα= v co s Η, yα= v sin Η, Η= Ξ,
(1)
其中: v 和 Ξ 分别为移动机器人的平移速度和角速
度; (x , y ) 为机器人两轮轴线中心的笛卡儿坐标描
述; Η为其前进方向与 x 轴的夹角. 本文研究机器人
(7)
引理 2[7] 若系统 (6) 是渐近稳定且系统齐次
度小于零, 则该系统为有限时间渐近稳定的.
引理 3[12 ] 假设 f ( t) : R + → R 为可导函数, 且
752
控 制 与 决 策
第 20 卷
当 t → ∞ 时存在有界极限. 若其导数函数可表示成 如下两个函数之和:
Α3) ,
(9)
并且系统 (3) 在有限时间 tΗ内到达 Ξ - Ξr = 0, 即 Ξ
= Ξr.
Step 2: 对系统 (3) 而言, 在 t > tΗ时只需考虑另
外两个状态的控制设计. 注意到此时原系统退化为
系统有限时间控制设计, 选择 Ξ 的控制律为
Ξ = Ξr + k 3 sigΑ3Ηe,
(8)
其中: k 3 > 0, 0 < Α3 < 1, 则有
Ηe = - k 3 sigΑ3Ηe.
因此, 系统 (3) 在有限时间 tΗ 内到达 Ηe = 0, 其中
tΗ =
Ηe (0) k3 (1 -
(1- Α3)
Ηe
0
0 1 Ηr - Η
由此导出的位姿坐标误差模型为
xαe = Ξy e - v + v rco s Ηe, yαe = - Ξx e + v r sin Ηe,
Ηe = Ξr - Ξ.
(3)
3 有限时间跟踪控制器的分步设计
为方便描述, 令函数 sigΑx = x Αsign (x ) , 其中 Α> 0, sign (x ) 为符号函数. 注意到该函数满足下列 性质:
摘 要: 对非完整移动机器人的有限时间轨迹跟踪控制问题进行讨论. 与基于非连续状态反馈的传统有限时间控制 算法相比, 基于连续状态反馈的有限时间控制算法更适合于控制工程应用. 利用该连续系统有限时间控制技术, 设计 一种连续的状态反馈跟踪控制算法. 使得对角速度为非零常数的期望轨迹, 非完整移动机器人能够实现全局跟踪, 并 能在有限时间内完全跟踪上期望轨迹. 仿真结果表明了该方法的有效性. 关键词: 非完整移动机器人; 轨迹跟踪; 有限时间 中图分类号: O 31 文献标识码: A
f (t) = g 1 (t) + g 2 (t) ,
其中 g 1
( t)
为一致连续函数,
并且lim g t→∞
2
( t)
=
0, 则有
lim g
t→∞
1
(
t)
=
0.
考虑到移动机器人的运动学模型特性, 将有限
时间控制技术应用于移动机器人的跟踪控制, 可按
如下步骤进行:
Step 1: 对系统 (3) 的状态 Ηe 按式 (5) 进行一阶
(6)
其中 f (x ) = (f 1 (x ) , …, f n (x ) ) T. 称系统齐次度为
k , 若存在 ( r1, …, rn) , ri > 0, i = 1, …, n , 对任意 Ε>
0, x ∈ R n 满足
f i (Εr1x 1, …, Εrnx n) = Εk+ rif i (x ).
sig1x =
x
,
d dx
x
Α+ 1 =
(Α+
1) sigΑx.
在设计有限时间跟踪控制器之前, 首先给出一
些相关的定义和引理.
引理 1[7] 一阶线性系统
xα= u
(4)
可被下列控制器在有限时间内镇定:
u = - k sigΑx ,
(5)
其中: k > 0, 0 < Α< 1.
实际上该系统有这样的特性: 对初态为 x (0) ≠
0 的状态 x ( t) , 系统 (4) 将在有限时间 ts 内到达 x =
0, 其中 ts = x (0) (1- Α) k (1 - Α). 值得注意的是系
统 (4) 到达原点 (平衡点) 后停留, 即有限时间收敛
到原点.
定义 1[7] 考虑如下非线性系统:
xα= f (x ) , x ∈ R n,
1 引 言
近年来, 非完整系统的控制问题一直受到广泛 的关注[1], 由于机器人技术的广泛应用, 研究非完整 移动机器人的跟踪问题具有重要的工程意义. 关于 跟踪问题, 根据期望点是否为时间的函数可分为轨 迹跟踪和路径跟踪. 本文以非完整移动机器人为主 要研究对象, 讨论其轨迹跟踪控制问题. 早期的非完整移动机器人轨迹跟踪控制方法主 要包括在跟踪误差模型基础上的泰勒线性化或动态 反馈线性化等方法[2, 3], 得到的是局部跟踪结果. 在
Abstract: T he fin ite2tim e tra jecto ry track ing con tro l p rob lem of a nonho lonom ic m ob ile robo t is discu ssed. In con tract to traditiona l fin ite tim e con tro l a lgo rithm s ba sed on non2con tinuou s feedback s, the fin ite tim e con tro l a lgo rithm s ba sed on con tinuou s feedback s a re m o re su itab le fo r app lica tion to con tro l engineering. U sing fin ite tim e con tro l techn iques fo r con tinuou s system s, a con tinuou s sta te feedback con tro l law fo r tra jecto ry track ing is develop ed. T he p ropo sed con tro l law can gua ran tee tha t the m ob ile robo t w ill track the desired tra jecto ry in the globa l sen se a s w ell a s in fin ite tim e w hen the desired ro ta te velocity is a nonzero con stan t. Sim u la tion resu lts show the effectiveness of the m ethod. Key words: N onho lonom ic m ob ile robo t; T ra jecto ry track ing; F in ite tim e
F in ite T im e Track ing Con trol A lgor ithm for Nonholonom ic M ob ile Robots
L I S h i2hua, T IA N Y u 2p ing
(D ep a rtm en t of A u tom a tic Con tro l, Sou thea st U n iversity, N an jing 210096, Ch ina. Co rresponden t: L I Sh i2hua, E2m a il: lsh@ seu. edu. cn)
第 20 卷 第 7 期
V o l. 20 N o. 7
控 制 与 决 策
C on trol and D ecision
2005 年 7 月
J u ly 2005
文章编号: 100120920 (2005) 0620750205
非完整移动机器人的有限时间跟踪控制算法研究
李世华, 田玉平
(东南大学 自动控制系, 南京 210096)
第7期
李世华等: 非完整移动机器人的有限时间跟踪控制算法研究
751
以实现全局指数跟踪. 在上述的轨迹跟踪控制系统研究结果中, 最好 的收敛性能是跟踪误差指数收敛于零, 因此这些控 制方法均属于无限时间控制问题, 即系统在无穷大 时间才能真正跟踪上参考轨迹. 从控制系统时间优 化的角度来看, 有限时间收敛的控制方法才是时间 最优的控制方法. 所谓有限时间控制问题是指能否 在有限时间内将系统控制到平衡点. 研究表明, 在系 统具有干扰和不确定情况下, 有限时间收敛的系统 往往具有更好的性能[7]. 但由此带来的一个问题是 有限时间控制器的设计和稳定性分析更为复杂. 关于有限时间控制器设计的方法有开环控制、 非连续反馈和连续反馈控制方法. 开环控制在实际 应用中局限很大; 以 bang2bang 控制为代表的非连 续反馈方法可以实现有限时间收敛, 但控制器不易 实现, 系统易产生抖动. 因此, 采用连续状态反馈是 值得关注和研究的一类方法. 但此时有限时间系统 对应的是分数幂的微分方程, 而目前关于分数幂非 线性微分方程的理论结果和分析工具很少, 因此进 行这方面的研究难度很大. 目前有限时间控制方法研究的对象主要局限在 低阶线性系统和特殊结构的非线性系统等. 文献[ 8 ] 提出一种终端滑动模态的有限时间控制设计方法, 缺点是二阶系统的终端滑动模态设计存在奇异情 况. [ 7 ]采用齐次系统的分析方法, 解决了二阶线性 系统的全局有限时间控制问题, 并给出了非线性自 治系统的有限时间稳定性定理. [ 9 ]针对 n 阶线性系 统和特殊形式的非线性系统, 提出一种有限时间控 制器设计方法, 遗憾的是为了实现有限时间控制, 必 须估计出控制器增益的取值范围. 近期, 作者提出了一些有限时间跟踪控制方法. 对参考模型角速度不为零的情况, 文献[ 10 ]利用[ 8 ] 的终端滑动模态方法设计一种有限时间控制律, 缺 点是控制律存在奇异, 必须采取附加的控制绕开奇 异点; 对同样的问题, 文献[ 11 ]利用[ 7 ]中二阶系统 有限时间技术, 结合反馈线性化技术, 实现了非完整 移动机器人在有限时间内对参考轨迹的完全跟踪, 且控制器没有奇异. 但文[ 10, 11 ]中的方法只是得到 了误差模型有限时间收敛结果, 没有给出全局有限 时间稳定性的分析和证明. 本文则针对非完整移动 机器人特点, 考虑参考模型角速度为非零常数情况, 提出了连续有限时间跟踪控制律, 并利用文献[ 7 ]的 齐次系统有限时间稳定定理证明了闭环系统的全局 有限时间稳定性. 对满足一定假设条件的角速度不 趋于零的期望轨迹, 非完整移动机器人能够实现全 局跟踪, 并在有限时间内完全跟踪上期望轨迹.
