半导体物理总复习
半导体物理复习梳理
第一章填空题：1、 写出三种立方单胞的名称：简立方，体心立方，面心立方；这三种单胞中所含的原子数分别是1，2，42、 在四面体结构的共价晶体中，四个共价键是以s 态和p 态波函数的线性组合为基础，构成了所谓的“杂化轨道”。
3、 金刚石型结构的结晶学原胞是立方对称的晶胞。
4、 闪锌矿结构的Ⅲ-Ⅴ族化合物和金刚石型结构一样，都是由两个面心立方晶格套构而成的，称这种晶格为双原子复式格子。
5、 纤锌矿型结构和闪锌型结构相接近，它也是以正四面体结构为基础构成的，但是它具有六方对称性。
6、 内壳层的电子，轨道交叠少，共有化运动弱，可忽略。
外层的价电子，轨道交叠多，共有化运动强，能级分裂大，被视为“准自由电子”。
7、 原来简并的N 个原子的s 能级，结合成晶体后分裂为N 个十分靠近的能级，形成能带(允带)，因N 值极大，能带被视为“准连续的”。
8、 Si 、Ge 具有一般晶体的共性，又有其特殊性：其能级分裂成能带时，存在轨道杂化。
9、 如图，当 时，形成稳定晶体，上下两带的状态数（各4N 个）不变,根据能量最小原理，低温下，下带填4N 个价电子是满的，称为满带或价带；而上带4N 个状态无电子是空的，称为导带；中间隔以禁带。
10、 在周期性势场内，电子的平均速度v 可表示为波包的群速度。
在能带极值附近的电子速度为：11、 半导体中电子在外加电场作用下，电子的加速度为：12、 半导体中除了导带上电子导电作用外，价带中还有空穴的导电作用。
对本征半导体，导带中出现多少电子，价带中相应地就出现多少空穴，导带上电子参与导电，价带上空穴也参与导电，这就是本征半导体的导电机构。
13、当磁场不变时，加高频电场Cw 垂直磁场，当电场频率B w =Cw 时，可观察到吸收峰，吸收峰的个数等于有效质量的个数。
14、 为了观察到明显的共振吸收峰, 要求半导体样品比较纯净, 而且一般是在低温下进行。
15、 右图为GaAs 的能带结构。
半导体物理复习归纳
半导体物理复习归纳————————————————————————————————作者: ————————————————————————————————日期:一、半导体的电子状态1、金刚石结构（Ｓi、Ge）Si、Ge原子组成，正四面体结构，由两个面心立方沿空间对角线互相平移１/４个空间对角线长度套构而成。
由相同原子构成的复式格子。
2、闪锌矿结构（GaAｓ)３-5族化合物分子构成，与金刚石结构类似,由两类原子各自形成的面心立方沿空间对角线相互平移1/４个空间对角线长度套构而成。
由共价键结合,有一定离子键。
由不同原子构成的复式格子。
3、纤锌矿结构（ＺnＳ)与闪锌矿结构类似，以正四面体结构为基础,具有六方对称性,由两类原子各自组成的六方排列的双原子层堆积而成。
是共价化合物，但具有离子性，且离子性占优。
4、氯化钠结构（NaＣl)沿棱方向平移1／2,形成的复式格子。
5、原子能级与晶体能带原子组成晶体时,由于原子间距非常小,于是电子可以在整个晶体中做共有化运动，导致能级劈裂形成能带。
6、脱离共价键所需的最低能量就是禁带宽度。
价带上的电子激发为准自由电子，即价带电子激发为导带电子的过程,称为本征激发。
7、有效质量的意义a.有效质量概括了半导体内部势场的作用（有效质量为负说明晶格对粒子做负功)b.有效质量可以直接由实验测定c.有效质量与能量函数对于k的二次微商成反比。
能带越窄,二次微商越小，有效质量越大。
8、测量有效质量的方法回旋共振。
当交变电磁场角频率等于回旋频率时,就可以发生共振吸收。
测出共振吸收时电磁波的角频率和磁感应强度,就可以算出有效质量。
为能观测出明显的共振吸收峰，要求样品纯度较高,且实验要在低温下进行。
9、空穴价带中空着的状态被看成带正电的粒子，称为空穴。
这是一种假想的粒子，其带正电荷+q，而且具有正的有效质量m p＊。
10、轻／重空穴重空穴:有效质量较大的空穴轻空穴：有效质量较小的空穴11、间接带隙半导体导带底和价带顶处于不同k值的半导体。
半导体物理复习资料
第一章 半导体中的电子状态1.导体、半导体、绝缘体的划分：Ⅰ导体内部存在部分充满的能带，在电场作用下形成电流；Ⅱ绝缘体内部不存在部分充满的能带，在电场作用下无电流产生； Ⅲ半导体的价带是完全充满的，但与之上面靠近的能带间的能隙很小，电子易被激发到上面的能带，使这两个能带都变成部分充满，使固体导电。
2.电子的有效质量是*n m ，空穴的有效质量是*p m ；**np m m -=，电量等值反号，波矢k 与电子相同 能带底电子的有效质量是正值，能带顶电子的有效质量是负值。
能带底空穴的有效质量是负值，能带顶空穴的有效质量是正值。
3.半导体中电子所受的外力dtdkh f ⋅=的计算。
4.引进有效质量的意义：概括了半导体内部势场的作用，使得在解决半导体中电子在外力作用下的运动规律时，可以不涉及半导体内部势场的作用。
第二章 半导体中杂质和缺陷能级1.施主能级：被施主杂质束缚的电子的能量状态称为施主能级E D ；施主能级很接近于导带底；受主能级：被受主杂质束缚的空穴的能量状态称为受主能级E A ；受主能级很接近于价带顶。
施主能级图 受主能级图2.浅能级杂质：杂质的电离能远小于本征半导体禁带宽度的杂质，电离后向相应的能带提供电子或空穴。
深能级杂质：能级位于禁带中央位置附近，距离相应允带差值较大。
深能级杂质起复合中心、陷阱作用；浅能级杂质起施主、受主作用。
3.杂质的补偿作用：半导体中同时含有施主和受主杂质，施主和受主先相互抵消，剩余的杂质发生电离。
在Ⅲ-Ⅴ族半导体中(Ga-As )掺入Ⅳ族杂质原子(Si )，Si 为两性杂质，既可作施主，亦可作受主。
设315100.1-⨯=cm N A ，316101.1-⨯=cm N D ；则316100.1-⨯=-=cm N N n A D 由p n n i ⋅=2，可得p 值；①p n ≈时，近似认为本征半导体，i F E E =；②p n μμ=时，本征电导p n σσ=； p n >>时，杂质能级靠近导带底；第三章 半导体中载流子的统计分布1.费米分布函数(简并半导体)⎪⎪⎭⎫ ⎝⎛⋅-+=Tk E E E f F 0exp 11)((本征)；⎪⎪⎭⎫ ⎝⎛⋅-+=T k E E E f F 0exp 2111)((杂质)；玻尔兹曼分布函数(非简并半导体) ⎪⎪⎭⎫ ⎝⎛⋅-=T k E A E f B0exp )(；2.费米能级：TF N F E ⎪⎭⎫⎝⎛∂∂==μ；系统处于热平衡状态，也不对外界做功的情况下，系统中增加一个电子所引起系统自由能的变化，等于系统的化学势，也就是等于系统的费米能级。
半导体物理总复习
隧道效应
单独的N型和P型半导体是电中性的,当这两 对于P型半导体和N型半导体结合面附近 种半导体结合形成PN结时，将在N型半导体和P 的电离施主和电离受主所带电荷称为空间电 型半导体的结合面上形成如下物理过程: 荷，它们所在的区域称为空间电荷区。 在空间电荷区，由于缺少多子，所以也 因浓度差 称耗尽层。 多子的扩散运动 由杂质离子形成空间电荷区 空间电荷区形成内建电场 内建电场促使少子漂移 内建电场阻止多子扩散
本征半导体： 不含杂质且结构非常完整的单晶半导体。 本征激发： 共价键上的电子激发成为准自由电子，亦即价带电子吸收能量被激发到 导带成为导带电子的过程，称为本征激发
有效质量的特点
决定于材料； E ② mn*只在能带极值附近有意义; ③ mn*可正可负; 在能带底部附近，E(k)曲线开口向上，d2E/dk2>0， mn*>0; 0 在能带顶部附近，E(k)曲线开口向下， 1/2 v a d2E/dk2<0， mn*<0; ④ mn*大小与能带宽窄有关; 0 内层:能带窄, d2E/dk2小, mn*大； 外层:能带宽, d2E/dk2大, mn*小. mn 因而，外层电子在外力作用下可以获得 + * 较大的加速度。 ⑤ 对于带顶和带底的电子,有效质量恒定。 0
本征区
● 饱和电离区的确定
载流子浓度随温度、掺杂浓度的变化规律 费米能级位置随温度、掺杂浓度的变化情况
图3-3、3-7、3-10、3-11、3-13、3-14、3-15
第四章
一、电导率、迁移率、电导率和平均自由 时间的关系 二、载流子的散射
1.电离杂质的散射：低温、掺杂浓度高 2.晶格散射：高温、掺杂浓度低
高度补偿：若施主杂质浓度与受主杂质浓度相差不大或二者相等，则不能提 供电子或空穴，这种情况称为杂质的高等补偿。
半导体物理_复习总结(刘恩科)
半导体物理
准费米能级
当半导体处于非平衡状态，不再具有统一的费米能 级，引入准费米能级
非平衡态下电子浓度：
n
ni
exp
Ei EFn k0T Βιβλιοθήκη 非平衡态下空穴浓度：p
ni
exp
Ei EFp k0T
以及其他大量电子的平均势场中运动，这个势场也是周期变化的， 并且它的周期与晶格周期相同。
半导体物理
半导体中的电子运动
半导体中E(k)与k的关系
电子速度与能量关系
电子有效质量
mn*
h2 d2E
dk 2
半导体物理
有效质量的意义：
f
a
1、概括了半导体内部势场 的作用 2、a是半导体内部势场和 外电场作用的综合效果 3、直接将外力与电子加速 度联系起来
(1) VG<0，多子积累 •绝对值较大时，，空穴聚集表面， C＝C0，AB段（半导体看成导通） •绝对值较小时，C0和Cs串联，C随 V增加而减小，BC段 (2)VG＝0 CFB－表面平带电容 (3) VG>0 •耗尽状态：VG增加，xd增大，Cs减小，CD段 •Vs>2VB时： EF段（低频）强反型，电子聚集表面， C＝C0 GH段（高频）：反型层中电子数量不能随高频信号而变，对电容无贡献， 还是由耗尽层的电荷变化决定（强反型达到xdm不随VG变化，电容保持最小 值）；GH段
玻尔兹曼分布函数
条件：E-EF>>k0T EEF
fB E e k0T
费米统计分布：受到泡利不相容原理限制 玻尔兹曼分布：泡利原理不起作用
半导体物理学复习
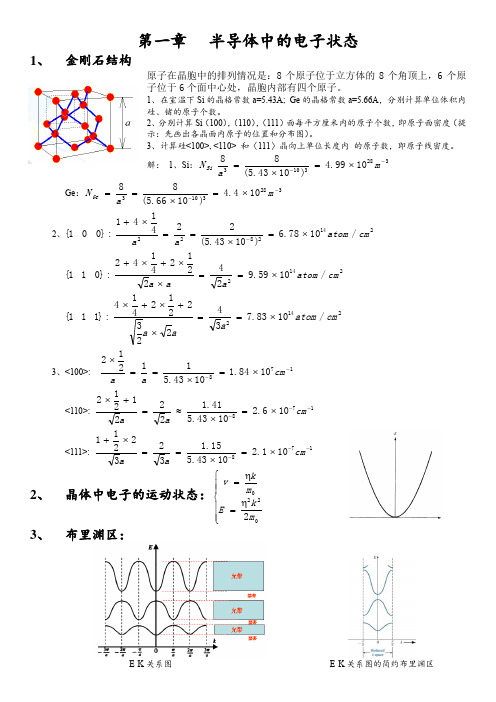
1、 金刚石结构
半导体中的电子状态
原子在晶胞中的排列情况是：8 个原子位于立方体的 8 个角顶上，6 个原 子位于 6 个面中心处，晶胞内部有四个原子。
1、在室温下 Si 的晶格常数 a=5.43A; Ge 的晶格常数 a=5.66A，分别计算单位体积内 硅、锗的原子个数。 2、 分别计算 Si （100） ， （110） ， （111） 面每平方厘米内的原子个数， 即原子面密度 （提 示：先画出各晶面内原子的位置和分布图） 。 3、计算硅<100>, <110>和〈111〉晶向上单位长度内的原子数，即原子线密度。 解： 1、Si： N Si Ge： N Ge
3、n 型半导体载流子浓度
ND E - ED 1 + 2 exp( F ) k0T ① 低温弱电离区：当温度很低时，大部分施主杂质被电子占据，只有少数杂质电离，使少量电 E - EF ND + )= = nD 子进入导带，称作低温弱电离： n0 = N C exp( - C E E k0T F 1 + 2 exp( - D ) k0T 1/ 2 1/ 2 N D NC EC ED N D NC ΔED EC + ED k0T ND exp( )= exp( ) 得到： EF = + ln( ) n0 = 2 2k0T 2 2k0T 2 2 2 NC N C exp(
8
a
3
8 4.99 10 28 m 3 10 3 (5.43 10 )
2、{1 0
{1 1
{1 1
3、<100>:
<110>:
<111>:
8 4.4 10 28 m 3 10 3 a (5.66 10 ) 1 14 2 4 2 0} : 6.78 10 14 atom / cm 2 2 2 8 2 a a (5.43 10 ) 1 1 2 4 2 4 2 4 9.59 10 14 atom / cm 2 0} : 2a a 2a 2 1 1 4 2 2 4 4 2 1} : 7.83 10 14 atom / cm 2 2 3 3a a 2a 2 1 2 1 2 1 1.84 10 7 cm 1 8 a a 5.43 10 1 2 1 2 1.41 2 2.6 10 7cm 1 8 5 . 43 10 2a 2a 1 1 2 2 1.15 2 2.1 10 7cm 1 8 5.43 10 3a 3a
半导体物理复习资料全
第一章 半导体中的电子状态1. 如何表示晶胞中的几何元素？规定以阵胞的基矢群为坐标轴，即以阵胞的三个棱为坐标轴，并且以各自的棱长为单位，也称晶轴。
2. 什么是倒易点阵（倒格矢）？为什么要引入倒易点阵的概念？它有哪些基本性质？ 倒格子： 2311232()a a b a a a π⨯=⋅⨯3122312()a a b a a a π⨯=⋅⨯1233122()a a b a a a π⨯=⋅⨯倒格子空间实际上是波矢空间，用它可很方便地将周期性函数展开为傅里叶级数，而傅里叶级数是研究周期性函数的基本数学工具。
3. 波尔的氢原子理论基本假设是什么？（1）原子只能处在一系列不连续的稳定状态。
处在这些稳定状态的原子不辐射。
（2）原子吸收或发射光子的频率必须满足。
（3）电子与核之间的相互作用力主要是库仑力，万有引力相对很小，可忽略不计。
（4）电子轨道角动量满足：h m vr nn π== 1,2,3,24. 波尔氢原子理论基本结论是什么？ （1） 电子轨道方程：0224πεe r mv = （2） 电子第n 个无辐射轨道半径为：2022meh n r n πε= （3） 电子在第n 个无辐射轨道大巷的能量为：222042821hn me mv E n n ε== 5. 晶体中的电子状态与孤立原子中的电子状态有哪些不同？（1）与孤立原子不同，由于电子壳层的交迭，晶体中的电子不再属于某个原子，使得电子在整个晶体中运动，这样的运动称为电子共有化运动，这种运动只能在相似壳间进行，也只有在最外层的电子共有化运动才最为显著。
（2）孤立原子钟的电子运动状态由四个量子数决定，用非连续的能级描述电子的能量状态，在晶体中由于电子共有化运动使能级分裂为而成能带，用准连续的能带来描述电子的运动状态。
6. 硅、锗原子的电子结构特点是什么？硅电子排布：2262233221p s p s s锗电子排布：22106262244333221p s d p s p s s价电子有四个：2个s 电子，2个p 电子。
半导体物理总复习
能带论 共有化运动 电子/空穴 有效质量
杂质能级（施主、受主） E EF c k0T
n0 = Nc exp
p0 = Nv exp
E EF
k 0T
v
分本征、杂质半导体两种情况讨论（变化规律的物理图像） 简并半导体及其禁带变窄效应
n0p0 = ni2
Chapter 3
外场作用下载流子的运动规律
11/98
12/98
13/98
18/98
19/98
20/98
21/98
22/98
23/98
2
半导体中载流子的统计分布
本章内容提要
n n n
热平衡状态，状态密度 费米能级与分布函数 电中性方程 载流子浓度 Vs 温度
n
n
简并半导体
24/98
产生载流子（本征激发/杂质电离）
电子由低能态向高能态跃迁
EF p < EF
n = Nc exp
p = Nv exp np = n0p0 exp
空穴准费米能级比平衡费米能级低
Ec EF n k0T
p E F Ev k0T
EF EF = ni exp = n0 exp k0T = p0 exp EF EFp k0T
n p
n
n
EF Ei
陷阱中心的特点
复合中心：
rn 能 rp 够俘获两种不同载流子而复合掉
而陷阱中心对两种载流子的俘获能力必然相差很大
Nt
越大，陷阱作用最强
杂质能级与平衡时的费米能级重合时，陷阱作用最强
61/98
5
p-n结
本章内容提要
n n n n
p-n结的形成及其能带图 p-n结伏安特性 p-n结电容 p-n结击穿 p-n结隧道效应
半导体物理--复习版
2012-9-7
4
2. 多电子原子
对多电子原子，电子能量同样是不连续的。由主量子 数、角量子数、磁量子数、自旋量子数描述。
2012-9-7
5
二、自由电子状态（一维）
一维恒定势场中的自由电子，遵守薛定谔方程
2
0
d ψ(x) dx
2
2
V ψ (x) E ψ (x)
k z
2m
z
E Ec
2
k 0z
2
1
2012-9-7
28
上式是一个椭球方程，各分母等于椭球的各个半轴长的平方，
这种情况下的等能面是环绕极值点k0的一系列的椭球面。其中
1 mx
* 2 1 E 2 2 k x
k0
内层电子占据了比较窄的满带，这些电子的有效质量mn* 比较大，外力作用下不易运动；
而价电子所处的能带较宽，电子的有效质量mn*较小，在
外力的作用下可以获得较大的加速度。
2012-9-7
25
六、k空间等能面
不同半导体的E(k)~k关系各不相同。即便对于同一种半 导体，沿不同k方向的E(k)~k关系也不相同。换言之，半 导体的E(k)~k关系可以是各向异性的。
k x k 0x E ( k ) Ec 2 mx
2
2
k
y
k 0y m
y
2
k z
k 0z mz
2即Biblioteka k x2m* x
E Ec
2
半导体物理复习资料
半导体物理复习资料一．填空题1.半导体中的载流子主要受到两种散射，它们分别是电离杂质散射和晶格震动散射。
2.纯净半导体Si中掺杂Ⅴ族元素，当杂质电离时释放电子。
这种杂质称施主杂质；相应的半导体称N型半导体。
3.当半导体中载流子浓度的分布不均匀时，载流子将做扩散运动；在半导体存在外加电压情况下，载流子将做漂移运动。
4.n0p0=n i2标志着半导体处于热平衡状态，当半导体掺入的杂质含量改变时，乘积n0p0是否改变？不改变；当温度变化时，n0p0改变否？改变。
5.硅的导带极小值位于布里渊区<100>方向上，根据晶体对称性共有6个等价能谷。
6.n型硅掺As后，费米能级向E C或上移动，在室外温度下进一步升高温度，费米能级向E i或下移动。
7.半导体中的陷阱中心使其中光电导灵敏度增加，并使其光电导衰减规律衰减时间延长。
8.若用氢取代磷化镓中的部分磷，结果是禁带宽度E g增大；若用砷的话，结果是禁带宽度E g减小。
9.已知硅的E g为1.12Ev，则本征吸收的波长限为1.11微米；Ge的E g为0.67eV，则本征吸收的波长限为1.85微米。
10.复合中心的作用是促进电子和空穴的复合，起有效复合中心的杂质能级必须位于E1或禁带中心线，而对电子和空穴的俘获系数r n或r p必须满足r n=r p。
11.有效陷阱中心位置靠近E F或费米能级。
12.计算半导体中载流子浓度时，不能使用玻尔兹曼统计代替费米统计的判定条件E c-E F≤2k0T以及E F-E V≤2k0T，这种半导体被称为简并半导体。
13.PN结电容可分为扩散电容和势垒电容两种。
14.纯净半导体Si中掺杂Ⅲ族元素的杂质，当杂质电离时在Si晶体的共价键中产生了一个空穴，这种杂质称受主杂质；相应的半导体称P型半导体。
15.半导体产生光吸收的方式本征、激子、杂质、晶格振动、半导体吸收光子后产生载流子，在均匀半导体中是电导率增加，可制成光敏电阻；在存在自建电场的半导体中产生光生伏特，可制成光电池；光生载流子发生辐射复合时，伴随着发射光子，这就是半导体的发光现象，利用这种现象可制成发光管。
半导体物理知识点汇总总结
半导体物理知识点汇总总结一、半导体物理基本概念半导体是介于导体和绝缘体之间的材料，它具有一些导体和绝缘体的特性。
半导体是由单一、多层、回交或互相稀释的混合晶形的二元、三元或多元化合物所组成。
它的特点是它的电导率介于导体和绝缘体之间，是导体的电导率∗101~1015倍，是绝缘体的电导率÷102~103倍。
半导体材料具有晶体结构，对它取决于结晶度的大小，织排效应特别大。
由于它的电导率数值在半导体晶体内并不等同，所以它是隔离的，具有相当大的飞行束度，并且不容易受到外界的干扰。
二、半导体晶体结构半导体是晶体材料中最均匀最典型的材料之一，半导体的基本结构是一个由原子排成的一种规则有序的晶体结构。
半导体原子是立方体的晶体，具有600个原子的立方体晶体结构，又称之为立方的晶体结构。
半导体晶体结构的代表性六面体晶体结构，是一种由两个或两个以上的六面全部说构成的立方晶体。
半导体晶体的界面都是由两个或两个以上的六面全部说构成的晶体包围构成，是由两个或两个以上的六面全部说构成的立方晶体。
半导体晶体的界面都是由两个或两个以上的六面全部说构成的晶点构成，是由两个或两个以上的六面全部说构成的晶点构成。
三、半导体的能带结构半导体的能带“带”是指其电子是在“带”中运动的，是光电子带，又称作价带，当其中的自由电子都填满时另一种平面，又称导电带，当其中的自由电子并不填满时其另一种平面在有一些能够使电子轻易穿越的东西。
半导体的能带是由两个非常临近的能带组成的，其中价带的最上一层电子不足，而导电带的下一层电子却相当到往动能，这一些动能可能直到加到电子摆脱它自己体原子，变成自由电子，并且在整体晶体里自由活动。
四、半导体的导电机理半导体的导电机理是在外加电压加大时一部分自由电子均可以在各自能带中加速骚扰，从而增加在给导电子处所需要的电压增大并最终触碰到另一种平面上产生电流就可以。
五、半导体的掺杂掺杂是指在纯净半导体中加入某些以外杂质元素的行为。
半导体物理总复习
f外 m a
* n
（3）电子的有效质量与晶体的能带结构有关
h2 m 2 d E dk 2
* n
利用有效质量可以对半导体的能带结构进 行研究 （4）有效质量可以通过回旋共振实验测得，并 椐此推出半导体的能带结构
4.空穴：空穴是几乎被电子填满的能带中未被电子占据的
少数空量子态，这少量的空穴总是处于能带顶附近。是价
高温本征激发区
n0= p0=ni
EF=Ei
费米能级仍用前面的公式得到EF=Ei
例题1 （同类型题103页1题）
导出能量在Ec和Ec+kT之间时，导带上的有效状 态总数（状态数/cm3)的表达式， 是任意常数。
例题2
（a)在热平衡条件下，温度T大于0K，电子能量位于费米 能级时，电子态的占有几率是多少？
n p 中处于准平衡分布，可以有各自的费米能级 E F 和E F
称为准费米能级，准费米能级分离的程度，即
n p 的大小，反映了与平衡态分离的程度 EF EF
4. 解释载流子的产生和复合，直接复合，间接复合，复合率
产 生：电子和空穴被形成的过程，如电子从价带跃迁到导 带，或 电子从杂质能级跃迁到导带的过程或空穴从 杂质能级跃迁到价带的过程 复 合：电子和空穴被湮灭或消失的过程
MIN
0
所以布里渊区边界为
k (2n 1)
a
（n=0，1，2……）
1.能带宽度为
E（k ) MAX E (k ) MIN
2 2 ma 2
2电子在波矢k状态的速度
1 dE 1 v (sin ka sin 2ka) dk ma 4
3、电子的有效质量 能带底部
半导体物理复习
半导体物理基础 总复习
掌握熟悉了解第一章半导体物理基础一、能带理论1、能带的形成、结构：导带、价带、禁带•当原子结合成晶体时，原子最外层的价电子实际上是被晶体中所有原子所共有，称为共有化。
•共有化导致电子的能量状态发生变化，产生了密集能级组成的准连续能带---能级分裂•价带：绝对0度条件下被电子填充的能量最高的能带；结合成共价键的电子填充的能带。
•导带：绝对0度条件下未被电子填充的能量最低的能带2、导体、半导体、绝缘体的能带结构特点•禁带的宽度区别了绝缘体和半导体；而禁带的有无是导体和半导体、绝缘体之间的区别；绝缘体是相对的，不存在绝对的绝缘体。
3、导电的前提：不满带的存在二、掺杂半导体1、两种掺杂半导体的能级结构。
2、杂质补偿的概念三、载流子统计分布1、费米函数、费米能级：公式1-7-9和1-7-10，及其简化公式1-7-11和1-7-122、质量作用定律，只用于本征半导体：公式1-7-273、用费米能级表示的载流子浓度：公式1-7-28和1-7-294、杂质饱和电离的概念（本征激发）5、杂质半导体费米能级的位置：公式1-7-33和1-7-37。
意义（图1-13，费米能级随着掺杂浓度和温度的变化）。
6、杂质补充半导体的费米能级四、载流子的运输1、（1.8节）载流子的运动模式：散射－漂移－散射。
平均弛豫时间的概念2、迁移率，物理意义：公式1-9-4和1-9-5（迁移率与电子自由运动时间和有效质量有关），迁移率与温度和杂质浓度的关系3、电导率，是迁移率的函数：公式1-9-10和1-9-114、在外电场和载流子浓度梯度同时存在的条件下，载流子运输公式：1-9-24～1-9-275、费米势：公式1-10-5：电势与费米能级的转换6、以静电势表示的载流子浓度1-10-6和1-10-7或1-10-9和1-10-107、爱因斯坦关系：反映了扩散系数和迁移率的关系。
在非热平衡状态下也成立。
公式1-10-11和1-10-12 五、非平衡载流子1、概念：平衡与非平衡（能带间的载流子跃迁）；过剩载流子2、大注入和小注入3、产生率、复合率、净复合率4、非平衡载流子的寿命：从撤销外力，到非平衡载流子消失。
半导体物理学期末总复习
半导体中的热平衡态
载流子的扩散
在半导体中，不同区域的载流子浓度不同，浓度高的区域的载流子会向浓度低的区域扩散，这种现象称为载流子的扩散。
载流子的漂移
当半导体中存在电场时，载流子会受到电场力的作用，从高电场强度区域向低电场强度区域移动，这种现象称为载流子的漂移。
载流子的输运过程
在半导体中，载流子的浓度分布取决于载流子的产生、复合、扩散、漂移等过程的综合作用。
太阳能电池
利用半导体物理器件的能带结构，可以制造出高效的太阳能电池。
半导体物理器件在新能源和环境中的应用
风能发电装置
利用半导体物理器件的高频特性，可以制造出高效的风能发电装置。
水质监测和污水处理
利用半导体物理器件的化学传感器作用，可以制造出用于水质监测和污水处理中的传感器。
THANK YOU.
谢谢您的观看
04
半导体的光学性质
光吸收
半导体对光的吸收主要取决于材料中的电子和原子结构。在光子能量大于或等于半导体带隙时，光子会被吸收并产生电子-空穴对。
光发射
光发射是半导体中电子从束缚态跃迁到自由态并辐射出光子的过程。光发射的能量与带隙密切相关，带隙越大，发射光的能量越高。
半导体中的光吸收与光发射
光电效应
5G和6G通信技术
随着5G和6G通信技术的不断发展，现代半导体器件需要适应更高的频率和更复杂的通信协议。
半导体物理器件在集成电路中的应用
存储器
半导体物理器件还可以应用于存储器中，例如动态随机存储器和闪存等。
传感器
半导体物理器件还可以应用于传感器中，例如光传感器、温度传感器和压力传感器等。
微处理器
半导体物理器件在集成电路中的应用最为广泛，其中微处理器是其中的代表。
半导体物理学复习提纲(重点)
第一章 半导体中的电子状态§ 锗和硅的晶体结构特征 金刚石结构的基本特征§ 半导体中的电子状态和能带 电子共有化运动概念绝缘体、半导体和导体的能带特征。
几种常用半导体的禁带宽度； 本征激发的概念§ 半导体中电子的运动 有效质量导带底和价带顶附近的E(k)~k 关系()()2*2nk E k E m 2h -0=； 半导体中电子的平均速度dEv hdk=； 有效质量的公式：222*11dk Ed h m n =。
§本征半导体的导电机构 空穴空穴的特征：带正电；p n m m **=-；n p E E =-；p n k k =-§ 回旋共振§ 硅和锗的能带结构 导带底的位置、个数； 重空穴带、轻空穴第二章 半导体中杂质和缺陷能级§ 硅、锗晶体中的杂质能级基本概念：施主杂质，受主杂质，杂质的电离能，杂质的补偿作用。
§ Ⅲ—Ⅴ族化合物中的杂质能级 杂质的双性行为第三章 半导体中载流子的统计分布热平衡载流子概念§状态密度定义式：()/g E dz dE =；导带底附近的状态密度：()()3/2*1/232()4n c c m g E VE E h π=-；价带顶附近的状态密度：()()3/2*1/232()4pv Vm g E V E E hπ=-§ 费米能级和载流子的浓度统计分布 Fermi 分布函数：()01()1exp /F f E E E k T =+-⎡⎤⎣⎦；Fermi 能级的意义：它和温度、半导体材料的导电类型、杂质的含量以及能量零点的选取有关。
1）将半导体中大量的电子看成一个热力学系统，费米能级F E 是系统的化学势；2）F E 可看成量子态是否被电子占据的一个界限。
3）F E 的位置比较直观地标志了电子占据量子态的情况，通常就说费米能级标志了电子填充能级的水平。
费米能级位置较高，说明有较多的能量较高的量子态上有电子。
半导体物理学总复习课
n0 = N D − N A + p0 ni2 p0 = n0
( N D − N A ) + (( N D − N A ) 2 + 4ni2 )1/2 = 2
强 n0 = ni + N A − ND 电 ≈ N A − ND 离 再求少子浓度 区
ni2 n0 = p0
载流子浓度的乘积
EC − EV n 0 p 0 = N C NV exp－ k0T Eg = N C NV exp－ kT 0
3/2
m∗ m∗ Eg n p 31 3 n 0 p 0 = 2.33 × 10 T exp－ 2 kT m0 0
− t
τ
∆n(t ) = ∆n(0)e
−
tБайду номын сангаас
τ
平衡时
n0、 p0
光注入后从非平 衡到平衡的过程
n = n0 + ∆n p = p0 + ∆p
σ＝( n0＋∆n ) qµn＋( p0＋∆p) qµp
= (n 0 qµ n ＋p 0 qµ p ) + (∆nqµ n ＋∆pqµ p )
= σ 0 (原光电导） ∆σ + （附加光电导）
N E F＝ E i + k 0Tarcsh D 2n i
EF＝ EC + ED k0T N D + ln 2N 2 2 C
EC + ED k0T N D EF＝ ln + 2N 2 2 C
ND EF＝EC + k0Tln N C
半导体物理学期末总复习
Si原子的能级
▪ 电子的能级是量子化的
n=3 四个电子
n=2 8个电子
+14
n=1
H
2个电子
Si
原子的能级的分裂
▪ 孤立原子的能级 4个原子能级的分裂
原子的能级的分裂
▪ 原子能级分裂为能带
半导体的能带结构
导带 Eg
价带
价带：0K条件下被电子填充的能量的能带 导带：0K条件下未被电子填充的能量的能带 带隙：导带底与价带顶之间的能量差
热平衡状态
▪ 在一定温度下，载流子的产生和载流子的复 合建立起一动态平衡，这时的载流子称为热 平衡载流子。
▪ 半导体的热平衡状态受温度影响，某一特定 温度对应某一特定的热平衡状态。
▪ 半导体的导电性受温度影响剧烈。
态密度的概念
▪ 能带中能量 E 附近每单位能量间隔内的量子态
数。 ▪ 能带中能量为 E （E dE）无限小的能量间隔内
半导体物理学
一．半导体中的电子状态 二．半导体中杂质和缺陷能级 三．半导体中载流子的统计分布 四．半导体的导电性 五．非平衡载流子 六．pn结 七．金属和半导体的接触 八．半导体表面与MIS结构 九．半导体的光学性质和光电与发光现象
晶体结构
▪ 半导体的晶格结构和结合性质 ▪ 半导体中的电子状态和能带 ▪ 半导体中的电子运动和有效质量 ▪ 本征半导体的导电机构 ▪ 空穴 ▪ 回旋共振 ▪ 硅和锗的能带结构 ▪ III－V族化合物半导体的能带结构 ▪ II－VI族化合物半导体的能带结构
k0T
k0T
k0T
k0T
玻尔兹曼分布函数
▪ 导带中电子分布可用电子的玻尔兹曼分布函数 描写（绝大多数电子分布在导带底）；价带中 的空穴分布可用空穴的玻尔兹曼分布函数描写 （绝大多数空穴分布在价带顶）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
过剩载流子：过剩电子和空穴的总称 过剩少子在复合前存在的平均时间。 2。小注入和大注入 小注入：过剩载流子的浓度远小于热平衡多子浓度的情况
大注入：过剩载流子的浓度接近或大于热平衡多子浓度的情况
半导体物理复习
第一章
一、基本概念
1. 能带，允带，禁带，K空间的能带图 能带: 在晶体中可以容纳电子的一系列能级 允带：分裂的每一个能带都称为允带。 禁带：晶体中不可以容纳电子的一系列能级 K空间的能带图：晶体中的电子能量随电子波矢k
的变化曲线，即E（K）关系。
（1）越靠近内壳层 的电子，共有化运动 弱，能带窄。
施主能级
受主能级
△ED △E
3.本征半导体，杂质半导体，杂质补偿半导体 本征半导体：没有杂质原子且晶体中无晶格缺陷 的纯净半导体 杂质半导体：掺有施主杂质的N型半导体或掺有 受主杂质的p型半导体都叫杂质半导体 杂质补偿半导体：同一半导体区域内既含有施主 杂质又含有受主杂质的半导体
第三章
一.基本概念 1。状态密度：单位体积单位能量中的量子态数量 2。费米能级：它是电子热力学系统的化学势，它标志在
2.扩散电流密度公式 33. .爱因斯坦关系:
J n,diff
qDn
dn dx
dp J p,diff qDp dx
D kT
q
4. 连续性方程
p t
Dp
2 p x 2
p
E
p x
E
p p x
p
p
gp
n t
Dn
2n x 2
n
E
n x
n
n
E x
n
n
gn
三.例题
例1. T 300K时，硅的掺杂浓度为N A 1014 cm 3 , N D 1015 cm 3 ,
式中a为晶格常数，试求 1、能带宽度；
2、电子在波矢k状态时的速度；
3、能带底部电子的有效质量；
4、能带顶部空穴的有效质量；
1、由 dE(k) 0 dk
得 k n （n=0，1，2…）
a
进一步分析
k (2n 1)
a
（n=0，1，2……）时，E（k）有极大值，E（k)
MAX
2 2 ma2
k 2n
kT ln
p0 NV
EF
Ei
kT ln
p0 ni
5.不同温区载流子浓度和费米能级的计
强电离区
n型半导体
n0 N D
p0
ni2 n0
补偿型半导体
p型半导体
p0 N A
n0
ni2 p0
费米能级仍用前面的公式
当N D N A时：
n0 N D N A
p0
ni2 n0
当N D
N
时
A
p0 N A ND
5 .什么是载流子的扩散运动？写出电子和空穴 的扩散电流密度方程
当半导体内部的载流子存在浓度梯度时，引 起载流子由浓度高的地方向浓度低的地方扩 散，扩散运动是载流子的有规则运动。
电子扩散电流： 空穴扩散电流：
J n,diff
qDn
dn dx
dp J p,diff qDp dx
二、基本公式
1. 漂移电流密度公式： J n nqn E J p pq p E
3。什么是载流子的散射？半导体中载流子的有哪两种主 要散射机制
没有外场的作用，载流子作无规则的热运动。载流子 在半导体中运动时，不断地与热振动的晶格原子或电 离的杂质离子发生碰撞，碰撞后载流子的运动速度的 大小和方向发生了改变。用波的概念，就是说电子波 在半导体中传播时遭到了散射。
半导体中载流子的散射机制： 晶格散射和电离杂质散 射
4. 半导体的电阻率（或电导率）与那些因素有关
n型半导体 p型半导体 本征半导体
nqn ,
1
nq n
pq p ,
1
pq p
ni qn
ni q p ,
ni qn
1
ni q p
电阻率与载流子浓度与迁移率有关，二者均 与杂质浓度和温度有关。
第五章 非平衡载流子
一、基本概念
1。过剩电子，过剩空穴，过剩载流子（非平衡载流子），非 平衡载流子的寿命？
mn*
2 d 2E
m (cos ka 1 cos 2ka)
dk 2
2
能带底部 k 2n
a
所以 mn* 2m
，
5、能带顶部 k (2n 1)
a
且
m*p mn*
，
所以能带顶部空穴的有效质量
m*p 2m
第二章
基本概念
1。施主杂质，施主能级，施主杂质电离能 施主杂质：能够施放电子而在导带中产生电子并形成正 电中心的杂质，称为施主杂质，掺有施主杂质的半导体 叫N型半导体。。 施主能级被施主杂质束缚的电子的能量状态称为施主能级 ED，施主能级位于离导带低很近的禁带中。 施主杂质电离能：导带底EC与施主能级ED的能量之差 ED=EC-ED就是施主杂质的电离能。施主杂质未电离时是 中性的，电离后成为正电中心
由题意得：
解之得：
例题3
求在下列条件下，均匀掺杂硅样品中平衡状态的空穴和电子浓 度及Ei，EF-Ei,并在硅样品的能带图中仔细标出他们的位置
（a）T=300K, NA<< ND, ND=1015/cm3 （b）T=300K, ,NA=1016/cm3, ND<<NA （c）T=300K, NA=91015/cm3, ND=1016/cm3 （d）T=450K, NA=0, ND=1014/cm3, （e）T=650K, NA=0, ND=1014/cm3
5。直接带隙半导体和间接带隙半导体
直接带隙半导体：导带低和价带顶对应的电子波矢相同
间接带隙半导体：导带低和价带顶对应的电子波矢不相同
二. 基本公式
有效质量 速度：
m*
h2 d 2E
ห้องสมุดไป่ตู้
dk 2
1 dE
h dk
例1、 一维晶体的电子能带可写为，
E（k )
2 ma2
(7 8
cos ka
1 8
cos 2ka)
f外 mn*a
mn*
h2 d 2E
（3）电子的有效质量与晶体的能带结构有关
dk 2
利用有效质量可以对半导体的能带结构进
行研究
（4）有效质量可以通过回旋共振实验测得，并
椐此推出半导体的能带结构
4.空穴：空穴是几乎被电子填满的能带中未被电子占据的 少数空量子态，这少量的空穴总是处于能带顶附近。是价 电子脱离原子束缚 后形成的电子空位，对应于价带顶的电 子空位。把半导体中的空穴看成一个带有电荷为+q，并以 该空状态相应的电子速度v(k)运动的粒子，它具有正的有 效质量，价带中大量电子的导电作用可以用少数空穴的导 电作用来描写。
n0
ni2 p0
过渡区
n型半导体：
p型半导体：
n0 p0 N D n0 p0 ni2
p0 n0 N A n0 p0 ni2
联立解方程求n0，p0
补偿型半导体： n0 N A p0 N D n0 p0 ni2
费米能级仍用前面的公式
高温本征激发区
n0= p0=ni EF=Ei
费米能级仍用前面的公式得到EF=Ei
3.什么是准费米能级？
在非平衡状态下，由于导带和价带在总体上处于非
平衡，因此就不能用统一的费米能级来描述导带中
的电子和价带中的空穴按能量的分布问题。但由于
导带中的电子和价带中的空穴按能量在各自的能带
中处于准平衡分布，可以有各自的费米能级
EFn
和E
p F
称为准费米能级，准费米能级分离的程度，即
E
n F
例题1 （同类型题103页1题）
导出能量在Ec和Ec+kT之间时，导带上的有效状 态总数（状态数/cm3)的表达式， 是任意常数。
例题2
（a)在热平衡条件下，温度T大于0K，电子能量位于费米 能级时，电子态的占有几率是多少？
(b)若EF位于EC，试计算状态在EC+kT时发现电子的几率 。
(c)在EC+kT时，若状态被占据的几率等于状态未 被占据的几率。此时费米能级位于何处？
dZ dE
4V
(2mn* ) 2 h3
(E
1
EC ) 2
价带态密度
3
gV
(E)
dZ dE
4V
(2mP* ) 2 h3
(EV
1
E) 2
2.费米分布函数
f (E)
1
EEF
1 e k0T
当E-EF>>kT时
波尔兹曼函数
EEF
f (E) e k0T
3.载流子的浓度
n0
Nc
exp (
EC E f k0T
（2）各分裂能级间 能量相差小，看作准 连续
（3）有些能带被电 子占满（满带），有 些被部分占满（半满 带），未被电子占据 的是空带。
原子能级
能带
2、半导体的导带，价带和禁带宽度
导带
Eg
价带
价带：0K条件下被电子填充的能量最高的能带 导带： 0K条件下未被电子填充的能量最低的能带 禁带：导带底与价带顶之间能带 禁带宽度：导带底与价带顶之间的能量差
非简并半导体：掺杂浓度较低，其费米能级EF在禁带中的
半导体
n型半导体
p型半导体
非简并
EC EF 2k0T
EV EF 2k0T
弱简并 0 EC EF 2k0T
0 EV EF 2k0T