信号检测与估计 第三章 信号的检测2
合集下载
第三章信号的检测 ,信号检测与估计
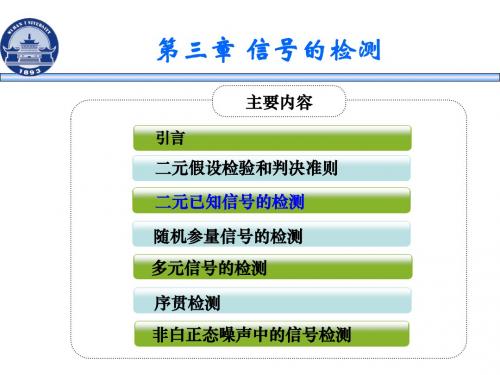
作业：
1 z2 exp( )dz 1 [ (1 ) E / N0 ] 2 2
x
[ x]
1 e 2
z2 2
dz
1 同理 ＝ p(G | H1 )dG＝ [ (1 ) E / N0 ]
l0*
Pe 1 [ (1 ) E / N0 ]
• 对于通信最佳检测系统，通常用最小总错误概 率准则。即贝叶斯准则C11=C00=0,C01=C10=1
(C10 C00 )q q l0 (C01 C 11 ) p p
• 通常先验概率p及q一般都设计得近似相等，这 样可得到更小的总错误概率。
• 假设p=q=1/2 ， 此时l0=q/p=1，则
H1
2 1 T T x ( s1 s0 ) ln l0 ( s1 s1 s0 s0 ) 2
H0
T
H1
代入得
T
0
x(t ) s1 (t )dt
0
* 1 1 x(t ) s0 (t )dt l0 N 0 ln l0 ( E1 E0 ) 2 2
H0
H1
0
T
Var[G | H 0 ] E{[G E (G | H 0 )]2 } N0 = 2
T
0
[s1 (t ) s0 (t )]2 dt N 0 E (1 )
[G ( E E0 )]2 1 p(G | H 0 ) exp{ } 2 N0 E (1 ) 2 N0 E (1 )
xt s1 t nt
xt s0 t nt
0t T
3.3.2 二元信号检测系统
信号检测与估计教学资料 第三章 信号检测与估计1new-PPT精选文档
4 二元信号判决概率
P H | H pH x | d, x ， i j 0 , 1 i j j
R i
P H | H pH x | j d, x ， i j 0 , 1 i j
R i
5 M元信号检测模型
信源
概率转移机构
信源的输出称为假设 将信源的输出(假设)以一定的 概率关系映射到整个观察空间中 接收端所有可能观测量的集合 将观察空间进行合理划分,使每个观测量 对应一个假设判断的方法
H H
1 1
4 二元信号判决概率
判决 假设
H0
H1
H0 H P 0H 0
H P 1H 0
H P 1H 1
H1 H P 0H 1
3 二元信号判决结果
判决 假设
H0
H1
H0 H0 H0
H H
1 0
H1 H0 H1
H H
1 1
四种检测状态 ① 目标不存在，干扰信号没有超过门限，检测没有发生 ② 目标存在，合成的信号（目标和干扰）超过门限，检测发生 ③ 目标不存在，干扰信号超过了门限，虚假的检测产生 ④ 目标存在，合成的信号（目标和干扰）没有超过门限，检测没有发生
2 二元信号检测判决域 二元信号的检测问题，可归结为对观察空间的划分问题，即按照 一定的准则，将观察空间R分别划分为R0和R1两个子空间。
H 0 成立
R0
H 1 成立
R0
R1
2 二元信号检测判决域
3 二元信号判决结果
判决 假设
H0
H1
H0 H0 H0
H H
1 0
H1 H0 H1
观测量落入观测空间后,就可以用来推断哪一个
电子科技大学第三章 信号检测与估计(2)
3.4.4 奈曼-皮尔逊准则
2 奈曼-皮尔逊准则的推导
在 PH1 H0 约束条件下,使正确判决概率PH1 H1最大的准则。
等价于
在 PH1 H0 约束条件下,使判决概率PH0 H1 最小的准则。 利用拉格朗日乘子 0，构建目标函数
J PH0 H1 PH1 H0
若 PH1 H0 ,J达到最小时，PH0 H1 也达到最小。
c00 c10 c00 PF P1 P1 c11 c00 c01 c11 PM P1 c10 c00 PF P1
平均代价C(P1)是先验概率P1的严格上凸函数
3.4.3 极小化极大准则
3.4.3 极小化极大准则
3.4.3 极小化极大准则
3 先验概率未知的情况下，可以采用的检测方法
P1c11 c00 c01 c11PM P1 c10 c00 PF P1
def
def
PF p x H0 dx PF P1g PM p x H1 dx PM P1g
R1
R0
C P1, P1g c00 c10 c00 PF P1g
P1 c11 c00 c01 c11 PM P1g c10 c00 PF P1g
大家晚上好
3.4 派生贝叶斯准则 (Generalized Bayes Criterion)
基本要求：
① 掌握最小平均错误概率准则和最大后验概 率准则
② 掌握极小化极大准则和奈曼-皮尔逊准则的 应用范围和基本原理
3.4.1 最小平均错误概率准则 (Minimum mean prob. of error criterion)
3.4.3 极小化极大准则
3.4.3 极小化极大准则
C P1, P1g c00 c10 c00 PF P1g
第三章 信号检测与估计
第三章 信号的统计检测理论
1
3.3 Bayes Criterion(贝叶斯准则)
基本要求： ① 充分理解平均代价(Average Risk)的概念 ② 贝叶斯准则的判决表达式 ③ 判决性能分析
贝叶斯准则的基本原理：在划分观察空间时，使平均风险最小.
2
1 平均代价的概念和贝叶斯准则
通信系统中，二元信号的平均解调错误概率：
PH1 c01 c11 px H1 0 PH0 c10 c00 px H0 0
因此，平均代价C的大小与判决区域R0有关。
把使被积函数取负值的观察值x值划分给R0区域，而把其余的观察值x值划分给R1，
即可保证平均代价最小。
12
1 平均代价的概念和贝叶斯准则
合并
C P H 0 c10 c00 p x H 0 dx c10 p x H 0 dx
P H1 c11 c01 p x H1 dx c11 p x H1 dx
R0 R0
R0
R0
11
合并
C c10 PH 0 c11 PH1 R PH1 c01 c11 p x H1 PH 0 c10 c00 p x H 0 dx 0
9
1 平均代价的概念和贝叶斯准则
3. 平均代价取到最小值的条件 C PH 0 c00 R px H 0 dx c10 R px H 0 dx 0 1 PH1 c01 R px H1 dx c11 R px H1 dx 0 1
注：一般假设
c10 c00 c01 c11
5
1 平均代价的概念和贝叶斯准则
1
3.3 Bayes Criterion(贝叶斯准则)
基本要求： ① 充分理解平均代价(Average Risk)的概念 ② 贝叶斯准则的判决表达式 ③ 判决性能分析
贝叶斯准则的基本原理：在划分观察空间时，使平均风险最小.
2
1 平均代价的概念和贝叶斯准则
通信系统中，二元信号的平均解调错误概率：
PH1 c01 c11 px H1 0 PH0 c10 c00 px H0 0
因此，平均代价C的大小与判决区域R0有关。
把使被积函数取负值的观察值x值划分给R0区域，而把其余的观察值x值划分给R1，
即可保证平均代价最小。
12
1 平均代价的概念和贝叶斯准则
合并
C P H 0 c10 c00 p x H 0 dx c10 p x H 0 dx
P H1 c11 c01 p x H1 dx c11 p x H1 dx
R0 R0
R0
R0
11
合并
C c10 PH 0 c11 PH1 R PH1 c01 c11 p x H1 PH 0 c10 c00 p x H 0 dx 0
9
1 平均代价的概念和贝叶斯准则
3. 平均代价取到最小值的条件 C PH 0 c00 R px H 0 dx c10 R px H 0 dx 0 1 PH1 c01 R px H1 dx c11 R px H1 dx 0 1
注：一般假设
c10 c00 c01 c11
5
1 平均代价的概念和贝叶斯准则
第三章信号的检测 ,信号检测与估计
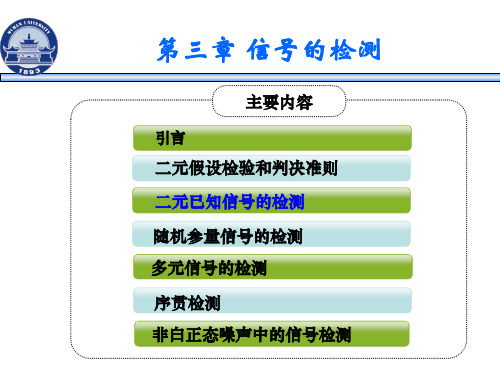
1 2
N k 1
s12k s02k
2
H0
H1
则
xT
(s1
s0 )
2
ln l0
1 2
(s1T
s1
s0T s0 )
H0
代入得
H1
T
0 x(t)s1(t)dt
T 0
x(t)s0 (t)dt
l0*
1 2
N0
ln
l0
1 2
(E1
E0 )
H0
3.3.3 二元通信系统的检测性能
第三章 信号的检测
主要内容
引言
二元假设检验和判决准则 二元已知信号的检测 随机参量信号的检测 多元信号的检测 序贯检测 非白正态噪声中的信号检测
§3.3 二元已知信号的检测
• 已知信号：信号出现后，所有的参数（幅度、
频率、相位、到达时间等）都已知。
• 二元已知信号在高斯白噪声中的检测：
假设H1： xt s1t nt
1
S1k
xk
t
2 N0
T
0 s1
t
xt
dt
lim N S0k xk 2
N
t 0
k 1
2
N0
T
0 s0
t
xt
dt
同理
N
lim
S12k
1
2 N
t 0
k 1
2
N0
s T 2
01
t dt E1 N0
N
lim
p xN H0 p xN H1
信号检测与估计理论(3)第三章 克拉美-罗下限
exp ⎧⎨− ⎩
1
2σ 2
N
−1
(
x[
n]
−
s[n;θ
])2
⎫ ⎬
n=0
⎭
3.3 WGN中信号的CRLB
一阶偏导
∑ ∂ ln
p(x;θ ) ∂θ
=
1
σ2
N −1
( x[n] −
n=0
s[n;θ ])
∂s[n;θ ] ∂θ
二阶偏导 数学期望
∑ ∂2
ln p(x;θ ) ∂θ 2
=
1
σ2
N −1 ⎨⎧( x[n] −
ln p (x;θ ∂θ 2
)⎤ ⎥ ⎦
（3-16）
显然，当估计获得CRLB时，其方差就是Fisher 信息的倒数。下界越小，信息越多。Fisher信 息有如下性质：
1、Fisher信息是非负的（根据（3-11）式）。 2、对于独立的观测，Fisher信息满足可加性。
由此，可以得出如下结论：对N个IID观测的 CRLB是单次观测的1/N倍。
3.3 WGN中信号的CRLB
(3-5)
与 p(x[0]; A) 有关，仅是A的函数。上式值越大，估计量的方差 就越小。
3.2 克拉美-罗下界（CRLB）
定理3-1（标量形式的CRLB）假设PDF p(x;θ ) 对
所有可能的 θ 满足“正则”条件
E
⎡ ⎢⎣
∂
ln
p(x;θ ∂θ
)
⎤ ⎥⎦
=
0
那么任何无偏估计 θˆ 的方差一定满足
−
1
2σ 2
N −1
(x[n] −
n=0
A)2
⎤ ⎥
⎦
信号检测与估计知识点总结(2)
第三章 估计理论1. 估计的分类矩估计：直接对观测样本的统计特征作出估计。
参数估计：对观测样本中的信号的未知参数作出估计。
待定参数可以是未知的确定量，也可以是随机量。
点估计：对待定参量只给出单个估计值。
区间估计：给出待定参数的可能取值范围及置信度。
(置信度、置信区间) 波形估计：根据观测样本对被噪声污染的信号波形进行估计。
预测、滤波、平滑三种基本方式。
✓ 已知分布的估计✓ 分布未知或不需要分布的估计。
✓ 估计方法取决于采用的估计准则。
2. 估计器的性能评价✧ 无偏性：估计的统计均值等于真值。
✧ 渐进无偏性：随着样本量的增大估计值收敛于真值。
✧ 有效性：最小方差与实际估计方差的比值。
✧ 有效估计：最小方差无偏估计。
达到方差下限。
✧ 渐进有效估计：样本量趋近于无穷大时方差趋近于最小方差的无偏估计。
✧ 一致性：随着样本量的增大依概率收敛于真值。
✧ Cramer-Rao 界： 其中为Fisher 信息量。
3. 最小均方误差准则模型：假定： 是观测样本，它包含了有用信号 及干扰信号 ，其中 是待估计的信号随机参数。
根据观测样本对待测参数作出估计。
最小均方误差准则：估计的误差平方在统计平均的意义上是最小的。
即使达到最小值。
此时 从而得到的最小均方误差估计为： 即最小均方误差准则应是观测样本Y 一定前提下的条件均值。
需借助于条)()(1αα-≥F V ⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡∂∂=⎭⎬⎫⎩⎨⎧∂∂-=2212122);,(ln );,(ln )(αααααm m y y y p E y y y p E F )(),()(t n t s t y +=θ)(t n T N ),,,(21θθθθ=),(θts {}{})ˆ()ˆ()ˆ,(2θθθθθθ--=T E e E {}0)ˆ,(ˆ2=⎥⎦⎤⎢⎣⎡=MSE e E d d θθθθθθθθθd Y f Y MSE )|()(ˆ⎰=件概率密度求解，是无偏估计。
信号检测与估计第三章
+∞
th1
⎛ N1μ − th1 ⎞ = Φ⎜ ⎟ ⎜ N 1σ ⎟ ⎝ ⎠
⎛ N1μ − N1σΦ −1 (1 − α1 ) ⎞ ⎛ N1 μ ⎞ −1 PD1 = Φ ⎜ = Φ⎜ − Φ (1 − α1 ) ⎟ ⎟ ⎜ ⎟ ⎜ ⎟ σ N σ 1 ⎝ ⎠ ⎝ ⎠
• 若采用符号检测器，其检验统计量为：
0 2,1
ARE
N1 = N2
0 2,1
渐近相对效率定义如下:
N1 ARE2,1 = lim ARE = lim H1 → H 0 H1 → H 0 N 2 N →+∞ N →+∞
N 2 →+∞
1
N 2 →+∞
1
渐近相对效率是检测器在 H1 → H 0 条件下样本数趋于无穷时 的相对效率。它是比较两种检测器性能的一种指标。
⎧ H 0 : f ( xi ) = f ( − xi ) ⎨ ⎩ H1 : f ( Asi + xi ) = f ( Asi − xi )
2）若只知道噪声分布的中位数为零，可表示为： 1 ⎧ H0 : F ( 0) = ⎪ ⎪ 2 ⎨ ⎪ H : F ( As ) = 1 1 i ⎪ ⎩ 2
定义非随机检验函数（连续型）：
( ) ( ) ( )
k >0
• 混合型噪声的概率密度函数为：
⎧ ⎧ x2 ⎫ ε 1− ε ⎪ 2 x f ( x) = exp ⎨ − 2 ⎬ + exp ⎨ − 2πσ 1 2σ 2 ⎩ 2σ 1 ⎭ ⎪ σ2 ⎩ ⎫ ⎪ ⎬ ⎪ ⎭
3.2.1 衡量检测器性能的指标
1. 检测器渐近相对效率 假设二元假设检验问题有两个检测器，若它们具有相同的 虚警概率和检测概率所需的观测样本数分别为 N1 , N 2 ， 则定义第2个检测器对于第1个的相对效率为:
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
H0
T
T
0
x(t ) s1 (t )dt
0
* 1 1 x(t ) s0 (t )dt l0 N 0 ln l0 ( E1 E0 ) 2 2
H0
H1
3.3.3 二元通信系统的检测性能
• 相关概念及推导 • 几种具体信号模型
– 相参相移键控 – 相参频移键控 – 启闭载波键控
Var[G | H0 ] N0 E(1 )
Pe 1 [ (1 ) E / N0 ]
几种具体信号模型
• 相参相移键控（CPSK）
s0 (t ) A sin 0t
0t T
0t T
s1 (t ) A sin(0t ) A sin 0t
xt s1 t nt
xt s0 t nt
0t T
3.3.2 二元信号检测系统
对x(t)在0~T范围内进行N次观测，则
p X H 0 p x1 x2 xN H 0 p x1 H 0 p x2 H 0 p xN H 0 p X H1 p x1 x2 xN H1 p x1 H1 p x2 H1 p xN H1
Err an I [Q(t ) cos( ) I (t )sin( )] an Q[ I (t ) cos( ) Q(t )sin( )] [an I * I (t ) an Q * Q(t )]sin( ) 2 K p sin( ) 2 K p
s t x t dt
0 1
T
S0 k xk 2 lim 2 N N0 t 0 k 1
N
s t x t dt
0 0
T
同理
S lim N 2 t 0 k 1
N
N
2 1k 2
1 N0
2 0
T
0
E1 s t dt N0
其性能较相参相移键控信号差3dB
启闭载波键控（CASK或OOK）
s0 (t ) 0 s1 (t ) A sin 0t 0t T
此时ρ＝0，E=E1/2，E0=0。 错误概率 判决门限
Pe 1 [ E1 / 2 N 0 ]
1 l ( E1 E0 ) E1 / 2 2
2 1
S02k 1 lim 2 N 2 N0 t 0 k 1
T
0
E0 s t dt N0
N足够大时，等式近似成立
令
x x1 , x2 ...xN
H1
T T
si si1 , si 2 ...siN
T
则 代入得
2 1 T T x ( s1 s0 ) ln l0 ( s1 s1 s0 s0 ) 2
0 0
T
T
• 则判决规则为
* G l0
H0
H1
• 检测系统的总错误概率：
1 1 Pe =q p p(G | H 0 )dG p(G | H1 )dG 2l* 2
0
l0*
E G | H 0 E s0 (t ) s1 (t )dt E[n(t )]s1 (t )dt 0 0
2 2 N p X H1 S1k xk S0 k xk S1k S0 k lX exp 2 2 2 2 p X H0 2 2 k 1
判决规则
N
l ( x ) l0
H0
N H1 N 2 1k 2 0k
* 0
按平均信号能量E来说，其性能与相参频移 键控系统相同。
x(t )
×
T
0
+ -
判决
S1 (t )
l
* 0
图3.10 启闭载波键控检测系统
3.3.4 雷达系统的检测性能
H 0： x(t ) n(t )
H1： x(t ) s1 (t ) n(t )
Ps0 (t ) 及 P s1 (t ) 未知，常用奈曼-皮尔逊准则。
l0*
Pe 1 [ (1 ) E / N0 ]
总错误概率，标志着二元通信系统的最佳检测性能。
除与信号平均能量及噪声强度有关，还与ρ 有关。
当ρ ＝－1时Pe最小。
回顾
• 贝叶斯准则 (C10 C00 )q l0 (C01 C 11 ) p –最小平均风险 • 最小总错误概率准则 – C00 = C11=0，C10 = C01=1 • 奈曼---皮尔逊准则 p ( l | H ) dl 0 –固定使PD最大 l0 • 极大极小准则 –安全平均风险
相关概念及推导
• 系统的检测性能，通常是指在假定的信号与噪 声的条件下系统的某种判决概率与输入信噪比 之间的关系。在这里我们求总错误概率Pe与输 入信噪比d之间的关系。
• 对于通信最佳检测系统，通常用最小总错误概 率准则。即贝叶斯准则C11=C00=0,C01=C10=1
(C10 C00 )q q l0 (C01 C 11 ) p p
则
E[G | H0 ] E E0
G E[G | H 0 ] n(t )[s1 (t ) s0 (t )]dt
0
T
Var[G | H 0 ] E{[G E (G | H 0 )]2 } N0 = 2
T
0
[s1 (t ) s0 (t )]2 dt N 0 E (1 )
最佳检测系统的方框图仍如前所示。 检验统计量
G x(t )s1 (t )dt
0 T
虚警概率
检测概率
p(G H 0 )dG
l0
PD p(G H1 )dG
l0
E[G | H0 ] E E0
Var[G | H0 ] N0 E(1 )
1 1 l N 0 ln l0 ( E1 E0 ) 2 2
E1 d 2 N0
工作特性
检测特性
当α给定之后，检测概率只与信号能量及噪声强度 之比有关
PSK/ASK/QAM/FSK解调
QPSK 解调
符号 同步 低通 滤波 匹配 滤波 抽取 判决 匹配 滤波 载波 同步 串并 转换
数据 输出
中频
ADC
cos( 0t 0)
低通 滤波
sin( 0t 0)
[G ( E E0 )]2 1 p(G | H 0 ) exp{ } 2 N0 E (1 ) 2 N0 E (1 )
因此
=
l0*
p(G | H
0
)dG
1 ( E1 E0 ) 2
[G ( E E0 )]2 1 exp{ }dG 2 N 0 E (1 ) 2 N 0 E (1 )
•
最大似然准则
– C00 = C11，C10 = C01，且P(H0) = P(H1)
•
最大后验概率准则
p( x | H1 ) 1 p( x | H 0 ) H0
H1
– (C10-C00)=( C01-C11) – 与最小总错误概率准则等效； – P(H1)= P(H0)时，与最大似然准则等效。
H1
x k s1k x k s0 k 1 s s ln l0 取对数得 2 2 2 2 k 1 k 1 k 1
H0
极限值
取极限情况
t 0, N 2 N 0 B N 0 2t B 1 2t
N S1k xk 2 2 lim 2 lim S1k xk t 可得 N N N N0 k 1 0 t 0 t 0 k 1 N
二元已知信号在高斯白噪声中的检测
T
0
x(t )s1 (t )dt
T
0
1 * 1 x(t )s0 (t )dt l0 N0 ln l0 ( E1 E0 )
H0
H1
2
2
二元通信系统中p=q=1/2
1 l0 ( E1 E0 ) 2
*
E[G | H0 ] E E0
条件概率密度
2 xk s0 k 1 p xk H 0 exp 2 2 2 2 xk s1k 1 p xk H1 exp 2 2 2
其中
似然比检验
在0~T时间内进行N次抽样，得到似然函数比为
• 通常先验概率p及q一般都设计得近似相等，这 样可得到更小的总错误概率。
• 假设p=q=1/2 ， 此时l0=q/p=1，则
1 1 1 l0 N 0 Inl0 ( E1 E0 ) ( E1 E0 ) 2 2 2
*
• 取检验统计量 G x(t)s1(t)dt x(t)s0(t)dt
* 0
代入得
0，E0 0，E E 2
1
p (G H 0 )
p (G H1 )
0
1 G2 exp N 0 E1 N 0 E1
(G E1 ) 2 1 exp N E N 0 E1 0 1
1 1 l N 0 ln l0 E1 2 2
T T T 2 E s0 (t )dt E[n(t )]s0 (t )dt 0 0 2 s0 (t ) s1 (t )dt s0 (t )dt 0 0 T T
T
令
1 T 2 1 2 E [ s0 (t ) s1 (t )]dt ( E0 E1 ) 2 0 2 1 T s0 (t ) s1 (t )dt E 0
T
T
0
x(t ) s1 (t )dt
0
* 1 1 x(t ) s0 (t )dt l0 N 0 ln l0 ( E1 E0 ) 2 2
H0
H1
3.3.3 二元通信系统的检测性能
• 相关概念及推导 • 几种具体信号模型
– 相参相移键控 – 相参频移键控 – 启闭载波键控
Var[G | H0 ] N0 E(1 )
Pe 1 [ (1 ) E / N0 ]
几种具体信号模型
• 相参相移键控（CPSK）
s0 (t ) A sin 0t
0t T
0t T
s1 (t ) A sin(0t ) A sin 0t
xt s1 t nt
xt s0 t nt
0t T
3.3.2 二元信号检测系统
对x(t)在0~T范围内进行N次观测，则
p X H 0 p x1 x2 xN H 0 p x1 H 0 p x2 H 0 p xN H 0 p X H1 p x1 x2 xN H1 p x1 H1 p x2 H1 p xN H1
Err an I [Q(t ) cos( ) I (t )sin( )] an Q[ I (t ) cos( ) Q(t )sin( )] [an I * I (t ) an Q * Q(t )]sin( ) 2 K p sin( ) 2 K p
s t x t dt
0 1
T
S0 k xk 2 lim 2 N N0 t 0 k 1
N
s t x t dt
0 0
T
同理
S lim N 2 t 0 k 1
N
N
2 1k 2
1 N0
2 0
T
0
E1 s t dt N0
其性能较相参相移键控信号差3dB
启闭载波键控（CASK或OOK）
s0 (t ) 0 s1 (t ) A sin 0t 0t T
此时ρ＝0，E=E1/2，E0=0。 错误概率 判决门限
Pe 1 [ E1 / 2 N 0 ]
1 l ( E1 E0 ) E1 / 2 2
2 1
S02k 1 lim 2 N 2 N0 t 0 k 1
T
0
E0 s t dt N0
N足够大时，等式近似成立
令
x x1 , x2 ...xN
H1
T T
si si1 , si 2 ...siN
T
则 代入得
2 1 T T x ( s1 s0 ) ln l0 ( s1 s1 s0 s0 ) 2
0 0
T
T
• 则判决规则为
* G l0
H0
H1
• 检测系统的总错误概率：
1 1 Pe =q p p(G | H 0 )dG p(G | H1 )dG 2l* 2
0
l0*
E G | H 0 E s0 (t ) s1 (t )dt E[n(t )]s1 (t )dt 0 0
2 2 N p X H1 S1k xk S0 k xk S1k S0 k lX exp 2 2 2 2 p X H0 2 2 k 1
判决规则
N
l ( x ) l0
H0
N H1 N 2 1k 2 0k
* 0
按平均信号能量E来说，其性能与相参频移 键控系统相同。
x(t )
×
T
0
+ -
判决
S1 (t )
l
* 0
图3.10 启闭载波键控检测系统
3.3.4 雷达系统的检测性能
H 0： x(t ) n(t )
H1： x(t ) s1 (t ) n(t )
Ps0 (t ) 及 P s1 (t ) 未知，常用奈曼-皮尔逊准则。
l0*
Pe 1 [ (1 ) E / N0 ]
总错误概率，标志着二元通信系统的最佳检测性能。
除与信号平均能量及噪声强度有关，还与ρ 有关。
当ρ ＝－1时Pe最小。
回顾
• 贝叶斯准则 (C10 C00 )q l0 (C01 C 11 ) p –最小平均风险 • 最小总错误概率准则 – C00 = C11=0，C10 = C01=1 • 奈曼---皮尔逊准则 p ( l | H ) dl 0 –固定使PD最大 l0 • 极大极小准则 –安全平均风险
相关概念及推导
• 系统的检测性能，通常是指在假定的信号与噪 声的条件下系统的某种判决概率与输入信噪比 之间的关系。在这里我们求总错误概率Pe与输 入信噪比d之间的关系。
• 对于通信最佳检测系统，通常用最小总错误概 率准则。即贝叶斯准则C11=C00=0,C01=C10=1
(C10 C00 )q q l0 (C01 C 11 ) p p
则
E[G | H0 ] E E0
G E[G | H 0 ] n(t )[s1 (t ) s0 (t )]dt
0
T
Var[G | H 0 ] E{[G E (G | H 0 )]2 } N0 = 2
T
0
[s1 (t ) s0 (t )]2 dt N 0 E (1 )
最佳检测系统的方框图仍如前所示。 检验统计量
G x(t )s1 (t )dt
0 T
虚警概率
检测概率
p(G H 0 )dG
l0
PD p(G H1 )dG
l0
E[G | H0 ] E E0
Var[G | H0 ] N0 E(1 )
1 1 l N 0 ln l0 ( E1 E0 ) 2 2
E1 d 2 N0
工作特性
检测特性
当α给定之后，检测概率只与信号能量及噪声强度 之比有关
PSK/ASK/QAM/FSK解调
QPSK 解调
符号 同步 低通 滤波 匹配 滤波 抽取 判决 匹配 滤波 载波 同步 串并 转换
数据 输出
中频
ADC
cos( 0t 0)
低通 滤波
sin( 0t 0)
[G ( E E0 )]2 1 p(G | H 0 ) exp{ } 2 N0 E (1 ) 2 N0 E (1 )
因此
=
l0*
p(G | H
0
)dG
1 ( E1 E0 ) 2
[G ( E E0 )]2 1 exp{ }dG 2 N 0 E (1 ) 2 N 0 E (1 )
•
最大似然准则
– C00 = C11，C10 = C01，且P(H0) = P(H1)
•
最大后验概率准则
p( x | H1 ) 1 p( x | H 0 ) H0
H1
– (C10-C00)=( C01-C11) – 与最小总错误概率准则等效； – P(H1)= P(H0)时，与最大似然准则等效。
H1
x k s1k x k s0 k 1 s s ln l0 取对数得 2 2 2 2 k 1 k 1 k 1
H0
极限值
取极限情况
t 0, N 2 N 0 B N 0 2t B 1 2t
N S1k xk 2 2 lim 2 lim S1k xk t 可得 N N N N0 k 1 0 t 0 t 0 k 1 N
二元已知信号在高斯白噪声中的检测
T
0
x(t )s1 (t )dt
T
0
1 * 1 x(t )s0 (t )dt l0 N0 ln l0 ( E1 E0 )
H0
H1
2
2
二元通信系统中p=q=1/2
1 l0 ( E1 E0 ) 2
*
E[G | H0 ] E E0
条件概率密度
2 xk s0 k 1 p xk H 0 exp 2 2 2 2 xk s1k 1 p xk H1 exp 2 2 2
其中
似然比检验
在0~T时间内进行N次抽样，得到似然函数比为
• 通常先验概率p及q一般都设计得近似相等，这 样可得到更小的总错误概率。
• 假设p=q=1/2 ， 此时l0=q/p=1，则
1 1 1 l0 N 0 Inl0 ( E1 E0 ) ( E1 E0 ) 2 2 2
*
• 取检验统计量 G x(t)s1(t)dt x(t)s0(t)dt
* 0
代入得
0，E0 0，E E 2
1
p (G H 0 )
p (G H1 )
0
1 G2 exp N 0 E1 N 0 E1
(G E1 ) 2 1 exp N E N 0 E1 0 1
1 1 l N 0 ln l0 E1 2 2
T T T 2 E s0 (t )dt E[n(t )]s0 (t )dt 0 0 2 s0 (t ) s1 (t )dt s0 (t )dt 0 0 T T
T
令
1 T 2 1 2 E [ s0 (t ) s1 (t )]dt ( E0 E1 ) 2 0 2 1 T s0 (t ) s1 (t )dt E 0