计量经济学作业excel图
计量经济学 知识点网络结构图

用EXCEL软件绘制经济图表

用EXCEL软件绘制经济图表课程:经济预测学时:2学时实验目的和意义:经济图表能够在最短的时间内、用最少的笔墨、在最小的空间里给观众最多的思想。
一个好的经济图表能够把复杂的思想在图表中清楚、准确、有效地表达出来。
通过本环节,要求学生能够熟练运用EXCEL软件绘制柱形图、饼图、雷达图、线图等各种经济图表,并养成用经济图表表达数据特征的好习惯。
E X C E L软件简介:EXCEL为微软公司特别针对运算工作所开发的一套软件。
发展至今,软件本身除了蕴含着强大的计算功能外,高级的VBA 程序自定义功能以及数据分析能力,更是让此软件更具成长性的关键特征,使其广泛应用于经济数据分析中。
如EXCEL中简单的加载宏功能,计算出数据分析中最重要的推论及假设工作,为经济管理人员推测品质控制过程是否出现瑕疵或预测公司未来收益。
EXCEL经济预测功能虽不及SPSS强大,但由于其具有很好的大众基础,使用方法简单,已经成为数据分析工作中最常用的软件之一。
实验目标与结果:要求学生能够熟练运用EXCEL软件绘制各种经济图表,养成用图表表达数据特征的好习惯,并对EXCEL其它的计算功能、VBA程序自定义功能以及数据分析功能有初步认识,为后面的经济预测方法讲授打下基础。
程序与步骤:(数据可采用《经济预测》教材中例题)(以折线图为例):1、打开EXCEL软件并输入原始数据。
2、在菜单中选取“插入―图表”命令,启动图表向导。
3、在“图表向导步骤4之1-图表类型”中,选取相应图表,再单击“下一步”按钮。
4、在“图表向导步骤4之2-图表源数据”中,在“数据区域”文本框中,输入或选取单元格范围,并在“系列产生在”选项按钮组中选择“列”,单击“下一步”按钮。
5、在“图表向导步骤4之3-图表选项”中,点击“标题”选项卡输入图表名称,点击“数据标志”选项卡,勾选“系列名称”选项,以使横纵坐标显示坐标名称(或选取系列名称使图表较乱可不选此项),点击“下一步”按钮。
计量经济学问题用Excel解决方法
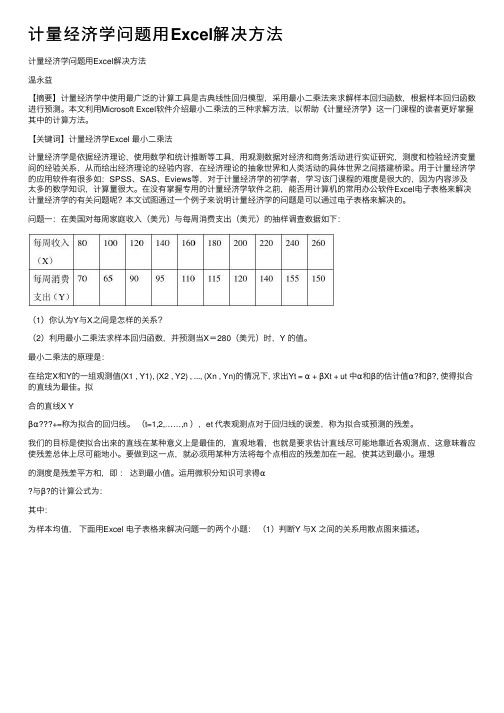
计量经济学问题⽤Excel解决⽅法计量经济学问题⽤Excel解决⽅法温永益【摘要】计量经济学中使⽤最⼴泛的计算⼯具是古典线性回归模型,采⽤最⼩⼆乘法来求解样本回归函数,根据样本回归函数进⾏预测。
本⽂利⽤Microsoft Excel软件介绍最⼩⼆乘法的三种求解⽅法,以帮助《计量经济学》这⼀门课程的读者更好掌握其中的计算⽅法。
【关键词】计量经济学Excel 最⼩⼆乘法计量经济学是依据经济理论,使⽤数学和统计推断等⼯具,⽤观测数据对经济和商务活动进⾏实证研究,测度和检验经济变量间的经验关系,从⽽给出经济理论的经验内容,在经济理论的抽象世界和⼈类活动的具体世界之间搭建桥梁。
⽤于计量经济学的应⽤软件有很多如:SPSS、SAS、Eviews等,对于计量经济学的初学者,学习该门课程的难度是很⼤的,因为内容涉及太多的数学知识,计算量很⼤。
在没有掌握专⽤的计量经济学软件之前,能否⽤计算机的常⽤办公软件Excel电⼦表格来解决计量经济学的有关问题呢?本⽂试图通过⼀个例⼦来说明计量经济学的问题是可以通过电⼦表格来解决的。
问题⼀:在美国对每周家庭收⼊(美元)与每周消费⽀出(美元)的抽样调查数据如下:(1)你认为Y与X之间是怎样的关系?(2)利⽤最⼩⼆乘法求样本回归函数,并预测当X=280(美元)时,Y 的值。
最⼩⼆乘法的原理是:在给定X和Y的⼀组观测值(X1 , Y1), (X2 , Y2) , ..., (Xn , Yn)的情况下, 求出Yt = α + βXt + ut 中α和β的估计值α?和β?, 使得拟合的直线为最佳。
拟合的直线X Yβα+=称为拟合的回归线。
(t=1,2,……,n ),et 代表观测点对于回归线的误差,称为拟合或预测的残差。
我们的⽬标是使拟合出来的直线在某种意义上是最佳的,直观地看,也就是要求估计直线尽可能地靠近各观测点,这意味着应使残差总体上尽可能地⼩。
要做到这⼀点,就必须⽤某种⽅法将每个点相应的残差加在⼀起,使其达到最⼩。
李子奈《计量经济学》第三版例题及习题的stata解答

第二章例.1(p24)(1)表中E(Y|X=800)即条件均值的求法,将数据直接复制到stata 中。
程序:sum y if x==800程序:程序:(2)图的做法: 程序:twoway(scatter y x )(lfit y x ),title("不同可支配收入水平组家庭消费支出的条件分布图")xtitle("每月可支配收入(元)")ytitle("每月消费支出(元)")xtick(500(500)4000)ytick(0(500)3500)、例.1(p37)将数据直接复制到stata中程序:(1)total xiyixiyi 4974750 1507821 1563822 8385678Total Std. Err. [95% Conf. Interval]return listscalars:-r(skip) = 0r(first) = 1r(k_term) = 0r(k_operator) = 0r(k) = 0r(k_level) = 0r(output) = 1r(b) = 4974750r(se) =g a=r(b) in 1#Scatter表示散点图选项,lfit表示回归线,title表示题目,xtick表示刻度,(500(500)4000)分别表示起始刻度,中间数表示以单位刻度,4000表示最后的刻度。
要注意的是命令中的符号都要用英文字符,否则命令无效。
这个图可以直接复制的,但是由于我的软件出问题,只能直接剪切,所以影响清晰度。
Total表示求和,return list命令可以引用其中的数据,接下来在第一列生成一个新的变量代表xiyi的和,同样生成一个b代表xi平方的,a除以b即可得到batatotal xi2return listg b=r(b) in 1di a/b.67(2)mean Yigen m=r(b) in 1mean Xi(g n=r(b) in 1di m-n*由此得到回归方程:Y=+例.2(p53)程序:(1)回归reg y x(2) >(3) 求X 的样本均值和样本方差:mean xx 11363.69 591.7041 10155.27 12572.11 Mean Std. Err. [95% Conf. Interval] Mean estimation Number of obs = 31sum x ,d (d 表示detail 的省略,这个命令会产生更多的信息)99% 20667.91 20667.91 Kurtosis 4.73926795% 19977.52 19977.52 Skewness 1.69197390% 16015.58 18265.1 Variance 1.09e+0775% 12192.24 16015.58Largest Std. Dev. 3294.46950% 9898.75 Mean 11363.6925% 9267.7 9000.35 Sum of Wgt. 3110% 9000.35 8941.08 Obs 31 5% 8920.59 8920.591% 8871.27 8871.27 Percentiles Smallest xdi r(Var)(特别注意Var 的大小写)例(P56) (1)reg Y X>Source SS df MS Number of obs = 29 F( 1, 27) = 2214.60 Model 2.4819e+09 1 2.4819e+09 Prob > F = 0.0000 Residual 30259023.9 27 1120704.59 R-squared = 0.9880 Adj R-squared = 0.9875 Total 2.5122e+09 28 89720219.8 Root MSE = 1058.6 Y Coef. Std. Err. t P>|t| [95% Conf. Interval]X .4375268 .0092973 47.06 0.000 .4184503 .4566033 _cons 2091.295 334.987 6.24 0.000 1403.959 2778.632(2)图的绘制:twoway (line Y X year),title("中国居民可支配总收入X与消费总支出Y 的变动图")~第三章例(p72)reg Y X1 X2&Source SS df MS Number of obs = 31F( 2, 28) = 560.57Model 166971988 2 83485994.2 Prob > F = 0.0000Residual 4170092.27 28 148931.867 R-squared = 0.9756Adj R-squared = 0.9739Total 171142081 30 5704736.02 Root MSE = 385.92Y Coef. Std. Err. t P>|t| [95% Conf. Interval]X1 .5556438 .0753076 7.38 0.000 .4013831 .7099046X2 .2500854 .1136343 2.20 0.036 .0173161 .4828547_cons 143.3266 260.4032 0.55 0.586 -390.0851 676.7383例.1(p85)g lnP1=ln(P1)g lnP0=ln(P0)g lnQ=ln(Q)g lnX=ln(X)Source SS df MS Number of obs = 22 F( 3, 18) = 258.84 Model .765670868 3 .255223623 Prob > F = 0.0000 Residual .017748183 18 .00098601 R-squared = 0.9773 Adj R-squared = 0.9736 Total .783419051 21 .037305669 Root MSE = .0314 lnQ Coef. Std. Err. t P>|t| [95% Conf. Interval]lnX .5399167 .0365299 14.78 0.000 .4631703 .6166631 lnP1 -.2580119 .1781856 -1.45 0.165 -.632366 .1163422 lnP0 -.2885609 .2051844 -1.41 0.177 -.7196373 .1425155 _cons 5.53195 .0931071 59.41 0.000 5.336339 5.727561 drop lnX lnP1 lnP0g lnXP0=ln(X/P0)g lnP1P0=ln(P1/P0)?reg lnQ lnXP0 lnP1P0Source SS df MS Number of obs = 22F( 2, 19) = 408.93Model .765632331 2 .382816165 Prob > F = 0.0000Residual .01778672 19 .000936143 R-squared = 0.9773Adj R-squared = 0.9749Total .783419051 21 .037305669 Root MSE = .0306lnQ Coef. Std. Err. t P>|t| [95% Conf. Interval]lnXP0 .5344394 .0231984 23.04 0.000 .4858846 .5829942lnP1P0 -.2753473 .1511432 -1.82 0.084 -.5916936 .040999_cons 5.524569 .0831077 66.47 0.000 5.350622 5.698515练习题13(p105)g lnY=ln(Y)g lnK=ln(K)g lnL=ln(L)reg lnY lnK lnLSource SS df MS Number of obs = 31 F( 2, 28) = 59.66 Model 21.6049266 2 10.8024633 Prob > F = 0.0000 Residual 5.07030244 28 .18108223 R-squared = 0.8099 Adj R-squared = 0.7963 Total 26.6752291 30 .889174303 Root MSE = .42554 lnY Coef. Std. Err. t P>|t| [95% Conf. Interval]lnK .6092356 .1763779 3.45 0.002 .2479419 .9705293 lnL .3607965 .2015915 1.79 0.084 -.0521449 .7737378 _cons 1.153994 .7276114 1.59 0.124 -.33645 2.644439第二问:test b_[lnk]+b_[lnl]==1*第四章¥例.4 (P116)(1)回归g lnY=ln(Y)g lnX1=ln(X1)g lnX2=ln(X2)reg lnY lnX1 lnX2Source SS df MS Number of obs = 31 F( 2, 28) = 49.60 Model 2.9609923 2 1.48049615 Prob > F = 0.0000 Residual .835744123 28 .029848004 R-squared = 0.7799 Adj R-squared = 0.7642 Total 3.79673642 30 .126557881 Root MSE = .17277 lnY Coef. Std. Err. t P>|t| [95% Conf. Interval]lnX1 .1502137 .1085379 1.38 0.177 -.072116 .3725435 lnX2 .4774534 .0515951 9.25 0.000 .3717657 .5831412 _cons 3.266068 1.041591 3.14 0.004 1.132465 5.39967于是得到方程:lnY=++(2)绘制参差图:"predict e, residg ei2=e^2scatter ei2 lnX2,title("图异方差性检验图")xtick(6ytick(0predict在回归结束后,需要对拟合值以及残差进行分析,需要使用此命令。
计量经济学实际案例

二、均值分析1、分性别对身高进行的比较假设男女身高相等,否定假设可认为男生身高明显高于女生。
2、分南北地区进行比较(1)身高假设两者均值相等,检验结果不能否定原假设,因而不能认为南北方身高有显著差异。
(2)体重通过假设两者均值相等,检验结果无法否定原假设,因而认为南北方体重没有明显差异。
3、分出生年份月份进行比较年份性别身高体重84 男均值172.00 56.00N 1 1总计均值172.00 56.00N 1 185 男均值180.33 70.67N 3 3女均值161.00 51.00N 2 2总计均值172.60 62.80N 5 586 男均值174.20 65.40N 20 20女均值162.11 52.28N 18 18总计均值168.47 59.1887 男均值178.50 66.58N 6 6女均值164.83 52.83N 18 18总计均值168.25 56.27N 24 2488 男均值170.50 65.00N 2 2女均值167.00 53.50N 2 2总计均值168.75 59.25N 4 489 女均值165.00 50.00N 1 1总计均值165.00 50.00N 1 1总计男均值175.28 65.80N 32 32女均值163.56 52.46N 41 41总计均值168.70 58.31N 73 73ANOVA 表由表可看出,各年份出生的人身高体重无显著性差异。
总计均值171.00 64.00N 6 6 3 男均值174.50 69.50N 4 4 女均值160.25 50.75N 4 4 总计均值167.38 60.13N 8 8 4 男均值181.25 68.50N 4 4 女均值162.25 52.00N 4 4 总计均值171.75 60.25N 8 8 5 男均值169.50 65.25N 2 2 女均值156.00 43.00N 1 1 总计均值165.00 57.83N 3 3 6 男均值175.00 63.00N 1 1 女均值171.50 57.50N 4 4 总计均值172.20 58.60N 5 5 7 男均值171.00 64.33N 3 3 女均值167.00 50.50N 2 2 总计均值169.40 58.80N 5 5 8 男均值179.20 64.90N 5 5 女均值161.50 52.50N 2 2 总计均值174.14 61.36N 7 7 9 男均值171.67 58.00N 3 3 女均值163.33 54.33N 3 3 总计均值167.50 56.1710 男均值174.67 61.83N 3 3总计均值174.67 61.83N 3 311 女均值162.50 51.67N 12 12总计均值162.50 51.67N 12 1212 男均值171.00 66.50N 2 2女均值167.00 57.00N 1 1总计均值169.67 63.33N 3 3总计男均值175.28 65.80N 32 32女均值163.56 52.46N 41 41总计均值168.70 58.31N 73 73ANOVA 表由表同样可得出,各月出生的人身高体重无显著性差异。
(1)用Excel作一元线性回归分析

实验四(1)用Excel作一元线性回归分析实验名称:回归分析实验目的:学会应用软件实验一元线性回归,多元线性回归和非线性回归模型的求解及应用模型解决相应地理问题。
1 利用Excel进行一元线性回归分析第一步,录入数据以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。
录入结果见下图(图1)。
图1第二步,作散点图如图2所示,选中数据(包括自变量和因变量),点击“图表向导”图标;或者在“插入”菜单中打开“图表(H)”。
图表向导的图标为。
选中数据后,数据变为蓝色(图2)(office2003)。
插入-图表(office2007)图2点击“图表向导”以后,弹出如下对话框(图3):图3在左边一栏中选中“XY散点图”,点击“完成”按钮,立即出现散点图的原始形式(图4):灌溉面积y(千亩)01020304050600102030灌溉面积y(千亩)图4第三步,回归观察散点图,判断点列分布是否具有线性趋势。
只有当数据具有线性分布特征时,才能采用线性回归分析方法。
从图中可以看出,本例数据具有线性分布趋势,可以进行线性回归。
回归的步骤如下:⑴ 首先,打开“工具”下拉菜单,可见数据分析选项(见图5)(office2003)。
数据-数据分析(office2007):图5 用鼠标双击“数据分析”选项,弹出“数据分析”对话框(图6):图6⑵然后,选择“回归”,确定,弹出如下选项表(图7):图7进行如下选择:X、Y值的输入区域(B1:B11,C1:C11),标志,置信度(95%),新工作表组,残差,线性拟合图(图8-1)。
或者:X、Y值的输入区域(B2:B11,C2:C11),置信度(95%),新工作表组,残差,线性拟合图(图8-2)。
注意:选中数据“标志”和不选“标志”,X、Y值的输入区域是不一样的:前者包括数据标志:最大积雪深度x(米)灌溉面积y(千亩)后者不包括。
这一点务请注意(图8)。
图8-1 包括数据“标志”图8-2 不包括数据“标志”⑶再后,确定,取得回归结果(图9)。
计量经济学EViews操作
计量经济学作业操作过程详解1.进入Eviews软件2.主菜单-->File--->Workfile3.打开工作文件范围选择框,选择Annual,分别输入1985,1998。
点击完成。
4.数据输入:方法一:导入excel文件中的数据1)在excel中先建立数据文件2)点击file/import/read text-lotus-excel选项,在对话框中选择已建立的excel文件4)打开后,在新的对话框中输入想要分析的变量名称,然后点击OK即可。
此时工作文件中出现变量图标。
方法二:手工数据输入主菜单--->Quick----->Empty Group分别输入变量Y、GDP的数据。
点击obs后面的灰色格子中分别输入Y、GDP。
(方法一:一个一个输入方法二:在Excel中输入完再复制粘贴)5.主菜单---->Quick----->Estimate Equation打开估计模型对话框,输入Y C GDP ,(如上图所示,注意字母之间要有空格)点击OK键。
得出Eviews的估计结果:其中12596.27为β(上面还要带个帽子,电脑打不出来),26.95415为1β。
第五步可以直接输入LS Y C GDP 等出结果6.一元线性回归模型的预测1)在工作文件主窗口点击procs/change workfile range(改变范围),弹出对话框,在对话框的end date栏中输入预测值的时间或序号,点击OK2)在工作文件窗口中双击解释变量文件,在变量窗口中点击edit+/-键,进入编辑模式,在变量窗口底端输入新序号的数值,再点击edit+/-键,关闭编辑模式3)再次进行估计,点击quick/estimate equation,在对话框中输入方程,注意样本范围应不包括新序号,点击OK得到估计结果4)点击结果窗口中的forecast键,产生对话框,在对话框中选择样本范围,点击OK可得预测曲线图。
计量经济学作业陈述部分
计量经济学作业陈述部分
β0的H0:β0=0; H1:β0≠0。
β1的H0:β1=0; H1:β1≠0。
在1%的显著性水平下,自由度为8的t分布的临界值是3.355。
t1的绝对值大于该临界值,说明解释变量收入在99%的置信度下显著,即通过了变量显著性检验;但t0的绝对值小于该临界值,表明在99%的置信度下,无法拒绝截距项为零的假设。
在5%的显著性水平下,自由度为8的t分布的临界值是2.306。
t1的绝对值大于该临界值,说明解释变量收入在95%的置信度下显著,即通过了变量的显著性检验;但t0的绝对值小于该临界值,表明在95%的置信度下,无法拒绝截距项为零的假设。
由EXCEL表格得:
(1)在显著性水平为5%下,β0的置信区间为(-326.4634622,110.5806339);β1的置信区间为(0.684606339,0.873292651)。
(2)可决系数R²=0.978407966
附:β1估=0.778949495 β0估=-107.9414141 β1估的标准差的估计值=0.040912036
β0估的标准差的估计值=94.7623799
t1=19.03961683 t0=-1.139074538
090320114丁宇菲。
经济学分析图解析图形表格
%responding:datamonitor heaith 48send/receive nobfications 46search 45track daity activity 45take pictures,audio,video 43tell time 42track exercise 41access video/audio content 38control smart home 28make mobite payments 28share health and data 25fashion accessory 25work purposes 24% of respondents data 截断误差2insurance (for definite discount)7038#N/Abrand (for lower prices)6938#N/Adoctor 6838#N/Ahealth industry subsidy 67380insurance(for potential discount)6738#N/Afamity 6638#N/A 0 10 20friends6438#N/A brand (advertising and promotion)6138#N/A employer5938Price respondents are wilting to paydata 100 or less11101-20024201-30025301-40020401-50011501-6006Over 600335 40 45 5100 orless 101-200 201-300 301-400 401-500 50作图数据第一组数据第二组数据%responding:data% of respondentsmonitor heaith48insurance (for definite discount)send/receive nobfications46brand (for lower prices)search45doctortrack daity activity45health industry subsidytake pictures,audio,video43insurance(for potential discount)tell time42famitytrack exercise41friendsaccess video/audio content38brand (advertising and promotion)control smart home28employermake mobite payments28share health and data25fashion accessory25work purposes2420 30 40 50步骤1删除图例,删除标题设置纵坐标标签为“无”刻度线为“无”,且逆序类别调整系类无间距为“40”设置刻度值最小为0,最大为50,间距为10,线条为“无”设置系列为RGB值为0,163,219设置背景色为无填充无线条设置网格线为灰色步骤2第二组数据需要对其进行处理因图表网格线中有不同颜色突出使用柱形图制作散点图选择误差2的数据插入柱形图删除图例,删除标题设置刻度值最大值为10选中柱形图添加误差线选中误差线那设置为“正偏差”“无线端”固定值为“10”颜色为“红”线粗为“1”设置横坐标轴在刻度线上选择数据与截断数据黏贴到图表中,选择新系列把新系列改成条形图把主纵坐标与横坐标设置不可见调出次要纵坐标设置次要横坐标 坐标交叉位置设置为“自动”,刻度值最大为70,最小为35,间距为5,无线条设置次要纵坐标为逆序刻度,横坐标轴交叉为“自动”,分列不显示,线条设置为白色,线粗比网格调出次要纵网格线设置条形图的重叠为100,间距为30画出截断图形,填充白色,复制图形后选择截断数据黏贴设置系列颜色设置横坐标数字显示格式[红色][=50]0;[>35]0;;设置背景无填充网格线灰色步骤3选择第三组数据插入柱形图设置刻度值为最大25,最小为0,设置无线条选中系列,设置分列间距为30,颜色设置为蓝色选中横坐标设置纵坐标交叉位置为“最大分类”,主要刻度线为“无”设置网格线为灰色设置背景无颜色步骤4对三个小图表进行排版成组图图表中分类标签为左对齐,这里使用文本框文字对齐因EXCEL图表中默认网格线与刻度值有一定距离而商业图表都是很靠近的所以这里需要模仿,做法为:复制一个一样大小的图表,底层只留刻度标签,其他设置无颜色顶层图表设置无刻度值,然后两个图表重叠,把顶层图表往上拉一点,让其与底层刻度靠近图1与图2排版好后,底部各画一个矩形填充白色放置图表最底层作为背景再绘制一个矩形填充灰色,放在两个图表最低端,遮住漏出来的一部分网格线,让系列与网格线平行第三个图表排版与上面图表一样,复制两个重叠45 50 55 60 65 70 0510152025501-600 Over 600用直线与文本框作为系列线与数据标记画矩形作为第三个图表背景选择整个图表区域设置单元格颜色为灰色进行美化第三组数据第二组辅助data Price respondents are wilting to pay data误差1误差2截断70100 or less110.238 69101-200240.238 68201-300250.238 67301-400200.238 67401-500110.238 66501-60060.238 64Over 60030.238 610.238 5938“1”小为35,间距为5,无线条线条设置为白色,线粗比网格线粗即可标签,其他设置无颜色让其与底层刻度靠近网格线,让系列与网格线平行。
计量经济学实验报告(范例)
3、估计参数
方法一:在EViews主页界面点击“Quick”菜单,点击“Estimate Equation”,出现“Equation specification”对话框,选OLS估计,即选击“Least Squares”,键入“Y C X”,点“ok”或按回车,即出现如表2那样的回归结果。
表表12002年中国各地区城市居民人均年消费支出和可支配收入地区城市居民家庭平均每人每年消费支出元y城市居民人均年可支配收入元x北京天津河北山西内蒙古辽宁吉林黑龙江上海江苏浙江安徽福建江西山东河南湖北湖南广东广西海南重庆四川贵州云南102846071919650692847109648598853426449738844620810464006042608713084736526631684549325596324504685608925574728988485413445459646360245413084598285827921246392933756667968523435605106652452626016610056132498081776411715606032409189366334647614366245406788526958561113720731532682272723804661080594408724056西藏陕西甘肃青海宁夏新疆695244527804506424504252610492563640807912633084615144617052606744689964作城市居民家庭平均每人每年消费支出y和城市居民人均年可支配收入x的散点图如图1
