数学实验(MATLAB版韩明版)5.1,5.3,5.5,5.6部分答案
MATLAB语言基础与应用(第二版)第5章 习题答案

第5章习题与答案5.1用矩阵三角分解方法解方程组123123123214453186920x x x x x x x x x +-=⎧⎪-+=⎨⎪+-=⎩ 解答:>>A=[2 1 -1;4 -1 3;6 9 -1] A =2 1 -1 4 -13 6 9 -1 >>b=[14 18 20]; b =14 18 20 >> [L, U, P]=lu(A) L =1.0000 0 0 0.6667 1.0000 0 0.3333 0.2857 1.0000 U =6.0000 9.0000 -1.0000 0 -7.0000 3.6667 0 0 -1.7143 P =0 0 1 0 1 0 1 0 0 >> y=backsub(L,P*b’) y =20.0000 4.6667 6.0000 >> x=backsub(U,y) x =6.5000 -2.5000 -3.5000 5.2 Cholesky 分解方法解方程组123121332352233127x x x x x x x ++=⎧⎪+=⎨⎪+=⎩ 解答:>> A=[3 2 3;2 2 0;3 0 12] A =3 2 32 2 03 0 12>> b=[5;3;7]b =537>> L=chol(A)L =1.7321 1.1547 1.73210 0.8165 -2.44950 0 1.7321>> y=backsub(L,b)y =-11.6871 15.7986 4.0415>> x=backsub(L',y)x =-6.7475 28.8917 49.93995.3解答:观察数据点图形>> x=0:0.5:2.5x =0 0.5000 1.0000 1.5000 2.0000 2.5000 >> y=[2.0 1.1 0.9 0.6 0.4 0.3]y =2.0000 1.1000 0.9000 0.6000 0.4000 0.3000 >> plot(x,y)图5.1 离散点分布示意图从图5.1观察数据点分布,用二次曲线拟合。
数学实验(MATLAB)课后习题答案
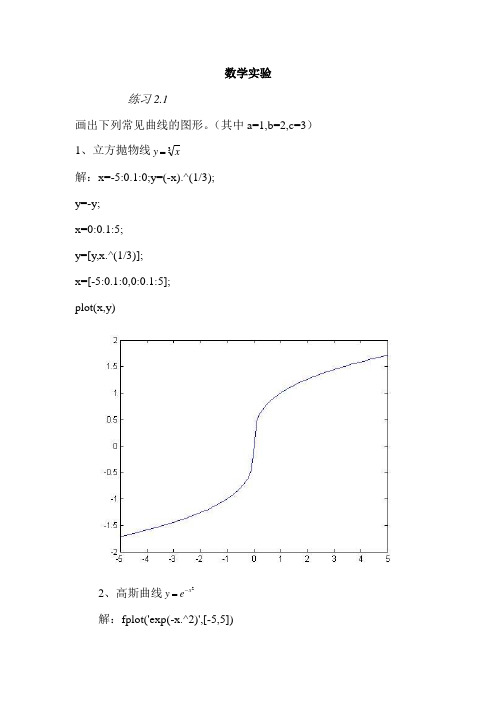
数学实验练习2.1画出下列常见曲线的图形。
(其中a=1,b=2,c=3)1、立方抛物线3xy=解:x=-5:0.1:0;y=(-x).^(1/3);y=-y;x=0:0.1:5;y=[y,x.^(1/3)];x=[-5:0.1:0,0:0.1:5];plot(x,y)2、高斯曲线2x e=y-解:fplot('exp(-x.^2)',[-5,5])3、笛卡儿曲线)3(13,1333222axy y x t at y t at x =++=+=解:ezplot('x.^3+y.^3-3*x*y',[-5,5])xyx.3+y.3-3 x y = 0或t=-5:0.1:5; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)4、蔓叶线)(1,1322322xa x y t at y t at x -=+=+=解:ezplot('y.^2-x.^3/(1-x)',[-5,5])xyy.2-x.3/(1-x) = 0或t=-5:0.1:5; x=t.^2./(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)5、摆线)cos 1(),sin (t b y t t a x -=-= 解:t=0:0.1:2*pi;x=t-sin(t); y=2*(1-cos(t)); plot(x,y)6、星形线)(sin ,cos 32323233a y x t a y t a x =+== 解:t=0:0.1:2*pi; x=cos(t).^3; y=sin(t).^3;plot(x,y)或ezplot('x.^(2/3)+y.^(2/3)-1',[-1,1])xyx.2/3+y.2/3-1 = 07、螺旋线ct z t b y t a x ===,sin ,cos 解:t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z) grid on8、阿基米德螺线θa r = 解:x =0:0.1:2*pi; r=x; polar(x,r)902701809、对数螺线θa e r = 解:x =0:0.1:2*pi; r=exp(x); polar(x,r)90270180010、双纽线))()((2cos 22222222y x a y x a r -=+=θ 解:x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-(x.^2-y.^2)',[-1,1]) grid onxy(x.2+y.2).2-(x.2-y.2) = 011、双纽线)2)((2sin 222222xy a y x a r =+=θ 解:x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-2*x*y',[-1,1]) grid onxy(x.2+y.2).2-2 x y = 012、心形线)cos 1(θ+=a r 解:x =0:0.1:2*pi; r=1+cos(x); polar(x,r)90270练习2.21、求出下列极限值。
高等数学实验报告matlab参考答案

成都大学高等数学实验报告(MATLAB版)班级姓名学号注意:1 这个答案可由教师保存;2 每个班级注意保存实验报告。
成都大学高等数学教研室2011年3月高等数学实验报告1 基本计算与作图班级 姓名 学号 完成时间 成绩一、实验内容基本计算,函数的表示,函数图形的显示.二、预期目标1.熟悉Matlab 软件的基本操作.2.掌握基本计算,函数的表示与函数的作图命令.3.学会利用Matlab 软件对函数进行分析研究.三、练习内容习题一1.计算下列各式的值:(写出格式及执行结果,(1)为例式) (1)1675; >> 75^16ans = 1.0023e+030 (2)i31-; (3)23sin ;>> sqrt(1-3*i) >>sin(23*pi/180) ans = 1.4426 - 1.0398i ans = 0.3907 (4)π2arcsin; (5)!88.>> asin(2/pi) >> factorial(88) ans = 0.6901 ans = 1.8548e+134 2.3tan,2π==b e a e,计算:(1)5332532b a ab a -+; (2))sec(arctana .>> a=sqrt(exp(exp(1))); b=tan(pi^2/3); >> a=sqrt(exp(exp(1))); b=tan(pi^2/3); >> 2*a^2+3*a*b^3-5*a^3*b^5 >> sec(atan(a)) ans =30.3255 ans =4.0192 3.在计算机上练习以下语句的输入:((1)为求解格式)(1)143212-+x bx ax ; (2)13ln 42sin 2+-⎪⎭⎫ ⎝⎛+x x x π;>> syms a b x >> syms x>> (3*a*x^2+4*b*x^(1/2))/(x-1) >> (sin(2*x+pi/4)-log(3*x))/sqrt(x^2+1)ans =(3*a*x^2+4*b*x^(1/2))/(x-1) ans = (sin(2*x+1/4*pi)-log(3*x))/(x^2+1)^(1/2) (3)xex x 22)2sin (cos -.>> syms x>> (cos(x)^2-sin(2*x))*exp(2*x) ans =(cos(x)^2-sin(2*x))*exp(2*x) 习题二(只写出输入格式) 1.作出13y x =的图象>> x=linspace(0,3,100); >> y=x.^(1/3); >> plot(x,y) 参见图12.作出14xy ⎛⎫=⎪⎝⎭的图象 3.作出14log y x =的图象 >> x=linspace(-2,2,50); >> fplot('log(x)/log(1/4)',[0.1,3])>> y= (1/4).^x; >> plot(x,y)参见图2 参见图3图1图2 图34.作出sin(2)4y x π=+在一个周期内的图象 5.作分段函数2,0()1,0x x f x x x ⎧≤=⎨+>⎩的图象。
MATLAB数学实验答案(全)

MATLAB数学实验答案(全)第⼀次练习教学要求:熟练掌握Matlab 软件的基本命令和操作,会作⼆维、三维⼏何图形,能够⽤Matlab 软件解决微积分、线性代数与解析⼏何中的计算问题。
补充命令vpa(x,n) 显⽰x 的n 位有效数字,教材102页fplot(‘f(x)’,[a,b]) 函数作图命令,画出f(x)在区间[a,b]上的图形在下⾯的题⽬中m 为你的学号的后3位(1-9班)或4位(10班以上) 1.1 计算30sin limx mx mx x →-与3sin lim x mx mxx →∞-syms xlimit((902*x-sin(902*x))/x^3) ans =366935404/3limit((902*x-sin(902*x))/x^3,inf)//inf 的意思 ans = 0 1.2 cos1000xmxy e =,求''y syms xdiff(exp(x)*cos(902*x/1000),2)//diff 及其后的2的意思 ans =(46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算221100x y edxdy +??dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1)//双重积分 ans = 2.13941.4 计算4224x dx m x +? syms xint(x^4/(902^2+4*x^2))//不定积分 ans =(91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求//⾼阶导数syms xdiff(exp(x)*cos(902*x),10) ans =-356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x)1.6 0x =的泰勒展式(最⾼次幂为4).syms xtaylor(sqrt(902/1000+x),5,x)//泰勒展式 ans =-(9765625*451^(1/2)*500^(1/2)*x^4)/82743933602 +(15625*451^(1/2)*500^(1/2)*x^3)/91733851-(125*451^(1/2)*500^(1/2)*x^2)/406802 + (451^(1/2)*500^(1/2)*x)/902 +(451^(1/2)*500^(1/2))/500 1.7 Fibonacci 数列{}n x 的定义是121,1x x ==12,(3,4,)n n n x x x n --=+=⽤循环语句编程给出该数列的前20项(要求将结果⽤向量的形式给出)。
数学实验作业1--答案

数学实验-作业1—及部分答案(要求:1. 每次上机课下课之前提交,文件名如:数学091朝鲁第一次作业.doc。
2. 交至邮箱:matlabzuoyetijiao@3.作业实行5分制,依次为A++,A+,A ,A-,A- -)4.作业中,需要编程实现的均要求列出你的代码,以及求解的结果)1.请上网或查阅各种资料并回答:MATLAB是什么?MATLAB能做什么?答:略2.请上网或查阅各种资料并回答:MATLAB语言突出的特点是什么?答:略3.在MATLAB软件中有几种获得帮助的途径?答:help函数,菜单栏help菜单。
4.请上网或查询MATLAB软件中inv函数的功能与特点。
答:用来求可逆矩阵的逆矩阵。
inv(A),即求已知矩阵A的逆矩阵。
5.请上网或查阅各种资料并回答:如何在MATLAB中建立向量和矩阵。
答:如在matlab中创建向量a=(2,-5,6,1);a=[2,-5,6,1];b= [2;-5;6;1];如在matlab中创建矩阵A=;A=[1,2,3;4,5,6;7,8,9];A =1 2 34 5 67 8 96.请上网或查阅各种资料并回答:在MATLAB中,向量和矩阵如何进行基本加减乘除四则运算,以及矩阵的乘法。
答:a=[2,-5,6,1];b= [1,2,3,4];求向量的和与差,直接输入a+b,a-b,即可,当然必须要求两个向量大小一致。
如:>> a=[2,-5,6,1];b= [1,2,3,4];>> a+bans =3 -3 9 5>> a-b1 -7 3 -3>> a.*bans =2 -10 18 4>> a./bans =2.0000 -2.5000 2.0000 0.2500>> a/b向量之间进行除法运算,使用不加点的矩阵除法“A/B”时,问题可以描述为:给定两个向量A、B,求一个常量x,使得A=x * B。
(完整版)MATLAB)课后实验答案[1]
![(完整版)MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/306ff29b690203d8ce2f0066f5335a8102d266cb.png)
(完整版)MATLAB)课后实验答案[1]实验⼀ MATLAB 运算基础1. 先求下列表达式的值,然后显⽰MATLAB ⼯作空间的使⽤情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =,其中2120.455i x +??=?- (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--L (4) 2242011122123t t z t t t t t ?≤=-≤,其中t =0:0.5:2.5 解:4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建⽴⼀个字符串向量,删除其中的⼤写字母。
解:(1) 结果:(2). 建⽴⼀个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:实验⼆ MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S=?,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对⾓阵,试通过数值计算验证2 2E R RS A O S +??=。
解: M ⽂件如下;5. 下⾯是⼀个线性⽅程组:1231112340.951110.673450.52111456x x x ??=???(1) 求⽅程的解。
(2) 将⽅程右边向量元素b 3改为0.53再求解,并⽐较b 3的变化和解的相对变化。
(3) 计算系数矩阵A 的条件数并分析结论。
解: M ⽂件如下:123d4e56g9实验三选择结构程序设计1. 求分段函数的值。
2226035605231x x x x y x x x x x x x ?+-<≠-?=-+≤<≠≠??--?且且及其他⽤if 语句实现,分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y 值。
解:M ⽂件如下:2. 输⼊⼀个百分制成绩,要求输出成绩等级A、B、C、D、E。
数学实验,课后题参考解答

>> D=det(A)
D =
a11*a22 - a12*a21
>> Y=inv(A)
Y =
[ a22/(a11*a22 - a12*a21), -a12/(a11*a22 - a12*a21)]
[ -a21/(a11*a22 - a12*a21), a11/(a11*a22 - a12*a21)]
>> bar(x,y)
>> bar(x,y,'stack')
6.
>> x=[60 43 51 26 19];
>> explode=[0 0 0 0 1];
>> pie(x,explode)
第四章习题
1.(P82)
>> syms x y;
>> f=(x^2-y^2)/(x^2+y^2);
>> limit(limit(f,y,0),x,0)
y =
(x*((- 4*x^2 + 4*x + 1)/x^2)^(1/2))/2 + 1/2
(8)
>> syms a n x0 V0;
>> x=dsolve('D2x+2*n*Dx+a^2*x','x(0)=x0','Dx(0)=V0');
>> x=simplify(x)
x =
(exp(-t*(n - (n^2 - a^2)^(1/2)))*(V0 + n*x0 + x0*(n^2 - a^2)^(1/2)))/(2*(n^2 - a^2)^(1/2)) - (exp(-t*(n + (n^2 - a^2)^(1/2)))*(V0 + n*x0 - x0*(n^2 - a^2)^(1/2)))/(2*(n^2 - a^2)^(1/2))
MATLAB)课后实验答案[1]
![MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/e6c0efc2e2bd960591c67719.png)
真验一 MATLAB运算前提之阳早格格创做1. 先供下列表白式的值,而后隐现MATLAB处事空间的使用情况并保存局部变量.(1)0 122sin851ze =+(2)21ln( 2z x=+,其中2120.455i x+⎡⎤=⎢⎥-⎣⎦(3)0.30.330.3sin(0.3)ln, 3.0, 2.9,,2.9,3.0 22a ae e az a a--+=++=--(4)2242011122123t tz t tt t t⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t解:4. 完毕下列支配:(1) 供[100,999]之间能被21整除的数的个数.(2) 修坐一个字符串背量,简略其中的大写字母.解:(1) 截止:(2). 修坐一个字符串背量比圆:ch='ABC123d4e56Fg9';则央供截止是:真验二 MATLAB矩阵领会与处理1. 设有分块矩阵33322322E RAO S⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E、R、O、S分别为单位矩阵、随机矩阵、整矩阵战对于角阵,试通过数值估计考证22E R RS AO S+⎡⎤=⎢⎥⎣⎦.解: M文献如下;5. 底下是一个线性圆程组:(1) 供圆程的解.(2) 将圆程左边背量元素b3改为0.53再供解,并比较b3的变更妥协的相对于变更.(3) 估计系数矩阵A的条件数并领会论断.解: M文献如下:真验三采用结构步调安排1. 供分段函数的值.用if语句真止,分别输出x=-5.0,-3.0,1.0,2.0,2.5,3.0,5.0时的y值.解:M文献如下:2. 输进一个百分造结果,央供输出结果等第A、B、C、D、E.其中90分~100分为A,80分~89分为B,79分~79分为C,60分~69分为D,60分以下为E.央供:(1) 分别用if语句战switch语句真止.(2) 输进百分造结果后要推断该结果的合理性,对于分歧理的结果应输出堕落疑息.解:M文献如下3. 硅谷公司职工的人为估计要领如下:(1) 处事时数超出120小时者,超出部分加收15%.(2) 处事时数矮于60小时者,扣收700元.(3) 其余按每小时84元计收.试编程按输进的工号战该号职工的工时数,估计应收人为.解:M文献下真验四循环结构步调安排1. 根据2222211116123nπ=++++,供π的近似值.当n分别与100、1000、10000时,截止是几?央供:分别用循环结媾战背量运算(使用sum函数)去真止.解:M文献如下:运止截止如下:2. 根据11113521yn=++++-,供:(1) y<3时的最大n值.(2) 与(1)的n值对于应的y值.解:M—文献如下:3. 思量以下迭代公式:其中a、b为正的教数.(1) 编写步调供迭代的截止,迭代的末止条件为|x n+1-x n|≤10-5,迭代初值x0=1.0,迭代次数没有超出500次.(2) 如果迭代历程支敛于r,那么r的准确值是(a,b)的值与(1,1)、(8,3)、(10,0.1)时,分别对于迭代截止战准确值举止比较.解:M 文献如下:运算截止如下;5. 若二个连绝自然数的乘积减1是素数,则称那二个边陲自然数是亲稀数对于,该素数是亲稀素数.比圆,2×3-1=5,由于5是素数,所以2战3是亲稀数,5是亲稀素数.供[2,50]区间内:(1) 亲稀数对于的对于数.(2) 与上述亲稀数对于对于应的所有亲稀素数之战. 解:M 文献:真验五 函数文献4. 设2411()(2)0.1(3)0.01f x x x =+-+-+,编写一个MATLAB 函数文献fx.m ,使得调用f(x)时,x 可用矩阵代进,得出的f(x)为共阶矩阵.解:运算截止:5. 已知(40)(30)(20)fyf f=+(1) 当f(n)=n+10ln(n2+5)时,供y的值.(2) 当f(n)=1×2+2×3+3×4+...+n×(n+1)时,供y的值.解:(1)(2).真验八数据处理与多项式估计2. 将100个教死5门功课的结果存进矩阵P中,举止如下处理:(1) 分别供每门课的最下分、最矮分及相映教死序号.(2) 分别供每门课的仄衡分战尺度圆好.(3) 5门课总分的最下分、最矮分及相映教死序号.(4) 将5门课总分按从大到小程序存进zcj中,相映教死序号存进xsxh.提示:上机调试时,为预防输进教死结果的贫苦,可用与值范畴正在[45,95]之间的随机矩阵去表示教死结果.解:M文献:运止截止:3. 某局里瞅测得某日6:00~18:00之间每隔2h的室内中温度(0C)如真验表1所示.真验表1 室内中温度瞅测截止(0C)时间h 6 8 10 12 14 16 18试用三次样条插值分别供出该日室内中6:30~18:30之间每隔2h各面的近似温度(0C).解:M文献:运止截止:4. 已知lgx正在[1,101]区间10个整数采样面的函数值如真验表2所示.真验表2 lgx正在10个采样面的函数值x 1 11 21 31 41 51 61 71 81 91 101试供lgx的5次拟合多项式p(x),并画造出lgx战p(x)正在[1,101]区间的函数直线.解:M文献:5. 有3个多项式P1(x)=x4+2x3+4x2+5,P2(x)=x+2,P3(x)=x2+2x+3,试举止下列支配:(1) 供P(x)=P1(x)+P2(x)P3(x).(2) 供P(x)的根.(3) 当x与矩阵A的每一元素时,供P(x)的值.其中:(4) 当以矩阵A为自变量时,供P(x)的值.其中A的值与第(3)题相共.解:M文献:真验九 数值微积分与圆程数值供解1. 供函数正在指定面的数值导数.真验六 下层画图支配3. 已知正在-5≤x ≤5区间画造函数直线.解:M 文献:2. 用数值要领供定积分.(1)210I π=⎰的近似值. (2) 2220ln(1)1x I dt x π+=+⎰ 解:M 文献:运止截止:3. 分别用3种分歧的数值要领解线性圆程组.解:M文献:运止截止:4. 供非齐次线性圆程组的通解.解:M文献:.5. 供代数圆程的数值解.(1) 3x+sin x-e x=0正在x0=1.5附近的根.(2) 正在给定的初值x0=1,y0=1,z0=1下,供圆程组的数值解.解:M文献:(2). M文献:运止截止:6. 供函数正在指定区间的极值. (1)3cos log ()x x x x x f x e ++=正在(0,1)内的最小值. (2) 33212112122(,)2410f x x x x x x x x =+-+正在[0,0]附近的最小值面战最小值.解:M 文献:8. 供微分圆程组的数值解,并画造解的直线. 解: 令y1=x,y2=y,y3=z; 那样圆程形成: '''0.51(0)0,(0)1,(0)1x yz y xz z xyx y z =⎧⎪=-⎪⎨=-⎪⎪===⎩,自变量是tM 文献:真验十 标记估计前提与标记微积分 一、1. 已知x=6,y=5,利用标记表白式供提示:定义标记常数x=sym(‘6’),y=sym(‘5’).解:M文献:运止截止:2. 领会果式.(1) x4-y4(2) 5135解:M文献:运止截止:5. 用标记要领供下列极限或者导数.解:M文献:运止截止:6. 用标记要领供下列积分.解:M文献:运止截止:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练习B的分布规律和分布函数的图形,通过观1、仿照本节的例子,分别画出二项分布()7.0,20察图形,进一步理解二项分布的性质。
解:分布规律编程作图:>> x=0:1:20;y=binopdf(x,20,;>> plot(x,y,'*')图像:yx分布函数编程作图:>> x=0::20;>>y=binocdf(x,20,>> plot(x,y)图像:《1x观察图像可知二项分布规律图像像一条抛物线,其分布函数图像呈阶梯状。
2、仿照本节的例子,分别画出正态分布()25,2N的概率密度函数和分布函数的图形,通过观察图形,进一步理解正态分布的性质。
解:概率密度函数编程作图:>> x=-10::10;>> y=normpdf(x,2,5);>> plot(x,y)图像:00.010.020.030.040.050.060.070.08x y分布函数编程作图:>> x=-10::10;>> y=normcdf(x,2,5);~>> plot(x,y)图像:01x y观察图像可知正态分布概率密度函数图像像抛物线,起分布函数图像呈递增趋势。
3、设()1,0~N X ,通过分布函数的调用计算{}11<<-X P ,{}22<<-X P , {}33<<-X P .解:编程求解:>> x1=normcdf(1)-normcdf(-1),x2=normcdf(2)-normcdf(-2),x3=normcdf(3)-normcdf(-3) x1 =x2 =)x3 =即:{}6827.011=<<-X P ,{}9545.022=<<-X P ,{}9973.033=<<-X P .4、设()7.0,20~B X ,通过分布函数的调用计算{}10=X P 与{}10<X P .解:编程求解:>> x1=binopdf(10,20,,x2=binocdf(10,20,-binopdf(10,20,x1 =x2 =即:{}0308.010==X P ,{}0171.010=<X P5、设()8~P X ,求:(1){}4≤X P ;(2){}52≤<X P .解:(1)编程求解:>> p=poisscdf(4,8)p =,即:{}0996.04=≤X P (2)编程求解:>> p=poisscdf(5,8)-poisscdf(2,8)p =即:{}1775.052=≤<X P6、(1)设()1,0~N X ,求01.0z ;(2)对2χ分布,求()8205.0χ;(3)对()1305.0t ;(4)对F 分布,求()10,1505.0F 。
解:(1)编程求解:>> norminvans =即:3263.201.0=z(2)编程求解:>> chi2inv,8)ans ='即:()5073.158205.0=χ (3)编程求解:>> tinv,13)ans =即:()7709.11305.0=t(4)编程求解:>> finv,15,10)ans =即:()8450.210,1505.0=F7、分别生成26⨯个和16⨯个均匀分布()1,0U 的随机数。
解:编程求解:>> A=unifrnd(0,1,6,2),B=rand(6,1)A =】B =@练习1.设()11,1~U X ,求该均匀分布的均值和方差。
解:编程求解:>> [m,v]=unifstat(1,11)m = 6v =2.设()16,0~N X ,求该正态分布的均值、标准差与方差。
解:编程求解:>> x=normrnd(0,16,5,5);\>> s=std(x),[m,v]=normstat(0,16)s =m = 0v = 2563.生成6列服从标准正态分布的随机数,每列200个数,每列中,标准差的均值都为1.解:编程如下:>> x=normrnd(0,1,200,6)x =%$、:、·&* ,~—|` ," { ;~ (,4、首先生成正态分布()16,0N 的容量为300的随机数的样本,然后画正态分布()16,0N 的直方图。
解:编程求解:>> x=normrnd(0,16,300,1); >> hist(x,7)/图像:0102030405060708090100xy练习1.泥厂用自动包装机包装水泥,每袋额定重量是kg 50,某日开工后随机抽查了9袋,称得重量如下: .设每袋重量服从正态分布,问包装机工作是否正常(取显著性水平05.0=α.) 解:假设检验:50,50::10≠=μμH H 编程如下:>> x=[ ]; >> [h,sig,ci]=ttest(x,50) h = 0 sig =.ci = 检验结果为:①布尔值h=0说明表示在显著性水平为下接受原假设0H ,说明包装机工作正常。
②置信水平为的置信区间为()3122.50,4878.49,它包含50,因此接受原假设。
③05.05911.0>=sig ,也说明能接受“包装机正常工作”的假设。
2.某工厂生产的某种型号的电池,其寿命(以小时计)长期以来服从方差为5000的正态分布,现有一批这种电池,从它的生产情况来看,寿命的波动性有所改变.现随机取26只电池,测出其寿命的样本方差9200=s .问根据这一数据能否推断这批电池的寿命的波动性较以往的有显著的变化(取显著性水平05.0=α.)解:假设检验:5000:5000:10≠=sig H sig H , 编程如下:建立M 文件,命名为:Untitled sigma0=5000; % 总体原始方差 sigma1=9200; % 样本方差&alpha=; % 显著性水平 n=26; % 样本容量chi2stat=(n-1)*sigma1/sigma0; % 卡方检验统计量 criticalValue1 =chi2inv(alpha/2,n-1); % 临界值 criticalValue2=chi2inv(1-alpha/2,n-1); % 临界值if (chi2stat>criticalValue1&&chi2stat<criticalValue2) % 判断并显示结论 disp('接受原假设,认为方差没有改变') elsedisp('拒绝原假设,认为方差发生了改变') end《运行M 文件,得结果:拒绝原假设,认为方差发生了改变3、某地某年高考后随机抽得15名男生、12名女生的数学考试成绩如下:男生:119 118 117 123 121 113 109 127 116 116 112 114 125 114 110女生:116 110 117 121 113 106 113 108 118 124 118 104从这27名学生的成绩能说明这个地区男、女生的数学考试成绩不相上下吗(显著性水平05.0=α.)解:假设:210:μμ=H验证数学成绩服从正态分布编程如下:>> x1=[119 118 117 123 121 113 109 127 116 116 112 114 125 114 110]; >> x2=[116 110 117 121 113 106 113 108 118 124 118 104]; >> subplot(1,2,1);normplot(x1);subplot(1,2,2);normplot(x2)`图像:1101151201250.020.05 0.10 0.250.50 0.75 0.900.950.98 DataP r o b a b i l i t yNormal Probability Plot1051101151200.050.10 0.250.500.750.900.95 DataP r o b a b i l i t yNormal Probability Plot由于正太概率图都显示出直线形态,因此数据x1和数据x2都可以认为如从正态分布. 检验编程如下:>> x1=[119 118 117 123 121 113 109 127 116 116 112 114 125 114 110]; >> x2=[116 110 117 121 113 106 113 108 118 124 118 104];>> [pt,sigt]=ttest2(x1,x2) pt = 0 sigt =可见,男、女生数学成绩不相上下,没有显著差异,接受假设。
·4、下面列出84个伊特拉斯坎男子头颅的最大宽度(单位:mm ):141 148 132 138 154 142 150 146 155 158 150 140 147 148 144 150 149 145 149 158 143 141 144 144 126 140 144 142 141 140 145 135 147 146 141 136 140 146 142 137 148 154 137 139 143 140 131 143 141 149 148 135 148 152 143 144 141 143 147 146 150 132 142 142 143 153 149 146 149 138 142 149 142 137 134 144 146 147 140 142 140 137 152 145请检验上述头颅的最大宽度数据是否来自正态总体(显著性水平05.0=α.) 解:编程:x=[141 148 132 138 154 142 150 146 155 158 150 140 147 148 144 150 149 145 149 158 143 141 144 144 126 140 144 142 141 140 145 135 147 146 141 136 140 146 142 137 148 154 137 139 143 140 131 143 141 149 148 135 148 152 143 144 141 143 147 146 150 132 142 142 143 153 149 146 149 138 142 149 142 137 134 144 146 147 140 142 140 137 152 145]; >> normplot(x) 图像:1301351401451501550.0030.01 0.02 0.05 0.10 0.25 0.50 0.75 0.90 0.95 0.98 0.990.997DataP r o b a b i l i t yNormal Probability Plot由于正太概率图都显示出直线形态,因此数据x1和数据x2都可以认为如从正态分布. 5、在一批灯泡中抽取300只做寿命试验,获得的数据见下表.对于给定的显著性水平05.0=α,问这批灯泡的寿命是否服从指数分布()⎩⎨⎧≤≥=-0,0,0,005.0t t e t f t ~解:编程:>> t=0:100:300; >> h=[121 78 43 58]; >> pi=*exp(-t* pi = >> t=[400 500 600 700];>> sum*exp(-t*) ans = >> n=300;>> sum((h-n*pi).^2/(n*pi)) ans = +003)>> syms x>> ff=@(x)(chi2pdf(x,4)); >> p=quadl(ff,ans,10000) p = 0由于α=<=05.00p ,所以显著性水平05.0=α下,这批灯泡的寿命不如从指数分布。
