理论力学第一章 质点力学-3
合集下载
理论力学1-3动 力 学1
y
i
j
i
j
0
质点系内力主矩为0
动量定律
•质点系的动量
质点系动量定理
(e) (i ) (e ) (i ) dpi dpi Fi Fi 0 Fi Fi dt dt dp 质点系的总动量对时间的导数 FR 等于作用于质点系的外力主矢 力重不能自举，须人乃举。 dt
动量矩定律
动量矩守恒定理
质点系动量矩定理
(e ) dLo Mo dt
１、
if
(e) Mo 0
then Lo C
２、
if
M
(e) l
0
then Ll C
动量矩定律
质点系动量矩定理
例题１：水平杆以角速度绕铅垂轴Oz转动。杆上有用一细绳连接 质量分别为mA=2(kg) 和 mB=0.5(kg)的物块A和B，两物块可沿水 平杆滑动。绳长为l=1(m)。已知当物块A离Oz轴的距离rA=0.6(m) 时，它相对与水平杆的速度vA=0.4(m/s),方向沿Ox轴；而此时水平 杆绕Oz轴的角速度 =0.5(rad/s),试求该瞬时水平杆的角加速度。 水平杆和细绳的质量及轴承的摩擦均略去不计。
动力学基本定律 质点运动微分方程
例：求解质量为ｍ的平面单摆中绳的张力。已知 t=0，=o，v=vo。 解: S l v S l S l
o
ml mg sin
FT
n
m
mg
2 FT mg cos ml d 1 2 g ( ) sin d 2 l 2 vo 2g 2 (cos 1) 2 l l 2 vo FT mg ((3 cos 2) 2 ) l
理论力学第一章质点力学
（3）牛顿第三定律
F1 F2
分别作用在两个物体上
重点加深理解的几个问题
(1)牛顿定律是经典力学的基础，核心是牛顿 第二定律； (2)三个定律相互独立;牛顿第一定律是牛顿 第二定律的前提. 牛顿第一定律定义了惯性系,对力给出了定性 定义(力是改变运动状态的原因). 牛顿第三定律与参考系选择无关. (但第三定律只对接触力严格成立). (3) 质量 引力质量＝惯性质量
二、经典力学的相对性原理
（1）惯性系与非惯性系 地球系可近似视为惯性系
x x vt y y （2）伽利略变换式 (不同惯性系之间的变换) z z t t
（3）相对性原理 (不同惯性系之间)
a a
相对性原理的实质:物理定律在不同惯性系是相同的 (物理规律是绝对的)
约束反作用力不作功.
例如 曲面约束的物理意义则表现为曲面的支撑力.
*关于力的属性的说明(3)
保守力、非保守力与耗散力
(线积分)
力的功 W
B
A
B F dr Fx dx Fy dy Fz dz 一般与路径有关.
A
若力的功(线积分)与实际路径无关,仅与始末位置有关, 这种力称为保守力(保守力场). (1)保守力必然存在势能函数
(转动参考系的牵连加速度为 a [ r ( r )] )
(平动参照系的平移加速度为 a0
ma0
)
(3).柯里奥利惯性力 Fc0 2m v
(转动参考系的柯里奥利加速度为aco 2 v
速度矢量方向沿轨道切线方向(运动方向)。
加速度矢量
a lim
t 0
F1 F2
分别作用在两个物体上
重点加深理解的几个问题
(1)牛顿定律是经典力学的基础，核心是牛顿 第二定律； (2)三个定律相互独立;牛顿第一定律是牛顿 第二定律的前提. 牛顿第一定律定义了惯性系,对力给出了定性 定义(力是改变运动状态的原因). 牛顿第三定律与参考系选择无关. (但第三定律只对接触力严格成立). (3) 质量 引力质量＝惯性质量
二、经典力学的相对性原理
（1）惯性系与非惯性系 地球系可近似视为惯性系
x x vt y y （2）伽利略变换式 (不同惯性系之间的变换) z z t t
（3）相对性原理 (不同惯性系之间)
a a
相对性原理的实质:物理定律在不同惯性系是相同的 (物理规律是绝对的)
约束反作用力不作功.
例如 曲面约束的物理意义则表现为曲面的支撑力.
*关于力的属性的说明(3)
保守力、非保守力与耗散力
(线积分)
力的功 W
B
A
B F dr Fx dx Fy dy Fz dz 一般与路径有关.
A
若力的功(线积分)与实际路径无关,仅与始末位置有关, 这种力称为保守力(保守力场). (1)保守力必然存在势能函数
(转动参考系的牵连加速度为 a [ r ( r )] )
(平动参照系的平移加速度为 a0
ma0
)
(3).柯里奥利惯性力 Fc0 2m v
(转动参考系的柯里奥利加速度为aco 2 v
速度矢量方向沿轨道切线方向(运动方向)。
加速度矢量
a lim
t 0
理论力学(周衍柏)第一章质点力学
（1）矢量形式的运动学方程
rr(t)
理论力学：Theoretical mechanics 当质点运动时r是时间t的单值连续函数。此方程常用来 进行理论推导。它的特点是概念清晰，是矢量法分析质点 运动的基础。
（2）直角坐标形式的运动学方程
x x(t)
y
y (t)
z z ( t )
这是常用的运动学方程，尤其当质点的轨迹未知时。它是 代数方程，虽然依赖于坐标系，但是运算容易。
说明： ① 参照物不同，对同一个物体运动的描述结果可能不同；
② 观察者是站在参照系的观察点上； ③ 不特别说明都以地球为参照系。
2. 坐标系
理论力学：Theoretical mechanics 为了定量研究的空间位置，就必须在参考系上建立坐标 系。参照系确定后，在参照系上选择适宜的坐标系，便于 用教学方式描述质点在空间的相对位置（方法）。
ji
解： 确定动系和静系 静系：河岸 动系：河流 研究对象：小船
理论力学：Theoretical mechanics
:0 牵连速度， ： 绝对速度， :相 对 速度
ji
由：
0
0
c2i
r d
dt
j
c1 cosi c1 sin
j
i
选取极坐标, 得
理论力学：Theoretical mechanics
0:人行走速度， ： 风速(相对于地)， :风 相对于人的速
度 由：
得： 理论力学：Theoretical mechanics
得： 解得：
y
2
2
理论力学：Theoretical mechanics
因此：x 4,y 4
风速： x2y2 4 2km/h
理论力学第一章质点力学(3)
这时 闭合路径积分等于零
F dr F dl 0
（保守力定义之三）
L
※ 假若场力的功与中间路径无关，或沿任何闭合路径运
动一周时，场力做的功为零，则该场力即为保守力。
□保守力的判据：
由场论知 F dl F ds 0
L
S
L 为任意
F 0
Fz Fy 0, y z
即：
cosq sinq 7q 6 7dq
98p 2 70p
例2 （P38）在上题中，如
Fx 2x 3y 4z 5, Fy z x 8, Fz x y z 12
则结果如何？
解：略
2015/3/24
第一章 质点力学(2)
16
§1、8 质点动力学的基本定理与基本守恒律
通过求解
阻力，则叫单摆。如单摆从幅角 q0（ q0不一定很小）
的地方自由落下，试用两种不同方法（机械能守恒与 运动定律 ）求摆锤通过最低点时的速度。
解： （1）机械能守恒
1 2
mv2
mgl
0
mgl
cosq0
于是得到 v 2gl 1 cosq0
2015/3/24
第一章 质点力学(2)
27
（2）运动定律求解
Fx x 2y z 5, Fy 2x y z, Fz x y z 6
求此质点沿螺旋线 x cosq, y sinq, z 7q 运行自q=0至 q=2p时，力对质点所作的功。
解： 先检验一下，作用力是不是保守力？
Fz Fy 11 0, y z
Fx Fz 11 0, z x
微分形式（又称“冲量定理” theorem of impulse）
积分形式 力对时间的积累
dP Fdt
大学物理理论力学 第一章 质点力学
d
ri
dri
rdi
ri
rj
dt
dt dt
d
rj
dr j r
dj
rdj
rj
rj
r2i
dt
dt
dt
dt
2.平面极坐标系——加速度
a（r r2）i（r 2r）j （r r2）i 1 d（r2）j 矢量的变化为矢量大小的 r dt
定义: bˆ iˆ ˆj 垂 直于密切面, 称为副发 线方向单位矢，
( iˆ , ˆj , bˆ )构成空间正
交自然坐标系。
a dviˆ v 2 ˆj 0bˆ
dt
法线平面 R n
v t
dv dt
d 2r dt 2
&r&
小结
1) 参照系，坐标系（立场和方法） 2)已知r=r(t), 求v, a 3)已知a, v, 求运动r=r(t)
运动描述法的应用——例题1 例题1
绳的一端连在小车的A点上，另一端跨过B 点绕在鼓轮C上，滑车离地的高度为h。若 小车以匀速度v沿着水平方向向右运动，求
2.平面极坐标系
在极限情况下， d 0 di i （与j的方向一致）
di 1 d d
dj j （沿i的负方向）
dj 1 d d
o
di
di d
dt d dt
j
dj dt
dj d d dt
i
dj
j
j'
i' di
d
交换律
A
B
B
A
理论力学知识总结
学生整理，时间有限，水平有限，仅供参考，如有纰漏，请以老师、课本为主。
第一章质点力学（1）笛卡尔坐标系 位置：k z j y i x ++=r速度：k z j y i x dtr d ...v ++== 加速度：k z j y i x dtv d ......a ++== （2）极坐标系坐标：j i e r θθsin cos += j i e θθθcos sin +-= r e r =r 速度：r r .v = .v θθr =加速度:2...θr r a r -= .....2θθθr r a += （3）自然坐标系（0>θd ） 坐标：ds r d e t =θd e d e t n = θρd ds = 速度：t e v v = 加速度：n t e v e v ρ2.a +=（4）相对运动（5）牛顿运动定律 牛顿第一定律：惯性定律 牛顿第二定律：)(a m v m P dtP d dt v d m F ==== 牛顿第三定律：2112F F -= （6）功、能量vF dt rd F dt dW P rFd dA ⋅=⋅=== （7）（7）有心力第二章 质点动力学的基本定理知识点总结： 质点动力学的基本方程质点动力学可分为两类基本问题:. (1) .已知质点的运动，求作用于质点的力; (2) 己知作用于质点的力，求质点的运动。
动量定理 动量：符号动量定理微分形式动量守恒定律：如果作用在质点系上的外力主失恒等于零，质点系的动量保持不变。
即：质心运动定理：质点对点O 的动量矩是矢量mv r J i ⨯= 质点系对点0的动量矩是矢量i ni nii i i v m r J J ∑∑=⨯==1若z 轴通过点0，则质点系对于z 轴的动量矩为∑==ni z z z J M J ][若C 为质点系的质心，对任一点O 有 c c c J mv r J +⨯=02. 动量矩定理∑∑=⨯=⨯=nie i i n i i i i M F r v m r dt d dt dJ )()( 动量矩守恒：合外力矢量和为零，则动量矩为常矢量。
理论力学第一章
将上式代入式（b） 得一次近似的微分方程
( gt 2 20 ) cos ， 0 ， g x y z
（f）
在式（d）的初始条件下 上式积分一次 得一次近似的速度
( gt 2 20t ) cos ，y 0 ，z gt 0 x
1 2 1 2 2 l2 r ( x ) 2 2 4
2 dx l r x 2 dt 4
（b）
上式再分离变量并积分 即 l t dx dt 1 0 2 l 2 x 2 4
求得套筒到达点A的时间t为
2 l l l2 1 4 1 ln(2 3 ) t ln 1 2 解出 将 2 rad/s 代入上式
将上式投影到轨迹的切向轴t上 得
d2s m 2 ( P FIe ) sin m( g a0 ) sin dt
当摆作微振动时 角很小 有 sin 且 s l 上式成为 d 2 m l 2 m( g a0 ) dt 令
2 0
g a0 l
将式（a）投影到
y 轴上得
t=0.2096s
F2 FIC 2m x （c） 由式（b）可得 当套筒到达端点A时 x l
2 l 2 l r x 3l 4 2
代入式（c）得
F2 3 2lm 3(2 rad/s) 2 0.5m 0.1kg 3.419N 又 对于惯性参考系 套筒运动的基本方程为
mar F FIe
mar F
（2）动参考系相对于定参考系作匀速直线平移 得 因 aC 0 和 ae 0 所以 FIe FIC 0 所有相对于惯性参考系作匀速直线平移的参考系 都是惯性参考系 发生在惯性参考系中的任何力学现象 都无助于发觉该参考系本身的运动情况 以上称为相对性原理
第一章质点力学
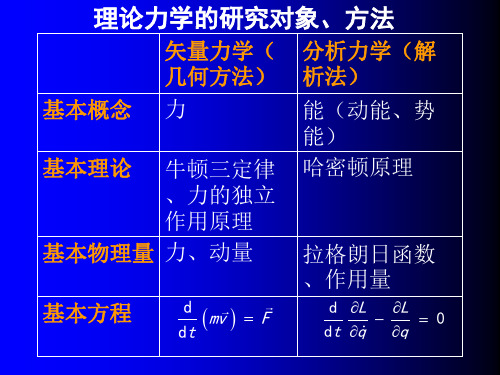
求：速度，加速度，轨道曲率半径。
解：
v4
x2 y2 1 4
5
a 16 x2 y2 32 an , at 0
v2 x2 y2 1 5 2.5
an
x2 y2 2
§1.3 平动参考系
绝对速度、相对速度与牵连速度
两种参考系：基本参考系S、运动参考系 S。
三种运动：质点的绝对运动、相对运动和牵连运动。 牵连速度：由于运动参考系的运动而使质点所具有 的相对基本参考系的运动速度叫做质点的牵连速度； 它等于运动参考系上与质点位置重合的空间点的速 度。
4. 自然坐标系、切向加速度、法向加速度
利用质点运动轨道本身的几何特性 (如切线、法 线方向等)来描述质点的运动. 这种方法称为自然坐 标法.
i. 弧长方程
在轨道上取一点 作O原点, 规定沿轨道的某一方向 为弧长的正方向, 质点位置可由原点 到质点O 间的一
段弧长 来确定s, 称为弧坐s 标.
s s(t)
特
逐个考虑
② 把作用分离到
体，按自由度来 分析
点
各个质点上 ② 作用体现为势能
③ 非自由质点运
，反映场的性质
动方程中存在
和结构
约束力
③ 拉格朗日方程中
不含约束力
第一章 质点力学
质点运动学
运动学物理量： 位移，速度，加 速度
运动学方程： 轨道方程
质点动力学
牛
顿
动力学学物理
运
量：动量，动
动
量矩，能量
定
3. 运动学方程和轨道
若用直角坐标系Oxyz代表参考系, 如图位置矢量 (简
称位矢)
r rer r r (t)
称为质点的运动学方程, 它 包括了质点运动的全部信息.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三. 保守力、非保守力、耗散力 1. 力场: 一般情况下：
若质点在某空间区域任意位置上，受到确定的力 F(r)，力是位置的单值有界可微函数，则该区域称 为力场，F 为场力。如：万有引力场、静电场。
2. 保守力场: 若力场是稳定的，当质点运动时，场力做功单 值地由始末位置确定（与轨道形状无关） ―― 该力 场称为保守力场。质点受到的场力为保守力。如电 磁力、重力等。
通过求解 F ma 可得运动规律,这是研究质点
动力学问题的基本方法！
存在问题：由于 F 形式复杂，求解十分困难；有
时并不需要全部解。
关于质点动力学的问题有其他研究及求解方法吗?
一、动量定理与动量守恒律 1. 动量: 定义： 物理学中一个非常重要的物理量。在机械运动的 范围内，质点间运动的传递通过动量的交换来实现 。动量是机械运动强弱的度量。 2. 动量定理 动量定理的微分形式变形并积分
同理：
Fx Fz Fz Fy 0, 0, z x y z
4. 势能:
函数V(x,y,z)成为质点在坐标(x,y,z) 处的势能。 势能的物理意义：保守力作的功等于势能的减少量 。 注： 1) 势能函数加上任意常数不影响势能差。 2) 仅当力场为保守力场时才可引入势能。 3) F与V的关系：
I N I N
桌面对小球的冲量
小球对桌面的冲量
(4) 在小球与桌面碰撞过程中应用动量定理 投影到x轴得标量方程 N P m2 m1 其中， 1 2gh1 , 2 2gh2
N P m2 m1
经典力学与量子力学的区别之一，隧穿效应
【例 2 】如图所示，一重锤固定一轻杆末端，将其 约束在竖直圆周上运动。假设初始角度为 θ0 ，忽 略空气阻力，求重锤经过最低点的速度。
解：(1) 分析用机械能守恒律的可能性 重锤受到哪些力？ 哪些做功哪些不做功？ 零势能 (2) 确定初末态时重锤的总机械能； 用机械能守恒定律求出速度
§1.7 功与能
一. 功和功率 1.质点在恒力作用下沿直线运动
F
r
其中， r 是力的作用点之位移
2.质点受变力沿曲线运动
dW F cos dr F dr 元功 dW
W
B A
B F dr F cos ds
A
功是标量，其值与坐标选取无关。在直角坐标系下 ： dr dxi dyj dzk
____动量定理的积分形式
具有普遍性 ：（1）牛顿第二定律原始形式 （2）相对论中亦适用
力对质点的冲量，是一个矢量。 力对时间的积累. 3. 动量守恒
若F 0, dp 0, p C
即：如果质点受到的合外力等于零， 则其动量守恒。常数由初值确定。
若F 0, 但Fx 0, dpx 0, p x c
W Fx dx Fy dy Fz dz sin 2 3sin 2 cos 2 28 sin d 0 15cos 12sin 49 84 98 2 226
2
§1.8 质点动力学的基本定理与基本守恒律
Jz J k
三、动量矩定理与动量矩守恒律(对固定点O) 1. 动量矩定理( 出发点：牛顿第二运动定律 )
动量矩定理的微分形式
投影式:
2.冲量矩
3.动量矩守恒律
若M 0, dJ 0, J C
即：如果质点受到的外力矩等于零,则其动量矩守 恒。常数由初值确定。 投影式:
A A
即合力对质点所做的功为各力对质点所做功的代数和 。
说明 ：
一般情况下，做功与路径有关 位移元 dr 是力的作用点的位移 做功与参照系的选取有关
4. 功率: 表述做功快慢的物理量。
二. 能
物体具有做功的本领，称它具有一定的能量。 力学中――机械能。 当能量发生变化时，总有一定数量的功表现出来 功是能量变化的度量。
若M 0, 但M x 0, dJx 0, J x c
即：如果质点在某方向上受到的外力矩为 0, 则该 方向上的动量矩守恒。
【例1】质点所受的力恒通过某一个定点，则质点必 在一平面上运动（如地球绕太阳运动，卫星绕地球 运动等）。试证明之。 解：由于力恒通过一个定点，那么力对该定点的力矩 : 所以 : J C r F 0
即：如果质点在某方向上受到的合外力为 0,则该方 向上的动量守恒。
例：一质量为0.01kg的小球，从 h1 0.256m 的高度
处由静止下落到水平桌面上，反弹后的最大高度为
h1 0.196m 。求小球与桌面碰撞时对桌面作用的冲量
是多少？
解法一：(1) 研究对象：小球 (2) 参照系：桌面，坐标系：ox (3) 受力分析：重力，桌面对小球的 正压力(冲力)， 用平均正压力代替 x
2. 动量矩(矢量)
对O点的动量矩：
i j k
i mzx mxz myx k mzy j mxy J r m x y z myz my mz mx
对x,y,z轴的投影：
不存在势能函数
F 做功与路径有关。
x cos , y =sin , z =7 dx sin d , dy cos d , dz 7 d Fx 2 cos 3sin 28 5 Fy 7 cos 8 Fz cos sin 7 12
ACB
F dr
BDA
ADB
F dr
F dr
l
W Fc dr 0
l
ACB
F dr
F dr
A
D
C
B
若力做功与路径有关，这种力为非保守力 (漩涡 力)，力场为非保守力场。如：摩擦力――与路径有 关――耗散能量――耗散力。
3. 保守力的判据:
F(r)为保守力的充要条件：
Байду номын сангаас
即：
证明:
充分条件 F 0 F (r )为保守力 必要条件
dW Fx dx Fy dy Fz dz -dV
与路径无关，只与始末位置有关。必存在一可微函数 V，使得 z
z
Fx 0 x y
Fy
r
分量式为：
x乘(1), y乘(2), z乘(3),并相加,得: 经过固定点的平面方程。
四、动能定理与机械能守恒律 1.动能定理
定义动能
质点动能的微分等于作用在该点上的力所作的元功
2. 若F为保守力场，那么 dW dV
dT dV
机械能守恒
五、势能曲线 质点受一维守恒力的作用，则质点的势能是其坐 标的函数。假设该一维坐标为x , 则V(x)–x图形称 为势能曲线。
x, y , z
x , y ,0
Fz dz
1 2 2 2 x y z 2 xy xz yz 5 x 6 z 2
W V 1,0,14 V 1,0,0 98 70
2
【例2】在例1中，如果
Fx 2x 3 y 4z 5, Fy z x 8, Fz x y z 12
Fy Fx Fy F F F x z z F F F 2 2F FxFzF F Fy F y 0, 1 1 0, 01 1 0 F z z Fyy x x 2 2 x z 0, 1 1 0, 1 1 x 2 y2 0, z 1 1 0, y 1 1 0 x z y x xy y z z x x y zz
0
求杆对重锤的作用力
m T mg cos l
2
T 3mg 2mg cos0
守恒律小结
基础：
2. 牛顿第二定律是二阶微分方程，守恒律是一阶的， 称为第一积分，能量守恒也称能量积分。用初积分比用 运动方程来的简单。
I I N mg m
2 gh1 2 gh2
小球对桌面的冲量方向竖直向下
解法二：将动量定理用于小球下落、与桌面碰撞和 上升的整个过程。
N P t1 t2 0
标量方程为 其中，
N P t1 t2 0
2h1 2h2 t1 , t2 g g
x cos , y sin , z 7 则结果如何？
Fz Fy 11 0 z y Fx Fz 4 1 3 0 F 0 x z Fy Fx 1 3 2 0 y x
缺点：无法求出T 的大小。(若考虑空气阻力，则不 能用机械能守恒)
(3) 尝试用动力学的方法 写出动力学方程(自然坐标或极坐标)
受力分析 注意：假设了速度的方向后，那么就应该考虑相关表 达式的正负。由于这里只关心速度的值，因此求解时 最好把dt换成dθ： 于是微分方程变为：
两边积分：
0
0
gl sin d d
F Fx i Fy j Fz k
W
B A A
B F dr （Fx dx Fy dy Fz dz）
n F Fi
i 1
3. 若质点受几个力F1 ,F2, ……,Fn作用, 合力
W
B
A
B B F d r Fi d r Fi d r Wi
解法二：选直线路径积分
W
14
0
Fz dz
14