理论力学第一章参考答案
1-8章的习题答案理论力学.doc

第一章静力学公理和物体的受力分析一、选择题与填空题1.C2.ACD3.A, B两处约束力的方向如图所示60°第二章平面力系一、选择题与填空题■1. B; D。
2. B。
3. F;向上。
4. B。
5. 4^M;方向与水平线成60角,指向 23L右下。
6. 10kN; 10kN ; 5kN; 5kN。
7. 100kN;水平向右。
二•计算题1. F B - -70 KN F AX =70 KN ,F Ay =120 KN , M A二-30KN m2. F AX - -qa F BX二 F qa F Ay =qa F F By 二 qa - F3. F= -5kN F Dy = 4.33kN F E-4.33kN F C =24.41kND xF B^ -17.08kN F AX=F BX = -5kN l^y = -14.08kN M A=T4.66kN mF AX =10N FAy =20N M A =15N mF CD =14.1N6F Ax=2.5kN F Ay=—2.16kN M A=」kN ,m F c =20.33kN7 F B=40kNF AX = —10kNFA ^-20kN M -50kN m F cx = 40kNF ey = 0F HX =300N F Hy =100N第三章空间力系少2(-8. F A ^ = -100N F Ay 二-300N F Ex 二-300N F Ey =100N F °y 二 200N整=一一A > X Y m 一:J E £c X一、选择题与填空题f—- - Fa 6 Fa 1.B。
2.B。
3. M x(F)=O ; M y(F) —H2 44.F x=-40.2N; F y=30-2N; M z=240.2 N m。
5.F z= F sin :;F y= F cos :cos :;M x(F)二 F(ccos'cos : bsin )。
理论力学第一章答案

• wfei@ • wfei@
ϕ +ϕ ϕ +ϕ m1g sinϕ1 − k cos 1 2 ⋅ (l − 2R) ⋅ sin 1 2 = 0 2 2 m g sinϕ − k cosϕ1 + ϕ2 ⋅ (l − 2R) ⋅ sinϕ1 + ϕ2 = 0 2 2 2 2
o
ϕ1 ϕ2
m2
m1
2.23 质量为m,电荷为q的粒子在轴对称电场 中运动。写出粒子的拉格朗日函数和运动微分方程。 v v v v 解: 由题中 E = E 0 e r ,B = B 0 k 令 ϕ = E 0 ln R v 1 v A = B 0 R eθ 2 v v 在柱坐标系中,有: = 1 mv 2 − q ϕ + q A ⋅ V , L 2 d ∂L ∂L − =0 代入: & dt ∂ q α ∂ qα
2 p 2p
代入完整保守体系的拉格朗日方程,
d dt & R2 & g R & R + R − ω 2R + R − 2 R p2 p p
2
= 0
m
&& & 化简得到, ( p 2 + R 2 ) ⋅ R + R ⋅ R 2 − p 2 ω 2 R + pgR = 0
z o
F
G P
∴ P ⋅ FG = F1 ⋅ EF + ( P'− F1 ) ⋅
若有
DF AC = ,则有:P ⋅ FG EF AB
AB DF AC
A B
P'
F'2
= P'⋅EF
C
即秤锤的重量P与重物P’在秤台的位置无关,且 P ' = P
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
《理论力学》课后习题解答(赫桐生版)
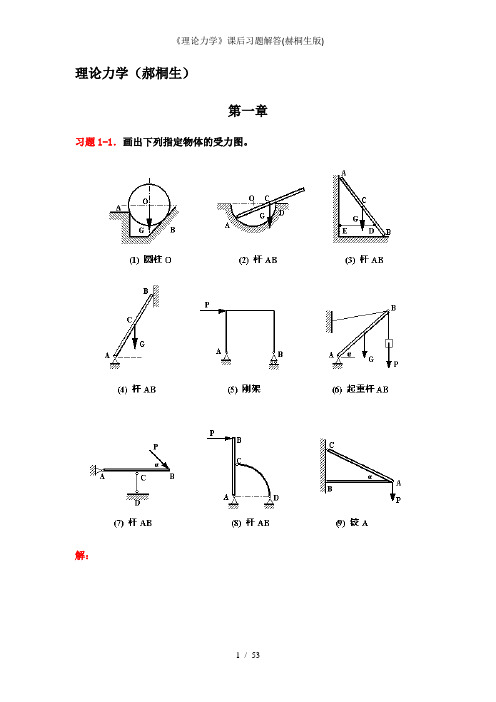
理论力学(郝桐生)第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1)研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB与水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
理论力学第一章题及解答(文末)

理论⼒学第⼀章题及解答(⽂末)第⼀章思考题1.1平均速度与瞬时速度有何不同?1.2 在极坐标系中,r v r =,θθ r v =.为什么2θ r r a r-=⽽⾮r ?为什么θθ r r a 20+=⽽⾮θθ r r +?你能说出r a 中的2θ r -和θa 中另⼀个θ r 出现的原因和它们的物理意义吗?1.3 在内禀⽅程中,n a 是怎样产⽣的?为什么在空间曲线中它总沿着主法线⽅向?当质点沿空间运动时,副法线⽅向的加速度b a 等于零,⽽作⽤⼒在副法线⽅向的分量b F ⼀般不等于零,这是不是违背了⽜顿运动定律呢?1.4 在怎样的运动中只有τa ⽽⽆n a ?在怎样的运动中⼜只有n a ⽽⽆τa ?在怎样的运动中既有n a ⽽⽆τa ?1.5dt r d 与dt dr 有⽆不同?dt v d与dtdv 有⽆不同?试就直线运动与曲线运动分别加以讨论. 1.6⼈以速度v 向篮球⽹前进,则当其投篮时应⽤什么⾓度投出?跟静⽌时投篮有何不同?1.7⾬点以匀速度v 落下,在⼀有加速度a 的⽕车中看,它⾛什么路经?1.8某⼈以⼀定的功率划船,逆流⽽上.当船经过⼀桥时,船上的渔竿不慎落⼊河中.两分钟后,此⼈才发现,⽴即返棹追赶.追到渔竿之处是在桥的下游600⽶的地⽅,问河⽔的流速是多⼤?1.9物体运动的速度是否总是和所受的外⼒的⽅向⼀致?为什么?1.10在那些条件下,物体可以作直线运动?如果初速度的⽅向和⼒的⽅向⼀致,则物体是沿⼒的⽅向还是沿初速度的⽅向运动?试⽤⼀具体实例加以说明.1.11质点仅因重⼒作⽤⽽沿光滑静⽌曲线下滑,达到任⼀点时的速度只和什么有关?为什么是这样?假如不是光滑的将如何?1.12为什么被约束在⼀光滑静⽌的曲线上运动时,约束⼒不作功?我们利⽤动能定理或能量积分,能否求出约束⼒?如不能,应当怎样去求?1.13质点的质量是1千克,它运动时的速度是k j i v 323++=,式中i 、j 、k 是沿x 、y 、z 轴上的单位⽮量。
理论力学习题答案

第一章静力学公理和物体的受力分析一、是非判断题1.1.1 在任何情况下,体内任意两点距离保持不变的物体称为刚体。
( ∨ ) 1.1.2 物体在两个力作用下平衡的必要与充分条件是这两个力大小相等、方向相反,沿同一直线。
( × )1.1.3 加减平衡力系公理不但适用于刚体,而且也适用于变形体。
( × ) 1.1.4 力的可传性只适用于刚体,不适用于变形体。
( ∨ ) 1.1.5 两点受力的构件都是二力杆。
( × ) 1.1.6只要作用于刚体上的三个力汇交于一点,该刚体一定平衡。
( × ) 1.1.7力的平行四边形法则只适用于刚体。
( × ) 1.1.8 凡矢量都可以应用平行四边形法则合成。
( ∨ ) 1.1.9 只要物体平衡,都能应用加减平衡力系公理。
( × ) 1.1.10 凡是平衡力系,它的作用效果都等于零。
( × ) 1.1.11 合力总是比分力大。
( × ) 1.1.12只要两个力大小相等,方向相同,则它们对物体的作用效果相同。
( × ) 1.1.13若物体相对于地面保持静止或匀速直线运动状态,则物体处于平衡。
( ∨ ) 1.1.14当软绳受两个等值反向的压力时,可以平衡。
( × ) 1.1.15静力学公理中,二力平衡公理和加减平衡力系公理适用于刚体。
( ∨ ) 1.1.16静力学公理中,作用力与反作用力公理和力的平行四边形公理适用于任何物体。
( ∨ ) 1.1.17 凡是两端用铰链连接的直杆都是二力杆。
( × ) 1.1.18 如图所示三铰拱,受力F ,F1作用,其中F作用于铰C的销子上,则AC、BC构件都不是二力构件。
( × )二、填空题1.2.1 力对物体的作用效应一般分为 外 效应和 内 效应。
1.2.2 对非自由体的运动所预加的限制条件称为 约束 ;约束力的方向总是与约束所能阻止的物体的运动趋势的方向 相反 ;约束力由 主动 力引起,且随 主动 力的改变而改变。
《理论力学》第一章基本概念及基本原理

第一章 基本概念及基本原理[习题1-1] 支座受力F ,已知kN F 10=,方向如图所示, 求力沿y x ,轴及沿'',y x 轴分解的结果,并求力F 在各轴上的投影.解:(1)F 沿y x ,轴分解的结果把F 沿y x ,轴分解成两个分力,如图所示. →→→→=⨯==i i i F F x 66.8866.01030cos 0)(kN →→→→=⨯==j j j F F y 55.01030sin 0)(kN (2)F 沿'',y x 轴分解的结果把F 沿'',y x 轴分解成两个分力,如图所示. 由图可知,力三角形是等腰三角形.故:→→→==''10'i i F F x )(kN→→→-=⨯-=''018.575cos 102'j j F y )(kN (3) F 在y x ,轴上的投影)(66.8866.01030cos 0kN F F x =⨯==)(55.01030sin 0kN F F y =⨯== (4) F 在'',y x 轴上的投影)(66.8866.01030cos 0'kN F F x =⨯==)(59.275cos 1075cos 00'kN F F y -=-=-=[习题1-2] 已知N F 1001=,N F 502=,N F 603=N F 804=,各力方向如图所示,试分别求各力在x 轴y 轴上的投影. 解:)(6.86866.010030cos 011N F F x =⨯==)(505.010030sin 011N F F y =⨯==)(305350cos 222N F F x =⨯==α力沿x,y 轴的分解图力沿x ’,y ’轴的分解图力沿x ’,y ’轴的投影图xF yFy 'x F ')(405450sin 222N F F y -=⨯-=-=α 0060cos 333=⨯==αF F x)(60160sin 333N F F y =⨯==α)(57.56135cos 80cos 0444N F F x -===α)(57.56135sin 80sin 0444N F F y ===α[习题1-3] 计算图中321,,F F F 三个力分别在z y x ,,轴上的投影.已知kN F 21=,kN F 12= , kN F 33=. 解:)(2.16.025311kN F F x -=⨯-=⨯-= )(6.18.025411kN F F y =⨯=⨯=01=z F)(424.05345sin 1cos sin 02222kN F F x =⨯⨯==θγ )(566.05445sin 1sin sin 02222kN F F y=⨯⨯==θγ)(707.045cos 1cos 0222kN F F z =⨯==γ03=x F03=y F)(333kN F F z ==[习题1-4] 已知kN F T 10=,求T F 分别在z y x ,,轴上的投影. 解:(591.75353510sin 22222F F T Txy =+++⨯==γ)(51.6355591.7cos 22kN F F Txy Tx =+⨯==θ题1-2图)3,)0,)(91.3353591.7sin 22kN F F Txy Ty =+⨯==θ)(51.6535510cos 222kN F F T Tz -=++⨯-=-=γ[习题1-5] 力F 沿正六面体的对角线AB 作用,kN F 100=,求F 在ON 上的投影. 解:如图所示,F 在AC 线上的投影为:)(345.88400300400400400100cos 22222kN CAB F F F OB AC =+++⨯===5.0400200tan ==NOD 057.265.0arctan ==NOD 00043.1857.2645=-=BONF 在ON 线上的投影为:)(811.8343.18cos 345.88cos 0kN BON F F O B O N ===[习题1-6] 已知N F 10=,其作用线通过A(4,2,0),B(1,4,3)两点,如图所示.试求力F 在沿CB 的T 轴上的投影. 解: 61.313)42()14(22==-+-=AD69.413361.322==+=AB 2361.322=-=DGF 在AD 上的投影为:M)(697.769.461.310cos N BAD F F AD =⨯== )(40.669.4310sin N BAD F F z =⨯==)(264.461.32697.7cos N ADG F F AD y =⨯==)(396.661.33697.7sin N ADG F F AD x =⨯==F 在T 轴上的投影为:)(251.75340.654264.4cos cos kN ECB F BCD F F z y T =⨯+⨯=+= [习题1-7] 图中圆轮在力F 和矩为M 的力偶作用下保持平衡,这是否说明一个力可与一个力偶平衡? 解:图中圆轮在力F 和矩为M 的力偶作用下保持平衡,这不能说明一个力可与一个力偶平衡.因为轮子的圆心处 有支座,该支座反力R 与F 构成一力偶,力偶矩),(F R M 与M 等值,共面,反向,故圆轮保持平衡.[习题1-8] 试求图示的力F 对A 点之矩,已知m r 2.01=m r 5.02=,N F 300=.010012030cos 60sin )30sin (60cos )(r F r r F F M A ⋅+--=)(15232.023300)5.02.05.0(5.0300)(m N F M A ⋅-=⨯⨯⨯+⨯-⨯-= [习题1-9] 试求图示绳子张力T F 对A 点及对B 点的矩.已知kN F T 10=,m l 2=,m R 5.0=,030=α.解:)(530sin 10sin 0kN F F T Tx ===α)(66.830cos 10cos 0kN F F T Ty ===α )(732.1866.0260sin 0m l OC =⨯==)(15.0260cos 0m l AC =⨯==)()()(Ty A Tx A T A F M F M F M +=)30cos 5.01(66.8)30sin 5.0732.1(500+⨯+-⨯-=)(5m kN ⋅=)()()(Ty B Tx B T B F M F M F M +=)30cos 5.01(66.8)30sin 5.0732.1(500-⨯--⨯-=)(320.12m kN ⋅-=[习题1-10] 已矩正六面体的边长为c b a ,,,沿AC 作用一力F ,试求力F 对O 点的矩矢量表达式. 解:zy xF F F c bak j iF M →→→=)(0式中,2222222222cos cos c b a Fa b a a c b a b a F F F x ++-=+⋅+++⋅-=⋅-=θγ2222222222sin cos cb a Fb ba b cb a b a F F F y ++-=+⋅+++⋅-=⋅-=θγ222222sin cb a Fc cb ac F F F z ++=++⋅==γ故cb ac b ak j i c b a FF M --++=→→→2220)(cc bak j i c b a F200222→→→++=baj ic c b a F→→⋅++=2222)(2222→→-++=j a i b c b a cF[习题1-11] 钢绳AB 中的张力kN F T 10=.写出该张力T F 对O 点的矩的矢量表达式.解:2)21()01(22=-+-=BC2318)04()12()10(222==-+-+-=ABzy xF F F k j iF M 42)(0→→→=式中,)(357.22123210cos cos kN F F T Tx =⋅⋅=⋅=θγ )(357.22123210sin cos kN F F T Ty -=⋅⋅-=⋅-=θγ)(428.923410sin kN F F T Tz -=⋅-=-=γ故428.9357.2357.2420)(0--=→→→k j i F M 357.2357.24428.9357.22---=→→→→jiki)(357.24)357.2428.9(2→→→→--⨯---=j i k i →→→-+-=k j i 714.4428.9428.9[习题1-12] 已知力→→→→+-=k j i F 32,其作用点的位置矢→→→→++=k j i r A 423,求力F 对位置矢为→→→→++=k j i r B 的一点B 的矩(力以N 计,长度m 以计).A解:→→→→→⨯-=⨯=F r r F r F M B A AB B )()(式中,→→→→++=k j i r A 423,→→→→++=k j i r B ,=-→→)(B A r r →→→++k j i 312 →→→→+-=k j i F 32故, =)(F M B ⨯++→→→)312(k j i )32(→→→+-k j i=-=→→→132312k j i=--→→→240312k j i 23522---→→→→k k j i 5222---=→→→k j i)425(2→→→+---=k j i→→→-+=k j i 8410 )(m N ⋅[习题1-13] 工人启闭闸门时,为了省力,常常用一根杆子插入手轮中,并在杆的一端C 施加力,以转动手轮.设手轮直径m AB 6.0=,AC 轩长m l 2.1=,在C 端用N F C 100=的力能将闸门开启,若不借用杆子而直接在手轮A,B 施加力偶),('F F ,问F 至少应多大才能开启闸门? 解:支座O 反力O R 与C F 构成一力偶),(0C F R 若要闸门能打开,则),('F F 与),(0C F R 必须 等效,即它们的力偶矩相等:)3.02.1(1006.0-⨯=⨯F )(150N F =[习题1-14] 作下列指定物体的示力图.物体重量,除图上已注明者外,均略去不计.假设接触处都是光滑的.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
dt
dt
的改变。在直线运动中规定了直线的正方向后,二者都可表示质点运动的加速度;在曲线运
动中,二者不同,
dv dt
=
aτ
+
a
nHale Waihona Puke ,而dv dt
=
aτ
。
课 后 答 案 网
1.6 答:不论人是静止投篮还是运动投篮,球对地的方向总应指向篮筐,其速度合成如题 1.6 球对人
人对地
题1-6图
其他物体由于受到质点的作用而对质点产生的反作用力。有人也许还会问:某时刻若
Fb与Rb 大小不等, ab 就不为零了?当然是这样,但此时刻质点受合力的方向与原来不同, 质点的位置也在改变,副法线在空间中方位也不再是原来 ab 所在的方位,又有了新的副法 线,在新的副法线上仍满足 Fb + Rb = 0即ab = 0 。这反映了牛顿定律得瞬时性和矢量性,
的极限情况,二者一致,在匀速直线运动中二者也一致的。
1.2 答:质点运动时,径向速度 V r 和横向速度 V θ的大小、方向都改变,而 ar 中的 ̇ṙ只反映 了 V r 本身大小的改变, aθ 中的 rθ̇̇ + rθ̇ 只是 V θ本身大小的改变。事实上,横向速度 V θ 方向的改变会引起径向速度 V r 大小大改变, − rθ̇2 就是反映这种改变的加速度分量;经向 速度 V r 的方向改变也引起 V θ的大小改变,另一个 ṙθ̇ 即为反映这种改变的加速度分量,故 ar = ̇ṙ − rθ̇2 , aθ = rθ̇̇ + 2ṙθ̇. 。这表示质点的径向与横向运动在相互影响,它们一起才能
a′
=
−a
,其相对运动方程
⎪⎧x′ ⎨
=
1 2
at
2
⎪⎩y′ = vt
消去 t 的轨迹
y′2 = 2v 2 x′ a
如题图,有人会问:车上的人看雨点的轨迹是向上凹而不是向下凹呢?因加速度总是在曲线
凹向的内侧, a ′ 垂直于 V ′ 方向的分量 a ′n 在改变着 V ′ 的方向,该轨迹上凹。
1.8 答:设人发觉干落水时,船已上行 s′ ,上行时船的绝对速度V船 − V水 ,则
r
r
r
事实上据“ ∇ ”算符的性质,上述证明完全可以简写为
w ∇×F = ∇× F(r)r= 0
这表明有心力场是无旋场记保守立场
1.17 答平方反比力场中系统的势能V (r) = − k 2m ,其势能曲线如题图 1.17 图所示,
r
课 后 答 案 网
题1-17图
由T + V (r) = E知T = E −V (r),因T > 0,故有E > V (r)。
s′ = ( V船 − V水 )× 2
①
课 后 答 案 网
船反向追赶竿的速度V船 + V水 ,设从反船到追上竿共用时间 t ,则 ( V船 + V水 )t = 600 + s′
②
又竿与水同速,则 V水(2 + t) = 600 ③
①+③=②得
V水 = 150m min
1.9 答:不一定一致,因为是改变物体运动速度的外因,而不是产生速度的原因,加速度的 方向与合外力的方向一致。外力不但改变速度的大小还改变速度的方向,在曲线运动中外力 与速度的方向肯定不一致,只是在加速度直线运动二者的方向一致。 1.10 答:当速度与物体受的合外力同一方位线且力矢的方位线不变时,物体作直线运动。 在曲线运动中若初速度方向与力的方向不一致,物体沿出速度的方向减速运动,以后各时刻 既可沿初速度方向运动,也可沿力的方向运动,如以一定初速度上抛的物体,开始时及上升 过程中初速度的方向运动,到达最高点下落过程中沿力的方向运动。 在曲线运动中初速度的方向与外力的方向不一致,物体初时刻速度沿初速度的反方向,但以 后既不会沿初速度的方向也不会沿外力的方向运动,外力不断改变物体的运动方向,各时刻 的运动方向与外力的方向及初速度的方向都有关。如斜抛物体初速度的方向与重力的方向不 一致,重力的方向决定了轨道的形状开口下凹,初速度的方向决定了射高和射程。 1.11 答:质点仅因重力作用沿光滑静止曲线下滑,达到任意点的速度只和初末时刻的高度 差有关,因重力是保守力,而光滑静止曲线给予质点的发向约束力不做功,因此有此结论 假如曲线不是光滑的,质点还受到摩擦力的作用,摩擦力是非保守力,摩擦力的功不仅与初 末位置有关,还与路径有关,故质点到达任一点的速度不仅与初末高度差有关,还与曲线形 状有关。 1.12 答:质点被约束在一光滑静止的曲线上运动时,约束力的方向总是垂直于质点的运动 方向,故约束力不做功,动能定理或能量积分中不含约束力,故不能求出约束力。但用动能
若 E < 0 ,其势能曲线对应于近日点 rmin 和远日点 rmax 之间的一段。近日点处
E − V (r) − T 即为进入轨道需要的初动能若 E > 0 则质点的运动无界,对应于双曲线轨道的
运动;若 E = 0 位于有界和无界之间,对应于抛物线轨道的运动;这两种轨道的运动都没有
1.13 质点的质量是 1 千克,它运动时的速度是 v = 3i + 2 j + 3k ,式中 i 、 j 、 k 是沿 x 、 y 、 z 轴上的单位矢量。求此质点的动量和动能的量值。 1.14 在上题中,当质点以上述速度运动到(1,2,3)点时,它对原点 O 及 z 轴的动量矩各
是多少?
1.15 动量矩守恒是否就意味着动量也守恒?已知质点受有心力作用而运动时,动量矩是守
既有 an 而无 aτ ?
�
�
1.5 dr 与 dr 有无不同? dv 与 dv 有无不同?试就直线运动与曲线运动分别加以讨论.
dt dt �
dt dt
1.6 人以速度 v 向篮球网前进,则当其投篮时应用什么角度投出?跟静止时投篮有何不同?
课 后 答 案 网
1.7 雨点以匀速度 v 落下,在一有加速度 a 的火车中看,它走什么路经?
第一章 思考题
1.1 平均速度与瞬时速度有何不同?在上面情况下,它们一致?
1.2 在极坐标系中,vr = ṙ , vθ = rθ̇ .为什么 ar = ̇ṙ − rθ̇2 而非 ṙ̇?为什么 a0 = rθ̇̇ + 2ṙθ̇ 而非 rθ̇̇ + ṙθ̇ ?你能说出 ar 中的 − rθ̇2 和 aθ 中另一个 ṙθ̇ 出现的原因和它们的物理意义
恒的,问它的动量是否也守恒?
1.16 如 F = F (r),则在三维直角坐标系中,仍有▽ × F = 0 的关系存在吗?试验之。
1.17 在平方反比引力问题中,势能曲线应具有什么样的形状?
1.18 我国发射的第一颗人造地球卫星的轨道平面和地球赤道平面的交角为 68.5 � ,比苏
联及美国第一次发射的都要大。我们说,交角越大,技术要求越高,这是为什么?又交角大 的优点是什么? 1.19 卢瑟福公式对引力库仑场来讲也能适用吗?为什么?
. er
e θ
w ∇×F = ∂ ∂ ∂r ∂θ
F(r) 0
e
ϕ
∂ ∂ϕ
=
∂F(r) e
∂ϕ θ
−
∂F (r
∂θ
)
e
ϕ
=0
0
a 由于坐标系的选取只是数学手段的不同,它不影响力场的物理性质,故在三维直角坐标系中
d 仍有∇ ×F = 0 的关系。在直角坐标系中
r = xi+ yj+ zk,F (r) = Fx (r)i+ Fy (i)j+ Fz (r)k
也反映了自然坐标系的方向虽质点的运动而变。
1.4 答:质点在直线运动中只有 aτ 而无an ,质点的匀速曲线运动中只有 an而无aτ ;质点作 变速运动时即有 at 又有an 。
1.5 答: dr 即反应位矢 r大小的改变又反映其方向的改变,是质点运动某时刻的速度矢量, dt
而 dr 只表示 r大小的改变。如在极坐标系中, dr = ṙi+ rθ̇j而 dr = ṙ 。在直线运动中,规
图所示,故人以速度 V 向球网前进时应向高于篮筐的方向投出。静止投篮是直接向篮筐投
出,(事实上要稍高一点,使球的运动有一定弧度,便于投篮)。
1.7 答:火车中的人看雨点的运动,是雨点的匀速下落运动及向右以加速度 a 的匀速水平直
线运动的合成运动如题 1.7 图所示,
题1-7图
o′x′y′
是固定于车的坐标系,雨点相对车的加速度
dt
dt
dt
dr
定了直线的正方向后,
=
dr 。且 dr
的正负可表示 dr 的指向,二者都可表示质点的运
dt dt dt
dt
动速度;在曲线运动中 dr ≠ dr ,且 dr 也表示不了 dr 的指向,二者完全不同。
dt dt dt
dt
dv 表示质点运动速度的大小,方向的改变是加速度矢量,而 dv 只是质点运动速度大小
沿力的方向还是沿初速度的方向运动?试用一具体实例加以说明.
1.11 质点仅因重力作用而沿光滑静止曲线下滑,达到任一点时的速度只和什么有关?为什
么是这样?假如不是光滑的将如何?
1.12 为什么被约束在一光滑静止的曲线上运动时,约束力不作功?我们利用动能定理或能
量积分,能否求出约束力?如不能,应当怎样去求?
定理 或 能 量 积 分 可 求 出 质 点 在 某 位 置 的 速 度 , 从 而 得 出 an ,有 牛 顿 运 动 方 程 Fn + Rn = man 便可求出 Rn ,即为约束力
1.13 答:动量
( ) p = mv = 1⋅
32 + 22 +
2
3
=
4
kg .m s
动能
1.14 答:
