第二章 计算题
宏观经济学(计算题)

1.某国企业在本国的总收益为200亿元,
在外国的收益为50亿元; 该国国民收入的劳动收入为120亿元, 在外国的劳动收入为10亿元; 外国企业在该国的收益为80亿元, 外国人在该国的劳动收入为12亿元。 求该国的GDP与GNP。
GNP= 200 +50+120+10=380
2. I=300 ,Y=5200 I=500, Y=6000 Y1=5400; Y2=5550; Y3=5662.5 Y4=5746.87
3.设消费函数为C=120+075Y。试求: (1)消费水平达到1120时,收入应为多少? (2)边际消费倾向和边际储蓄倾向各部为多少? (3)收入为3000时,消费水平为多少?
利润 10-7.5=2.5 40-5-10=25 27.5
3.假设GDP为5000万美元,个人可支配收入为4100万美 元,政府预算赤字为200万美元,消费为3800万美元, 贸易赤字为100万美元。 计算:(1)储蓄(2)投资(3)政府支出 个人储蓄=个人可支配收入-消费=4100-3800=300万 政府储蓄=预算盈余(或赤字)=-200万
6、(1)Y = 1837.5 (2)KI = 2.5
T = 267.5 Kg =2.5
C = 1337.5 Kt = -1.875
第六章: IS-LM模型
1.假设货币需求为L=0.2y-1000r,货币供给量为200美元, C=90+0.8Yd,t=50美元,i=140-300r美元,g=50美元。 (1)请写出IS和LM方程,并求均衡收入、利率和投资; (2)若其它条件不变,g增加20美元,均衡收入、利率和 投资各为多少
(1)最终产品为项链售价为40万美元。故GDP为40万美元。 (2)增值法 第一阶段增值:10万美元—0万美元=10万美元 第二阶段增值:40万美元—10万美元=30万美元 合计增值 40万美元
微观经济学计算题02192

第二章需求、供给计算题1、假设X商品的需求曲线为直线,Q X=40 0。
5P X,,Y商品的需求曲线也为直线,X与Y的需求线在Px=8的那一点相交,在Px=8的那一点上,X的需求弹性的绝对值只有的Y的需求弹性的绝对值的一半,请根据上述条件求Y的需求函数。
解:当P X=8时,Q X=36,且|E X|=1/9,故|E Y|=2/9,设Y商品的需求函数为Q Y=a—bP Y, 由此可得b=1,由于36=a—8,得a=44,故Y商品的需求函数为Q Y=44—P Y。
2、某人每周收入120元,全部花费在X和Y两种商品上,他的效用函数为U=XY,P X=2元,P Y=3元.求(1)为获得最大效用,他会购买几单位X和Y?(2)货币的边际效用和总效用各多少?(3)假如X的价格提高44%,Y的价格不变,为使他保持原有的效用水平,收入必须增加多少?解:(1)由U=XY,得MU X=Y,MU Y=X,根据消费者均衡条件得Y/2=X/3考虑到预算方程为2X+3Y=120解得X=30,Y=20(2)货币的边际效用λ=MU X/P X=Y/P X=10总效用TU=XY=600(3)提价后P X=2。
88 新的消费者均衡条件为Y/2。
88=X/3由题意知XY=600,解得X=25,Y=24将其代入预算方程M=2。
88×25+3×24=144元ΔM=144—120=24元因此,为保持原有的效用水平,收入必须增加24元。
3、证明需求曲线P=a/Q上的点均为单一弹性证明:dQ/dP=—aP-2, E d=(dQ/dP)(P/Q)=(-aP—2)(P/aP—1)=-1,故| E d|=1,为单一弹性。
4、1986年7月某外国城市公共汽车票价从32美元提高到40美元,1986年8月的乘客为880万次,与1985年同期相比减少了12%,求需求的弧弹性.解:由题设, P1=32, P2=40, Q2=880Q1=880/(1—12%)=880/88%=1000于是,Ed=[(Q2-Q1)/( P2—P1)]×[(P1+P2)/(Q1+Q2)]≈—0。
第二章+有理数的运算+有理数的加减混合运算同步练习2024-2025学年人教版数学七年级上册

第二章有理数的运算有理数的加减混合运算第一课时学习目标进一步巩固有理数加法、减法法则和运算;能熟练地将加减混合运算统一成加法运算;理解运算符号和性质符号的意义;运用加法运算律进行简算.课堂学习检测一、填空题1. 计算有理数加减混合运算时,通常先把减法转化为,然后将正数、负数分别 .2. 4-5-1=-5-1+4的根据是 .3. 计算: (1) (-0.7)-(-0.8)+(-0.9)= ;(2)(−0.25)+(−34)−(+43)=¯.4. 把-6-(+7)+(-2)-(-9)写成省略括号的代数和形式为 .二、选择题5. 下列计算中错误的是 ( ).(A) -2-(-2)=0 (B) -3-4-5=-12(C) -7-(-3)=-10 (D) 12-15=-36. 如果三个数的和为零,那么这三个数一定是 ( ).(A) 两个正数,一个负数(B) 两个负数,一个正数(C) 三个都是零(D) 其中两个数之和等于第三个数的相反数7. 已知|m-3|+|n+2|=0, 则m+2n的值为 ( ).(A) -1 (B) 1 (C) 4 (D) 7三、计算题8. -8-8+6. 9.−312+4.4−2.4+312.10. -17+(-33)-10-(-16). 11. -2.1-1.1+(-16.2)-(-13.3).12.(−6.5)−(−414)+8.75−(+312)+5.13.(+235)+(−734)−(−3.75)−(+6.2).14.−4.4−(−0.1)−813+1123+(−113).综合·运用·诊断一、选择题15. 有理数a ,b ,c ,d 在数轴上的对应点的位置如图所示,则正确的结论是( ). (A )a <−4(B )b +d >0(C )−a −d <0(D )|a|<|d|16. 若|a|=4, |b|=3, 且a, b 异号, 则 |a −b|=( ).(A) 7 (B) ±1 (C) 1 (D) 1或7二、填空题17. 有理数a ,b ,c 在数轴上的对应点的位置如图所示, 用“>”或“<”填空: (1) |a| |b|; (2) a+b+c 0; (3) a-b+c 0; (4) a+c b; (5) c-b a.三、计算题18.13−12+56−12+56.19.−513+21112−1614−356.20. 1-2+3-4+5-6+…+99-100.拓展·探究·思考解答题21. 已知有若干个数,第1个数记为( a₁,第2个数记为a₂, 第3个数记为a₃, ……a₁,第n个数记为 an. 若a1=−13,从第2个数起,每个数都等于1与前面那个数的差的倒数.(1) 分别求出a₁,a₁,a₁的值;(2) 求a1+a2+a3+⋯+a36的值.第二课时学习目标能熟练地进行有理数加减混合运算,并且会解决简单的实际问题.课堂学习检测一、选择题1. 如果两个有理数的和为负数,那么这两个数 ( ).(A) 都是负数 (B) 至少有一个是负数(C) 有一个是0 (D) 绝对值不相等2. 已知|x|=3,|y|=2,且x-y=-5,则x+y等于 ( ).(A) 5 (B) -5 (C) 1 (D) -13. 2, -7, -12的和比它们的绝对值的和小 ( ).(A) -38 (B) -4 (C) 4 (D) 38二、计算题4. (+132)-(+124)-(+16)+0+(-132)+(+16).5.(+325)+(−278)−(−535)−(+18).6.−357+15.5−627−512.7.−23−34+112+34−2+23.综合·运用·诊断解答题8. 计算:1-2-3+4+5-6-7+8+…+2 021-2022-2 023+2024.9. 阅读下面的计算方法. 计算: −556+(−923)+1712. 解:原式 =[(−5)+(−56)]+[(−9)+(−23)]+(17+12) =[(−5)+(−9)+17]+[(−56)+(−23)+12] =3+(--1)=2.上面的方法叫拆项法. 请参考上面的方法计算: −201056−201323+40023+102356.。
管理会计计算题及答案
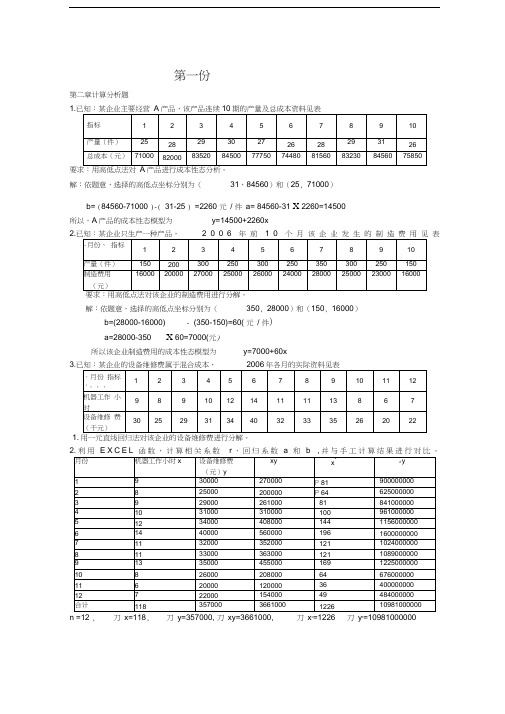
第一份第二章计算分析题1.要求:用高低点法对产品进行成本性态分析。
解:依题意,选择的高低点坐标分别为(31,84560)和(25, 71000)b= (84560-71000 )-( 31-25 ) =2260 元/ 件a= 84560-31 X 2260=14500所以,A产品的成本性态模型为y=14500+2260x2.表解:依题意,选择的高低点坐标分别为(350, 28000)和(150, 16000)b=(28000-16000) - (350-150)=60( 元/ 件)a=28000-350 X 60=7000(元)所以该企业制造费用的成本性态模型为y=7000+60x3.1. 用一元直线回归法对该企业的设备维修费进行分解。
n =12 , 刀x=118, 刀y=357000, 刀xy=3661000, 刀x2=1226 刀y2=109810000002 2r=(12 X 3661000-118 X 357000)十 (12X 1226-118 )x( 12X 10981000000-357000 )〜0.9785 T + 1 (x 与y 基本正相关)b=(12 X 3661000-118 X 357000) - (12 X 1226-118 2)=2292 元/ 小时a=(357000-2292 X 118) - 12=7212 元因此,该企业的成本性态模型为: y=7212+2292x第三章变动成本法计算成本题(注:计算变动非生产成本的业务量用销售量)1.已知:某公司从事单一产品生产, 连续三年销售量均为 1000件,而三年的产量分别为 1000件、1200件和800件。
单位产品售价为 200元,管理费用与销售费用均为固定成本,两项 费用各年总额均为50000元,单位产品变动生产成本为90元,固定性制造费用为 20000元,第一年的期初存货量为零。
(1) 分别采用变动成本法和完全成本法计算第一年的营业利润。
西方经济学(微观部分)计算题

第二章需求、供给和均衡价格1、假定在某市场上A 、B 两厂商是生产同种有差异的产品的竞争者,A 厂商的需求曲线为PA=80-2QA ,B 厂商的需求曲线为为PB=100—QB,两厂商目前的销售量分别为 QA1=20, QB1=40, 求:(1)B 厂商的需求价格弹性系数(2)如果B 厂商降价后,B 厂商的需求量增加为QB2=60,同时使竞争对手A 厂商的销售量减少为 QA2=10,那么A 厂商对B 厂商的需求交叉价格弹性系数为多少? 解答:(1)根据B 厂商的需求函数可知,当QB1=40时,PB1=60再根据需求的价格点弹性公式: 计算可得:eBd=—(-1)×1。
5=1.5 故当QB1=40时,该商品的需求价格弹性为1.5. (2)根据B 厂商的需求函数可知,当QB2=60时,PB2=40根据A 厂商的需求函数可知,当QA1=20时,PA1=40; QA2=10时,PA2=60 再根据需求的交叉价格弹性公式:计算可得: eABd=(-10×100)/(—20×30)=5/32、已知需求函数Qd=14-3P,供给函数Qs=2+6P ,求该商品的均衡价格,以及均衡时的需求价格弹性和供给价格弹性。
解答:由供求均衡Qs=Qd 得14-3P=2+6P P=4/3 Q=10 所以3、某商品的价格由24元上升到30元后,需求量相应减少10%,问该商品的需求弧弹性是多少?该商品价格变化对总收益有何影响? 解答:ed 小于1,商品价格与总收益成正方向变动。
4、假定某消费者关于某种商品的消费数量Q 与收入M 之间的函数关系为M=100Q2,求:当收入M=6400时的需求的收入点弹性。
解答:由以知条件M=100 Q2,可得Q =于是有:112100Q Md d=0lim d P QPdQPe P Q dP Q∆→∆=-•=-•∆1212limA B B d P B A A Q P P e P Q Q ∆→∆+=•∆+3/430.410d dQ Pe dP Q =-•=⨯=3/460.810s dQ P e dP Q =•=⨯=212121210.9302490.9302419d Q Q p p Q Qe Q Q p p Q Q ----=-÷=-÷=++++进一步,可得:111100)21002Q m MM Q d e d=•=••=观察并分析以上计算过程即其结果,可以发现,当收入函数M=aQ2(其中a 〉0 为常数)时,则无论收入M 为多少,相应的需求的点弹性恒等于1/2。
管理会计第二章练习题
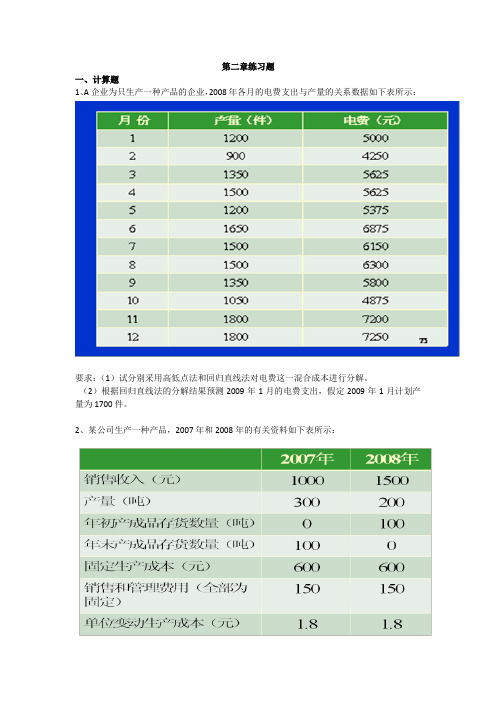
第二章练习题一、计算题1、A企业为只生产一种产品的企业,2008年各月的电费支出与产量的关系数据如下表所示:要求:(1)试分别采用高低点法和回归直线法对电费这一混合成本进行分解。
(2)根据回归直线法的分解结果预测2009年1月的电费支出,假定2009年1月计划产量为1700件。
2、某公司生产一种产品,2007年和2008年的有关资料如下表所示:要求:(1)用完全成本法为该公司编制这两年的比较利润表,并说明为什么销售增加50%,营业净利反而大为减少。
(2)用变动成本法根据相同资料编制比较利润表,并将它同(1)中的比较利润表进行比较,指出哪一种成本法比较重视生产,哪一种比较重视销售。
3、已知A企业从事单一产品的生产,连续三年销量均为1000件,而这三年产量分别为1000件,1200件和800件,单位产品售价为200元/年;管理费用与销售费用均为固定费用,这两项费用各年总额均为50000元;单位产品变动成本(包括直接材料、直接人工、变动制造费用)为90元;固定制造费用为20000元。
要求:(1)根据上述资料,不考虑销售税金,分别采用变动成本法和完全成本法计算各年税前利润;(2)根据计算结果,简单分析完全成本法与变动成本法对损益计算的影响。
二、选择题1、下列费用中属于酌量性固定成本的是()。
A、厂房、机器设备的租赁费B、保险费C、不动产税D、业务招待费2、下列各种混合成本可以用模型y=a+bx表示的是()。
A、半变动成本B、半固定成本C、延伸变动成本D、变动成本3、假设每个质检员最多检验1000件产品,也就是说产量每增加1000件就必须增加一名质检员,且在产量一旦突破1000件的倍数时就必须增加。
那么,该质检员的工资成本属于()。
A、半变动成本B、半固定成本C、延伸变动成本D、变动成本4、当企业实行计时工资制时,其支付给职工的正常工作时间内的工资总额是固定不变的;但当职工的工作时间超过正常水平,企业须按规定支付加班工资,且加班工资的多少与加班时间的长短存在正比例关系。
微观经济学课后题部分答案

第二章计算题2、某产品的市场需求函数为:Q =a —bP ,这里a,b >0。
(1)求市场价格为P 0时的需求价格弹性.(2)当a =3,b =1.5时,需求价格弹性为1。
5,求市场价格为多少? 并求此时的市场需求量.(3)求价格上升能带来市场销售额增加的市场价格范围。
解:(1)需求价格弹性:根据需求函数:Q =a -bP 可得:,所以当,所以(2)当a =3,b=0.5时,E d =1.5,即解此可得:P=1。
2,此时的市场需求为:(3)市场总的销售额为:TR -PQ =P (a —bP )=aP —bP 2对TR 求P 的一阶导数可得:要使价格上升能带来市场销售额的增加,就必须使>0,所以a-2bP >0即P <为价格上升能带来市场销售额增加的市场价格范围。
3、假定表1是供给函数在一定价格范围内的供给表。
(1)求出价格3元和5元之间的供给的价格的弧弹性。
(2)根据给出的供给函数,求P=4元时的供给价格点弹性。
(3)根据该供给函数或供给表做出几何图形,利用几何方法求出P=4元时的供给价格的点弹性。
它与(2)的结果相同吗?表1 某商品的供给表价格/元2 3 4 5 6 供给量 1 3 5 7 9解:(1)根据供给价格弧弹性的中点公式,根据商品供给表中的数据,可知价格3元和5元之间的供给价格弧弹性为(2)根据供给价格点弹性公式,根据供给函数和表中给出的数据,可知价格4元时的需求价格点弹性为(3)如上图所示,线性供给曲线与横坐标相交于A 点,B 点为该供给曲线上价格为4元时的点。
从几何意义看,根据点弹性的定义,C 点的供给的价格弹性可以表示为:Es=(dQ/dP)*P/Q=(AC /BC )*(BC/OC)=AC/OC=(5—(-3))/5=1。
6,结果相同。
5、假定某消费者的需求的价格弹性,需求的收入弹性.求:(1)在其他条件不变的情况下,商品价格下降2%对需求数量的影响。
(2)在其他条件不变的情况下,消费者收入提高5%对需求数量的影响。
微观经济学计算题

微观经济学计算题第二章需求、供给和均衡价格1. 已知某一时期内某商品的需求函数为Q d=50-5P,供给函数为Q s=-10+5P。
(1)求均衡价格P e和均衡数量Q e,并作出几何图形.(2)假定供给函数不变,由于消费者收入水平提高,使需求函数变为Q d=60-5P。
求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(3)假定需求函数不变,由于生产技术水平提高,使供给函数变为Q s=-5+5P.求出相应的均衡价格P e和均衡数量Q e,并作出几何图形。
(5)利用(1)、(2)和(3),说明需求变动和供给变动对均衡价格和均衡数量的影响。
解答:(1)将需求函数Q d=50-5P和供给函数Q s=-10+5P代入均衡条件Q d=Q s,有50-5P=-10+5P得P e=6将均衡价格P e=6代入需求函数Q d=50-5P,得Q e=50-5×6=20或者,将均衡价格P e=6代入供给函数Q s=-10+5P,得Q e=-10+5×6=20所以,均衡价格和均衡数量分别为P e=6,Q e=20。
如图2—1所示。
图2—1(2)将由于消费者收入水平提高而产生的需求函数Q d=60-5P和原供给函数Q s=-10+5P代入均衡条件Q d=Q s,有60-5P=-10+5P得P e=7将均衡价格P e=7代入Q d=60-5P,得Q e=60-5×7=25或者,将均衡价格P e=7代入Q s=-10+5P,得Q e=-10+5×7=25所以,均衡价格和均衡数量分别为P e=7,Q e=25。
如图2—2所示。
图2—2(3)将原需求函数Q d=50-5P和由于技术水平提高而产生的供给函数Q s=-5+5P代入均衡条件Q d=Q s,有50-5P=-5+5P, 得P e=5.5将均衡价格P e=5。
5代入Q d=50-5P,得Q e=50-5×5。
5=22.5或者,将均衡价格P e=5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 热力学第二定律计算题1.有一绝热体系如图2.1所示,中间隔板为导热壁,右边容积为在左边容积的2倍,已知气体的C v,m =28.03J ·mol -1,请求: (1)不抽掉隔板达平衡后的ΔS 。
(2)抽去隔板达平衡后的ΔS 。
解:(1)不抽掉隔板最后达热平衡,温度为T ,设左边为室1,右边为室2: )298(2)283(1)()(2,1,22T T T T C n T T C n m v N m v o −×=−×−=−解出T=293(K )2,1,1122T Tn C n T T nC n S m v N m v O +=∆ 10248.0298293103.282283293103.281−⋅=××+××=K J n n(2)抽去隔板后的熵变有两部分组成,一部分为上述热熵变化,另一部分为等温混合熵变。
110248.0−⋅=∆K J SVV R n V V R n S N O 23ln 3ln222+=∆ 121191.1588.15231314.8231314.81−−⋅=∆+∆=∆⋅=××+××=K J S S S K J n n2. 体系经绝热不可逆过程由A 态变到B 态。
请论证不可能用一个绝热可逆过程使体系从B 态回到A 态。
解:体系经绝热不可逆过程由A 态变到B 态,据熵增加原理可知AB A B S S S S S >>−=∆即01图 2假设用一个绝热可逆过程使体系能够从B 态回到A 态,据熵增加原理得AB B A S S S S S >>−=∆即02此结果与S B >S A 矛盾,故作假设不真,因此此题结论得证。
3. 在298.15K 的等温情况下,两个瓶子中间有旋塞连通。
开始时,一个瓶中放0.2molO 2,压力为0.2×101325Pa ,另一个瓶中放0.8molN 2,压力为0.8×101325Pa ,打开旋塞后,两气互相混合。
计算。
(1)终了时瓶中的压力;(2)混合过程中的Q ,W ,ΔU ,ΔS ,ΔG ;(3)如设等温下可逆地使气体回到原状,计算机过程中的Q 和W 。
1013252.015.298314.82.0)1(:222×××==O O O p RT n V 解302447.0m =1013258.015.298314.88.0222×××==N N N p RT n V302447.0m =02447.0215.298314.81×××==总总终V RT n p (2)以两个球内气体为体系,混合过程没有对外做功,W=0,又是等温过程,ΔU=0,则Q=0。
22222211N N O O N O mix V Vn R n V V nR n S S S 总总+=∆+∆=∆ 176.5314.8]2ln 8.02ln 2.0[−⋅=××+×=K J S T S T H G mix mix mix mix ∆−=∆−∆=∆0 J K J K 1719)763.5)(2.298(1−=⋅−=− (3)等温可逆分离使气体各回原态JQ W U J K J K S T Q R mix R 1719,01719)763.5)(2.298(1=−==∆−=⋅−=∆−=−4.将一玻璃球放入真空容器中,球中已封入1mol 水(101325Pa ,373K ),真空容器内部恰好容纳1mol 的水蒸气(101325Pa ,373K ),若保持整个体系的温度为373K ,小球被击破后,水全部汽化成水蒸气,计算Q ,W ,ΔU ,ΔH ,ΔS ,ΔG ,ΔA 。
根据计算结果判断这一过程是否是自发过程;用哪一个热力学性质作为判据?已知水的蒸发热为40668.5J ·mol -1(条件是温度373K ,压力为101325Pa )解:ΔH =(1mol )(40668.5J ·mol -1)=40668.5J 向真空蒸发 W=0JJ J K mol KJ mol J nRT H pV H V V p H Vp H pV H Q W Q U g g 375671.31015.40668)373)(314.8)(1(5.40668)()(111=−=⋅⋅−=−∆=−∆=−−∆=∆−∆=∆−∆==+=∆−−JJ J S T U A G K J K J T Q S r301015.4066837567003.109373/5.406681−=−=∆−∆=∆=∆⋅===∆−该过程是恒温容过程,故可用∆A 作判据,因为∆A<0,故该过程自发。
5. 在298K ,101300Pa 下,若使1mol 铅与醋酸铜液在可逆情况下作用,可得电功91838.8J,同时吸热213635J ,试计算ΔU ,ΔH ,ΔS ,ΔA 和ΔG 。
解:W 体积功=0 W 电功= -91838.8J Q=213635JΔU=Q+W=213635J-91838.8J=121796J 对凝聚相反应,ΔH ≈ΔU=121796JJ W G J W A K J K J T Q S r 8.918388.918389.7162982136351−=′=∆−=′=∆⋅===∆−6.证明dV V T C dp p T C TdS p p vv ⎟⎠⎞⎜⎝⎛∂∂+⎟⎟⎠⎞⎜⎜⎝⎛∂∂= 解:设S=S (p,V ) dVV T C dp P T C TdS dV V T T C dp P T TC dV V T T S dp P T T S dV V S dp p S dS pp v v P p vvp p v v p v⎟⎠⎞⎜⎝⎛∂∂+⎟⎠⎞⎜⎝⎛∂∂==⎟⎠⎞⎜⎝⎛∂∂+⎟⎠⎞⎜⎝⎛∂∂=⎟⎠⎞⎜⎝⎛∂∂+⎟⎠⎞⎜⎝⎛∂∂+⎟⎠⎞⎜⎝⎛∂∂⎟⎠⎞⎜⎝⎛∂∂=⎟⎠⎞⎜⎝⎛∂∂+⎟⎟⎠⎞⎜⎜⎝⎛∂∂=则7.证明对理想气体绝热可逆过程dG=(C P -S)dT 证明:由G 的定义G=H-TS 得dG=dH-TdS-SdT (1) 理想气体 dH=C P dT 绝热可逆过程 dS=0将上述二式代入(1),得理想气体绝热可逆过程dG=(C P -S)dT8.甲苯正常沸点(383K )下气化热为3619J •g -1,现将1mol 甲苯在383K 等温等压完全气化,求该过程Q ,W ;并求甲苯的△U m ,△H m ,△S m ,△A m ,△G m ,若甲苯向真空气化(终态同上),上述各量又是什么?解析:正常沸点是指p 0下液-气可逆相变温度,是一种平衡相变,因此Q=△H m =361.9J •g -1×92.14g •mol -1=33.35kJ •mol -1kJ RT pV V V p pdV W gV vg m m g m 184.3)(11−=−=−=−−=−=∫△U m =Q+W=30.16kJ •mol -1 1106.87−−⋅⋅=∆=∆mol K J TH S mm △A m =△U m -T △S m =-3.184kJ •mol -1△G m =0若向真空气化,由于始终态相同,因此凡状态函数各改变量均不变,同上面所得。
W=0,Q=△U m =30.16kJ •mol -19.已知298K 时下列数据(见下表),求算298K 时甲醇的 饱和蒸气压。
物质)/(1−Θ⋅∆mol kJ H m f)/(11−−Θ⋅⋅mol K J S mH 2(g )0 130.57O 2(g) 0 205.03 C(石墨) 0 5.740 CH 3OH (1) -288.7 127.0 CH 3OH (g )-200.7 239.9解:提到饱和蒸气压,应联想到设计过程中要有包括在蒸气压的压力下的可逆相变。
此题解法很多,关键在于如何设计可逆过程,根据所设计的过程(图9-1,图9-2)作相应的求算。
方法1.令298K ,其饱和蒸气压力P(298K ,Θp )H 2(g )+O 2(g )+C(石墨CH 3OH (g )(298K,Θp )d Θp )CH 3OH (1) ge (298K ,p) CH3OH (1) 3OH (g )(298.K,p)图9-1反应c 与d 的S H ∆∆及可由已知数据求得,然后根据可求,S T H G ∆−∆=∆△1G=-16.11 kJ •mol -1 △2G=-166.47 kJ •mol -1△3G=0(压力对凝聚相的Gibbs 自由能影响很小) △4G=0(可逆相变))/ln(5p p RT G Θ=∆(令气相为理想气体)∴△1G=△2G+△5G 得kPa p p p 44.17,8112.5/==Θ方法2,298,1(3p K OH CH ),298,(p K g,298,13K CH ),298,(3p K g CH图9-2△S=△1S+△2S+△3S△1S=0(压力凝聚相熵的影响很小) △H=△1H+△2H+△3H△1H=0(压力对凝聚相焓的影响很小) △3H=0(理想气体焓只是温度函数) △H=△2H )/ln(,32Θ=∆∆=∆∴p p R S THS )/ln(32Θ+∆=∆+∆=∆p p R THS S S 可求。
方法3 过程同方法2∫Θ∆=∆−∆ΘppVdp p K G p K G ),298(),298(]0),298([/1=∆==−=∆p K G p RT V V V V gm m g m 代入积分10.证明绝热可逆过程的温度与压力的关系为PPS C T V T p T ⎟⎠⎞⎜⎝⎛∂∂=⎟⎟⎠⎞⎜⎜⎝⎛∂∂ 解析:证明方法很多,我们以此题为例介绍几种常用方法。
方法1 从热力学基本方程出发 dH=TdS+Vdp dp T V P H dT T H dp T V dH T dS T p −⎟⎠⎞⎜⎝⎛∂∂+⎟⎠⎞⎜⎝⎛∂∂=−=][1 dp V p H T dT T C T P ][1−⎟⎟⎠⎞⎜⎜⎝⎛∂∂+=由dH=TdS+Vdp 可得 V T V T V p S T p H P T T+⎟⎠⎞⎜⎝⎛∂∂−=+⎟⎟⎠⎞⎜⎜⎝⎛∂∂=⎟⎟⎠⎞⎜⎜⎝⎛∂∂ 将此式代入式,得 dp T V dT T C dS PP ⎟⎠⎞⎜⎝⎛∂∂−=即,1dp T V C T dS dS dT P P ⎟⎠⎞⎜⎝⎛∂∂+=PPS C T V T p T ⎟⎠⎞⎜⎝⎛∂∂=⎟⎟⎠⎞⎜⎜⎝⎛∂∂∴ 方法2 从Maxwell 关系式出发P PPP P P P S C T V T T S T T V T T S T V S V p T ⎟⎠⎞⎜⎝⎛∂∂=⎟⎠⎞⎜⎝⎛∂∂⎟⎠⎞⎜⎝⎛∂∂=⎟⎠⎞⎜⎝⎛∂∂⎟⎠⎞⎜⎝⎛∂∂=⎟⎠⎞⎜⎝⎛∂∂=⎟⎟⎠⎞⎜⎜⎝⎛∂∂ 方法3 从循环关系出发 1−=⎟⎠⎞⎜⎝⎛∂∂⎟⎠⎞⎜⎝⎛∂∂⎟⎟⎠⎞⎜⎜⎝⎛∂∂P T S T S S P p T P PP P PT SC T V T T S T V T S p S p T ⎟⎠⎞⎜⎝⎛∂∂=⎟⎠⎞⎜⎝⎛∂∂⎟⎠⎞⎜⎝⎛∂∂=⎟⎠⎞⎜⎝⎛∂∂⎟⎟⎠⎞⎜⎜⎝⎛∂∂−=⎟⎟⎠⎞⎜⎜⎝⎛∂∂ 方法4 应用Jacobi 行列式TP TP TT PP S p S T S p s T p p S p T T S T T p T pS p T S T S p S T P T ⎟⎟⎠⎞⎜⎜⎝⎛∂∂⎟⎠⎞⎜⎝⎛∂∂⎟⎟⎠⎞⎜⎜⎝⎛∂∂⎟⎠⎞⎜⎝⎛∂∂⎟⎟⎠⎞⎜⎜⎝⎛∂∂⎟⎟⎠⎞⎜⎜⎝⎛∂∂⎟⎠⎞⎜⎝⎛∂∂⎟⎠⎞⎜⎝⎛∂∂=∂∂∂=∂∂=⎟⎠⎞⎜⎝⎛∂∂,)(),(),(),(),(PPPP P S C T V T S p S T S p S ⎟⎠⎞⎜⎝⎛∂∂−=⎟⎠⎞⎜⎝⎛∂∂−⎟⎟⎠⎞⎜⎜⎝⎛∂∂−=⎟⎠⎞⎜⎝⎛∂∂−⎟⎟⎠⎞⎜⎜⎝⎛∂∂=11.乙烯蒸气压与温度关系为20421.810375.8lg 75.113.83413+×−+−=ΘK T K T T k pp g试求乙烯在正常沸点169.3K 时的摩尔气化焓和摩尔气化熵。
