自动控制原理第8章习题解——邵世凡
自动控制原理习题及答案(冯巧玲)
第二章习题及答案2-1 试建立题2-1图所示各系统的微分方程 [其中外力)(t F ，位移)(t x 和电压)(t u r 为输入量；位移)(t y 和电压)(t u c 为输出量；k （弹性系数），f （阻尼系数），R （电阻），C （电容）和m （质量）均为常数]。
解（a ）以平衡状态为基点，对质块m 进行受力分析（不再考虑重力影响），如图解2-1(a)所示。
根据牛顿定理可写出22)()(dtyd m dt dy f t ky t F =-- 整理得)(1)()()(22t F m t y m k dt t dy m f dtt y d =++（b ）如图解2-1(b)所示，取A,B 两点分别进行受力分析。
对A 点有 )()(111dtdydt dx f x x k -=- （1） 对B 点有 y k dtdydt dx f 21)(=- （2） 联立式（1）、（2）可得：dtdx k k k y k k f k k dt dy2112121)(+=++ (c) 应用复数阻抗概念可写出)()(11)(11s U s I csR cs R s U c r ++= （3） 2)()(R s Uc s I =（4） 联立式（3）、（4），可解得：CsR R R R Cs R R s U s U r c 212112)1()()(+++=微分方程为:r r c c u CR dt du u R CR R R dt du 121211+=++ (d) 由图解2-1（d ）可写出[]Css I s I s I R s U c R R r 1)()()()(++= （5） )()(1)(s RI s RI Css I c R c -= （6） []Css I s I R s I s U c R c c 1)()()()(++= （7）联立式（5）、（6）、（7），消去中间变量)(s I C 和)(s I R ，可得：1312)()(222222++++=RCs s C R RCs s C R s U s U r c 微分方程为 r r r c c c u RC dt du CR dt du u R C dt du CR dt du 222222221213++=++ 2-2 试证明题2-2图中所示的力学系统(a)和电路系统(b)是相似系统（即有相同形式的数学模型）。
自动控制原理第6章习题解——邵世凡
习 题 66-1 设控制系统的开环传递函数为：()()()s s s s G 1.015.0110++= 绘出系统的Bode 图并求出相角裕量和幅值裕量。
若采用传递函数为(1+0.23s)/(1+0.023s)的串联校正装置，试求校正后系统的幅值和相角裕度，并讨论校正后系统的性能有何改进。
6—2设控制系统的开环频率特性为()()()()ωωωωωj j j j H j G 25.01625.011++= ①绘出系统的Bode 图，并确定系统的相角裕度和幅值裕度以及系统的稳定性； ②如引入传递函数()()()0125.025.005.0++=s s s G c 的相位滞后校正装置，试绘出校正后系统的Bode 图，并确定校正后系统的相角裕度和幅值裕度。
6 3设单位反馈系统的开环传递函数为()()()8210++=s s s s G 设计一校正装置，使静态速度误差系数K v =80，并使闭环主导极点位于s=-2±j23。
6-4设单位反馈系统的开环传递函数为()()()93++=s s s K s G ①如果要求系统在单位阶跃输入作用下的超凋量σ =20％，试确定K 值；②根据所确定的K 值，求出系统在单位阶跃输入下的调节时间t s 。
，以及静态速度误差系数； ③设计一串联校正装置，使系统K v ≥20，σ≤25％，t s 减少两倍以上。
6 5 已知单位反馈系统开环传递函数为()()()12.011.0++=s s s K s G 设计校正网络，使K v ≥30，γ≥40º，ωn ≥2.5，K g ≥8dB 。
6-6 由实验测得单位反馈二阶系统的单位阶跃响应如图6-38所示．要求①绘制系统的方框图，并标出参数值；②系统单位阶跃响应的超调量σ =20％，峰值时间t p =0.5s ，设计适当的校正环节并画出校正后系统的方框图。
6-7设原系统的开环传递函数为()()()15.012.010++=s s s s G 要求校正后系统的相角裕度γ=65º。
任彦硕《自动控制原理》全部答案
R1
R2
+
1 sC2
Ur (s) R1C2s
(d)
Ur (s) R1
=
Uc (s)
( R2
//
1 sC2
)
⇒ T(s) = Uc(s) Ur (s)
=
R2 R1
1 R2C2s +1
题 2-2：试用运算法建立题 2-2 图所示 LC、RLC 电网络的动态结构图，并求解
自 u i (t) 至 u o (t) 信号传输的传递函数。
b)
R 2 uc(t) C2 −
R1 u r(t)
Rb
R2 C2
− +
c)
− uc(t)
R1 u r(t)
Rb
题 2-1 图 电网络
C3 R3 C2 R2
− +
d)
− uc(t)
(a) T (s) = Uc (s) =
R2
+
1 sC2
=
R2C1C2s + C1
Ur (s)
R1
+
R2
+
1 sC1
+
1 sC2
−
Ms2
X1(s)
=
ms2
X
2
⇒ X1(s) =
ms2 + ks + f
F (s) s2[Mms2 + (M + m)ks + (M + m) f ]
(b)
⎧ ⎪⎪m ⎨
⎪ ⎪⎩
f1
d 2 x1(t) + dt 2
d[x1(t) − dt
f1
d[
x1
(t) − dt
自动控制原理课后习题答案.docx
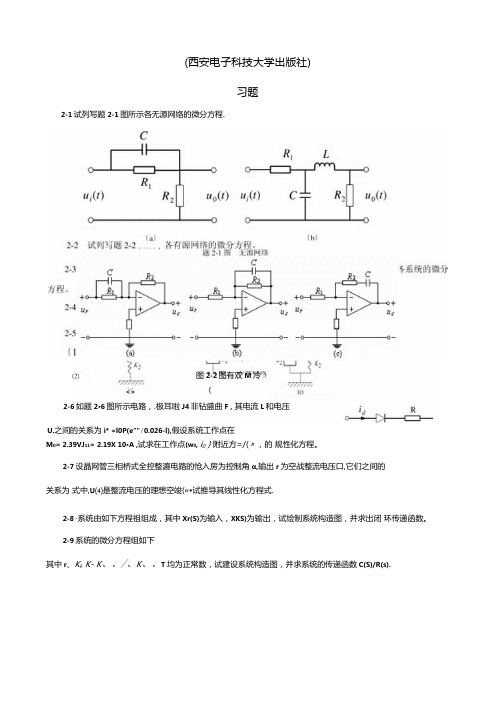
(西安电子科技大学出版社)习题2-1试列写题2-1图所示各无源网络的微分方程.M 0= 2.39VJ 11= 2.19X 10∙A ,试求在工作点(w 0, i 0｝附近方=/(〃，的 规性化方程。
2-7设晶网管三相桥式全控整漉电路的怆入房为控制角α,输出r 为空战整流电压口,它们之间的 关系为 式中,U ⑷是整流电压的理想空竣(«•试推导其线性化方程式.2-8 ∙系统由如下方程祖组成，其中Xr(S)为输入，XKS)为输出，试绘制系统构造图，并求出闭 环传递函数。
2-9系统的微分方程组如下其中r 、K l . K- K 、、/、K 、、T 均为正常数，试建设系统构造图，并求系统的传递函数C(S)/R(s).图2-2图有双M 冷 ⑵(W <»U.之间的关系为i* =l0P(e""∕0.026-l),假设系统工作点在 2-6如题2∙6图所示电路，.极耳啦J4非钻盛曲F ，其电流L 和电压2-10试化简即2-10图所示的系统构造图.并求传递函数C(S)11R(S), K(S) C(S)/ C(S) R(S) 筑书规图所材 Gl C(S) G,卡G 5佛与函数 国S) C(S) G) 5 “七； Hl 弟统 £(S) M(S)2-16零初 设某 2-17 g (t) = 7-5e 6f . 咫2∙ 15图求系统 的传速函数, 始条件下的输出响试求该系统的传递 2-18系统的 W'> I 控制系统构造t f 1*1 2-16 W 系统构造图 R(S) ΛU) 2-15 E(S) C (Λ I I - L_rτ∏J ∙13图 系统G:" r ,(5) E(S)凤 F) R ⑸M ⑸松) ⅛4和脉冲响应函数, 单位脉冲响应为。
自动控制原理智慧树知到课后章节答案2023年下邵阳学院
自动控制原理智慧树知到课后章节答案2023年下邵阳学院邵阳学院第一章测试1.系统和输入已知，求输出并对动态特性进行研究，称为（）答案:系统分析2.通过测量输出量，产生一个与输出信号存在确定函数比例关系值的元件称为（）答案:反馈元件3.在直流电动机调速系统中，霍尔传感器是用作（）反馈的传感器。
答案:电流4.系统已给出，确定输入，使输出尽可能符合给定的最佳要求，称为（）答案:最优控制5.时域分析的性能指标，哪个指标是反映相对稳定性的（）答案:最大超调量6.直接对控制对象进行操作的元件称为（）答案:执行元件7.主要用来产生偏差的元件称为（）答案:比较元件8.主要用于产生输入信号的元件称为（）答案:给定元件9.“现代控制理论”的主要内容是以（）为基础，研究多输入、多输出等控制系统的分析和设计问题。
答案:状态空间模型10.主要用于稳定控制系统，提高性能的元件称为（）答案:校正元件第二章测试1.系统的数学模型是指（）的数学表达式。
答案:系统的动态特性2.答案:3.答案:4.答案:5.答案:56.答案:207.答案:108.关于传递函数，错误的说法是 ( )答案:传递函数不仅取决于系统的结构参数，给定输入和扰动对传递函数也有影响9.答案:比例、积分、微分10.答案:第三章测试1.答案:临界稳定2.答案:0.53.为了保证系统稳定，则闭环极点都必须在（）上答案:s左半平面4.答案:不稳定5.答案:愈小6.答案:型别 v < 2 7.答案:28.非单位负反馈系统，其前向通道传递函数为G(S)，反馈通道传递函数为H(S)，当输入信号为R(S)，则从输入端定义的误差E(S)为 ( )答案:9.答案:2010.答案:欠阻尼系统第四章测试1.答案:2.在系统中加入适当的开环零点或极点可以改善系统的稳态和动态性能，增加开环极点，根轨迹将向左偏移（）答案:错3.答案:-24.答案:对5.答案:16.答案:-1.57.答案:(1,5];(-∞,7]8.答案:0为起始点;-3为起始点9.答案:210.根轨迹定义为闭环传递函数的某个参数，由0变化到无穷大时，系统的闭环特征根在S平面上的变化轨迹( )答案:错第五章测试1.答案:2.闭环系统的动态性能主要取决于开环对数幅频特性的( )答案:中频段3.惯性环节和积分环节的频率特性在（）上相等答案:幅频特性的斜率4.答案:圆5.答案:6.二阶振荡环节乃奎斯特图中与虚轴交点的频率为( )答案:固有频率7.一般为使系统有较好的稳定性,希望相位裕量g为（）答案:8.若系统的传递函数在右半S平面上没有零点和极点，则该系统称作（）答案:最小相位系统9.答案:610.答案:第六章测试1.单位负反馈系统型数为2，闭环幅频特性的零频值为（）。
自动控制原理第4章习题解——邵世凡
第四章 习题4-1 绘制具有下列开环传递函数的负反馈系统的根轨迹1、()()()()54*++=s s s K s H s G解：首先确定开环传递函数中的零极点的个数各是多少。
由开环传递函数可知 m=0，n=3，n -m=3。
即，有限零点为0个，开环极点为3个。
其中，3个开环极点的坐标分别为：p 1=0，p 2=-4，p 3=-5。
然后，在[s]平面上画出开环极点的分布情况，根据根轨迹方程的幅角条件：首先确定实轴上的闭环系统的根轨迹。
如图所示。
接着再通过所需参数的计算画出比较精确的根轨迹通过画实轴上的根轨迹图可知，有3条闭环根轨迹，分别从p 1=0，p 2=-4，p 3=-5出发奔向无穷远处的零点。
在这一过程中，从p 1=0，p 2=-4两个极点出发的根轨迹在实轴上相遇后进入复平面，因此，有必要进行分离点的坐标计算，渐进线在实轴上的坐标点和渐进线的角度计算，以及与虚轴交点的计算。
根据公式有：渐进线303054011-=----=--=∑∑==mn zp n i mj jiσ()() ,,331212ππππϕ±±=+=-+=k mn k a从p 1=0，p 2=-4两个极点出发的根轨迹在实轴上相遇后将沿着±60º进入复平面，分离点：设：()1=s N ；()()()s s s s s s s D 2095423++=++=；()0'=s N ；()201832'++=s s s D则有：()()()()()0201832''=++-=⋅-⋅s s s D s N s D s N[s ]0201832=++s s解得方程的根为s 1= -4.5275（不合题意舍去）；s 2= -1.4725 得分离点坐标：d = -1.4725。
与虚轴的交点：在交点处，s=j ω，同时也是闭环系统的特征根，必然符合闭环特征方程，于是有：()020********=++--=+++*=*K j j K s s sj s ωωωω整理得： 0203=-ωω；092=-*ωK 解得01=ω；203,2±=ω；18092==*ωK 最后，根据以上数据精确地画出根轨迹。
《自动控制原理》---丁红主编---第八章习题答案
8-1已知非线性环节的特性如图8.1a 所示，试计算该环节的描述函数。
答：方法一：由图8.1a 所示，,0...............0...............⎩⎨⎧<->+=x A Kx x A Kx y 令代入则可以得到, 因为非线性特性为奇函数，所以=0,A 1=,B 1==在此处键入公式。
可以得到B 1=KX+4,所以该非线性环节的描述函数为 。
方法二：图8.1a 所示的非线性特性可以看作是图8.1b ，图8.1c 叠加而成的。
图8.1b 对应的非线性环节的描述函数为。
图8.1c 对应的为理想继电器非线性，其描述函数为。
所以，图8.1a 对应的飞线性特性描述函数为。
8.2.试绘制0=++x x x &&&非线性系统的相平面图。
答：y 0 -a a x k （a ） y 0 xk （b ） y（c ）0 -aa x由题意，此方程可以改写为：,开关线为x=0。
当x>0时，相轨迹方程对应的特征方程为+λ+1=0，，由可以得到.故奇点为稳定的焦点。
当x<0时，相轨迹方程对应的特征方程为+λ-1=0,,由可以得到此时的奇点为（0,0），奇点为鞍点，推导等倾线方程。
令=α，可以得到等倾线方程为,令等倾线的斜率为k ，即可以得到，得到,列写表格如下表所示。
K -3 -2 -10 1 2 3 +∞,8.3.系统方框图如图8-29所示，其中K>0，T>0。
当非线性元件N分别为理想继电特性;死区继电特性;滞环继电特性;带死区和滞环的继电特性，在cc&-相平面上绘制相平面图。
8-29系统方框图（1）具有死区的三位置继电特性线性部分的微分方程为当继电特性为具有死区的三位置继电特性时，上式可以写成分段微分方程为：C(t)r = 0- )1(+TssKN(e)e)开关线为,两条开关将相平面划分为三个线性区域，下面分区绘制相轨迹在区域，相轨迹方程为：类似于具有饱和特性的非线性控制系统时的讨论，像平面与该区域无奇点，相轨迹均渐进于的直线。
自动控制原理习题及解答
dt 2
dt
（2-1)
此方程为二阶非线性齐次方程。
（5）线性化
由前可知，在θ ＝0 的附近，非线性函数 sinθ ≈θ ，故代入式（2-1）可得线
性化方程为
ml d 2θ + al dθ + mgθ = 0
dt 2
dt
例 2-3 已知机械旋转系统如图 2-3 所示，试列出系统运动方程。
图 2-3 机械旋转系统
U (s) = Z(s) I (s)
如果二端元件是电阻 R、电容 C 或电感 L，则复阻抗 Z(s)分别是 R、1/C s 或 L s。
(2) 用复阻抗写电路方程式：
I1
(S)
=
[U
r
(S
)
−
U
C1
(S )]
⋅
1 R1
U
c1
(S)
=
[I1(S
)
−
I
2
(S )]
⋅
1 C1s
I
2
(S
)
=
[U
c1
(S)
=1−
(L1
+
L2
+
L3 )
−
L1 L2
=1+
1 R1C1S
+
1 R2C2 S
+
1 R2 C1 S
（2－2）
式中，J 为摆杆围绕重心 A 的转动惯量。
摆杆重心 A 沿 X 轴方向运动方程为：
m d 2xA = H dt 2
即
m d 2 (x + l sinθ ) = H
（2
dt 2
－3）
摆杆重心 A 沿 y 轴方向运动方程为：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
习题8
8—1 三个非线性系统的非线性环节一样，线性部分分别为
①G㈤一赢；②G㈤一志；③G㈤一高等揣。
试问用描述函数法分析时，哪个系统分析的准确度高?
8 2试求图8～41所示非线性特性的描述函数
8—3 试求图8—42所示非线性特性的描述函数。
8—4求图8 43所示非线性描述函数。
8—5求图8 44所示非线性描述函数。
8 非线性系统理论§265
8—6 求出图8—45所示非线性控制系统线性部分的传递函数。
8—7一非线性系统其前向通路中有一描述函数N(A)一去e j寻的非线性元件，线性部分传递函数为试用描述函数法确定系统是否存在自激振荡，若有，求出自激振荡参数。
8 8试用描述函数分析图8 46所示系统必然存在自激振荡，
y．z，e的稳态波形。
8 9若非线性系统的微分方程为
试求系统的奇点．并概略绘制奇点附近的相轨迹。
并求出自激振荡振幅和振荡频率，并画出
8 10 非线性系统结构如图8—47所示，系统开始是静止的，输入信号r(￡)一4×1(f)，试写出切换线方程，确定奇点的位置和类型，作出该系统的相平面图，并分析系统的运动特点。
8—11 已知非线性系统的微分方程为
图8 47题8—10非线性系统
i1一T1(T；+z；一1)(T；+上；～9)一z2(z；+T；一4)
j 2一z2(z；+卫!一1)(工}+z；～9)+z1(zi+T；一4)
试分析系统奇点的类型，判断系统是否存在极限环。
8 12绘制图8 48所示非线性系统的相轨迹，分析系统的运动特性(B>O，B。
<4K)。
8—13 已知非线性系统如图8—49所示，粗略绘制系统在单位阶跃及斜坡输入r一、，T+R 作用下系统的相轨迹，并分析系统的运动特性(T>O，4KT>1)。
8—14一非线性控制系统如图8—50所示，请绘制系统在如下情况下的相轨迹，并分析系统的运动特性。
初始状态为P(O)：3．5，i(O)一O。
8—15一位置继电控制系统结构如图8—51所示．当输入幅度为4的阶跃函数，绘制从y(0)一一3，j(O)一O出发的相轨迹，求系统运动的最大速度、超调量及峰值时间。
8 16一继电控制系统如图8 52所示，输人为单位阶跃，绘制从y(O)一一8，，(O)一O 出发的相轨迹，分
析系统是否存在周期运动．若存在周期运动，求出周期振荡的振幅和振荡频率。
8一17非线性控制系统如图8—53所示。
已知y(O)一2，'(O)一O，绘制系统相轨迹。
并求出f一10时的y
和』值。
8 18已知继电控制系统如图8 54所示，绘制系统相轨迹。
已知y(0)一一2．5，多(0)一O。
并判断系统是
否存在周期运动，若存在，求出振荡参数。