第2章 平面问题的基本理论_习题.
合集下载
弹性力学复习思考题

其中: 为曲梁圆周边界上的分布载荷。 其中: q 为曲梁圆周边界上的分布载荷。 M, Q分别为梁截面上弯矩与剪力。 分别为梁截面上弯矩与剪力。 分别为梁截面上弯矩与剪力 应力函数: 结合应力分量与应力函数的关系确定 应力函数:
2 σθ = 2 r
= f (r)
= f (r) sin θ
= f (r) cosθ
力偶、 (9)半无限平面体在边界上作用力偶、集中力、分布力下,应力函数 )半无限平面体在边界上作用力偶 集中力、分布力下 、应力分量、位移分量的确定? 应力分量、位移分量的确定? 应力分量、位移分量的确定? (10)圆孔附近应力集中问题应力函数 、应力分量、位移分量的确定? ) (11)叠加法的应用。 )叠加法的应用。
X = l(1+ )αT,
Y = m(1+ )αT
(5)温度应力问题求解的基本思路与方法: )温度应力问题求解的基本思路与方法: (a)求出满足位移平衡方程(6-18)的一组特解(此时,无需满足 )求出满足位移平衡方程( )的一组特解(此时, 边界条件;用位移势函数求解)。 边界条件;用位移势函数求解)。 (b)不计变温,求出满足平衡方程(6-18)的一组补充解(常由应 )不计变温,求出满足平衡方程( )的一组补充解( 力函数求解,其边界条件为特解给出的面力)。 力函数求解,其边界条件为特解给出的面力)。 的概念; 与位移分量的关系; (6)位移势函数 ψ 的概念;位移势函数 ψ 与位移分量的关系;温 ) 度应力问题中, 满足的方程; 度应力问题中,位移势函数 ψ 满足的方程;应力分量的位移势 的表示。 函数 ψ 的表示。
王俊民 编 徐秉业 编
《弹性力学学习方法及解题指导》 弹性力学学习方法及解题指导》
同济大学出版社 机械工业出版社
弹性力学-2-平面问题的基本理论

2015-1-16
4 弹性力学
2.1 平面应力问题与平面应变问题
弹性力学空间问题共有应力、应变和位
移共15个未知函数,且均为 f (x, y, z)。
弹性力学平面问题共有应力、应变和位
移8个未知函数,且均为f (x, y,)。
2015-1-16
5 弹性力学
2.1 平面应力问题与平面应变问题
什么条件下 空间问题可简化为平面问题
px n l l
py n m m
又由于:
px xl xy m p y xyl y m
32 弹性力学
2015-1-16
2.2 平面问题中一点的应力状态 问题3:若经过该点的某一斜面上的切应力为0, 求此斜面上的主应力σ和应力主方向α 从而可得
2015-1-16 25 弹性力学
2.2 平面问题中一点的应力状态 应力是与作用面有关的。σx,σy和τxy作为 基本未知函数,只是表示一点的坐标平面上的 应力分量(左图)。而校核强度时需要知道过 此点的任意斜面上的应力p。斜面上的应力p可 以按坐标轴分解为(px,py),也可沿法向和切 向分解为正应力σn和切应力τn(右图)。
z , zx , zy 0
2015-1-16 10 弹性力学
2.1 平面应力问题与平面应变问题
因此,此类问题的未知量只剩下Oxy面内 的三个应力分量: x , y , xy
所以此类问题称为平面应力问题。 由于板很薄,等厚度,外力和约束沿z 方向不变,因此应力也沿厚度z方向均匀分 布,应力x,y和xy只是坐标x, y的函数。
取如图所示的微分三角板或三棱柱
PAB,当平面AB无限接近于P点时, 该平面上的应力即为所求。
理论力学平面力系的简化和平衡

原力偶系的合力偶矩
n
M Mi i 1
只受平面力偶系作用的刚体平衡充要条件:
n
M Mi 0 i 1
对BC物块对B点取矩,以逆时针为正列方程应为:
M 2 M B (FC ) M FCY a FCx b M FC (b a) cos45 0
[例] 在一钻床上水平放置工件,在工件上同时钻四个等直径 的孔,每个钻头的力偶矩为 m1m2 m3 m4 15Nm 求工件的总切削力偶矩和A 、B端水平反力?
两轴不平行即 条件:x 轴不 AB
可,矩心任意
连线
mA (Fi ) 0 mB (Fi ) 0 mC (Fi ) 0
③三矩式 条件:A,B,C不在
同一直线上
上式有三个独立方程,只能求出三个未知数。
4. 平面一般力系的简化结果分析
简化结果: 主矢R ,主矩 MO ,下面分别讨论。 ① R =0, MO =0,则力系平衡,下节专门讨论。 ② R =0,MO≠0 即简化结果为一合力偶, MO=M 此时刚
解除约束,可把支反
力直接画在整体结构
的原图上)
解除约束
由
mA (Fi
)
0
P2a N B
3a0,
N B
2P 3
X 0 XA 0
Y 0 YB NB P0,
YA
P 3
2.5物体系统的平衡、静定与超静定问题
1、物体系统的平衡问题 物体系统(物系):由若干个物体通过约束所组成的系统叫∼。 [例]
外力:外界物体作用于系统上的力叫外力。 内力:系统内部各物体之间的相互作用力叫内力。
N2个物体受平面汇交力系(或平面平行力系)
X 0 Y 0
2*n2个独立平衡方程
N3个物体受平 X 0 面任意力系 Y 0
弹性力学9-位移分量的求出、简支梁均布荷载

其中有三个关于 y 的待定函数:f(y), f(y1) , f(y2)。
第二章 平面问题的基本理论 3.4 简支梁受均布荷载
(3)由相容方程求应力函数
将上步所得应力函数的一般形式代入无体力情况下的相 容方程,整理后有
1 4 f ( y ) 2 4 f1 ( y ) 4 f 2 ( y) 2 f ( y) x x 2 0 4 4 4 2 2 y y y y
代入第三式,并整理可得
v
M
2 EI
y f 2 ( x)
2
df1 ( y ) df 2 ( x) M x dy dx EI
第二章 平面问题的基本理论 3.3 位移分量的求出
(2 )位移分量
df1 ( y ) df 2 ( x) M x dy dx EI
等式左右两边分别为 y 和 x 的函数,要想对于所有的 y 和 x 均成立,只可能两边都等于同一常数w:
M
l
1、形变分量与位移分量
M
x
1
h
(1)形变分量 将上节所求应力分量代入物理方程 y (2-8) 1 x ( x y ) E M x y 1 I y ( y x ) E y xy 0 2(1 ) xy xy E
M x y EI M y y EI xy 0
(c)几何方程积分计算位移表达式 (d)利用位移边界条件,确定常数。
第二章 平面问题的基本理论 本节内容 3.4 简支梁受均布荷载
内容要点: 用半逆解法求解梁的平面问题;体会理解半逆解法的 解题过程。
第二章 平面问题的基本理论 3.4 简支梁受均布荷载
半逆解法步骤回顾:
(1)对于给定的弹性力学问题,根据弹性体的几何形状、 受力特征和变形的特点或已知的一些简单结论,如材料力学 得到的初等结论,假设部分或全部应力分量的函数形式; (2)按式(2-24),由应力推出应力函数 的一般形式( 含待定函数项);
弹性力学 第二讲 平面问题的基本理论

第二讲 平面问题的基本理论
本讲学习指南
本讲将系统地平面问题的基本理论-基本方程和边 界条件,及两种基本解法,是弹性力学中最具典型性和 代表性的内容,是后续内容学习的基础。要求掌握的内 容如下: 1、两类平面问题的定义; 2、关于一点应力状态的分析; 3、平面区域内的平衡微分方程、几何方程与物理 方程; 4、平面边界上的应力和位移边界条件的建立,及 圣维南原理的应用; 5、按位移求解方法和按应力求y x
fy 0
2q0 3 s y 3 xy f ( x) y g ( x) hl
主要内容
平面应力问题与平面应变问题 平面问题的平衡微分方程 平面问题中的一点应力状态分析 平面问题的几何方程与刚体位移 平面问题的物理方程 平面问题的边界条件 圣维南原理及应用 按位移法求解平面问题 按应力求解平面问题及相容方程 常体力情况下的简化与应力函数
平面AB上的正应力sn即为上
面所求的全应力p向法线方向n 的投影: s lp mp
n x y
平面AB上的切应力tn即为上
面所求的全应力P向切线方向的 投影: 2 2 2 t n px p y s n 或
t n mpx lp y
过一点任意斜面的主应力与主方向
问题3:若经过该点的某一斜面上的切应力为0,求此斜
§2.2 平面问题的平衡微分方程
平面问题的平衡微分方程是考虑平面问题的静力学条 件,根据弹性体内微分单元的静力平衡条件来推导出应力 分量与体力分量之间的关系。
如图,在弹性体内任一点
取一微小的正平行六面体,其 x、y方向的尺寸分别为dx、dy ,为计算方便,设它在z方向 的尺寸为单位长度1。
平面问题的平衡微分方程
本讲学习指南
本讲将系统地平面问题的基本理论-基本方程和边 界条件,及两种基本解法,是弹性力学中最具典型性和 代表性的内容,是后续内容学习的基础。要求掌握的内 容如下: 1、两类平面问题的定义; 2、关于一点应力状态的分析; 3、平面区域内的平衡微分方程、几何方程与物理 方程; 4、平面边界上的应力和位移边界条件的建立,及 圣维南原理的应用; 5、按位移求解方法和按应力求y x
fy 0
2q0 3 s y 3 xy f ( x) y g ( x) hl
主要内容
平面应力问题与平面应变问题 平面问题的平衡微分方程 平面问题中的一点应力状态分析 平面问题的几何方程与刚体位移 平面问题的物理方程 平面问题的边界条件 圣维南原理及应用 按位移法求解平面问题 按应力求解平面问题及相容方程 常体力情况下的简化与应力函数
平面AB上的正应力sn即为上
面所求的全应力p向法线方向n 的投影: s lp mp
n x y
平面AB上的切应力tn即为上
面所求的全应力P向切线方向的 投影: 2 2 2 t n px p y s n 或
t n mpx lp y
过一点任意斜面的主应力与主方向
问题3:若经过该点的某一斜面上的切应力为0,求此斜
§2.2 平面问题的平衡微分方程
平面问题的平衡微分方程是考虑平面问题的静力学条 件,根据弹性体内微分单元的静力平衡条件来推导出应力 分量与体力分量之间的关系。
如图,在弹性体内任一点
取一微小的正平行六面体,其 x、y方向的尺寸分别为dx、dy ,为计算方便,设它在z方向 的尺寸为单位长度1。
平面问题的平衡微分方程
弹性力学-第二章 平面问题基本理论 (徐芝纶第五版)
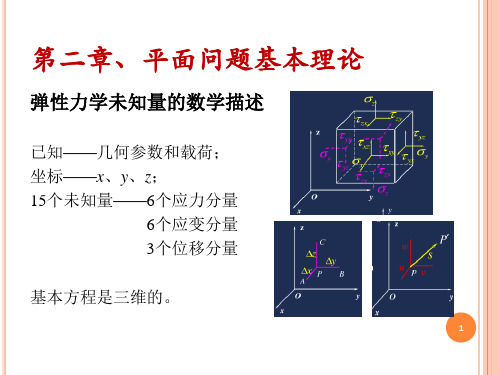
基本方程是二维的。
平面应力问题
平面应变问题
3
1.平面应力问题
支承板
z x
y
(2) 受力特性
外力(体力、面力)和约束,仅平行于 板面作用,沿z方向不变化。
(1) 几何特性
一个方向的尺寸比另两个 方向的尺寸小得多。
——平板
4
1.平面应力问题
(3) 应力特征
由于板面上不受力,有
sx =sx(x,y)
sy =sy(x,y)
53
54
55
56
习题
57
第二章 教学参考资料 (一)本章学习要求及重点
本章系统地介绍了平面问题的基本理论: 基本方程和边界条件,及两种基本解法。这 些内容在弹性力学中具有典型性和代表性。 因此,学好平面问题的基本理论,就可以方 便地学习其他各章。为此,我们要求学生深 入地理解本章的内容,掌握好以下几点:
)
f
y
0.
68
(2)用位移表示的应力边界条件
E
1
2
[l
(
u x
v
y
)m12
(
u y
v x
)]s
fx,
E
1
2
[m(
v y
u
x
)l12
(
u y
v x
)]s
fy.
(在s 上ss)
69
(3)位移边界条件
(u)s u , (v)s v.
(在Su上)
70
4、按应力求解平面问题(平面应力问题),
应力分量 σ x , σ y ,t x必y 须满足下列全部条件:
sx =sx(x,y) sy =sy(x,y) txy =txy(x,y) sz =sz (x,y) txz =tyz =0
平面应力问题
平面应变问题
3
1.平面应力问题
支承板
z x
y
(2) 受力特性
外力(体力、面力)和约束,仅平行于 板面作用,沿z方向不变化。
(1) 几何特性
一个方向的尺寸比另两个 方向的尺寸小得多。
——平板
4
1.平面应力问题
(3) 应力特征
由于板面上不受力,有
sx =sx(x,y)
sy =sy(x,y)
53
54
55
56
习题
57
第二章 教学参考资料 (一)本章学习要求及重点
本章系统地介绍了平面问题的基本理论: 基本方程和边界条件,及两种基本解法。这 些内容在弹性力学中具有典型性和代表性。 因此,学好平面问题的基本理论,就可以方 便地学习其他各章。为此,我们要求学生深 入地理解本章的内容,掌握好以下几点:
)
f
y
0.
68
(2)用位移表示的应力边界条件
E
1
2
[l
(
u x
v
y
)m12
(
u y
v x
)]s
fx,
E
1
2
[m(
v y
u
x
)l12
(
u y
v x
)]s
fy.
(在s 上ss)
69
(3)位移边界条件
(u)s u , (v)s v.
(在Su上)
70
4、按应力求解平面问题(平面应力问题),
应力分量 σ x , σ y ,t x必y 须满足下列全部条件:
sx =sx(x,y) sy =sy(x,y) txy =txy(x,y) sz =sz (x,y) txz =tyz =0
弹性力学简明教程 第2章 平面问题的基本理论

一 、求AB面上的正应力σn和切应力τn
设px、py为斜面AB的应力p在x、y 轴上的投影。斜面 AB的长度为 ds, 则AB=ds, PB=lds, PA=mds 。 由平衡条件∑Fx=0 得:
l ds m d s p x ds x l ds xy m ds f x 0 2
除以ds ,然后令ds→0, 得:
B'
一、位移与形变
刚体位移
如果各点(或部分点)间的相对距离发生变化, 则物体发生了变形。这种变形一方面表现在微 线段长度的变化,称为线应变;一方面表现在 微线段间夹角的变化,称为切应变。
O
A
O
A'
B
B'
二、几何方程
几何方程——描述任一点的微线段上形变分量 与位移分量之间的关系。 P点的形变分量与位移分量的关系?
0 l 1
当 l2 = 1 时,
0 l 2 1
n nmax 1 ( 1 2 ) 2 1
当 l2 = 0 时,
n n min 2
可见:两个主应力就是最大与最小的正应力。
五、求最大与最小的切应力
任意斜面上的切应力 n lm( y x ) (l 2 m 2 ) xy
y
二、几何方程
PA的线应变在小变形
时是由x 方向的位移 引起的,因此PA的线 应变为
P' A' PA x PA
o u
P
x
u
dx
v
P'
A
u dx x
A'
v
v dx x
y
u (u dx) u AA' PP' u x dx PA x v (v dx) v v x PA的转角为 dx x
第2章 平面问题的基本理论

u = u ( x, y ) ,v = v ( x, y )
例2(习题 ) (习题2-4) 按平面应变问题特征来分析, 按平面应变问题特征来分析, 本题中
ox
z
y
只有
ε x = ε x ( x, y ) ,ε y = ε y ( x, y ) ,γ xy = γ xy ( x, y )
思考题 设有厚度很大(即 向很长)的基础梁放置在地基上 的基础梁放置在地基上,如果 设有厚度很大 即 z 向很长 的基础梁放置在地基上 如果 想把它近似地简化为平面问题处理,问应如何考虑 问应如何考虑? 想把它近似地简化为平面问题处理 问应如何考虑
2、平面应变问题 (1) 几何特征: 几何特征: 常截面的柱体,长度>>截面的长 截面的长、 常截面的柱体,长度>>截面的长、宽; (2) 受力特征: ∥xy面,沿厚度不变; 受力特征: xy面 沿厚度不变; 体力f 作用于体内; 体力fx、fy作用于体内; 面力f 作用于柱面; 面力fx、fy作用于柱面; 约束u 作用于柱面。 约束u、v 作用于柱面。
一、斜截面上的应力 求解: 边长 求解: AB=ds, PB=lds, PA=mds. AB=ds, PB=lds, PA= l=cos(n,x), m=sin(n,y) =cos(n =sin(n (1) 求(px,py)
2-3 平面问题中一点的应力状态
一、斜截面上的应力 l=cos(n,x), m=sin(n,y) =cos(n =sin(n (2) 求( σn , τn )
ω
─ 表示物体绕原点的刚体转动。 表示物体绕原点的刚体转动。
v = f 2 ( x ) = v0 + ω x
结论: 形变确定, 结论: 形变确定,位移不完全确定 : 从物理概念看, 、 确定 物体还可作刚体位移。 确定, 从物理概念看,ε、γ确定,物体还可作刚体位移。
例2(习题 ) (习题2-4) 按平面应变问题特征来分析, 按平面应变问题特征来分析, 本题中
ox
z
y
只有
ε x = ε x ( x, y ) ,ε y = ε y ( x, y ) ,γ xy = γ xy ( x, y )
思考题 设有厚度很大(即 向很长)的基础梁放置在地基上 的基础梁放置在地基上,如果 设有厚度很大 即 z 向很长 的基础梁放置在地基上 如果 想把它近似地简化为平面问题处理,问应如何考虑 问应如何考虑? 想把它近似地简化为平面问题处理 问应如何考虑
2、平面应变问题 (1) 几何特征: 几何特征: 常截面的柱体,长度>>截面的长 截面的长、 常截面的柱体,长度>>截面的长、宽; (2) 受力特征: ∥xy面,沿厚度不变; 受力特征: xy面 沿厚度不变; 体力f 作用于体内; 体力fx、fy作用于体内; 面力f 作用于柱面; 面力fx、fy作用于柱面; 约束u 作用于柱面。 约束u、v 作用于柱面。
一、斜截面上的应力 求解: 边长 求解: AB=ds, PB=lds, PA=mds. AB=ds, PB=lds, PA= l=cos(n,x), m=sin(n,y) =cos(n =sin(n (1) 求(px,py)
2-3 平面问题中一点的应力状态
一、斜截面上的应力 l=cos(n,x), m=sin(n,y) =cos(n =sin(n (2) 求( σn , τn )
ω
─ 表示物体绕原点的刚体转动。 表示物体绕原点的刚体转动。
v = f 2 ( x ) = v0 + ω x
结论: 形变确定, 结论: 形变确定,位移不完全确定 : 从物理概念看, 、 确定 物体还可作刚体位移。 确定, 从物理概念看,ε、γ确定,物体还可作刚体位移。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
v
g
(ly y 2 ),
o
思考题 1、 试用位移法求解图(b)的位移和 应力。 2、试将弹性力学中平面问题的位移 法与结构力学的位移法相比,有那 些相同 和不同之处? 选择习题 2—10。
l
x
o
x
g
g
y
图(a)
y
图 (b )
例2 厚度δ =1的悬臂梁,受一端的集中力 F 的作用。已求得其位移的解答是
思考题 1.试证明微分体绕 z 轴的平均转动分量是 (
1 v u ). 2 x y
2.当应变为常量时,εx=a , εy=b , γxy=c ,试求出对应的位移分量。
选择习题 2—7、2—19。
思考题
1.试证:由主应力可以求出主应变,且两者方向一致。
2.试证:三个主应力均为压应力,有时可以产生拉裂现象。 试根据空间问题的物理方程进行解释。
y
l
σy
yx
q1
y h 边界, 2 x (σ y ) y h q , ( τ yx ) y h 0. 2 2 l y h 边界, 2 (σ y ) y h 0, ( τ yx ) y h q1.
2 2
例2 列出边界条件:
y b边界: (σ y ) y b 0, ( τ yx ) y b 0. x a边界: (σ x ) x a y 2 q( ) , ( τ xy ) x a 0. b
3.试证:在自重作用下,圆环(平面应力问题) 比圆筒(平面应变问题)的变形大。 试根据它们的物理方程来解释这种现象。
例1 列出边界条件:
h/2 h/2
σy
0, x l边界, (σ x ) x l 0,
o
x
xy
σx
(v) x 0 0. ( τ xy ) x l 0.
h/2
h / 2 h/2
( x ) x 0 d y F , ( x ) x 0 y d y M , ( xy ) x 0 d y Fs。
在小边界x = l,当平衡微分方程和其它各 边界条件都已满足的条件下,三个积分的边 界条件必然满足,可以不必校核。
h / 2 h/2
o
l
x
o
x
g
g
y
y
2v g . 2 y E
y = 0 , l ,位移边界条件 (v)y=0=0 ∴ B=0 (v)y=l=0 ∴ A
g
2E l.
v
g
2E
y 2 Ay B.
2E g y (l 2 y ), 2E g σy (l 2 y ). 2
h / 2
例2 试列出图中的边界条件。 解:(a)在主要边界x= 0, b,应精确满足下列边界 条件:
O
F
300
x
b/2 b/2
gy
h q y (h b, 1)
x0 xl
σ x gy, σ x 0,
xy 0; xy q。
在小边界y = 0应用圣维 南原理,列出三个积分 的近似边界条件,当板 厚δ =1时, 注意:
Fx2 y Fy3 Fy3 Fl 2 Fh2 u ( ) y, 2 EI 6 EI 6 IG 2 EI 8IG Fxy2 Fx3 Fxl2 Fl3 v 。 2 EI 6 EI 2 EI 3EI
第二章 平面问题的 基本理论
例如:深梁问题
例1(习题2-3) 试分析不受面力的空间体表面薄层中的应力状态。
选择坐标系如图。 因该表面无任何面力,fx、fy、fz = 0,故表面上 (σz , τzx , τzy)=0 在近表面很薄一层 (σz , τzx , τzy)→0 ∴ 接近平面应力问题。
例2(习题2-4) 按平面应变问题特征来分析, 本题中
ox
z
y
只有
x x x,y , y y x,y , xy xy x,y
思考题 设有厚度很大(即 z 向很长)的基础梁放置在地基上,如果 想把它近似地简化为平面问题处理,问应如何考虑?
思考题
1.试检查,同一方程中的各项,其量纲必然相同(可用来 检验方程的正确性)。 2.将条件ΣMc=0 ,改为对某一角点的ΣM=0,将得出什么结 果? 3.微分体边上的应力若考虑为不均匀分布,将得出什么结 果?
q b b q
a o
a
q x
yx xy
q
σx
σy
y
思考题
M
x o q n y
(a )
o
σy
A
x
g
A
x
y
(b )
y
(d )
B
(c )
A
1、若在斜边界面上,受有常量的法向分布压力q作用,试列出应力边界条件,(图(a))。 2、证明在无面力作用的0A边上,σy不等于零(图 (b))。 3、证明在凸角A点附近,当无面力作用时,其应力为零(图(c))。 4、试导出在无面力作用时,AB边界上的 σx , σy , τxy 之间的关系。(图(d))。 5、试比较平面应力问题和平面应变问题的基本方程和边界条件的异同,并 进一步说明它们的解答的异同。 选择习题 2—13
(b)
3F , 0 2 b 3F ( ) x d x b, 0 y y 0 4 b F ( ) d x 。 0 yx y 0 2
b
( y ) y 0 d x
在列力矩的条件时两边均是 对原点O的力矩来计算的。
对于y = h的小边界可以 不必校核。
四、按位移求解(位移法)的优缺点: 适用性广─ 可适用于任何边界条件。 求函数式解答困难,但在近似解法 (变分法、差分法、有限单元法) 中有着广泛的应用。 例1 考虑两端固定的一维杆件。 图(a), 只受重力作用,fx=0 , fy=ρg。 试用位移法求解。 解:为了简化,设μ = 0 位移u = 0,v = v ( y ) 按位移求解,位移应满足式(b),(c),(d)。 代入式(b),第一式自然满足, 第二式成为
例1 试列出图中的边界条件。 解:(a)在主要边界y = ±h/2应精确满足下列边 界条件:
x y q( ) 2 , l y h / 2, y 0, y h / 2,
xy 0; xy q1.
在小边界x = 0应用圣维 南原理,列出三个积分 的近似边界条件,当板 厚δ =1时,
