几个开环与闭环自动控制系统的例子
开环控制系统与闭环控制系统的区别及相关的实例
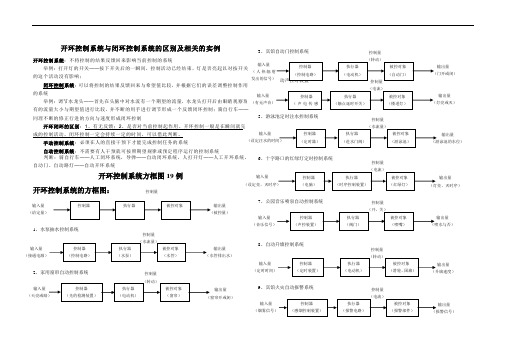
开环控制系统与闭环控制系统的区别及相关的实例开环控制系统:不将控制的结果反馈回来影响当前控制的系统举例:打开灯的开关——的这个活动没有影响; 闭环控制系统:可以将控制的结果反馈回来与希望值比较,的系统 举例:调节水龙头——有的流量大小与期望值进行比较,并不断的用手进行调节形成一个反馈闭环控制;骑自行车同理不断的修正行进的方向与速度形成闭环控制 自动控制系统:不需要有人干预就可按照期望规律或预定程序运行的控制系统 判断:骑自行车——人工闭环系统,导弹——自动闭环系统,人打开灯——人工开环系统,自动门、自动路灯——自动开环系统 开环控制系统方框图19例 开环控制系统的方框图: 1、水泵抽水控制系统 2、家用窗帘自动控制系统3、宾馆自动门控制系统 5、游泳池定时注水控制系统6、十字路口的红绿灯定时控制系统7、公园音乐喷泉自动控制系统8、自动升旗控制系统9、宾馆火灾自动报警系统 控制量控制量控制量控制量 控制量 控制量控制量 控制量 输入量 (定时时间) 控制量10、宾馆自动叫醒服务系统11、活动猴控制系统 12、公共汽车车门开关控制系统13、家用缝纫机缝纫速度控制系统14、普通电风扇控制系统15、普通全自动洗衣机控制系统16、手电筒控制装置 17、宾馆自动门加装压力传感器防意外事故自动控制系统 18、可调光台灯控制系统19、电吹风控制系统控制量 控制量(压缩空控制量控制量控制量 控制量 控制量控制量控制量闭环控制系统方框图12例闭环控制系统的方框图:1、投篮2、供水水箱的水位自动控制系统3、加热炉的温度自动控制系统4、抽水马桶的自动控制系统5、花房温度控制系统给定量被控量给定量被控量给定量被控量给定量被控量给定量给定量 被控量控制量6、夏天房间温度控制系统7、家用电饭锅保温控制系统8、家用电冰箱温度控制系统9、宾馆使用多台热水器串联电辅助加热自动控制系统10、粮库温、湿度自动控制系统11、自动电热水壶控制系统给定量被控量房内实被控量给定量 控制量被控量 冰箱实给定量 给定量被控量—80℃) 控制量被控量 粮库内给定量(设定控制量给定量控制量。
开环系统的例子及原理

开环系统的例子及原理
开环系统是一种物理或电气系统,其运作过程中没有反馈信号回路,而是通过输入信号来控制输出信号。
这种系统通常用于简单的控制任务,例如,灯泡的开关就是一个开环系统。
以下是一些开环系统的例子:
1. 简单的灯光控制系统:在室内,我们可以使用开关控制灯光。
当我们打开开关时,电流流过灯泡,将灯泡点亮。
这是一个开环系统,因为我们无法知道灯泡实际上是否真的点亮了。
如果灯泡损坏或电线断开,我们就无法得知,除非我们再次打开开关。
2. 自动售货机:自动售货机是另一个常见的开环系统例子。
当我们投入硬币时,自动售货机会释放物品。
然而,自动售货机并不会检查是否释放了正确的物品,或者是否有足够的物品供应。
这是一个开环系统,因为投入硬币并不能保证我们得到我们想要的物品。
开环系统的原理很简单:输入信号会直接影响输出信号,而不需要任何反馈机制。
这种系统通常很简单,但也因此容易出错。
如果输入信号有误或输出信号无法实现预期目标,就需要进行调整或修复。
因此,开环系统在复杂的控制任务中通常不太实用。
相比之下,闭环系统通过反馈机制来调整输出信号,因此更加精确和可靠。
- 1 -。
开环与闭环控制

开环与闭环控制1.普通机械式电饭煲简单的工作过程如下:接通电源,拨动杠杆按钮,给出做饭指令,磁钢吸合,拉住与之相连的杠杆,杠杆拨动微动开关,微动开关在杠杆的按压下接通加热回路,磁钢铝壳帽与锅底接触,开始加热。
当饭熟时(不再有水的沸腾),锅底温度升高,磁钢温度达到150℃时失去磁性,在弹簧力作用下,杠杆下移,微动开关恢复常态,结束加热状态。
此时电源仍是接通状态,由于双金属片温控器的作用,电饭煲进入保温状态(70度以下),这就是电饭煲接通电源后即使不按键也能得到温水的原因。
但不按下杠杆按键则煮不熟饭。
由上面的工作过程可知,普通电饭煲虽然简单,但其控制过程还是比较复杂的。
其工作流程为:给出“做饭”指令——进入加热状态——判断是否达到150度,没有达到,继续加热,如果达到,则进入保温状态。
从这个流程知道,电饭煲的控制,从总体上说,仍是一个开环控制。
因为,输入一个“做饭”指令,输出的就是“做饭”状态。
如果输入的是“温水”指令,则输出的状态就是“温水”状态。
即输入量和输出量是一一对应的。
但是,其局部环节还有反馈。
其参考方块图如下:3.宾馆、酒店的“自动叫醒服务系统”是一个开环控制系统。
参考框图如下:4.家用缝纫机的缝纫速度控制系统缝纫机“转速控制系统”的控制对象应该是“缝纫机”不应该是“机针”。
对缝纫机来说,还有其它控制系统,如“针距控制系统”、“倒车控制系统”等,这些系统的控制对象都是缝纫机。
参考框图如下:注:有些学生会认为这个控制系统是一个闭环控制系统,理由是人可以不断调整缝纫的转速。
其实这种理解是错误的。
它不是闭环的原因是:第一,它输入的转速不是恒定的,没法与输出转速进行比较。
第二,“人”作为操作者,对控制系统施加控制指令的行为不能视为“人作为某个环节参与了控制系统”。
5.走道路灯的声光控制系统声光自动控制白炽灯开关的基本工作原理如下:白天或夜晚光线较亮时,光控部分将开关自动关断,声控部分不起作用。
当光线较暗时,光控部分将开关自动打开,负载电路的通断受控于声控部分。
自动控制理论_哈尔滨工业大学_1 第1章自动控制理论概述_(1.2.1) 1.2开环控制和闭环控制

一、开环控制系统
例:烤面包机
输入—定时器设定的时间 输出—面包的颜色 控制对象—烤箱的加热系统
输入量
控制器
控制量
输出量
被控对象
• 控制器与被控对象之间只有正向的控制作用。 • 输出量对控制量没有影响。
一、开环控制系统
例:直流电动机转速开环控制系统
一、开环控制系统
开环控制系统的特点:
对于惯性较大的系统,若参数配合不当,控制性能可能变 得很差,甚至出现发散或等幅振荡等不稳定的情况。
三、自动控制系统的概念
反馈:
将检测出来的输出量送回到系统的输入端,并与输 入信号比较的过程。
反馈
负反馈(反馈信号与输入信号相减),减小偏差。 正反馈(反馈信号与输入信号相加),增大偏差。
对于主反馈必须采用负反馈。
1. 结构简单、造价低、容易设计调整。
2. 没有抗干扰的能力,因此精度较低。
3. 系统的控制精度取决于给定信号的标定精度及被控对 象参数的稳定性。
应用场合:
1. 控制量的变化规律可以预知。 2. 可能出现的干扰可以抑制。 3. 被控量很难测量。 应用较为广泛,如家电、加热炉、水泵等等。
二、闭环控制系统
二、闭环控制系统
阀门 进水
减速器 电动机
电位器
连 杆
放大 器
浮子 水池
较完善的水位自动控制系统
实际 水位
出 水
采用误差累积式控制(积分)保证精确的水位
二、闭环控制系统
闭环控制系统定义: 通过反馈回路使系统构成闭环并按偏差的性质产生控
制作用,以求减小或消除偏差的控制系统。
闭环控制系统的特点: 1. 对外部或内部干扰(如内部件参数变动)的影响不敏感。 2. 由于采用反馈装置,导致设备增多,系统设计调整复杂。 3. 精度较高,很大程度上由反馈测量元件精度决定。 4. 闭环系统存在稳定性问题。
自动控制原理_高等教育出版社_王万良__课后答案

G1 ( s )
R ( s) + −
G2 ( s )
C ( s)
图题 2.7 解:传递函数为:
C ( s) G2 ( s )[1 + G1 ( s)] = R( s ) 1 + G2 ( s)
2.8 简化图题 2.8 所示系统的结构图,并求传递函数 C ( s) 。 R( s )
2.4 设运算放大器放大倍数很大,输入阻抗很大,输出阻抗很小。求图题 2.4 所示运算放大 电路的传递函数。其中, u i 为输入变量, u o 为输出变量。
R1
i
C
− +
ui
R2
图题 2.4
uo
解:
iR1 = u i 1 − id t = u o C ∫
整理得传递函数为:
uo (s) 1 =− ui ( s) R1CS
2.13
求图题 2.13 所示系统结构图的传递函数 C ( s) / R( s) 和 C ( s ) / N ( s ) 。
N(s) G3 (s) R(s)
⊗ −
G1 (s)
⊗
−
G2 (s) G4 (s) G5 (s)
⊗
C(s)
⊗
H(s)
图题 2.13 解:求 C ( s) / R( s) 时,令 N(s)=0,系统结构图变为
2.10 简化图题 2.10 所示系统的结构图,并求传递函数
C ( s) 。 R(s)
+
G3 (s )
R( s ) + −
G1 ( s) G 4 (s)
G 2 ( s)
开环控制系统和闭环控制系统的例子

开环控制系统和闭环控制系统的例子
1. 你知道家里面的那种普通电扇吗?它就是开环控制系统的例子呀!你打开开关,它就一直转,完全不管周围温度啥样,只知道傻乎乎地转,这多直接!
2. 哎呀,那些自动贩卖机不也是嘛!你投了币,选择了商品,它就按照设定好的程序给你出货,根本不会因为你的喜好改变而改变,这是典型的开环控制系统呀!
3. 咱再想想,公园里的那种定时喷泉,到点就喷,管它有没有人看呢,可不就是开环控制系统嘛,多么形象!
4. 像空调的温度控制系统就是闭环控制系统啦!它会感知室内温度,热了就制冷,冷了就制热,这多贴心啊,不停地调整来让你舒服!
5. 还有啊,你想想汽车的定速巡航,它能根据车速的实际情况去调整油门,让车保持在设定的速度,这可是闭环控制系统在发挥作用呢!
6. 你家里如果有那种智能扫地机器人,它在清扫的过程中会根据环境去改变路线,避免碰撞,这就是闭环控制系统呀,多厉害!
7. 血压计不也是嘛!它能实时测量你的血压,然后告诉你结果,这就是一个不断反馈和调整的过程,闭环控制系统就在为你的健康服务呢!
8. 很多工厂里的生产线上的自动控制系统也是闭环的呀!它会根据产品的质量情况去调整生产参数,这不就是在努力做到最好吗,就像人一样会自我改进!
9. 智能灌溉系统也挺神奇的哟!它可以根据土壤的湿度来决定要不要浇水,多智能呀,绝对是闭环控制系统的优秀代表呢!
我觉得开环控制系统和闭环控制系统都有各自厉害的地方,在我们生活中真的太重要啦!它们让我们的生活变得更加方便、高效和智能呢!。
生活中闭环控制的例子及其工作原理

生活中闭环控制的例子及其工作原理
闭环控制也称为反馈控制,在生活中有很多应用。
它通过测量系统输出并调节输入来达成预期效果。
下面介绍几个常见的闭环控制的例子及其工作原理。
1. 空调系统
空调系统是一个广泛应用闭环控制的例子。
当温度传感器测量室内温度高于设定温度时,系统会自动调节空调机组以降低室内温度。
当室温达到设定温度后,控制系统关闭空调机组,防止温度过低。
这个过程中,系统不断检测并调整空气质量,以确保室内空气清新舒适。
2. 水箱自动灌溉系统
在农业生产中,为了保证作物生长,常常需要用到水箱自动灌溉系统。
这个系统会通过土壤湿度传感器检测土壤水分,根据检测结果调节阀门控制水流的供应。
当土壤水分过低时,系统自动开启阀门供水,当土壤水分达到设定值时,系统自动关闭阀门以免过度浇水。
3. 火车轮轴压力监控系统
火车轮轴压力监控系统可以帮助保障列车行驶安全。
系统通过监测轮轴压力变化来检测轮轴摩擦等异常,确保列车运行平稳。
当轮轴压力异常时,系统会自动停车并报警以保证列车安全。
这些示例说明了闭环控制在自动调节、追踪目标、预警反应等方面的优势。
其原理基础是运用感知技术、信息反馈、逻辑判断以及动态调整等手段,自适应控制系统以实现优化控制。
其中分为开环控制和闭环控制,前者没有了解系统反馈的信息,只控制输入,后者则通过测量与系统连通的输出来调整输入,来达到预期效果。
因此,在生活和工业生产中,闭环控制是非常实用的方案。
它可以提高系统的稳定性和可靠性,减少人工干预和人为错误,提高效率,降低成本,提高生产能力,实现更好的节能效果。
运动技能与控制的开环,闭环论述题

在运动技能和控制领域,开环和闭环是两种常用的控制系统模型,用于描述人类在执行运动任务时的动作控制过程。
开环控制系统:
开环控制是一种预先设定的控制系统,动作的执行不受外部反馈的影响。
在开环控制中,执行者根据任务的要求和先前的经验,通过预定的运动模式和指令来完成动作。
开环控制的特点:
执行者在动作进行过程中没有实时的反馈信息。
控制过程主要基于内部模型和预设的指令。
对环境变化和误差没有实时的修正机制。
例子:高尔夫球挥杆是一个典型的开环控制过程。
高尔夫球手在进行挥杆动作时,根据目标、距离和风向等因素,预先设定挥杆的力度和方向,而在挥杆过程中没有实时的视觉或感觉反馈来修正动作。
闭环控制系统:
闭环控制是一种通过实时的感觉反馈来修正和调整运动执行的控制系统。
执行者接收来自感觉器官的反馈信息,根据这些信息来调整动作以达到预期的目标。
闭环控制的特点:
执行者通过感觉反馈来实时监控和调整动作。
控制过程可以根据反馈信息对误差进行修正。
环境变化和任务需求的变化可以通过反馈信息进行适应性调整。
例子:乒乓球发球是一个典型的闭环控制过程。
发球者在发球过程中会通过观察乒乓球的轨迹、听觉反馈和触觉反馈等来调整发球的速度、角度和旋转,以确保球的落点和球的轨迹符合预期。
综上所述,开环控制和闭环控制是描述人类运动技能和控制过程的两种模型。
在实际运动中,开环和闭环控制往往同时存在,根据任务的不同和执行者的经验水平,可以灵活地选择合适的控制策略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2-1 试求出图P2-1中各电路的传递函数。
图P2-12-2 试求出图P2-2中各有源网络的传递函数。
图P2-22-3 求图P2-3所示各机械运动系统的传递函数。
(1)求图(a )的 ()()?=s X s X r c (2)求图(b )的()()?=s X s X r c (3)求图(c )的()()?12=s X s X (4)求图(d )的 ()()?1=s F s X图P2-32-4 图P2-4所示为一齿轮传动机构。
设此机构无间隙、无变形,求折算到传动轴上的等效转动惯量、等效粘性摩擦系数和()()()s M s s W 2θ=。
图P2-4 图P2-52-5 图P2-5所示为一磁场控制的直流电动机。
设工作时电枢电流不变,控制电压加在励磁绕组上,输出为电机角位移,求传递函数()()()s u s s W r θ=。
2-6 图P2-6所示为一用作放大器的直流发电机,原电机以恒定转速运行。
试确定传递函数()()()s W s U s U r c =,设不计发电机的电枢电感和电阻。
图P2-62-7 已知一系统由如下方程组组成,试绘制系统方框图,并求出闭环传递函数。
()()()()()()[]()s X s W s W s W s W s X s X c r 87111--=()()()()()[]s X s W s X s W s X 36122-= ()()()()[]()s W s W s X s X s X c 3523-= ()()()s X s W s X c 34=2-8 试分别化简图P2-7和图P2-8所示的结构图,并求出相应的传递函数。
图P2-7 图P2-82-9 求如图P2-9所示系统的传递函数()()()s X s X s W r c =1,()()()s X s X s W N c =2。
图P2-92-10 求如图P2-10所示系统的传递函数。
图P2-102-11 求图P2-11所示系统的闭环传递函数。
图P2-11 图P2-122-13 画出图P2-13所示结构图的信号流图,用梅逊公式求传递函数:()()()s X s X s W r c =1,()()()s N s X s W c =2。
图P2-132-14 画出图P2-14所示系统的信号流图,并分别求出两个系统的传递函数()()s X s X r c 11,()()s X s X r c 22。
图P2-143-1 一单位反馈控制系统的开环传递函数为()()11+=s s s W K 。
求:(1)系统的单位阶跃响应及动态特性指标??、t r 、t S 、?; (2)输入量x r (t )=t 时,系统的输出响应;(2)输入量x r (t )为单位脉冲函数时,系统的输出响应。
3-2 一单位反馈控制系统的开环传递函数为()()1+=s s K s W kK τ,其单位阶跃响应曲线如图P3-1所示,图中的X m =,t m =。
试确定系统参数K k 及 ? 值。
图P3-13-3 一单位反馈控制系统的开环传递函数为()()n nK s s s W ξωω22+=。
已知系统的x r (t )=1(t ),误差时间函数为()t t e e t e 73.37.14.04.1---=,求系统的阻尼比ξ、自然振荡角频率n ω、系统的开环传递函数和闭环传递函数、系统的稳态误差。
3-4 已知单位反馈控制系统的开环传递函数为()()1+=s s K s W kK τ,试选择K k及?值以满足下列指标。
当x r (t )=t 时,系统的稳态误差e (?)≤;当x r (t )=1(t )时,系统的?%≤30%,t S (5%)≤。
3-5 已知单位反馈控制系统的闭环传递函数为()2222nn nB s ss W ωξωω++=,试画出以n ω为常数、ξ为变数时,系统特征方程式的根在s 复平面上的分布轨迹。
3-6 一系统的动态结构图如图P3-2所示,求在不同的K k 值下(例如,K k =1、K k =3、K k =7)系统的闭环极点、单位阶跃响应、动态指标及稳态误差。
图P3-23-7 一闭环反馈控制系统的动态结构图如图P3-3所示。
(1)求当?%≤20%、t S (5%)=时,系统的参数K 1及?值。
(2)求上述系统的位置误差系数K p 、速度误差系数K v 、加速度误差系数K a 及其相应的稳态误差。
图P3-33-8 一系统的动态结构图如图P3-4所示。
求 (1)1.0,021==ττ时,系统的%δ、%)5(s t(2)0,1.021==ττ时,系统的%δ、%)5(s t(3)比较上述两种校正情况下的暂态性能指标及稳态性能。
图P3-43-9 如图P3-5所示系统,图中的()s W g 为调节对象的传递函数,()s W c 为调节器的传递函数。
如果调节对象为()()()1121++=s T s T K s W gg ,T 1 > T 2 ,系统要求的指标为:位置稳态误差为零,调节时间最短,超调量%δ≤ %,问下述三种调节器中哪一种能满足上述指标其参数应具备什么条件三种调节器为(a )()p c K s W =; (b) ()()ss K s W pc 1+=τ; (c) ()()()1121++=s s K s W pc ττ。
图P3-53-10 有闭环系统的特征方程式如下,试用劳斯判椐判断系统的稳定性,并说明特征根在复平面上的分布。
(1)05042023=+++s s s (2)010042023=+++s s s (3)08862234=++++s s s s (4)0722********=-++-+s s s s s (5)0121222189323456=++++++s s s s s s 3-11 单位反馈系统的开环传递函数为()()()()15.0115.02++++=s s s s s K s W k k试确定使系统稳定的K k 值范围。
3-12 已知系统的结构图如图P3-6所示,试用劳斯判椐确定使系统稳定的K f 值范围。
图P3-63-13 如果采用图P3-7所示系统,问τ取何值时,系统方能稳定 3-14 设单位反馈系统的开环传递函数为()()()s s s Ks W k 167.0133.01++=,要求闭环特征根的实部均小于–1,求K 值应取的范围。
图P3-73-15 设有一单位反馈系统,如果其开环传递函数为 (1)()()()15410++=s s s s W k(2)()()()()1541.0102+++=s s s s s W k求输入量为()t t x r =和()2542t t t x r ++=时系统的稳态误差。
3-16有一单位反馈系统,系统的开环传递函数为()sK s W k k =。
求当输入量为()221t t x r =和()t t x r ωsin =时,控制系统的稳态误差。
3-17有一单位反馈系统,其开环传递函数为()()15103-+=s s s s W k ,求系统的动态误差系数;并求当输入量为()2211t t t x r ++=时,稳态误差的时间函数()t e s 。
3-18 一系统的结构图如图P3-8所示,并设()()ss T K s W 1111+=,()()s T s K s W 2221+=。
当扰动量分别以()s s N 1=∆、21s作用于系统时,求系统的扰动稳态误差。
图P3-83-19 一复合控制系统的结构图如图P3-9所示,其中1231==K K ,T 2=,K 2=2。
(1)求输入量分别为()1=t x r ,()t t x r =,()221t t x r =时,系统的稳态误差; (2)求系统的单位阶跃响应,及其%δ,s t 值。
图P3-9 图P3-103-20 一复合控制系统如图P3-10所示,图中()bsas s W c +=2,()()()s s s s W g 2.011.0110++=。
如果系统由1型提高为3型系统,求a 值及b 值。
4-1 求下列各开环传递函数所对应的负反馈系统的根轨迹。
(1))2)(1()3()(+++=s s s K s W g K(2))2)(3()5()(+++=s s s s K s W g K(3))10)(5)(1()3()(++++=s s s s K s W g K4-2 求下列各开环传递函数所对应的负反馈系统的根轨迹。
(1)32)2()(2+++=s s s K s W g K(2))22)(2()(2+++=s s s s K s W gK(3))22)(3()2()(2++++=s s s s s K s W g K(4))164)(1()1()(2++-+=s s s s s K s W g K(5)2)125.0)(1()11.0()(+++=s s s s K s W g K4-3 已知单位负反馈系统的开环传递函数为)22)(1()(2+++=s s Ts s Ks W K求当4=K 时,以T 为参变量的根轨迹。
4-4 已知单位负反馈系统的开环传递函数为)1()()(2++=s s a s K s W K求当41=K 时,以a 为参变量的根轨迹。
4-5 已知单位负反馈系统的开环传递函数为)22)(16()(2+++=s s s K s W gK试用根轨迹法确定使闭环主导极点的阻尼比5.0=ξ和自然角频率2=n ω时g K 值。
4-6 已知单位正反馈系统的开环传递函数为2)4)(1)(1()(+-+=s s s K s W gK试绘制其根轨迹。
4-7 设系统开环传递函数为)4)(2()1()(2+++=s s s s K s W g K试绘制系统在负反馈与正反馈两种情况下的根轨迹。
4-8 设单位负反馈系统的开环传递函数为)11.0()1()(2++=s s s K s W K 如果要求系统的一对共轭主导根的阻尼系数为,用根轨迹法确定(1) 串联相位迟后环节,设15=a k 。
(2) 串联相位引前环节,设15=a k 。
4-9 已知单位负反馈系统的开环传递函数为)20)(4()(++=s s s K s W gK设要求)/1(12s k v ≥、%25%≤δ、s t s 7.0≤,试确定串联引前校正装置的传递函数,并绘制校正前、后的系统根轨迹。
4-10 设单位负反馈系统的开环传递函数为)5)(4()(++=s s s K s W gK要求校正后)/1(30s k v ≥、主导极点阻尼比707.0=ξ,试求串联迟后校正装置的传递函数。
4-11 已知负反馈系统的开环传递函数为)12()(+=s s Ks W K要使系统闭环主导极点的阻尼比5.0=ξ、自然振荡角频率5=n ω、)/1(50s k v ≥时,求串联迟后—引前校正装置的传递函数,并绘制校正前、后的系统根轨迹。
