平面的法向量与平面的向量表示(含答案)
高二数学选修课件:3-2-2平面的法向量与平面的向量表示

人 教 B 版 数 学
第三章
空间向量与立体几何
[例 1]
如图, ABCD 是直角梯形, ∠ABC=90° SA⊥ ,
人 教 B 版 数 学
1 平面 ABCD,SA=AB=BC=1,AD=2,求平面 SCD 与平 面 SAB 的法向量.
第三章
空间向量与立体几何
[分析] 解答本题可先建立空间直角坐标系,写出每
个平面内两个不共线向量的坐标,再利用待定系数法求出 平面的法向量.
人 教 B 版 数 学
[解析]
∵AD、AB、AS 是三条两两垂直的线段,
→ → → ∴以 A 为原点,以AD、AB、AS的方向为 x 轴,y 轴, 1 z 轴的正方向建立坐标系, A(0,0,0), 2, 则 D( 0,0), C(1,1,0), → =(1,0,0),是平面 SAB 的法向量, S(0,0,1),AD 2 设平面 SCD 的法向量 n=(1,λ,μ),
第三章
空间向量与立体几何
人 教 B 版 数 学
第三章
空间向量与立体几何
人 教 B 版 数 学
第三章
空间向量与立体几何
1.知识与技能
掌握平面的法向量的概念及性质. 理解平面的向量表示. 2.过程与方法 用向量的观点认识平面、利用平面的法向量证明平行人ຫໍສະໝຸດ 教 B 版 数 学或垂直问题.
3.情感态度与价值观 培养学生转化的数学思想,增强应用意识.
第三章
空间向量与立体几何
人 教 B 版 数 学
第三章
空间向量与立体几何
重点:平面法向量的概念及性质. 难点:利用法向量法解决几何问题.
人 教 B 版 数 学
第三章
空间向量与立体几何
人 教 B 版 数 学
高中数学空间向量与立体几何1.2空间向量在立体几何中的应用1.2.2空间中的平面与空间向量学案含解析

1.2.2 空间中的平面与空间向量导思1.什么是平面的法向量?它在解决线面位置关系中有何用途? 2.什么是三垂线定理及其逆定理?1.平面的法向量(1)定义:如果α是空间中的一个平面,n 是空间中的一个非零向量,且表示n 的有向线段所在的直线与平面α垂直,则称n 为平面α的一个法向量.此时也称n 与平面α垂直,记作n ⊥α. (2)性质:如果A ,B 是平面α上的任意不同两点,n 为平面α的一个法向量,则: 1 若直线l ⊥α,则l 的任意一个方向向量都是平面α的一个法向量 2 对任意实数λ≠0,λn 是平面α的一个法向量 3向量AB → 一定与n 垂直,即AB →·n =0平面α的法向量唯一吗?它们有什么共同特征? 提示:不唯一,都平行.2.空间线面的位置关系与空间向量若v 是直线l 的一个方向向量,n 1,n 2分别是平面α1,α2的一个法向量,则:1 n 1∥v ⇔l ⊥α12 n 1⊥v ⇔l ∥α1或l ⊂α13 n 1⊥n 2⇔α1⊥α24 n 1∥n 2⇔α1∥α2或α1,α2重合已知v 是直线l 的一个方向向量,n 是平面α的一个法向量,如果n ⊥v ,那么直线l 一定与平面α平行吗?提示:不一定,也可能l ⊂α. 3.三垂线定理及其逆定理 射影已知平面α和一点A ,过点A 作α的垂线l ,设l 与α相交于点A′,则A′就是点A在平面α内的射影,也称为投影.三垂线定理如果平面内的一条直线与平面的一条斜线在该平面内的射影垂直,则它也和这条斜线垂直.三垂线定理的逆定理如果平面内的一条直线和这个平面的一条斜线垂直,则它也和这条斜线在该平面内的射影垂直.1.辨析记忆(对的打“√”,错的打“×”).(1)已知直线l垂直于平面α,向量a平行直线l,则a是平面α的法向量.()(2)若平面外的一条直线的方向向量与平面的法向量垂直,则该直线与平面平行.()(3)若a是平面α的一条斜线,直线b垂直于a在α内的射影,则a⊥b.()提示:(1)×.向量a必须为非零向量.(2)√.(3)×.因为b不一定在平面α内,所以a与b不一定垂直.2.若a=(1,2,3)是平面γ的一个法向量,则下列向量中能作为平面γ的法向量的是() A.(0,1,2) B.(3,6,9)C.(-1,-2,3) D.(3,6,8)【解析】选B.向量(1,2,3)与向量(3,6,9)共线.3.(教材例题改编)已知PO⊥平面ABC,且O为△ABC的垂心,则AB与PC的关系是________.【解析】因为O为△ABC的垂心,所以CO⊥AB.又因为OC为PC在平面ABC内的射影,所以由三垂线定理知AB⊥PC.答案:垂直关键能力·合作学习类型一 平面的法向量(数学运算)1.若两个向量AB → =(1,2,3),AC →=(3,2,1),则平面ABC 的一个法向量 为( )A .(-1,2,-1)B .(1,2,1)C .(1,2,-1)D .(-1,2,1)2.已知点A(2,-1,2)在平面α内,n =(3,1,2)是平面α的一个法向量,则下列点P 中,在平面α内的是( ) A .P(1,-1,1)B .P ⎝⎛⎭⎫1,3,32C .P ⎝⎛⎭⎫1,-3,32D .P ⎝⎛⎭⎫-1,3,-343.正四棱锥如图所示,在向量PA → -PB → +PC → -PD → ,PA → +PC → ,PB → +PD → ,PA → +PB → +PC →+PD →中,不能作为底面ABCD 的法向量的是________.【解析】AB → =(1,2,3),AC →=(3,2,1), 设平面ABC 的一个法向量n =(x ,y ,z),则⎩⎪⎨⎪⎧n ·AB →=x +2y +3z =0n ·AC →=3x +2y +z =0 ,取x =-1,得平面ABC 的一个法向量为(-1,2,-1).2.选B.设P(x ,y ,z),则AP →=(x -2,y +1,z -2); 由题意知,AP → ⊥n ,则n ·AP →=0;所以3(x -2)+(y +1)+2(z -2)=0,化简得3x +y +2z =9. 验证得在A 中,3×1-1+2×1=4,不满足条件; 在B 中,3×1+3+2×32 =9,满足条件; 同理验证C 、D 不满足条件.3.连接AC ,BD ,交于点O ,连接OP ,则OP → 是底面ABCD 的一个法向量,PA → -PB → +PC → -PD →=BA → +DC → =0,不能作为底面ABCD 的法向量;PA → +PC → =-2OP →,能作为底面ABCD 的法向量;PB → +PD → =-2OP → ,能作为底面ABCD 的法向量;PA → +PB → +PC → +PD → =-4OP →,能作为底面ABCD 的法向量.答案:PA → -PB → +PC → -PD →求平面ABC 的一个法向量的方法1.平面垂线的方向向量法:证明一条直线为一个平面的垂线,则这条直线的一个方向向量即为所求.2.待定系数法:步骤如下:类型二 三垂线定理及其逆定理的应用(直观想象、逻辑推理)【典例】如图所示,三棱锥P-ABC 中,PA ⊥平面ABC ,若O ,Q 分别是△ABC 和△PBC 的垂心,求证:OQ ⊥平面PBC.【思路导引】利用三垂线定理及其逆定理证明【证明】如图,连接AO 并延长交BC 于点E ,连接PE.因为PA ⊥平面ABC ,AE ⊥BC(由于O 是△ABC 的垂心), 所以PE ⊥BC ,所以点Q 在PE 上.因为⎩⎪⎨⎪⎧AE ⊥BC ,PE ⊥BC ,AE ∩PE =E ⇒BC ⊥平面PAE ⇒BC ⊥OQ.①连接BO 并延长交AC 于点F ,则BF ⊥AC. 连接BQ 并延长交PC 于点M ,则BM ⊥PC. 连接MF.因为PA ⊥平面ABC ,BF ⊥AC , 所以BF ⊥PC(三垂线定理).因为⎩⎪⎨⎪⎧BM ⊥PC ,BF ⊥PC ,BM ∩BF =B ⇒PC ⊥平面BMF ⇒PC ⊥OQ.②由①②,知OQ ⊥平面PBC.利用三垂线定理及其逆定理证明线线垂直的基本环节在正方体ABCD-A 1B 1C 1D 1中,求证:A 1C ⊥平面BDC 1.【证明】连接AC,CD1,在正方体中,AA1⊥平面ABCD,所以AC是A1C在平面ABCD内的射影,又AC⊥BD,所以BD⊥A1C.同理D1C是A1C在平面CDD1C1内的射影.所以C1D⊥A1C.又C1D∩BD=D,所以A1C⊥平面BDC1.类型三利用空间向量证明线面、面面的位置关系(逻辑推理)证明平行问题角度1【典例】如图,在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点.设Q 是CC1上的点.当点Q在什么位置时,BQ∥平面PAO?【思路导引】建立恰当的坐标系,设出点Q的坐标,由BQ∥平面PAO确定其位置即可.【解析】建立如图所示的空间直角坐标系Dxyz,设正方体棱长为2,则O(1,1,0),A(2,0,0),P(0,0,1),B(2,2,0),D 1(0,0,2). 再设Q(0,2,c),所以OA → =(1,-1,0),OP →=(-1,-1,1), BQ →=(-2,0,c),BD 1=(-2,-2,2). 设平面PAO 的法向量为n =(x ,y ,z), 则⎩⎪⎨⎪⎧n ·OA →=0,n ·OP →=0, 所以⎩⎪⎨⎪⎧x -y =0,-x -y +z =0,令x =1,则y =1,z =2.所以平面PAO 的一个法向量为n =(1,1,2). 若BQ ∥平面PAO ,则n ⊥BQ ,所以n ·BQ → =0,即-2+2c =0,所以c =1, 故当Q 为CC 1的中点时,BQ ∥平面PAO.本例若把“Q 是CC 1上的点”改为“Q 是CC 1的中点”,其他条件不变,求证:平面D 1BQ ∥平面PAO.【证明】建立如图所示的空间直角坐标系,设正方体棱长为2,则O(1,1,0),A(2,0,0),P(0,0,1),B(2,2,0),D 1(0,0,2),Q(0,2,1), 所以OA → =(1,-1,0),OP →=(-1,-1,1), BQ →=(-2,0,1),BD 1=(-2,-2,2). 设平面PAO 的法向量为n 1=(x ,y ,z), 则⎩⎪⎨⎪⎧n 1·OA →=0n 1·OP →=0 ,所以⎩⎪⎨⎪⎧x -y =0-x -y +z =0,令x =1,则y =1,z =2.所以平面PAO 的一个法向量为n 1=(1,1,2).同理可求平面D 1BQ 的一个法向量为n 2=()1,1,2 , 因为n 1=n 2,所以n 1∥n 2, 所以平面D 1BQ ∥平面PAO.角度2证明垂直问题【典例】在如图所示的几何体中,平面CDEF 为正方形,平面ABCD 为等腰梯形,AB ∥CD ,AB =2BC ,∠ABC =60°,AC ⊥FB. (1)求证:AC ⊥平面FBC ;(2)线段ED 上是否存在点Q ,使平面EAC ⊥平面QBC ?证明你的结论.【思路导引】(1)利用余弦定理和勾股定理的逆定理可得AC ⊥BC ,再利用已知AC ⊥FB 和线面垂直的判定定理即可证明;(2)通过建立空间直角坐标系,利用两个平面的法向量是否垂直即可. 【解析】(1)因为AB =2BC ,∠ABC =60°,在△ABC 中,由余弦定理可得AC 2=AB 2+BC 2-2AB ·BCcos 60°=3BC 2, 所以AC 2+BC 2=4BC 2=AB 2, 所以∠ACB =90°,所以AC ⊥BC. 又因为AC ⊥FB ,FB ∩BC =B , 所以AC ⊥平面FBC.(2)线段ED 上不存在点Q ,使平面EAC ⊥平面QBC. 证明如下:因为AC ⊥平面FBC , 所以AC ⊥FC.因为CD ⊥FC ,所以FC ⊥平面ABCD.所以CA ,CF ,CB 两两互相垂直,如图建立空间直角坐标系.在等腰梯形ABCD 中,可得CB =CD.设BC =1,所以C(0,0,0),A(3 ,0,0),B(0,1,0),D(32 ,-12 ,0),E ⎝ ⎛⎭⎪⎪⎫32,-12,1 .所以CE → =⎝⎛⎭⎪⎪⎫32,-12,1 ,CA →=(3 ,0,0),CB →=(0,1,0).设平面EAC 的法向量为n =(x ,y ,z), 则⎩⎪⎨⎪⎧n ·CE →=0n ·CA →=0 ,所以⎩⎨⎧32x -12y +z =03x =0,取z =1,得n =(0,2,1).假设线段ED 上存在点Q , 设Q ⎝⎛⎭⎪⎫32,-12,t (0≤t≤1),所以CQ →=⎝ ⎛⎭⎪⎫32,-12,t . 设平面QBC 的法向量为m =(a ,b ,c),则⎩⎪⎨⎪⎧m ·CB →=0m ·CQ →=0 ,所以⎩⎨⎧b =032a -12b +tc =0,取c =1,得m =⎝ ⎛⎭⎪⎫-2t 3,0,1 .要使平面EAC ⊥平面QBC ,只需m·n =0, 即-23t×0+0×2+1×1=0,此方程无解.所以线段ED上不存在点Q,使平面EAC⊥平面QBC. 利用空间向量证明平行、垂直问题的常用思路线面平行(1)求出直线l的方向向量是a,平面α的法向量是u,只需证明a⊥u,即a·u=0.(2)在平面内找一个向量与已知直线的方向向量是共线向量即可.面面平行(1)转化为相应的线线平行或线面平行.(2)求出平面α,β的法向量u,v,证明u∥v即可说明α∥β.线面垂直求出平面内两条相交直线的方向向量,证明直线的方向向量和它们都垂直.面面垂直(1)转化为线面垂直.(2)求解两个平面的法向量,证明两个法向量垂直.1.已知正方体ABCD-A1B1C1D1的棱长为2,E,F分别是BB1,DD1的中点,求证:(1)FC1∥平面ADE;(2)平面ADE∥平面B1C1F.【解析】如图所示建立空间直角坐标系,则有D(0,0,0),A(2,0,0),C(0,2,0),C1(0,2,2),E(2,2,1),F(0,0,1),B1(2,2,2),所以FC1=(0,2,1),DA → =(2,0,0),AE → =(0,2,1).(1)设n 1=(x 1,y 1,z 1)是平面ADE 的法向量,则n 1⊥DA → ,n 1⊥AE → ,即⎩⎪⎨⎪⎧n 1·DA →=2x 1=0n 1·AE →=2y 1+z 1=0 ⇒⎩⎪⎨⎪⎧x 1=0z 1=-2y 1 , 令z 1=2⇒y 1=-1,所以n 1=(0,-1,2),因为n 1·1FC =-2+2=0,所以n 1⊥1FC , 又因为FC 1⊄平面ADE ,即FC 1∥平面ADE.(2)因为11C B =(2,0,0),设n 2=(x 2,y 2,z 2)是平面B 1C 1F 的一个法向量. 由n 2⊥1FC ,n 2⊥11C B ,得21222112FC 2y z 0C B 2x 0⎧=+=⎪⎨==⎪⎩n n ⇒⎩⎪⎨⎪⎧x 2=0z 2=-2y 2. 令z 2=2⇒y 2=-1,所以n 2=(0,-1,2),所以n 1=n 2,所以平面ADE ∥平面B 1C 1 F.2.在正方体ABCD-A 1B 1C 1D 1中,E 是BC 的中点,在CC 1上求一点P ,使平面A 1B 1P ⊥平面C 1DE.【解析】以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,如图所示,设正方体棱长为2,且P(0,2,a),则D(0,0,0),E(1,2,0),C 1(0,2,2),A 1(2,0,2),B 1(2,2,2),则DE → =(1,2,0),1DC =(0,2,2),设n 1=(x 1,y 1,z 1)且n 1⊥平面DEC 1,则⎩⎪⎨⎪⎧x 1+2y 1=0y 1+z 1=0 ,取n 1=(2,-1,1). 又1A P =(-2,2,a -2),11A B =(0,2,0),设n 2=(x 2,y 2,z 2)且n 2⊥平面A 1B 1P ,则⎩⎪⎨⎪⎧-2x 2+2y 2+(a -2)z 2=0y 2=0 ,取n 2=(a -2,0,2). 由平面A 1B 1P ⊥平面C 1DE ,得n 1·n 2=0,1的中点.【补偿训练】在四棱锥P-ABCD 中,底面ABCD 是正方形,侧棱PD 垂直于底面ABCD ,PD =DC ,E 是PC 的中点,作EF ⊥PB 于点F.求证:(1)PA ∥平面EDB.(2)PB ⊥平面EFD.K【证明】建立如图所示的空间直角坐标系.D 是坐标原点,设DC =a.(1)连接AC 交BD 于G ,连接EG ,依题意得D(0,0,0),A(a ,0,0),P(0,0,a),E ⎝⎛⎭⎫0,a 2,a 2 . 因为底面ABCD 是正方形,所以G 是此正方形的中心,故点G 的坐标为⎝⎛⎭⎫a 2,a 2,0 ,所以EG → =⎝⎛⎭⎫a 2,0,-a 2 .又PA → =(a ,0,-a),所以PA → =2EG → ,这表明PA ∥EG.而EG ⊂平面EDB ,且PA ⊄平面EDB ,所以PA ∥平面EDB.(2)依题意得B(a ,a ,0),PB → =(a ,a ,-a),DE → =⎝⎛⎭⎫0,a 2,a 2 ,所以PB → ·DE → =0+a 22 -a 22 =0,所以PB → ⊥DE → ,即PB ⊥DE.又已知EF ⊥PB ,且EF∩DE =E ,所以PB ⊥平面EFD.课堂检测·素养达标1.设直线l 的方向向量为a ,平面α的法向量为n ,l ⊄α,则使l ∥α成立的是( )A .a =(1,-1,2),n =(-1,1,-2)B .a =(2,-1,3),n =(-1,1,1)C .a =(1,1,0),n =(2,-1,0)D .a =(1,-2,1),n =(1,1,2)【解析】l 的方向向量为a ,平面α的法向量为n ,l ⊄α,使l ∥α成立,所以a·n =0, 在A 中,a·n =-1-1-4=-6,故A 错误;在B 中,a·n =-2-1+3=0,故B 成立;在C 中,a·n =2-1=1,故C 错误;在D 中,a·n =1-2+2=1,故D 错误.2.(教材练习改编)若平面α与β的法向量分别是a =(2,4,-3),b =(-1,2,2),则平面α与β的位置关系是( )A .平行B .垂直C .相交但不垂直D .无法确定 【解析】选B.a·b =(2,4,-3)·(-1,2,2)=-2+8-6=0,所以a ⊥b ,所以平面α与平面β垂直.3.已知平面α内有一个点M(1,-1,2),平面α的一个法向量是n =(6,-3,6),则下列点P 中在平面α内的是( )A .P(2,3,3)B .P(-2,0,1)C .P(-4,4,0)D .P(3,-3,4)【解析】选A.设平面α内一点P(x ,y ,z),则:MP → =(x -1,y +1,z -2),因为n =(6,-3,6)是平面α的法向量,所以n ⊥MP → ,n ·MP → =6(x -1)-3(y +1)+6(z -2)=6x -3y +6z -21,所以由n ·MP → =0得6x -3y +6z -21=0,所以2x -y +2z =7,把各选项的坐标数据代入上式验证可知A 适合.4.正三棱锥P-ABC 中,BC 与PA 的位置关系是________.【解析】如图,在正三棱锥P-ABC 中,P 在底面ABC 内的射影O 为正三角形ABC 的中心,连接AO ,则AO 是PA 在底面ABC 内的射影,且BC ⊥AO ,所以BC ⊥PA.答案:BC ⊥PA。
平面向量的平面方程与法向量

平面向量的平面方程与法向量平面向量是指在平面内既有大小又有方向的向量,通过平面向量可以确定平面上的一些特征,其中包括平面方程和法向量。
本文将详细介绍平面向量的平面方程与法向量的相关概念和性质。
1. 平面向量的表示与性质平面向量通常用箭头表示,箭头的方向表示向量的方向,而箭头的长度表示向量的大小。
平面向量的表示可以用两点表示,即从一个点A指向另一个点B得到的向量,记作AB。
根据平行四边形法则,平面向量的大小等于其对应的对角线的大小。
对于平面向量$\vec{a}$和$\vec{b}$,其性质如下:- 加法性质:$\vec{a}+\vec{b}=\vec{b}+\vec{a}$,即向量的加法满足交换律;- 数乘性质:$k(\vec{a}+\vec{b})=k\vec{a}+k\vec{b}$,即数与向量的加法满足分配律;- 数乘性质:$(k+l)\vec{a}=k\vec{a}+l\vec{a}$,即不同数与向量相乘满足分配律。
2. 平面向量的平面方程平面向量的平面方程表示了该向量所在平面的特征。
平面方程的一般形式为$Ax+By+Cz+D=0$,其中A、B和C是方程的系数,D是常数。
需要注意的是,A、B和C不全为0。
以平面上一点P(x, y, z)为例,该点到平面上已知点Q的向量为$\vec{n}$,若平面上的任意一点M(x', y', z')到点Q的向量为$\vec{p}$,则平面方程可以表示为$\vec{np}=0$。
3. 平面向量的法向量对于平面向量的平面方程而言,平面的法向量起着重要的作用。
法向量是垂直于给定平面的向量,可以用来描述平面的方向和倾斜度。
对于平面的法向量,有以下性质:- 若$\vec{n}$是平面方程$Ax+By+Cz+D=0$的法向量,则$\vec{n}(A, B, C)$;- 若平面有一个与$\vec{n}$同向的法向量,其中$\vec{n}$有大小和方向,$\vec{m}=k\vec{n}$,其中k是一个实数。
法向量1

A
B
x
F E
Dy
C
小结:
想想看,这节课我们都学到了什么? 1、怎么求法向量? 2、利用法向量证明平行与垂直问题
作业:练习册:47-48页
目标:
会求法向 量并用法 向量解题
请各位老师批评指正 谢谢
课前小测答案:
1、 a b x1x2 y1 y2 z1z2
2、a b 0
3、 E(1, 1 ,2) F 1 ,1,1
2、线面垂直性质定理: (1)垂直于同一平面的直线互相平行 (2)垂直面的直线,垂直面内所有直线
目标:
会求法向 量并用法 向量解题
3、线面平行判定定理:不在面内直线平行面内一条直线, 则线面平行
4、面面平行判定定理:两条相交直线平行于同一个 平面,则两个平面平行
新知教学
1、已知平面 ,如果向量 n 的基线与
即xy
y z
赋值:x 1 n (1,1,1)
步骤1-2-1
目标:
会求法向
(1)设 n x, y, z
量并用法 向量解题
(2)找出平面内不共
线向量 v1,v2
n
v1
0
n v2 0
(3)解方程组,赋值
应用1 :ABCD是直角梯形,ABC SA 平面ABCD SA AB BC 1 AD
x2 y2 z2 1 法向量是否
n (1,1,1)
唯一?
思考:求平面ABC的单位法向量坐标
求法向量方法
设法向量 n x, y, z
AB (1,1,0) BC 0,1,1
n AB 0 n BC 0
x y 0 y z 0
最新人教版高中数学选修一第一单元《空间向量与立体几何》测试卷(包含答案解析)

一、选择题1.在棱长为1的正方体1111ABCD A B C D -中,,M N 分别为111,BD B C 的中点,点P 在正方体的表面上运动,且满足MP CN ⊥,则下列说法正确的是( )A .点P 可以是棱1BB 的中点 B .线段MP 的最大值为32C .点P 的轨迹是正方形D .点P 轨迹的长度为2+52.设O ABC -是正三棱锥,1G 是ABC 的重心,G 是1OG 上的一点,且13OG GG =,若OG xOA yOB zOC =++,则x y z ++=( ).A .14B .12C .34D .13.已知()1,1,2P -,()23,1,0P 、()30,1,3P ,则向量12PP 与13PP 的夹角是( ) A .30B .45C .60D .904.如图,三棱柱111ABC A B C -中,底面边长和侧棱长都相等,1160BAA CAA ∠=∠=︒,则异面直线1AB 与1BC 所成角的余弦值为( )A 30B 6C 3D 65.如图,在正方体1111ABCD A B C D -中,M ,N ,P 分别为棱AD ,1CC ,11A D 的中点,则1B P 与MN 所成角的余弦值为( )A .3010B .15-C .7010D .156.在平行六面体ABCD A B C D ''''-中,若2AC x AB y BC z CC →→→→''=++,则x y z ++=( ) A .52B .2C .32D .1167.以下四个命题中,正确的是( ) A .若1123OP OA OB =+,则P 、A 、B 三点共线 B .若{,,}a b c 为空间的一个基底,则{,,}a b b c c a +++构成空间的另一个基底 C .()a b c a b c ⋅=⋅⋅D .ABC 为直角三角形的充要条件是·0AB AC =8.已知正四面体ABCD 的棱长为a ,点E ,F 分别是,BC AD 的中点,则AE AF ⋅的值为( ) A .2aB .212a C .214a D .234a 9.已知空间直角坐标系O xyz -中,()1,2,3OA =,()2,1,2OB =,()1,1,2OP =,点Q 在直线OP 上运动,则当QA QB ⋅取得最小值时,点Q 的坐标为( )A .131,,243⎛⎫⎪⎝⎭B .133,,224⎛⎫⎪⎝⎭C .448,,333⎛⎫⎪⎝⎭D .447,,333⎛⎫⎪⎝⎭10.已知()2,1,3a =-,()1,4,2b =--,()7,5,c λ=,若a 、b 、c 三向量共面,则实数λ等于( ) A .9B .647C .657D .66711.如图所示,直三棱柱111ABC A B C -的侧棱长为3,底面边长11111A C B C ==,且11190A C B ∠=,D 点在棱1AA 上且12AD DA =,P 点在棱1C C 上,则1PD PB ⋅的最小值为( )A .52B .14-C .14D .52-12.如图,在菱形ABCD 中,23ABC π∠=,线段AD 、BD 的中点分别为E 、F .现将ABD ∆沿对角线BD 翻折,当二面角A BD C --的余弦值为13时,异面直线BE 与CF 所成角的正弦值是( )A .356B .16C .265D .1513.如图,在60︒二面角的棱上有两点A 、B ,线段AC 、BD 分别在这个二面角的两个面内,并且都垂直于棱AB ,若4AB AC BD ===,则线段CD 的长为( )A .3B .16C .8D .42二、填空题14.已知直四棱柱1111ABCD A B C D -中,12AA =,底面ABCD 是直角梯形,A ∠为直角,//AB CD ,4AB =,2AD =,1DC =,则异面直线1BC 与DC 所成角的余弦值为______.15.如图:二面角α﹣l ﹣β等于120°,A 、B 是棱l 上两点,AC 、BD 分别在半平面α、β内,AC ⊥l ,BD ⊥l ,AB =AC =BD =1,则CD 的长等于__.16.已知(5,3,1)a =,22,,5b t ⎛⎫=-- ⎪⎝⎭.若a 与b 的夹角为钝角,则实数t 的取值范围是________.17.已知直线l 的一个方向向量(4,3,1)d =,平面α的一个法向量(,3,5)n m =-,且//l α,则m =____18.若(2,3,1)a =-,(2,0,3)b =,(0,2,2)c =,则()a b c ⋅+=_____ 19.设平面α的法向量为(1,2,2)-,平面β的法向量为(2,,4)λ,若α∥β,则λ的值为______20.已知()1,1,2AB =-,()1,1,BC z =-,()1,,1BP x y =--.若BP ⊥平面ABC ,则||CP 的最小值为___________.21.已知空间四边形OABC 中,OA a =,OB b =,OC c =,点M 在OA 上,2OM MA =,点N 在BC 上,3BN NC =,则MN 等于__________.(用a ,b ,c 表示)22.已知(2,1,3),(1,4,2),(3,5,)a b c λ=-=-=-,若,,a b c 三向量共面,则实数λ=_____.23.如图,在空间四边形OABC 中,M ,N 分别为OA 、BC 的中点,点G 在线段MN 上,且3MG GN =,用向量OA 、OB 、OC 表示向量OG ,设OG x OA y OB z OC =⋅+⋅+⋅,则x 、y 、z 的和为______.24.在空间直角坐标系中,(2,0,1)a x =--,(1,,2)b y =,且|2|13a b +=,则2m x y =+的取值范围是_____.25.平行六面体1111ABCD A B C D -中,底面ABCD 是边长为1的正方形,12AA = 11120A AD A AB ∠=∠=︒,则对角线1BD 的长度为___.26.在平行六面体1111ABCD A B C D -中,已知1160BAD A AB A AD ∠=∠=∠=︒,14,3,5AD AB AA ===,1AC =__.【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】在正方体1111ABCD A B C D -中,以点D 为坐标原点,分别以DA 、DC 、1DD 方向为x 轴、y 轴、z 轴正方向,建立空间直角坐标系,根据MP CN ⊥,确定点P 的轨迹,在逐项判断,即可得出结果. 【详解】在正方体1111ABCD A B C D -中,以点D 为坐标原点,分别以DA 、DC 、1DD 方向为x 轴、y 轴、z 轴正方向,建立空间直角坐标系, 因为该正方体的棱长为1,,M N 分别为111,BD B C 的中点, 则()0,0,0D ,111,,222M ⎛⎫ ⎪⎝⎭,1,1,12N ⎛⎫⎪⎝⎭,()0,1,0C , 所以1,0,12CN ⎛⎫=⎪⎝⎭,设(),,P x y z ,则111,,222MP x y z ⎛⎫=--- ⎪⎝⎭,因为MP CN ⊥, 所以1110222x z ⎛⎫-+-= ⎪⎝⎭,2430x z +-=,当1x =时,14z =;当0x =时,34z =; 取11,0,4E ⎛⎫ ⎪⎝⎭,11,1,4F ⎛⎫ ⎪⎝⎭,30,1,4G ⎛⎫ ⎪⎝⎭,30,0,4H ⎛⎫ ⎪⎝⎭, 连接EF ,FG ,GH ,HE ,则()0,1,0EF GH ==,11,0,2EH FG ⎛⎫==- ⎪⎝⎭, 所以四边形EFGH 为矩形,则0EF CN ⋅=,0EH CN ⋅=,即EF CN ⊥,EH CN ⊥, 又EFEH E =,且EF ⊂平面EFGH ,EH ⊂平面EFGH ,所以CN ⊥平面EFGH , 又111,,224EM ⎛⎫=-⎪⎝⎭,111,,224MG ⎛⎫=- ⎪⎝⎭,所以M 为EG 中点,则M ∈平面EFGH ,所以,为使MP CN ⊥,必有点P ∈平面EFGH ,又点P 在正方体的表面上运动, 所以点P 的轨迹为四边形EFGH , 因此点P 不可能是棱1BB 的中点,即A 错; 又1EF GH ==,52EH FG ==,所以EF EH ≠,则点P 的轨迹不是正方形;且矩形EFGH 的周长为2222+⨯=+C 错,D 正确; 因为点M 为EG 中点,则点M 为矩形EFGH 的对角线交点,所以点M 到点E 和点G的距离相等,且最大,所以线段MP ,故B 错. 故选:D. 【点睛】关键点点睛:求解本题的关键在于建立适当的空间直角坐标系,利用空间向量的方法,由MP CN ⊥,求出动点轨迹图形,即可求解.2.C解析:C【分析】利用空间向量的基本定理可计算得出1111333OG OA OB OC =++,由已知条件可得出134OG OG =,进而可求得x 、y 、z 的值,由此可求得结果.【详解】如下图所示,连接1AG 并延长交BC 于点D ,则点D 为BC 的中点,1G 为ABC 的重心,可得123AG AD =, 而()()111222OD OB BD OB BC OB OC OB OB OC =+=+=+-=+, ()1122123333OG OA AG OA AD OA OD OA OA OD =+=+=+-=+ ()()12113323OA OB OC OA OB OC =+⋅+=++,所以,13311111144333444OG OG OA OB OC OA OB OC ⎛⎫==++=++ ⎪⎝⎭, 所以,14x y z ===,因此,34x y z ++=. 故选:C. 【点睛】方法点睛:对于空间向量的基底分解的问题,一般需要利用向量的加减法法则进行处理,也可以借助一些相应的结论对运算进行简化.3.D解析:D 【分析】设向量12PP 与13PP 的夹角为θ,计算出向量12PP 与13PP 的坐标,然后由12131213cos PP PP PP PP θ⋅=⋅计算出cos θ的值,可得出θ的值.【详解】设向量12PP 与13PP 的夹角为θ, ()()()123,1,01,1,22,2,2PP =--=-,()()()130,1,31,1,21,2,1PP =--=-,则12131213cos 0PP PP PP PP θ⋅==⋅,所以,90θ=,故选D.【点睛】本题考查空间向量的坐标运算,考查利用向量的坐标计算向量的夹角,考查计算能力,属于中等题.4.D解析:D 【分析】根据三棱柱的边长和角度关系,设棱长为1,分别求得AB AC ⋅、1AB AA ⋅、1AC AA ⋅的数量积,并用1,,AA AC AB 表示出1AB 和1BC ,结合空间向量数量积的定义求得11AB BC ⋅,再求得1AB 和1BC ,即可由向量的夹角公式求得异面直线1AB 与1BC 所成角的余弦值. 【详解】三棱柱111ABC A B C -中,底面边长和侧棱长都相等,1160BAA CAA ∠=∠=︒,设棱长为1,则111cos602AB AC ⋅=⨯⨯︒=,1111cos602AB AA ⋅=⨯⨯︒=,1111cos602AC AA ⋅=⨯⨯︒=. 11AB AB AA =+,11BC AA AC AB =+-,所以()()1111AB BC AB AA AA AC AB ⋅=+⋅+-221111AB AA AB AC AB AA AA AC AA AB =⋅+⋅-++⋅-⋅11111112222=+-++-= 而()222111123AB AB AA AB AB AA AA =+=+⋅+=,()2111BC AA AC AB =+-==,所以111111cos 2AB BC AB BC AB BC ⋅<⋅>===⋅, 故选:D. 【点睛】本题考查了空间向量的线性运算,空间向量数量积的定义与运算,异面直线夹角的向量求法,属于中档题.5.A解析:A 【分析】如图以A 为原点,分别以1,,AB AD AA 所在的直线为,,x y z 轴建立空间直角坐标系,求出1B P 和MN 的坐标,设1B P 与MN 所成的角为θ,利用11cos B P MN B P MNθ=⋅⋅即可求解.【详解】如图以A 为原点,分别以1,,AB AD AA 所在的直线为,,x y z 轴建立空间直角坐标系,设正方体的棱长为2,则()0,1,0M ,()2,2,1N ,()12,0,2B ,()0,1,2P , 所以()12,1,0B P =-,()2,1,1MN =, 设1B P 与MN 所成的角为θ, 所以1122130cos 1056B P MN B P MNθ=⋅-⨯+==⨯⋅, 1B P 与MN 所成角的余弦值为3010,故选:A 【点睛】 方法点睛:求空间角的常用方法:(1)定义法,由异面直线所成角、线面角、二面角的定义,结合图形,作出所求空间角,再结合题中条件,解对应三角形,即可求出结果;(2)向量法:建立适当的空间直角坐标系,通过计算向量夹角(直线方向向量与直线方向向量、直线方向向量与平面法向量,平面法向量与平面法向量)余弦值,即可求出结果.6.A解析:A 【分析】根据空间向量的线性运算,得出AB BC AC AC CC CC →→→→→→⎛⎫=+=++ ⎪⎭'''⎝,结合题意,即可求出11,2y z ==,从而得出x y z ++的值. 【详解】解:由空间向量的线性运算,得AB BC AC AC CC CC →→→→→→⎛⎫=+=++ ⎪⎭'''⎝,由题可知,2AC x AB y BC z CC →→→→''=++, 则1,1,21x y z ===,所以11,2y z ==, 151122x y z ∴++=++=. 故选:A. 【点睛】本题考查空间向量的基本定理的应用,以及空间向量的线性运算,属于基础题.7.B解析:B 【分析】对于A ,P ,A , B 三点共线时,(1)OP OA OB λμλμ=++=,故A 不正确;对于B , ,,a b b c c a +++不共线,所以 {,,}a b b c c a +++构成空间的另一个基底,故B 正确;对于C ,设,a b θ<>=,则|()||||||||cos |a b c a b c θ=,故C 不正确;对于D ,·0AB AC =时,A ∠为直角,反之也可以是B ,C ∠为直角,故D 不正确. 【详解】对于A ,P ,A , B 三点共线时,(1)OP OA OB λμλμ=++=,1123OP OA OB =+,P ∴,A ,B 三点共线不成立,故A 不正确;对于B ,若{,,}a b c 为空间的一个基底,则,,a b c 不共线,∴,,a b b c c a +++不共线,∴{,,}a b b c c a +++构成空间的另一个基底,故B 正确;对于C ,设,a b θ<>=,则|()||||||||cos |a b c a b c θ=,故C 不正确;对于D ,·0AB AC =时,A ∠为直角,故ABC ∆为直角三角形,反之也可以是B ,C ∠为直角,故D 不正确. 故选:B 【点睛】本题主要考查命题真假的判断,考查向量共线的条件,考查向量的数量积的计算,考查充要条件的判定,意在考查学生对这些知识的理解掌握水平.8.C解析:C【分析】把要求数量积的两个向量表示成以四面体的棱长为基底的向量的表示形式,写出向量的数量积,问题转化成四面体的棱之间的关系,因为棱长和夹角已知,得到结果.【详解】 解:11()22AE AF AB AC AD =+ 1()4AB AD AC AD =+ 1(cos60cos60)4a a a a =⨯⨯︒+⨯⨯︒ 2221111()4224a a a =+= 故选:C.【点睛】本题考查空间向量的数量积,解题的关键是把要用的向量写成以已知几何体的一个顶点为起点的向量为基地的形式,再进行运算.9.C解析:C【分析】设(,,)Q x y z ,根据点Q 在直线OP 上,求得(,,2)Q λλλ,再结合向量的数量积和二次函数的性质,求得43λ=时,QA QB ⋅取得最小值,即可求解. 【详解】设(,,)Q x y z ,由点Q 在直线OP 上,可得存在实数λ使得OQ OP λ=,即(,,)(1,1,2)x y z λ=,可得(,,2)Q λλλ,所以(1,2,32),(2,1,22)QA QB λλλλλλ=---=---,则2(1)(2)(2)(1)(32)(22)2(385)QA QB λλλλλλλλ⋅=--+--+--=-+,根据二次函数的性质,可得当43λ=时,取得最小值23-,此时448(,,)333Q . 故选:C.【点睛】 本题主要考查了空间向量的共线定理,空间向量的数量积的运算,其中解答中根据向量的数量积的运算公式,得出关于λ的二次函数是解答的关键,着重考查运算与求解能力. 10.C解析:C【分析】由题知,a 、b 、c 三个向量共面,则存在常数,p q ,使得c pa qb =+,由此能求出结果.【详解】因为()2,1,3a =-,()1,4,2b =--,()7,5,c λ=,且a 、b 、c 三个向量共面, 所以存在,p q 使得c pa qb =+.所以()()7,5,2,4,32p q p q p q λ=--+- ,所以274532p q q p p q λ-=⎧⎪-=⎨⎪=-⎩, 解得331765,,32777p q p q λ===-= . 故选:C.【点睛】本题主要考查空间向量共面定理求参数,还运用到向量的坐标运算. 11.B解析:B【分析】由题易知1,,AC BC CC 两两垂直,以C 为坐标原点,建立如图所示的空间直角坐标系,设()03PC a a =≤≤,可知()0,0,P a ,进而可得1,PD PB 的坐标,然后求得1PD PB ⋅的表达式,求出最小值即可.【详解】由题意可知,1,,AC BC CC 两两垂直,以C 为坐标原点,建立如图所示的空间直角坐标系,则()10,1,3B ,()1,0,2D ,设()03PC a a =≤≤,则()0,0,P a ,所以()1,0,2P a D =-,()10,1,3a PB =-,则()()2151002324a a a PD PB ⎛⎫=++--=-- ⎪⎝⋅⎭,当52a =时,1PD PB ⋅取得最小值14-. 故选:B.【点睛】本题考查两个向量的数量积的应用,考查向量的坐标运算,考查学生的计算求解能力,属于中档题.12.A解析:A【分析】过E 作EH BD ⊥,交BD 于H 点,设二面角A BD C --的大小为α,设BE 与CF 的夹角为θ,则0,2π⎡⎤θ∈⎢⎥⎣⎦,由向量数量积的运算律得出CF BE CF HE ⋅=⋅,由题意可得出12HE BE =,利用数量积的定义可求出cos ,CF BE <>的值,即可求出cos θ的值,进而利用同角三角函数的平方关系可求出sin θ的值.【详解】如下图所示,过E 作EH BD ⊥,交BD 于H 点,设BE 与CF 的夹角为θ,则0,2π⎡⎤θ∈⎢⎥⎣⎦, 记二面角A BD C --的大小为α,()CF BE CF BH HE CF HE ⋅=⋅+=⋅, 即()cos CF BE CF HE πα⋅=⋅-,即11cos ,23CF BE CF BE CF BE ⎛⎫⋅<>=⋅⋅- ⎪⎝⎭, 1cos ,6CF BE ∴<>=-,所以1cos 6θ=,即35sin 6θ=, 故选:A .【点睛】本题考查异面直线所成角的计算,同时也考查了二面角的定义,涉及利用空间向量数量积的计算,考查计算能力,属于中等题.13.D解析:D【分析】分别过点A 、点D 作BD 、AB 的平行线相交于点E ,连接CE ,则由题意可知ACE ∆为等边三角形,CDE ∆为直角三角形,求解CD 即可.【详解】分别过点A 、点D 作BD 、AB 的平行线相交于点E ,连接CE ,则四边形ABDE 为平行四边形.线段AC 、BD 分别在这个二面角的两个面内,并且都垂直于棱AB .AC AB ∴⊥,AE AB ⊥则CAE ∠为二面角的平面角,即60CAE ∠=4AB AC BD ===4AC BD AE AB DE ∴=====,如图所示.ACE ∴∆为等边三角形,4CE =AC DE ⊥,AE DE ⊥,AC AE A ⋂=,AC ⊂平面ACE ,AE ⊂平面ACE DE ∴⊥平面ACE又CE ⊂平面ACE∴DE CE ⊥在Rt CDE ∆中22224442CD CE DE =+=+=故选:D【点睛】本题考查空间的距离问题,属于中档题.二、填空题14.【分析】本题首先可结合题意绘出空间直角坐标系然后根据空间直角坐标系得出以及最后根据即可得出结果【详解】因为四棱柱使直四棱柱为直角所以可以以为坐标原点以所在直线分别为轴轴轴建立如图所示的空间直角坐标系 解析:31717 【分析】本题首先可结合题意绘出空间直角坐标系,然后根据空间直角坐标系得出()0,1,0DC =以及()12,3,2BC =--,最后根据111cos ,DC BC DC BC DC BC ⋅=⋅即可得出结果.【详解】因为四棱柱1111ABCD A B C D -使直四棱柱,A ∠为直角,//AB CD , 所以可以以D 为坐标原点,以DA 、DC 、1DD 所在直线分别为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系,则()0,0,0D ,()2,4,0B ,()0,1,0C ,()10,1,2C ,故()0,1,0DC =,()12,3,2BC =--,因为1DC =,222123217BC =++=,所以1113317cos ,1717DC BC DC BC D BC C ⋅-===⋅, 故异面直线DC 与1BC 所成的角的余弦值为31717, 故答案为:31717. 【点睛】 方法点睛:求空间中两条异面直线所成角的大小是立体几何中最为常见的基本题型之一.这类问题的求解一般有两条途径:其一是平移其中的一条直线或两条直线,将其转化为共面直线所成角,然后再构造三角形,通过解三角形来获得答案;其二是建立空间直角坐标系,借助空间向量的数量积公式求出两向量的夹角的大小,从而得出结果. 15.2【分析】求CD 的长即为由向量的加法可得利用向量的数量积运算即可得出答案【详解】∵AB 是棱l 上两点ACBD 分别在半平面αβ内AC ⊥lBD ⊥l 因为所以因为所以故答案为:2【点睛】本题主要考查空间向量的解析:2【分析】求CD 的长即为CD ,由向量的加法可得CD CA AB BD =++,利用向量的数量积运算即可得出答案.【详解】∵A 、B 是棱l 上两点,AC 、BD 分别在半平面α、β内,AC ⊥l ,BD ⊥l ,0,0∴⋅=⋅=CA AB BD AB ,,60︒<>=CA BD因为1AB AC BD ===,所以111cos602︒⋅=⨯⨯=CA BD , 因为CD CA AB BD =++, 所以2()12=++==CD CA AB BD故答案为:2【点睛】本题主要考查空间向量的加法,减法及几何意义和空间向量的数量积,考查了运算求解能力和转化的数学思想,属于一般题目. 16.【分析】由根据与的夹角为钝角由且求解【详解】因为所以因为与的夹角为钝角所以且由得所以若与的夹角为则存在使即所以解得故答案为:【点睛】本题主要考查平面向量的数量积的应用还考查了运算求解的能力属于中档题解析:6652,,5515⎛⎫⎛⎫-∞-⋃- ⎪ ⎪⎝⎭⎝⎭ 【分析】由(5,3,1)a =,22,,5b t ⎛⎫=--⎪⎝⎭,根据a 与b 的夹角为钝角,由0a b ⋅<且,180a b ︒〈〉≠求解.【详解】因为(5,3,1)a =,22,,5b t ⎛⎫=-- ⎪⎝⎭, 所以2525(2)31355a b t t ⎛⎫⋅=⨯-++⨯-=- ⎪⎝⎭, 因为a 与b 的夹角为钝角,所以0a b ⋅<且,180a b ︒〈〉≠,由0a b ⋅<,得52305t -<, 所以5215t <. 若a 与b 的夹角为180︒,则存在0λ<,使a b λ=, 即2(5,3,1)2,,5t λ⎛⎫=-- ⎪⎝⎭, 所以523215t λλλ⎧⎪=-⎪=⎨⎪⎪=-⎩, 解得65t =-, 故答案为: 6652,,5515⎛⎫⎛⎫-∞-⋃- ⎪ ⎪⎝⎭⎝⎭ 【点睛】本题主要考查平面向量的数量积的应用,还考查了运算求解的能力,属于中档题. 17.【分析】由题意可得根据线面平行可得则进而得到解得即可【详解】解:由题意可得则解得【点睛】本题主要考查了直线与平面的位置关系根据线面平行线面垂直的性质得到平面的法向量与平行于平面的直线垂直考查了空间向 解析:1-【分析】由题意可得,根据线面平行可得d n ⊥,则=0d n ,进而得到4950m +-=,解得即可.【详解】解:由题意可得d n ⊥,则4950m +-=解得1m =-【点睛】本题主要考查了直线与平面的位置关系,根据线面平行、线面垂直的性质得到平面的法向量与平行于平面的直线垂直,考查了空间向量垂直的坐标表示.18.3【分析】根据向量加法以及向量数量积的坐标表示得结果【详解】【点睛】本题考查空间向量加法与数量积考查基本求解能力属于基础题解析:3【分析】根据向量加法以及向量数量积的坐标表示得结果.【详解】()()() 2,3,12,2,5465 3.a b c ⋅+=-⋅=-+=,【点睛】本题考查空间向量加法与数量积,考查基本求解能力. 属于基础题. 19.-4【解析】分析:设平面的法向量平面的法向量由∥可得因此存在实数使得再利用向量共线定理的坐标运算即可求得结果详解:设平面的法向量平面的法向量因为∥所以所以存在实数使得所以有解得故答案为点睛:该题考查 解析:-4【解析】分析:设平面α的法向量m ,平面β的法向量n ,由α∥β,可得m n ∥,因此存在实数k ,使得m kn =,再利用向量共线定理的坐标运算即可求得结果.详解:设平面α的法向量(1,2,2)m =-,平面β的法向量(2,,4)n λ=,因为α∥β,所以m n ∥,所以存在实数k ,使得m kn =,所以有12224k k k λ=⎧⎪-=⎨⎪=⎩,解得4λ=-,故答案为4-. 点睛:该题考查的是向量平行的条件,以及向量平行时坐标所满足的关系,在解题的过程中,首先需要利用两个平面平行的条件,得到其法向量共线的结论,之后根据坐标的关系求得结果.20.【分析】利用平面得到两个向量垂直从而利用坐标运算得到之间的关系然后再利用模的坐标表示求解最值即可【详解】因为平面都在平面内所以所以又因为所以解得所以所以所以的最小值为故答案为:【点睛】方法点睛:解答【分析】利用BP ⊥平面ABC ,得到两个向量垂直,从而利用坐标运算得到y ,x ,z 之间的关系,然后再利用模的坐标表示求解最值即可.【详解】因为BP ⊥平面ABC ,,AB BC 都在平面ABC 内,所以,BP AB BP BC ⊥⊥,所以,BP AB BP BC ⊥⊥,又因为()1,1,2AB =-,()1,1,BC z =-,()1,,1BP x y =--,所以(1)20(1)0BP AB x y BP BC x y z ⎧⋅=-++=⎨⋅=---=⎩, 解得1y x =--,2x z =所以(2,1,1)CP BP BC x y z =-=-+--,所以2222||(2)(1)(1)CP x y z =-+++--()()()222212x x x =-+-+--2655x =+, 所以||CP【点睛】方法点睛:解答立体几何中的最值问题一般有两种方法:一是几何意义,特别是用平面几何的有关结论来解决,非常巧妙;二是将立体几何中最值问题转化为函数问题,然后根据函数的特征选用配方法、三角函数有界法、函数单调性法以及均值不等式法求解. 21.【分析】利用向量加法和减法的三角形法则以及向量线性运算的运算律即可用表示【详解】因为所以【点睛】主要考查向量的线性运算法则以及运算律属于基础题 解析:213344a b c -++ 【分析】利用向量加法和减法的三角形法则,以及向量线性运算的运算律即可用,,a b c 表示MN【详解】因为213344MN a b c =-++ 所以//AC BC【点睛】主要考查向量的线性运算法则以及运算律,属于基础题.22.【分析】由题意结合向量基本定理得到方程组求解方程组即可确定的值【详解】由题意可知存在实数满足:据此可得方程组:求解方程组可得:故答案为【点睛】本题主要考查空间向量基本定理方程的数学思想等知识意在考查 解析:1-【分析】由题意结合向量基本定理得到方程组,求解方程组即可确定λ的值.【详解】由题意可知,存在实数,m n 满足:c ma nb =+,据此可得方程组:325432m n m n m n λ-=-⎧⎪=-+⎨⎪=+⎩,求解方程组可得:111m n λ=-⎧⎪=⎨⎪=-⎩. 故答案为1-.【点睛】本题主要考查空间向量基本定理,方程的数学思想等知识,意在考查学生的转化能力和计算求解能力.23.【分析】利用向量的加法公式得出再由得出的值即可得出的和【详解】即故答案为:【点睛】本题主要考查了用空间基底表示向量属于中档题 解析:78【分析】 利用向量的加法公式得出111222MN OA OB OC =-++,再由1324OG OM MG OA MN =+=+,得出,,x y z 的值,即可得出,,x y z 的和. 【详解】MN MA AB BN =++11111()22222OA OB OA OC OB OA OB OC =+-+-=-++ 13131112424222OG OM MG OA MN OA OA OB OC ⎛⎫∴=+=+=+-++ ⎪⎝⎭813388OA OB OC =++ 133,,888x y z ∴=== 即78x y z ++=故答案为:78【点睛】本题主要考查了用空间基底表示向量,属于中档题. 24.【分析】推导出由得到从而由此能求出的取值范围【详解】在空间直角坐标系中整理得:的取值范围是故答案为:【点睛】本题考查代数式的取值范围的求法考查空间向量坐标运算法则椭圆的参数方程等基础知识考查运算求解解析:⎡⎣【分析】推导出2(a b x +=,2y ,3),由|2|13a b +=2214x y +=,从而2cos sin x y θθ=⎧⎨=⎩,(02)θπ≤<,由此能求出2m x y =+的取值范围. 【详解】在空间直角坐标系中,(2,0,1)a x =--,(1,,2)b y =,∴2(,2,3)a b x y +=,|2|13a b +=,∴=2244x y +=,∴2214x y +=, ∴2cos sin x y θθ=⎧⎨=⎩,(02)θπ≤<,2sin 4cos )m x y θθθα∴=+=+=+,tan 4α=.2m x y ∴=+的取值范围是[.故答案为:[.【点睛】本题考查代数式的取值范围的求法,考查空间向量坐标运算法则、椭圆的参数方程等基础知识,考查运算求解能力,求解时注意三角函数中辅助角公式及有界性的应用. 25.2【分析】利用两边平方后利用向量数量积计算公式计算得【详解】对两边平方并化简得故【点睛】本小题主要考查空间向量的加法和减法运算考查空间向量数量积的表示属于中档题解析:2【分析】利用11BD AD AA AB =+-,两边平方后,利用向量数量积计算公式,计算得1BD . 【详解】对11BD AD AA AB=+-两边平方并化简得21BD 2221AD AA AB =++11222AD AA AD AB AA AB +⋅-⋅-⋅211212cos1200212cos1204=+++⨯⨯--⨯⨯=,故12BD =.【点睛】本小题主要考查空间向量的加法和减法运算,考查空间向量数量积的表示,属于中档题. 26.【分析】先由空间向量的基本定理将向量用一组基底表示再利用向量数量积的性质计算即可【详解】∵六面体ABCD ﹣A1B1C1D1是平行六面体∵=++∴=(++)2=+++2+2+2又∵∠BAD=∠A1AB【分析】 先由空间向量的基本定理,将向量1AC 用一组基底1AA AD AB ,,表示,再利用向量数量积的性质22a a =,计算1AC 即可【详解】∵六面体ABCD ﹣A 1B 1C 1D 1是平行六面体,∵1AC =1AA +AD +AB ∴21AC =(1AA +AD +AB )2=21AA +2AB +2AD +21AA AD ⋅+21AA AB ⋅+2AB AD ⋅ 又∵∠BAD=∠A 1AB=∠A 1AD=60°,AD=4,AB=3,AA 1=5,∴21AC =16+9+25+2×5×4×cos60°+2×5×3×cos60°+2×3×4×cos60°=97 ∴197AC =【点睛】本题考察了空间向量的基本定理,向量数量积运算的意义即运算性质,解题时要特别注意空间向量与平面向量的异同。
平面的法向量和方向向量

平面的法向量和方向向量平面的法向量和方向向量是平面几何中的重要概念,它们在描述平面的性质和运动方向时起到了关键作用。
本文将分别介绍平面的法向量和方向向量,并探讨它们的应用和相关性质。
一、平面的法向量平面的法向量是指垂直于该平面的向量。
设平面P上有一条直线L,经过L上的两点A和B可以确定一条向量AB。
如果向量AB垂直于平面P,那么向量AB就是平面P的法向量。
平面的法向量有以下性质:1. 法向量与平面上任意两个垂直向量的内积为零。
设向量a和向量b是平面P上的两个垂直向量,向量n是平面P的法向量,则有a·n=0,b·n=0。
2. 平面上的两个垂直向量的内积为零时,它们是平面的法向量的倍数关系。
设向量a和向量b是平面P上的两个垂直向量,向量n是平面P的法向量,则有a·n=0,b·n=0,因此存在实数k,使得a=k·n,b=k·n。
3. 平面上的两个非零向量的叉积是平面的法向量的倍数。
设向量a 和向量b是平面P上的两个非零向量,向量n是平面P的法向量,则有向量a×b=k·n,其中k为实数。
平面的法向量在几何和物理学中有广泛的应用。
例如,在计算平面上的点到另一平面的距离时,可以利用平面的法向量来求解。
同时,在力学中,平面的法向量也被用来描述平面上的压力和力的作用方向。
二、平面的方向向量平面的方向向量是指平面上的一个非零向量,它表示了平面上的一个方向。
设平面P上有一条直线L,经过L上的两点A和B可以确定一条向量AB。
如果向量AB不是平面P的法向量,那么向量AB 就是平面P的方向向量。
平面的方向向量有以下性质:1. 平面上的两个非零向量的线性组合是平面的方向向量。
设向量a 和向量b是平面P上的两个非零向量,向量c=k1·a+k2·b,其中k1和k2为实数,则向量c是平面P的方向向量。
2. 平面上的两个方向向量的叉积是平面的法向量。
平面的法向量

g = xm + yn , l g = xl m + yl n , l
∵ l m = 0, l n = 0 , ∴ l g = 0, 即l ⊥ g .
g l m
m
n
n g
l ∴ l ⊥ g , 即 l 垂 直 于 平 面 α内 任 一 直 线 . ⊥ α .
6.有关平面的斜线概念, 6.有关平面的斜线概念, 有关平面的斜线概念 三垂线定理及其逆定理 P104
答:a⊥PO
为什么呢? 为什么呢?
三垂线定理
三垂线定理:在平面内的一条直线, 三垂线定理:在平面内的一条直线,如果和这个平面的 一条斜线的射影垂直,那么它也和这条斜线垂直。 一条斜线的射影垂直,那么它也和这条斜线垂直。
PA⊥α a α
P
PA⊥a ② a⊥平面PAO
AO⊥a PO 平面PAO
①
③
a⊥PO
a α A o
数式板书
三垂线定理
对三垂线定理的说明: 对三垂线定理的说明: 1、三垂线定理描述的是PO(斜线)、AO(射 三垂线定理描述的是PO(斜线) AO(射 PO(斜线 影)、a(直线)之间的垂直关系。 a(直线 之间的垂直关系。 直线) 2、a与PO可以相交,也可以异面。 PO可以相交,也可以异面。 可以相交 3、三垂线定理的实质是平面的一条斜线和 平面内的一条直线垂直的判定定理。 平面内的一条直线垂直的判定定理。 4、三垂线定理的图形是由“四线一面”五 三垂线定理的图形是由“四线一面” 个部件组成——垂线 斜线、射影、面内一线、 垂线、 个部件组成——垂线、斜线、射影、面内一线、 平面
高中数学选修2 高中数学选修2-1
3.2.2平面的法向量与 3.2.2平面的法向量与 平面的向量表示
法向量与平面的向量表示
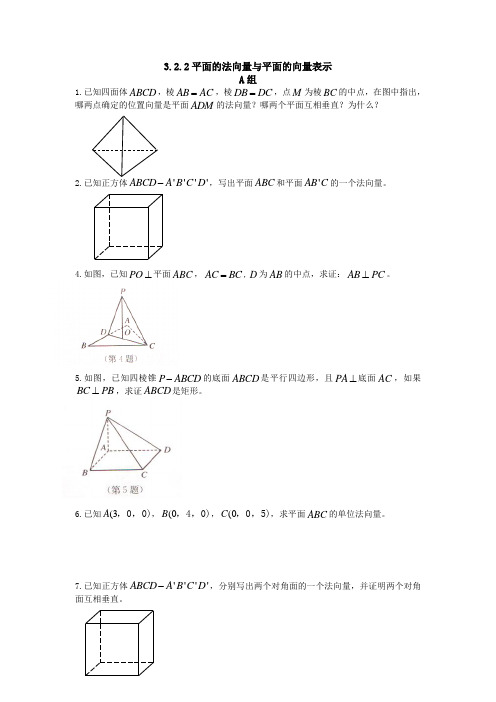
3.2.2平面的法向量与平面的向量表示
A 组
1.已知四面体ABCD ,棱AB AC =,棱DB DC =,点M 为棱BC 的中点,在图中指出,哪两点确定的位置向量是平面ADM 的法向量?哪两个平面互相垂直?为什么?
2.已知正方体''''ABCD A B C D -,写出平面ABC 和平面'AB C 的一个法向量。
4.如图,已知PO ⊥平面ABC ,AC BC =,D 为AB 的中点,求证:AB PC ⊥。
5.如图,已知四棱锥P ABCD -的底面ABCD 是平行四边形,且PA ⊥底面AC ,如果BC PB ⊥,求证ABCD 是矩形。
6.已知(3A ,0,0),(0B ,4,0),(0C ,0,5),求平面ABC 的单位法向量。
7.已知正方体''''ABCD A B C D -,分别写出两个对角面的一个法向量,并证明两个对角面互相垂直。
8.已知四面体ABCD 的棱AB CD ⊥,AC BD ⊥,求证:AD BC ⊥。
B 组
9.直四棱柱1111ABCD A BC D -中,底面ABCD 是矩形,121 3.AB AD AA ===,, M 是BC 的中点.在1DD 上是否存在一点N ,使1MN DC ⊥?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面的法向量与平面的向量表示
一、基础过关
1.若平面α、β的法向量分别为u =(2,-3,5),v =(-3,1,-4),则
( ) A .α∥β B .α⊥β
C .α、β相交但不垂直
D .以上均不正确 2.若直线l 的一个方向向量为a =(2,5,7),平面α的一个法向量为u =(1,1,-1),则( )
A .l ∥α
B .l ⊥α
C .l ⊂α
D .A 、C 都有可能
3.已知平面α内有一个点A (2,-1,2),α的一个法向量为n =(3,1,2),则下列点P 中,在平面α内的是
( ) A .(1,-1,1)
B.⎝⎛⎭⎫1,3,32
C.⎝
⎛⎭⎫1,-3,32 D.⎝⎛⎭⎫-1,3,-32 4.若n 1,n 2分别是平面α,β的法向量,且α⊥β,n 1=(1,2,x ),n 2=(x ,x +1,x ),则x 的值为
( ) A .1或2
B .-1或-2
C .-1
D .-2
5.设平面α的法向量为(1,2,-2),平面β的法向量为(-2,-4,k ),若α∥β,则k 等于( )
A .2
B .-4
C .4
D .-2
6.已知A (1,0,0)、B (0,1,0)、C (0,0,1),则平面ABC 的一个单位法向量是
( ) A.⎝⎛⎭⎫33
,33,-33 B.⎝⎛⎭⎫33,-33,33 C.⎝⎛⎭⎫-33,33,33 D.⎝⎛⎭
⎫-33,-33,-33 7.已知平面α和平面β的法向量分别为a =(1,1,2),b =(x ,-2,3),且α⊥β,则x =________.
8.下列命题中:
①若u ,v 分别是平面α,β的法向量,则α⊥β⇔u·v =0;
②若u 是平面α的法向量且向量a 与α共面,则u·a =0;
③若两个平面的法向量不垂直,则这两个平面一定不垂直.
正确的命题序号是________.
9.已知点P 是平行四边形ABCD 所在的平面外一点,如果AB →=(2,-1,-4),AD →=(4,2,0),
AP →=(-1,2,-1).对于结论:①AP ⊥AB ;②AP ⊥AD ;③AP →是平面ABCD 的法向量; ④AP →∥BD →.
其中正确的是________.(填序号)
二、能力提升
10.在正方体ABCD —A 1B 1C 1D 1中,E ,F 分别是棱AB ,BC 的中点,试在棱BB 1上找一点
M ,使得D 1M ⊥平面EFB 1.
11.如图所示,△ABC 是一个正三角形,EC ⊥平面ABC ,BD ∥CE ,且CE
=CA =2BD ,M 是EA 的中点.求证:平面DEA ⊥平面ECA .
12.如图,在四棱锥P —ABCD 中,P A ⊥底面ABCD ,AB ⊥AD ,∠ABC
=60°,P A =AB =BC ,AD =
233
AB ,E 是PC 的中点. 证明:PD ⊥平面ABE .
三、探究与拓展
13.如图所示,四棱锥P —ABCD 中,底面ABCD 是直角梯形,AB ∥CD ,
∠DAB =60°,AB =AD =2CD ,侧面P AD ⊥底面ABCD ,且△P AD
为等腰直角三角形,∠APD =90°,M 为AP 的中点. 求证:DM ∥平面PCB .
答案
1.C 2.D 3.B 4.B 5.C 6.D
7.-4
8.①②③
9.①②③
10.解 建立如图所示的空间直角坐标系Dxyz ,设正方体的棱长为
2,则E (2,1,0),F (1,2,0),D 1(0,0,2),B 1(2,2,2).
设M (2,2,m ),则EF →=(-1,1,0),B 1E →=(0,-1,-2),D 1M →=
(2,2,m -2).
∵D 1M ⊥平面EFB 1,∴D 1M ⊥EF ,D 1M ⊥B 1E ,
∴D 1M →·EF →=0且D 1M →·B 1E →=0,
于是⎩⎪⎨⎪⎧
-2+2=0,-2-2(m -2)=0, ∴m =1, 故取B 1B 的中点为M 就能满足D 1M ⊥平面EFB 1.
11.证明 建立如图所示的空间直角坐标系Cxyz ,不妨设CA =2,
则CE =2,BD =1,C (0,0,0),A (3,1,0),B (0,2,0),E (0,0,2),D (0,2,1).
所以EA →=(3,1,-2),CE →=(0,0,2),ED →=(0,2,-1).
分别设面CEA 与面DEA 的法向量是n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,
z 2),
则⎩⎪⎨⎪⎧ n 1·EA →=0,n 1·CE →=0,即⎩⎨⎧
3x 1+y 1-2z 1=0,2z 1=0. 解得⎩⎨⎧ y 1=-3x 1,z 1
=0. ⎩⎪⎨⎪⎧ n 2·EA →=0,n 2·ED →=0, 即⎩⎨⎧
3x 2+y 2-2z 2=0,2y 2-z 2=0. 解得⎩⎨⎧ x 2=3y 2,z 2=2y 2.
不妨取n 1=(1,-3,0),n 2=(3,1,2),
因为n 1·n 2=0,所以两个法向量相互垂直.
所以平面DEA ⊥平面ECA .
12.证明 ∵P A ⊥底面ABCD ,AB ⊥AD ,
∴AB 、AD 、AP 两两垂直,建立如图所示的空间直角坐标系,
设P A =AB =BC =1,则P (0,0,1)、A (0,0,0)、B (1,0,0)、
D ⎝⎛⎭
⎫0,233,0. ∵∠ABC =60°,∴△ABC 为正三角形.
∴C ⎝⎛⎭⎫12,32,0,E ⎝⎛⎭
⎫14,34,12. ∴AB →=(1,0,0),AE →=⎝⎛⎭
⎫14,34,12, ∴设平面ABE 的一个法向量为n =(x ,y ,z ),
则⎩⎪⎨⎪⎧ x =0,14x +34y +12z =0,
令y =2,则z =-3,∴n =(0,2,-3).
∵PD →=⎝⎛⎭
⎫0,233,-1,显然PD →=33n ,∴PD →∥n , ∴PD →⊥平面ABE ,即PD ⊥平面ABE .
13.证明 取AD 的中点G ,连接PG ,GB .
∵侧面P AD ⊥底面ABCD .
∵PG ⊥AD ,∴PG ⊥底面ABCD ,
∴PG ⊥BG .又∵BG ⊥AD ,
∴直线DA 、GB 、GP 两两互相垂直,故可以分别以直线DA ,GB ,GP 为x 轴、y 轴和z 轴建立如图所示的空间直角坐标系Gxyz ,
设PG =a ,C (x ,y ,z ),则可求得
P (0,0,a ),A (a,0,0),B (0,3a,0),D (-a,0,0),
则GP →=(0,0,a ),AB →=(-a ,3a,0),PB →=(0,3a ,-a ).
∵AB =2DC ,且AB ∥CD ,
∴AB →=2DC →,即(-a ,3a,0)=2[(x ,y ,z )-(-a,0,0)].
∴(x ,y ,z )=⎝⎛⎭⎫-32a ,32a ,0,即C ⎝⎛⎭
⎫-32a ,32a ,0. ∴BC →=⎝⎛⎭
⎫-32a ,-32a ,0. 设n =(x 0,y 0,z 0)是平面PBC 的法向量,
则n ·BC →=0且n ·PB →=0,
∴⎩⎪⎨⎪⎧ -32ax 0-32ay 0=03ay 0-az 0=0⇒⎩⎪⎨⎪⎧ x 0=-33y 0,z 0=3y 0, 取y 0=3,得n =(-1,3,3).
∵点M 是AP 的中点,∴M ⎝⎛⎭⎫a 2
,0,a 2, ∴DM →=⎝⎛⎭⎫a 2,0,a 2-(-a,0,0)=⎝⎛⎭⎫32
a ,0,a 2. DM →·n =⎝⎛⎭⎫32
a ,0,a 2·(-1,3,3)=0,∴DM →⊥n . ∵DM ⊄平面PCB ,∴DM ∥平面PCB .。
