01第1章质点运动学
01第一章质点运动学

Az
P(x,y,z) A
o
Ax
cos Ay A
Ay
y
cos Az A cos2 cos2 cos2 1
x
第 14 页
因此,一个矢量可以表示为三个分矢量之和;也可以由其 大小和三个方向角决定(四个变量?)。可以写为:
A Ax i Ay j Az k ( Ax , Ay , Az )
或:
t2
t1
t2 t2 t2 A(t )dt Ax (t )dt i Ay (t )dt j Az (t )dt k t1 t1 t1
第 20 页
第二节 质点运动的描述
一、参考系 坐标系
瞬时速度:刻画t 时刻位矢的即时变化率
dr dt
A r r(t)
B'' B' B
r dr v lim dt t 0 t
r(t+t)
o
显然,v 和 r(t) 曲线的斜率有一一对应关系!
第 26 页
平均速率: 在t 时间内,质点所经过路程s对时间的变化率
s v t
A B AB cos
A · B = A B cos(A, B) 表示:两个矢量的标积是 一个标量,其大小是第一个矢量的大小乘以第二 个矢量在第一个矢量上的投影。 (A, B) 是指这两 个矢量的夹角()。
第 10 页
1) A · B = B · A B 2)如果: A⊥B 则 A · B = 0 反之 亦成立。 3)两个矢量平行、反平行时,标积 最大、最小。
dx(t ) dy (t ) dz (t ) v i j k dt dt dt
(完整版)大学物理01质点运动学习题解答

第一章质点运动学一选择题1.以下说法中,正确的选项是:()A.一物体若拥有恒定的速率,则没有变化的速度;B.一物体拥有恒定的速度,但仍有变化的速率;C.一物体拥有恒定的加快度,则其速度不行能为零;D. 一物体拥有沿x 轴正方向的加快度而有沿x 轴负方向的速度。
解:答案是 D。
2.长度不变的杆 AB,其端点 A 以 v0匀速沿 y 轴向下滑动, B 点沿 x 轴挪动,则 B 点的速率为:()A . v0 sinB .v0 cos C.v0 tan D.v0 / cos解:答案是 C。
简要提示:设 B 点的坐标为 x, A 点的坐标为 y,杆的长度为l,则x2y2l 2对上式两边关于时间求导:dx dy0,因dxv,dyv0,所以2 x 2 ydtdt dt dt2xv2yv0 = 0即v=v0 y/x =v0tan所以答案是 C。
3.如图示,路灯距地面高为 H,行人身高为 h,若人以匀速 v 背向路灯行走,灯y人头A H vv0hθvx影sB选择题 3图选择题 2图则人头影子挪动的速度u 为()H h Hv h HA.vB.H H h H h 解:答案是 B 。
简要提示:设人头影子到灯杆的距离为 x ,则x s h , x Hs , x H H hdx H ds HvuH h dt Hdt h所以答案是 B 。
4. 某质点作直线运动的运动学方程为x = 3t-5t 3 + 6 (SI),则该质点作A. 匀加快直线运动,加快度沿 x 轴正方向.B. 匀加快直线运动,加快度沿 x 轴负方向.C. 变加快直线运动,加快度沿 x 轴正方向.D. 变加快直线运动,加快度沿x 轴负方向.()解: 答案是 D5. 一物体从某一确立高度以v 0 的初速度水平抛出,已知它落地时的速度为v t ,那么它的运动时间是: ()v t - v 0v t v 0v t2 22v v 0 v t A.B.C.gD.2 gg2 g解:答案是 C 。
大学精品课件:01第一章质点运动学

第二节 质点运动的描述
一、参考系 坐标系
参考系(Reference Frame) :
确定一个物体的位置总是相对于某一物体或某一物体系来确定,那 么这—物体或物体系就作为描述物体位置的基准,称为参考系。
坐标系(Coordinates) :
确定了参考系后,为了能够定量地描
r
r
r
第4页
运动方程(Motion Equation):
矢量形式:
rv(t)
v x(t)i
y(t)
v j
v z(t)k
x x(t)
参数形式:
y
y(t)
z z(t)
轨道方程( Track Equation ):
F (x, y, z) 0 G (x, y, z) 0
一般情况:Q rv s, vv v
当t0时:Q rv drv , s ds, drv ds, vv v
第 12 页
三、加速度(Acceleration)
t1时刻,质点位于A处,速度为v(t) t2时刻,质点位于A处,速度为v(t+t) t时间内,速度增量为:
瞬时速度:刻画t 时刻速度的即时变化率
lim vv
rv drv
t0 t dt
o
dr
dt
A
B''
B'
r
B
r(t) r(t+t)
显然,v 和 r(t) 曲线的斜率有一一对应关系!
第9页
速度在直角坐标系中的解析表示:
rv(t) x(t)iˆ y(t) ˆj z(t)kˆ
大学物理上第一章质点运动学ppt

加法法则
当有两个或多个质点同时运动时,它们的速 度可以通过矢量加法进行合成。
速率
速度的大小称为速率,用标量符号表示。
04 质点的加速度
瞬时加速度
定义
瞬时加速度是指在某一时刻, 质点运动速度的变化率。
计算公式
$a = frac{dv}{dt}$,其中$a$是 瞬时加速度,$v$是质点的速度, $t$是时间。
定义
平均速度是指在一段时间内质点位移量与时间的比值。
关系
瞬时速度是平均速度在时间趋于零时的极限值,即平 均速度的极限状态就是瞬时速度。
应用
在分析质点运动规律时,通常先求平均速度,再通过 极限思想求得瞬时速度。
速度的矢量性质
矢量表示
速度是一个矢量,具有大小和方向,可以用 矢量符号表示。
方向与正方向
速度的方向与质点运动的方向一致,通常规 定正方向为速度的方向。
重力加速度,大小为 $9.8m/s^{2}$,方向竖 直向下。
圆周运动
圆周运动的定义
质点在平面或空间以一定半径作圆周运动的运动形式。
圆周运动的描述参数
线速度、角速度、周期和频率。
圆周运动的向心加速度
大小为$a = v^{2}/r$,方向指向圆心。
相对运动
相对运动的定义
01
两个物体相对于第三个参照物的运动。
质点运动学的基本概念
质点
没有大小、形状,只有质量的 理想化模型,用于描述实际物 体的运动。
速度
描述质点运动快慢和方向的物 理量。
参考系
用来确定质点位置和描述其运 动的参照物。
位移
质点在空间中的位置变化量。
加速度
描述质点速度变化快慢和方向 的物理量。
第1章质点运动学

➢ 存在绝对空间与绝对时间,二者相互独立; ➢ 绝对空间是三维均匀各向同性的固定不动的欧几里德空间; ➢ 绝对时间是大小连续变化的、方向是从过去到未来; ➢ 在空间的所有点,时间皆是均匀的、单值的,不依赖质点
的运动。
2. 质点与质点系
质点
➢ 尺寸足够小的一小部分物质,即仅有质量,有空间占位而 无尺寸的物质
S’ P
S r r'
o’ o
r r'图1.1r 在直角坐标系的形式
直角坐标系 • 一组正交基矢: {i , j , k} • 三个互为正交的坐标轴:x , y , z
记为:o-xyz
r可表示为: r xi yj zk
其中:x=rcosα, y=rcosβ, z=rcosγ
z
r
γ
β
α
y
➢ 当所研究物体的运动可忽略物体的尺寸时,只有平动而无 转动的物体时可用质点模型
质点系或力学系统 ➢ 质点以某种方式组成的集合
3. 运动学的任务
确定质点(系统)的运动。包括
➢ 研究描述运动的方法; ➢ 确定组成力学系统的点的速度、加速度和其它运动学量
的方法
1.2 运动与参照系
1. 参照系与坐标系
• r 与参照系有关,但在同一参照系下,
∆r只与起点与终点的相对位置有关,与参 照点的选择无关。
② 速度 • 平均速度 v 定义为
v r t
• (瞬时)速度 v 定义为
r dr v lim r v
t0 t dt
讨论
• v是矢量,方向沿运动轨迹曲线的切向。 演示
• 在直角坐标系中的形式
其中:
r rr o
r r ,
ro r r
质点运动学30p.ppt

x
y
R cost R sin t
(2)、轨迹方程——质点运动所经过的空间径迹。
从运动方程中消去时间t 可得轨迹方程。
如:匀速率圆周运动的轨迹方程为 x2 y2 R2
2、位移
zA
位移:反映 位置矢量变化的
大小和方向的物理量。
r rB rA
rA
r
B
O
rB
x
y
(xB xA)i ( yB yA) j (zB zA)k
a
=
v2 Δ
tv1=
9
i
+
2
j
5. t =1s 时刻的瞬时加速度
a
=
dv dt
=6t
i+2j
= 6i + 2 j
§1. 2 直线运动及其几何图线描述法
一、直线运动规律
运动方程: x = x( t )
x
位移(大小): Δ x
速度(大小): v
=
dx dt
x2
加速度(大小): a =
dv dt
d 2x =
3、坐标系
为了定量地确定质点在空间的位置而固定在参照系上 的一个计算系统。 (直角坐标、自然坐标、球坐标、极坐标、柱面坐标等)
对物体运动的描写决定于参照系而不是坐标系
二、描述质点运动的基本物理量
1、位置矢量(位矢、矢径)
z
描述P点的位置,从O到P的有向线
段0P(或r)称为点P的位置矢量。
γ
k
r xi yj zk a O
Δr
Δy
φ Δx
O
5
x 10 15 (cm)
Δ x =12(cm) Δ y =12.6 (cm)
第一章 质点运动学
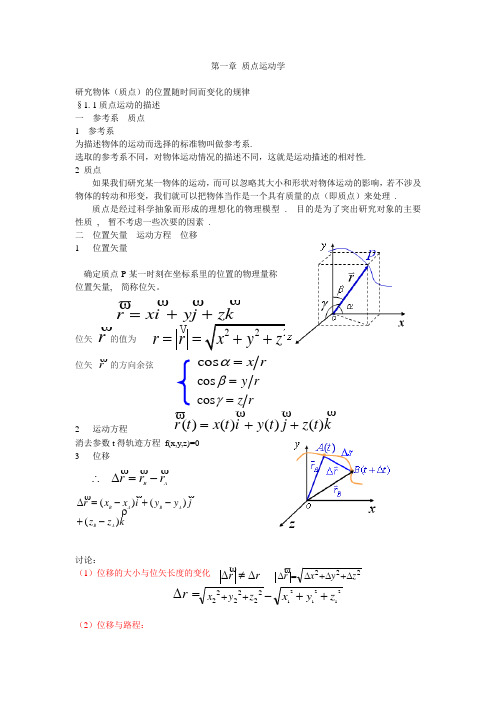
第一章 质点运动学研究物体(质点)的位置随时间而变化的规律 §1. 1质点运动的描述 一 参考系 质点 1 参考系为描述物体的运动而选择的标准物叫做参考系.选取的参考系不同,对物体运动情况的描述不同,这就是运动描述的相对性. 2 质点如果我们研究某一物体的运动,而可以忽略其大小和形状对物体运动的影响,若不涉及物体的转动和形变,我们就可以把物体当作是一个具有质量的点(即质点)来处理 .质点是经过科学抽象而形成的理想化的物理模型 . 目的是为了突出研究对象的主要性质 , 暂不考虑一些次要的因素 . 二 位置矢量 运动方程 位移 1 位置矢量确定质点P 某一时刻在坐标系里的位置的物理量称位置矢量, 简称位矢。
j y i x r+=位矢的值为位矢 的方向余弦2 运动方程k t z j t y i t x t r)()()()(++=消去参数t 得轨迹方程 f(x,y,z)=03 位移讨论:(1)位移的大小与位矢长度的变化(2)位移与路程:r r == r r r x =αcos r y =βcos rz =γcos A B r r r -=∆∴kz z j y y i x x r A B A B A B)()()(-+-+-=∆rr ∆≠∆ 222z y x r ∆+∆+∆=∆212121z y x ++-222222z y x ++=∆r一般情况, 位移大小不等于路程 当Δt →0时,ds r d r =⇒∆三 速度 1 平均速度Δt 时间内,质点从P 1到P 22 瞬时速度当Δt →0时平均速度的极限值叫做瞬时速度, 简称速度即 大小:方向:沿质点运动轨迹的切线方向或讨论:(1)速度与速率: 瞬时速度速度与速率 平均速率与平均速度 平均速率四 加速度(反映速度变化快慢的物理量) 1) 平均加速度与 同方向 2)(瞬时)加速度(1)直角坐标系加速度加速度大小 加速度方向(2)自然坐标系在运动轨迹上任取一点o, 在某时刻t ,质点位于P 处, 沿轨迹某一方向量得的曲线长度r s∆≠∆kt z j t y i t x∆∆+∆∆+∆∆=∆∆=t r v t r t r t d d lim 0=∆∆=→∆v kt z j t y i t x d d d d d d ++=kv j i zy x ++=v v v 222zy x v v v v ++=v v x=αCOS v vy=βCOS v v z=γCOS t d d et s =v == v v d d st=v ts∆∆=v a t ∆=∆v∆ v a0d lim d t a t t∆→∆==∆v v 22d d d d r a t t == v k dt z dv j dt y dv i dt x dv++=y z a j a k + a =222222d d d d d d d d d d d d x x y y x at t y a t t a t t ======z z v v v z a a x=αCOS aay =βCOS a a z=γCOSS=S(t)即为以自然坐标系表示的质点运动方程切线坐标:沿轨迹上任一点的切线方向,切向单位矢量 法线坐标:沿轨迹上任一点的法线方向,法向单位矢量 *注意:ne t e , 随质点移动ttttee dtd d dse e dt dsρωθθ====v v其中ρ=ds/d θ 曲率半径加速度:切向加速度(速度大小变化引起)t a d d t v=切向单位矢量的时间变化率法向加速度(速度方向变化引起)ρρωω22nv v ===a即nnttnte a e a e v e dt dv a+=+=ρ2加速度大小:22nt a a a += ,方向:tna a =ϕtg 讨论:(1)一般情况下,dtdva ≠例 匀速率圆周运动 0,0=≠dtdv a(2)在讨论圆周运动和曲线运动时常采用自然坐标系,即nnttnte a e a e rv e dt dv a+=+=2§1. 2 圆周运动圆周运动一般采用自然坐标系加速度:nnttnte a e a e rv e dt dv a+=+=2t e e t d d d d tt v v +=t a d d v =n d d et θ=∆∆→∆t e t t 0lim =t e d d t加速度大小:22n t a a a += ,方向:tn aa =ϕtgta d d t v =rr a 22nvv ===ωωdtd dtd ωαθω==(1)匀速率圆周运动:速率v 和角速度ω 都为常量 .n2n n e r e a a ω==(2)匀变速率圆周运动α=常量,当t=0时,θ=θ0,ω=ω0。
第1章质点运动学

dr rd
dr
dθ
k
r
ω dθ k
O r dθ P
v dr
Or P
ω dω
Or P
Or P
β dω
2.
速度与角v速度dr的矢d量θ 关 k系式r
dθ
k
r
ω
r
dt dt 大小 v ω r (标量式)
dt 方向 ω
r
(由右手法则确定)
3.
加速度与角加速度的矢量关系式
a
dv
d(ω
vdv g sin ds sin dy
ds
从图中分析看出
dy P ds
Ox
sin ds dy
v
vdv
v0
y y0
gdy
v2
v
2 0
2g( y0
y)
§1.5 圆周运动的角量描述 角量与线量
的关系
一. 角位置与角位移 θ θ (t) 角位置(运动学方程)
yQ
P
O
x
当 t
为质点圆周运动的角位移 按右手法则确定 的正负变化
dt t0 t t0 t t0 s t ρ
ds dt
dτ dt
v
1vn ρ
v2 ρ
n
an
曲率半径
法向加速度: 大小为 v 2 ρ
方向为 n
意义: 反映速度方向变化的快慢
加速度
a
an
n
aτ
τ
v2 ρ
n
dv dt
τ
d2 dt
2sτ
(
ds dt
)2
1 ρ
n
例 一汽车在半径R=200 m 的圆弧形公路上行驶,其运动学 方程为s =20t 0.2 t 2 (SI) .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A = Ax i + Ay j + Az k
dA dAx dAy dAz = i+ j+ k dt dt dt dt
第 19 页
使用类似的方法可以处理矢量函数的积分。如矢量函数 A(t) 对 t 的积分:
Ax (t )dt i + Ay (t )dt j + Az (t )dt k A ( t )d t =
第 26 页
运动方程(Motion Equation): 矢量形式:
r (t ) = x(t )i + y(t ) j + z (t )k
参数形式:
x = x(t ) y = y (t ) z = z (t )
F (x, y, z) = 0 G(x, y, z) = 0
y
A
Dr
Dr
Ds
B
r (t )
O
r (t + Dt )
D r = D x i + D yj + D z k z
2 2 2 Dr = Dx + Dy + Dz
注意
Dr Dr
2
A ( x1 , y1 , z1 ) B( x2 , y2 , z 2 ):
公转:质点模型 自转:质点系模型
第 25 页
三、位置矢量(Position Vector)
从坐标原点o出发,指向质点所在位置 P 的一有向线段。
z
位矢用坐标值表示为:
r = xi + yj + zk
r= x +y +z
2 2 2
o
r
P(x,y,z)
y
x
x y z cos = , cos = , cos = r r r
A+ B = C
B B B C
A
A
第6页
矢量加法的三角形法则,多矢量加法:
C B
Ai
A5 A4
A3 A2
A
A1
显然,矢量加法服从: 交换律 结合律
( A + B) + C = A + ( B + C )
A+ B = B + A
第7页
A = Ax i + Ay j + Az k
B = Bx i + By j + Bz k
第 15 页
矢量点乘的解析表示: 因为有如下关系:
i i = j j = k k =1 i j = j k = k i = 0
或:
t2
t1
t2 t2 t2 A(t )dt = Ax (t )dt i + Ay (t )dt j + Az (t )dt k t1 t1 t1
第 20 页
6.梯度
定义算符▽为:
=i
散度
旋度
+ j +k x y z
标量场函数Ψ(x,y,z)的梯度(gradient)
A = = i +j +k x y z
A是一个矢量,表示函数Ψ(x,y,z) 在空间某点的最大空间变化率, 矢量的方向垂直于函数Ψ(x,y,z)的等值面指向函数值增大的方向
E = -U ( x, y, z )
第 21 页
A B = ( Ax i + Ay j + Az k ) ( Bx i + By j + Bz k ) = Ax Bx + Ay By + Az Bz
第 16 页
矢量叉乘的解析表示:
i i = j j = k k = 0 i j = k, j k = i , k i = j
因此,一个矢量可以表示为三个分矢量之和;也可以由其 大小和三个方向角决定(四个变量?)。可以写为:
A = Ax i + Ay j + Az k = ( Ax , Ay , Az )
矢量加法(减法)的解析表示:
A B = ( Ax i + Ay j + Az k ) ( Bx i + By j + Bz k ) = ( Ax Bx )i + ( Ay By ) j + ( Az Bz )k
2 2
D r = x2 +y2 +z2 - x + y + z
第 29 页
2 1
2 1
2 1
二、速度(Velocity)
平均速度:刻画速度Dt 时间内平均变化率 在Dt 时间内发生位移 则平均速度:
Dr v= Dt
Dr
dr dt
A Dr r(t)
B'' B' B
瞬时速度:刻画t 时刻速度的即时变化率
第一章 质点运动学 Chap.1 Kinematics
本章要点
矢量及其运算 位矢、位移、速度、加速度的定义 曲线运动的自然坐标系描述 运动学的两类问题
第2页
第一节 矢量( Vector )
一、矢量的定义和表示方法
矢量:既有大小又有方向的量,如速度、力、位移等 标量:仅有大小而与空间方向无关的量,由单一的数和单 位描写,如质量、密度等 矢量的表示:
A B = ( Axi + Ay j + Az k) (Bxi + By j + Bz k) = ( Ay Bz - Az By )i + ( Az Bx - Ax Bz ) j + ( Ax By - Ay Bx )k
利用行列式,可表达为:
A B = Ax Ay Az Bx By Bz
矢量场的旋度还是一个矢量。若一个矢量场在空间某个范围内 的旋度为0,我们就说该矢量场为无旋场,若矢量场的旋度不 为0,则称该矢量场是有旋场
斯托克斯定理
L
Adl = A dS
S
第 23 页
第二节 位置矢量
一、参考系 坐标系
参考系(Reference Frame) : 确定一个物体的位置总是相对于某一物体或某一物体系来确定,那 么这—物体或物体系就作为描述物体位置的基准,称为参考系。 坐标系(Coordinates) : 确定了参考系后,为了能够定量地描 述一个物体的运动,必需在选定的参 考系上建立一个合适的坐标系 。常见 的坐标系有直角坐标系、自然坐标系、 球坐标系、柱坐标系、极坐标系等。
高斯定理:
第 22 页
S
AdS = AdV
V
矢量场函数A(x,y,z)的旋度(curl)
i j k Az Ay Ay Ax Ax Az A = i +k + j = z x y x y z z y x Ax Ay Az
A⊥B 则
B
2)如果:
A B = 0
B cos(A, B)
A
3)两个矢量平行、反平行时,标积 最大、最小。
第 11 页
矢量的叉乘(矢积)(Vector Product):
A B = C
A B = C = AB sin( A, B )
两个矢量的矢积是一个矢量,其大小是第 一个矢量的大小与第二个矢量的大小以及 两矢量夹角的正弦值,这三者的乘积,方 向按右手螺旋法则确定。C矢量与A、B矢 量构成的平面永远垂直!它的几何意义是A、 B矢量构成的平行四边形的有向面积。
矢量场函数A(x,y,z)的散度(divergence)
A( x, y, z ) = Ax i + Ay j + Az k
Ax Ay Az A = + + x y z
矢量场的散度是个标量。若一个矢量场在空间某个范围内的 散度为0,我们就说该矢量场为无源场,若矢量场的散度不为 0,则称该矢量场是有源场。
z
r
参考系
o y
x
第 24 页
二、质点
质点系
质点(Particle):将宏观物理抽象为只有质量而不计大小、形状的 点(粒子),是力学中的一个重要的理想模型。 质点系(Particle System):很多质点按一定规律组成的一个质点 系统。通过描述质点系中所有质点的 运动情况,从而了解整个质点系的运 动(求和,积分)。
第9页
矢量的点乘(标积)(Scalar Product):
A B = AB cos q
表示:两个矢量的标积是一个标量,其大 小是第一个矢量的大小乘以第二个矢量在 第一个矢量上的投影。 (q 是这两个矢量 的夹角)。
第 10 页
A B = AB cos q
1)
A B = B A
消去时间 参数(t)
轨道方程( Track Equation ):
第 27 页
第三节 质点的位移、速度、加速度
一、位移(Displacement)
设质点作曲线运动
z
A Dr r(t)
Ds
B
t 时刻位于A点,位矢 r (t )
t+Dt时刻位于B点,位矢 r (t + Dt )
x
r(t+Dt)
一般情况: Dr Ds, v v
当Dt0时: Dr dr , Ds ds, dr = ds, v = v
