北师大版九年级上册数学期末考试试题附标准答案
北师大版九年级上册数学期末考试试卷及答案

北师大版九年级上册数学期末考试试题一、单选题1.下列方程,是一元二次方程的是()A .2 310x x +-=B .2 51y x -=C . 210x +=D .21 1x x +=2.下面几何体的主视图是()A .B .C .D .3.若△ABC ∽△DEF ,且△ABC 与△DEF 的面积比是94,则△ABC 与△DEF 的对应高的比为()A .23B .8116C .94D .324.若正方形的对角线长为2,则这个正方形的面积为()A .2B .4CD .5.如图,点A 为反比例函数k y x=的图象上一点,过A 作AB ⊥x 轴于点B ,连接OA ,已知△ABO 的面积为3,则k 值为()A .-3B .3C .-6D .66.如图,线段AB 两个端点的坐标分别为(2,2)(2.5,0.8)A B 、,以原点O 为位似中心,在第一象限内将线段AB 扩大为原来的2倍后得到线段CD ,则端点C 的坐标为()A .(3,1.6)B .(4,3.2)C .(4,4)D .(6,1.6)7.由于疫情得到缓和,餐饮行业逐渐回暖,某地一家餐厅重新开张,开业第一天收入约为5000元,之后两天的收入按相同的增长率增长,第3天收入约为6050元,若设每天的增长率为x ,则x 满足的方程是()A .5000(1+x )=6050B .5000(1+2x )=6050C .5000(1﹣x )2=6050D .5000(1+x )2=60508.如图,正比例函数11y k x =的图像与反比例函数22k y x =的图象相交于A 、B 两点,其中点A 的横坐标为2,当12y y >时,x 的取值范围是()A .x <-2或x >2B .x <-2或0<x <2C .-2<x <0或0<x <2D .-2<x <0或x >29.如图,正方形ABCD 中,E 为BC 中点,连接AE ,DF AE ⊥于点F ,连接CF ,FG CF ⊥交AD 于点G ,下列结论:①CF CD =;②G 为AD 中点;③~DCF AGF ∆∆;④23AF EF =,其中结论正确的个数有()A .1个B .2个C .3个D .4个10.如图,菱形ABCD的边AB的垂直平分线交AB于点E,交AC于点F,连接DF.当100BAD∠=︒时,则CDF∠=()A.15︒B.30°C.40︒D.50︒二、填空题11.方程x2=x的解为___.12.若关于x的一元二次方程ax2+4x﹣2=0有实数根,则a的取值范围为___.13.一个不透明的盒子里装有除颜色外无其他差别的白珠子6颗和黑珠子若干颗,每次随机摸出一颗珠子,放回摇匀后再摸,通过多次试验发现摸到白珠子的频率稳定在0.3左右,则盒子中黑珠子可能有__颗.14.已知矩形ABCD,当满足条件______时,它成为正方形(填一个你认为正确的条件即可).15.反比例函数kyx=的图象经过点(1,﹣2),则k的值为_____.16.如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点A′处,此时点B落在点B′处.已知折痕EF=13,则AE的长等于_________.17.如图,菱形ABCD中,对角线AC与BD相交于点O,且AC=8,BD=6,则菱形ABCD 的高DH=_____.三、解答题18.解方程:2x2﹣4x﹣1=0.19.如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E.求证:△ABD∽△CBE.20.如图,小明站在路灯B下的A处,向前走5米到D处,发现自己在地面上的影子DC 是2米.若小明的身高DE是1.8米,则路灯B离地面的高度AB是多少米?21.如图,已知矩形ABCD的两条对角线相交于点O,∠ACB=30°,AB=2.(1)求AC的长及∠AOB的度数;(2)以OB,OC为邻边作菱形OBEC,求菱形OBEC的面积.22.有一块长60m,宽50m的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中黑色部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为am)区域将铺设塑胶地面作为运动场地.(1)设通道的宽度为xm,则a=(用含x的代数式表示);(2)若塑胶运动场地总的占地面积为2430m2,则通道的宽度为多少?23.已知,如图,正比例函数y=ax的图象与反比例函数图象交于A点(3,2),(1)试确定上述正比例函数和反比例函数的表达式.(2)根据图象回答:在第一象限内,当反比例函数值大于正比例函数值时x的取值范围?(3)M(m,n)是反比例函数上一动点,其中0大于m小于3,过点M作直线MN平行x 轴,交y轴于点B.过点A作直线AC平行y轴,交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由.24.如图1,在平面直角坐标系中,已知直线l:y=kx+b与x轴交于点A,与y轴交于点B,与直线CD相交于点D,其中AC=14,C(﹣6,0),D(2,8).(1)求直线l的函数解析式;(2)如图2,点P为线段CD延长线上的一点,连接PB,当△PBD的面积为7时,将线段BP 沿着y轴方向平移,使得点P落在直线AB上的P'处,求点P′到直线CD的距离;(3)若点E 为直线CD 上的一点,则在平面直角坐标系中是否存在点F ,使以点A ,D ,E ,F 为顶点的四边形为菱形?若存在,求出所有满足条件的点F 的坐标;若不存在,请说明理由.25.如图,一次函数y=x+b 和反比例函数y=xk (k≠0)交于点A (4,1).(1)求反比例函数和一次函数的解析式;(2)求△AOB 的面积;(3)根据图象直接写出一次函数的值大于反比例函数的值的x 的取值范围.26.如图,在矩形ABCD 的边AB 上取一点E ,连接CE 并延长和DA 的延长线交于点G ,过点E 作CG 的垂线与CD 的延长线交于点H ,与DG 交于点F ,连接GH .(1)当tan 2BEC ∠=且4BC =时,求CH 的长;(2)求证:DF FG HF EF ⋅=⋅;(3)连接DE ,求证:CDE CGH ∠=∠.参考答案1.A 【分析】根据一元二次方程的概念(只含有一个未知数,并且未知数项的最高次数是二次的整式方程叫做一元二次方程),逐一判断.【详解】A.2310x x +-=,符合一元二次方程的定义,故本选项正确;B.251y x -=,方程含有两个未知数,故本选项错误;C.210x +=,未知数项的最高次数是一次,故本选项错误;D.211x x+=,不是整式方程,故本选项错误.故答案选A.【点睛】本题重点考查了满足一元二次方程的条件:(1)该方程为整式方程.(2)该方程有且只含有一个未知数.(3)该方程中未知数的最高次数是2.2.B 【分析】主视图是从物体正面看所得到的的图形.【详解】解:从几何体正面看,从左到右的正方形的个数为:2,1,2.故选:B .【点睛】本题考查了三视图,主视图是从物体的正面看得到的视图,解答时学生易将三种试图混淆而错误地选其它选项.3.D 【分析】根据相似三角形的面积比等于相似比的平方,再结合相似三角形的对应高的比等于相似比解答即可.【详解】解:∵△ABC ∽△DEF ,△ABC 与△DEF 的面积比是94,∴△ABC 与△DEF 的相似比为32,∴△ABC 与△DEF 对应高的比为32,故选:D .【点睛】本题考查的是相似三角形的性质,相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.4.A 【分析】根据正方形的性质,对角线平分、相等、垂直且平分每一组对角求解.【详解】如图所示:∵四边形ABCD 是正方形,∴AO=BO=12AC=1cm ,∠AOB=90°,由勾股定理得,2,S 正=2)2=2cm2.故选A .【点睛】考查正方形的性质,解题关键是根据对角线平分、相等、垂直且平分每一组对角进行分析.5.C 【分析】先设出A 点的坐标,由△AOB 的面积可求出xy 的值,即xy =﹣6,即可写出反比例函数的解析式.【详解】解:设A 点坐标为A (x ,y ),由图可知A 点在第二象限,∴x <0,y >0.又∵AB ⊥x 轴,∴|AB|=y ,|OB|=|x|,∴S △AOB 12=⨯|AB|×|OB|12=⨯y×|x|=3,∴﹣xy =6,∴k =﹣6.故选:C .【点睛】本题考查了反比例函数系数k 的几何意义,解题的关键是掌握过双曲线上的任意一点分别向两条坐标轴作垂线,与坐标轴围成的矩形面积就等于|k|,本知识点是中考的重要考点,同学们应高度关注.6.C 【分析】根据位似中心的定义可得:2:1OC OA =,由此即可得出答案.【详解】解:由题意得::2:1OC OA =,则端点C 的坐标为(22,22)C ⨯⨯,即为(4,4)C ,故选:C .【点睛】本题考查了位似图形的性质,理解定义是解题关键.7.D 【分析】根据开业第一天收入约为5000元,之后两天的收入按相同的增长率增长,第3天收入约为6050元列方程即可得到结论.【详解】解:设每天的增长率为x ,依题意,得:5000(1+x )2=6050.故选:D .【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.8.D 【分析】先根据反比例函数与正比例函数的性质求出B 点坐标,再由函数图象即可得出结论.【详解】解:∵反比例函数与正比例函数的图象均关于原点对称,∴A 、B 两点关于原点对称,∵点A 的横坐标为2,∴点B 的横坐标为-2,∵由函数图象可知,当-2<x <0或x >2时函数y 1=k 1x 的图象在22k y x=的上方,∴当y 1>y 2时,x 的取值范围是-2<x <0或x >2.故选:D .9.D 【分析】如图(见解析),过点C 作CM DF ⊥于点M ,先根据三角形全等的判定定理证出ADF DCM ≅ ,根据全等三角形的性质可得AF DM =,再利用正切三角函数可得1tan 1tan 42BE AB ∠=∠==,从而可得AF FM DM ==,然后根据线段垂直平分线的判定与性质即可判断①;先根据等腰三角形的性质可得25∠=∠,从而可得17∠=∠,再根据等腰三角形的判定可得DG FG =,然后根据角的和差可得36∠=∠,最后根据等腰三角形的判定可得AG FG =,由此即可判断②;先根据上面过程可知3256=∠∠∠=∠=,再根据相似三角形的判定即可判断③;设(0)AF x x =>,从而可得2DF x =,先利用勾股定理可得5,2AD AB BC AE x ====,再根据线段的和差可得32EF x =,由此即可判断④.【详解】解:如图,过点C 作CM DF ⊥于点M ,四边形ABCD 是正方形,,90AB BC CD AD B BAD ADC ∴===∠=∠=∠=︒,2190∴∠+∠=︒,DF AE ⊥ ,90,1390AFD DMC ∴∠=∠=︒∠+∠=︒,32∴∠=∠,在ADF 和DCM △中,9032AFD DMC AD DC∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,()ADF DCM AAS ∴≅ ,AF DM ∴=,点E 是BC 的中点,1122BE BC AB ∴==,349031∠+∠=︒=∠+∠ ,41∴∠=∠,1tan 1tan 42BE AB ∴∠=∠==,12AFDF ∴=,即2DF AF =,DF DM FM AF FM =+=+ ,2AF AF FM ∴=+,即AF FM =,DM FM ∴=,又CM DF ⊥ ,CF CD ∴=,结论①正确;25∴∠=∠,FG CF ⊥ ,90CFG ADC ∴∠=︒=∠,17∴∠=∠,DG FG ∴=,又139076∠+∠=︒=∠+∠ ,36∴∠=∠,AG FG ∴=,AG DG ∴=,即G 为AD 中点,结论②正确;由上已得:32536,2,∠=∠∠∠∠=∠=,56∴∠=∠,在DCF 和AGF 中,2356∠=∠⎧⎨∠=∠⎩,DCF AGF ∴ ,结论③正确;设(0)AF x x =>,则2DF x =,BC AB AD ∴====,122BE BC ∴==,52AE x ∴==,32EF AE AF x ∴=-=,3223AF x EF x ∴==,结论④正确;综上,结论正确的个数有4个,故选:D .10.B 【分析】连接BF ,根据菱形的对角线平分一组对角线可得∠BAC=50°,根据线段垂直平分线上的点到两端点的距离相等可得AF=BF ,根据等边对等角可得∠FBA=∠FAB ,再根据菱形的邻角互补求出∠ABC ,然后求出∠CBF ,最后根据菱形的对称性可得∠CDF=∠CBF .【详解】解:如图,连接BF ,在菱形ABCD 中,∠BAC=12∠BAD=12×100°=50°,∵EF 是AB 的垂直平分线,∴AF=BF ,∴∠FBA=∠FAB=50°,∵菱形ABCD 的对边AD ∥BC ,∴∠ABC=180°-∠BAD=180°-100°=80°,∴∠CBF=∠ABC-∠ABF=80°-50°=30°,由菱形的对称性,∠CDF=∠CBF=30°.故选:B .11.0x =或1x =【分析】利用因式分解法解方程即可;【详解】2x x =,20x x -=,()10x x -=,0x =或1x =;故答案是:0x =或1x =.12.2a ≥-且0a ≠##a≠0且a≥-2【分析】根据题意可知0∆≥,代入求解即可.【详解】解:一元二次方程ax 2+4x ﹣2=0,,4,2a a b c ===-,∵关于x 的一元二次方程ax 2+4x ﹣2=0有实数根,∴0∆≥且0a ≠,即244(2)0a -⨯-≥,0a ≠解得:2a ≥-且0a ≠故答案为:2a ≥-且0a ≠.13.14【分析】在同样条件下,大量反复试验时,随机事件发生的频率逐渐稳定在概率附近,可以从比例关系入手,列出方程求解.【详解】解:由题意可得,60.36n=+,解得n=14.经检验n=14是原方程的解故估计盒子中黑珠子大约有14个.故答案为:14.14.AB=BC【详解】解:∵四边形ABCD是矩形,∴(1)当AB=BC时,矩形ABCD是正方形;(2)当AC⊥BD时,矩形ABCD是正方形.故答案为:AB=CD(或AC⊥BD).15.﹣2.【分析】将点(1,﹣2)代入kyx=,即可求解.【详解】∵反比例函数kyx=的图象经过点(1,﹣2),∴k21-=,解得k=﹣2.故答案为-2.16.16924【分析】过点F作FG⊥AD,垂足为G,连接AA′,在△GEF中,由勾股定理可求得EG=5,轴对称的性质可知AA′⊥EF,由同角的余角相等可证明∠EAH=∠GFE,从而可证明△ADA′≌△FGE,故此可知GE=DA′=5,最后在△EDA′利用勾股定理列方程求解即可.【详解】解:过点F作FG⊥AD,垂足为G,连接AA′.在Rt△EFG中,5=,∵轴对称的性质可知AA′⊥EF,∴∠EAH+∠AEH=90∘,∵FG⊥AD,∴∠GEF+∠EFG=90∘,∴∠DAA′=∠GFE,在△GEF 和△DA′A 中,90EGF D FG AD DAA GFE ∠=∠=︒⎧⎪=⎨⎪∠'=∠⎩,∴△GEF ≌△DA′A ,∴DA′=EG=5,设AE=x,由翻折的性质可知EA′=x ,则DE=12−x ,在Rt △EDA′中,由勾股定理得:A′E 2=DE 2+A′D 2,即x 2=(12−x)2+52,解得:x=16924,故答案为16924,【点睛】本题主要考查正方形、轴对称、全等三角形的性质及勾股定理等相关知识.利用辅助线构全等形、利用勾股定理建立方程是解题的关键.17.4.8【分析】根据菱形的性质得到AC ⊥BD ,求出OA ,OB ,由勾股定理求出AB ,再利用菱形的面积公式得到12AC•BD=AB•DH ,由此求出答案.【详解】解:在菱形ABCD 中,AC ⊥BD ,∵AC=8,BD=6,∴OA=12AC=12×8=4,OB=12BD=12×6=3,在Rt △AOB 中,==5,∵DH ⊥AB ,∴菱形ABCD 的面积=12AC•BD=AB•DH ,即12×6×8=5DH ,解得DH=4.8.故答案为:4.8.【点睛】此题考查了菱形的性质,勾股定理,熟记菱形的性质并熟练应用解决问题是解题的关键.18.【分析】用配方法解一元二次方程即可.【详解】解:∵2x2﹣4x ﹣1=0,∴2x2﹣4x=1,则x2﹣2x=12,∴x2﹣2x+1=32,即(x ﹣1)2=32,则x ﹣,∴.【点睛】此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确使用,把左边配成完全平方式,右边化为常数.19.证明见解析.【分析】根据等腰三角形三线合一的性质可得AD ⊥BC ,然后求出∠ADB=∠CEB=90°,再根据两组角对应相等的两个三角形相似证明.【详解】∵在△ABC 中,AB=AC ,BD=CD ,∴AD ⊥BC .又∵CE ⊥AB ,∴∠ADB=∠CEB=90°,又∵∠B=∠B ,∴△ABD ∽△CBE .【点睛】本题考查了相似三角形的判定,正确找到相似的条件是解题的关键.20.路灯B 离地面的高度 6.3AB =米【分析】根据ED ∥AB ,得出△ECD ∽△BCA ,进而得出比例式求出即可.【详解】解:由题图知,2DC =米, 1.8=ED 米,5AD =米,∴527=+=+=AC AD DC (米).∵ED AB ∥,∴ECD BCA ∽△△.∴ED DC AB AC =,即1.827AB =.∴路灯B 离地面的高度 1.87 6.32AB ⨯==(米).【点睛】此题主要考查了相似三角形的应用,得出△ECD ∽△EBA 是解决问题的关键.21.(1)4AC =,60AOB ∠=︒;(2)菱形OBEC 的面积是【分析】(1)根据AB 的长结合“在直角三角形中,30°所对的直角边等于斜边的一半”可得出AC 的长度,根据矩形的对角线互相平分可得出OBC 为等腰三角形,从而利用外角的知识可得出∠AOB 的度数;(2)先求出△OBC 和的面积,从而可求出菱形OBEC 的面积.(1)解:在矩形ABCD 中,90ABC ∠=︒,在Rt ABC 中,30ACB ∠=︒.∴24AC AB ==.∴2AO OB ==.又∵2AB =,∴AOB 是等边三角形.∴60AOB ∠=︒.(2)解:在Rt ABC 中,由勾股定理,得BC ==.∴122ABC S =⨯⨯= .∴12BOC ABC S S ==△△.∴菱形OBEC 的面积是【点睛】本题考查矩形的性质、菱形的性质及勾股定理的知识,熟练掌握矩形的性质、菱形的性质及勾股定理是解题的关键.22.(1)6032x-(2)通道的宽度为2m .【分析】(1)结合图形可得:荒地的长为60m ,内部两个矩形的宽为am ,通道宽为xm ,可得方程等式,化简即可得;(2)结合图形,利用大面积减去黑色部分的面积可得方向,求解即可得.(1)解:结合图形可得:荒地的长为60m ,内部两个矩形的宽为am ,通道宽为xm ,∴2360a x +=,6032x a -=,故答案为:6032x -;(2)解:根据题意得:(502)(603)2430---⋅=x x x a ,∵6032x a -=,∴603(502)(603)24302x x x x ----⋅=,解得122,38x x ==(不合题意,舍去).∴通道的宽度为2m .【点睛】题目主要考查列代数式及一元二次方程的应用,理解题意,找准面积之间的关系是解题关键.23.(1)6y x =,23y x =;(2)03x <<;(3)理由见解析【分析】(1)把A 点坐标分别代入两函数解析式可求得a 和k 的值,可求得两函数的解析式;(2)由反比例函数的图象在正比例函数图象的下方可求得对应的x 的取值范围;(3)用M 点的坐标可表示矩形OCDB 的面积和△OBM 的面积,从而可表示出四边形OADM 的面积,可得到方程,可求得M 点的坐标,从而可证明结论.【详解】解:(1)∵将()3,2A 分别代入k y x =,y ax =中,得23k =,32a =,∴6k =,23a =,∴反比例函数的表达式为:6y x =,正比例函数的表达式为23y x =.(2)∵()3,2A 观察图象,得在第一象限内,当03x <<时,反比例函数的值大于正比例函数的值;(3)BM DM=理由:∵//MN x 轴,//AC y 轴,∴四边形OCDB 是平行四边形,∵x 轴y ⊥轴,∴OCDB 是矩形.∵M 和A 都在双曲线6y x=上,∴6BM OB ⨯=,6OC AC ⨯=,∴132OMB OAC S S k ==⨯= ,又∵6OADM S =四边形,∴33612OMB OAC OBDC OADM S S S S =++=++= 矩形四边形,即12OC OB ⋅=,∵3OC =,∴4OB =,即4n =∴632m n ==,∴32MB =,33322MD =-=,∴MB MD =.【点睛】本题为反比例函数的综合应用,涉及知识点有待定系数法、函数与不等式、矩形及三角形的面积和数形结合思想等.在(2)中注意数形结合的应用,在(3)中用M 的坐标表示出四边形OADM 的面积是解题的关键.24.(1)直线l 的函数解析式为43233y x =-+(2)点P '到直线CD 的距离为2(3)存在点1(8F +或2(8F --或3(6,14)F -或4(33,25)F ,使以点A ,D ,E ,F 为顶点的四边形为菱形.【分析】(1)用待定系数法即可求解;(2)由△PBD 的面积求出点P 的坐标,进而求出点P'(5,4),构建△P'DN 用解直角三角形的方法即可求解;(3)分AD 是菱形的边、AD 是菱形的对角线两种情况,利用图像平移和中点公式,分别求解即可.(1)解:∵14,(6,0)=-AC C ,点A 在点C 右侧,∴(8,0)A .∵直线l 与直线CD 相交于点(2,8)D ,∴80,28,k b k b +=⎧⎨+=⎩解得4,332.3k b ⎧=-⎪⎪⎨⎪=⎪⎩∴直线l 的函数解析式为43233y x =-+.(2)解:如图1,过点P 作PN y ⊥轴于点N ,作'∥PP y 轴,交AB 于点P ',过点P '作'⊥P M CD 于点M ,过点D 作DE y ⊥轴于点E ,设CD 与y 轴交于点F,0设直线CD 的解析式为y mx n =+,∵(6,0),(2,8)-C D ,∴60,28,m n m n -+=⎧⎨+=⎩解得 1.6.m n =⎧⎨=⎩∴直线CD 的解析式为6y x =+.(0,6)F ∴∴6OC OF ==.∴OCF OFC∠=∠∵OC OF ⊥,∴45OCF OFC ∠=∠=︒∵直线l 的解析式为43233y x =-+,∴320,3B ⎛⎫⎪⎝⎭.∴323OB =.∴3214633=-=-=BF OB OF .设(,6)+P a a ,∵7=-= PBD PBF DBF S S S ,∴11722⋅-⋅=BF PN BF DE ,即114(2)723⨯-=a ,解得5a =.∴(5,11)P .∵将线段BP 沿着y 轴方向平移,使得点P 落在直线AB 上的P '处,∴4325433-⨯+=.∴(5,4)'P .∴1147='-=PP .∵45PCA OCF ∠=∠=︒,PP AC '⊥∴45'︒∠=MPP .∵'⊥P M CD ,∴45PP M P PM ''∠=∠=︒∴PMP ' 是等腰直角三角形.∴==''P M ,即点P '到直线CD 的距离为2.(3)解:①如图2,当AD 、AF 为边时,∵(8,0),(2,8)A D ,∴10==AD .∵四边形ADEF 是菱形,∴,10==∥DE AF AD AF .∵直线CD 的解析式为6y x =+,∴可设直线AF 的解析式为y x b =+.∵(8,0)A ,∴80b +=,解得8b =-.∴直线AF 的解析式为8y x =-.设(,8)-F c c ,∴10===AF AD ,解得8=±c∴12(8(8+--F F .当AD 、AE 为边时,∵(8,0),(2,8)A D ,∴10==AD .∵四边形ADFE 是菱形,∴,10∥DF AE AD AE ==.∵直线CD 的解析式为6y x =+,∴可设直线AF 的解析式为y x b =-+.∵(8,0)A ,∴-80b +=,解得8b =.∴直线AF 的解析式为8y x =-+.设(,8)F d d -+,∴10DF AD ===,解得6d =-或8d =(舍去),∴3(6,14),F -.②如图3,当AD 为对角线时,则,=∥DF AF AF DE .由①得直线AF 的解析式为8y x =-.设(,8)-F t t ,∵(2,8),(8,0)D A ,2222(2)(88)(8)(8)t t t t -+--=-+-解得33t =.∴4(33,25)F .综上所述,存在点1(852,52)F +或2(852,52)F --或3(6,14)F -或4(33,25)F 使以点A ,D ,E ,F 为顶点的四边形为菱形.【点睛】本题考查的是二次函数综合运用,涉及到二次函数的性质、平行四边形的性质、图形的平移、面积的计算等,分类求解解题的关键.25.(1)反比例函数的解析式为:y=4x ;一次函数的解析式为:y=x ﹣3;(2)S △AOB =152;(3)一次函数的值大于反比例函数的值的x 的取值范围为:﹣1<x <0或x >4.【分析】(1)把A 的坐标代入y=k x ,求出反比例函数的解析式,把A 的坐标代入y=x+b 求出一次函数的解析式;(2)求出D 、B 的坐标,利用S △AOB =S △AOD +S △BOD 计算,即可求出答案;(3)根据函数的图象和A 、B 的坐标即可得出答案.【详解】(1)∵反比例函数y=k x的图象过点A (4,1),∴1=k 4,即k=4,∴反比例函数的解析式为:y=4x.∵一次函数y=x+b (k≠0)的图象过点A (4,1),∴1=4+b ,解得b=﹣3,∴一次函数的解析式为:y=x ﹣3;(2)∵令x=0,则y=﹣3,∴D (0,﹣3),即DO=3.解方程4x=x ﹣3,得x=﹣1,∴B (﹣1,﹣4),∴S △AOB =S △AOD +S △BOD =12×3×4+12×3×1=152;(3)∵A (4,1),B (﹣1,﹣4),∴一次函数的值大于反比例函数的值的x 的取值范围为:﹣1<x <0或x >4.【点睛】本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了观察函数图象的能力.26.(1)10CH =;(2)见解析;(3)见解析【分析】(1)根据已知条件先求出CE 的长,再证明∠=∠BEC ECH ,在Rt △CHE 中解三角形可求得EH 的长,最后利用勾股定理求CH 的长;(2)证明∽∆∆GFE HFD ,进而得出结果;(3)由(2)∽∆∆GFE HFD 得∠=∠EGF FHD ,进而sin sin ∠=∠EGF FHD ,即=CD CE CG CH ,再结合∠=∠ECD DCE ,可得出∽∆∆CDE CGH ,进一步得出结果.【详解】(1)解:∵矩形ABCD ,EH CG ⊥,∴90∠=︒=∠=∠BCD CEH B .而90BEC BCE ∠+∠=︒,90∠+∠=︒BCE ECH ,∴∠=∠BEC ECH ,又∵4BC =,tan 2BEC ∠=,∴2BE =,易得CE ==∴tan 2∠==EH ECH CE ,∴EH =∴10CH ==.(2)证明:∵矩形ABCD ,EH CG ⊥,∴∠=∠CEH HDG ,而∠=∠GFE DFH ,∴∽∆∆GFE HFD ,∴=DF FH EF FG,∴⋅=⋅DF FG EF FH ;(3)证明:由(2)∽∆∆GFE HFD 得∠=∠EGF FHD ,∴sin sin ∠=∠EGF FHD ,即=CD CE CG CH,而∠=∠ECD DCE ,∴∽∆∆CDE CGH ,∴CDE CGH ∠=∠.【点睛】本题主要考查相似三角形的判定与性质以及解直角三角形,关键是掌握基本的概念与性质.。
北师大版九年级上册数学期末考试试卷含答案解析

北师大版九年级上册数学期末考试试题一、选择题。
(每小题只有一个正确答案)1.在一个四边形ABCD 中,依次连结各边中点的四边形是菱形,则对角线AC 与BD 需要满足条件()A .垂直B .相等C .垂直且相等D .不再需要条件2.如图,在矩形ABCD 中,AB=3,BC=4,将其折叠,使AB 边落在对角线AC 上,得到折痕AE ,则点E 到点B 的距离为()A .32B .2C .52D .33.下列方程中,是关于x 的一元二次方程的是A .()()12132+=+x x B .02112=-+x x C .02=++c bx ax D .1222-=+x x x 4.已知点()12,A y -、B (-1,y 2)、C (3,y 3)都在反比例函数4y x=的图象上,则y 1、y 2、y 3的大小关系是()A .y 1<y 2<y 3B .y 3<y 2<y 1C .y 3<y 1<y 2D .y 2<y 1<y 35.学生冬季运动装原来每套的售价是100元,后经连续两次降价,现在的售价是81元,则平均每次降价的百分数是A .9%B ..5%C .9.5%D .10%6.二次三项式243x x -+配方的结果是()A .2(2)7x -+B .2(2)1x --C .2(2)7x ++D .2(2)1x +-7.函数x ky =的图象经过(1,-1),则函数2-=kx y 的图象是2222-2-2-2-2O OOOy y y y xxxxA .B .C .D.8.如图,矩形ABCD ,R 是CD 的中点,点M 在BC 边上运动,E 、F 分别是AM 、MR 的中点,则EF 的长随着M 点的运动A .变短B .变长C .不变D.无法确定9.如图,点A 在双曲线=6上,且OA =4,过A 作AC ⊥轴,垂足为C ,OA 的垂直平分线交OC 于B ,则△ABC 的周长为()A .47B .5C .27D .2210.如图,在△ABC 中,点D 、E 分别在AB 、AC 上,DE ∥BC .若AD=4,DB=2,则的值为.二、填空题11.反比例函数2k y x+=的图象在一、三象限,则k 应满足_________.12.把一个三角形改做成和它相似的三角形,如果面积缩小到原来的12倍,边长应缩小到原来的____倍.13.已知一元二次方程22(1)7340a x ax a a -+++-=有一个根为0,则a 的值为_______.14.已知534a b c ==,则232a b c a b c++=++_______15.如图,已知点A 在反比例函数(0)ky x x=<的图象上,AC y ⊥轴于点C ,点B 在x 轴的负半轴上,若2ABC S = ,则k 的值为_________.16.如图,在Rt △ABC 中,∠ACB=90°,CD ⊥AB 于D ,若AD=1,BD=4,则CD=_____.17.若关于x 的一元二次方程()21210k x x -+-=有两个不相等的实数根,则k 的取值范围是______.三、解答题18.解方程(1);(2).19.(8分)已知,如图,AB 和DE 是直立在地面上的两根立柱.AB=5m ,某一时刻AB 在阳光下的投影BC=3m .B(1)请你在图中画出此时DE 在阳光下的投影;(2)在测量AB 的投影时,同时测量出DE 在阳光下的投影长为6m ,请你计算DE 的长.20.(10分)如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.(1)BD与CD有什么数量关系,并说明理由;(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.21.已知甲同学手中藏有三张分别标有数字11,,124的卡片,乙同学手中藏有三张分别标有数字1,3,2的卡片,卡片外形相同.现从甲乙两人手中各任取一张卡片,并将它们的数字分别记为,a b.(1)请你用树形图或列表法列出所有可能的结果.(2)现制定这样一个游戏规则:若所选出的能使得有两个不相等的实数根,则甲获胜;否则乙获胜.请问这样的游戏规则公平吗?请你用概率知识解释22.如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE,已知∠BAC=30°,EF⊥AB,垂足为F,连接DF(1)试说明AC=EF;(2)求证:四边形ADFE是平行四边形.23.某商场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出500张,每张盈利0.3元.为了尽快减少库存,商场决定采取适当的降价措施,调查发现,如果这种贺年卡的售价每降低0.1元,那么商场平均每天可多售出100张,商场要想平均每天盈利120元,每张贺年卡应降价多少元?24.如图,已知A (−4,n ),B (2,−4)是一次函数y =kx +b 的图象和反比例函数my x=的图象的两个交点;(1)求反比例函数和一次函数的解析式;(2)求直线AB 与x 轴的交点C 的坐标及△AOB 的面积;(3)求不等式kx +b −mx<0的解集(请直接写出答案).25.在平面直角坐标系中,直线l 1:y =x +5与反比例函数y =kx(k ≠0,x >0)图象交于点A(1,n );另一条直线l 2:y =﹣2x +b 与x 轴交于点E ,与y 轴交于点B ,与反比例函数y =k x(k ≠0,x >0)图象交于点C 和点D (12,m ),连接OC 、OD .(1)求反比例函数解析式和点C 的坐标;(2)求△OCD 的面积.26.(12分)如图,在ABC △中,5AB =,3BC =,4AC =,动点E (与点A C ,不重合)在AC 边上,EF AB ∥交BC 于F 点.CE FA B(1)当ECF△的面积与四边形EABF的面积相等时,求CE的长;(2)当ECF△的周长与四边形EABF的周长相等时,求CE的长;(3)试问在AB上是否存在点P,使得EFP△为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出EF的长.参考答案1.B【解析】试题分析:如图:∵四边形EFGH是菱形,∴EH=FG=EF=HG=12BD=12AC,故AC=BD.故选B.考点:中点四边形.2.A【解析】试题分析:由于AE是折痕,可得到AB=AF,BE=EF,设出未知数,在Rt△EFC中利用勾股定理列出方程,通过解方程即可得到答案.设BE=x,∵AE为折痕,∴AB=AF,BE=EF=x,∠AFE=∠B=90°,Rt△ABC中,,∴Rt△EFC中,FC=5-3=2,EC=4-X,∴,解得,故选A.考点:本题考查的是图形折叠的性质及勾股定理点评:熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等的知识是解答此题的关键.3.A【解析】试题分析:A、由原方程得到3x2+4x+1=0,符合一元二次方程的定义,故本选项正确;B、该方程中分母中含有未知数.不属于整式方程,故本选项错误;C、当a=0时.该方程不是一元二次方程.故本选项错误;D、由原方程得到2x+1=0,即未知数的最高次数是1.故本选项错误;故选A.考点:一元二次方程定义4.D【分析】分别把各点坐标代入反比例函数y=4x,求出y1,y2,y3的值,再比较大小即可.【详解】∵点A(-2,y1)、B(-1,y2)、C(3,y3)都在反比例函数y=4x的图象上,∴y1=-2,y2=-4,y3=4 3,∵-4<-2<4 3,∴y2<y1<y3.故选D.【点睛】本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.5.D【解析】试题分析:设平均每次降价的百分数是x,依题意得100(1-x)2=81,解方程得x1=0.1,x2=1.9(舍去)所以平均每次降价的百分数是10%.故选D.考点:一元二次方程的应用6.B【解析】试题分析:在本题中,若所给的式子要配成完全平方式,常数项应该是一次项系数-4的一半的平方;可将常数项3拆分为4和-1,然后再按完全平方公式进行计算.解:x2-4x+3=x2-4x+4-1=(x-2)2-1.故选B.考点:配方法的应用.7.A【解析】试题分析:∵函数xky=的图象经过(1,-1),∴k=-1,∴函数2-=kxy的解析式为:y=-x-2,函数y=-x-2的图像过二、四象限过(0,-2),(-2,0)点,故选A考点:1.反比例函数图像2.一次函数8.C【解析】试题分析:∵E,F分别是AM,MR的中点,∴EF=12AR.∵R是定点,∴AR的定长.∴无论M运动到哪个位置EF的长不变.故选C.考点:1.动点问题;2.三角形中位线定理.9.C【解析】试题分析:∵OA的垂直平分线交OC于B,∴AB=OB,∴△ABC的周长=OC+AC,设OC=a,AC=b,则:ab=6,a2+b2=16,解得a+b=27,即△ABC的周长=OC+AC=27.故选C考点:反比例函数图象上点的坐标特征10.2 3【解析】试题分析::∵DE∥BC,∴△ADE∽△ABC,∴AD:AB=DE:BC,∵AD=4,DB=2,∴AD:AB=DE:BC=2:3.则的值为2 3.考点:相似三角形的判定与性质.11.k>-2【解析】试题分析:反比例函数:当时,图象在第一、三象限;当时,图象在第二、四象限.由题意得,考点:本题主要考查了反比例函数的性质点评:本题属于基础应用题,只需学生熟练掌握反比例函数的性质,即可完成.12.2【解析】试题分析::∵改做的三角形与原三角形相似,且面积缩小到原来的倍,∴边长应缩小到原来的2倍.考点:相似三角形的性质13.-4【解析】【分析】将x=0代入原方程可得关于a的方程,解之可求得a的值,结合一元二次方程的定义即可确定出a的值.【详解】把x=0代入一元二次方程(a-1)x2+7ax+a2+3a-4=0,可得a2+3a-4=0,解得a=-4或a=1,∵二次项系数a-1≠0,∴a≠1,∴a=-4,故答案为-4.【点睛】本题考查了一元二次方程的一般式以及一元二次方程的解,熟知一元二次方程二次项系数不为0是解本题的关键.14.15 26【解析】试题分析:设=k ,则a=5k ,b=3k ,c=4k ,25641532153826a b c k k k a b c k k k ++++==++++考点:比例的性质15.-4【分析】连结OA ,由AC ⊥y 轴,可得AC ∥x 轴,可知S △ACB =S △ACO =2,可得=4k ,由反比例函数图像在第二象限(x<0),可知k<0,可求k=-4.【详解】解:连结OA ,∵AC ⊥y 轴,∴AC ∥x 轴,∴S △ACB =S △ACO =2,∴1=22k ,∴=4k ,∵反比例函数图像在第二象限(x<0),∴k<0,∴k=-4.故答案为:-4.【点睛】本题考查反比例函数解析式,掌握反比例函数的性质,关键是反比例函数中k 的几何意义.16.2.【分析】首先证△ACD ∽△CBD ,然后根据相似三角形的对应边成比例求出CD 的长.【详解】解:Rt △ACB 中,∠ACB=90°,CD ⊥AB ;∴∠ACD=∠B=90°﹣∠A ;又∵∠ADC=∠CDB=90°,∴△ACD ∽△CBD ;∴CD 2=AD•BD=4,即CD=2.故答案为:2【点睛】本题考查相似三角形的判定与性质.17.0k >且1k ≠【分析】根据题意,结合一元二次方程的定义和根的判别式可得关于k 的不等式,然后解不等式即可求解.【详解】解:∵关于x 的一元二次方程()21210k x x -+-=有两个不相等的实数根,∴21024(1)(1)0k k -≠⎧⎨∆=--⨯->⎩,10k k ≠⎧⎨>⎩,∴k 的取值范围是0k >且1k ≠,故答案为:0k >且1k ≠.【点睛】本题考查了一元二次方程的定义、根的判别式、解一元一次不等式,熟练掌握一元二次方程的根的判别式与根的关系是解答的关键.18.(1)1x =2x =.(2)【详解】试题分析:(1)用公式法(2)用分解因式法试题解析:(1)因为(()245248∆=--⨯-⨯=,所以x =即1x =2x =.(2)移项得,分解因式得,解得考点:解一元二次方程19.(1)见解析;(2)DE=10m【解析】试题分析:(1)根据投影的定义,作出投影即可;(2)根据在同一时刻,不同物体的物高和影长成比例;构造比例关系AB BC DE EF =.计算可得DE试题解析:(1)如图:连接AC ,过点D 作DE//AC ,交直线BC 于点F ,线段EF 即为DE 的投影(2)∵AC//DF ,∴∠ACB=∠DFE.∵∠ABC=∠DEF=90°∴△ABC ∽△DEF.53,.6AB BC DE EF DE ∴=∴= ∴DE=10(m )考点:平行投影20.(1)BD=CD .(2)当△ABC 满足:AB=AC 时,四边形AFBD 是矩形.【解析】试题分析:(1)根据两直线平行,内错角相等求出∠AFE=∠DCE ,然后利用“角角边”证明△AEF 和△DEC 全等,根据全等三角形对应边相等可得AF=CD ,再利用等量代换即可得证;(2)先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD 是平行四边形,再根据一个角是直角的平行四边形是矩形,可知∠ADB=90°,由等腰三角形三线合一的性质可知必须是AB=AC.试题解析:(1)BD=CD.理由如下:∵AF∥BC,∴∠AFE=∠DCE,∵E是AD的中点,∴AE=DE,在△AEF和△DEC中,,∴△AEF≌△DEC(AAS),∴AF=CD,∵AF=BD,∴BD=CD;(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.理由如下:∵AF∥BD,AF=BD,∴四边形AFBD是平行四边形,∵AB=AC,BD=CD,∴∠ADB=90°,∴▱AFBD是矩形.考点:1.矩形的判定2.全等三角形的判定与性质.21.(1)列表见解析;(2)不公平,理由见解析.【分析】(1)首先根据题意画出树状图,然后根据树状图即可求得所有等可能的结果;(2)利用一元二次方程根的判别式,即可判定各种情况下根的情况,然后利用概率公式求解即可求得甲、乙获胜的概率,比较概率大小,即可确定这样的游戏规是否公平.【详解】(1)列表如下:a b12312(12,1)(12,2)(12,3)14(14,1)(14,2)(14,3)1(1,1)(1,2)(1,3)(2)要使方程210ax bx ++=有两个不相等的实根,即△=240b a ->,满足条件的有5种可能:1111,2,,2,,3,,3,(1,3)2424⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭∴甲获胜的概率为()59P =甲,乙获胜的概率为()49P =乙,5499> 即此游戏不公平.22.证明见解析.【分析】(1)一方面Rt △ABC 中,由∠BAC=30°可以得到AB=2BC ,另一方面△ABE 是等边三角形,EF ⊥AB ,由此得到AE=2AF ,并且AB=2AF ,从而可证明△AFE ≌△BCA ,再根据全等三角形的性质即可证明AC=EF .(2)根据(1)知道EF=AC ,而△ACD 是等边三角形,所以EF=AC=AD ,并且AD ⊥AB ,而EF ⊥AB ,由此得到EF ∥AD ,再根据平行四边形的判定定理即可证明四边形ADFE 是平行四边形.【详解】证明:(1)∵Rt △ABC 中,∠BAC=30°,∴AB=2BC .又∵△ABE 是等边三角形,EF ⊥AB ,∴AB=2AF .∴AF=BC .∵在Rt △AFE 和Rt △BCA 中,AF=BC ,AE=BA ,∴△AFE ≌△BCA (HL ).∴AC=EF .(2)∵△ACD 是等边三角形,∴∠DAC=60°,AC=AD .∴∠DAB=∠DAC+∠BAC=90°.∴EF ∥AD .∵AC=EF ,AC=AD ,∴EF=AD .∴四边形ADFE 是平行四边形.考点:1.全等三角形的判定与性质;2.等边三角形的性质;3.平行四边形的判定.23.每张贺年卡应降价0.1元.【分析】设每张贺年卡应降价x 元,等量关系为:(原来每张贺年卡盈利-降价的价格)×(原来售出的张数+增加的张数)=120,把相关数值代入求得正数解即可.【详解】设每张贺年卡应降价x 元,根据题意得:(0.3-x )(500+1000.1x )=120,整理,得:21002030x x +-=,解得:120.1,0.3x x ==-(不合题意,舍去),∴0.1x =,答:每张贺年卡应降价0.1元.24.(1)8y x=-,2y x =--;(2)C 点坐标为(2,0)-,6;(3)40x -<<或2x >.【分析】(1)先把B 点坐标代入代入m y x =求出m 得到反比例函数解析式,再利用反比例函数解析式确定A 点坐标,然后利用待定系数法求一次函数解析式;(2)根据x 轴上点的坐标特征确定C 点坐标,然后根据三角形面积公式和AOB 的面积AOC BOC S S ∆∆=+进行计算;(3)观察函数图象得到当4x <-或02x <<时,一次函数图象都在反比例函数图象下方.【详解】解:(1)把(2,4)-B 代入m y x=得2(4)8m =⨯-=-,所以反比例函数解析式为8y x =-,把(4,)A n -代入8y x=-得48n -=-,解得2n =,则A 点坐标为(4,2)-,把(4,2)A -,(2,4)-B 分别代入y kx b =+得4224k b k b -+=⎧⎨+=-⎩,解得12k b =-⎧⎨=-⎩,所以一次函数的解析式为2y x =--;(2)当0y =时,20x --=,解得2x =-,则C 点坐标为(2,0)-,∴AOC BOCAOB S S S ∆∆∆=+11222422=⨯⨯+⨯⨯6=;(3)由kx +b −m x <0可得kx +b <m x故该不等式的解为40x -<<或2x >.【点睛】本题考查了反比例函数与一次函数综合.(1)中理解函数图象上的点都满足函数关系式是解题关键;(2)中掌握“割补法”求图形面积是解题关键;(3)中掌握数形结合思想是解题关键.25.(1)y =6x ,点C (6,1);(2)1434.【分析】(1)点A (1,n )在直线l 1:y =x +5的图象上,可求点A 的坐标,进而求出反比例函数关系式,点D 在反比例函数的图象上,求出点D 的坐标,从而确定直线l 2:y =﹣2x +b 的关系式,联立求出直线l 2与反比例函数的图象的交点坐标,确定点C 的坐标,(2)求出直线l 2与x 轴、y 轴的交点B 、E 的坐标,利用面积差可求出△OCD 的面积.【详解】解:(1)∵点A (1,n )在直线l 1:y =x +5的图象上,∴n =6,∴点A (1,6)代入y =k x 得,k =6,∴反比例函数y =6x ,当x =12时,y =12,∴点D (12,12)代入直线l 2:y =﹣2x +b 得,b =13,∴直线l 2:y =﹣2x +13,由题意得:6213y x y x ⎧=⎪⎨⎪=-+⎩解得:111212x y ⎧=⎪⎨⎪=⎩,2261x y =⎧⎨=⎩,∴点C (6,1)答:反比例函数解析式y =6x,点C 的坐标为(6,1).(2)直线l 2:y =﹣2x +13,与x 轴的交点E (132,0)与y 轴的交点B (0,13)∴S △OCD =S △BOE ﹣S △BOD ﹣S △OCE11311113143131312222224=⨯⨯-⨯⨯⨯=答:△OCD 的面积为1434.【点睛】本题考查了待定系数法求反比例函数解析式、反比例函数与一次函数交点问题、以及反比例函数与几何面积的求解,解题的关键是灵活处理反比例函数与一次函数及几何的关系.26.(1)CE =22;(2)CE 的长为724;(3)在AB 上存在点P ,使△EFP 为等腰直角三角形,此时EF =3760或EF =49120【解析】试题分析:(1)因为EF ∥AB ,所以容易想到用相似三角形的面积比等于相似比的平方解题;(2)根据周长相等,建立等量关系,列方程解答;(3)先画出图形,根据图形猜想P 点可能的位置,再找到相似三角形,依据相似三角形的性质解答.试题解析:(1)∵△ECF 的面积与四边形EABF 的面积相等∴S △ECF :S △ACB =1:2又∵EF ∥AB ∴△ECF ∽△ACB.,21)(2==∆∆CA CE S S ACB ECF 且AC =4∴CE =22;(2)设CE 的长为x∵△ECF ∽△ACB ∴CB CF CA CE =∴CF=x 43.由△ECF 的周长与四边形EABF 的周长相等,得EFx x x EF x +-++-=++)433(5)4(43解得724=x ∴CE 的长为724;(3)△EFP 为等腰直角三角形,有两种情况:①如图1,假设∠PEF =90°,EP =EF图1A B由AB =5,BC =3,AC =4,得∠C =90°∴Rt △ACB 斜边AB 上高CD =512设EP =EF =x ,由△ECF ∽△ACB ,得CD EP CD AB EF -=,即5125125xx -=,解得3760=x ,即EF =3760,当∠EFP´=90°,EF =FP´时,同理可得EF =3760.②如图2,假设∠EPF =90°,PE =PF 时,点P 到EF 的距离为EF 21。
九年级数学上册第一学期期末综合测试卷(北师版 2024年秋)

九年级数学上册第一学期期末综合测试卷(北师版2024年秋)一、选择题(每题3分,共30分)1.(教材P57复习题T13变式)关于x的一元二次方程(a-1)x2+a2-1=0的一个根是0,则a的值为()A.1B.-1C.1或-1 D.122.先贤孔子曾说过“鼓之舞之”,这是“鼓舞”一词最早的起源,如图是喜庆集会时击鼓瞬间的情景及鼓的立体图形,该立体图形的主视图是()3.如图,要使▱ABCD成为矩形,则可添加的一个条件是()A.AB=AD B.OA=OC C.AD=BC D.AC=BD(第3题)(k≠0)的图象经过点P(1,-2),则这个函数的图象位于4.已知反比例函数y=kx()A.第一、三象限B.第二、三象限C.第二、四象限D.第三、四象限5.(2023山东省实验中学月考)如图是一次数学活动课上制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数(当指针恰好指在分界线上时,不记,重转),则记录的两个数都是正数的概率为()A.18B.16C.14D.12(第5题)(第6题)6.如图,在△ABC 中,DE ∥BC ,∠ADE =∠EFC ,AD BD =53,CF =6,则DE 的长为()A .6B .8C .10D .127.如图,△ADC 是由等腰直角三角形EOG 经过位似变换得到的,位似中心在x轴的正半轴上,位似比为12,已知EO =1,D 点坐标为(2,0),则这两个三角形的位似中心的坐标是()B .(1,0)C .(0,0)(第7题)(第8题)8.(2023合肥一模)如图,Rt △BOC 的一条直角边OC 在x 轴的正半轴上,双曲线y =kx 过△BOC 的斜边OB 的中点A ,与另一直角边BC 相交于点D.若△BOD的面积是6,则k 的值是()A .-6B .-4C .4D .69.如图,△ABC 中,∠C =90°,AB =10,AC =8,线段DE 的两个端点D ,E 分别在边AC ,BC 上滑动,且DE =4,若点M ,N 分别是DE ,AB 的中点,则MN 的最小值为()A .2B .3C .3.5D .4(第9题)(第10题)10.(2023东营)如图,正方形ABCD的边长为4,点E,F分别在边DC,BC上,且BF=CE,AE平分∠CAD,连接DF,分别交AE,AC于点G,M,P是线段AG上的一个动点,过点P作PN⊥AC,垂足为点N,连接PM,有下列四个结论:①AE垂直平分DM;②PM+PN的最小值为32;③CF2=GE·AE;④S△ADM=62.其中正确的是()A.①②B.②③④C.①③④D.①③二、填空题(每题3分,共24分)11.如图,已知ADAE=ACAB,AD=3cm,AC=6cm,BC=8cm,则DE=________.(第11题)(第13题) 12.已知点A(-2,y1),B(a,y2),C(3,y3)在反比例函数y=-4x的图象上,且-2<a<0,则y1,y2,y3的大小关系是________.13.如图所示的是一个几何体的三视图,则这个几何体的侧面积为________.14.(2023营口二模)某水果销售网络平台以2.6元/kg的成本价购进20000kg沃柑.如下表是平台销售部通过随机取样,得到的“沃柑损坏率”统计表的一部分,从而可大约估计每千克沃柑的实际售价定为________元时(精确到0.1元),可获得13000元利润.(销售总金额-损耗总金额-销售部分成本=销售总利润)沃柑总质量n/kg (100200300400500)损坏沃柑质量m/kg…10.4419.6330.6239.5450.67沃柑损坏的频率mn(精确到0.001)…0.1040.0980.1020.0990.10115.若关于x的方程x2-3x+m=0有两个不相等的实数根,且m≥-3,则从满足条件的所有整数m中随机选取一个,恰好是负数的概率是________.16.【新趋势学科内综合】若矩形ABCD的两邻边长分别为一元二次方程x2-7x +12=0的两个实数根,则矩形ABCD的对角线长为________.17.如图,已知点A是一次函数y=13x图象上y轴右侧的一点,过点A作x轴的垂线l,B是l上一点(点B在A上方),在AB的右侧以AB为斜边作等腰直角三角形ABC,反比例函数y=kx(x>0)的图象过点B,C,若△OAB的面积为12,则△ABC的面积是________.18.如图,在平面直角坐标系中,菱形ABCD的顶点A,B在x轴上,AB=2,A(1,0),∠DAB=60°,将菱形ABCD绕点A旋转90°后,得到菱形AB1C1D1,则点C1的坐标是________.三、解答题(19~20题每题8分,21~25题每题10分,共66分)19.解下列方程:(1)(x+1)2-4=0;(2)x(x-2)=x-2.20.(2023鄂州)如图,点E是矩形ABCD的边BC上的一点,且AE=A D. (1)尺规作图:作∠DAE的平分线AF,交BC的延长线于点F,连接DF.(保留作图痕迹,不写作法);(2)试判断四边形AEFD的形状,并说明理由.21.画出如图所示的几何体的三视图.22.(新考向传统文化)藏毯作为青海省非物质文化遗产项目之一,与波斯毯、东方毯并称为世界三大名毯.西宁作为藏毯之都,生产的藏毯已成为青海名副其实的特色产品,更是一张通往世界的“金名片”.(1)为了调查一批藏毯的质量,质检人员从中随机抽取了100件产品进行检测.本次抽样调查的样本容量是________;(2)6月10日是我国文化和自然遗产日.某校举办非遗文化进校园活动,决定从A,B,C,D四名同学中随机抽取两人作为“小小宣传员”,为大家介绍青海藏毯文化.请用画树状图或列表的方法求出A,B两人同时被选中的概率.23.【新考向传统文化】正月十五是中华民族的传统节日——元宵节,家家挂彩灯、户户吃汤圆已成为世代相沿的习俗.某手工汤圆店计划在元宵节前用21天的时间生产袋装手工汤圆,已知每袋汤圆需要0.3斤汤圆馅和0.5斤汤圆粉,而汤圆店每天能生产450斤汤圆馅或300斤汤圆粉(每天只能生产其中一种).(1)若这21天生产的汤圆馅和汤圆粉恰好配套,且全部及时加工成汤圆,则总共生产了多少袋手工汤圆?(2)为保证手工汤圆的最佳口感,汤圆店计划把这21天生产的汤圆放在近10天内销售.据统计,每袋手工汤圆的成本为13元,售价为25元时每天可售出225袋,售价每降低2元,每天可多售出75袋.汤圆店按售价25元销售2天后,余下8天进行降价促销,第10天结束后将还未售出的手工汤圆以15元/袋的价格全部卖给古城小吃店,若最终获利40500元,则促销时每袋应降价多少元?24.如图,一次函数y=ax+b的图象与x轴交于点A(4,0),与y轴交于点B,与反比例函数y=kx(x>0)的图象交于点C,D.若BO:OA=2:1,BC=3A C.(1)求一次函数和反比例函数的表达式;(2)求△OCD的面积.25.【新视角动点探究题】如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC =8cm,动点P从点B出发,在BA边上以5cm/s的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以4cm/s的速度向点B匀速运动,运动时间为t s(0<t<2),连接PQ.(1)若△BPQ和△ABC相似,求t的值;(2)连接AQ,CP,若AQ⊥CP,求t的值.答案一、1.B 2.B3.D4.C5.C6.C7.A8.C 点拨:过点A 作AE ⊥OC 于点E ,则AE ∥BC ,∠OEA =∠OCB =90°.∴∠OAE =∠OBC .∴△OAE ∽△OBC .∴S △OAE S △OBC==14.∵S △OAE =k2,∴S △OBC =4S △OAE =2k .∴S △OBC =S △OCD +S △BOD =k2+6=2k ,解得k =4.9.B10.D 点拨:∵四边形ABCD 为正方形,∴BC =CD =AD ,∠ADE =∠DCF =90°.∵BF =CE ,∴DE =FC .∴△ADE ≌△DCF (SAS ).∴∠DAE =∠FDC .∵∠ADE =90°,∴∠ADG +∠FDC =90°.∴∠ADG +∠DAE =90°.∴∠AGD =∠AGM =90°.∵AE 平分∠CAD ,∴∠DAG =∠MAG .又∵AG =AG ,∴△ADG ≌△AMG (ASA ).∴DG =GM ,∴AE 垂直平分DM .故①正确.易知∠ADE =∠DGE =90°,∠DAE =∠GDE ,∴△ADE ∽△DGE ,∴DE GE =AE DE.∴DE 2=GE ·AE .又∵DE =CF ,∴CF 2=GE ·AE .故③正确.∵正方形ABCD 的边长为4,∴在Rt △ABC 中,AC =AB 2+BC 2=42+42=4 2.∵△ADG ≌△AMG ,∴AM =AD =4.由图可知△ADM 中AM 边上的高与△ADC 中AC 边上的高相等,设△ADM 中边AM 上的高为h ,则△ADC 中AC 边上的高为h .∵12×AC ×h =12×AD ×DC ,∴h =AD ×DC AC=2 2.∴S △ADM =12·AM ·h =12×4×22=42.故④不正确.∵DM ⊥AG ,DG =GM ,∴点M 关于线段AG 的对称点为点D .过点D 作DN ′⊥AC 于点N ′,连接PD ,如图所示.则PD =PM .∴PM +PN =PD +PN ≥DN ′.∴PM +PN 的最小值即为DN ′.又∵DN ′=h =22,∴PM +PN 的最小值为2 2.故②不正确.综上所述,正确的是①③.二、11.4cm 12.y 3<y 1<y 213.16πcm 214.3.615.1216.517.8点拨:过点C 作CD ⊥y 轴于点D ,交AB 于点E .∵AB ⊥x 轴,∴CD ⊥AB .又∵△ABC 是等腰直角三角形,∴BE =AE =CE .设AB =2a ,则BE =AE =CE =a .设,13x ,13x +2+a ,13x +∵点B ,C 均在反比例函数y =kx(x >0)的图象上,∴+2(x +a +解得x =32a .∵S △OAB =12AB ·DE =12·2a ·x =12,∴ax =12.∴32a 2=12.∴a 2=8.∴S △ABC =12AB ·CE =12·2a ·a =a 2=8.18.(1-3,3)或(1+3,-3)点拨:当菱形ABCD 绕点A 顺时针旋转90°时,如图①,延长C 1D 1交x 轴于点E .易得C 1D 1=AD 1=AD =AB =2.∵∠DAB =60°,∠D 1AD =90°,∴∠D 1AB =30°.∵在菱形ABCD 中,AB ∥CD ,∴∠ADC =120°.∴∠AD 1C 1=∠ADC =120°.∴∠AD 1E =60°.∴∠AED 1=90°.∴ED 1=12AD 1=1.∴C 1E =2+1=3,AE =22-12=3,∴OE =1+3,∴C 1(1+3,-3).当菱形ABCD 绕点A 逆时针旋转90°时,如图②,延长C 1D 1交x 轴于点F .同理可得OF =3-1,C 1F =3.∴C 1(1-3,3).综上所述,C1的坐标为(1-3,3)或(1+3,-3).三、19.解:(1)移项,得(x+1)2=4,两边开平方,得x+1=±2,即x+1=2或x+1=-2.∴x1=1,x2=-3.(2)移项,得x(x-2)-(x-2)=0.提取公因式,得(x-1)(x-2)=0,∴x-1=0或x-2=0,∴x1=1,x2=2. 20.解:(1)作图如图所示.(2)四边形AEFD是菱形.理由如下:∵在矩形ABCD中,AD∥BC,∴∠DAF=∠AFE.∵AF平分∠DAE,∴∠DAF=∠EAF.∴∠AFE=∠EAF.∴AE=EF.∵AE=AD,∴AD=EF.又∵AD∥EF,∴四边形AEFD是平行四边形.又∵AE=AD,∴平行四边形AEFD是菱形.21.解:如图所示.22.解:(1)100(2)根据题意列表如下:第一人A B C D 第二人A—BA CA DA B AB —CB DB C AC BC —DC DADBDCD—由表格可知,共有12种等可能的结果,其中A ,B 两人同时被选中的结果共有2种,即AB ,BA ,所以P (A ,B 两人同时被选中)=16.23.解:(1)设总共生产了a 袋手工汤圆,依题意得0.3a 450+0.5a300=21,解得a =9000.答:总共生产了9000袋手工汤圆.(2)设促销时每袋应降价x 元,若刚好10天全部卖完,则依题意得225×2×(25-13)+8×(25-13-x )(225+752x )=40500,整理得x 2-6x +45=0,∵Δ=(-6)2-4×45<0,∴方程无解.∴10天不能全部卖完.∴第10天结束后将还未售出的手工汤圆以15元/袋的价格全部卖给古城小吃店的利润为(15-13)[9000-2×225-+752x=13500-600x (元).依题意得225×2×(25-13)+8×(25-13-x +752x13500-600x =40500,整理得,x 2-4x =0,解得x 1=0,x 2=4.∵要促销,∴x =4.即促销时每袋应降价4元.24.解:(1)∵A (4,0),∴OA =4.又∵BO :OA =2:1,∴OB =8.∴B (0,8).∵A ,B 两点在直线y =ax +b 上,a +b =0,=8,=-2,=8.∴一次函数的表达式为y =-2x +8.如图,过点C 作CE ⊥OA 于点E .∵BC =3AC ,∴AB =4AC .易知CE ∥OB ,∴△ACE ∽△ABO .∴CE OB =AE OA =AC AB =14.∴CE =2,AE =1.∴OE =3.∴C (3,2).∵点C 在反比例函数y =kx(x >0)的图象上,∴k =3×2=6.∴反比例函数的表达式为y =6x.(2)由(1)=-2x +8,=6x .1=1,1=6.2=3,2=2.∴D (1,6).如图,过点D 作DF ⊥y 轴于点F ,则DF =1.∴S △OCD =S △AOB -S △BOD -S △COA =12·OA ·OB -12·OB ·DF -12·OA ·CE =12×4×8-12×8×1-12×4×2=8.25.解:(1)由题易知AB =10cm ,BP =5t cm ,CQ =4t cm ,∴BQ =(8-4t )cm .当△PBQ ∽△ABC 时,有BP BA =BQ BC ,即5t 10=8-4t8,∴t =1.当△QBP ∽△ABC 时,有BQ BA =BP BC,即8-4t 10=5t 8,∴t =3241.∴若△BPQ 和△ABC 相似,则t =1或t =3241.(2)如图,过点P 作PD ⊥BC 于点D ,则PD ∥AC .易得△PBD ∽△ABC .∴BP AB =PD AC =BD BC.由(1)知AB =10cm ,BP =5t cm ,可求得PD =3t cm ,BD =4t cm ,∴CD =(8-4t )cm.∵AQ ⊥CP ,∠ACB =90°,∴∠CAQ +∠ACP =90°,∠DCP +∠ACP =90°.∴∠CAQ =∠DCP .又∵∠CDP =∠ACQ =90°,∴△CPD ∽△AQC .∴CD AC =PD QC ,即8-4t 6=3t 4t =34.∴t =78.点易错:解答动态问题时,要注意分类讨论思想的应用.相似三角形对应边的位置不同,解出来的t 值也不同,应充分考虑所有可能出现的情况,避免漏解.。
北师大版九年级上册数学期末考试试卷及答案

北师大版九年级上册数学期末考试试题一、单选题1.如图所示的几何体的俯视图是()A .B .C .D .2.已知反比例函数ky x的图象经过点(﹣3,6),则k 的值是()A .﹣18B .﹣2C .2D .183.方程x 2=3x 的解为()A .x =3B .x =0C .x 1=0,x 2=﹣3D .x 1=0,x 2=34.如图,△ABO ∽△CDO ,若BO =8,DO =4,CD =3,则AB 的长是()A .2B .3C .4D .65.如图,l 1∥l 2∥l 3,直线a ,b 与l 1、l 2、l 3分别相交于点A 、B 、C 和点D 、E 、F ,若AB :AC=2:5,DE =6,则EF 的长是()A .15B .10C .9D .26.如图,菱形OABC 的顶点C 的坐标为(3,4),顶点A 在x 轴的正半轴上.反比例函数ky x=(x >0)的图象经过顶点B ,则k 的值为()A .12B .16C .20D .327.同一时刻,小明在阳光下的影长为2米,与他邻近的旗杆的影长为6米,小明的身高为1.6米,则旗杆的高为()A .3.2米B .4.8米C .5.2米D .5.6米8.关于x 的方程230x x n -+=有两个不相等的实数根,则n 的取值范围是()A .n <94B .n ≤94C .n >94-D .n >949.在平面直角坐标系中,已知点A (﹣4,2),B (﹣6,﹣4),以原点O 为位似中心,相似比为12,把△ABO 缩小,则点A 的对应点A′的坐标是()A .(﹣2,1)B .(﹣8,4)C .(﹣8,4)或(8,﹣4)D .(﹣2,1)或(2,﹣1)10.已知反比例函数y =abx的图象如图所示,则二次函数y =ax 2-2x 和一次函数y =bx+a 在同一平面直角坐标系中的图象可能是()A .B .C .D .二、填空题11.若32b a =,则a b b +的值等于__.12.若两个相似三角形的相似比是1:2,则它们的周长比是________.13.在一个不透明的盒子里,装有4个黑球和若干个白球,它们除颜色外都相同.搅匀后从中任意摸出一个球,记下颜色再把它放回盒子中.不断重复实验多次后,摸到黑球的频率逐渐稳定在0.2左右.则据此估计盒子中大约有白球___________个.14.已知关于x 的一元二次方程20x x k -+=的一个根是2,则k 的值是______.15.如图,已知 ABC ∽ AMN ,点M 是AC 的中点,AB =6,AC =8,则AN =_____.16.端午节期间,某食品专卖店准备了一批粽子,每盒利润为50元,平均每天可卖300盒,经过调查发现每降价1元,可多销售10盒,为了尽快减少库存,决定采取降价措施,专卖店要想平均每天盈利16000元,设每盒粽子降价x 元,可列方程________.17.已知,一次函数1y x =-+与反比例函数2y x=-的图象交于点A 、B ,在x 轴上存在点P (n ,0),使△ABP 为直角三角形,则P 点的坐标是______.18.如图,OA OB OC ==且30ACB ∠=︒,则AOB ∠的大小是______度.三、解答题19.解方程:2450x x --=.20.如图,在平行四边形ABCD 中,点P 是AB 边上一点(不与A ,B 重合),过点P 作PQ ⊥CP ,交AD 边于点Q ,且∠QPA =∠PCB .求证:四边形ABCD 是矩形.21.如图,D 、E 、F 分别是ABC 各边的中点,连接DE 、EF 、AE .(1)求证:四边形ADEF 为平行四边形;(2)加上条件后,能使得四边形ADEF 为菱形,请从①90BAC ∠=︒;②AE 平分BAC ∠;③AB AC =,这三个条件中选择一个条件填空(写序号),并加以证明.22.2016年,某楼盘以每平方米8000元的均价对外销售,因为楼盘滞销,房地产开发商为了加快资金周转,决定进行降价促销,经过连续两年下调后,2018年的均价为每平方米6480元()1求平均每年下调的百分率;()2假设2019年的均价仍然下调相同的百分率,张强准备购买一套100平方米的住房,他持有现金20万元,可以在银行贷款40万元,张强的愿望能否实现?为什么?(房价每平方米按照均价计算)23.如图,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.(1)经过几秒△PCQ的面积为△ACB的面积的1 3?(2)经过几秒,△PCQ与△ACB相似?24.如图,矩形ABCD中,点E在边CD上,将△BCE沿BE折叠,点C落在AD边上的点F处,过点F作FG∥CD交BE于点G,连接CG.(1)求证:四边形CEFG是菱形;(2)若AB=6,AD=10,求四边形CEFG的面积.25.如图是一矩形广告牌ACGE,2AE 米,为测量其高度,某同学在B处测得A点仰角为45︒,该同学沿GB 方向后退6米到F 处,此时测得广告牌上部灯杆顶端P 点仰角为37︒.若该同学眼睛离地面的垂直距离为1.7米,灯杆PE 的高为2.25米,求广告牌的高度(AC 或EG 的长).(精确到1米,参考数据:sin 370.6︒≈,tan370.75︒≈)26.如图,在▱ABCD 中过点A 作AE ⊥DC ,垂足为E ,连接BE ,F 为BE 上一点,且∠AFE=∠D .(1)求证:△ABF ∽△BEC ;(2)若AD=5,AB=8,sinD=45,求AF 的长.27.已知C 、D 是双曲线()0ky k x=>上的两点,过点C 作CA ⊥x 轴点A ,过点D 作DE ⊥x 轴点E ,交OC 于点F .(1)如图1,若点D 坐标为(1,1),OE :OA=1:3,则DOF S =(2)如图2,延长OD ,AC 相交于点B ,若点D 为OB 的中点.①当6OBCS = ,求k 的值;②若点C 的坐标是(6,1),试求四边形DFCB 的面积.参考答案1.A2.A3.D4.D5.C6.D7.B8.A9.D 10.C11.53或者5:312.1:2 13.16 14.-215.16316.()()503001016000x x -+=17.(3,0)或(-3,0)或⎫⎪⎪⎝⎭或⎫⎪⎪⎝⎭18.60.19.125,1x x ==-【详解】解:2450x x --=(5)(1)0x x -+=50x ∴-=或10x +=解得:125,1x x ==-.20.见解析【分析】根据垂直的性质可得90QPC ∠=︒,利用各角之间的等量关系可得90B ∠=︒,再由矩形的判定定理即可证明.【详解】证明:∵PQ CP ⊥,∴90QPC ∠=︒,∴1809090QPA BPC ∠+∠=︒-︒=︒,∵QPA PCB ∠=∠,∴90BPC PCB ∠+∠=︒,∴()18090B BPC PCB ∠=︒-∠+∠=︒,∵四边形ABCD 是平行四边形,∴四边形ABCD 是矩形.21.(1)见解析;(2)②或③,见解析【分析】(1)先证明//EF AB ,根据平行的传递性证明EF //AD ,即可证明四边形ADEF 为平行四边形.(2)选②AE 平分BAC ∠,先证明DAE FAE ∠=∠,由四边形ADEF 是平行四边形ADEF ,得出AF EF =,即可证明平行四边形ADEF 是菱形.选③AB AC =,由//DE AC 且12DE AC =,AB AC =得出EF DE =,即可证明平行四边形ADEF 是菱形.【详解】(1)证明:已知D 、E 是AB 、BC 中点∴//DE AC又∵E 、F 是BC 、AC 的中点∴//EF AB ∵//DE AF ∴EF //AD∴四边形ADEF 为平行四边形(2)证明:选②AE 平分BAC ∠∵AE 平分BAC ∠∴DAE FAE ∠=∠又∵平行四边形ADEF ∴//EF DA ∴=∠∠FAE AEF ∴AF EF=∴平行四边形ADEF 是菱形选③AB AC =∵//EF AB 且12EF AB =//DE AC 且12DE AC =又∵AB AC =∴EF DE=∴平行四边形ADEF 为菱形故答案为:②或③【点睛】本题考查菱形的判定、平行四边形的性质及判定,熟练进行角的转换是关键,熟悉菱形的判定是重点.22.(1)平均每年下调的百分率为10%;(2)能,理由见解析【分析】(1)根据增长率问题的列式方法列出一元二次方程,解方程;(2)根据第一问求出的增长率算出2019年的房价,看张强的钱是否足够.【详解】解:()1设平均每年下调的百分率为x ,()2800016480x -=,解得:120.110%, 1.9x x ===(不合题意舍去),答:平均每年下调的百分率为10%;()()26480110%10058320058.32-⨯==,由于20406058.32+=>,所以张强的愿望能实现.【点睛】本题考查一元二次方程的应用题,解题的关键是掌握增长率问题的列式方法.23.(1)2秒或4秒;(2)125秒或1811秒【分析】(1)分别表示出线段PC 和线段CQ 的长后利用S △PCQ =13S △ABC 列出方程求解;(2)设运动时间为ts ,△PCQ 与△ACB 相似,当△PCQ 与△ACB 相似时,则有CP CQ=CA CB或CP CQ=CB CA,分别代入可得到关于t 的方程,可求得t 的值.【详解】解:(1)设经过x 秒△PCQ 的面积为△ACB 的面积的13,由题意得:PC=2xm ,CQ=(6﹣x )m ,则12×2x (6﹣x )=13×12×8×6,解得:x=2或x=4.故经过2秒或4秒,△PCQ 的面积为△ACB 的面积的13;(2)设运动时间为ts ,△PCQ 与△ACB 相似.当△PCQ 与△ACB 相似时,则有CP CQ =CA CB 或CP CQ=CB CA,所以2686t t -=,或2668t t -=,解得t=125,或t=1811.因此,经过125秒或1811秒,△OCQ 与△ACB 相似;24.(1)见解析(2)四边形CEFG 的面积为203.【分析】(1)根据题意和翻折的性质,可以得到△BCE ≌△BFE ,再根据全等三角形的性质和菱形的判定方法即可证明结论成立;(2)根据题意和勾股定理,可以求得AF 的长,进而求得EF 和DF 的值,从而可以得到四边形CEFG 的面积.(1)证明:由题意可得,△BCE ≌△BFE ,∴∠BEC=∠BEF ,FE=CE ,∵FG ∥CE ,∴∠FGE=∠CEB ,∴∠FGE=∠FEG ,∴FG=FE ,∴FG=EC ,∴四边形CEFG 是平行四边形,又∵CE=FE ,∴四边形CEFG 是菱形;(2)解:∵矩形ABCD 中,AB=6,AD=10,BC=BF ,∴∠BAF=90°,AD=BC=BF=10,∴AF=8,∴DF=2,设EF=x ,则CE=x ,DE=6-x ,∵∠FDE=90°,∴22+(6-x )2=x 2,解得,x=103,∴CE=103,∴四边形CEFG 的面积是:CE•DF=103×2=203.【点睛】本题考查翻折变化、菱形的性质和判定、矩形的性质,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.25.广告牌的高度为17米【分析】首先延长DH 交EG 于M ,交AC 于N ,构造直角三角形,可得到EM AN =,设AN x =,表示出PM,在Rt AND ∆中得到AN ND x ==,628MH x x =++=+,在Rt PHM ∆中运用勾股定理求解即可.【详解】依题意:6DH BF ==米, 1.7DB HF ==米, 2.25PE =米,如图设直线DH 交EG 于M ,交AC 于N ,则EM AN =.设AN x =m 则 2.25PM x =+,在Rt AND ∆中,∵45ADN ∠=︒,∴AN ND x ==,∵2AE MN ==,则628MH x x =++=+,在Rt PHM ∆中,∵tan 37PM MH ︒=,∴ 2.250.758x x +≈+,解得15x ≈,∴15 1.717AC AN NC =+=+≈(米),∴广告牌的高度为17米.【点睛】本题考查了解直角三角形的应用仰角俯角的问题,准确构造直角三角形和找准角度是解题的关键.26.(1)证明见解析;(2)【分析】(1)由平行四边形的性质得出AB ∥CD ,AD ∥BC ,AD=BC ,得出∠D+∠C=180°,∠ABF=∠BEC ,证出∠C=∠AFB ,即可得出结论;(2)由勾股定理求出BE ,由三角函数求出AE ,再由相似三角形的性质求出AF 的长.【详解】(1)证明:∵四边形ABCD 是平行四边形,∴AB ∥CD ,AD ∥BC ,AD=BC ,∴∠D+∠C=180°,∠ABF=∠BEC ,∵∠AFB+∠AFE=180°,∴∠C=∠AFB ,∴△ABF ∽△BEC ;(2)解:∵AE ⊥DC ,AB ∥DC ,∴∠AED=∠BAE=90°,在Rt △ABE 中,根据勾股定理得:==在Rt △ADE 中,AE=AD•sinD=5×45=4,∵BC=AD=5,由(1)得:△ABF ∽△BEC ,∴AF AB BC BE=,即5AF =解得:.27.(1)49;(2)①4;②274【分析】(1)将D 代入双曲线解析式中求出k ,根据反比例函数k 的几何意义和相似三角形的性质求解即可;(2)①设D (m ,k m),则可求得点B 、C 的坐标,根据反比例函数k 的几何意义和OBC ABC OAC S S S =- 列出k 的方程求解即可;②根据点C 坐标可得出OA ,进而可求得OE 和点B 、D 的坐标,根据相似三角形的性质可求得EF 和DF ,利用梯形的面积公式求解即可.【详解】解(1)将D (1,1)代入k y x =,得k=1,∴11||22ODE OAC S S k === ,∵CA ⊥x 轴,DE ⊥x 轴,∴DE ∥AC ,∵OE :OA=1:3,∴△OEF ∽△OAC ,∴19OEF OAC S S = ,∴1112918OEF S =⨯= ,∴1142189DOF S =-= ;(2)①设D (m ,km ),∵点D 为OB 的中点,∴B (2m ,2k m ),C (2m ,2km ),∵6OBC ABC OAC S S S -== ,∴2112622k m k m ⨯⨯-=,∴4k =;②∵点C (6,1),∴OA =6,AC=1,∵点D 是OB 的中点,DE ∥AC ,D 在反比例函数6y x =上,∴OE =12OA =3,点D (3,2),∴点B (6,4),DE=2,又∵△OEF ∽△OAC ,∴12EFAC =,∴EF=12,∴DF =2-12=32,BC =3,EA =3∴四边形DFCB 的面积=312733224+⨯⨯=().。
北师大版九年级上册数学期末考试试卷及答案

北师大版九年级上册数学期末考试试题一、选择题。
(每小题只有一个正确答案)1.下列长度的各组线段中,能构成比例的是()A .2,5,6,8B .3,6,9,18C .1,2,3,4D .3,6,7,92.如图,正比例函数y 1=k 1x 和反比例函数y 2=2k x的图象都经过点A (2,﹣1),若y 1>y 2,则x 的取值范围是()A .﹣1<x <0B .x >2C .﹣2<x <0或x >2D .x <﹣2或0<x <23.关于反比例函数y =﹣3x,下列说法错误的是()A .图象经过点(1,﹣3)B .图象分布在第一、三象限C .图象关于原点对称D .图象与坐标轴没有交点4.如图,在Rt ABC 中,90ABC ∠=︒,点F 为AC 中点,DE 是ABC 的中位线,若6DE =,则BF =()A .6B .4C .3D .55.已知1x =是关于x 的方程22(1)10k x k x -+-=的根,则常数k 的值为()A .0B .1C .0或1D .0或-18.6.关于x 的一元二次方程210kx x -+=有两个不相等的实数根,则k 的取值范围是A .14k <B .14k >C .14k <且0k ≠D .14k >且0k ≠7.某企业今年1月份产值为x 万元,2月份的产值比1月份减少了10%,则2月份的产值是()A .(1﹣10%)x 万元B .(1﹣10%x )万元C .(x ﹣10%)万元D .(1+10%)x 万元8.下列说法正确的是()A .对角线互相垂直的四边形是菱形B .矩形的对角线互相垂直C .一组对边平行的四边形是平行四边形D .四边相等的四边形是菱形9.如图,在正方形OABC 中,OA =6,点E 、F 分别在边BC ,BA 上,OE =,若∠EOF=45°,则点F 的纵坐标为()A .2B .53C D 1-10.如图,在△ABC 中,DE ∥BC ,AD =9,DB =3,CE =2,则AC 的长为()A .6B .7C .8D .9二、填空题11.矩形纸片ABCD ,长8cm AD =,宽4cm AB =,折叠纸片,使折痕经过点B ,交AD 边于点E ,点A 落在点A '处,展平后得到折痕BE ,同时得到线段BA ',EA ',不再添加其它线段,当图中存在30 角时,AE 的长为__________厘米.12.已知y 与2x+1成反比例,且当x=1时,y=2,那么当x=﹣2时,y=______.13.在一只不透明的口袋中放入红球6个,黑球2个,黄球n 个,这些球除颜色不同外,其它无任何差别.搅匀后随机从中摸出一个恰好是黄球的概率为13,则放入口袋中的黄球总数n=__.14.如图,在平面直角坐标系中,边长为4的等边△OAB 的OA 边在x 轴的正半轴上,反比例函数y=k x(x >0)的图象经过AB 边的中点C ,且与OB 边交于点D ,则点D 的坐标为_____.15.如图,已知在ABC 中,90ACB ∠=︒,2AC =,4BC =.D 为ABC 所在平面内的一个动点,且满足90BDC ∠=︒,E 为线段AD 的中点,连结CE ,则线段CE 长的最大值为______.16.如图,矩形ABOC 的面积为3,反比例函数y =k x的图象过点A ,则k =_____.17.关于x 的方程(m ﹣2)x 2﹣2x +1=0是一元二次方程,则m 满足的条件是_____.三、解答题18.解方程(1)3x 2+8x +4=0(配方法)(2)2310x x --=(公式法)(3)4x (2x +1)=3(2x +1)(4)3x 2-x -2=019.设一元二次方程260x x k -+=的两根分别为1x 、2x .(1)若12x =,求2x 的值;(2)若5k =,且1x 、2x 分别是Rt ABC ∆的两条直角边的长,试求Rt ABC ∆的面积.20.如图,在平行四边形ABCD 中,ABD ∠的平分线BE 交AD 于点E ,CDB ∠的平分线DF 交BC 于点F .求证:四边形DEBF 是平行四边形.21.如图,E 是矩形ABCD 的边BC 延长线上的一点,连接AE ,交CD 于F ,把ABE ∆沿CB 向左平移,使点E 与点C 重合,ADF CBG ∆≅∆吗?请说明理由.22.如图,四边形ABCD 是矩形,E 是BC 边上一点,点F 在BC 的延长线上,且CF =BE .(1)求证:四边形AEFD 是平行四边形;(2)连接ED ,若∠AED =90°,AB =4,BE =2,求四边形AEFD 的面积.23.如图,A 是反比例函数k y x=()0k <图象上的一点,过点A 作AB x ⊥轴于点B ,连0A ,AOB 的面积为2,点A 的坐标为()1,m -.(1)求反比例函数的解析式.(2)若一次函数3y ax =+的图象经过点A ,交双曲线的另一支于点()4,C n ,交y 轴于点D ,若y 轴上存在点P ,使PAC △的面积为5,求点P 的坐标.24.在抗击“新冠病毒”期间,某路口利用探测仪对过往的物体进行检查,探测仪A 测得某物体的仰角∠BAD =35°,俯角∠DAC =45°,探测仪到货物表面的距离AD =3米,求货物高BC 的长.(sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,结果精确到0.1)25.如图,点P 是正方形ABCD 对角线AC 上一动点,点E 在射线BC 上,且PE =PB ,连接PD ,O 为AC 中点.(1)如图1,当点P 在线段AO 上时,试猜想PE 与PD 的数量关系和位置关系.(2)①如图2,当点P 在线段OC 上时,(1)中的猜想还成立吗?请说明理由.②图2,试用等式来表示PB 、BC 、CE 之间的数量关系,并证明.参考答案1.B【解析】分析:分别计算各组数中最大与最小数的积和另外两数的积,然后根据比例线段的定义进行判断.详解:∵3×18=6×9,∴3,6,9,18成比例.故选B .点睛:本题考查了比例线段:判定四条线段是否成比例,只要把四条线段按大小顺序排列好,判断前两条线段之比与后两条线段之比是否相等即可,求线段之比时,要先统一线段的长度单位,最后的结果与所选取的单位无关系.2.D【解析】如图,∵点A 坐标(2,﹣1),又∵正比例函数y 1=k 1x 和反比例函数y 2=2k x都是关于原点对称,∴它们的交点A 、B 关于原点对称,∴点B坐标(﹣2,1),∴由图象可知,y1>y2时,x<﹣2,或0<x<2,故选D.3.B【解析】【分析】反比例函数y=kx(k≠0)的图象k>0时位于第一、三象限,在每个象限内,y随x的增大而减小;k<0时位于第二、四象限,在每个象限内,y随x的增大而增大.根据反比例函数的性质并结合其对称性对各选项进行判断.【详解】A、把点(1,﹣3)代入函数解析式,﹣3=﹣3,故本选项正确,不符合题意,B、∵k=﹣2<0,∴图象位于二、四象限,且在每个象限内,y随x的增大而增大,故本选项错误,符合题意,C、反比例函数的图象可知,图象关于原点对称,故本选项正确,不符合题意D、∵x、y均不能为0,故图象与坐标轴没有交点,故本选项正确,不符合题意.故选:B.【点睛】本题主要考查的是反比例函数的性质,是中考中比较常见的知识点,一般难度不大,需熟练掌握.4.A【分析】由DE是ABC的中位线,可得AC=12,在Rt ABC中,点F为AC中点,可得BF=6即可.【详解】解:∵DE是ABC的中位线,∴AC=2DE=2×6=12,∵在Rt ABC 中,90ABC ∠=︒,点F 为AC 中点,∴BF =1112622AC =⨯=,故选择A .【点睛】本题考查三角形中位线与三角形中线性质,掌握三角形中位线与三角形中线性质是解题关键.5.C【详解】试题分析:①当1k =时,方程22(1)10k x k x -+-=为一元一次方程,解为1x =;②1k ≠时,方程22(1)10k x k x -+-=为一元二次方程,把1x =代入方程22(1)10k x k x -+-=可得:2110k k -+-=,即20k k -=0,可得(1)0k k -=,即k=0或1(舍去);故选C .考点:一元二次方程的解.6.C【分析】根据一元二次方程kx 2-x+1=0有两个不相等的实数根,知△=b 2-4ac >0,然后据此列出关于k 的方程,解方程即可.【详解】解:∵kx 2-x+1=0有两个不相等的实数根,∴△=1-4k >0,且k≠0,解得,k <14且k≠0;故答案是:k <14且k≠0.【点睛】本题考查了一元二次方程ax 2+bx+c=0(a≠0)的根的判别式△=b 2-4ac :当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.解题时,注意一元二次方程的“二次项系数不为0”这一条件.7.A【分析】1、本题属于列代数式的题目,解答此类题目首先要弄清楚语句中各个量之间的关系;2、细查题意,由2月份比1月份减少了10%先表示出2月份的产值为(1-10%)x 万元.【详解】由2月份比1月份减少了10%得2月份的产值是(1-10%)x 万元.故答案选A.【点睛】本题考查了列代数式,解题的关键是弄清楚题目中各个量之间的关系.8.D【详解】选项A ,菱形的对角线互相垂直,当对角线互相垂直的四边形不一定是菱形;选项B ,矩形的对角线相等但不一定垂直;选项C ,一组对边平行且相等的四边形是平行四边形;选项D ,四边相等的四边形是菱形.故选D.9.A【分析】延长BA 到点M ,使AM =CE ,连接OM ,由题意易得△OCE ≌△OAM ,则有OE =OM ,∠COE =∠AOM ,然后可得∠EOF =∠MOF ,进而可得△EOF ≌△MOF ,则有FM =EF ,根据勾股定理可得CE =3,设AF =x ,则EF =3+x ,BE =3,BF =6-x ,最后根据勾股定理建立方程求解即可.【详解】解:延长BA 到点M ,使AM =CE ,连接OM ,如图所示:∵四边形OABC 是正方形,OA =6,∴6,90OA OC AB BC OCE OAM OAF B COA ====∠=∠=∠=∠=∠=︒,∴△OCE ≌△OAM ,∴OE =OM ,∠COE =∠AOM ,∵∠EOF =45°,∴45COE AOF ∠+∠=︒,∴45AOM AOF ∠+∠=︒,∴∠EOF =∠MOF ,∵OF =OF ,OE =OM ,∴△EOF ≌△MOF (SAS ),∴EF FM AF AM AF CE ==+=+,∵OE =∴在Rt △OEC 中,3CE ==,设AF =x ,则EF =3+x ,BE =3,BF =6-x ,∴在Rt △EBF 中,222BE BF EF +=,∴()()222363x x +-=+,解得:2x =,∴点F 的纵坐标为2;故选A .【点睛】本题主要考查正方形的性质、勾股定理及图形与坐标,熟练掌握正方形的性质、勾股定理及图形与坐标是解题的关键.10.C【分析】利用平行线分线段成比例定理得到=AD AE DB EC ,利用比例性质求出AE ,然后计算AE +EC 即可.【详解】解:∵DE ∥BC ,∴=AD AE DB EC ,即9=32AE ,∴AE =6,∴AC =AE +EC =6+2=8.故选:C .【点睛】本题考查的是平行线分线段成比例定理,灵活运用定理、找准对应关系是解题的关键.11.3或8-【分析】分∠ABE=30°或∠AEB=30°或∠ABA′=30°时三种情况,利用锐角三角函数进行求解即可.【详解】解:当∠ABE=30°时,∵AB=4cm ,∠A=90°,∴AE=AB·tan30°=3cm ;当∠AEB=30°时,则∠ABE=60°,∵AB=4cm ,∠A=90°,∴AE=AB·tan60°=;当∠ABE=15°时,∠ABA′=30°,延长BA′交AD 于F ,如下图所示,设AE=x ,则EA′=x ,sin 603x EF ==︒,∵AF=AE+EF=ABtan30°=3,∴x +,∴8x =-∴8AE =-cm .故答案为:3或8-【点睛】本题考查了矩形与折叠,以及分类讨论的数学思想,分类讨论是解答本题的关键.12.-2【解析】试题分析:设反比例函数的解析式为:y=2r1,根据题意可得y=62r1,当x=-2时,y=-2.考点:待定系数法求反比例函数解析式.【详解】试题分析:随机从口袋中摸出一个恰好是黄球的概率为13,说明黄球的数目是口袋中所有球的数目的13,则可列方程:1623n n =++,解得:n=4.考点:概率的定义.14.3)【分析】由等边三角形的性质可求出B (2,,然后由中点坐标公式求出C (3,从而可求出反比例函数解析式,再求出直线OB 的解析式,然后与反比例函数解析式联立可求出点D 的坐标.【详解】∵△AOB 是等边三角形,边长为4,∴B (2,,∵BC =CA ,∴C (3),把点C 坐标代入k y x=上,得到k∵直线OB 的解析式为y,由y y x ⎧=⎪⎨=⎪⎩,解得3x y ⎧=⎪⎨=⎪⎩或3x y ⎧=⎪⎨=-⎪⎩∴D3),3).【点睛】本题考查了等边三角形的性质,待定系数法求函数关系式,反比例函数与一次函数的交点,求出反比例函数与直线OB 的解析式是解答本题的关键.15.1+取BC 的中点O ,连接OA 、OD ,取AO 中点M ,连接CM 、EM ,根据三角形斜边上的中线性质得出122OD BC ==,再根据三角形中位线性质得出112EM OD ==,然后根据勾股定理及角形斜边上的中线性质得出12CM OA ==最后根据两点之间线段最短即可得出答案.【详解】解:取BC 的中点O ,连接OA 、OD ,取AO 中点M ,连接CM 、EM在Rt △CDB 中,O 为斜边BC 的中点122OD BC ∴==在△AOD 中,AE =DE ,AM =OM 112EM OD ∴==在Rt △ACO 中,AC =OC =2AO ∴==∴12CM OA ==在△CME 中,1CE CM EM ≤+即CE 1.1.【点睛】本题考查了直角三角形斜边上的中线性质、三角形中位线性质、勾股定理、两点之间线段最短等知识点,熟练掌握性质定理和添加合适的辅助线是解题的关键.16.-3【分析】根据比例系数k 的几何含义:在反比例函数y=k x的图象中任取一点,过这一个点向x 轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|即可解题.【详解】解:∵矩形ABOC 的面积为3,∴|k|=3.∴k=±3.又∵点A 在第二象限,∴k<0,∴k=−3.故答案为−3.【点睛】本题考查了反比例函数系数k 的几何意义,反比例函数图象上点的坐标特征,属于简单题,熟悉反比例函数的图像和性质是解题关键.17.2m ≠【分析】根据一元二次方程的定义ax 2+bx+c=0(a≠0),列含m 的不等式求解即可.【详解】解:∵关于x 的方程(m ﹣2)x 2﹣2x+1=0是一元二次方程,∴m-2≠0,∴m≠2.故答案为:m≠2.【点睛】本题考查了一元二次方程的概念,满足二次项系数不为0是解答此题的关键.18.(1)x 1=23-,x 2=2-;(2)x 1=32+,x 2=32;(3)x 1=34,x 2=12-;(4)x 1=1,x 2=23-【分析】(1)将方程常数项移到右边,未知项移到方程左边,方程两边同时除以3将二次项系数化为1,然后方程两边都加上一次项系数一半的平方,左边化为完全平方式,右边合并为一个非负常数,开方转化为两个一元一次方程,求出一次方程的解即可得到原方程的解;(2)化成一般形式后用公式法解比较方便;(3)把右边的项移到左边,用提公因式的方法因式分解解方程;(4)化成一般形式后用公式法解比较方便;【详解】解:(1)23840x x ++=,∴2384x x +=-,∴28433x x +=-,∴28164163939x x ++=-+,∴24439x ⎛⎫+= ⎪⎝⎭,∴4233x +=±,解得:x 1=23-,x 2=2-;(2)2310x x --=,则a =1,b =-3,c =-1,∵b 2-4ac =9+4=13>0,∴x解得:x 1,x 2(3)()()421321x x x +=+,∴()()4213210x x x +-+=,∴()()04321x x -+=,∴4x -3=0或2x +1=0,解得:x 1=34,x 2=12-;(4)2320x x --=,则a =3,b =-1,c =-2,∵b 2-4ac =1+24=25>0,∴x ,解得:x 1=1,x 2=23-.【点睛】此题考查了解一元二次方程-配方法、公式法及因式分解法,利用因式分解法解方程时,首先将方程右边化为0,左边的多项式化为积的形式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.19.解:(1)24x =(2)2.5.【分析】(1)利用根与系数的关系12b x x a +=-求解;(2)解一元二次方程,然后利用三角形面积公式进行计算求解.【详解】解:∵一元二次方程260x x k -+=的两根分别为1x 、2x ∴12b x x a +=-,即226x +=∴24x =;(2)当5k =时,2650x x -+=解得:121,5x x ==∵1x 、2x 分别是Rt ABC ∆的两条直角边的长∴115 2.52Rt ABC S ∆=⨯⨯=【点睛】本题考查一元二次方程根与系数的关系及解一元二次方程,掌握公式和解方程的一般步骤正确计算是本题的解题关键.20.详见解析【分析】根据平行四边形性质得出AB=CD ,∠A=∠C .求出∠ABD=∠CDB .推出∠ABE=∠CDF ,根据ASA 推出△ABE ≌△CDF 即可证得DE=BF ;再又DE ∥BF 可得.【详解】证明:在□ABCD 中,AB=CD ,∠A=∠C,AD=BC .∵AB ∥CD ,∴∠ABD=∠CDB .∵BE 平分∠ABD ,DF 平分∠CDB ,∴∠ABE=12∠ABD ,∠CDF=12∠CDB .∴∠ABE=∠CDF .∵在△ABE 和△CDF 中,A C AB DC ABE CDF ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABE ≌△CDF (ASA ).∴AE=CF∴AD-AE=BC-CF,即DE=BF又AD ∥BC∴四边形DEBF 是平行四边形【点睛】本题考查了平行线的性质,平行四边形的性质和判定,全等三角形的性质和判定,角平分线定义等知识点的应用,熟练运用平行四边形的判定和性质是关键.21.见解析【解析】【分析】根据平移的性质得到∠GCB=∠DAF ,然后利用ASA 证得两三角形全等即可.【详解】解:△ADF ≌△CBG ;理由:∵把△ABE 沿CB 向左平移,使点E 与点C 重合,∴∠GCB=∠E ,∵四边形ABCD 是矩形,∴∠E=∠DAF ,∴∠GCB=∠DAF ,在△ADF 与△CBG 中,90D GBC GCB DAF BC AD ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩,∴△ADF ≌△CBG (ASA ).【点睛】本题考查了矩形的性质及全等三角形的判定等知识,解题的关键是了解矩形的性质与平移的性质,难度不大.22.(1)见解析;(2)40【分析】(1)先根据矩形的性质得到AD∥BC,AD=BC,然后证明AD=EF可判断四边形AEFD 是平行四边形;(2)连接DE,如图,先利用勾股定理计算出AE=ABE∽△DEA,利用相似比求出AD,然后根据平行四边形的面积公式计算.【详解】(1)证明:∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∵BE=CF,∴BE+EC=EC+CF,即BC=EF,∴AD=EF,∴四边形AEFD是平行四边形;(2)解:连接DE,如图,∵四边形ABCD是矩形,∴∠B=90°,在Rt△ABE中,AE∵AD∥BC,∴∠AEB=∠EAD,∵∠B=∠AED=90°,∴△ABE∽△DEA,∴AE:AD=BE:AE,∴AD =2=10,∵AB =4,∴四边形AEFD 的面积=AB ×AD =4×10=40.【点睛】本题考查了矩形的性质,平行四边形的性质与判定,相似三角形的性质与判定,掌握以上知识点是解题的关键.23.(1)4y x=-;(2)点P 的坐标为()0,1或()0,5.【分析】(1)根据反比例函数系数的几何意义,利用△AOB 的面积即可求出m 值,然后把点A 的坐标代入反比例函数解析式,计算即可得到k 的值.(2)先一次函数的解析式,再求出点C 坐标为(4,−1),设P 点坐标为(0,c ),根据题意有:113134522c c ⨯-⨯+⨯-⨯=,解方程即可求得.【详解】解:(1)依题意得1122m ⨯⨯=,∴4m =,∴()1,4A -,把点()1,4A -代入k y x=得41k =-,∴4k =-,∴反比例函数解析式为4y x =-;(2)∵()1,4A -,代入一次函数3y ax =+,得4=-a +3,解得a =-1∴3y x =-+令x =0,y =3,∴D (0,3)将点()4,C n 代入4y x=-,得:1n =-,则点C 坐标为()41-,,设点P 坐标为()0,c ,∴PD =3c -PAC △的面积为5,∴113134522c c ⨯-⨯+⨯-⨯=,解得:1c =或5c =,则点P 的坐标为()0,1或()0,5.【点睛】本题考查了反比例函数和一次函数图象的交点问题,反比例函数系数的几何意义,反比例函数图象上点的坐标特征,即过双曲线上任意一点引x 轴、y 轴垂线,所得矩形面积为|k |,三角形的面积是12|k |.24.这件货物高约5.1米.【分析】根据解直角三角形的解法得出BD ,CD 的长即可.【详解】解:∵tan ∠BAD =BD AD ,tan ∠CAD =CD AD ,∴BD =AD tan ∠BAD =3×tan35°≈2.1,CD =AD tan ∠CAD =3×1=3,∴BC =BD +CD =2.1+3=5.1(米)答:这件货物高约5.1米.【点睛】本题主要考查了解直角三角形的应用,关键是根据题意作出辅助线,构造直角三角形.25.(1)PD =PE 且PD ⊥PE ,理由见详解;(2)①(1)中猜想成立,理由见详解;②2222BC CE PB +=,证明见详解.【分析】(1)根据点P 在线段AO 上,利用三角形的全等判定可以得出问题;(2)①利用三角形全等得出BP =PD ,由PB =PE 可得PE =PD ,要证PE ⊥PD 可从三方面分析,当点E 在线段BC 上(E 与B 、C 不重合)时,当点E 与点C 重合时,点P 恰好在AC 中点处,当点E 在BC 的延长线上时,分别分析即可求解;②连接DE ,由①知PE =PD ,PE ⊥PD ,由勾股定理可得22222DE PD PE PE =+=,由四边形ABCD 是正方形可得BC =DC ,∠BCD =∠DCE =90°,根据222DC CE DE +=知22222BC CE DE PE +==,然后结合PE =PB 可求解.【详解】解:(1)PD=PE且PD⊥PE,理由如下:∵四边形ABCD是正方形,∴BC=DC,∠BCP=∠DCP=45°,∵PC=PC,∴△BCP≌△DCP(SAS),∴PB=PD,∠PBC=∠PDC,∵PE=PB,∴PD=PE,∠PBC=∠PEB,∴∠PDC=∠PEB,∴∠PDC+∠PEC=180°,由四边形PECD内角和为360°,∴∠DPE+∠DCE=180°,∵∠DCE=90°,∴∠DPE=90°,∴PD=PE且PD⊥PE;(2)①(1)中结论仍成立,理由如下:∵四边形ABCD是正方形,∴BA=DA,∠BAP=∠DAP=45°,∵PA=PA,∴△BAP≌△DAP(SAS),∴PB=PD,∵PE=PB,∴PD=PE,a、当点E与点C重合时,点P恰好在AC中点处,此时PE⊥PD;b、当点E在BC的延长线上时,如图所示:∵△BAP ≌△DAP ,∴∠ABP =∠ADP ,∴∠CDP =∠CBP ,∵BP =PE ,∴∠CBP =∠PEC ,∴∠PDC =∠PEC ,∵∠1=∠2,∴∠DPE =∠DCE =90°,∴PE ⊥PD ,综上所述:PD =PE 且PD ⊥PE 仍成立;②数量关系:2222BC CE PB +=,证明如下:如图2,连接DE ,由①可得PD =PE 且PD ⊥PE ,∴22222DE PD PE PE =+=,∵四边形ABCD 是正方形,∴BC =DC ,∠BCD =∠DCE =90°,∴在Rt △DCE 中,222DC CE DE +=,∴22222BC CE DE PE +==,∵PE =PB ,∴2222BC CE PB +=.【点睛】本题主要考查正方形的性质、勾股定理及全等三角形的性质与判定,熟练掌握正方形的性质、勾股定理及全等三角形的性质与判定是解题的关键.。
北师大版九年级上册数学期末考试试卷附答案详解

北师大版九年级上册数学期末考试试题一、选择题。
(每小题只有一个正确答案)1.在下面的四个几何体中,同一几何体的主视图与俯视图相同的是()A .B .C .D .2.如图,Rt △ABC 中,∠C=90°,AB=2,BC=1,则sinA 等于()A .2BC .12D 3.如图,点P 在△ABC 的边AC 上,要判断△ABP ∽△ACB ,添加一个条件,不正确的是A .∠ABP=∠CB .∠APB=∠ABC C .AP ABAB AC=D .AB ACBP CB=4.如果两个相似三角形的相似比是1:4,那么这两个相似三角形的周长比是()A .2:1B .1:16C .1:4D .1:25.要使菱形ABCD 成为正方形,需要添加的条件是()A .AB=CDB .AD=BCC .AB=BCD .AC=BD 6.已知点A (3,a )与点B (5,b )都在反比例函数y=﹣2x的图象上,则a 与b 之间的关系是()A .a >bB .a <bC .a≥bD .a=b7.某池塘中放养了鲫鱼1000条,鲮鱼若干条,在几次随机捕捞中,共抓到鲫鱼200条,鲮鱼400条,估计池塘中原来放养了鲮鱼()A .500条B .1000条C .2000条D .3000条8.一元二次方程x 2﹣2x+3=0根的情况是()A .有两个不相等的实数根B .有两个相等的实数根C .没有实数根D .无法判断9.已知反比例函数ky x=的图象经过点(﹣1,5),则此反比例函数的图象位于()A .第一、二象限B .第二、三象限C .第二、四象限D .第一、三象限10.如图,一次函数1(0)y kx b k =+≠的图象与反比例函数2my x=(m 为常数且0m ≠)的图象都经过()()1,2,2,1A B --,结合图象,则不等式mkx b x+>的解集是()A .1x <-B .10x -<<C .1x <-或02x <<D .10x -<<或2x >二、填空题11.方程22x x =的根是________.12.如图,已知DE ∥BC ,AE=3,AC=5,AB=6,则AD=_____.13.如图,过反比例函数y=6x(x >0)图象上的一点A ,作x 轴的垂线,垂足为B 点,连接OA ,则S △AOB =_____14.如图,菱形ABCD 中,对角线AC 与BD 相交于点O ,且AC=8,BD=6,则菱形ABCD 的高DH=_____.15.如图,在A时测得旗杆的影长是4米,B时测得旗杆的影长是16米,若两次的日照光线恰好垂直,则旗杆的高度是______米.16.已知矩形的长是3,宽是2,另一个矩形的周长和面积分别是已知矩形周长和面积的2倍,那么新矩形的长是_____.三、解答题17.计算:2sin30°+4cos30°·tan60°-cos245°18.由于提倡环保节能,自行车已成为市民日常出行的主要工具之一,据某自行车经销店4至6月份统计,某品牌自行车4月份销售200辆,6月份销售338辆,求该品牌自行车销售量的月平均增长率.19.如图,在6×8网格图中,每个小正方形边长均为1,点O和△ABC的顶点均在小正方形的格点上.(1)以O为位似中心,在网格图中作△A′B′C′,使△A′B′C′和△ABC位似,且相似比为1:2;(2)连接(1)中的BB′,CC′,求四边形BB′C′C的周长.(结果保留根号)20.如图,某幢大楼顶部有广告牌CD,小宇身高MA为1.89米,他站在立在离大楼45米的A 处测得大楼顶端点D的仰角为30°;接着他向大楼前进15米,站在点B处测得广告牌顶端点C 的仰角为45°.(1)求这幢大楼的高DH ;(2)求这块广告牌CD 的高度.(.732,计算结果保留一位小数)21.在一个不透明的口袋里装有若干个除颜色外其余均相同的红、黄、蓝三种颜色的小球,其中红球2个,篮球1个,若从中任意摸出一个球,摸到球是红球的概率为12.(1)求袋中黄球的个数;(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,求两次摸到球的颜色是红色与黄色这种组合(不考虑红、黄球顺序)的概率.22.某超市服装专柜在销售中发现:某男装上衣的进价为每件30元,当售价为每件50元时,每周可卖出200件,现需降价处理,经过市场调查,发现每降价1元,每周可多卖出20件.(1)为占有更大的市场份额,当降价为多少元时,每周盈利为4420元?(2)当降价为多少元时,每周盈利额最大?最大盈利多少元?23.如图,一次函数y=x+b 和反比例函数y=xk(k≠0)交于点A (4,1).(1)求反比例函数和一次函数的解析式;(2)求△AOB 的面积;(3)根据图象直接写出一次函数的值大于反比例函数的值的x 的取值范围.24.如图,以△ABC 的各边,在边BC 的同侧分别作三个正方形ABDI ,BCFE ,ACHG .(1)求证:△BDE ≌△BAC ;(2)求证:四边形ADEG 是平行四边形.(3)直接回答下面两个问题,不必证明:①当△ABC 满足条件_____________________时,四边形ADEG 是矩形.②当△ABC 满足条件_____________________时,四边形ADEG 是正方形?25.如图,直线y=﹣23x+c 与x 轴交于点A (3,0),与y 轴交于点B ,抛物线y=﹣43x 2+bx+c 经过点A ,B ,M (m ,0)为x 轴上一动点,点M 在线段OA 上运动且不与O ,A 重合,过点M 且垂直于x 轴的直线与直线AB 及抛物线分别交于点P ,N .(1)求点B 的坐标和抛物线的解析式;(2)在运动过程中,若点P 为线段MN 的中点,求m 的值;(3)在运动过程中,若以B ,P ,N 为顶点的三角形与△APM 相似,求点M 的坐标;参考答案1.D【详解】试题分析:主视图、俯视图是分别从物体正面和上面看,所得到的图形.因此,A、圆柱主视图、俯视图分别是长方形、圆,主视图与俯视图不相同,故A选项错误;B、圆锥主视图、俯视图分别是三角形、有圆心的圆,主视图与俯视图不相同,故B选项错误;C、三棱柱主视图、俯视图分别是长方形,三角形,主视图与俯视图不相同,故C选项错误;D、球主视图、俯视图都是圆,主视图与俯视图相同,故D选项正确.故选D.考点:简单几何体的三视图.2.C【解析】【分析】结合图形运用三角函数定义求解.【详解】∵AB=2、BC=1,∴sinA=1=2 BC AB,故选C.【点睛】本题考查的是锐角三角函数的定义,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.3.D【详解】试题分析:A.当∠ABP=∠C时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;B.当∠APB=∠ABC时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;C.当AP ABAB AC时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误;D.无法得到△ABP∽△ACB,故此选项正确.故选D.考点:相似三角形的判定.4.C【分析】直接根据相似三角形周长的比等于相似比即可得出结论.【详解】∵两个相似三角形的相似比是1:4,∴这两个相似三角形的周长比是1:4.故选C.【点睛】本题考查的是相似三角形的性质,熟知相似三角形对应周长的比等于相似比是解答此题的关键.5.D【分析】根据有一个角是直角的菱形是正方形即可解答.【详解】如图,∵四边形ABCD是菱形,∴要使菱形ABCD成为一个正方形,需要添加一个条件,这个条件可以是:∠ABC=90°或AC=BD.故选D.【点睛】本题考查了正方形的判定,解答此题的关键是熟练掌握正方形的判定定理,正方形的判定方法:①先判定四边形是矩形,再判定这个矩形有一组邻边相等;②先判定四边形是菱形,再判定这个菱形有一个角为直角.③还可以先判定四边形是平行四边形,再用①或②进行判定.6.B【分析】直接利用反比例函数的增减性分析得出答案.【详解】∵点A(3,a)与点B(5,b)都在反比例函数y=﹣2x的图象上,∴每个象限内y随x的增大而增大,则a<b.故选B.【点睛】此题主要考查了反比例函数的增减性,正确记忆反比例函数的性质是解题关键.7.C【分析】先根据题意可得到鲫鱼与鲮鱼之比为1:2,再根据鲫鱼的总条数计算出鲮鱼的条数即可.【详解】由题意得:鲫鱼与鲮鱼之比为:200:400=1:2,∵鲫鱼1000条,∴鲮鱼条数是:1000×2=2000.故答案选:C.【点睛】本题主要考查了用样本估计总体,关键是知道样本的鲫鱼与鲮鱼之比就是池塘内鲫鱼与鲮鱼之比.8.C【分析】直接利用根的判别式进而判断,即可得出答案.【详解】∵a=1,b=﹣2,c=3,∴b2﹣4ac=4=4﹣4×1×3=﹣8<0,∴此方程没有实数根.故选C.【点睛】此题主要考查了根的判别式,当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.9.C 【分析】把点(-1,5)代入反比例函数ky x=得到关于k 的一元一次方程,解之,即可得到反比例函数的解析式,根据反比例函数的图象和性质,即可得到答案.【详解】解:把点(﹣1,5)代入反比例函数ky x=得:1k-=5,解得:k =﹣5,即反比例函数的解析式为:y =5x-,此反比例函数的图象位于第二、第四象限,故选:C .【点睛】本题考查了反比例函数图象上点的坐标特征,反比例函数的图象,反比例函数的性质,正确掌握代入法,反比例函数的图象和性质是解题的关键.10.C 【分析】根据一次函数图象在反比例函数图象上方的x 的取值范围便是不等式mkx b x+>的解集.【详解】解:由函数图象可知,当一次函数()10y kx b k =+≠的图象在反比例函数2my x=(m 为常数且0m ≠)的图象上方时,x 的取值范围是:1x <-或02x <<,∴不等式mkx b x+>的解集是1x <-或02x <<.故选C .【点睛】本题是一次函数图象与反比例函数图象的交点问题:主要考查了由函数图象求不等式的解集.利用数形结合是解题的关键.11.x 1=0,x 2=2【分析】先移项,再用因式分解法求解即可.【详解】解:∵22x x =,∴22=0x x -,∴x(x-2)=0,x 1=0,x 2=2.故答案为:x 1=0,x 2=2.【点睛】本题考查了一元二次方程的解法,常用的方法有直接开平方法、配方法、因式分解法、求根公式法,灵活选择合适的方法是解答本题的关键.12.3.6.【分析】根据平行线分线段成比例定理得出比例式,代入求出即可.相似三角形的判定推出【详解】解:∵DE ∥BC ,∴AE ADAC AB=,∴356AD =,解得:AD =3.6,故答案为:3.6.【点睛】本题考查了平行线分线段成比例定理,能根据平行线得出比例式是解此题的关键.13.3【分析】设A (x ,6x ),则有OB=x ,AB=6x,根据三角形面积公式可得答案.【详解】设A (x ,6x )则有,OB=x ,AB=6x∴S△AOB =162xx⨯⨯=3,故答案为:3,【点睛】本题考查反比例函数系数k的几何意义,记住:反比例函数的图象上任意一点向坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是12|k|,且保持不变.14.4.8.【详解】试题分析:在菱形ABCD中,AC⊥BD,∵AC=8,BD=6,∴OA=12AC=12×8=4,OB=12BD=12×6=3,在Rt△AOB中,由勾股定理可得AB=5,∵DH⊥AB,∴菱形ABCD的面积=12AC•BD=AB•DH,即12×6×8=5•DH,解得DH=4.8.考点:菱形的性质.15.8【分析】如图,∠CPD=90°,QC=4m,QD=9m,利用等角的余角相等得到∠QPC=∠D,则可判断Rt△PCQ∽Rt△DPQ,然后利用相似比可计算出PQ.【详解】解:如图,∠CPD=90°,QC=4m,QD=16m,∵PQ⊥CD,∴∠PQC=90°,∴∠C+∠QPC=90°,而∠C+∠D=90°,∴∠QPC=∠D,∴Rt△PCQ∽Rt△DPQ,∴PQ QCQD PQ=,即416PQPQ=,∴PQ=8,即旗杆的高度为8m.故答案为8.【点睛】本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.平行投影中物体与投影面平行时的投影是全等的.也考查了相似三角形的判定与性质.16.【分析】设新矩形的长为x,则新矩形的宽为(10-x),根据新矩形的面积为12,即可得出关于x的一元二次方程,解之取其较大值即可得出结论.【详解】设新矩形的长为x,则新矩形的宽为(10﹣x),根据题意得:x(10﹣x)=2×3×2,整理得:x2﹣10x+12=0,解得:x1=5x2∵x≥10﹣x,∴x≥5,∴故答案为:【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.17.132【解析】分析:将sin30°=12,详解:原式=2×12+2=1+6-12=132点睛:考查了特殊角的三角函数值,解答本题的关键是掌握一些特殊角的三角函数值,请牢记以下特殊三角函数值:18.月平均增长率为30%.【分析】设该品牌自行车销售量的月平均增长率为x ,根据4月、6月份的销售量,即可得出关于x 的一元二次方程,解之取其正值即可得出结论.【详解】设该品牌自行车销售量的月平均增长率为x ,根据题意得:200(1+x )2=338,解得:x 1=0.3=30%,x 2=﹣2.3(不合题意,舍去).答:该品牌自行车销售量的月平均增长率为30%.【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.19.(1)见解析;(2)【分析】(1)直接利用位似图形的性质得出对应点位置进而得出答案;(2)利用勾股定理得出各线段长,进而得出答案.【详解】(1)如图所示:△A′B′C′,即为所求;(2)四边形BB′C′C 的周长为:.【点睛】此题主要考查了位似变换,正确得出对应点位置是解题关键.20.(1)楼高DH 为27.9米;(2)广告牌CD 的高度为4.0米.【解析】【分析】在Rt △DME 与Rt △CNE ;应利用ME-NE=AB=15构造方程关系式,进而可解即可求出答案.【详解】解:(1)在Rt △DME 中,ME=AH=45;由tan 30°=DE ME ,得DE=45×3≈15×1.732=25.98;又因为EH=MA=1.89,故大楼DH=DE+EH=25.98+1.89=27.87≈27.9.(2)在Rt △CNE 中,NE=45-15=30,由tan 45°=CE NE,得CE=NE=30,因而广告牌CD=CE-DE=30-25.98≈4.0.答:楼高DH 为27.9米,广告牌CD 的高度为4.0米.【点睛】本题要求学生借助仰角关系构造直角三角形,并结合图形利用三角函数解直角三角形.21.(1)袋中黄球的个数1个;(2)两次摸到球的颜色是红色与黄色这种组合的概率为1 3 .【分析】(1)首先设袋中的黄球个数为x个,然后根据古典概率的知识列方程,求解即可求得答案;(2)首先画树状图,然后求得全部情况的总数与符合条件的情况数目,求其二者的比值即可.【详解】(1)设袋中的黄球个数为x个,∴21= 212x++,解得:x=1,经检验,x=1是原方程的解,∴袋中黄球的个数1个;(2)画树状图得:,∴一共有12种情况,两次摸到球的颜色是红色与黄色这种组合的有4种,∴两次摸到球的颜色是红色与黄色这种组合的概率为:4 12 =13【点睛】此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件.注意方程思想的应用.22.(1)当降价为7元时,每周盈利为4420元;(2)当降价为5元时,每周盈利额最大,最大盈利4500元.【分析】(1)设降价为x元,根据“总利润=每件利润×销售量”列出关于x的方程,解之得出x的值,再根据要占有更大的市场份额,即销量尽可能的大取舍即可得;(2)设每周盈利为y,根据以上所列相等关系列出函数解析式,将其配方成顶点式后利用二次函数的性质求解可得.【详解】(1)设降价为x元,根据题意,可得:(50﹣x ﹣30)(200+20x )=4420,整理,得:x 2﹣10x+21=0,解得:x 1=3,x 2=7,因为要占有更大的市场份额,即销量尽可能的大,所以x=7,答:当降价为7元时,每周盈利为4420元;(2)设每周盈利为y ,则y=(50﹣x ﹣30)(200+20x )=﹣20x 2+200x+4000=﹣20(x ﹣5)2+4500,所以当x=5时,y 取得最大值,最大值为4500,答:当降价为5元时,每周盈利额最大,最大盈利4500元.【点睛】本题主要考查了二次函数的应用,最值问题一般的解决方法是转化为函数问题,根据函数的性质求解.23.(1)反比例函数的解析式为:y=4x ;一次函数的解析式为:y=x ﹣3;(2)S △AOB =152;(3)一次函数的值大于反比例函数的值的x 的取值范围为:﹣1<x <0或x >4.【分析】(1)把A 的坐标代入y=k x,求出反比例函数的解析式,把A 的坐标代入y=x+b 求出一次函数的解析式;(2)求出D 、B 的坐标,利用S △AOB =S △AOD +S △BOD 计算,即可求出答案;(3)根据函数的图象和A 、B 的坐标即可得出答案.【详解】(1)∵反比例函数y=k x 的图象过点A (4,1),∴1=k 4,即k=4,∴反比例函数的解析式为:y=4x.∵一次函数y=x+b (k≠0)的图象过点A (4,1),∴1=4+b,解得b=﹣3,∴一次函数的解析式为:y=x﹣3;(2)∵令x=0,则y=﹣3,∴D(0,﹣3),即DO=3.解方程4x=x﹣3,得x=﹣1,∴B(﹣1,﹣4),∴S△AOB =S△AOD+S△BOD=12×3×4+12×3×1=152;(3)∵A(4,1),B(﹣1,﹣4),∴一次函数的值大于反比例函数的值的x的取值范围为:﹣1<x<0或x>4.【点睛】本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了观察函数图象的能力.24.(1)见解析;(2)见解析;(3)①∠BAC=135°;②∠BAC=135°且AC【分析】(1)根据全等三角形的判定定理SAS证得△BDE≌△BAC;(2)由△BDE≌△BAC,可得全等三角形的对应边DE=AG.然后利用正方形对角线的性质、周角的定义推知∠EDA+∠DAG=180°,易证ED∥GA;最后由“一组对边平行且相等”的判定定理证得结论;(3)①根据“矩形的内角都是直角”易证∠DAG=90°.然后由周角的定义求得∠BAC=135°;②由“正方形的内角都是直角,四条边都相等”易证∠DAG=90°,且AG=AD.由正方形ABDI和正方形ACHG的性质证得:AC=.【详解】(1)∵四边形ABDI、四边形BCFE、四边形ACHG都是正方形,∴AC=AG,AB=BD,BC=BE,∠GAC=∠EBC=∠DBA=90°,∴∠ABC=∠EBD(同为∠EBA的余角).在△BDE和△BAC中,∵BD BADBE ABCBE BC=⎧⎪∠=∠⎨⎪=⎩,∴△BDE≌△BAC(SAS);(2)∵△BDE≌△BAC,∴DE=AC=AG,∠BAC=∠BDE.∵AD是正方形ABDI的对角线,∴∠BDA=∠BAD=45°.∵∠EDA=∠BDE﹣∠BDA=∠BDE﹣45°,∠DAG=360°﹣∠GAC﹣∠BAC﹣∠BAD=360°﹣90°﹣∠BAC﹣45°=225°﹣∠BAC,∴∠EDA+∠DAG=∠BDE﹣45°+225°﹣∠BAC=180°,∴DE∥AG,∴四边形ADEG是平行四边形(一组对边平行且相等).(3)①当四边形ADEG是矩形时,∠DAG=90°.则∠BAC=360°﹣∠BAD﹣∠DAG﹣∠GAC=360°﹣45°﹣90°﹣90°=135°,即当∠BAC=135°时,平行四边形ADEG是矩形;②当四边形ADEG是正方形时,∠DAG=90°,且AG=AD.由①知,当∠DAG=90°时,∠BAC=135°.∵四边形ABDI是正方形,∴AD.又∵四边形ACHG是正方形,∴AC=AG,∴AC=,∴当∠BAC=135°且AC=时,四边形ADEG是正方形.【点睛】本题综合考查了正方形的判定与性质,全等三角形的判定与性质,平行四边形的判定与性质等知识点.解题时,注意利用隐含在题干中的已知条件:周角是360°.25.(1)B(0,2),抛物线解析式为y=﹣43x2+103x+2;(2)m的值为1 2;(3)当以B,P,N为顶点的三角形与△APM相似时,点M的坐标为(2.5.0)或(118,0).【分析】(1)把A点坐标代入直线解析式可求得c,则可求得B点坐标,由A、B的坐标,利用待定系数法可求得抛物线解析式;(2)用m可表示出M、P、N的坐标,由题意可知有P为线段MN的中点,可得到关于m 的方程,可求得m的值.(3)由M点坐标可表示P、N的坐标,从而可表示出MA、MP、PN、PB的长,分∠NBP=90°和∠BNP=90°两种情况,分别利用相似三角形的性质可得到关于m的方程,可求得m的值,从而得到点M的坐标.【详解】(1)∵y=﹣23x+c与x轴交于点A(3,0),与y轴交于点B,∴0=﹣2+c,解得c=2,∴B(0,2),∵抛物线y=﹣43x2+bx+c经过点A,B,∴12302b cc-++=⎧⎨=⎩,解得1032bc⎧=⎪⎨⎪=⎩,∴抛物线解析式为y=﹣43x2+103x+2;(2)由(1)可知直线解析式为y=﹣23x+2,∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,∴P(m,﹣23m+2),N(m,﹣43m2+103m+2),∵P为线段MN的中点时,∴有2(﹣23m+2)=﹣43m2+103m+2,解得m=3(三点重合,舍去)或m=1 2.故m的值为1 2.(3)由(1)可知直线解析式为y=﹣23x+2,∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,∴P(m,﹣23m+2),N(m,﹣43m2+103m+2),∴PM=﹣23m+2,AM=3﹣m,PN=﹣43m2+103m+2﹣(﹣23m+2)=﹣43m2+4m,∵△BPN和△APM相似,且∠BPN=∠APM,∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°,当∠BNP=90°时,则有BN⊥MN,∴N点的纵坐标为2,∴﹣43m2+103m+2=2,解得m=0(舍去)或m=2.5,∴M(2.5,0);当∠NBP=90°时,过点N作NC⊥y轴于点C,则∠NBC+∠BNC=90°,NC=m ,BC=﹣43m 2+103m+2﹣2=﹣43m 2+103m ,∵∠NBP=90°,∴∠NBC+∠ABO=90°,∴∠ABO=∠BNC ,∴Rt △NCB ∽Rt △BOA ,∴NC CB =OB OA,∴2π=2410333m m -+,解得m=0(舍去)或m=118,∴M (118,0);综上可知,当以B ,P ,N 为顶点的三角形与△APM 相似时,点M 的坐标为(2.5.0)或(118,0).【点睛】本题为二次函数的综合应用,涉及待定系数法、函数图象的交点、相似三角形的判定和性质、勾股定理、线段的中点、方程思想及分类讨论思想等知识.在(1)中注意待定系数法的应用,在(2)中得到m 的方程是解题的关键,在(3)中利用相似三角形的性质得到关于m 的方程是解题的关键,注意分两种情况.本题考查知识点较多,综合性较强,分情况讨论比较多,难度较大.。
北师大版数学九年级上册期末考试试卷含答案
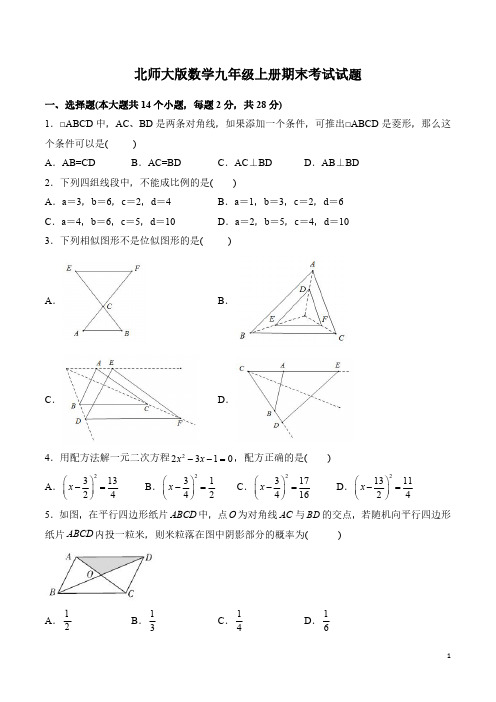
北师大版数学九年级上册期末考试试题一、选择题(本大题共14个小题,每题2分,共28分)1.□ABCD中,AC、BD是两条对角线,如果添加一个条件,可推出□ABCD是菱形,那么这个条件可以是()A.AB=CD B.AC=BD C.AC⊥BD D.AB⊥BD2.下列四组线段中,不能成比例的是()A.a=3,b=6,c=2,d=4B.a=1,b=3,c=2,d=6C.a=4,b=6,c=5,d=10D.a=2,b=5,c=4,d=103.下列相似图形不是位似图形的是()A.B.C.D.4.用配方法解一元二次方程22310x x--=,配方正确的是()A.231324x⎛⎫-=⎪⎝⎭B.23142x⎛⎫-=⎪⎝⎭C.2317416x⎛⎫-=⎪⎝⎭D.2131124x⎛⎫-=⎪⎝⎭5.如图,在平行四边形纸片ABCD中,点O为对角线AC与BD的交点,若随机向平行四边形纸片ABCD内投一粒米,则米粒落在图中阴影部分的概率为()A.12B.13C.14D.166.如图,要使ABC ACD ∆∆ ,需补充的条件不能是()A .ADC ACB∠=∠B .ABC ACD ∠=∠C .AD AC AC AB =D .AD BC AC DC⋅=⋅7.若反比例函数21k y x +=的图象位于第一、三象限,则k 的取值可以是()A .﹣3B .﹣2C .﹣1D .08.如图,直线12//l l ,:2:3AF FB =,:2:1BC CD =,则:AE EC 是()A .1:2B .1:4C .2:1D .3:29.在一个不透明的布袋中,有黄色、白色的玻璃球共有20个,除颜色外,形状、大小、质地等完全相同.小刚每次换出一个球后放回,通过多次摸球实验后发现摸到黄色球的频率稳定在40%,则布袋中白色球的个数很可能是()A .8个B .15个C .12个D .16个10.如图,在矩形ABCD 中,AB =a (a <2),BC =2.以点D 为圆心,CD 的长为半径画弧,交AD 于点E ,交BD 于点F .下列哪条线段的长度是方程2240x ax +-=的一个根()A .线段AE 的长B .线段BF 的长C .线段BD 的长D .线段DF 的长11.如图,在四边形ABCD 中,//AD BC ,DE BC ⊥,垂足为点E ,连接AC 交DE 于点F ,点G 为AF 的中点,2ACD ACB ∠=∠.若3DG =,1EC =,则DE 的长为()A12B10C8D612.如图1,有一张长32cm,宽16cm的长方形硬纸片,裁去角上2个小正方形和2个小长方形(图中阴影部分)之后,恰好折成如图2所示的有盖纸盒.若纸盒的底面积是2130cm,则纸盒的高为()A.2cm B.2.5cm C.3cm D.4cm13.已知一次函数y=kx+b的图象如图,那么正比例函数y=kx和反比例函数y=bx在同一坐标系中的图象的形状大致是()A.B.C.D.14.如图,四边形ABCD为菱形,BF∥AC,DF交AC的延长线于点E,交BF于点F,且CE:AC=1:2.则下列结论:①△ABE≌△ADE;②∠CBE=∠CDF;③DE=FE;④S△BCE:S四边形ABFD=1:10.其中正确结论的个数是()A .1个B .2个C .3个D .4个二、填空题(本题共3个小题;每个小题4分,共12分)15.若干个桶装方便面摆放在桌子上,小明从三个不同方向看到的图形(分别是:主视图,左视图,和俯视图)如图所示,则这一堆方便面共有__________个16.方程()()130x x --=的解是__________.17.已知在Rt ABC ∆中,90,3,4C BC cm AC cm ︒∠===,点,M N 分别在边AC AB 、上,将ABC ∆沿直线MN 对折后,点A 正好落在对边BC 上,且折痕MN 截ABC ∆所成的小三角形(即对折后的重叠部分)与ABC ∆相似,则折折痕MN =__________cm三、解答题(本题共8道题,18-20每题6分,21-245每题8分,25题10分,满分60分)18.我们定义一种关于“★”的新运算:a ★b ab a b =+-,试根据条件回答问题.(1)计算:2★()=3-_____;(2)若x ★()11x +=,求x 的值.19.己知:如图,点A 在反比例函数()0k y x x =>的图像上,且点A 的横坐标为2,作AH 垂直于x 轴,垂足为点H ,3AOHS = .(1)求AH 的长;(2)求k 的值;(3)若()11,M x y 、()22,N x y 在该函数图像上,当120x x <<时,比较1y 与2y 的大小关系.20.2019年,市教育局在全市中小学中选取了63所学校从学生的思想品德、学业水平、学业负担、身心发展和兴趣特长五个维度进行了综合评价.评价小组在选取的某中学全体学生中随机抽取了若干名学生进行问卷调查,了解他们每天在课外用于学习的时间,并绘制成如下不完整的统计图.根据上述信息,解答下列问题:(1)本次抽取的学生人数是______;扇形统计图中的圆心角 等于______;补全统计直方图.(2)被抽取的学生还要进行一次50米跑测试,每4人一组进行.在随机分组时,小红、小花两名女生被分到同一个小组,请用列表法或画树状图求出她俩在抽道次时抽在相邻两道的概率.21.一批发市场某服装批发价为240元/件.为拉动消费,该批发市场规定:当批发数量超过10件时,给予降价优惠,但批发价不得低于150元/件.经市场调查发现,优惠时批发价y(元/件)与x(件)之间成一次函数关系,当批发数量为15件时,批发价为210元/件;当批发数量为22件时,批发价为168元/件.(1)求批发价y(元/件)与x(件)之间的一次函数表达式;(2)在该市场降价优惠期间,某顾客一次性支付了3600元,求该顾客批发了多少件服装?22.已知,如图,矩形ABCD中,AD=6,DC=7,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,AD上,AH=2,连接CF.(1)当四边形EFGH为正方形时,求DG的长;(2)当DG=6时,求△FCG的面积;(3)求△FCG的面积的最小值.23.如图是小亮晚上在广场散步的示意图,图中线段AB表示站立在广场上的小亮,线段PO表示直立在广场上的灯杆,点P表示照明灯的位置.(1)在小亮由B沿OB所在的方向行走的过程中,他在地面上的影子的变化情况为______;(2)请你在图中画出小亮站在AB处的影子;(3)当小亮离开灯杆的距离 4.2OB m =时,身高(AB )为1.6m 的小亮的影长为1.6m ,问当小亮离开灯杆的距离6OD m =时,小亮的影长是多少m ?24.饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热,此过程中水温y (℃)与开机时间x (分)满足一次函数关系,当加热到100℃时自动停止加热,随后水温开始下降,此过程中水温y (℃)与开机时间x (分)成反比例关系,当水温降至20℃时,饮水机又自动开始加热……,重复上述程序(如图所示),根据图中提供的信息,解答问题:(1)当0≤x <8时,求水温y (℃)与开机时间x (分)的函数关系式.(2)求图中t 的值;(3)若在通电开机后即外出散步,请你预测散步42分钟回到家时,饮水机内的温度约为多少℃?25.如图所示,在△ABC 中,BA =BC =20cm ,AC =30cm ,点P 从A 点出发,沿着AB 以每秒4cm 的速度向B 点运动;同时点Q 从C 点出发,沿CA 以每秒3cm 的速度向A 点运动,设运动时间为x秒.(1)当x 为何值时,PQ //BC ;(2)当13BCQABC S S ∆∆=时,求S △BPQ :S △ABC 的值;(3)△APQ 能否与△CQB 相似?若能,求出时间x 的值;若不能,说明理由.答案一、选择题1.C.2.C .3.D .4.C.5.C.6.D.7.D .8.C .9.B .10.B.11.C .12.C .13.C .14.D .二、填空题15.516.11x =,23x =17.32或158.三、解答题18.解:(1)根据题中的新定义得:2★()()36231-=-+--=-;故答案为: 1-;(2)根据题中的新定义得:x ★()()()111x x x x x +=++-+=21x x +-∴21x x +-=1∴220x x +-=∴(2)(1)0x x +-=∴122,1x x =-=故答案是:-2或1.19.解:(1)∵点A 的横坐标为2,∴OH=2∵3AOH S = ∴12OH·AH=3解得:AH=3(2)∵OH=2,AH=3∴点A 的坐标为(2,3)将点A 的坐标代入ky x =中,得32k=解得:k=6(3)∵k=6>0∴反比例函数在第一象限内,y 随x 的增大而减小∵()11,M x y 、()22,N x y 在该函数图像上,且120x x <<∴1y >2y .20.(1)34-小时的人数有6人,占总人数20%,∴总人数有:620÷%30=(人),23-小时的人数有:30376212----=(人),占总人数为:1210030⨯%40=%,36040α=︒⨯%144=︒.补全直方图如下:;(2)列表法:小红,小花12341()2,1()3,1()4,12()1,2()3,2()4,23()1,3()2,3()4,34()1,4()3,4()3,461122P ==.21.解:(1)根据题意,则设一次函数的解析式为:y kx b =+,∴1521022168k b k b +=⎧⎨+=⎩,解得:6300k b =-⎧⎨=⎩,∴6300y x =-+;(2)根据题意,则可列方程:(6300)3600x x -+=,解得:1220,30x x ==当20x =时,6300180x -+=>150当30x =时,6300120x -+=<150,不合题意,舍去答:该顾客批发了20件服装.22.解:(1)∵四边形EFGH 为正方形,∴HG=HE ,∠EAH=∠D=90°,∵∠DHG+∠AHE=90°,∠DHG+∠DGH=90°,∴∠DGH=∠AHE ,∴△AHE ≌△DGH(AAS),∴DG=AH=2;(2)过F 作FM ⊥DC ,交DC 延长线于M ,连接GE ,∵AB∥CD,∴∠AEG=∠MGE,∵HE∥GF,∴∠HEG=∠FGE,∴∠AEH=∠MGF,在△AHE和△MFG中,∠A=∠M=90°,HE=FG,∴△AHE≌△MFG(AAS),∴FM=HA=2,即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2,因此S△FCG =12×FM×GC=12×2×(7-6)=1;(3)设DG=x,则由(2)得,S△FCG=7-x,在△AHE中,AE≤AB=7,∴HE2≤53,∴x2+16≤53,∴37,∴S△FCG的最小值为37,此时37,∴当37时,△FCG的面积最小为(7-37).23.(1)因为光是沿直线传播的,所以当小亮由B处沿BO所在的方向行走到达O处的过程中,他在地面上的影子长度的变化情况为变短;(2)如图所示,BE 即为所求(3)先设OP=x,则当OB=4.2米时,BE=1.6米,∴ 1.6 1.6, 4.2 1.6AB BE OP OE x ==+即∴x=5.8米当OD=6米时,设小亮的影长是y 米,∴DF CDDF OD OP=+∴ 1.66 5.8yy =+y=167(米)即小亮的影长是167米。
北师大版九年级上册数学期末考试试卷及答案

北师大版九年级上册数学期末考试试题一、单选题1.如图所示的几何体的主视图是()A.B.C.D.2.如果2a=5b,那么下列比例式中正确的是()A.25ab=B.25ab=C.52ab=D.25a b=3.已知m,n是方程x2+2x﹣5=0的两个实数根,则下列选项错误的是()A.m+n=﹣2B.mn=﹣5C.m2+2m﹣5=0D.m2+2n﹣5=04.已知反比例函数6yx=-,下列说法中正确的是()A.该函数的图象分布在第一、三象限B.点()2,3在该函数图象上C.y随x的增大而增大D.该图象关于原点成中心对称5.如图,某游乐场山顶滑梯的高BC为50米,滑梯的坡比为5:12,则滑梯的长AB为A.100米B.110米C.120米D.130米6.已知不透明的袋中只装有黑、白两种球,这些球除颜色外都相同,其中白球有30个,黑球有n个.随机地从袋中摸出一个球,记录下颜色后,放回袋子中并摇匀,再从中摸出一个球,经过如此大量重复试验,发现摸出的黑球的频率稳定在0.4附近,则n的值约为()A.20B.30C.40D.507.如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是()A B .136C .1D .568.如图,在平面直角坐标系中,OAB 与OCD 位似,点O 是它们的位似中心,已知()4,2A -,()2,1C -,则OAB 与OCD 的面积之比为()A .1:1B .2:1C .3:1D .4:19.如图,在ABC 中,E 、F 分别是AB 和AC 上的点,且EF BC ∥,且10AB =,6AE =,5AF =,那么AC 的长是()A .253B .103C .325D .31010.如图,在菱形ABCD 中,8AC =,3tan 4BAO ∠=,则菱形ABCD 的面积是()A .12B .24C .48D .20二、填空题11.已知△ABC ∽△A B C ''',AD 和A D ''是它们的对应中线,若AD =8,A D ''=6,则△ABC 与△A B C '''的周长比是_____.12.已知关于x 的一元二次方程(a ﹣2)x 2+2x+1=0有两个不相等的实数根,则a 的取值范围是_____.13.抛物线212y x =向左平移1个单位,再向上平移2个单位后,所得抛物线表达式为______.14.如图,在菱形ABCD 中,对角线AC 、BD 相交于点O ,E 为AB 中点,68AC BD ==,,则线段OE 的长为________________.15.如图,小树AB 在路灯O 的照射下形成投影BC .若树高AB =2m ,树影BC =3m ,树与路灯的水平距离BP =4m .则路灯的高度OP 为_____m .16.如图,在平行四边形ABCD 中,点E 是AB 的中点,CE 和BD 交于点O ,若1EOB S =△,则四边形AEOD 的面积为___________.17.如图,点A 的坐标为(1,0),点B 的坐标为(1,2),将 OAB 绕点A 第一次顺时针旋转90°得到 O 1AB 1,将 O 1AB 1绕点B 1第二次顺时针旋转90°得到 O 2A 1B 1,将 O 2A 1B 1绕点B 1第三次顺时针旋转90°得到 O 3A 2B 1,…,如此进行下去,则点O 2021的坐标为__.三、解答题18.用适当的方法解方程:(1)2410x x -=+;(2)22350x x --=.19.计算:2cos45°+(﹣12)-1+(2020)0+|2|.20.如图,小明想在自己家的窗口A 处测量对面建筑物CD 的高度,他首先量出窗口A 到地面的距离AB 为1.5m ,又测得从A 处看建筑物底部C 的俯角为30°,看建筑物顶部D 的仰角为45°,且AB ,CD 都与地面垂直,点A ,B ,C ,D 在同一平面内.则建筑物CD 的高度_____m .21.已知:△ABC 在坐标平面内,三个顶点的坐标分别为A (0,3),B (3,4),C (2,2).(正方形网格中,每个小正方形的边长是1个单位长度)(1)画出△ABC 向下平移4个单位得到的△A 1B 1C 1,并直接写出C 1点的坐标;(2)以点B 为位似中心,在网格中画出△A 2BC 2,使△A 2BC 2与△ABC 位似,且位似比为2︰1,并直接写出C 2点的坐标及△A 2BC 2的面积.22.如图,在Rt △ABC 中,∠BAC =90°,AD 是边BC 上的中线,过点A 作AE //BC ,过点D 作DE //AB ,DE 与AC ,AE 分别交于点O ,E ,连接EC .(1)求证:四边形ADCE 是菱形;(2)若AB =AO ,OD =1,则菱形ADCE 的周长为.23.如图,在 ACB中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.(1)求证: BDE∽ CEF;(2)当点E移动到BC的中点时,且BD=3,CF=2,则DEEF的值为.24.某超市准备进一批每个进价为40元的小家电,经市场调查预测,售价定为50元时可售出400个;定价每增加1元,销售量将减少10个.(1)设每个定价增加x元,此时的销售量是多少?(用含x的代数式表示)(2)超市若准备获得利润6000元,并且使进货量较少,则每个应定价为多少元?25.在矩形ABCD中,AD=6,AB=3E是边AD上的一个动点,连接BE,以BE 为一边在其左上方作矩形BEFG,过点F作直线AD的垂线,垂足为点H,连接DF.(1)当BE=EF时.①求证:FH=AE;②当 DEF 的面积是358时,求线段DE 的长;(2)如图2,当BE ,且射线FE 经过CD 的中点时,请直接写出线段FH 长.26.如图,一次函数1y x =--的图像与反比例函数ky x=的图像交于点A 、B ,与x 轴交于点C ,1AOCS =△.(1)求点A 的坐标与反比例函数的表达式.(2)设直线AB 与y 轴相交于点D ,经过计算可知点B 的坐标为()2,3-.若点Q 是y 轴上一点,是否存在点Q ,使得AQD AOB S S =△△?若存在,求出点Q 的坐标;若不存在,请说明理由.(3)求1kx x--≥的x 的取值范围.参考答案1.D 2.C 3.D4.D 5.D 6.A 7.D 8.D 9.A 10.B 11.4:312.3a <且2a≠【分析】根据一元二次方程的定义及根的判别式△>0,即可得出关于a 的一元一次不等式组,解之即可得出结论.【详解】∵关于x 的一元二次方程(a ﹣2)x 2+2x+1=0有两个不相等的实数根,∴22024(2)10a a -≠⎧⎨=--⨯>⎩,解得:a <3且a≠2.故答案为:a <3且a≠213.21212y x =++()【分析】根据函数图象向左平移加,向上平移加,可得答案.【详解】解:把抛物线212y x =向左平移1个单位,再向上平移2个单位,则所得抛物线的解析式是21212yx =++(),故答案为:21212y x =++().14.52【分析】由菱形的性质可得3OA OC ==,4OB OD ==,AO BO ⊥,由勾股定理求出AB ,再根据直角三角形斜边上的中线性质即可得出结果.【详解】解: 四边形ABCD 是菱形,6AC =,8BD =,3OA OC ∴==,4OB OD ==,AO BO ⊥,在Rt AOB 中,由勾股定理得:5AB ===,E 为AB 中点,1522OE AB ∴==故答案为:52.15.143【分析】由于OP 和AB 与地面垂直,则AB ∥OP ,根据相似三角形的判定可证△ABC ∽△OPC ,然后利用相似三角形的性质即可求出OP 的长.【详解】解:∵AB ∥OP ,∴△ABC ∽△OPC ,∴AB CBOP CP =,即2334OP =+,∴OP =143m .故答案为:143.16.5【分析】由在平行四边形ABCD 中,点E 是AB 的中点,可知CD ∥AB ,1122BE AB CD ==,则△DOC ∽△BOE ,则2OD OC CD OB OE BE ===,进而可得2COD EOD S CD S BE ⎛⎫= ⎪⎝⎭△△,则2241CODS ==△,解得4CODS = ,由32BD OB OD OD =+=,可知334622BCD COD S S ==⨯=△△,由四边形ABCD 为平行四边形,可知6ABDBCD S S == ,进而可知615ABD BOE AEOD S S S =-=-=△△四边形.【详解】解:∵在平行四边形ABCD 中,点E 是AB 的中点,∴CD ∥AB ,1122BE AB CD ==,∴△DOC ∽△BOE ,∴2OD OC CDOB OE BE===,∴2COD EOD S CD S BE ⎛⎫= ⎪⎝⎭△△,∴2241CODS ==△,∴4CODS = ,32BD OB OD OD =+=,∴334622BCD COD S S ==⨯=△△,∵四边形ABCD 为平行四边形,∴6ABDBCD S S == ,∴615ABD BOE AEOD S S S =-=-=△△四边形,故答案为:5.17.(2021,1)【分析】根据题意得出O 点坐标变化规律,进而得出点O 2021的坐标位置,进而得出答案.【详解】解:∵点A 的坐标为(1,0),点B 的坐标为(1,2),△AOB 是直角三角形,∴OA =1,AB =2,将△OAB 绕点A 第一次顺时针旋转90°得到△O 1AB 1,此时O 1为(1,1),将△O 1AB 1绕点B 1第二次顺时针旋转90°得到△O 2A 1B 1,得到O 2为(1+2+1,2),再将△O 2A 1B 1绕点B 1第三次顺时针旋转90°得到△O 3A 2B 1,得到O 3(1+2+2,﹣1),…,依此规律,∴每4次循环一周,O 1(1,1),O 2(4,2),O 3(5,﹣1),O 4(4,0),∵2021÷4=505…1,∴点O 2021(505×4+1,1),即(2021,1).故答案为(2021,1).18.(1)12x =-,22x =;(2)11x =-,252x =;【分析】(1)用配方法求一元二次方程的解,首先把-1转化为4-5的形式,则前三项可凑成完全平方式,再通过用平方根的方法求解即可.(2)直接用十字相乘法解一元二次方程.(1)解:2410x x -=+24450x x ++-=()2250x +-=,()225x +=,2x +=12x =-,22x =-;(2)解:22350x x --=()()1250x x +-=10x +=或250x -=,11x =-,252x =.19.1【分析】根据题意直接利用零指数幂的性质以及绝对值的性质和负整数指数幂的性质、特殊角的三角函数值分别化简即可得出答案.【详解】解:2cos45°+(﹣12)-1+(20200+|2|=2×2﹣2+1+2﹣2+1+2=1.20【分析】作AE ⊥CD 于E ,则四边形ABCE 为矩形,CE =AB =1.5m .解Rt △ACE 可得AE 的长,再解Rt △ADE 可得DE 的长,最后根据CD =CE+DE 计算即可.【详解】解:如图,作AE ⊥CD 于E ,则四边形ABCE 为矩形,∴CE =AB =1.5m ,AE =BC ,在Rt △ACE 中,tan ∠CAE =CEAE,∴AE =tan CE CAE ∠= 1.5tan 30︒=2(m ),在Rt △ADE 中,∵∠DAE =45°,∴△ADE 为等腰直角三角形,∴DE =AE ,又∵CE =AB =1.5m ,∴CD =CE+DE =m ).答:建筑物CD .21.解:(1)如图,△A 1B 1C 1即为所求,C 1(2,-2).(2)如图,△A 2BC 2即为所求,C 2(1,0),△A 2BC 2的面积:10【详解】分析:(1)根据网格结构,找出点A 、B 、C 向下平移4个单位的对应点1A 、1B 、1C 的位置,然后顺次连接即可,再根据平面直角坐标系写出点1C 的坐标;(2)延长BA 到2A 使A 2A =AB ,延长BC 到2C ,使C 2C =BC ,然后连接A 2C 2即可,再根据平面直角坐标系写出2C 点的坐标,利用△2A B 2C 所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.本题解析:(1)如图,△A 1B 1C 1即为所求,C 1(2,-2)(2)如图,△2A B 2C 为所求,2C (1,0),△2A B2C的面积:6×4−12×2×6−12×2×4−12×2×4=24−6−4−4=24−14=10,22.(1)见解析;(2)【分析】(1)先证四边形ABDE为平行四边形,再证得AE=CD,得四边形ADCE是平行四边形,然后根据直角三角形斜边上的中线性质得AD=CD,即可得出结论;(2)先由菱形的性质得AD=AE=CE=CD,AC⊥DE,OA=OC,再证OD是△ABC的中位线,得AB=2OD=2,则AO=AB=2,然后由勾股定理求出AD的长即可解决问题.【详解】解:(1)证明:∵AE∥BC,DE∥AB,∴四边形ABDE为平行四边形,∴AE=BD,∵AD是边BC上的中线,∴BD=CD,∴AE=CD,∴四边形ADCE是平行四边形,又∵∠BAC=90°,AD是边BC上的中线,∴AD=12BC=CD,∴平行四边形ADCE是菱形;(2)解:∵四边形ADCE是菱形,∴AD=AE=CE=CD,AC⊥DE,OA=OC,∵BD=CD,∴OD是△ABC的中位线,∴AB=2OD=2,∴AO=AB=2,∴AD∴菱形ADCE的周长=4AD=故答案为:23.(1)见解析;(2)2【分析】(1)由相似三角形的判定可证 BDE ∽ CEF ;(2)由相似三角形的性质可得DBBECE CF =,可求BE =CE ,即可求解.【详解】(1)证明:∵AB =AC ,∴∠B =∠C ,∵∠BDE =180°﹣∠B ﹣∠DEB ,∠CEF =180°﹣∠DEF ﹣∠DEB ,又∵∠DEF =∠B ,∴∠BDE =∠CEF ,∴ BDE ∽ CEF ;(2)解:∵点E 是BC 的中点,∴BE =CE ,∵ BDE ∽ CEF ,∴DBBECE CF =,∴BE 2=DB•CF =6,∴BE =CE ,∵ BDE ∽ CEF ,∴DEDBEF CE =故答案为:224.(1)40010x -;(2)每个定价70元.【分析】(1)根据销售量=400-10x 列关系式;(2)总利润=每个的利润×销售量,销售量为400-10x ,列方程求解,根据题意取舍;【详解】(1)根据题意得出:40010x -;(2)()()10400106000x x +-=整理得:2302000x x -+=,解得120x =,210x =(舍去),∴每个定价70元.25.(1)①证明见详解;②52或72;11;【分析】(1)①根据正方形的性质和全等三角形的性质与判定解答即可;②根据全等三角形的性质和三角形的面积公式解答即可;(2)根据矩形的性质和相似三角形的判定和性质解答即可.(1)①证明:∵EH⊥AE,∴∠FEH+∠HFE=90°,∵四边形BEFG为矩形,∴∠FEH+∠AEB=90°,∴∠AEB=∠HFE,在△FHE与△EAB中,90BAE EHFHFE AEBBE EF∠=∠=︒⎧⎪∠=∠⎨⎪=⎩,∴△FHE≌△EAB(AAS),∴FH=AE;②解:∵△FHE≌△EAB,∴AE=FH,∵AD=6,设DE=x,AE=6-x,∴35182DEFS DE FH==⋅△,可得:()135628x x-=,解得:152x=,272x=,即线段DE的长度为:52或72;(2)解:FH⊥AE,∴∠FEH+∠HFE=90°,∵四边形BEFG为矩形,∴∠FEH +∠AEB=90°,∴∠AEB=∠HFE ,∴△FHE ∽△EAB ,∴FH EF AE BE =∵AB =,∴HE EF AB BE ==∴HE=2,延长EF 交DC 于点Q ,如图所示,∵Q 是CD 的中点,∴1122DQ CD AB ===,设FH 为x ,则AE =,则6DE =-,∵∠DEQ=∠FEH ,=90°,∴△EDQ ∽△EHF ,∴FH HE DQ DE =,=解得:11x =+,21x =,∴线段FH 11.26.(1)()3,2A -,6y x =-;(2)存在,20,3Q ⎛⎫ ⎪⎝⎭或80,3⎛⎫- ⎪⎝⎭;(3)3x ≤-或02x <≤【分析】(1)直线AB 与x 轴的交点()1,0C -,由1AOC S =△,可求得点A 的纵坐标,然后代入一次函数求得点A 的坐标,把点A 的坐标代入反比例函数即可求得反比例函数解析式.(2)结合题意可以求得AOB 的面积,然后设设点()0,Q y ,然后用三角形的面积公式列等式,求解即可得出答案;(3)根据A 、B 点的坐标和图象得出答案.【详解】解:(1)直线AB :1y x =--与x 轴的交点C ,令y =0,则1=0x --,解得:x =﹣1,∴点()1,0C -.设(),A x y ,∵1AOC S =△,∴1112y ⨯⨯=∴2y =,∴(),2A x 将点A 代入1y x =--得,3x =-,∴()3,2A -,∴6k =-,∴反比例函数解析式为:6y x =-;(2)存在,理由如下:∵1152113222AOB S =⨯⨯+⨯⨯=△,设点()0,Q y ,直线AB 与y 轴的交点为()0,1-,则153122ADQ S y =⨯⨯+=△,∴23y =或83y =-,∴20,3Q ⎛⎫ ⎪⎝⎭或80,3⎛⎫- ⎪⎝⎭(3)∵一次函数与反比例函数交于点()3,2A -、B ()2,3-,∴由图像可知:要使1kx x--≥∴3x ≤-或02x <≤。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北师大版九年级上册数学期末考试试题及答案一、选择题(每小题4分,共24分)下列各小题均有四个答案,其中只有一个是正确地,请将正确答案地代号字母填入题后括号内.1.Rt 90ABC C BAC 在△中,=,地角平分线AD 交BC 于点D ,2CD =,则点D 到AB 地距离是()A .1B .2C .3D .42.一元二次方程230xx 地解是()A .0xB .1203x x ,C .1210,3x x D .13x3.顺次连结任意四边形各边中点所得到地四边形一定是()b5E2RGbCAPA .平行四边形B .菱形C .矩形D .正方形4.小明拿一个等边三角形木框在阳光下玩,等边三角形木框在地面上形成地投影不可能...是ABC D p1EanqFDPw5.某农场地粮食总产量为1500吨,设该农场人数为x 人,平均每人占有粮食数为y 吨,则y 与x 之间地函数图象大致是()DXDiTa9E3d6.在李咏主持地“幸运52”栏目中,曾有一种竞猜游戏,游戏规则是:在20个商标牌中,有5个商标牌地背面注明了一定地奖金,其余商标牌地背面是一张“哭脸”,若翻到“哭脸”就不获奖,参与这个游戏地观众有三次翻牌地机会,且翻过地牌不能再翻.有一位观众已翻牌两次,一次获奖,一次不获奖,那么这位观众第三次翻牌获奖地概率是RTCrpUDGiTA .15B .29C .14D .518二、填空题(每小题3分,共27分)7.如图,地面A 处有一支燃烧地蜡烛(长度不计),一个人在A 与墙BC 之间运动,则他在墙上地投影长度随着他离墙地距离变小而.(填“变大”、“变小”或“不变”).5PCzVD7HxADACBBCAxyxyxyxyA .B .C .D .ABCDE FO8.反比例函数2kyx(k 为常数,0k )地图象位于第象限.9.根据天气预报,明天地降水概率为15%,后天地降水概率为70%,假如小明准备明天或者后天去放风筝,你建议他__________天去为好.jLBHrnAILg 10.随机掷一枚均匀地正方体骰子,骰子停止后朝上地点数小于3地概率是.11.如图,矩形ABCD 地对角线AC 和BD 相交于点O ,过点O 地直线分别交AD 和BC 于点E 、F ,23AB BC ,,则图中阴影部分地面积为.12.如图,50ABCAD ,垂直平分线段BC 于点D ABC ,地平分线BE 交AD 于点E ,连结EC ,则AEC 地度数是.13.已知关于x 地方程0322mmx x 地一个根是1x ,那么m.14.要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排21场比赛,应邀请个球队参加比赛.[来源:学#科#网Z#X#X#K]xHAQX74J0X15.已知梯形地两底边长分别为6和8,一腰长为7,则另一腰长a 地取值范围是.三、解答题(本题共8道小题,第16小题8分,第9 ~ 20小题各9分,第21、22小题各10分,第23题11分,共75分)LDAYtRyKfE16.下图是一个立体图形地三视图,请根据视图写出该立体图形地名称,并计算该立体图形地体积(结果保留).Zzz6ZB2Ltk17.如图,反比例函数k y x地图象与一次函数y mx b 地图象交于(13)A ,,(1)B n ,两点.(1)求反比例函数与一次函数地解析式;(2)根据图象回答:当x 取何值时,反比例函数地值大于一次函数地值.CDBEA正视图左视图俯视图101010yxAOB18.九年级(1)班要举行一场毕业联欢会,规定每个同学同时转动下图中①、②两个转盘(两个转盘分别被二等分和三等分),若两个转盘停止后指针所指地数字之和为奇数,则这个同学要表演唱歌节目;若数字之和为偶数,则要表演其他节目.试求出这个同学表演唱歌节目地概率(要求用画树状图或列表方法求解).dvzfvkwMI119.如图,已知在□ABCD 中,E 、F 是对角线BD 上地两点,BE =DF ,点G 、H 分别在BA 和DC 地延长线上,且AG =CH ,连接GE 、EH 、HF 、FG .rqyn14ZNXI求证:四边形GEHF 是平行四边形.20.请写出一元二次方程地求根公式,并用配方法推导这个公式.21.小强家有一块三角形菜地,量得两边长分别为40m ,50m ,第三边上地高为30m ,请你帮小强计算这块菜地地面积(结果保留根号).EmxvxOtOco12231转盘②转盘①22.某农场去年种植了10亩地地南瓜,亩产量为2000kg ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产地新品种南瓜,已知南瓜种植面积地增长率是亩产量地增长率地2倍,今年南瓜地总产量为60 000kg ,求南瓜亩产量地增长率.SixE2yXPq523.如图,点O 是等边ABC △内一点,110AOB BOC,.将BOC △绕点C按顺时针方向旋转60得ADC △,连接OD .(1)求证:COD △是等边三角形;(2)当150时,试判断AOD △地形状,并说明理由;(3)探究:当为多少度时,AOD △是等腰三角形?ABCDO110九年级(上)期末试卷数学参考答案和评分标准(北师大版)一、1.B 2.C3.A4.B 5.B 6.B二、7.变小8.二、四9.明10.1311.312.115°(填115不扣分)13.25314.715.5<a <9三、16.解:该立体图形为圆柱.因为圆柱地底面半径5r,高10h,所以圆柱地体积22510250Vr h(立方单位).答:所求立体图形地体积为250立方单位. ……………………………8分17.解:(1)(13)A ,在k y x地图象上,3k,3yx2分又(1)B n ,在3y x地图象上,3n,即(31)B ,3分313m b m b ,解得:1m,2b,6分反比例函数地解析式为3y x,一次函数地解析式为2yx ,7分(2)从图象上可知,当3x 或01x 时,反比例函数地值大于一次函数地值.9分18.解:列表如下:1 21 2 3 234转盘①和转盘②5分由上表可知,所有等可能结果共有6种,其中数字之和为奇数地有3种,P (表演唱歌)31629分6ewMyirQFL19.证明:∵四边形ABCD 是平行四边形∴AB =CD ,AB ∥CD∴∠GBE =∠HDF …………………………………………………2分又∵AG =CH ∴BG =DH 又∵BE =DF∴△GBE ≌△HDF …………………………………5分∴GE =HF ,∠GEB =∠HFD ∴∠GEF =∠HFE ∴GE ∥HF∴四边形GEHF 是平行四边形.……………………………9分20.见教材.写出公式3分,推导正确6分,共9分.21.解:分两种情况:(1)如图(1)当ACB 为钝角时,BD 是高,90ADB.在Rt BCD △中,40BC,30BD221600900107CD BCBD.2分在Rt ABD △中,50AB,2240AD ABBD.4分40107ACAD CD,211(40107)30(6001507)(m )22ABCS AC BD△.5分(2)如图(2)3 4 5BBDCA图(1)当ACB 为锐角时,BD 是高,90ADBBDC,在Rt ABD △中,5030ABBD,,2240ADABBD.同理221600900107CD BC BD ,7分(40107)ACAD CD,8分211(40107)30(6001507)(m )22ABCS AC BD △.9分综上所述:2(6001507)(m )ABC S △10分22.解:设南瓜亩产量地增长率为x ,则种植面积地增长率为2x .1分根据题意,得10(12)2000(1)60000x x .6分解这个方程,得10.5x ,22x (不合题意,舍去).9分答:南瓜亩产量地增长率为50%.10分kavU42VRUs23.(1)证明:CO CD ∵,60OCD°,COD ∴△是等边三角形.3分(2)解:当150°,即150BOC°时,AOD △是直角三角形.5分BOC ADC ∵△≌△,150ADCBOC∴°.又COD ∵△是等边三角形,60ODC∴°.90ADO ∴°.即AOD △是直角三角形.7分(3)解:①要使AOAD ,需AODADO .190AOD∵°,60ADO °,19060∴°°.125∴°.②要使OAOD ,需OADADO .180()50OADAODADO ∵°°,6050∴°°.110∴°.③要使OD AD ,需OAD AOD .19050∴°°.140∴°.综上所述:当地度数为125°,或110°,或140°时,ABC △是等腰三角形.11分版权申明本文部分内容,包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some p arts, including text, pictures, and design. Copyright is personal ownership.y6v3ALoS89 用户可将本文地内容或服务用于个人学习、研究或欣赏,以及其他非商业性或非盈利性用途,但同时应遵守著作权法及其他相关法律地规定,不得侵犯本网站及相关权利人地合法权利.除此以外,将本文任何内容或服务用于其他用途时,须征得本人及相关权利人地书面许可,并支付报酬.M2ub6vSTnPUsers may use the contents or services of this articlefor personal study, research or appreciation, and othernon-commercial or non-profit purposes, but at the same time,they shall abide by the provisions of copyright law and otherrelevant laws, and shall not infringe upon the legitimaterights of this website and its relevant obligees. In addition, when any content or service of this article is used for other purposes, written permission and remuneration shall beobtained from the person concerned and the relevantobligee.0YujCfmUCw转载或引用本文内容必须是以新闻性或资料性公共免费信息为使用目地地合理、善意引用,不得对本文内容原意进行曲解、修改,并自负版权等法律责任.eUts8ZQVRdReproduction or quotation of the content of this articlemust be reasonable and good-faith citation for the use of news or informative public free information. It shall notmisinterpret or modify the original intention of the contentof this article, and shall bear legal liability such ascopyright.sQsAEJkW5T。
