【数学】2.1.1 合情推理 课件(人教A版选修1—2)
合集下载
高二数学选修1-2 《2.1合情推理》新课标人教版精选教学PPT课件

B
C
c2=a2+b2 类比: S2△ABC =S2△AOB+S2△AOC+S2△BOC
归纳推理
由部分到整体、特殊到一般的推理; 以观察分析为基础,推测新的结论; 具有发现的功能; 结论不一定成立.
类比推理
由特殊到特殊的推理; 以旧的知识为基础,推测新的结果; 具有发现的功能; 结论不一定成立.
小结 ☞
感谢父母给了我生命和无私的爱; 感谢老师给了我知识和看世界的眼睛;
感谢朋友给了我友谊和支持; 感谢完美给了我信任和展示自己能力的机会;
感谢邻家的小女孩给我以纯真无邪的笑脸; 感谢周围所有的人给了我与他人交流勾通时的快乐; 感谢生活所给予我的一切,虽然并不全都是美满和幸福;
感谢天空,给我提供了一个施展的舞台 感谢大地,给我无穷的支持与力量; 感谢太阳,给我提供光和热;
感谢伤痛,让我学会了坚忍,也练就了我释怀生命之起落的本能; 感谢生活,让我在漫长岁月的季节里拈起生命的美丽;
感谢有你,尽管远隔千里,可你寒冬里也给我温暖的心怀; 感谢关怀,生命因你而多了充实与清新;
感谢所有的一切~ ~ ~ ~ ~ ~ 感谢我身边每一位好友,为你祝福,为的敲起祈祷钟!伴你走过每一天。他是一个劫匪,坐过牢,之后又杀了人,穷途末路之际他又去抢银行。 是一个很小的储蓄所。抢劫遇到了从来没有过的不顺利,两个女子拼命反抗,他把其中一个杀了,另一个被劫持上了车。因为有人报了警,警车越来越近了,他劫持着这个女子狂逃,把车都开飞了,撞了很多人,轧了很多小摊。 这个刚刚21岁的女孩子才参加工作,为了这份工作,她拼命读书,毕业后又托了很多人,没钱送礼,是她哥卖了血供她上学为她送礼,她父母双亡,只有这一个哥哥。
可能有生命存在
由两类对象具有某些类似特征和其中 一类对象的某些已知特征,推出另一类对 象也具有这些特征的推理称为类比推理.
高中数学选修1-2精品课件8:2.1.1 合情推理

)
r2 l2 lr l+r A. 2 B.2 C.2 D. 2
【解析】三角形的高对应扇形的半径,三角形的底对应 扇形的弧长,所以可猜测为 S=12rl=l2r. 【答案】C
4.等差数列{an}中,an>0,公差d>0,则有a4·a6>a3·a7, 类比上述性质,在等比数列{bn}中,若bn>0,q>1,写 出b5,b7,b4,b8的一个不等关系________+33+…+n3=(1+2+3+…+n)2, 即 13+23+33+…+n3=n(n2+1)2.
(2)【解析】由a1=1=21-1,a2=3=22-1,a3=7 =23-1,a4=15=24-1,a5=31=25-1,可归纳猜 想出an=2n-1(n∈N*). 【答案】2n-1(n∈N*)
类型2 图形中的归纳推理 典例2 有两种花色的正六边形地面砖,按下图的规律 拼成若干个图案,则第6个图案中有菱形纹的正六边形 的个数是( )
sin2nπ+1 -2 + sin2n2+π 1 -2 + sin2n3+π 1 -2 + … + sin22nn+π1-2=________. (2)已知数列{an}的第 1 项 a1=1,且 an+1=1+anan(n=1, 2,3,…),试归纳出这个数列的通项公式.
(1)【解析】根据已给出的等式归纳推理求解. 通过观察已给出等式的特点,可知等式右边的43是个固 定数,43后面第一个数是等式左边最后一个数括号内角 度中 π 的系数的分子的一半,43后面第二个数是第一个
数的下一个自然数,所以,所求结果为43×n×(n+1), 即43n(n+1). 【答案】43n(n+1)
(2)解:当 n=1 时,a1=1;
当 n=2 时,a2=1+1 1=12;
1 当 n=3 时,a3=1+2 12=13;
人教A版高中数学选修1-2《2.1.1合情推理》课件

以上属于什么推理?
答案 推理.
答案
属于归纳推理 .符合归纳推理的定义特征,即由部分对
象具有某些特征,推出该类事物的全部对象都具有这些特征的
梳理
(1)定义:由某类事物的 部分对象 具有某些特征,推出该类事物的 全部 对象 都具有这些特征的推理,或者由个别事实 概括出 一般结论 的 推理,称为归纳推理. (2)特征:由 部分 到 整体 ,由个别到 一般 .
答案
梳理
(1)定义:由两类对象具有某些 类似 特征和其中一类对象的某些 已知 特征, 推出 另一类对象 也具有这些特征的推理称为类比推理. (2)特征:由 特殊 到 特殊 的推理.
知识点三
合情推理
思考1
归纳推理与类比推理有何区别与联系? 答案 区别:归纳推理是由特殊到一般的推理;而类比推理是
由个别到个别的推理或是由特殊到特殊的推理.
1
2
3
4
5
解析
答案
规律与方法
1.合情推理主要包括归纳推理和类比推理 .数学研究中,在得到一个新结
论前,合情推理能帮助猜测和发现结论,在证明一个数学结论之前,合
情推理常常能为证明提供思路与方向.
2.合情推理的过程概括为
从具体问题出发 ― → 观察、分析、比较、联想 ― → 归纳、类比 ― → 提出猜想
跟踪训练 2
黑白两种颜色的正六边形地面砖按如图的规律拼成若干个
图案,则第n个图案中黑色地面砖的块数是________. 5n+1
解析
观察图案知,从第一个图案起,每个图案中黑色地面砖的个数组
成首项为 6 ,公差为5 的等差数列,从而第n 个图案中黑色地面砖的块数
为6+(n-1)×5=5n+1.
人教版选修2-2《2.1.1合情推理》课件(共23张PPT)
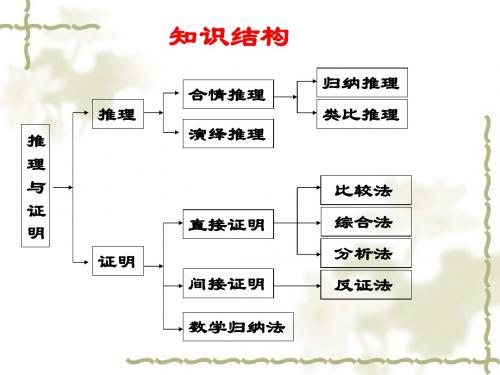
三棱锥
4
4
6
四棱锥
5
5
8
三棱柱
5
6
9
五棱锥
6
6
10
立方体
6
8
12
正八面体
8
6
12
五棱柱
截角正方体
尖顶塔
猜想 F+V-E=2 欧拉公式
多面体 面数(F) 顶点数(V) 棱数(E)
三棱锥
4
4
6
四棱锥
5
5
8
三棱柱
5
6
9
五棱锥
6
6
10
立方体
6
8
12
正八面体86Fra bibliotek12五棱柱
7
10
15
截角正方体 7
10
15
尖顶塔
7.利用等差数列性质类比等比数列性质
歌德巴赫猜想的提出过程:
3+7=10,3+17=20,13+17=30,
改写为:10=3+7,20=3+17,30=13+17.
6=3+3, 8=3+5,
10=5+5, 12=5+7, 14=7+7, 16=5+11,
18 =7+11, …,
1000=29+971, 1002=139+863,
…
这种由某类事物的部分对象具有某些特征, 推出该类事物的全部对象都具有这些特征 的推理,或者由个别事实概栝出一般结论 的推理,称为归纳推理.(简称;归纳)
解;设an表示移动n块金属片时的移动次数. 当n=1时,a1=1 当n=2时,a2= 3
2
1
3
解;设an表示移动n块金属片时的移动次数. 当n=1时,a1=1
高中数学选修1-2精品课件6:2.1.1 合情推理

4.若把正整数按下图所示的规律排序,则从 2 014 到 2 016 的箭头方向依次为( )
1 4→5 8→9 12 ↓ ↑ ↓ ↑ ↓ ↑ ……
2→3 6→7 10→11 A.↓→ B.→↓ C.↑→ D.→↑
【答案】D 【解析】根据箭头方向找规律,每相邻四个数字,箭头方 向相同,2014÷4=503余2,故从2014到2016与从2到4的方向 一致,故选D.
(2)分成两列数,奇数位的数:32,16,( ),4,2.偶数位的 数:31,26,( ),16,11,所以括号中的数依次是 8,21.
2.观察下列式子:1+212<32,1+212+312<54,1+212+312+412 <78,…,由此可以归纳出的一般结论是__________.
【答案】1+212+312+…+n12+n+112<2n2+n 1(n∈N*) 【解析】不等式的左边是i12的前 n+1 项和,右边的分母是 2n, 分子是 2n+1,故一般性的结论是 1+212+312+…+n12+n+112 <2n2+n 1(n∈N*).
4.合情推理 归 纳 推 理 和 类 比 推 理 都 是 根 据 _已__有__的__事__实___ , 经 过 观__察__、__分__析__、__比__较__、__联__想__,再进行___归__纳___、___类__比___,然后 提出__猜__想____的推理.我们把它们称为合情推理.通俗地说, 合情推理是指“合乎情理”的推理.
5.归纳推理是由部分到_整__体___,由具体到_抽__象___,由特 殊到_一__般___,从个别事实中概括出_一__般__结__论___的思维模式. 类比推理是在__两__类__不__同__的事物之间进行对比,找出若干相同 或相似之处之后,推测在其他方面也可能存在__相__同__或__相__似___
数学:2[1].1《合情推理与演绎证明--合情推理》PPT课件(新人教A版-选修1-2)
![数学:2[1].1《合情推理与演绎证明--合情推理》PPT课件(新人教A版-选修1-2)](https://img.taocdn.com/s3/m/33509701bd64783e08122b1f.png)
2
1
3
解;设an表示移动n块金属片时的移动次数. 当n=1时,a1=1 当n=2时,a2= 3 猜想 an= 2n -1 当n=3时,a3= 7 当n=4时,a4= 15
2
1
3
歌德巴赫猜想的提出过程:
…
这种由某类事物的部分对象具有某些特征, 推出该类事物的全部对象都具有这些特征 的推理,或者由个别事实概栝出一般结论 的推理,称为归纳推理.(简称;归纳) 归纳推理的几个特点;
1.归纳是依据特殊现象推断一般现象,因而,由归纳 所得的结论超越了前提所包容的范围. 2.归纳是依据若干已知的、没有穷尽的现象推断尚 属未知的现象,因而结论具有猜测性. 3.归纳的前提是特殊的情况,因而归纳是立足于观 察、经验和实验的基础之上. 归纳是立足于观察、经验、实验和对有限资料分 析的基础上.提出带有规律性的结论. 需证明
这就是著的哥德巴赫猜想。欧拉在6月30日给他的回信中说, 他相信这个猜想是正确的,但他不能证明。叙述如此简单的问 题,连欧拉这样首屈一指的数学家都不能证明,这个猜想便引 起了许多数学家的注意。从提出这个猜想至今,许多数学家都 不断努力想攻克它,但都没有成功。当然曾经有人作了些具体 的验证工作,例如: 6 = 3 + 3, 8 = 3 + 5, 10 = 5 + 5 = 3 + 7, 12 = 5 + 7, 14 = 7 + 7 = 3 + 11,16 = 5 + 11, 18 = 5 + 13, . . . . 等等。有人对33×108以内且大过6之偶数一 一进行验算,哥德巴赫猜想(a)都成立。但严格的数学证明尚 待数学家的努力。从此,这道著名的数学难题引起了世界上成 千上万数学家的注意。200年过去了,没有人证明它。哥德巴 赫猜想由此成为数学皇冠上一颗可望不可及的“明珠”。到了 20世纪20年代,才有人开始向它靠近。
2.1.1合情推理 课件(人教A版选修1-2)

A 版
数
(1)观察:通过观察个别事物发现某些相同性质.
学
(2)概括、归纳:从已知的相同性质中概括、归纳出一
个明确表述的一般性命题.
(3)猜测一般性结论:在一般情况下,如果归纳的个别
情况越多,越具有代表性,那么猜测出的一般性结论也就
越可靠.
第二章 推理与证明
3.对类比推理的理解
类比推理是在两类不同的事物之间进行对比,找出若
推理称为类比推理(简称 类比 ) . 简 言 之 , 类 比 推 理 是 由
特殊到特殊 的推理.
第二章 推理与证明
3.合情推理
பைடு நூலகம்
归纳推理和类比推理都是根据 已有的事实 ,
人
经过 观察、分析、比较、联想 ,再进行 归纳、类比 ,
教 A
版
然后提出 猜想 的推理.我们把它们称为合情推理.通俗 数 学
地说,合情推理是指“ 合乎情理 ”的推理.
第二章 推理与证明
[答案]
(1)21
1 (2)516
13 (3)44
(4)8
21
[解析] 要在括号里填上适当的数,必须正确地判断
出每列数所具有的规律,为此必须进行仔细的观察和揣
人 教
A
摩.
版 数
学
(1)考察相邻两数的差:
5-1=4,9-5=4,
13-9=4,17-13=4
可见,相邻两数之差都是4.按此规律,括号里的数减
干相同或相似之处之后,推测在其他方面也可能存在相同
或相似之处的一种推理模式.
人 教
A
类比推理的关键在于明确指出两类对象在某些方面的 版
数
学
相似特征.
4.类比推理的一般步骤
人教A版高中数学选修1-2课件2.1.1合情推理

KETANGHEZUOTANSUO
解析:由已知交点依次写为(1,12),(2,22),(3,32),…, ∴命题 n 中交点为(n,n2),直线中系数依次为 1,2,3,…,∴命题 n 中直线的 系数为 n.
双曲线中系数依次为 13,23,33,…,∴命题 n 中双曲线的系数为 n3, ∴命题 n 为:点(n,n2)是直线 y=nx 与双曲线 y=������������3的一个交点.
.
思路分析:解答本题的关键是确定好类比对象.平面中圆类比空间
中球,平面中长度类比空间中面积,平面中面积类比空间中体积.
答案:13R(S△ABC+S△ACD+S△BCD+S△ABD)
2.1.1 合情推理
问题导学 当堂检测
一二
课前预习导学 课堂合作探索
KEQIANYUXIDAOXUE
KETANGHEZUOTANSUO
.
答案:夹在两平行平面之间的平行线段相等
2.1.1 合情推理
目标导航 预习引导
课前预习导学
KEQIANYUXIDAOXUE
课堂合作探索
KETANGHEZUOTANSUO
2.合情推理及其推理过程 (1)合情推理的含义 归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、 联想,再进行归纳、类比,然后提出猜想的推理,它们统称为合情推理. (2)合情推理的思维过程 从具体问题出发→观察、分析、比较、联想
2.1.1 合情推理
问题导学 当堂检测
一二
课前预习导学 课堂合作探索
KEQIANYUXIDAOXUE
KETANGHEZUOTANSUO
一、归纳推理及其应用
活动与探究
归纳推理有什么特点? 答:(1)归纳推理是由部分到整体,由个别到一般的推理; (2)归纳推理的前提是部分的、个别的事实,因此归纳推理的结论超 出了前提所界定的范围,其前提和结论之间的联系不是必然的,而是偶 然的.所以“前提真而结论假”的情况是有可能发生的; (3)在进行归纳推理的时候,总是搜集一定的事实材料,有了个别性 的、特殊性的事实作为前提,然后才能进行归纳推理,因此归纳推理要在 观察和实验的基础上进行; (4)归纳推理能够发现新事实、获得新结论,是作出科学发现的重要 手段.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这种由某类事物的部分 对象具有某些特征 ,推 出该类 事物的全部对象都具有 这 些特征的推 论, 或者由个别事实概括出 一般结论的推理 ,称 为归纳推理 简称归纳.简言之,归纳推理是由 部分到整体、由个别到 一般的推理 .
例如 ,由铜、铁、铝、金、银 等 金 属能导电 , 归纳出" 一切金属都能导电 " ; 由直角三角形、 等腰三角形、等边三角 形的内角和都是 1800 , 归纳出 " 所有三角形的内角和都 是1800 " 这些都是归纳推理.在统计学中, 我们总是从 所研究的对象全体中抽 取一部分进行观测或 试验以取得信息, 从而对整体作出推断 , 这也 是归纳推理 .
与ΔRtABC的直角边边长a, b 相对应的, 是四面体P DEF 的面ΔDEF, ΔFPD, 和ΔDPE的 面积S1, S 2和S3 ;
B
c a
C
与ΔRtABC的斜边边长c相对 应的, 是四面体P DEF 的面 ΔPEF的面积S. 由此 ,我们可以类比ΔRtABC 中的勾股定理, 猜想出四面体 E P DEF四个面的面积的关系 .
例3 类比平面内直角三角形 的勾股定理 , 试给出 B 空间四面体性质的猜想 . 分 析 考虑 到直 角三角形的 c 两条边垂直, 所以我们可以选 a 取有3个面两两垂直的四面体 , A C b 作为直角三角形的类比 对象. 1 如图2.1 1所示,与Rt ΔABC P 相对应 , 是四面体P DEF; S2 D S 3 与Rt ΔABC的两条边交成 1个 S1 F 直角相对应的 , 是四面体P E 2 ABC的3个面在一个顶点处 图2.1 1 构成3个直二面角 ;
继续上述过程 , 你能提出一个猜想吗 ?
根据上述过程 , 哥德巴赫大胆地猜想: 任何一个 不小于6 的偶数都等于两个奇质 数的和.这是正 确的吗? 多少年来 , 许多优秀的数学家都在 努力 证明这个猜想 , 而且取得了很好的进展 .
现在, 我们来考察一下哥德巴 赫提出猜想的推理 过程 : 通过对一些偶数的验证 , 他发现它们总可 以表示成两个奇质数之 和,而且没有出现反例 .于 是, 提出猜想 " 任何一个不小于 6的偶数都等于 两个奇质数之和 ".
探究 你认为平面几何中的哪 一类图形 可以作为四面体的类比 对象 ?
我们可以从不同的角度 出发确定类比对象 , 如围成 四面体的几何元素的数 目、位置关系、度量等. 基 本原则是要根据当前问 题的需要, 选择适当的类比 对象 .例如 , 从构成几何体的元素数 目看 ,四面体由 4个面围成,它是空间中由数目最少 的基本元素(平 面)围成的封闭几何体 ; 在平面内 ,两条直线不能围成 一个封闭的图形 ,而3条直线可以围成一个三 角形,即 三角形是平面内由数目 最少的基本元素 (直线)围成 的封闭图形 .从这个角度看 , 我们可以把三角形作为 四面体的类比对象 . 下面, 我们就来看一个通过类 比平面的几何中的结论 , 得到立体图形性质的猜 想的例子 .
b 1
A
P
S S3 D 2 S1
F
2
图2.1 1
解 如图2.1 1 所示 , 我们知 道, 在 Rt ΔABC中,由勾股定, 得 c a b .
2 2 2
B
c a
C
于是 ,类比直角三角形的勾股 定理, 在四面体 P DEF 中 ,我
2 2 们猜想 S2 S1 S2 S . 2 3成立
第二章 推理与证明
2.1.1 合情推理
数学中有各种各样的猜 想, 如著名的哥德巴赫 (Goldbach )猜想、费马 (Fermat )猜想、地图的 " 四色猜想"、歌尼斯堡七桥猜想等 等.某些猜想 的证明吸引了大批的数 学家 和数学爱好者 ,有 的人甚至为之耗费了毕 生心血 .你知道这些数 学猜想是怎样提出来的 吗 ? 下面看一下哥德巴 赫提出猜想的过程 .
圆的 道这样的 点, 切点到圆心的距离等于
平面是存 半径; 对于球, 我们推测可能存在
已经知
例如,圆有切线, 切线与圆交于一
,与球交于一点 , 该点 在的,即球 这样的平面
的切平面 . 到球心的距离等于球的,由此猜 想空间中不共面的四个 点确定一个球 ;等等.
据说哥德巴赫无意中观 察到 : 3 7 10,3 17 20,13 17 30, 他有意把上面的式子改 写成 : 10 3 7,20 3 17,30 13 17.
其中反映出这样一个规 律: 偶数 奇质数 奇质数. 于是哥德巴赫产生了一 个想法 : 10,20,30都是偶 数,那么其他偶数是否也有 类似的规律呢? 显然,第一个等于两个奇质数 之和的偶数是 6, 即 6 3 3, 再看看超过6的偶数 : 8 3 5,10 5 5,12 5 7,14 7 7,16 5 11 , 1000 29 971 ,1002 139 863,
例 4 如图2.1 2所示, 有三根针和套在一根针 上的若 干金属片 .按下列规则 , 把金属片从一根针上全 部移到 另一根针上 . 1 3 1.每次只能移动 2 1个金属片 ; 2.较大的金属片
不能放在较小的 图2.1 2 金属片上面 . 试推测: 把n个金属片从 1号针移到 3号针, 最少需要 移动多少次? 分析 我们从移动 1 ,2,3,4个金属片的情形入手 , 探究其 中的规律性 , 进而归纳出移动n个金属片所需的次数 .
开普勒 ( Ke pler ,1571 1630 ) 说 : " 我珍惜类 比胜过任何 别的东西 ,它 是我最可信 赖的老师 ,它 能揭示自然 界的秘密 ."
根据同样的思路, 我们还可以 定义并且研究4维球、 5维球直 至n维球.研究n维球时,总可以 类比n 1维球的情形 , 从中获 得启发和联想.
例 2 类比实数的加法和乘法 ,列出它们相似的 运算性质 .
分析 实数的加法和乘法都是 由两个数参与运算 , 都满足一定的运算律 , 都存在逆运算 ,而且"0" "1" 分 别在加法和乘法中占有 特殊的地位 .因此我们可以 从上述4个方面来类比这两种运 算.
解 1两个实数经过加法运算 或乘法运算后 ,所 得的结果仍然是一个实 数. 2从运算律的角度考虑 , 加法和乘法都满足交换 律和结合律 ,即 ab ba ab ba a b c a b c abc abc
这种由两类对象具有某些类 似特征和其中一类对象的某 些已知特征, 推出另一类对象 也具有这些特征的推理称为 类比推理 简称类比.简言之, 类比推理是由特殊到特殊的 推理.
在数学中 , 我们可以由已知解决的 问题 和已经获得的知识出发 , 通过类比而提 出新问题和作出新发现 .例如, 数学家波 利亚Polya 曾指出:" 类比是一个伟大的 引路人 , 求解立体几何问题往往 有赖于 平面几何中的类比问题 ." 数学中还有向 量与数的类比 , 无限与有限的类比 ,不等 与相等的类比 , 等等.
思考 科学家做出上述猜想的 推理过程是怎样的 ? 在提出上述猜想过程中 , 科学家对比了火星与地 球 之间的某些相似特征 ,然后从地球的一个已知 特征 (有性命存在)出发, 猜测火星也可能具有这 个特征.
数学研究中也常常进行 这样的推理 .例如, 在研究 球体时, 我们会自然地联想到圆 .对于圆 , 我们已经 有了比较充分的研究 , 定义了圆的一些概念 , 发现 了圆的一些性质 (表2 1).由球与圆在形状上和概 念上都有类似的地方 , 即具有完美的对称性 , 都是 到定点的距离等于定长 的点的集合,因此我们推 测对于圆的特征 , 球也可能具有 .
应用归纳推理可以发现 新事实 , 获得新结论 . 下面是一个数学中的例 子.
an 例1 已知数列an 的第 1项a1 1 , 且an1 1 an n 1,2, , 试归纳出这个数列的通 项公式.
分析 数列的通项公式表示的 是数列an 的第n 项an与序号之间的对应关系 .为此,我们先根据已知 的递推公式 ,算出数列的前几项 . 1 1 ; 解 当n 1时, a1 1; 当n 2时, a 2 1 1 2 1 1 1 1 3 2 . 当n 3 时, a3 ;当n 4时, a 4 1 4 1 3 1 1 3 2
b 1
A
P
这个结论是正确的吗 ? 请同 学们自己证明 .
S S3 D 2 S1
E
F
2
图2.1 1
我们把前面所进行的推 理过程概括为 :
从具体问 题出发
观察、分析、 比较、联想
归纳、 类比
提出 猜想
法国数学家拉普拉 斯(Laplace,1749 1827)曾经说过 :" 即 使在数学里 , 发现真 理的主要工具也是 归纳和类比 ."
数学中还有许多集合具 有这4条运算性质 .法国天才的 Galois 提出了 数学家伽罗瓦 " 群的概念 , 用来表示具有 这种运算性质的集合 .
运用类比推理常常先要 寻找合适的类 比对象 , 例如 , 在立体几何中 ,为了研究 四面体的性质 , 我们可在平面几何中寻 找一个研究过的对象 , 通过类比这个对 象的性质 , 获得四面体性质的猜想 以及 证明这些猜想的思路 .
可见,归纳推理和类比推 理都是根据已有的事实 , 经过观察、分析、比较、 联想, 再进行归纳类比, 然 后提出猜想的推理, 我们 把他们统称为合情推理 (plausible reasoning).
通俗地说, 合情推理是指 " 合乎情理" 的推理.数学研究中 , 得到一个新结论 之前, 合情推理常常能帮助我 们猜想 和发现结论 ; 证明一个数学结论之前 , 合情推 理常常能为我们提供证 明思 路和方向 . 下面再来看一个例子 .
探究 类比圆的特征 , 填写表2 1中球的相关 特征,并说说推理的过程 .
