物理几何光学竞赛讲解及试题
高中物理竞赛几何光学测试题(含详细解析)

几何光学测试题1、如图(a )所示,一细长的圆柱形均匀玻璃棒,其一个端面是平面(垂直于轴线),另一个端面是球面,球心位于轴线上.现有一很细的光束沿平行于轴线方向且很靠近轴线人射.当光从平端面射人棒内时,光线从另一端面射出后与轴线的交点到球面的距离为a ;当光线从球形端面射人棒内时,光线在棒内与轴线的交点到球面的距离为b .试近似地求出玻璃的折射率n 。
2、内表面只反射而不吸收光的圆筒内有一半径为R 的黑球,距球心为2R 处有一点光源S ,球心O 和光源S 皆在圆筒轴线上,如图所示.若使点光源向右半边发出的光最后全被黑球吸收,则筒的内半径r 最大为多少?3、如图1中,三棱镜的顶角α为60︒,在三棱镜两侧对称位置上放置焦距均为 30.0cm f =的两个完全相同的凸透镜L 1和 L 2.若在L 1的前焦面上距主光轴下方14.3cm y =处放一单色点光源S ,已知其像S '与S 对该光学系统是左右对称的.试求该三棱镜的折射率.4、如图(a )所示,两平面镜A 和B 的镜面分别与纸面垂直,两镜面的交线过图中的O 点,两镜面间夹角为︒=15α,今自A 镜面上的C 点处沿与A 镜面夹角︒=30β的方向在纸面内射出一条光线,此光线在两镜面经多次反射后而不再与镜面相遇。
设两镜面足够大,1=CO m 。
试求:(1)上述光线的多次反射中,最后一次反射是发生在哪块镜面上? (2)光线自C 点出发至最后一次反射,共经历多长的时间?5、有一水平放置的平行平面玻璃板H ,厚3.0 cm ,折射率 1.5n =。
在其下表面下2.0 cm 处有一小物S ;在玻璃扳上方有一薄凸透镜L ,其焦距30cm f =,透镜的主轴与玻璃板面垂直;S 位于透镜的主轴上,如图(a )所示。
若透镜上方的观察者顺着主轴方向观察到S 的像就在S 处,问透镜与玻璃板上表面的距离为多少?6、望远镜的物镜直径D =250cm ,其焦距f =160m 。
全国中学生物理竞赛真题汇编---光学 参考答案
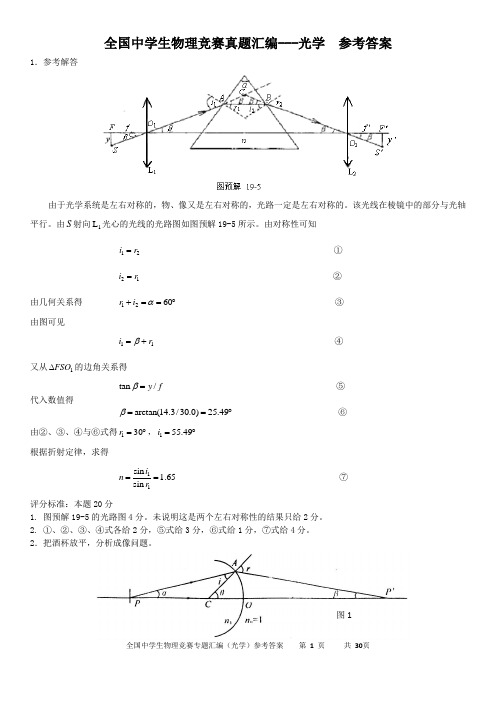
全国中学生物理竞赛真题汇编---光学 参考答案1.参考解答由于光学系统是左右对称的,物、像又是左右对称的,光路一定是左右对称的。
该光线在棱镜中的部分与光轴平行。
由S 射向1L 光心的光线的光路图如图预解19-5所示。
由对称性可知12i r = ①21i r = ②由几何关系得 1260r i α+==︒ ③ 由图可见11i r β=+ ④又从1FSO ∆的边角关系得tan /y f β= ⑤代入数值得arctan(14.3/30.0)25.49β==︒ ⑥由②、③、④与⑥式得130r =︒,155.49i =︒ 根据折射定律,求得11sin 1.65sin i n r == ⑦ 评分标准:本题20分1. 图预解19-5的光路图4分。
未说明这是两个左右对称性的结果只给2分。
2. ①、②、③、④式各给2分,⑤式给3分,⑥式给1分,⑦式给4分。
2.把酒杯放平,分析成像问题。
图11.未斟酒时,杯底凸球面的两侧介质的折射率分别为n 1和n 0=1。
在图1中,P 为画片中心,由P 发出经过球心C 的光线PO 经过顶点不变方向进入空气中;由P 发出的与PO 成α 角的另一光线PA 在A 处折射。
设A 处入射角为i ,折射角为r ,半径CA 与PO 的夹角为θ ,由折射定律和几何关系可得n 1sin i =n 0sin r (1) θ =i +α (2)在△PAC 中,由正弦定理,有sin sin R PCiα= (3) 考虑近轴光线成像,α、i 、r 都是小角度,则有1n r i n =(4) Ri PCα=(5) 由(2)、(4)、(5)式、n 0、n l 、R 的数值及 4.8PC PO CO =-=cm 可得θ =1.31i (6) r =1.56i (7)由(6)、(7)式有r >θ (8)由上式及图1可知,折射线将与PO 延长线相交于P ',P ' 即为P 点的实像.画面将成实像于P ' 处。
中学生物理竞赛系列练习试题几何光学

中学生物理竞赛系列练习题第十章 几何光学1、如图所示,一物体在曲率半径为12cm 的凹面镜的顶点左方4cm 处,求相的位置及横向放大率,并作出光路图。
d = 30cm ,求物体PQ 的像P ′Q ′与PQ 之间的距离d 2 。
答案:d 2 = 10cm 3、有一凹面镜,球心为C ,内盛透明液体,已知C 至液面的高度CE = 40.0cm ,主轴CO 上有一物体A 。
当物离液面的高度AE = 30.0cm 时,A 的实像和物恰好处于同一高度。
实验时光圈直径很小,可以保证近轴光线成像。
试求该透明液体的折射率n 。
解法一:第一次,折射 v 1 = n ·AE = 30n 第二次,反射 u 2 = 30n + OE f = 2OE 40+v 2 = OE40n 60)OE n 30)(OE 40(+-++第三次,折射 u 3 = v 2 - OE = OE40n 60OE 80nOE 30n 1200+-+-v 3 = nu 3 = 30即 180n 2+(6OE - 240)n - 8OE = 0 得 n 1 = 34 ,n 2 = -30OE (舍去)解法二:据光路图(水中反射线应指向C )。
再根据题意“近轴光线”,可以近似处理 sini ≈ tgi ,易得结论。
n = rsin i sin ≈tgrtgi = AECE答案:n =1.33 。
4、内径为r 、外径为R(R>r)的玻璃管内装满了发光的液体。
液体在伦琴射线的照射下发绿光,玻璃对绿光的折射率为n1,液体对绿光的折射率为n2。
从旁边看玻璃管,玻璃管的厚度象是零,那么r/R应满足什么条件?答案:当n1≤n2时,Rr≥1n1;当n1≥n2时,Rr≥2n15、凸透镜焦距为10cm ,凹透镜焦距为4cm ,两透镜相距12cm共主轴放置。
已知物在凸透镜左方20cm处,计算像的位置及横向放大率,并作出光路图。
答案:凹透镜左方8cm处;横向放大率为1(望远镜?)光路图如下——6、在折射率为5/3的透明液体中,有一会聚透镜L ,它在液体中的焦距为7cm ,主轴竖直。
2020年高中物理竞赛习题专题十一:几何光学(Word版含解析)

【预赛 三一 自招】高中物理竞赛模拟专题之《几何光学》1 如图所示,一储油圆桶,底面直径与桶高均为d .当桶内无油时,从某点A 恰能看到桶底边缘上的某点B .当桶内油的深度等于桶高一半时,在A 点沿AB 方向看去,看到桶底上的C 点,C 、B 相距.4d由此可得油的折射率以及光在油中传播的速度为() (A)17s m 10106,102-⋅⨯ (B) 17s m 10106,210-⋅⨯ (C)18s m 10105.1,210-⋅⨯ (D) 18s m 10105.1,102-⋅⨯ 分析与解 如图所示,C 点发出的光线经O 点折射后射向A 点,则由折射定律r n i n sin sin 0=(n 为油的折射率,0n 为空气的折射率),可知油的折射率210/45sin sin sin ===OC CD i r n .光在折射率为n 的介质中速度n c v =,因而可进一步求得光在油中传播的速度1718s m 10106s m 2/10103--⋅⨯=⋅⨯==n c v .故选(B ).题 13-1 图2 在水中的鱼看来,水面上和岸上的所有景物,都出现在一倒立圆锥里,其顶角为( ) (A )48.8(B )41.2(C )97.6(D )82.4分析与解 本题是一个全反射的应用题.根据水的折射率,光线从空气射入水中时反射光的临界角 8.481arcsin≈=ni c,其中n =1.33为水的折射率.如图所示,当光线以90 的最大入射角射入水中时,折射角为r ,故所有射入水中的光线的折射角均小于r ,根据空间旋转对称,水面上所有的景物都落在顶角为 6.9722c==i r 的锥面内.故选(C ).题 13-2 图3 一远视眼的近点在1 m 处,要看清楚眼前10 cm 处的物体,应佩戴怎样的眼镜() (A ) 焦距为10 cm 的凸透镜 (B ) 焦距为10 cm 的凹透镜 (C ) 焦距为11 cm 的凸透镜 (D ) 焦距为11 cm 的凹透镜 分析与解 根据薄透镜的成像公式f p p '=-'111,可由物距p 和像距p '计算透镜的像方焦距f '.根据题意,物距p =-0.1 m ,像距p '=-1 m ,则代入公式可求得像方焦距cm 11m 11.0=≈'f .像方焦距为正数,故为凸透镜.正确答案为(C )4 一平行超声波束入射于水中的平凸有机玻璃透镜的平的一面,球面的曲率半径为10 cm ,试求在水中时透镜的焦距.假设超声波在水中的速度为11s m 1470-⋅=u ,在有机玻璃中的速度为12s m 2680-⋅=u .分析 薄透镜的像方焦距公式为210r n n r n n n f Li L i---=',弄清公式中各值代表的物理意义即可求解本题.这里i n n 、0分别为透镜前后介质的折射率,由题意透镜前后介质均为水,故水n n n i ==0;L n 为透镜的折射率;1r 为透镜平的一面的曲率半径,即∞=1r ;2r 为透镜凸的一面的曲率半径,即2r = - 10 cm.解 由上述分析可得cm 1.2211212122221112-=-=-=---='u u rn n r r n n r n n n f i5 将一根短金属丝置于焦距为35 cm 的会聚透镜的主轴上,离开透镜的光心为50 cm处,如图所示. (1) 试绘出成像光路图;(2)求金属丝的成像位置.分析 (1) 凸透镜的成像图只需画出两条特殊光线就可确定像的位置.为此作出以下两条特殊光线:过光心的入射光线折射后方向不变;过物方焦点的入射光线通过透镜入射后平行于主光轴.(2)在已知透镜像方焦距f '和物距p 时,利用薄透镜的成像公式f p p '=-'111即可求得像的位置.解 (1)根据分析中所述方法作成像光路图如图所示. (2) 由成像公式可得成像位置为cm 117cm 355035)50(=+-⨯-='+'='f p f p p题 13-5 图6 一架显微镜的物镜和目镜相距为 20 cm ,物镜焦距为7 mm ,目镜的焦距为 5 mm ,把物镜和目镜均看做是薄透镜.试求:(1)被观察物到物镜的距离;(2)物镜的横向放大率;(3)显微镜的视角放大率.分析 (1)图示为显微镜的工作原理图.使用显微镜观察物体时,是将物体置于物镜物方焦点o f 外侧附近.调节物镜与目镜的间距d ,使物体经物镜放大成实像(显微镜的中间像)在目镜物方焦点e f 附近.由题意,图中d 和e f 已知,可以求得中间像到物镜的距离,即物体对物镜的像距ef d p -='.则利用薄透镜成像公式就可求得物体到物镜的距离p .(2)物镜的横向放大率可由公式pp V'=直接求出.而显微镜的视角放大率由公式e o 0f f s M ∆-=计算.其中∆为物镜像方焦点到目镜物方焦点的距离.解 (1)由分析可知,显微镜的中间像对物镜的距离(像距)为cm 195e =-='f d p而像方焦距f '=7 mm ,则由薄透镜成像公式f p p '=-'111可得观察物到物镜的距离为 mm -7.3mm 19571957=-⨯='-'''=p f p f p(2)物镜的横向放大率为7.26-='=pp V (3)由分析知mm 188mm 57200e o =--=--=∆)(f f d,则显微镜的视角放大率)5()7(188250-⨯-⨯-=M 1343-≈题 13-6 图7 一天文望远镜,物镜与目镜相距90 cm ,放大倍数为 8⨯(即8倍),求物镜和目镜的焦距.分析 望远镜的放大率为e o f f M''--=,其中o f '和e f '分别为物镜和目镜的像方焦距.而通常物镜的像方焦点和目镜的物方焦点几乎重合,即目镜和物镜的间距为两者焦距之和,而题中已知o f '+e f '=90 cm ,由此可求o f '和e f '.解 由分析可知8e o =''=f f M ,又o f '+e f '=90 cm ,则得物镜和目镜的像方焦距为⎩⎨⎧='='cm10cm80e o f f。
全国高中物理竞赛几何光学专题

若透镜是放置在空气中,则 ,薄透镜的物像位置关系式可以改写为
这时,焦距表示为
而定义薄透镜的光焦度 是
式中为透镜的折射,为透镜前后表面的曲半径.
⑵物像的放大率,若物像空间的折射率相同,薄透镜的垂直放大率是
2、凸透镜焦距为20cm,一点光源以速度40cm/s沿透镜主轴远离透镜,求当点光源距透镜为60cm时像点的移动速度。
解:设某一时刻此点光源成像的物距为 ,像矩为 ,则由透镜成像公式得
即
当点光源由上述位置移动一个很小的距离 时,其成像的物距变为 ,令其对应的像矩移动 ,则其对应的像矩变为 ,又依成像公式有
1.先求凸球面的曲率半径 。平行于主光轴的光线与平面垂直,不发生折射,它在球面上发生折射,交主光轴于 点,如图(a)所示。 点为球面的球心, ,由正弦定理,可得
(1)
由折射定律知
(2)
当 、 很小时, , , ,由以上两式得
(3)
所以
(4)
2.凸面镀银后将成为半径为 的凹面镜,如图(b)所示
令 表示物所在位置, 点经平面折射成像 ,根据折射定律可推出
几何光学
【知识点】
1、几何光学的基本定律
⑴光的直线传播定律在各向同性均匀介质中,光沿着直线传播,称为光的直线传播定律。
⑵光的独立传播定律不同发光点发出的光束在空间某点相遇时,彼此互不影响,各光束独立传播,称为光的独立传播定律。
⑶光的折射定律与反射定律入射光线、反射光线和分界面上入射点的法线三者在同一平面内:入射角和反射角的绝对值相等而符号相反,即入射光线和反射光线位于法线的两侧.即
同理,这时轴向放大率表示为
物理竞赛试题与解答(光学)

几何光学7.证明:光线相继经过几个平行分介面的多层介质时,出射光线的方向只与入射方向及两边的折射率有关,与中间各层介质无关。
证:因为界面都是平行的,所以光线在同一层介质中上界面的折射角相等。
如图所示,由折射定律有1212sin sin i n n i = 1312323sin sin sin i n n i n n i ==……………..1111sin sin sin i n n i n n i kk k k k ==--由此可见,最后出射光线的方向只与当初入射方向及两边介质的折射率有关。
8.顶角α很小的棱镜称为光楔。
证明光楔使垂直入射的光线产生偏向角()αδ1-=n ,其中是光楔的折射率。
证明:由于光线垂直入射,帮光线在第一个界面不发生折射。
仅在第二个界面有折射如图,根据折射定律22'sin sin i i n =以及几何关系α=2i ,故 2'sin sin i n =α当α很小时,有22''sin ,sin i i ≈≈αα则上式可写成2'i n =α所以偏向角为()αααδ1'22-=-=-=n n i i这个近似公式,在干涉、衍射、偏振中经常要用到。
9.如图1所示,两个顶角分别为0160=ϕ和0230=ϕ的棱镜胶合在一起(090=∠BCD )。
折射率有下式给出: 2111λb a n += 2222λb a n +=其中 1.11=a 25110nm b = 3.12=a 242105nm b ⨯=(1)确定使得从任何方向入射的光线在经过AC 面时不发生折射的波长0λ,并求出此情形下的折射率n 1和n 2(2)画出入射角相同的波长为红λ、0λ和蓝λ的三种不同光线的路径; (3)确定组合棱镜的最小偏向角(对于满足(1)中条件的波长);(4)计算平行于DC 入射且在离开组合棱镜时仍平行于DC 的光线的波长。
φ1φ2n1n2A BDC图1图2λ0解:(1)如果满足)()(0201λλn n = ,则波长为0λ的光线从任何方向入射在AC 面上将不发生折射,所以0λ满足关系式:222211λλb a b a +=+解得 nm a a b b 50021120=--=λ在此情形下折射率为 5.1)()(0201==λλn n(2)对波长比0λ长的红光,n 1和n 2均小于1.5。
高中物理竞赛几何光学测试题(含详细解析)

几何光学测试题1、如图(a )所示,一细长的圆柱形均匀玻璃棒,其一个端面是平面(垂直于轴线),另一个端面是球面,球心位于轴线上.现有一很细的光束沿平行于轴线方向且很靠近轴线人射.当光从平端面射人棒内时,光线从另一端面射出后与轴线的交点到球面的距离为a ;当光线从球形端面射人棒内时,光线在棒内与轴线的交点到球面的距离为b .试近似地求出玻璃的折射率n 。
2、内表面只反射而不吸收光的圆筒内有一半径为R 的黑球,距球心为2R 处有一点光源S ,球心O 和光源S 皆在圆筒轴线上,如图所示.若使点光源向右半边发出的光最后全被黑球吸收,则筒的内半径r 最大为多少?3、如图1中,三棱镜的顶角α为60︒,在三棱镜两侧对称位置上放置焦距均为 30.0cm f =的两个完全相同的凸透镜L 1和 L 2.若在L 1的前焦面上距主光轴下方14.3cm y =处放一单色点光源S ,已知其像S '与S 对该光学系统是左右对称的.试求该三棱镜的折射率.4、如图(a )所示,两平面镜A 和B 的镜面分别与纸面垂直,两镜面的交线过图中的O 点,两镜面间夹角为︒=15α,今自A 镜面上的C 点处沿与A 镜面夹角︒=30β的方向在纸面内射出一条光线,此光线在两镜面经多次反射后而不再与镜面相遇。
设两镜面足够大,1=CO m 。
试求:(1)上述光线的多次反射中,最后一次反射是发生在哪块镜面上? (2)光线自C 点出发至最后一次反射,共经历多长的时间?5、有一水平放置的平行平面玻璃板H ,厚3.0 cm ,折射率 1.5n =。
在其下表面下2.0 cm 处有一小物S ;在玻璃扳上方有一薄凸透镜L ,其焦距30cm f =,透镜的主轴与玻璃板面垂直;S 位于透镜的主轴上,如图(a )所示。
若透镜上方的观察者顺着主轴方向观察到S 的像就在S 处,问透镜与玻璃板上表面的距离为多少?6、望远镜的物镜直径D =250cm ,其焦距f =160m 。
高中几何光学竞赛题

1如图,三角形ABC 为某透明介质的横截面,O 为BC 边的中点,位于截面所在平面内的一束光线自O 以角i 入射,第一次到达AB 边恰好发生全反射。
已知θ=15°,BC 边长为2L,该介质的折射率为2。
求:①入射角i;②从入射到发生第一次全反射所用的时间(设光在真空中的速度为c,可能用到:6sin 75=tan152=-1【解析】①根据全反射规律可知,光线在AB 边上某点P 的入射角等于临界角C,由折射定律得1sin C n=① 代入数据得C=45°②设光线在BC 边上的折射角为r,由几何关系得 r=30°③ 由折射定律得sin sin inr=④ 联立③④式,代入数据得 i=45°⑤②在△OPB 中,根据正弦定律得00sin 75sin 45OP L=⑥设所用时间为t,光线在介质中的速度为v,得OP=vt ⑦c v v=⑧ 联立⑥⑦⑧式,代入数据得t =2一半径为 6 m 的半圆柱玻璃砖,上方有平行横截面直径AB 的固定直轨道,轨道上有一小车,车上固定一与轨道成45°角的激光笔,发出的细激光束始终在与横截面平行的平面上.打开激光笔,并使小车从左侧足够远的地方以恒定速度向右运动,结果在半圆柱玻璃砖的弧面有激光射出的时间持续了1 s .不考虑光在AB 面上的反射,已知该激光在该玻璃砖中的折射率为 2 ,光在空气中的传播速度大小为c .求: ①该激光在玻璃砖中传播的速度大小; ②小车向右匀速运动的速度v 0的大小.7、①由n =v c得,激光在玻璃中的传播速度为v =n c = 22c (2分)②激光从玻璃射向空气,发生全反射的临界角为 C =arcsin n 1=45°(1分) n =sin θsin 45°,θ=30°(2分)设激光射到M 、N 两点时,折射光线恰好在弧面发生全反射,激光从M 点到N 点的过程弧面有激光射出 由正弦定理得sin 45°MO =sin 60°R ,得MO = 36R (1分) 同理可得ON =36R (1分)又t =v0MN(2分) 可得v 0=4 m/s(1分)3一个半圆柱形玻璃砖,其横截面是半径为R 的半圆,AB 为半圆的直径,O 为圆心,如图所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
B
F2 B′
F1 O
A′
L1
A
L2
F2
B′
A′
B F1 O
A F2
B′
F1 B O
L1
L2
A′
L1 L2
在对光具组中某一镜进行计算时,u、v、f 都应
从该镜的光心算起。
最后成像的虚实,由最后一次成像决定。
总的放大率等于各次放大率的乘积。
1.物与屏相距L=80cm,在其间放一个薄凸透镜,透镜 放在两个不同的位置,都可以在光屏上得到物体的像。 已知这两个像长之比为1/9,求此透镜的焦距f。
薄透镜成像问题
一、薄透镜成像公式的推导
二、薄透镜
1.折射面是两个球面,或者一个是球面另一个是平面的 透明体,叫透镜。
通常,厚度比球面半径小得多的透镜,叫做薄透 镜。
2. 透镜的中心叫光心。过光心的直线叫光轴,其中与 透镜垂直的光轴叫主光轴,其余的叫副光轴。
3. 平行于主光轴(或副光轴)的近轴光线经透镜后将 会聚(或反向延长后相交)于主光轴(或副光轴)上 的一点,该点称为焦点(或副焦点)。
L
1.0cm
H 2.0cm S
3.0cm
7.在焦距为15cm的凸透镜O右边40cm处放一平面镜, 平面镜垂直于主轴,有一点光源S放在O的左面主轴上 离O为10cm处,求最后成的像的位置。
透镜左边17.4cm处。
8.有两个焦距分别为f1和f2的凸透镜,如果把这两个透
镜作适当的配置,则可使一垂直于光轴的小物体在原
15cm
2.如图所示,位于凸透镜L的焦点F处的点光源S射到透 镜上的光,经透镜折射后,在距透镜2倍焦距处与主光 轴垂直的光屏上,留下直径为d的亮斑。现沿主光轴移 动S一段距离,使在屏上留下亮斑的直径变为d/2。已
知此透镜的焦距为f,求物点S移动的距离。
L
S d
F
O
F
3f 或 f /3
3.如图所示,全反射棱镜上方6cm处放置一物体AB, 棱镜直角边长为6cm,棱镜右侧10cm处放置一焦距为
锥的顶点位于焦点F,锥高等于2f,锥的母线与其中心
轴线的夹角等于 ,求圆锥面的像。 L
F
2
2f
f
圆锥面的像是一个一端在透镜右方距透镜3f/2,另 一端位于无穷远处的半径为R=f tan 的圆柱面,是
实像。
10.一个焦距为f 的会聚透镜,在其左侧的主光轴上离 透镜2f 处有一小光源,在右侧屏上观察到此光源的清
10cm/s,向远离透镜方向运动。
6.有一个水平放置的平行平面玻璃板H,厚3.0cm,折 射率n=1.5,在其下表面下2.0cm处有一小物S;在玻璃
板上方有一薄透镜L,其焦距f=30cm,透镜的主轴与
玻璃板面垂直;S位于透镜的主轴上,如图所示。若透 镜上方的观察者顺着主轴方向观察到S的像就在S处, 问透镜与玻璃板上表面的距离为多少?
x1
(n 1)d nf (n 1)d
f
x2
(n 1)d n
11.如图所示,外形一样,折射率均为n的两个薄平凸透 镜,一个透镜的平面镀银,另一个透镜的凸面镀银。 如果光线从未镀银的一面入射,它们的焦距之比为多 少?
f : f′= n : (n-1)
12.如图所示,容器中装有深度为2h的某种液体,其折射
其变化率△r/ △ x=4/3。求透镜L1和L2的焦距f1和f2各为
多少?
L1
A
L2
f1 =f2= 2cm
O
O′
14.一薄透镜一侧有一球面物,球心在透镜的主轴上, 透镜两边的介质均为空气,透镜焦距为f。试给出一种 方案,能使此球面物通过此透镜成像仍为一球面。假 设球面各部分发出的光线均不被球面的其他部分挡住。
f1=10cm的凸透镜,凸透镜右侧15cm处再放置一焦距为 f2=10cm的凹透镜,求此光学系统成像的位置和放大率
(全反射棱镜的折射率n=1.5)。
BA
15cm
位置为凹透镜右侧距离凹透镜10cm处,是正立实像。 放大率为2。
4.光屏与遮光板互相平行,两者相距为b,遮光板上有 一个半径为r的圆孔。今在此孔中嵌入透镜,设透镜与
由于只讨论近轴光线,所以所有副焦点都位于 垂直于主光轴的平面内,称为焦平面。
4.焦点到光心的距离叫焦距。 如果透镜两侧介质相同,则两个焦距相等;如
果两侧介质不同,则两个焦距的关系为:
f1 : f2 = n1 :n2
式中f1、f2相应为物方焦距和像方焦距, n1、n2相应为 物方和像方介质的折射率。
O1
O2
d
(1)目镜上方5.1m处;(2)m=10。
4cm和2cm。固定A与L1而使L2左右移动,发现仅有一
个位置能使L2接收到经L1射过来的全部光线,即将L2固 定于此位置,然后在L2的右侧垂直于主光轴再置一光
屏,以x表示光屏与L2的距离,使x由零逐渐增大时,
发现:当x小于某值时,光屏上可见到一个大小不变的
光斑;当x大于此值时,圆形光斑的半径r随x线性增加,
做为一般讨论,除特殊说明外,均限于两侧介 质相同的薄透镜的近轴光线成像问题。
三、薄透镜成像公式
11 1 uv f
应用时的注意点:
1.透镜两侧介质折射率应相等。 2.必须是近轴光线。 3.符号法则:实正虚负。
4.放大率:
m v u
四、薄透镜成像作图
1.三条特殊光线的作用
(1)通过光心的光线不改变方向; (2)平行于主光轴的光线,折射后通过焦点(或反 向延长线过焦点); (3)通过焦点(或对方焦点)的光线,折射后平行 于主光轴。
设球面的半径为R,球心到光心的距离为u0,那么 应满足
R = u0 (u0 2 f )
15.图示是一种反射式望远镜的示意图,已知凹镜集焦 距f1=100cm,平面镜与凹镜主轴成45°角,凹镜主轴与 平面镜交于O2,O1O2=0.95m,目镜(凸透镜)光心到 凹镜主轴的距离d=0.15m,两镜主轴相互垂直。目镜焦 距f2=10.2cm。 求:(1)通过目镜看到的物体像的位置; (2)此望远镜的放大率m。
孔等大,且其主光轴与光屏垂直,再在此透镜的主光
轴上与光心相距为a处置一点光源S,因而在光屏上形 成一个半径为R的圆形光斑。已知a=30cm,b=20cm, r=1cm,R=5cm。试求此透镜的焦距。
(1)若为凸透镜,f=3cm; (2)若为凹透镜,f=-6cm。
5.有一个凸透镜,其焦距为20cm,一点光源以40cm/s 的速度沿主光轴匀速靠近透镜,求点光源与透镜相距 60cm时,像点移动的速度。
A
F2 B′
A
B
F1 O
A′
B F1
O
F2
L
L
2.一般光线的作图
对于任意一条光线SA,过光心O作副光轴OP平 行于SA,SA与焦平面MN交于P点,连接AP或AP的 反向延长线即为SA的折射光线。
A
M P
S
F1
O F2
N L
M A
S F1
O
F2
PN
L
3.注意:
(1)物点上所发出的任意一条光线,经成像系统作 用后,必定会通过像点;
位置成一等大、倒立的像,如图所示。试求出满足上 述要求的配置方案中各透镜的位置。
物
L1
L2
像
取焦距较小的L1放在物右方u处,把焦距较大的L2放
在L1右方d处,其中
d 2 f1 f2
u 2 f1 f2 ( f2 f1 )
9.在焦距为f 的凸透镜L的主光轴上放置 一个发光圆锥
面(如图所示),圆锥的中心轴线与主光轴重合,圆
(2)平行于副光轴的光线,经过透镜作用后,一定 通过焦平面与副光轴的交点。
五、光具组成像 由两个或两个以上的光学器具组成的光学系统,
叫光具组。
光线在传播过程中经过多次折射或反射,可以 依次成像,经第一镜成像后的反射或折射光线,对 于第二镜来说则是入射光线,因此,第一镜的像是 第二镜的物。
若第一镜成的像在第二镜之前,不论像是实像 还是虚像,对第二镜来说均看作实物。反之。若经 第一镜成的像在第二镜之后,则不论是实像还是虚 像均为虚物。
率为n,中心有圆孔的不透明板恰好位于液体深度的一
半,圆孔内镶嵌一个空心薄壁凸透镜,其半径恰好等
于孔的半径r,该透镜在液体中的焦距长为f,一个点光
源S位于透镜的主轴上且距液面高度为H,求在点光源 照射下,容器底部亮圆的半径大小。
R = r[1+ h(u f ) ] uf
S H
h h
13.如图所示,两凸透镜L1和L2及一发光圆盘A共轴(透 镜主光轴为OO′)放置,A、L1、L2的半径分别为1cm、
晰的像。现在光源和透镜的位置保持不变而在光路中
插入一个厚度为d(d<f)的平板玻璃(平板与光轴垂
直),若还要在屏上得到光源清晰的像,则屏应怎样
移动(分别就玻璃放在光源和透镜之间以及玻璃放在 透镜和光屏之间两种情况讨论)?
(1)玻璃放在光源和透镜之间时,右移△x1; (2)玻璃放在光源和屏之间时,右移△x2;
