偏微分实验报告1
偏微分方程数值解第三次上机实验报告
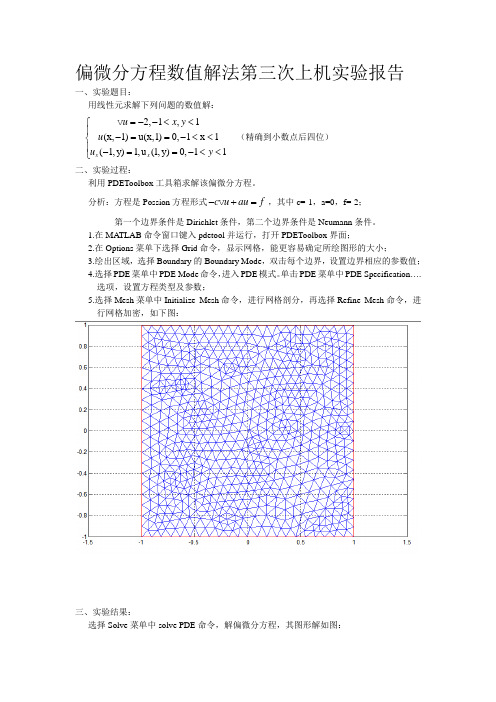
偏微分方程数值解法第三次上机实验报告一、实验题目:用线性元求解下列问题的数值解:2,1,1(x,1)u(x,1)0,1x 1(1,y)1,u (1,y)0,11xx u x y u u y =--<<⎧⎪-==-<<⎨⎪-==-<<⎩ (精确到小数点后四位)二、实验过程:利用PDEToolbox 工具箱求解该偏微分方程。
分析:方程是Possion 方程形式c u au f -+=,其中c=-1,a=0,f=-2; 第一个边界条件是Dirichlet 条件,第二个边界条件是Neumann 条件。
1.在MA TLAB 命令窗口键入pdetool 并运行,打开PDEToolbox 界面;2.在Options 菜单下选择Grid 命令,显示网格,能更容易确定所绘图形的大小;3.绘出区域,选择Boundary 的Boundary Mode ,双击每个边界,设置边界相应的参数值;4.选择PDE 菜单中PDE Mode 命令,进入PDE 模式。
单击PDE 菜单中PDE Specification ….选项,设置方程类型及参数;5.选择Mesh 菜单中Initialize Mesh 命令,进行网格剖分,再选择Refine Mesh 命令,进行网格加密,如下图:三、实验结果:选择Solve 菜单中solve PDE 命令,解偏微分方程,其图形解如图:图1 图形解图2 三维图形解图3 解的等值线图和矢量场图选择Mesh菜单中的Export Mesh,得到结点xy坐标;选择Solve菜单中的Export Solution…,得到每个节点处的值,输出u,即解的数值。
四、实验总结:通过本次试验,掌握了利用Matlab中的PDE求解工具得到PDE的解的方法,并对偏微分方程的形式有了更多的掌握。
偏微分方程报告范文

偏微分方程报告范文偏微分方程是研究多变量函数的微分方程,其中函数的未知量既依赖于自变量,又依赖于多个自变量。
偏微分方程在物理学、工程学和经济学等领域中有着广泛的应用。
本报告将介绍偏微分方程的基本概念、求解方法和应用领域。
一、偏微分方程的基本概念偏微分方程是由未知函数的偏导数和自变量构成的方程。
常见的偏微分方程包括波动方程、传热方程和扩散方程等。
偏微分方程根据阶数可分为一阶和二阶偏微分方程。
一阶偏微分方程中只涉及到未知函数的一阶偏导数,一般可以通过变量分离的方法求解。
二阶偏微分方程中涉及到未知函数的二阶偏导数,求解方法一般包括分离变量法、特征线法和变换法等。
二、偏微分方程的求解方法1.分离变量法:假设未知函数可以表示为两个只依赖于单个自变量的函数的乘积形式,然后将该形式代入到偏微分方程中,再将方程两边关于不同的自变量求积分,从而得到方程的通解。
2.特征线法:通过特征线曲线的方法将偏微分方程转化为常微分方程。
先找出特征线曲线,然后在特征线上引入新的变量,使得偏微分方程变为常微分方程,进而求解。
3.变换法:通过适当的变量变换,将原偏微分方程转化为一个更容易求解的形式。
常用的变换方法有坐标变换、函数变换和变量替换等。
三、偏微分方程的应用领域1.物理学:偏微分方程在物理学中有着广泛的应用。
例如,波动方程可以描述声波、光波和电磁波等在介质中的传播;传热方程可以描述热传导过程;薛定谔方程和波恩-奥本海默方程可以描述量子力学中的粒子行为等。
2.工程学:偏微分方程在工程学中被广泛应用于流体力学、结构力学和电磁场等领域。
例如,纳维-斯托克斯方程用于描述流体的运动;弹性方程用于描述结构的变形和应力分布等。
3.经济学:偏微分方程在经济学中应用较多,尤其是在金融学中。
例如,布莱克-斯科尔斯方程用于定价期权;黑-舒尔斯方程用于描述衍生品的定价和风险管理等。
通过对偏微分方程的研究和求解,可以更好地理解自然界的现象和规律,并为解决实际问题提供数学模型和解决方法。
偏微分方程实验1

预备实验偏微分方程工具箱的功能和利用一、实验目的PDE Toolbox提供了研究和求解空间二维偏微分方程问题的一个壮大而又灵活有效的环境。
本次实验了解PDE Toolbox的功能和PDE图形用户界面。
PDE Toolbox的功能包括:设置PDE 定解问题,即设置二维定解区域、边界条件和方程的形式和系数;用有限元法求解PDE,即网格的生成、方程的离散和求出数值解;解得可视化。
二、实验内容一、解偏微分方程的一个例子解Poisson方程:f∆-,边界条件为齐次dirichlet类型。
u=第一步:启动MATLAB,键入pdetool,按回车键确信即可启动GUI(图形用户界面),然后在options菜单下选择grid命令,打开栅格。
栅格的利用,能利用户容易确信所画图形的大小。
第二步:散布完成平面几何造型:R1-C1-E1+R2+C2。
用菜单或快捷工具别离画矩形R1,矩形R2,椭圆E1,圆C1,圆C2。
画圆时,第一选中椭圆工具,按鼠标右键并拖动即可,或在按Ctrl的同时,拖动鼠标也可绘制图。
然后在set formula栏,进行编辑并用算术运算符将图形对象名称连接起来,或删除默许的表达式直接键入R1-C1-E1+R2+C2。
选择Boundary菜单中Boundary Mode 命令,进入边界模式。
单击Boundary 菜单中Remove All Subdomain Borders选项,去掉子域边界,若是想将几何信息和边界信息进行存储,应选择Boundary菜单中的Export Decomposed Geometry, Boundary Cond’s…命令,将它们别离贮存于g,b变量中,通过MATLAB形成M文件。
第三步:选取边界,单击Boundary菜单中Specify Boundary Conditions…选项,打开Boundary Conditions对话框,输入边界条件,本例取缺省条件,即将全数边界设为齐次dirichlet条件,边界颜色显示为红色。
偏微分方程稳定性判断 实验报告

2
方法
前向差分法 注:用有限差分方法来求偏微分方程的近似解 ,想法是对自变量建立网格并把偏微分方程离散化 ,把连续问题 变成有限多个方程的离散化问题.若这个偏微分方程是线性的,那么它的离散方程也是线性的.
实验 2
云南财经大学实验报告
系 (院):统数学院 专 业:信息与计算科学 班 级:信计 07-1 学 号:200705001507 姓 名:邹凌波 课程名称:偏微分方程数值解法 实验时间:2010 年 5 月 24 日 指导教师:陈龙伟
云南财经大学教务处制
填表说明
1.实验名称 要用最简练的语言反映实验的内容。 2.实验目的 目的要明确,要抓住重点,可以从理论和实践两个方面考虑。在
τ
2h
程序:
附录 1
实验 内容 (算 法、
程 序、 步骤 和方 法)
function u=bjdlfc(xa,xb,ya,yb,M,N) %xa、xb 为 x 方向的起始与终止值;ya、yb 为 t 方向的起始与终止值; %M、N 分别为空间步数与时间步数. c=1;%c 为差分方程中的参数 h=(xb-xa)/M;m=M-1;n=N;%h、k 分别为空间与时间步长;k=(yb-ya)/N; k=(yb-ya)/N; sigma=c*k/(2*h);%网格比 a=diag(ones(m,1))+diag(-sigma*ones(m-1,1),1); a=a+diag(sigma*ones(m-1,1),-1);%定义矩阵 A lside=l(ya+(0:n)*k);rside=r(ya+(0:n)*k); u(:,1)=f(xa+(1:m)*h)';%初始条件 for j=1:n
偏微分实验

微分方程数值解实验指导(一)实验一: 二阶椭圆型方程差分格式的程序实现1. 实验内容用五点差分格式求解Poisson 方程边值问题⎩⎨⎧∂∈=∈=-=∆,),(,0,),(,:2G y x u G y x f u (1) 其中}1|||,||),{(<=y x y x D 。
(1)用正方形网格)(h k =列出相应的差分方程。
(2)对161,81,51,21=h 分别求出数值解,观察数值解的情况,分析计算结果。
(最好画出数值解的图形)注意:在区域G 的边界上为齐次Dirichlet 条件,在这类边界上不需要给出差分格式。
2. 实验目的及要求按照给定的差分格式编程实现求出数值解;结合格式的相容性和收敛性条件简单分析计算结果。
要求在实验课上算出数值结果;按要求格式写出实验报告;下次实验课前交本次实验的实验报告。
3. 实验原理与实验过程: 以下是求解问题的步骤第一步: 对求解区域作网格剖分。
按照要求得网格剖分图如下(图1为21=h 的情况,图2为51=h 的情况)-1-0.8-0.6-0.4-0.20.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81区域划分示意图图1-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81区域划分示意图图2第二步: 差分法的目的是:求边值问题的解),(y x u 在节点),(j i y x 的近似值ij u (m j n i ,...,2,1,,2,1==, )。
为此,需要构造逼近微分方程定解问题的差分格式。
采用五点差分格式,取定x 轴和y 轴方向的步长相等,即h=k ,作两族与坐标轴平行的直线:ih x i +-=1,i=0,1,…,2/h,jh y j +-=1,j=0,1,…,2/h,两族直线的交点为网点(或节点)。
位于G 内的节点为内点,位于G 的边界上的节点为界点。
偏微分方程数值及matlab实验报告

偏微分方程数值实验报告八实验题目:利用有限差分法求解.0)1(,0)1(),()()(==-=+''-u u x f x u x u 真解为)1()(22x e x u x -=-实现算法:对于两点边值问题,)(,)(,,d 22βα==∈=-b u a u l x f dxu(1)其中),(b a l =f b a ),(<为],[b a l =上的连续函数,βα,为给定常数.其相应的有限差分法的算法如下:1.对求解区域做网格剖分,得到计算网格.在这里我们对区间l 均匀剖分n 段,每个剖分单元的剖分步长记为nab h -=.2.对微分方程中的各阶导数进行差分离散,得到差分方程.运用的离散方法有:方法一:用待定系数和泰勒展开进行离散)()()()(d )(d 111122++--++≈i i i i i i i i x u x u x u x x u ααα方法二:利用差商逼近导数21122)()(2)()(d )(d h x u x u x u x x u i i i i i -++-≈(2)将(2)带入(1)可以得到)()()()(2)(211u R x f h x u x u x u i i i i i +=+---+,其中)(u R i 为无穷小量,这时我们丢弃)(u R i ,则有在i x 处满足的计算公式:1,...,1)()()(2)(211-==+---+n i x f hx u x u x u i i i i ,(3)3.根据边界条件,进行边界处理.由(1)可得βα==n u u ,0(4)称(3)(4)为逼近(1)的差分方程,并称相应的数值解向量1-n U 为差分解,i u 为)(i x u 的近似值.4.最后求解线性代数方程组,得到数值解向量1-n U .实验题目:用Lax-Wendroff 格式求解方程:.4sin 1),1(],1,0[,2sin 1)0,(,0),1,0(,02t t u x x x u t x u u x t ππ+=∈+=>∈=- (1) (精确解).2(2sin 1t x u ++=π) 数值边值条件分别为: (a )).(20101n 0nn nu u hu u -+=+τ (b ).1n 0nu u =(c ).02-12111n 0=++++n n u u u请将计算结果与精确解进行比较。
数统学院_偏微分方程数值解实验报告1

1.6905
0.0000
Hale Waihona Puke 0.02501.02531.0253
0.0000
0.5500
1.7333
1.7333
0.0000
0.0500
1.0513
1.0513
0.0000
0.5750
1.7772
1.7771
0.0001
0.0750
1.0779
1.0779
0.0000
0.6000
1.8222
0.0080
0.9500
2.5557
2.5857
0.0300
0.4500
1.5597
1.5683
0.0087
0.9750
2.6196
2.6512
0.0316
0.4750
1.5987
1.6080
0.0094
1.0000
2.6851
2.7183
0.0332
0.5000
1.6386
1.6487
0.0101
0.0001
0.1750
1.1913
1.1912
0.0000
0.7000
2.0138
2.0138
0.0001
0.2000
1.2214
1.2214
0.0000
0.7250
2.0648
2.0647
0.0001
0.2250
1.2523
1.2523
0.0000
0.7500
2.1171
2.1170
0.0001
1.7716
1.8221
0.0506
偏微分方程数值解上机实验报告(matlab做的)

偏微分方程数值解法上机报告(一)一、实验题目:用Ritz-Galerkin 方法求解边值问题2u '',01(0)0,(1)1u x x u u ⎧-+=<<⎨==⎩的第n 次近似()n u x ,基函数()sin(),1,2,...,i x i x i n ϕπ==.二、实验目的:通过本次上机实验,理解求解初值问题的变分问题的最重要的近似解法——Ritz-Galerkin 方法,以便为学习有限元法打好基础。
此外,要熟悉用Matlab 解决数学问题的基本编程方法,提高运用计算机解决问题的能力。
三、实验代码:n=5;syms x;for i=1:np(i)=sin(i*pi*x);q(i)=-i^2*pi^2*sin(i*pi*x);endfor i=1:nb(i)=2*int(p(i),0,1);for j=1:nA(i,j)=int((-q(j)+p(j))*p(i),0,1);endendt=inv(A)*b'四、运行结果:t=2251799813685248/3059521645650671/pi281474976710656/9481460623939047/pi281474976710656/43582901062631895/pi五、总结:通过本次上机,我了解了Ritz-Galerkin 方程 n j j p f cj p i p a n i i ,...,2,1)),(,())(),((1==∑=,明白了用Ritz-Galerkin 方法解决边值问题的变分问题的基本原理,并接近一步提高自己的编程动手能力,受益匪浅。
偏微分方程数值解法上机报告(二)一、 实验题目:用线性元求下列边值问题的数值解2''2sin ,0142(0)0,'(1)0y y x x y y ππ⎧-+=<<⎪⎨⎪==⎩二、 实验目的:通过本次上机,熟悉和掌握用Galerkin 法观点出发导出的求解处置问题数值解的线性有限元法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x=a:h1:b
y=c:h2:d
m=length(x);
n=length(y);
ee=;
[Y,X]=meshgrid(y,x);
?
Z=zeros(m,n);
U=zeros(m,n);
for i=2:m-1
U(i,1)=feval(g1x,x(i));
U(i,n)=feval(g2x,x(i));
g1x=inline('0');
g2x=inline('0');
…
g1y=inline('sin(pi*y)');
g2y=inline('exp(2)*sin(pi*y)');
[X,Y,Z]=chfenmethed(f,g1x,g2x,g1y,g2y,a,b,c,d,h1,h2);
function [X,Y,Z]=chfenmethed(f,g1x,g2x,g1y,g2y,a,b,c,d,h1,h2)
2、给出所用程序代码;
function varargout=liu(varargin)
T=1;a=1;h=1/20;k=1/10;
]
f=inline('0','x','t');
fx=inline('exp(x)');
ft1=inline('exp(t)');
ft2=inline('exp(1+t)');
C=A;
UU=zeros(1,m-2);
f1=UU;
for j=2:n
tk1=*(t(j-1)+t(j));
for i=2:m-1
UU(i-1)=f0(x(i),t(j));
f1(i-1)=r/2*U(i-1,j-1)+(1-r)*U(i,j-1)+r/2*U(i+1,j-1)+k*feval(f,x(i),tk1);
实验成绩
评阅时间
评阅教师
…
》
微分方程数值解法实验课:实验三
实验题目
利用显式差分格式计算二阶双曲型方程定解问题
实验目的
掌握双曲型方程显式差分格式的建立及其求法
实验地点及时间
机房2452012年11月2日
实验内容:
利用显式差分格式计算二阶双曲型方程定解问题
^
实验习题:
用显式差分格式求解双曲型方程定解问题
end
f1(1)=f1(1)+r/2*U(1,j);
*
f1(m-2)=f1(m-2)+r/2*U(m,j);
U(2:m-1,j)=zgf(A,B,C,f1);
Z(2:m-1,j)=abs(U(2:m-1,j)-UU');
end
function x=zgf(A,B,C,f)
n=length(B);
B1=zeros(1,n-1);
实验习题
用五点差分格式求解椭圆型方程边值问题
~
该问题的精确解为
要求:1、写出数值求解格式;
2、给出所用程序代码;
function varargout=hu(varargin)
a=0;b=2;c=0;d=1;h1=1/10;h2=1/20;
f=inline('(pi^2-1)*exp(x)*sin(pi*y)','x','y');
[X,T,Z]=chfenmethed(f,fx,ft1,ft2,a,T,h,k);
function [X,T,Z]=chfenmethed(f,fx,ft1,ft2,a,T,h,k)
x=0:h:a
t=0:k:T
m=length(x);
n=length(t);
r=a*k/h^2;
!
[T,X]=meshgrid(t,x);
(feval(fx1,x(i+1))-2*feval(fx1,x(i))+feval(fx1,x(i-1))+feval(f,x(i),0)));
end
for j=1:n
U(j,1)=feval(ft1,t(j));
U(j,m)=feval(ft2,t(j));
end
—
UU=f0(X,T);
for i=2:n-1
该问题的精确解为:
要求:
1.写出数值求解格式;
2.给出所用程序代码;
function varargout=wang(varargin)
a=1;T=1;b=;h=1/5;k=1/20;
f=inline('0','x','t');
fx1=inline('exp(x)');
/
fx2=inline('exp(x)');
z=exp(x+t)
3.给出实验结果。x =
0
t =
Columns 1 through 18
0
Columns 19 through 21
z =
…
实验总结:本次实验我学会了利用显式差分格式计算二阶双曲型方程定解问题,掌握双曲型方程显式差分格式的建立及其求法,学会了其对应的Matlab语言的编写。
实验成绩
end
x1(n)=Y(n);
for i=n-1:-1:1
x1(i)=Y(i)-B1(i)*x1(i+1);
end
x=x1;
)
function z=f0(x,t)
z=exp(x+t)
3、给出实验结果。
xtz
00
:
实验总结:本次实验我学会了利用Crank-Nicolson差分格式计算抛物型方程定解问题,掌握了用Matlab为其编写程序。
Z=zeros(m,n);
U=zeros(m,n);
for i=1:m
U(i,1)=feval(fx,x(i));
end
for j=2:n
U(1,j)=feval(ft1,t(j));
U(m,j)=feval(ft2,t(j));
end
A=-r/2*ones(1,m-2);
:
B=(1+r)*ones(1,m-2);
t=0:k:T
m=length(x);
n=length(t);
s=a*k/h;
[X,T]=meshgrid(x,t);—ຫໍສະໝຸດ Z=zeros(n,m);
U=zeros(n,m);
for i=2:m-1
U(1,i)=feval(fx1,x(i));
U(2,i)=U(1,i)+k*feval(fx2,x(i))+k^2/2*(a^2/h^2*...
3、给出实验结果。
x =
0
y =
@
0
z =
………
实验总结:通过本次实验,我学会了运用五点差分法解决椭圆型方程Dirichlet边值问题,并且学会了运用Matlab进行程序的编写并且调试。
实验成绩
评阅时间
评阅教师
?
微分方程数值解法实验课:实验二
实验题目
利用Crank-Nicolson差分格式计算抛物型方程定解问题
for j=2:m-1
U(i+1,j)=s^2*U(i,j-1)+2*(1-s^2)*U(i,j)+s^2*U(i,j+1)-U(i-1,j)+k^2*feval(f,x(j),t(i));
Z(i+1,j)=abs(U(i+1,j)-f0(x(j),t(i+1)));
end
end
function z=f0(x,t)
Y=zeros(1,n);
x1=zeros(1,n);
B1(1)=C(1)/B(1);
for i=2:n-1
?
B1(i)=C(i)/(B(i)-A(i)*B1(i-1));
end
Y(1)=f(1)/B(1);
for i=2:n
Y(i)=(f(i)-A(i)*Y(i-1))/(B(i)-A(i)*B1(i-1));
青岛农业大学
微分方程数值解法实验报告
姓 名:
学 院:
专 业:
班 级:
学 号:
/
完成时间:
2012年11月4日
微分方程数值解法实验课:实验一
~
实验题目
利用五点差分格式求解椭圆型方程Dirichlet边值问题
实验目的
掌握五点差分格式的建立及其求法
实验地点及时间
机房2452012年10月23日
实验内容:
利用五点差分格式求解椭圆型方程Dirichlet边值问题
实验目的
掌握Crank-Nicolson差分格式的建立及其求法
实验地点及时间
机房1272012年10月31日
实验内容:
*
利用Crank-Nicolson差分格式计算抛物型方程定解问题
实验习题:
用Crank-Nicolson差分格式求解抛物型方程定解问题:
该问题的精确解为:
要求:
1、写出数值求解格式;
end
for j=1:n
U(1,j)=feval(g1y,y(j));
U(m,j)=feval(g2y,y(j));
end
for i=2:m-1
(
for j=2:n-1
qu=f0(x(i),y(j));
Z(i,j)=abs(qu-U(i,j));
end
end
function z=f0(x,y)
z=exp(x)*sin(pi*y)
