偏微分方程数值解实验报告
偏微分方程数值解第三次上机实验报告
偏微分方程数值解法第三次上机实验报告一、实验题目：用线性元求解下列问题的数值解：2,1,1(x,1)u(x,1)0,1x 1(1,y)1,u (1,y)0,11xx u x y u u y =--<<⎧⎪-==-<<⎨⎪-==-<<⎩ （精确到小数点后四位）二、实验过程：利用PDEToolbox 工具箱求解该偏微分方程。
分析：方程是Possion 方程形式c u au f -+=，其中c=-1，a=0，f=-2； 第一个边界条件是Dirichlet 条件，第二个边界条件是Neumann 条件。
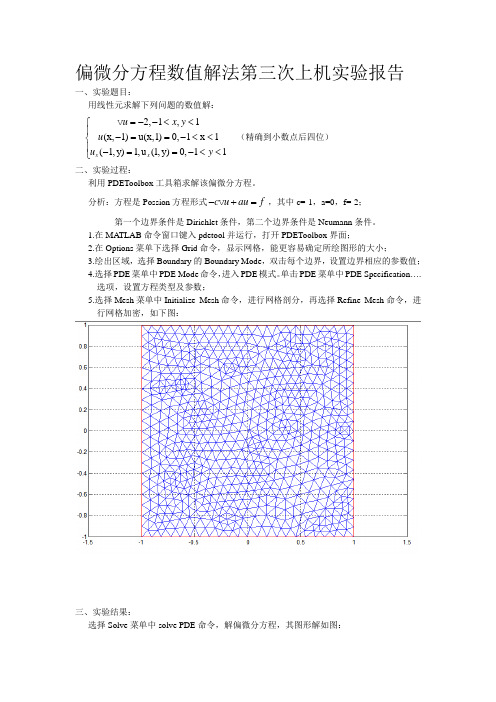
1.在MA TLAB 命令窗口键入pdetool 并运行，打开PDEToolbox 界面；2.在Options 菜单下选择Grid 命令，显示网格，能更容易确定所绘图形的大小；3.绘出区域，选择Boundary 的Boundary Mode ，双击每个边界，设置边界相应的参数值；4.选择PDE 菜单中PDE Mode 命令，进入PDE 模式。
单击PDE 菜单中PDE Specification ….选项，设置方程类型及参数；5.选择Mesh 菜单中Initialize Mesh 命令，进行网格剖分，再选择Refine Mesh 命令，进行网格加密，如下图：三、实验结果：选择Solve 菜单中solve PDE 命令，解偏微分方程，其图形解如图：图1 图形解图2 三维图形解图3 解的等值线图和矢量场图选择Mesh菜单中的Export Mesh，得到结点xy坐标；选择Solve菜单中的Export Solution…，得到每个节点处的值，输出u，即解的数值。
四、实验总结：通过本次试验，掌握了利用Matlab中的PDE求解工具得到PDE的解的方法，并对偏微分方程的形式有了更多的掌握。
偏微分方程数值算法和matlab实验报告
偏微分方程数值实验报告六实验题目：用Ritz-Galerkin 方法求边值问题2(0)0,(1)1u u x u u ''-+===⎧⎨⎩01x << 的第n 次近似()n u x ，基函数为(),i 1,2,.()..x n i sin i x πφ==并用表格列出0.25，0.5,0.75三点处的真解和1,2,3,4n =时的数值解。
实验算法：将上述边值问题转化为基于虚功方程的变分问题为： 求10()u H I ∈，满足10(,)(,(v H ,))a u v x x I ∀∈=-其中1100(u''v uv)(,)(,)dx (u'v'uv)dx a u v Lu v +=-+==⎰⎰ 记(x)sin()w x π=，引入10()H I 的n 维近似子空间12{,},,n n U φφφ=⋯(),i 1,2,,i sin i x n πφ==⋯利用Ritz-Galerkin 公式：1()(f,),j 1,,,2,n j i jj a n φφφ==⋯=∑，则问题关于n U 下的近似变分问题解1()()n i i n i c u x x φ==∑中的系数12(,,,)T nn c c c c =⋯∈满足12()(,,)n j i j j a x φφφ==∑程序代码：%主函数pde=modeldata();I=[0,1];%积分精度quadorder=10;n=[1,2,3,4];for i=1:length(n)uh{i}=Galerkin(pde,I,n(i),quadorder); endshowsolution(uh{1},'-bo');hold onshowsolution(uh{2},'-rx');hold onshowsolution(uh{3},'-.ko');hold onshowsolution(uh{4},'--k*');hold offtitle('the solution of the un');xlabel('x');ylabel('u');legend('n=1','n=2','n=3','n=4');%计算这三点的数值解x=[1/4,1/2,3/4];un=zeros(length(n),3);for i=1:length(n)[v, ]=basis(x,n(i));un(i,:)=(v'*uh{i})';endformat shortedisp('un');disp(un);%存储数据function pde=modeldata()pde=struct('f',@f);function z=f(x)z=x.*x;endend%Galerkin方法function uh=Galerkin(pde,I,n,quadorder) h=I(2)-I(1);[lambda,weight]=quadpts1d(I,quadorder);nQuad=length(weight);A=zeros(n,n);b=zeros(n,1);for q=1:nQuadgx=lambda(q);w=weight(q);x=[0.25;0.5;0.75];[phi,gradPhi]=basis(gx,n);A=A+(-gradPhi*gradPhi'+phi*phi')*w; b=b+pde.f(gx)*phi*w;endA=h*A;b=h*b;uh=A\b;end%构造基函数function [phi,gradPhi]=basis(x,n)m=length(x);w=sin(pi*x);v=ones(n,m);v(2:end,:)=bsxfun(@times,v(2:end,:),x);v=cumprod(v,1);phi=bsxfun(@times,v,w);gw=pi*cos(pi*x);gv=[zeros(1,m);v(1:end-1,:)];gv(3:end,:)=bsxfun(@times,(2:n-1)',gv(3:end,:)); gradPhi=bsxfun(@times,v,gw)+bsxfun(@times,gv,w); end%数值解的图像function showsolution(u,varargin)x=0:0.01:1;n=length(u);[v, ]=basis(x,n);y=v'*u;plot(x,y,varargin{:});% varargin: an input variable in a functionend%系数矩阵Afunction [lambda,weight] = quadpts1d(I,quadorder)numPts = ceil((quadorder+1)/2);if numPts> 10numPts = 10;endswitch numPtscase 1A = [0 2.0000000000000000000000000];case 2A = [0.57735026918962576450914881.0000000000000000000000000-0.57735026918962576450914881.0000000000000000000000000];case 3A = [ 00.88888888888888888888888890.77459666924148337703585310.5555555555555555555555556-0.7745966692414833770358531 0.5555555555555555555555556];case 4A = [0.33998104358485626480266580.65214515486254614262693610.8611363115940525752239465 0.3478548451374538573730639-0.3399810435848562648026658 0.6521451548625461426269361-0.8611363115940525752239465 0.3478548451374538573730639];case 5A = [ 00.56888888888888888888888890.5384693101056830910363144 0.47862867049936646804129150.9061798459386639927976269 0.2369268850561890875142640-0.5384693101056830910363144 0.4786286704993664680412915-0.9061798459386639927976269 0.2369268850561890875142640];case 6A = [0.23861918608319690863050170.46791393457269104738987030.6612093864662645136613996 0.36076157304813860756983350.9324695142031520278123016 0.1713244923791703450402961-0.2386191860831969086305017 0.4679139345726910473898703-0.6612093864662645136613996 0.3607615730481386075698335-0.9324695142031520278123016 0.1713244923791703450402961];case 7A = [00.41795918367346938775510200.4058451513773971669066064 0.38183005050511894495036980.7415311855993944398638648 0.27970539148927666790146780.9491079123427585245261897 0.1294849661688696932706114-0.4058451513773971669066064 0.3818300505051189449503698-0.7415311855993944398638648 0.2797053914892766679014678-0.9491079123427585245261897 0.1294849661688696932706114];case 8A = [0.18343464249564980493947610.36268378337836198296515040.5255324099163289858177390 0.31370664587788728733796220.7966664774136267395915539 0.22238103445337447054435600.9602898564975362316835609 0.1012285362903762591525314-0.1834346424956498049394761 0.3626837833783619829651504-0.5255324099163289858177390 0.3137066458778872873379622-0.7966664774136267395915539 0.2223810344533744705443560-0.9602898564975362316835609 0.1012285362903762591525314];case 9A = [00.33023935500125976316452510.3242534234038089290385380 0.31234707704000284006863040.6133714327005903973087020 0.26061069640293546231874290.8360311073266357942994298 0.18064816069485740405847200.9681602395076260898355762 0.0812743883615744119718922-0.3242534234038089290385380 0.3123470770400028400686304-0.6133714327005903973087020 0.2606106964029354623187429-0.8360311073266357942994298 0.1806481606948574040584720-0.9681602395076260898355762 0.0812743883615744119718922];case 10A = [0.14887433898163121088482600.29552422471475287017389300.4333953941292471907992659 0.26926671930999635509122690.6794095682990244062343274 0.21908636251598204399553490.8650633666889845107320967 0.14945134915058059314577630.9739065285171717200779640 0.0666713443086881375935688-0.1488743389816312108848260 0.2955242247147528701738930-0.4333953941292471907992659 0.2692667193099963550912269-0.6794095682990244062343274 0.2190863625159820439955349-0.86506336668898451073209670.1494513491505805931457763-0.97390652851717172007796400.0666713443086881375935688];endlambda = (I(2)+I(1)+(I(2)-I(1))*A(:,1))/2; weight = A(:,2)*(I(2)-I(1))/2;数值解：x=x=3/4x=1/21/4u-3.0184e-02 -4.2686e-02 -3.0184e-02 1u-2.1919e-02 -4.2686e-02 -3.8448e-02 2u-2.3232e-02 -4.0652e-02 -3.9761e-02 3u-2.3472e-02 -4.0652e-02 -3.9521e-02 4图像：00.10.20.30.40.50.60.70.80.91the solution of the unx u。
偏微分方程数值求解的算法研究与实现
偏微分方程数值求解的算法研究与实现随着计算机技术的日益发展，偏微分方程数值求解成为了热门的数值计算领域之一。
偏微分方程（PDE）是许多科学和工程领域的数学模型。
它们描述了物理过程，因此在流体动力学、机械工程、材料科学以及生命科学中都有广泛应用。
在本文中，我们将讨论偏微分方程数值求解的算法研究与实现。
一、偏微分方程的数值解法偏微分方程最常见的数值解法是有限差分法（FDM）、有限元法（FEM）和谱方法（SP）。
FDM是将PDE的导数转化为差分方程的方法。
它将解域划分为网格，并在每个网格点上估计解（即差分）。
通过这种方法，PDE可以被重写成一个差分方程组。
FEM通过将解域划分为有限数量的单元，然后估计每个单元内的解。
这个过程包括将PDE转化为一系列局部的差分方程，并将它们组合成一个大的线性方程组。
最后，SP使用特定的基函数表示解，通常是正交多项式。
这个过程产生一个矩阵形式的线性方程。
二、偏微分方程数值求解中的挑战偏微分方程数值求解涉及到许多挑战。
首先，PDE的数值解是无限精度的，但在计算机上是有限精度的，这意味着数值误差会在计算过程中逐渐累积。
其次，由于PDEs具有复杂的非线性行为，因此需要使用高阶算法才能在合理的时间内获得解。
最后，PDEs在解域的不同区域上可能具有不同的特征，这需要使用适当的算法来解决。
三、算法研究与实现针对偏微分方程数值求解中的挑战，研究者们一直在开发新的算法和优化现有算法。
许多研究都集中在如何提高数值解的精度和计算效率上。
在FDM中，高精度的近似解可以通过使用更高阶导数的差分来获得。
例如，中心差分代替前向或后向差分可以更准确地计算二阶导数。
在FEM中，使用高阶元素可以获得更好的精度。
此外，研究者还开发了基于多层网格技术的自适应算法，这些算法可以根据解的特性在解域的不同区域使用不同的网格大小来提高计算效率。
在SP中，使用高阶谱方法可以获得更好的精度和更高的计算效率。
除了以上算法，其他一些更复杂的方法也被广泛研究。
微分方程数值解法实验报告
微分方程数值解法实验报告2篇微分方程数值解法实验报告（一）在实际科学与工程问题中，我们经常会遇到微分方程的求解。
然而，许多微分方程往往没有解析解，这就需要我们利用数值方法来获得近似解。
本篇实验报告将介绍两种常见的微分方程数值解法：欧拉方法和改进的欧拉方法。
一、欧拉方法欧拉方法是最简单的微分方程数值解法之一。
其基本原理为离散化微分方程，将微分方程中的导数用差商代替。
设要求解的微分方程为dy/dx = f(x, y)，步长为h，则可用以下公式进行递推计算：y_{n+1} = y_n +hf(x_n, y_n)二、算法实现为了对欧拉方法进行数值实验，我们以一阶线性常微分方程为例：dy/dx = x - y, y(0) = 1步骤如下：（1）选择合适的步长h和求解区间[a, b]，这里我们取h=0.1，[a, b] = [0, 1]；（2）初始化y_0 = 1；（3）利用欧拉方法递推计算y_{n+1} = y_n + 0.1(x_n - y_n)；（4）重复步骤（3），直到x_n = 1。
三、实验结果与讨论我们通过上述步骤得到了在[0, 1]上的近似解y(x)。
下图展示了欧拉方法求解的结果。
从图中可以看出，欧拉方法得到的近似解与精确解有一定的偏差。
这是因为欧拉方法只是通过递推计算得到的近似解，并没有考虑到更高阶的误差。
所以在需要高精度解时，欧拉方法并不理想。
四、改进的欧拉方法针对欧拉方法的不足，我们可以考虑使用改进的欧拉方法（也称为改进的欧拉-柯西方法）。
它是通过利用前后两个步长欧拉方法得到的结果作为差商的中间项，从而提高了求解精度。
一阶线性常微分方程的改进欧拉方法可以表示为：y_{n+1} = y_n + h(f(x_n, y_n) + f(x_{n+1}, y_n + hf(x_n,y_n)))/2五、算法实现与结果展示将改进的欧拉方法应用于前述的一阶线性常微分方程，我们同样选择h=0.1，[a, b] = [0, 1]。
偏微分方程的数值解法研究
偏微分方程的数值解法研究偏微分方程是数学中的一个重要分支，它研究的是包含未知函数及其偏导数的方程。
这类方程在物理、工程、金融等领域中有着广泛的应用。
然而，由于偏微分方程的复杂性，往往难以找到解析解。
因此，数值解法成为解决偏微分方程的重要手段之一。
数值解法是通过离散化空间和时间，将连续的偏微分方程转化为离散的代数方程组，从而求得近似解。
常用的数值解法有有限差分法、有限元法和谱方法等。
有限差分法是最常用的数值解法之一。
它将求解区域划分为有限个网格点，并通过差分近似来逼近偏微分方程中的导数。
例如，对于一维热传导方程，我们可以将求解区域划分为若干个等距的网格点，然后利用中心差分公式来近似一阶导数。
通过迭代计算，可以逐步求得方程的数值解。
有限元法是另一种常用的数值解法。
它将求解区域划分为若干个小区域，称为有限元。
每个有限元内部的解通过插值函数来逼近，然后通过加权残差法将偏微分方程转化为代数方程组。
有限元法在处理复杂的几何形状和边界条件时具有优势，因此在工程领域得到广泛应用。
谱方法是一种基于傅里叶级数展开的数值解法。
它利用傅里叶级数的收敛性和正交性质，将未知函数展开为一系列基函数的线性组合。
通过选取适当的基函数和展开系数，可以将偏微分方程转化为代数方程组。
谱方法在处理高精度问题时具有优势，但对几何形状和边界条件的要求较高。
除了以上三种常见的数值解法，还有很多其他方法可以用于求解偏微分方程。
例如，有限体积法、边界元法等。
每种数值解法都有其适用的范围和优势，选择合适的方法需要根据具体问题的特点和求解要求进行综合考虑。
在实际应用中，数值解法的稳定性和收敛性是非常重要的考虑因素。
稳定性保证了数值解的长期行为是合理的，而收敛性则保证了数值解能够逼近真实解。
为了提高数值解法的稳定性和收敛性，常常需要选择合适的网格划分、时间步长和插值函数等参数，并进行误差估计和收敛性分析。
总之，偏微分方程的数值解法在科学计算和工程实践中发挥着重要作用。
数统学院_偏微分方程数值解实验报告1
1.6905
0.0000
Hale Waihona Puke 0.02501.02531.0253
0.0000
0.5500
1.7333
1.7333
0.0000
0.0500
1.0513
1.0513
0.0000
0.5750
1.7772
1.7771
0.0001
0.0750
1.0779
1.0779
0.0000
0.6000
1.8222
0.0080
0.9500
2.5557
2.5857
0.0300
0.4500
1.5597
1.5683
0.0087
0.9750
2.6196
2.6512
0.0316
0.4750
1.5987
1.6080
0.0094
1.0000
2.6851
2.7183
0.0332
0.5000
1.6386
1.6487
0.0101
0.0001
0.1750
1.1913
1.1912
0.0000
0.7000
2.0138
2.0138
0.0001
0.2000
1.2214
1.2214
0.0000
0.7250
2.0648
2.0647
0.0001
0.2250
1.2523
1.2523
0.0000
0.7500
2.1171
2.1170
0.0001
1.7716
1.8221
0.0506
微分方程数值解实验报告三
Columns 61 through 65
0.4598 0.4598 0.4598 0.4598 0.4598
Columns 66 through 70
0.4598 0.4598 0.4598 0.4598 0.4598
Columns 71 through 75
0.4597 0.4597 0.4597 0.4597 0.4597
Columns 56 through 60
0.4597 0.4597 0.4597 0.4597 0.4597
Columns 61 through 65
0.4597 0.4597 0.4597 0.4597 0.4597
Columns 66 through 70
0.4597
parabolicFD(80,3200)
ans =
Columns 1 through 5
0.4599 0.4599 0.4599 0.4599 0.4599
Columns 6 through 10
0.4599 0.4599 0.4599 0.4599 0.4599
Columns 11 through 15
0.4599 0.4599 0.4599 0.4599 0.4599
Columns 16 through 20
0.4599 0.4599 0.4599 0.4599 0.4599
Columns 21 through 25
0.4599 0.4599 0.4599 0.4599 0.4599
Columns 26 through 30
Columns 21 through 25
0.4598 0.4598 0.4598 0.4598 0.4598
偏微分方程数值及matlab实验报告(8)
偏微分方程数值及m a t l a b实验报告(8)-标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII偏微分方程数值实验报告八实验题目：利用有限差分法求解.0)1(,0)1(),()()(==-=+''-u u x f x u x u 真解为)1()(22x e x u x -=-实现算法：对于两点边值问题,)(,)(,,d 22βα==∈=-b u a u l x f dxu(1)其中),(b a l =f b a ),(<为],[b a l =上的连续函数，βα，为给定常数.其相应的有限差分法的算法如下：1.对求解区域做网格剖分，得到计算网格.在这里我们对区间l 均匀剖分n 段，每个剖分单元的剖分步长记为nab h -=.2.对微分方程中的各阶导数进行差分离散，得到差分方程.运用的离散方法有：方法一:用待定系数和泰勒展开进行离散)()()()(d )(d 111122++--++≈i i i i i i i i x u x u x u x x u ααα方法二：利用差商逼近导数21122)()(2)()(d )(d h x u x u x u x x u i i i i i -++-≈(2)将(2)带入(1)可以得到)()()()(2)(211u R x f h x u x u x u i i i i i +=+---+,其中)(u R i 为无穷小量，这时我们丢弃)(u R i ，则有在i x 处满足的计算公式：1,...,1)()()(2)(211-==+---+n i x f hx u x u x u i i i i ，(3)3.根据边界条件，进行边界处理.由(1)可得βα==n u u ,0(4)称(3)(4)为逼近(1)的差分方程，并称相应的数值解向量1-n U 为差分解，i u 为)(i x u 的近似值.4.最后求解线性代数方程组，得到数值解向量1-n U .实验题目：用Lax-Wendroff 格式求解方程：.4sin 1),1(],1,0[,2sin 1)0,(,0),1,0(,02t t u x x x u t x u u x t ππ+=∈+=>∈=- （1） （精确解).2(2sin 1t x u ++=π） 数值边值条件分别为：（a ）).(20101n 0nn n u u hu u -+=+τ（b ）.1nn u u = （c ）.02-12111n 0=++++n n u u u 请将计算结果与精确解进行比较。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
偏微分方程数值解实验报告1、用有限元方法求下列边值问题的数值解：''()112x -y +y =2sin ,0<x <,42y(0)=0,y'()=0.ππ⎧⎪⎨⎪⎩其中其精确解为 24x y =sin()2ππ，取h=0.1要求：（1）将精确解与用有限元得到的数值解画在同一图中（2）1hH u u -、2h L u u -、01h x max u -u ≤≤2、用线性元求解下列问题的数值解：x x u(x,-1)=u(x,1)=0,-1<x <1,u (-1,y)=1,u u =0=-2,-1<x,,-1<y <1.y <1,⎧∆⎪⎨⎪⎩ 精确到小数点后第六位，并画出解曲面。
3、用Crank-Nicolson 差分法求解Burger 方程0,(0,1),(0,5),,[01]t (1).t x xx v +vv =v ,x t v(x,0)=sin2x x ;v =v ,t =0ννπ>∈∈⎧⎨∈(0,)⎩，其中取1ν= 要求画出解曲面。
迭代格式如下：1221212111111111122142212n nn n n n j j j j j j n n n n n n j j j j j j V V V V V V h h V V V V V V h h τ++++++++++-+-⎧⎫-()-()()-()⎪⎪++⎨⎬⎪⎪⎩⎭⎧⎫-+-+⎪⎪=+⎨⎬⎪⎪⎩⎭1、%Ritz Galerkin方法求解方程function u1=Ritz(x)%定义步长h=1/100;x=0:h:1;n=1/h;a=zeros(n-1,1);b=zeros(n,1);c=zeros(n-1,1);d=zeros(n,1);%求解Ritz方法中内点系数矩阵for i=1:1:n-1b(i)=(1/h+h*pi*pi/12)*2;d(i)=h*pi*pi/2*sin(pi/2*(x(i)+h))/2+h*pi*pi/2*sin(pi/2*x(i+1))/2; end%右侧导数条件边界点的计算b(n)=(1/h+h*pi*pi/12);d(n)=h*pi*pi/2*sin(pi/2*(x(i)+h))/2;for i=1:1:n-1a(i)=-1/h+h*pi*pi/24;c(i)=-1/h+h*pi*pi/24;end%调用追赶法u=yy(a,b,c,d)%得到数值解向量u1=[0,u]%对分段区间做图plot(x,u1)%得到解析解y1=sin(pi/2*x);hold onplot(x,y1,'o')legend('数值解','解析解')function x=yy(a,b,c,d)n=length(b);q=zeros(n,1);p=zeros(n,1);q(1)=b(1);p(1)=d(1);for i=2:1:nq(i)=b(i)-a(i-1)*c(i-1)/q(i-1);p(i)=d(i)-p(i-1)*c(i-1)/q(i-1);endx(n)=p(n)/q(n);for j=n-1:-1:1x(j)=(p(j)-a(j)*x(j+1))/q(j);endxx =Columns 1 through 110.0157 0.0314 0.0471 0.0628 0.0785 0.0941 0.1097 0.1253 0.1409 0.1564 0.1719Columns 12 through 220.1874 0.2028 0.2181 0.2335 0.2487 0.2639 0.2790 0.2940 0.3090 0.3239 0.3387Columns 23 through 330.3535 0.3681 0.3827 0.3972 0.4115 0.4258 0.4400 0.4540 0.4679 0.4818 0.4955Columns 34 through 440.5091 0.5225 0.5358 0.5490 0.5621 0.5750 0.5878 0.6004 0.6129 0.6253 0.6374Columns 45 through 550.6495 0.6613 0.6730 0.6846 0.6959 0.7071 0.7181 0.7290 0.7397 0.7501 0.7604Columns 56 through 660.7705 0.7805 0.7902 0.7997 0.8090 0.8182 0.8271 0.8358 0.8444 0.8527 0.8608Columns 67 through 770.8687 0.8763 0.8838 0.8910 0.8981 0.9049 0.9114 0.9178 0.9239 0.9298 0.9355Columns 78 through 880.9409 0.9461 0.9511 0.9558 0.9603 0.9646 0.9686 0.9724 0.9759 0.9793 0.9823Columns 89 through 990.9851 0.9877 0.9901 0.9921 0.9940 0.9956 0.9969 0.9981 0.9989 0.9995 0.9999Column 1001.0000u =Columns 1 through 110.0157 0.0314 0.0471 0.0628 0.0785 0.0941 0.1097 0.1253 0.1409 0.1564 0.1719Columns 12 through 220.1874 0.2028 0.2181 0.2335 0.2487 0.2639 0.2790 0.2940 0.3090 0.3239 0.3387Columns 23 through 330.3535 0.3681 0.3827 0.3972 0.4115 0.4258 0.4400 0.4540 0.4679 0.4818 0.4955Columns 34 through 440.5091 0.5225 0.5358 0.5490 0.5621 0.5750 0.5878 0.6004 0.6129 0.6253 0.6374Columns 45 through 550.6495 0.6613 0.6730 0.6846 0.6959 0.7071 0.7181 0.7290 0.7397 0.7501 0.7604Columns 56 through 660.7705 0.7805 0.7902 0.7997 0.8090 0.8182 0.8271 0.8358 0.8444 0.8527 0.8608Columns 67 through 770.8687 0.8763 0.8838 0.8910 0.8981 0.9049 0.9114 0.9178 0.9239 0.9298 0.9355Columns 78 through 880.9409 0.9461 0.9511 0.9558 0.9603 0.9646 0.9686 0.9724 0.9759 0.9793 0.9823Columns 89 through 990.9851 0.9877 0.9901 0.9921 0.9940 0.9956 0.9969 0.9981 0.9989 0.9995 0.9999Column 1001.0000u1 =Columns 1 through 110 0.0157 0.0314 0.0471 0.0628 0.0785 0.0941 0.1097 0.1253 0.1409 0.1564Columns 12 through 220.1719 0.1874 0.2028 0.2181 0.2335 0.2487 0.2639 0.2790 0.2940 0.3090 0.3239Columns 23 through 330.3387 0.3535 0.3681 0.3827 0.3972 0.4115 0.4258 0.4400 0.4540 0.4679 0.4818Columns 34 through 440.4955 0.5091 0.5225 0.5358 0.5490 0.5621 0.5750 0.5878 0.6004 0.6129 0.6253Columns 45 through 550.6374 0.6495 0.6613 0.6730 0.6846 0.6959 0.7071 0.7181 0.7290 0.7397 0.7501Columns 56 through 660.7604 0.7705 0.7805 0.7902 0.7997 0.8090 0.8182 0.8271 0.8358 0.8444 0.8527Columns 67 through 770.8608 0.8687 0.8763 0.8838 0.8910 0.8981 0.9049 0.9114 0.9178 0.9239 0.9298Columns 78 through 880.9355 0.9409 0.9461 0.9511 0.9558 0.9603 0.9646 0.9686 0.9724 0.9759 0.9793Columns 89 through 990.9823 0.9851 0.9877 0.9901 0.9921 0.9940 0.99560.9969 0.9981 0.9989 0.9995Columns 100 through 1010.9999 1.0000ans =Columns 1 through 100 0.0157 0.0314 0.0471 0.0628 0.0785 0.0941 0.1097 0.1253 0.1409Columns 11 through 200.1564 0.1719 0.1874 0.2028 0.2181 0.2335 0.2487 0.2639 0.2790 0.2940Columns 21 through 300.3090 0.3239 0.3387 0.3535 0.3681 0.3827 0.3972 0.4115 0.4258 0.4400Columns 31 through 400.4540 0.4679 0.4818 0.4955 0.5091 0.5225 0.5358 0.5490 0.5621 0.5750Columns 41 through 500.5878 0.6004 0.6129 0.6253 0.6374 0.6495 0.6613 0.6730 0.6846 0.6959Columns 51 through 600.7071 0.7181 0.7290 0.7397 0.7501 0.7604 0.7705 0.7805 0.7902 0.7997Columns 61 through 700.8090 0.8182 0.8271 0.8358 0.8444 0.8527 0.8608 0.8687 0.8763 0.8838Columns 71 through 800.8910 0.8981 0.9049 0.9114 0.9178 0.9239 0.9298 0.9355 0.9409 0.9461Columns 81 through 900.9511 0.9558 0.9603 0.9646 0.9686 0.9724 0.9759 0.9793 0.9823 0.9851Columns 91 through 1000.9877 0.9901 0.9921 0.9940 0.9956 0.9969 0.9981 0.9989 0.9995 0.9999Column 1011.00002、function [ u ] = Q_2( P )format longif nargin<1P=16;endf=2;beta=-1;x=linspace(-1,1,P+1);h=2/P;%%%Q=P*P-1;Qi=(P-1)*(P-1);pos=zeros(Q,2);i=2;j=2;for n=1:Qipos(n,1)=x(i);pos(n,2)=x(j);j=j+1;if mod(n,P-1)==0i=i+1;j=2;endendfor j=1:P-1pos(j+Qi,1)=-1;pos(j+Qi,2)=x(j+1);pos(j+Qi+P-1,1)=1;pos(j+Qi+P-1,2)=x(j+1);end%%b=zeros(Q,1);for n=(Qi+1):(Qi+P-1)b(n)=beta*h;endfv=f*h*h/6;for n=1:Qib(n)=b(n)+6*fv;endfor n=1:P-1b(Qi+n)=b(Qi+n)+fv*3;b(Qi+n+P-1)=b(Qi+n+P-1)+fv*3;end%%K=zeros(Q);for n=1:QiK(n,n)=4;endfor n=Qi+1:Qi+P-1K(n,n)=2;K(n+P-1,n+P-1)=2;endfor i=1:Qifor j=i+1:Qif abs(pos(i,1)-pos(j,1))+abs(pos(i,2)-pos(j,2))==hK(i,j)=-1;end;endendfor i=Qi+1:Qi+P-1for j=i+1:Qi+P-1if abs(pos(i,1)-pos(j,1))+abs(pos(i,2)-pos(j,2))==hK(i,j)=-0.5;end;if abs(pos(i+P-1,1)-pos(j+P-1,1))+abs(pos(i+P-1,2)-pos(j+P-1,2))==h K(i+P-1,j+P-1)=-0.5;endendendfor i=1:Qfor j=i+1:QK(j,i)=K(i,j);endendu=linsolve(K,b);[X,Y]=meshgrid(x,x);U=zeros(P+1);U(2:P,1)=u(Qi+1:Qi+P-1);U(2:P,P+1)=u(Qi+P:Q);U(2:P,2:P)=reshape(u(1:Qi),P-1,P-1);surf(X,Y,U);xlabel('x');ylabel('y');zlabel('u');str=strcat(['N =',num2str(P)],[', 步长h =',num2str(h)]); title(str);hold offend3、a=0;b=1;t1=0;t2=5;h=0.01;tao=0.01;n1=(t2-t1)/tao;n2=(b-a)/h;eps=10^-8;V=zeros(n1+1,n2+1);M=zeros(n2-1,n2-1);m=zeros(n2-1,1);x=zeros(n2+1,1);y=zeros(n2+1,1);y1=zeros(n2+1,1);temp=zeros(n2+1,1);for i=2:n2r=(i-1)*h;V(1,i)=sin(2*pi*r);x(i)=V(1,i);enda=1/tao+1/h^2;y=x;for i=2:n1+1while norm((y-temp),2)>eps %应改为向量2-范数%构造Mfor j=1:n2-1if j==1M(1,1)=a-y(2);M(1,2)=y(3)/(2*h)-1/(2*h^2);endif j==n2-1M(n2-1,n2-2)=-1/(2*h^2);M(n2-1,n2-1)=a-y(n2)/(2*h);endif j~=1 && j~=n2-1M(j,j-1)=-1/(2*h^2);M(j,j)=a-y(j+1);M(j,j+1)=y(j+2)/(2*h)-1/(2*h^2);endend%构造mfor j=1:n2-1m(j)=(y(j+1)-x(j+1))/tao+(x(j+2)^2-x(j+1)^2+y(j+2)^2-y(j+1)^2)/(4*h)-(x(j+2)-2*x(j+1)+x(j)+y(j+2)-2*y(j+1)+y(j))/(2*h^2);endtemp=y;y(2:n2)=y(2:n2)-inv(M)*m;%y=y1;endV(i,:)=y';x=y;y=zeros(n2+1,1);endxx = 0:h:1;yy = 0:tao:5;surf(xx,yy,V)。