偏微分方程上机实验报告.doc
偏微分方程数值解第三次上机实验报告
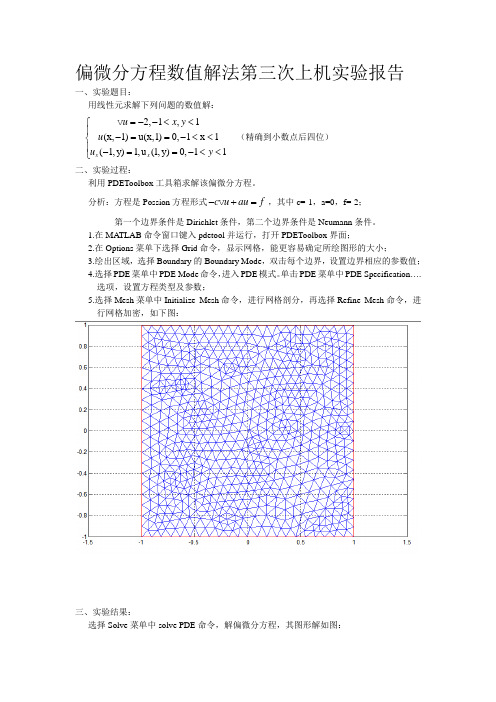
偏微分方程数值解法第三次上机实验报告一、实验题目:用线性元求解下列问题的数值解:2,1,1(x,1)u(x,1)0,1x 1(1,y)1,u (1,y)0,11xx u x y u u y =--<<⎧⎪-==-<<⎨⎪-==-<<⎩ (精确到小数点后四位)二、实验过程:利用PDEToolbox 工具箱求解该偏微分方程。
分析:方程是Possion 方程形式c u au f -+=,其中c=-1,a=0,f=-2; 第一个边界条件是Dirichlet 条件,第二个边界条件是Neumann 条件。
1.在MA TLAB 命令窗口键入pdetool 并运行,打开PDEToolbox 界面;2.在Options 菜单下选择Grid 命令,显示网格,能更容易确定所绘图形的大小;3.绘出区域,选择Boundary 的Boundary Mode ,双击每个边界,设置边界相应的参数值;4.选择PDE 菜单中PDE Mode 命令,进入PDE 模式。
单击PDE 菜单中PDE Specification ….选项,设置方程类型及参数;5.选择Mesh 菜单中Initialize Mesh 命令,进行网格剖分,再选择Refine Mesh 命令,进行网格加密,如下图:三、实验结果:选择Solve 菜单中solve PDE 命令,解偏微分方程,其图形解如图:图1 图形解图2 三维图形解图3 解的等值线图和矢量场图选择Mesh菜单中的Export Mesh,得到结点xy坐标;选择Solve菜单中的Export Solution…,得到每个节点处的值,输出u,即解的数值。
四、实验总结:通过本次试验,掌握了利用Matlab中的PDE求解工具得到PDE的解的方法,并对偏微分方程的形式有了更多的掌握。
孙志忠北京理工大学偏微分方程数值解上机作业

偏微分方程数值解大作业目录第一题 (3)第二题 (7)第三题 (16)第四题 (20)第五题 (26)第六题(附加题1) (39)第七题(附加题2) (45)第八题(附加题3) (51)第一题习题13.(1)解曲线图图1 (2)误差曲线图图2(3)表格表1 部分点处精确解和取不同步长时所得的数值解表2 取不同步长时部分结点处数值解的误差的绝对值和数值解的最大误差(4)MATLAB源代码M=64;a=0;b=pi/2;h=(b-a)/M;x=[a+h:h:b-h];u=zeros(M-1,M-1);u(1,1)=(2/h^2)+(x(1)-1/2)^2;u(1,2)=-(1/h^2);u(M-1,M-1)=(2/h^2)+(x(M-1)-1/2)^2;u(M-1,M-2)=-(1/h^2);for i=2:M-2u(i,i-1)=-(1/h^2);u(i,i)=(2/h^2)+(x(i)-1/2)^2;u(i,i+1)=-(1/h^2);endf=zeros(M-1,1)f(1)=(x(1).*x(1)-x(1)+5/4).*sin(x(1));f(M-1)=(x(M-1).*x(M-1)-x(M-1)+5/4).*sin(x(M-1))+1/h^2; for j=2:M-2f(j)=(x(j).*x(j)-x(j)+5/4).*sin(x(j));endy=inv(u)*f; true=sin(x); plot(x,y'-true)第二题习题二(P67 第3题)(1)h=1/4, τ=1/4精确解数值解误差(2)h=1/8, τ=1/8精确解数值解误差(3)h=1/16, τ=1/16精确解数值解误差(4)h=1/32, τ=1/32精确解数值解误差(5)h=1/64, τ=1/64精确解精确解误差(6)表格(7)Matlab代码function[p,e,u,x,y,k]=fivepoint(h,m,n,kmax,ep)%五点差分法和G-S迭代法解椭圆型方程%kmax为最大迭代次数;%m,n分别为x,y方向的网格数;%ep为精度;%u为差分解,p为精确解,e为误差;%例如在命令行窗口输入[p,e,u,x,y,k]=fivepoint(1/64,64,64,10000,1e-10);%代表步长为1/64,精度为10^(-10),最大迭代次数为10000的五点差分格式syms temp;u=zeros(n+1,m+1);x=0+(0:m)*h;y=0+(0:n)*h;for(j=1:n+1)u(j,1)=sin(y(j))+cos(y(j));u(j,m+1)=exp(1)*(sin(y(j))+cos(y(j)));endfor(i=1:m+1)u(1,i)=exp(x(i));u(n+1,i)=exp(x(i))*(sin(1)+cos(1));endt=zeros(n-1,m-1);for(k=1:kmax)for(j=2:n)for(i=2:m)temp=(u(j,i+1)+u(j,i-1)+u(j+1,i)+u(j-1,i))/4; t(j,i)=(temp-u(j,i))*(temp-u(j,i));u(j,i)=temp;endendt(j,i)=sqrt(t(j,i));if(k>kmax)break;endif(max(max(t))<ep)break;endendfor(j=1:n+1)for(i=1:m+1)p(j,i)=(sin(y(j))+cos(y(j)))*exp(x(i));e(j,i)=abs(u(j,i)-p(j,i));endend代码使用说明:在命令行窗口输入[p,e,u,x,y,k]=fivepoint(1/64,64,64,10000,1e-10);代表步长为1/64,精度为10^(-10),最大迭代次数为10000的五点差分格式surf(x,y,p)可作出近似解曲线surf(x,y,u)可作出精确解曲线surf(x,y,e)可作出误差曲线注意精度不要选取的太低,否则随着步长减小误差反而增大。
偏微分方程报告范文

偏微分方程报告范文偏微分方程是研究多变量函数的微分方程,其中函数的未知量既依赖于自变量,又依赖于多个自变量。
偏微分方程在物理学、工程学和经济学等领域中有着广泛的应用。
本报告将介绍偏微分方程的基本概念、求解方法和应用领域。
一、偏微分方程的基本概念偏微分方程是由未知函数的偏导数和自变量构成的方程。
常见的偏微分方程包括波动方程、传热方程和扩散方程等。
偏微分方程根据阶数可分为一阶和二阶偏微分方程。
一阶偏微分方程中只涉及到未知函数的一阶偏导数,一般可以通过变量分离的方法求解。
二阶偏微分方程中涉及到未知函数的二阶偏导数,求解方法一般包括分离变量法、特征线法和变换法等。
二、偏微分方程的求解方法1.分离变量法:假设未知函数可以表示为两个只依赖于单个自变量的函数的乘积形式,然后将该形式代入到偏微分方程中,再将方程两边关于不同的自变量求积分,从而得到方程的通解。
2.特征线法:通过特征线曲线的方法将偏微分方程转化为常微分方程。
先找出特征线曲线,然后在特征线上引入新的变量,使得偏微分方程变为常微分方程,进而求解。
3.变换法:通过适当的变量变换,将原偏微分方程转化为一个更容易求解的形式。
常用的变换方法有坐标变换、函数变换和变量替换等。
三、偏微分方程的应用领域1.物理学:偏微分方程在物理学中有着广泛的应用。
例如,波动方程可以描述声波、光波和电磁波等在介质中的传播;传热方程可以描述热传导过程;薛定谔方程和波恩-奥本海默方程可以描述量子力学中的粒子行为等。
2.工程学:偏微分方程在工程学中被广泛应用于流体力学、结构力学和电磁场等领域。
例如,纳维-斯托克斯方程用于描述流体的运动;弹性方程用于描述结构的变形和应力分布等。
3.经济学:偏微分方程在经济学中应用较多,尤其是在金融学中。
例如,布莱克-斯科尔斯方程用于定价期权;黑-舒尔斯方程用于描述衍生品的定价和风险管理等。
通过对偏微分方程的研究和求解,可以更好地理解自然界的现象和规律,并为解决实际问题提供数学模型和解决方法。
偏微分方程实验1

预备实验偏微分方程工具箱的功能和利用一、实验目的PDE Toolbox提供了研究和求解空间二维偏微分方程问题的一个壮大而又灵活有效的环境。
本次实验了解PDE Toolbox的功能和PDE图形用户界面。
PDE Toolbox的功能包括:设置PDE 定解问题,即设置二维定解区域、边界条件和方程的形式和系数;用有限元法求解PDE,即网格的生成、方程的离散和求出数值解;解得可视化。
二、实验内容一、解偏微分方程的一个例子解Poisson方程:f∆-,边界条件为齐次dirichlet类型。
u=第一步:启动MATLAB,键入pdetool,按回车键确信即可启动GUI(图形用户界面),然后在options菜单下选择grid命令,打开栅格。
栅格的利用,能利用户容易确信所画图形的大小。
第二步:散布完成平面几何造型:R1-C1-E1+R2+C2。
用菜单或快捷工具别离画矩形R1,矩形R2,椭圆E1,圆C1,圆C2。
画圆时,第一选中椭圆工具,按鼠标右键并拖动即可,或在按Ctrl的同时,拖动鼠标也可绘制图。
然后在set formula栏,进行编辑并用算术运算符将图形对象名称连接起来,或删除默许的表达式直接键入R1-C1-E1+R2+C2。
选择Boundary菜单中Boundary Mode 命令,进入边界模式。
单击Boundary 菜单中Remove All Subdomain Borders选项,去掉子域边界,若是想将几何信息和边界信息进行存储,应选择Boundary菜单中的Export Decomposed Geometry, Boundary Cond’s…命令,将它们别离贮存于g,b变量中,通过MATLAB形成M文件。
第三步:选取边界,单击Boundary菜单中Specify Boundary Conditions…选项,打开Boundary Conditions对话框,输入边界条件,本例取缺省条件,即将全数边界设为齐次dirichlet条件,边界颜色显示为红色。
《微分方程数值解》实验指导书2010

第1页共18页微分方程数值解实验指导书李光云数学与计算科学学院O 一0十月第2页共18页一、概述本课程实验指导书是根据陆金甫,关治编著的《偏微分方程数值解法(第二版)》编写的。
通过上机实验,可帮助学生理解偏微分方程数值计算方法的基本思想,巩固学生所学过的算法,同时让学生进一步学习和掌握Matlab软件在数值计算方面中的应用。
二、实验环境本书选择的实验环境是计算机以及软件Matlab(版本6.5以上)一套。
三、实验课时安排共7次实验,16课时,试验五为综合设计性试验4课时,其它实验2个课时。
四、实验要求上机完成实验指导书中所规定的内容,自行按实验指导书要求完成程序设计和调试,并提交每次实验的实验报告,附带算法程序清单和算法输出结果。
五、实验考核要求上机完成试验内容,并提交一份算法程序清单和数值结果。
第3页共18页实验一 双曲型方程的迎风格式、实验目的1、 掌握双曲型方程的迎风格式的算法思想 ,格式稳定的条件;2、 培养编程与上机调试能力。
、实验课时:2个课时 三、实验准备1、 了解偏微分方程的分类,以及双曲型方程的特点;2、 熟悉求解偏微分方程有限差分法的基本原理,双曲型方程迎风格式的推导和 特点,熟悉用迎风格式求解双曲型方程的算法步骤;3、 熟悉Matlab 软件的基本命令及其数值计算中的基本命令和函数。
4、 了解双曲型方程迎风格式稳定的条件。
四、实验内容用双曲型方程的迎风格式n nU j -U j 」0, hn 1 nnnU j —U jU j1—U j c a 0,Th其中,• ,h 分别为时间步长和空间步长。
求解初值问题賦”,ts,I u(x,0 )=u°(x ),其中,p!,x",U。
八 0,x 0.五、基本思想及主要步骤考虑对流方程:U :ua 0,x . ,t 0* *-t:x其a 为给定常数。
其迎风格式的基本思想是在方程中关于空间的偏导数用在特征线n 1 nU j Uja 0 a<0.计算〔0,1〕区间的u 值至t n 二0.5,并画出解的图形。
(完整word版)数值线性代数第二版徐树方高立张平文上机习题第四章实验报告
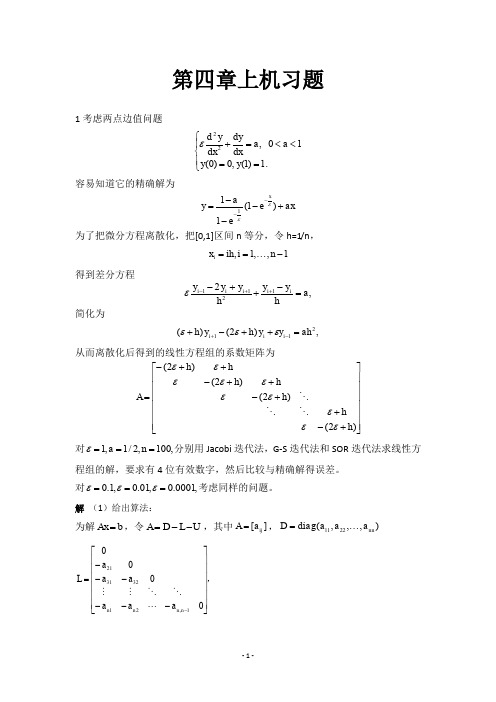
第四章上机习题1考虑两点边值问题⎪⎩⎪⎨⎧==<<=+.1)1(,0)0(10 ,22y y a a dx dy dx y d ε 容易知道它的精确解为ax e e ay x +---=--)1(111εε为了把微分方程离散化,把[0,1]区间n 等分,令h=1/n ,1,,1,-==n i ih x i得到差分方程,21211a hy y h y y y i i i i i =-++-++-ε简化为 ,)2()(211ah y y h y h i i i =++-+-+εεε从而离散化后得到的线性方程组的系数矩阵为⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+-++-++-++-=)2()2()2()2(h h h h h h h A εεεεεεεεεε 对,100,2/1,1===n a ε分别用Jacobi 迭代法,G-S 迭代法和SOR 迭代法求线性方程组的解,要求有4位有效数字,然后比较与精确解得误差。
对,0001.0,01.0,1.0===εεε考虑同样的问题。
解 (1)给出算法:为解b Ax =,令U L D A --=,其中][ij a A =,),,,(2211nn a a a diag D = ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=-00001,21323121n n n n a a a a a a L,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------=-0000,122311312 n n n n a a a a a a U 利用Jacobi 迭代法,G-S 迭代法,SOR 迭代法解线性方程组,均可以下步骤求解: step1给定初始向量x0=(0,0,...,0),最大迭代次数N ,精度要求c ,令k=1 step2令x=B*x0+gstep3若||x-x0||2<c ,算法停止,输出解和迭代次数k ,否则,转step4 step4若k>=N,算法停止,迭代失败,否则,令x0=x ,转step2在Jacobi 迭代法中,B=D -1*(L+U),g=D -1*b在G-S 迭代法中,B=D -1*(L+U),g=D -1*b在SOR 迭代法中,B=(D-w*L)-1*[(1-w)*D+w*U],g=w*(D-w*L)-1*b另外,在SOR 迭代法中,上面算法step1中要给定松弛因子w ,其中0<w<2 为计算结果,规定w=0.5。
数统学院_偏微分方程数值解实验报告1

1.6905
0.0000
Hale Waihona Puke 0.02501.02531.0253
0.0000
0.5500
1.7333
1.7333
0.0000
0.0500
1.0513
1.0513
0.0000
0.5750
1.7772
1.7771
0.0001
0.0750
1.0779
1.0779
0.0000
0.6000
1.8222
0.0080
0.9500
2.5557
2.5857
0.0300
0.4500
1.5597
1.5683
0.0087
0.9750
2.6196
2.6512
0.0316
0.4750
1.5987
1.6080
0.0094
1.0000
2.6851
2.7183
0.0332
0.5000
1.6386
1.6487
0.0101
0.0001
0.1750
1.1913
1.1912
0.0000
0.7000
2.0138
2.0138
0.0001
0.2000
1.2214
1.2214
0.0000
0.7250
2.0648
2.0647
0.0001
0.2250
1.2523
1.2523
0.0000
0.7500
2.1171
2.1170
0.0001
1.7716
1.8221
0.0506
偏微分方程解的几道算例(差分、有限元)-含matlab程序(1)

A(i-1,i)=-r; A(i,i-1)=-r; end end u=zeros(N+1,M+1); u(N+1,:)=u1; for k=1:N b=u(N+2-k,2:M)+0.02; u(N+1-k,2:M)=inv(A)*b';%求解迭代方程组 end uT=u(1,:);%0.25时刻的解 %精确解与数值解画图 x1=[0,x,1]; plot(x1,uT,'o') hold u_xt = exp (-pi*pi*T)*sin (pi*x1) + x1.*(1 - x1); plot (x1, u_xt, ' r') e=u_xt-uT; 六点格式 function [e]=six(dx,dt,T) %用六点对称格式求解,dx为x方向步长,dt为t方向步长 % e为误差 M=1/dx; N=T/dt; %得到第一层的值 u1=zeros(1,M+1); x=[1:M-1]*dx; u1([2:M])= sin(pi*x)+x.*(1 - x); %网比 r=dt/dx/dx;r2=2+2*r;r3=2-2*r; %构造三对角矩阵A for i=1:M-1 A(i,i)=r2;
0.0070 0.0027
-0.0097 -0.0037
-0.0013 -0.0005
0.0082 0.0000
-0.0114 0.0000
-0.0015 0.0000
0.0087 -0.0120
-0.0016
注:这里的"误差"=精确解-数值解. 2.精确解与数值解结果图像对比
“向前差分格式”:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上机实验2:五点差分格式法偏微分方程(Matlab )实验报告——五点差分格式法 一、 实验题目设G 是形如下图的十字形域,由五个相等的单位正方形组成,用五点差分格式求下列边值问题的数值解:22221,u uG x y ∂∂+=-∂∂∂于u=0,于G二、 实验原理取定沿X 轴和Y 轴方向的步长1h 和2h ,()122212h h h =+,作两族与坐标轴平行的直线:x=i 1h ,y=j 2h ,,0,1,2,i j =±±若(,i j x y )为正则内点,沿x,y 方向分别用二阶中心差商代替xx yy u u 和则得1,1,,1,1221222[]i j ij i ji j ij i j ij u u u u u u f h h +-+--+-+-+=特别取正方形网格:12h h h ==,则原差分方程可简化为21,,11,,11()44ij i j i j i j i j ij h u u u u u f --++-+++=三、 实验程序1)function uxy = EllIni2Uxl(x,y)format long ;uxy = 0;2)function uxy = EllIni2Uxr(x,y)format long;uxy = y*(2-y);3)function uxy = EllIni2Uyl(x,y)format long;uxy = 0;4)function uxy = EllIni2Uyr(x,y)format long;if x < 1uxy = x;elseuxy = 2 - x;end5)function u = peEllip5(nx,minx,maxx,ny,miny,maxy) format long;hx = (maxx-minx)/(nx-1);hy = (maxy-miny)/(ny-1);u0 = zeros(nx,ny);for j=1:nyu0(j,1) = EllIni2Uxl(minx,miny+(j-1)*hy);u0(j,nx) = EllIni2Uxr(maxx,miny+(j-1)*hy);endfor j=1:nxu0(1,j) = EllIni2Uyl(minx+(j-1)*hx,miny);u0(ny,j) = EllIni2Uyr(minx+(j-1)*hx,maxy);endA = -4*eye((nx-2)*(ny-2),(nx-2)*(ny-2));b = ones((nx-2)*(ny-2),1).*(-1);for i=1:(nx-2)*(ny-2)if mod(i,nx-2) == 1if i==1A(1,2) = 1;A(1,nx-1) = 1;b(1) = - u0(1,2) - u0(2,1);elseif i == (ny-3)*(nx-2)+1A(i,i+1) = 1;A(i,i-nx+2) = 1;b(i) = - u0(ny-1,1) - u0(ny,2);elseA(i,i+1) = 1;A(i,i-nx+2) = 1;A(i,i+nx-2) = 1;b(i) = - u0(floor(i/(nx-2))+2,1);endendelseif mod(i,nx-2) == 0if i == nx-2A(i,i-1) = 1;A(i,i+nx-2) = 1;b(i) = - u0(1,nx-1) - u0(2,nx);elseif i == (ny-2)*(nx-2)A(i,i-1) = 1;A(i,i-nx+2) = 1;b(i) = - u0(ny-1,nx) - u0(ny,nx-1);elseA(i,i-1) = 1;A(i,i-nx+2) = 1;A(i,i+nx-2) = 1;b(i) = - u0(floor(i/(nx-2))+1,nx);endendelseif i>1 && i< nx-2A(i,i-1) = 1;A(i,i+nx-2) = 1;A(i,i+1) = 1;b(i) = - u0(1,i+1);elseif i > (ny-3)*(nx-2) && i < (ny-2)*(nx-2) A(i,i-1) = 1;A(i,i-nx+2) = 1;A(i,i+1) = 1;b(i) = - u0(ny,mod(i,(nx-2))+1);elseA(i,i-1) = 1;A(i,i+1) = 1;A(i,i+nx-2) = 1;A(i,i-nx+2) = 1;endendendendendul = A\b;for i=1:(ny-2)for j=1:(nx-2)u(i,j) = ul((i-1)*(nx-2)+j);endendformat short;四、实验结果>> u=peEllip5(25,0,3,25,0,3)u =Columns 1 through 61.14482.28963.26714.0750 4.73725.27632.2896 4.7466 6.7036 8.2957 9.5977 10.65833.2670 6.7035 9.5050 11.8066 13.6994 15.24744.0749 8.2955 11.8064 14.7262 17.1460 19.13514.7370 9.5973 13.6990 17.1457 20.0233 22.40115.2759 10.6576 15.2465 19.1343 22.4005 25.11205.7089 11.5108 16.4951 20.7444 24.3324 27.32286.0490 12.1816 17.4787 22.0159 25.8619 29.07756.3055 12.6880 18.2221 22.9785 27.0220 30.41066.4851 13.0426 18.7432 23.6540 27.8369 31.34816.5922 13.2542 19.0543 24.0573 28.3237 31.90826.6294 13.3278 19.1623 24.1973 28.4924 32.10196.5977 13.2651 19.0700 24.0771 28.3467 31.93326.4964 13.0648 18.7754 23.6946 27.8841 31.39956.3231 12.7225 18.2720 23.0417 27.0957 30.49116.0736 12.2298 17.5486 22.1047 25.9657 29.19135.7415 11.5747 16.5879 20.8626 24.4710 27.47565.3175 10.7395 15.3659 19.2868 22.5803 25.31134.7891 9.7000 13.8492 17.3385 20.2519 22.65624.1389 8.4221 11.9923 14.9662 17.4326 19.45773.3445 6.8572 9.7318 12.1014 14.0546 15.65152.3820 4.9303 6.9762 8.6530 10.0330 11.16071.25322.50583.58964.50165.2637 5.8950 Columns 7 through 125.70956.0499 6.3068 6.4869 6.5946 6.6327 11.5119 12.1833 12.6905 13.0461 13.2590 13.3341 16.4966 17.4810 18.2256 18.7482 19.0610 19.1713 20.7461 22.0186 22.9826 23.6600 24.0656 24.2085 24.3339 25.8647 27.0264 27.8435 28.3330 28.5051 27.3238 29.0798 30.4148 31.3547 31.9178 32.1153 29.7693 31.7160 33.1982 34.2426 34.8684 35.0871 31.7146 33.8168 35.4193 36.5492 37.2260 37.461533.1947 35.4172 37.1129 38.3090 39.0249 39.272834.2366 36.5445 38.3062 39.5489 40.2920 40.547534.8591 37.2178 39.0186 40.2884 41.0465 41.305135.0737 37.4491 39.2621 40.5395 41.3007 41.5577 34.8848 37.2427 39.0411 40.3067 41.0590 41.3099 34.2896 36.5959 38.3529 39.5873 40.3187 40.5588 33.2780 35.4985 37.1872 38.3711 39.0695 39.2944 31.8328 33.9329 35.5265 36.6403 37.2938 37.4988 29.9289 31.8739 33.3454 34.3698 34.9665 35.1472 27.5331 29.2885 30.6112 31.5272 32.0552 32.2070 24.6039 26.1358 27.2838 28.0725 28.5202 28.6384 21.0904 22.3671 23.3156 23.9590 24.3148 24.3945 16.9329 17.9266 18.6526 19.1329 19.3854 19.4216 12.0633 12.7537 13.2351 13.5347 13.6723 13.6596 6.4058 6.7898 6.9996 7.0985 7.1096 7.0427Columns 13 through 186.6020 6.5019 6.3302 6.0826 5.7530 5.3325 13.2733 13.0755 12.7361 12.2473 11.5970 10.7682 19.0818 18.7906 18.2915 17.5734 16.6195 15.4061 24.0918 23.7135 23.0660 22.1354 20.9014 19.3358 28.3635 27.9059 27.1234 26.0007 24.5150 22.6350 31.9512 31.4230 30.5211 29.2291 27.5227 25.3694 34.9031 34.3137 33.3090 31.8719 29.9775 27.5926 37.2603 36.6196 35.5294 33.9721 31.9226 29.348039.0571 38.3751 37.2167 35.5644 33.3930 30.669840.3201 39.6070 38.3981 36.6757 34.4151 31.583741.0688 40.3347 39.0928 37.3254 35.0078 32.1078 41.3152 40.5704 39.3129 37.5254 35.1829 32.2534 41.0640 40.3185 39.0632 37.2803 34.9450 32.0249 40.3124 39.5766 38.3409 36.5877 34.2917 31.4203 39.0503 38.3344 37.1363 35.4380 33.2139 30.4309 37.2600 36.5745 35.4318 33.8140 31.6951 29.0414 34.9165 34.2716 33.2024 31.6909 29.7112 27.228831.9871 31.3931 30.4153 29.0362 27.2300 24.962328.4318 27.8985 27.0295 25.8084 24.2105 22.201824.2032 23.7396 22.9959 21.9575 20.6016 18.896619.2468 18.8607 18.2571 17.4239 16.3420 14.983813.5018 13.1993 12.7480 12.1390 11.3586 10.38596.9016 6.6868 6.3964 6.0257 5.5674 5.0103 Columns 19 through 234.8087 4.1651 3.3801 2.4318 1.32549.7373 8.4714 6.9236 5.0218 2.635213.9009 12.0597 9.8209 7.0967 3.756117.4005 15.0454 12.2038 8.7880 4.683220.3200 17.5175 14.1611 10.1681 5.438822.7271 19.5436 15.7548 11.2845 6.044524.6754 21.1749 17.0301 12.1707 6.517326.2071 22.4504 18.0201 12.8507 6.869727.3546 23.3995 18.7492 13.3421 7.110928.1421 24.0436 19.2352 13.6577 7.247528.5864 24.3978 19.4901 13.8060 7.284028.6980 24.4711 19.5214 13.7923 7.223028.4809 24.2673 19.3322 13.6187 7.065727.9336 23.7849 18.9214 13.2846 6.811827.0481 23.0174 18.2838 12.7864 6.459525.8106 21.9528 17.4100 12.1176 6.005524.2003 20.5732 16.2859 11.2686 5.444922.1885 18.8537 14.8917 10.2260 4.771119.7377 16.7613 13.2014 8.9724 3.976216.7993 14.2523 11.1802 7.4861 3.051813.3107 11.2685 8.7810 5.7401 1.99499.1911 7.7299 5.9352 3.6985 0.82824.3378 3.5247 2.5313 1.2905 -0.3180>>。
