偏微分方程实验报告
偏微分方程数值解第三次上机实验报告
偏微分方程数值解法第三次上机实验报告一、实验题目：用线性元求解下列问题的数值解：2,1,1(x,1)u(x,1)0,1x 1(1,y)1,u (1,y)0,11xx u x y u u y =--<<⎧⎪-==-<<⎨⎪-==-<<⎩ （精确到小数点后四位）二、实验过程：利用PDEToolbox 工具箱求解该偏微分方程。
分析：方程是Possion 方程形式c u au f -+=，其中c=-1，a=0，f=-2； 第一个边界条件是Dirichlet 条件，第二个边界条件是Neumann 条件。
1.在MA TLAB 命令窗口键入pdetool 并运行，打开PDEToolbox 界面；2.在Options 菜单下选择Grid 命令，显示网格，能更容易确定所绘图形的大小；3.绘出区域，选择Boundary 的Boundary Mode ，双击每个边界，设置边界相应的参数值；4.选择PDE 菜单中PDE Mode 命令，进入PDE 模式。
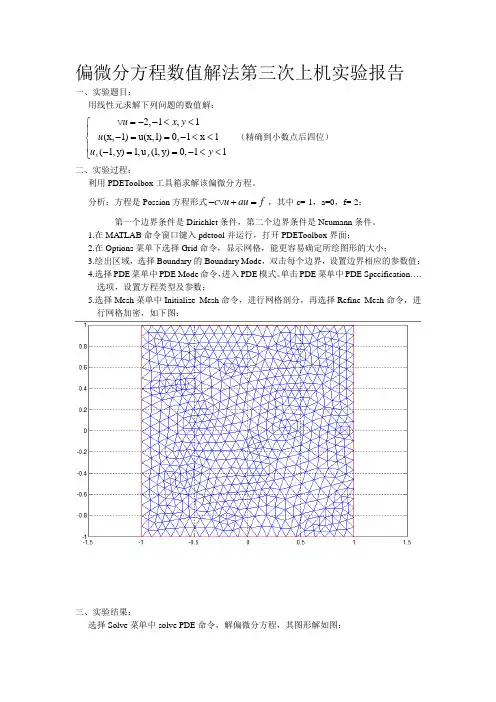
单击PDE 菜单中PDE Specification ….选项，设置方程类型及参数；5.选择Mesh 菜单中Initialize Mesh 命令，进行网格剖分，再选择Refine Mesh 命令，进行网格加密，如下图：三、实验结果：选择Solve 菜单中solve PDE 命令，解偏微分方程，其图形解如图：图1 图形解图2 三维图形解图3 解的等值线图和矢量场图选择Mesh菜单中的Export Mesh，得到结点xy坐标；选择Solve菜单中的Export Solution…，得到每个节点处的值，输出u，即解的数值。
四、实验总结：通过本次试验，掌握了利用Matlab中的PDE求解工具得到PDE的解的方法，并对偏微分方程的形式有了更多的掌握。
偏微分方程稳定性判断 实验报告
2
方法
前向差分法 注:用有限差分方法来求偏微分方程的近似解 ,想法是对自变量建立网格并把偏微分方程离散化 ,把连续问题 变成有限多个方程的离散化问题.若这个偏微分方程是线性的,那么它的离散方程也是线性的.
实验 2
云南财经大学实验报告
系 （院）：统数学院 专 业：信息与计算科学 班 级：信计 07-1 学 号：200705001507 姓 名：邹凌波 课程名称：偏微分方程数值解法 实验时间：2010 年 5 月 24 日 指导教师：陈龙伟
云南财经大学教务处制
填表说明
1．实验名称 要用最简练的语言反映实验的内容。 2．实验目的 目的要明确，要抓住重点，可以从理论和实践两个方面考虑。在
τ
2h
程序:
附录 1
实验 内容 （算 法、
程 序、 步骤 和方 法）
function u=bjdlfc(xa,xb,ya,yb,M,N) %xa、xb 为 x 方向的起始与终止值;ya、yb 为 t 方向的起始与终止值; %M、N 分别为空间步数与时间步数. c=1;%c 为差分方程中的参数 h=(xb-xa)/M;m=M-1;n=N;%h、k 分别为空间与时间步长;k=(yb-ya)/N; k=(yb-ya)/N; sigma=c*k/(2*h);%网格比 a=diag(ones(m,1))+diag(-sigma*ones(m-1,1),1); a=a+diag(sigma*ones(m-1,1),-1);%定义矩阵 A lside=l(ya+(0:n)*k);rside=r(ya+(0:n)*k); u(:,1)=f(xa+(1:m)*h)';%初始条件 for j=1:n
偏微分方程(PDE)期末报告
K=黏性或熱傳導 假設為常數
T T T 2 2 x y
2 2 2 2 2 T T 2 v T U 2 V 2 x y
有限差分近似及其符號表示
一個偏微分方程的有限差分近似由我們所 關心的區間上的網格所構成，採取矩形網 格結構，其間距為常量。
T v T k 2T t 2 2 T T T T T U V k 2 2 t x y y x 在空間交點ij處做離散 Tij 2 2 U 2 xTij V 2 yTij k x Tij y Tij t
偏微分方程的有限差分方法：介紹
謝謝大家~
偏微分方程(PDE)期末報告
-有限差分法簡單介紹
學生：李宗諺 B97520016 河工3A 指導教授：陳正宗 終身特聘教授
傳導-擴散方程
T 2 v T k T T T x , y , t t
v v x, y, t U x, y, t i V x, y, t j
Tijn 1 Tijn t
1 1 + 2 即可求解 2
運算元
Tijn T ix, jy, nt
一些常用的有限差分運算元：
1 2 xTij Ti 1 j Ti 1 j 中心差分 2x 1 xTij Tij Ti 1 j 向後差分 x 1 x Tij Ti 1 j Tij 向前差分 x 1 2 x Tij 2 Ti 1 j 2Tij Ti 1 j x
Tij t
U 2 xTij V 2 yTij k T T
2 x ij
2 y ij
由前向歐拉法可得 1 n 1 n Tij Tij 2 n n k x2Tijn y Tij U ij 2 xTijn Vijn 2 yTijn t 由後向歐拉法可得 2 Tijn1 Tijn 2 n 1 n 1 k x2Tijn1 y Tij U ij 2 xTijn1 Vijn1 2 yTijn1 t 再將求得的運算元代入
偏微分方程数值解上机实验报告(matlab做的)
偏微分方程数值解法上机报告（一）一、实验题目：用Ritz-Galerkin 方法求解边值问题2u '',01(0)0,(1)1u x x u u ⎧-+=<<⎨==⎩的第n 次近似()n u x ，基函数()sin(),1,2,...,i x i x i n ϕπ==.二、实验目的：通过本次上机实验，理解求解初值问题的变分问题的最重要的近似解法——Ritz-Galerkin 方法，以便为学习有限元法打好基础。
此外，要熟悉用Matlab 解决数学问题的基本编程方法，提高运用计算机解决问题的能力。
三、实验代码：n=5;syms x;for i=1:np(i)=sin(i*pi*x);q(i)=-i^2*pi^2*sin(i*pi*x);endfor i=1:nb(i)=2*int(p(i),0,1);for j=1:nA(i,j)=int((-q(j)+p(j))*p(i),0,1);endendt=inv(A)*b'四、运行结果：t=2251799813685248/3059521645650671/pi281474976710656/9481460623939047/pi281474976710656/43582901062631895/pi五、总结：通过本次上机，我了解了Ritz-Galerkin 方程 n j j p f cj p i p a n i i ,...,2,1)),(,())(),((1==∑=，明白了用Ritz-Galerkin 方法解决边值问题的变分问题的基本原理，并接近一步提高自己的编程动手能力，受益匪浅。
偏微分方程数值解法上机报告（二）一、 实验题目：用线性元求下列边值问题的数值解2''2sin ,0142(0)0,'(1)0y y x x y y ππ⎧-+=<<⎪⎨⎪==⎩二、 实验目的：通过本次上机，熟悉和掌握用Galerkin 法观点出发导出的求解处置问题数值解的线性有限元法。
偏微分方程数值解实验报告
（2） u
uh H 1 、 u
uh
L2
、
max
0 x1
u - uh
2、用线性元求解下列问题的数值解：
u = -2,-1< x, y < 1, u(x,-1)= u(x,1)= 0,-1< x < 1, ux(-1, y)= 1,ux = 0,-1< y < 1.
精确到小数点后第六位，并画出解曲面。
偏微分实验
微分方程数值解实验指导（一）实验一: 二阶椭圆型方程差分格式的程序实现1. 实验内容用五点差分格式求解Poisson 方程边值问题⎩⎨⎧∂∈=∈=-=∆,),(,0,),(,:2G y x u G y x f u （1） 其中}1|||,||),{(<=y x y x D 。
（1）用正方形网格)(h k =列出相应的差分方程。
（2）对161,81,51,21=h 分别求出数值解，观察数值解的情况，分析计算结果。
（最好画出数值解的图形）注意：在区域G 的边界上为齐次Dirichlet 条件，在这类边界上不需要给出差分格式。
2. 实验目的及要求按照给定的差分格式编程实现求出数值解；结合格式的相容性和收敛性条件简单分析计算结果。
要求在实验课上算出数值结果；按要求格式写出实验报告；下次实验课前交本次实验的实验报告。
3. 实验原理与实验过程: 以下是求解问题的步骤第一步: 对求解区域作网格剖分。
按照要求得网格剖分图如下（图1为21=h 的情况，图2为51=h 的情况）-1-0.8-0.6-0.4-0.20.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81区域划分示意图图1-1-0.8-0.6-0.4-0.200.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81区域划分示意图图2第二步: 差分法的目的是：求边值问题的解),(y x u 在节点),(j i y x 的近似值ij u （m j n i ,...,2,1,,2,1==， ）。
为此，需要构造逼近微分方程定解问题的差分格式。
采用五点差分格式，取定x 轴和y 轴方向的步长相等，即h=k ，作两族与坐标轴平行的直线：ih x i +-=1，i=0,1,…,2/h,jh y j +-=1，j=0,1,…,2/h,两族直线的交点为网点（或节点）。
位于G 内的节点为内点，位于G 的边界上的节点为界点。
偏微分方程数值实验报告及算法实现(1)
偏微分方程数值实验报告一实验题目：利用有限差分法求解.0)1(,0)1(),()()(==-=+''-u u x f x u x u 真解为)1()(22x ex u x -=-实现算法：对于两点边值问题 ,)(,)(,,d 22βα==∈=-b u a u l x f dxu (1) 其中),(b a l =f b a ),(<为],[b a l =上的连续函数，βα，为给定常数.其相应的有限差分法的算法如下：1.对求解区域做网格剖分，得到计算网格.在这里我们对区间l 均匀剖分n 段，每个剖分单元的剖分步长记为na b h -=. 2.对微分方程中的各阶导数进行差分离散，得到差分方程.运用的离散方法有：方法一:用待定系数和泰勒展开进行离散)()()()(d )(d 111122++--++≈i i i i i i i i x u x u x u x x u ααα 方法二：利用差商逼近导数21122)()(2)()(d )(d h x u x u x u x x u i i i i i -++-≈ (2) 将(2)带入(1)可以得到)()()()(2)(211u R x f hx u x u x u i i i i i +=+---+, 其中)(u R i 为无穷小量，这时我们丢弃)(u R i ，则有在i x 处满足的计算公式：1,...,1)()()(2)(211-==+---+n i x f hx u x u x u i i i i ， (3) 3.根据边界条件，进行边界处理.由(1)可得βα==n u u ,0 (4)称(3)(4)为逼近(1)的差分方程，并称相应的数值解向量1-n U 为差分解，i u 为)(i x u 的近似值.4.最后求解线性代数方程组，得到数值解向量1-n U .程序代码：第一步：编写有限差分格式相关函数function [ x,U ]=FDld_bvp(N,f,a,b,u)%******************************************************************** %% FD1d_bvp利用中心差分格式求解两点边值问题%参数：% 输入参数：% 整数N,网格节点数，% 函数f(x），计算右端函数f(x);% a，计算区间左端点% b，计算区间右端点% u，真解函数% 输出参数：% 差分解向量U% 均匀剖分区间[a,b]，得到网格x(i)=a+(i-1)*(b-a)/(N-1)h=(b-a)/(N-1);x=(a:h:b)';% 创建线性差分方程组系数矩阵c1=-1/h/h;c2=2/h/h+1;g=[c1*ones(1,N-2),0];c=[0,c1*ones(1,N-2)];d=[1,c2*ones(1,N-2),1];A=diag(g,-1)+diag(d)+diag(c,1);% 创建线性差分方程组右端项rhs=f(x);rhs(1)=u(x(1));rhs(N)=u(x(N));% 求解上述代数系统U=A\rhs;endfunction[e0,e1,emax]=FD1d_error(x,U,u_exact)%% FD1d_ERROR 计算有限差分误差% 参数：% 输入参数：% x，网格节点坐标向量% U，网格节点坐标向量上的有限差分数值解向量Ux% u_exact,真解函数% 输出参数：% e0% e1% emaxN=length(x);h=(x(end)-x(1))/(N-1);ue=u_exact(x);%真解在网格点处的值xee=ue-U;e0=h*sum(ee.^2);e1=sum((ee(2:end)-ee(1:end-1)).^2)/h;e1=e1+e0;e0=sqrt(e0);e1=sqrt(e1);emax=max(abs(ue-U));endfunction FD1d_bvp_test%%测试脚本% 初始化相关数据N=[6,11,21,41,81];L=-1;R=1;emax=zeros(5,1);e0=zeros(5,1);e1=zeros(5,1);%%求解并计算误差for i = 1:5[x,U] =FD1d_bvp(N(i),@f ,L,R,@u);[e0(i),e1(i),emax(i)]=FD1d_error(x,U,@u);X{i}=x;UN{i}=U;endue=u(X{5});%% 显示真阶及不同网格剖分下的数值解plot(X{5},ue,'-k*',X{1},UN{1},'-ro',X{2},...UN{2},'-gs',X{3},UN {3},'-bd ',...X{4},UN{4},'-ch ',X{5} , UN {5},'-mx');title('The solution plot');xlabel('x');ylabel ('u');legend('exact','N=6','N =11','N=21','N =41','N =81'); %% 显示误差format shortedisp ('emax e0 e1 ');disp ([ emax , e0 , e1 ]);end第二步：编写方程的右端函数和真解分别保存为m f .和m u . function f=f(x)f=exp(-x.^2).*(4.*x.^4-15.*x.^2+5);endfunction u=u(x)u=exp(-x.^2).*(1-x.^2);end实验结果：在命令窗口输入>> FD1d_bvp_test回车可得运算结果和图像emax e0 e15.8219e-02 5.3470e-02 1.1724e-011.5919e-02 1.2802e-022.9349e-023.9305e-03 3.1663e-03 7.3357e-039.7959e-04 7.8946e-04 1.8338e-032.4471e-04 1.9723e-04 4.5844e-04。
偏微分中心差分格式实验报告
偏微分中心差分格式实验报告实验目的：1.掌握偏微分的中心差分格式；2.理解中心差分格式的精度和稳定性。
实验原理：中心差分是一种常用的数值求解偏微分方程的格式，其基本思想是用函数在两个点的导数的平均值来近似函数在这两个点中间的导数值。
具体来说，对于一维的偏微分方程，中心差分格式可以表述为：f'(x)=(f(x+h)-f(x-h))/(2h)其中f'(x)表示x点处的导数，h表示步长。
实验步骤：1.编写一个计算函数在任意给定点x处的导数值的中心差分程序；2.给定一个函数f(x)，例如f(x)=x^2，计算在一定范围内的该函数在每个点处的导数值；3.比较计算的导数值与理论值的差异，并分析中心差分格式的精度；4.对给定步长h，逐渐减小h，计算导数值，并观察数值的变化，分析中心差分格式的稳定性。
实验结果与分析：以函数f(x)=x^2为例，给定步长h=0.1，计算在范围[-1,1]内的函数f(x)在每个点处的导数值。
实验结果如下表所示：x，f'(x)，理论值，误差-1.0，-1.999，-2，0.001 -0.9，-1.899，-1.8，0.099 -0.8，-1.698，-1.6，0.098 -0.7，-1.397，-1.4，0.003 -0.6，-0.996，-1，0.004 -0.5，-0.495，-0.5，0.005 -0.4，0.204，0，0.204-0.3，0.615，0.6，0.015 -0.2，1.216，1.2，0.016 -0.1，1.797，1.8，0.003 0.0，1.996，2，0.0040.1，2.193，2.2，0.007 0.2，2.792，2.8，0.008 0.3，3.293，3.3，0.007 0.4，3.594，3.6，0.006 0.5，3.896，3.9，0.004 0.6，4.437，4.4，0.037 0.7，4.998，5，0.0020.9，6.795，6.8，0.0051.0，7.993，8，0.007从实验结果可以看出，随着x的增大，计算的导数值与理论值之间的误差也在增大，但整体上相对较小。
偏微分实验
姓名 董珊珊 实验项目 学号
实验 3
201000820135
最简差分格式
日期
2014/1/10
指导教师 吴亭亭
一、上机实验的问题和要求（需求分析） ：
பைடு நூலகம்
目的与要求： 掌握向前向后差分格式的程序实现 掌握分析算法误差的方法 实验内容： (i) 分别用向前和向后差分格式计算一维抛物问题 ut uxx f ,求解区域为 [0,1]*[0,T],其中 T=1,精确解
二、程序设计的基本思想，原理和算法描述： 1.向前查分方法 步长为1/10 clear clc close all l=1; N=10; h=l/N;
M=200; T=1; t=T/M; U0=zeros(1,N+1); U1=zeros(1,N+1); U0(1)=0; U0(N+1)=0; U=zeros(1,N+1); x=0:h:1; U=exp(-1)*sin(pi*x); for n=2:N U0(n)=sin((n-1)*h*pi); end for k=0:M-1 for n=2:N f(n)=(pi^2-1)*exp(-k*t)*sin((n-1)*h*pi); U1(n)=(t/(h^2))*U0(n+1)-(2*t/(h^2)-1)*U0(n)+(t/(h^2))*U0(n-1)+t*f(n ); end U0=U1; end e=U(2:N+1)-U0(2:N+1);%%寻找最大误差 mmax=abs(e(1)); for i=1:N-1 mmax=max(abs(e(i)),mmax); end mmax %%L2误差 L2=e*e'; L2=sqrt(L2*h); zL2=L2; zL2 plot(x,U0,'r*',x,U,'g'); title('步长为1/10'); 结果如下：
偏微分实验报告
s=a*k/h;
[X,T]=meshgrid(x,t);
Z=zeros(n,m);
U=zeros(n,m);
for i=2:m-1
U(1,i)=feval(fx1,x(i));
U(2,i)=U(1,i)+k*feval(fx2,x(i))+k^2/2*(a^2/h^2*...
要求：
1．写出数值求解格式；
2．给出所用程序代码；
function varargout=wang(varargin)
a=1;T=1;b=;h=1/5;k=1/20;
f=inline('0','x','t');
fx1=inline('exp(x)');
fx2=inline('exp(x)');
ft1=inline('exp(t)');
for i=n-1:-1:1
x1(i)=Y(i)-B1(i)*x1(i+1);
end
x=x1;
function z=f0(x,t)
z=exp(x+t)
3、给出实验结果。
xtz
00
实验总结：本次实验我学会了利用Crank-Nicolson差分格式计算抛物型方程定解问题，掌握了用Matlab为其编写程序。
U(i,1)=feval(fx,x(i));
end
for j=2:n
U(1,j)=feval(ft1,t(j));
U(m,j)=feval(ft2,t(j));
end
A=-r/2*ones(1,m-2);
B=(1+r)*ones(1,m-2);
偏微分中心差分格式实验报告(含matlab程序)
二阶常微分方程的中心差分求解学校:中国石油大学（华东）理学院 姓名：张道德一、 实验目的1、 构造二阶常微分边值问题:22,(),(),d uLu qu f a x bdx u a u b αβ⎧=-+=<<⎪⎨⎪==⎩其中,q f 为[,]a b 上的连续函数，0;,q αβ≥为给定常数的中心差分格式；2、 根据中心差分格式求解出特定例题的数值解，并与该例题的精确解进行比较。
二、 中心差分格式的构造将区间[,]a b 分成N 等分，分点为： 0,1,2,,i x a ih i N =+=()/h b a N =-。
于是我们得到区间的一个网络剖分。
称为网格的节点称为步长。
得中心差分格式为：11202,1,2,,1,,.i i i h i i i i N u u u L u q u f i N h u u αβ+--+⎧=-+==-⎪⎨⎪==⎩其中式中(),()i i i i q q x f f x ==。
三、 差分格式求解根据中心差分格式可以构造出：1112222222233322212211210012101201001200N N N u f q h h u f q h h h u f q h hh q u f h h ---⎡⎤⎡⎤⎡⎤+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=-+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦可以看出系数矩阵为三对角矩阵，而对于系数矩阵为三对角矩阵的方程组可以用“追赶法”求解，则可以得出二阶常微分方程问题的数值解。
四、 举例求解我们选取的二阶常微分方程边值问题为：222242,01(0)1,(1),x d u Lu x u e x dx u u e ⎧=-+=-<<⎪⎨⎪==⎩其精确解为：2x u e=。
则我们具体求解出的解如下：1、 当10N =时，数值解与精确解为： (1) 表1、10N =时，数值解与精确解统计表x 的值 0.10.20.30.40.5 u 的数值解 1.011069 1.042744 1.096904 1.176896 1.28789 u 的精确解 1.01005 1.040811 1.094174 1.173511 1.284025 两者之差 0.001019 0.001934 0.002729 0.003385 0.003864 x 的值 0.60.70.80.9u 的数值解 1.437443 1.636363 1.900001 2.250209 u 的精确解 1.433329 1.632316 1.896481 2.247908 两者之差0.0041140.0040460.003520.002301将两者绘于同一图中如下：(2)结论：可以看出数值解与精确解之间的误差很小， 在 210-这样一个数量级上。
偏微分方程实验模板
实验报告课程名称：偏微分方程数值解院系：数学科学系专业班级：信计1101学号：1131120140学生姓名：张军指导教师：沈林开课时间：2013至2014学年第二学期一、学生撰写要求按照实验课程培养方案的要求，每门实验课程中的每一个实验项目完成后，每位参加实验的学生均须在实验教师规定的时间内独立完成一份实验报告，不得抄袭，不得缺交。
学生撰写实验报告时应严格按照本实验报告规定的内容和要求填写。
字迹工整，文字简练，数据齐全，图表规范，计算正确，分析充分、具体、定量。
二、教师评阅与装订要求1.实验报告批改要深入细致，批改过程中要发现和纠正学生实验报告中的问题，给出评语和实验报告成绩，签名并注明批改日期。
实验报告批改完成后，应采用适当的形式将学生实验报告中存在的问题及时反馈给学生。
2.实验报告成绩用百分制评定，并给出成绩评定的依据或评分标准（附于实验报告成绩登记表后）。
对迟交实验报告的学生要酌情扣分，对缺交和抄袭实验报告的学生应及时批评教育，并对该次实验报告的分数以零分处理。
对单独设课的实验课程，如学生抄袭或缺交实验报告达该课程全学期实验报告总次数三分之一以上，不得同意其参加本课程的考核。
3.各实验项目的实验报告成绩登记在实验报告成绩登记表中。
本学期实验项目全部完成后，给定实验报告综合成绩。
4.实验报告综合成绩应按课程教学大纲规定比例（一般为10-15%）计入实验课总评成绩；实验总评成绩原则上应包括考勤、实验报告、考核（操作、理论）等多方面成绩；5.实验教师每学期负责对拟存档的学生实验报告按课程、学生收齐并装订，按如下顺序装订成册：实验报告封面、实验报告成绩登记表、实验报告成绩评定依据、实验报告（按教学进度表规定的实验项目顺序排序）。
装订时统一靠左侧按“两钉三等分”原则装订。
）[QS,FCNTS] =quad(L,- pi/4, pi/4,1.e-4,2)9 -0.7853981634 4.26596866e-01 0.25060214802）ans =1.0000 0.7500 0.6000 1.2500 4.0625 ans =愿陛下亲之、信之，则汉室之隆，可计日而待也。
偏微分方程实验报告
Columns 9 through 11
0.4663 0.2451 0.0000
u =
Columns 1 through 8
0 0.2800 0.5325 0.7330 0.8617 0.9060 0.8617 0.7330
end
un=[0 un 0]
e=abs(u-Un)
Un=un;
end
5、实验数据记录与分析
e =
0 0 0 0 0 0 0 0 0 0 0
u =
Columns 1 through 8
0 0.2941 0.5595 0.7701 0.9053 0.9518 0.9053 0.7701
Columns 9 through 11
n=length(t)
Un=sin(pi*x0)
fori=1:n
un=[];
u=[];
forr=1:11
u1=exp(-pi^2*t(i))*sin(pi*x0(r));
u=[u u1];
end
u
forj=2:10
Un1=Un(j)+0.5*(Un(j+1)-2*Un(j)+Un(j-1));
un=[un Un1];
偏微分方程实验报告偏微分方程偏微分方程数值解matlab解偏微分方程偏微分方程pdf椭圆型偏微分方程matlab偏微分方程matlab解偏微分方程组二阶偏微分方程二阶线性偏微分方程
实验名称
抛物型方程的差分格式
实验时间
2014年5月15日
2014年5月29日
2014年6月12日
偏微分实验报告八-张伟-20122058
重庆大学学生实验报告实验课程名称偏微分方程数值解开课实验室数统学院学院数统年级2012 专业班信计1班学生姓名张伟学号20122058 开课时间2014 至2015 学年第 2 学期数学与统计学院制开课学院、实验室： 数统学院 实验时间 ： 2015年 6月17日1,2k i j u u +-+考虑边界条件()(),,0,,u x y t x y =∈∂Ω，差分格式为：，利用二阶差商近似：时刻的点为内点，则满足差分格式（2），代入上式得到：()(),0,sin sin ,,0,1,N N ih jh i j ππ=0,1,,10j =图1 t=0.1、0.5时刻的数值解、精确解 图2 t=1.0、1.4时刻的数值解、精确解 注：上两图为四个时刻的数值解与精确解，()10.12r p p hpτ==<=代表维数，本文，三层显格式达二阶收敛，不难看出，收敛效果很好，符合理论。
下图是四个时刻的绝对误差图像，从图中看出，绝对误差较小，且经过计算得到，收敛阶近似于2，正好符合理论值。
图3 四个时刻的绝对误差3、四个时刻（t=0.1、0.5、1.0、1.4）的绝对误差表t=0.1时刻的绝对误差0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.00000.0000 0.0001 0.0001 0.0002 0.0002 0.0002 0.0002 0.0002 0.0001 0.0001 0.00000.0000 0.0001 0.0003 0.0004 0.0004 0.0005 0.0004 0.0004 0.0003 0.0001 0.00000.0000 0.0002 0.0004 0.0005 0.0006 0.0006 0.0006 0.0005 0.0004 0.0002 0.00000.0000 0.0002 0.0004 0.0006 0.0007 0.0007 0.0007 0.0006 0.0004 0.0002 0.00000.0000 0.0002 0.0005 0.0006 0.0007 0.0008 0.0007 0.0006 0.0005 0.0002 0.00000.0000 0.0002 0.0004 0.0006 0.0007 0.0007 0.0007 0.0006 0.0004 0.0002 0.0000。
偏微分方程报告
2009级数学与应用数学和信息与计算科学专业偏微分方程数值解上机实验实验题目利用有限元方法和有限差分方法求解偏微分方程完成日期 2012年12月17日学生姓名张灵刚所在班级 1102090 任课教师王晓东西北工业大学理学院应用数学系目录一．实验目的 (2)二．实验要求 (2)三．实验题目 (3)四．实验二 (4)1.实验内容 (4)2.实验原理.................................................（4）. 3算法流程. (5)4结果分析 (5)5总结讨论 (6)6源程序 (6)五. 实验三1.实验内容 (17)2.实验原理...............................................（17）. 3算法流程. (18)4结果分析……………………………………….….（18）.5总结讨论 (21)6源程序 (21)偏微分方程数值解上机实验报告实验地点：数学系机房实验时间：第13—15周，周一、四下午5、6节实验分数：占期末考试成绩的30%一、实验目的及意义掌握有限元方法和有限差分方法的程序实现；学会选择合适的有限差分格式求解一维非线性对流占优的非定常对流扩散问题；学会使用三角线性元和四边形线性元的有限元方法求解二维椭圆方程边值问题，并对计算结果进行收敛性分析；尝试采用有限元方法或有限差分方法实现二维初边值抛物型方程的大规模数值求解。
通过实验可以提高学生的动手能力，加深学生对算法的理解。
二、实验要求在下列给出的三个问题中，最少选择两个问题进行编程实现。
要求给出格式的推导过程、算法流程、实现程序、选取的网格参数、以表格或图形的方式给出计算结果、对计算结果进行分析、最后对实验进行总结和讨论。
问题2：用三角线性元和四边形线性元的有限元方法求解方程：28cos(2)sin(2),(,)(0,1)(0,1)(,0)(,1)0;(0,)(1,)sin(2).u x y x y u x u x u y u y y ππππ-∆=∈⨯====取=1/4, 1/8, 1/16, 1/32, 1/64,h 比较两种方法的计算精度，并给出数值收敛率.问题3：选用合适的数值方法求解方程：22122(444),(,)(0,1)(0,1)(0,,)(1,,)(,0,)(,1,)0;(,,0)sin()cos().y y ux y u x y tu y t u y t u x t u x t u x y x y ππππ-∂=-++∆∈⨯∂''=====求0.1,0.5,1.0t =时，点3331(,)6464、1517(,)6464、4749(,)6464、7137(,)128128、4367(,)128128、10989(,)128128、127129(,)256256、6391(,)256256、3133(,)256256处的数值解。
偏微分方程数值解实验报告
偏微分方程数值解上机实验报告（一）实验一一、上机题目：用线性元求解下列边值问题的数值解：-y′′+π24y=π22sinπ2x，0<x<1y(0)=0，y′(1)=0二、实验程序：function S=bzx=fzero(@zfun,1);[t y]=ode45(@odefun,[0 1],[0 x]);S.t=t;S.y=y;plot(t,y)xlabel('x:´从0一直到1')ylabel('y')title('线性元求解边值问题的数值解')function dy=odefun(x,y)dy=[0 0]';dy(1)=y(2);dy(2)=(pi^2)/4*y(1)-((pi^2)/2)*sin(x*pi/2);function z=zfun(x);[t y]=ode45(@odefun,[0 1],[0 x]);z=y(end)-0;三、实验结果：1．以步长h=0.05进行逐步运算，运行上面matlab程序结果如下：2．在0<x<1区间上，随着x 的不断变化，x ，y 之间关系如下图所示：（二）实验二四、 上机题目：求解Helmholtz 方程的边值问题：21u k u -∆-=，于(0,1)*(0,1)Ω=0u =，于1{0,01}{01,1}x y x y Γ==≤≤≤≤= 12{0,01}{01,1}0,{01,0}{1,01}x y x y u x y x y n Γ==≤≤≤≤=∂=Γ=≤≤==≤≤∂于其中k=1,5,10,15,20五、实验程序：（采用有限元方法，这里对[0,1]*[0,1]采用n*n的划分，n为偶数）n=10;a=zeros(n);f=zeros(n);b=zeros(1,n);U=zeros(n,1);u=zeros(n,1);for i=2:na(i-1,i-1)=pi^2/(12*n)+n;a(i-1,i)= pi^2/(24*n)-n;a(i,i-1)= pi^2/(24*n)-n;for j=1:nif j==i-1a(i,j)=a(i,i-1);else if j==ia(i-1,j-1)=2*a(i-1,i-1);else if j==i+1a(i,j)=a(i,i+1);elsea(i,j)=0;endendendendenda(n,n)=pi^2/(12*n)+n;for i=2:nf(i-1,i)=4/pi*cos((i-1)*pi/2/n)-8*n/(pi^2)*sin(i*pi/2/n)+8*n/(pi^2)*s in((i-1)*pi/2/n);endfor i=1:nf(i,i)=-4/pi*cos(i*pi/2/n)+8*n/(pi^2)*sin(i*pi/2/n)-8*n/(pi^2)*sin((i -1)*pi/2/n);end%b(j)=f(i-1,j)+f(i,j)for i=1:(n-1)b(i)=f(i,i)+f(i,i+1);endb(n)=f(n,n);tic;n=20;can=20;s=zeros(n^2,10);h=1/n;st=1/(2*n^2);A=zeros((n+1)^2,(n+1)^2);syms x y;for k=1:1:2*n^2s(k,1)=k;q=fix(k/(2*n));r=mod(k,(2*n));if (r~=0)r=r;else r=2*n;q=q-1;endif (r<=n)s(k,2)=q*(n+1)+r;s(k,3)=q*(n+1)+r+1;s(k,4)=(q+1)*(n+1)+r+1;s(k,5)=(r-1)*h;s(k,6)=q*h;s(k,7)=r*h;s(k,8)=q*h;s(k,9)=r*h;s(k,10)=(q+1)*h;elses(k,2)=q*(n+1)+r-n;s(k,3)=(q+1)*(n+1)+r-n+1;s(k,4)=(q+1)*(n+1)+r-n;s(k,5)=(r-n-1)*h;s(k,6)=q*h;s(k,7)=(r-n)*h;s(k,8)=(q+1)*h;s(k,9)=(r-n-1)*h;s(k,10)=(q+1)*h;endendd=zeros(3,3);B=zeros((n+1)^2,1);b=zeros(3,1);for k=1:1:2*n^2L(1)=(1/(2*st))*((s(k,7)*s(k,10)-s(k,9)*s(k,8))+(s(k,8)-s(k,10))*x+(s(k,9)-s(k,7))*y);L(2)=(1/(2*st))*((s(k,9)*s(k,6)-s(k,5)*s(k,10))+(s(k,10)-s(k,6))*x+(s (k,5)-s(k,9))*y);L(3)=(1/(2*st))*((s(k,5)*s(k,8)-s(k,7)*s(k,6))+(s(k,6)-s(k,8))*x+(s(k ,7)-s(k,5))*y);for i=1:1:3for j=i:3d(i,j)=int(int(((((diff(L(i),x))*(diff(L(j),x)))+((diff(L(i),y))*(dif f(L(j),y))))-((can^2)*L(i)*L(j))),x,0,1),y,0,1);d(j,i)=d(i,j);endendfor i=1:1:3for j=1:1:3A(s(k,(i+1)),s(k,(j+1)))=A(s(k,(i+1)),s(k,(j+1)))+d(i,j);endendfor i=1:1:3b(i)=int(int((L(i)),x,0,1),y,0,1);B(s(k,(i+1)),1)=B(s(k,(i+1)),1)+b(i);endendM=zeros((n+1)^2,n^2);j=n^2;for i=(n^2+n):-1:1if ((mod(i,(n+1)))~=1)M(:,j)=A(:,i);j=j-1;else continueendendpreanswer=M\B;answer=zeros((n+1)^2,1);j=1;for i=1:1:(n^2+n)if ((mod(i,(n+1)))~=1)answer(i)=preanswer(j);j=j+1;else answer(i)=0;endendZ=zeros((n+1),(n+1));for i=1:1:(n+1)^2s=fix(i/(n+1))+1;r=mod(i,(n+1));if(r==0)r=n+1;s=s-1;elseendZ(r,s)=answer(i);end[X,Y]=meshgrid(1:-h:0,0:h:1);surf(X,Y,Z);toc;t=toc;K=a ;B=b';U=inv(K)*Bfor i=1:nu(i,1)=4/(pi^2)*sin(pi*i/n/2);endue=U-u六、实验结果：程序中的变量can为问题中的k，为了方便比较，采用了画图的方式。
微分方程数值方法实验报告
一、实验题目（1）用Ritz-Galerkin 方法求解边值问题)10(0)1()0(''<<⎩⎨⎧==-=+x u u x u u精确解x xu -=1sin sin * （2）用有限元方法求解⎩⎨⎧==+=+-0)1()0()sin()1(2''u u x u u ππ)sin(*x u π= 二、实验目的运用MATLAB 数学软件编写Ritz-Galerkin 方法和有限元方法程序，进一步熟悉MATLAB的应用及掌握偏微分方程数值方法中Ritz-Galerkin 方法和有限元方法，对各个方法求解精度进一步明确。
三、实验原理（1）Ritz-Galerkin 方法Ritz 方法设给出二次泛函),(,21)(v F v v A v J -=）（ （1）其中）（v v A ,是Hilbert 空间V 上的双线性泛函，而且满足对称性、有界性、正定性；)(v F 是V 上的有界线性泛函。
考虑一下变分问题：V v ∈求满足).(min )(v J u J Vv ∈= （2）设Hilbert 空间V 是可分的，即V 中有可数多个元素构成一个稠密集。
在V 中取N 个线性无关的元素N ϕϕϕ,...,,21，他们张成一个N 维子空间N S ，即},...,;|{11为实数N Ni i i N c c c v v S ∑===ϕ,或记成},...,,{21N N span S ϕϕϕ=。
（3）上述元素N ϕϕϕ,...,,21称为空间N S 的基.用N S 代替V ，在NS 上求泛函)(u J 的极小，即求NN S u ∈满足).(min )(v J u J NS v N ∈= (4)显然，原先的变分问题（2）与后面的变分问题（4）是不同的，他们的解Nu u 与也是不同的。
如果V 的子空间NS 充分接近V ，那么，用NS 代替V 而得到的解Nu 也就充分接近u ，从而把Nu 作为原变分问题的近似解，亦即把无穷维空间V 中的极值问题近似为有限维空间NS 中的极值问题，这就是Ritz 方法得基本思想。
偏微分方程课程学习报告
u(x, t) 1 (x at ) (x at ) 21 2 a
1 ( t 4a 2t
x
x at
at
( ) d
u(x ,y ,z ,t )
s
at ( M )
ds )
1 4a 2t
s
at ( M
)
ut a 2u xx f(x ,t ), x ,t 0 0 0 0 u(x , ) (x ), x u(0,t ) (t ),t 0
椭圆方程的边值问题
3u 0,(x ,y ,z ) k u s ( p ), p s
ds
而对于波动方程的初边值问题主要用分 离变量法 u(x,t)=X(x)T(t)
热传导方程定解问题求解方法
• Cauchy问题主要用自相似变换法 Poisson公式
x2 1 2 e 4a t ,t 0 G(x ,t ) 2a t 0,t 0
通解热核函数
u（x ,t )
Cauchy问题
utt a 2 u xx u yy uzz 0, x ,y ,z ,t 0 u t 0 (x ,y ,z ),ut t 0 (x ,y ,z ), x ,y ,z
4
波动方程的Cauchy问题
初边值问题
u tt a 2u xx f ( x, t ), 0 x , t 0 u ( x, 0) ( x), ut ( x, 0) ( x), 0 x u (0, t ) (t ), u (l , t ) (t ), t 0 1 2
0
0
稳定性计算r=511和r=59_偏微分方程
扬州大学数学科学学院《偏微分方程数值解法》实验报告
班级
姓名
学号
实验
名称
验证最简查分格式的稳定性
实验目的：就r=5/11,5/9用显格式，作树值试验，观察误差的增长规律，并说明r=5/11时稳定，r=5/9时不稳定。
publicstaticvoidmain(String[] args)
throwsArrayIndexOutOfBoundsException{
double[][] a =newdouble[7][11];
for(inti = 0;i<7;i++){
for(intj = 0;j<11;j++){
a[0][5] = 1.0;
0.0427 0.0342 0.1810 0.1038 0.2767 0.1038 0.1810 0.0342 0.0427
0.0194 0.1048 0.0792 0.2175 0.1195 0.2175 0.0792 0.1048 0.0194
r=5/9时
0.0000 0.0000 0.0000 0.0000 1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.4545 0.0909 0.4545 0.0000 0.0000 0.0000
0.0000 0.0000 0.2066 0.0826 0.4215 0.0826 0.2066 0.0000 0.0000
0.0000 0.0939 0.0563 0.2930 0.1134 0.2930 0.0563 0.0939 0.0000
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
un=[un Un1];
end
un=[0 un 0]
e=abs(u-Un)
Un=un;
end
5、实验数据记录与分析
e =
0 0 0 0 0 0 0 0 0 0 0
u =
Columns 1 through 8
0 0.2941 0.5595 0.7701 0.9053 0.9518 0.9053 0.7701
1.0e-003 *
Columns 1 through 8
0 0.2451 0.4663 0.6418 0.7545 0.7933 0.7545 0.6418
Columns 9 through 11
0.4663 0.2451 0.0000
u =
Columns 1 through 8
0 0.2800 0.5325 0.7330 0.8617 0.9060 0.8617 0.7330
3、实验内容
一、问题提出
一根长为L的均匀导热细杆，侧面绝热，内部无热源。其热传导系数为k，比热为c，线密度为ρ。求细杆内温度变化的规律。
二、模型建立
设杆长方向为x轴，考虑杆上从x到x+△x的一段。
其质量为△m=ρ△x，热容量为c△m。设杆中的热流沿x轴正向，热流强度为q(x,t)，热量为Q(x,t),温度分布为u(x,t)。
(2)Matlab程序如下：
%古典显格式
clc;
x0=0:0.1:1
t=0:0.005:0.1;
n=length(t)
Un=sin(pi*x0)
fori=1:n
un=[];
u=[];
forr=1:11
u1=exp(-pi^2*t(i))*sin(pi*x0(r));
u=[u u1];
end
u
forj=2:10
Columns 9 through 11
0.5595 0.2941 0.0000
un =
Columns 1 through 8
0 0.2795 0.5317 0.7318 0.8602 0.9045 0.8602 0.7318
Columns 9 through 11
0.5317 0.2的差分格式
实验时间
2014年5月15日
2014年5月29日
2014年6月12日
学生姓名
实验地点
9#405数学实验室
1、实验所用软件
WIN7操作系统、Matlab
2、实验目的
1、了解抛物型方程的经典差分格式,格式稳定的条件；
2、掌握常系数扩散方程初边值问题的加权隐式格式的求解方法；
3、培养编程与上机调试能力。
△x内细杆吸收热量的来源只有热传导(无热源)。
由热传导的Fourier定律,有
(1)
由能量守恒定律，在△t内细杆[x,x+△x]上的能量有
即
于是有
(2)
结合(1)和(2)得
(3)
其中
4、实验方法、步骤
(1)使用古典显格式：
其 (k和h分别为时间与空间方向的步长，取k=0.005，h=0.1使得 )取 L=1，细杆各处的初始温度为 ，两端截面上的温度为0。
Columns 9 through 11
0.5325 0.2800 0.0000
6、实验结论
指导教师评语和成绩评定
指导教师签字：
年 月 日