偏微分方程(PDE)期末报告
偏微分方程式(PDE)就是指含有偏导函数(partial

Chapt e r 2 Intro d ucti o n to Parti a l Diffe r enti a l Equat i ons偏微分方程式(PDE )就是指含有偏導函數(parti a l deriv a tive s )的方程式,在常微分方程式(ODE )中,未知函數只是單變數函數,而在PDE 中,未知函數則為多變數函數。
在實際的工程或物理問題中,所欲分析的物理量(即未知函數)常受到不只一個變數的影響,所以一般多以PDE 來表示。
2.1 PDE 的分類(a) 以階數(order )區分:PDE 的階數為方程式中的最高偏導函數的階數。
例如,u u t xx =為2階PD E ,u u t x =為1階PD E ,u uu x t xxx =+s i n 為3階PD E 。
(b) 以是否線性(linea r ity )區分:若PDE 中的相依變數(即未知函數)及其偏導函數均為一次方(無乘方)且無彼此相乘的情況,則稱為線性PDE ,反之為非線性PDE 。
例如,A u Bu Cu D u Eu Fu G xx xy yy x y +++++= (1)其中A , B , C , D , E , F , G 為常數,或x , y 的函數。
(1)式為線性的2階PDE 。
而為非線性uu u xx t +=0之PDE 。
(c) 以是否齊性區分:以(1)式為例,G = 0時為齊性,G ≠ 0時為非齊性。
(d) 以係數類型區分:分為常係數與變係數之PDE 。
(e) 所有像(1)式之線性P DE 均可分為三大類型: 當B 2-4AC = 0,為拋物線型(parab o lic),如熱方程式。
當B 2-4AC > 0,為雙曲線型(hyper b olic ),如波動方程式。
偏微分方程解法工作总结
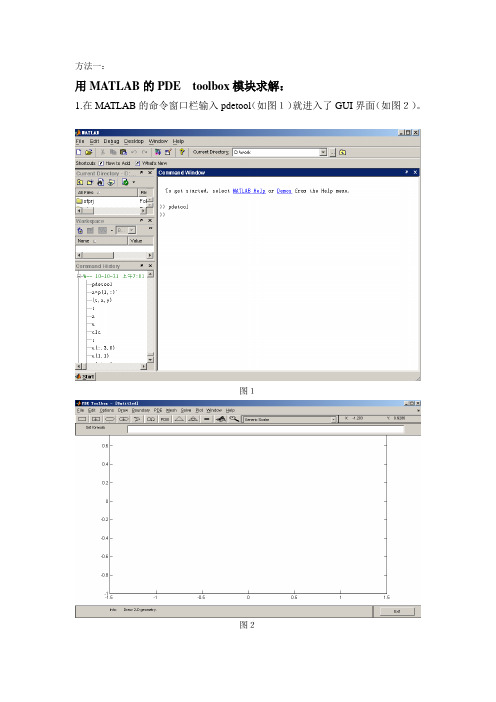
方法一:用MATLAB的PDE toolbox模块求解:1.在MATLAB的命令窗口栏输入pdetool(如图1)就进入了GUI界面(如图2)。
图1图2在Option的下拉菜单中选择Grid选项,就会出现相应的网格,如图3。
这样做的好处就是能方便图形的定位。
图33.选择所需要的图形。
在求解本题时,所求解的二维区域是矩形,因而点击第二行的矩形快捷键,并进行相应的放置。
如图4。
图44.根据边界调整坐标轴的范围及图形的大小。
坐标的调整:选择Option菜单中的Axeslimits,输入相应坐标的范围。
本题中取x的范围为[020],y的范围为[014]。
图形大小的调整:用鼠标双击所需调整的图形,在相应的窗口中输入所需的尺寸。
本例中取left=0,bottom=0,width=20,height=12。
得到图5。
图55.边界的设置。
选择Boundary下拉菜单中的Boundary Mode命令,得到图6。
图7双击相应的边界,输入相应的边界条件。
在本例中,x=20和y=12处的边界设置如图8。
x=0和y=0处的边界设置如图9。
图8图96.求解方程的输入。
选择PDE下拉菜单中的PDE Mode,并双击图形,得到图10的对话框。
由于本例中所求方程为:1)(2222=∂∂+∂∂-∂∂yTx T t T 因而选择第二种方程形式Parabolic ,其对应的方程形式为:f au u c tud=+∇⋅∇-∂∂)(对应的d=1,c=1,a=0,f=1。
如图10所示。
图9图107.初始条件的设定。
当所求微分方程涉及对时间变量t的偏微分时,就需要设置初始条件。
本例就是这种情况。
选择Solve的下拉菜单中的Parameter项,得到如图11的对话框。
其中第一栏表示计算机求解时时间变量t的范围,本例取0:300。
第二栏表示时间变量t=0时,变量u的取值,本例中设置为u(t=0)=200。
后两栏为相对及绝对强度的设置,在本例中不需要设置。
偏微分方程报告范文

偏微分方程报告范文偏微分方程是研究多变量函数的微分方程,其中函数的未知量既依赖于自变量,又依赖于多个自变量。
偏微分方程在物理学、工程学和经济学等领域中有着广泛的应用。
本报告将介绍偏微分方程的基本概念、求解方法和应用领域。
一、偏微分方程的基本概念偏微分方程是由未知函数的偏导数和自变量构成的方程。
常见的偏微分方程包括波动方程、传热方程和扩散方程等。
偏微分方程根据阶数可分为一阶和二阶偏微分方程。
一阶偏微分方程中只涉及到未知函数的一阶偏导数,一般可以通过变量分离的方法求解。
二阶偏微分方程中涉及到未知函数的二阶偏导数,求解方法一般包括分离变量法、特征线法和变换法等。
二、偏微分方程的求解方法1.分离变量法:假设未知函数可以表示为两个只依赖于单个自变量的函数的乘积形式,然后将该形式代入到偏微分方程中,再将方程两边关于不同的自变量求积分,从而得到方程的通解。
2.特征线法:通过特征线曲线的方法将偏微分方程转化为常微分方程。
先找出特征线曲线,然后在特征线上引入新的变量,使得偏微分方程变为常微分方程,进而求解。
3.变换法:通过适当的变量变换,将原偏微分方程转化为一个更容易求解的形式。
常用的变换方法有坐标变换、函数变换和变量替换等。
三、偏微分方程的应用领域1.物理学:偏微分方程在物理学中有着广泛的应用。
例如,波动方程可以描述声波、光波和电磁波等在介质中的传播;传热方程可以描述热传导过程;薛定谔方程和波恩-奥本海默方程可以描述量子力学中的粒子行为等。
2.工程学:偏微分方程在工程学中被广泛应用于流体力学、结构力学和电磁场等领域。
例如,纳维-斯托克斯方程用于描述流体的运动;弹性方程用于描述结构的变形和应力分布等。
3.经济学:偏微分方程在经济学中应用较多,尤其是在金融学中。
例如,布莱克-斯科尔斯方程用于定价期权;黑-舒尔斯方程用于描述衍生品的定价和风险管理等。
通过对偏微分方程的研究和求解,可以更好地理解自然界的现象和规律,并为解决实际问题提供数学模型和解决方法。
偏微分方程课程学习报告

u(x, t) 1 (x at ) (x at ) 21 2 a
1 ( t 4a 2t
x
x at
at
( ) d
u(x ,y ,z ,t )
s
at ( M )
ds )
1 4a 2t
s
at ( M
)
ut a 2u xx f(x ,t ), x ,t 0 0 0 0 u(x , ) (x ), x u(0,t ) (t ),t 0
椭圆方程的边值问题
3u 0,(x ,y ,z ) k u s ( p ), p s
ds
而对于波动方程的初边值问题主要用分 离变量法 u(x,t)=X(x)T(t)
热传导方程定解问题求解方法
• Cauchy问题主要用自相似变换法 Poisson公式
x2 1 2 e 4a t ,t 0 G(x ,t ) 2a t 0,t 0
通解热核函数
u(x ,t )
Cauchy问题
utt a 2 u xx u yy uzz 0, x ,y ,z ,t 0 u t 0 (x ,y ,z ),ut t 0 (x ,y ,z ), x ,y ,z
4
波动方程的Cauchy问题
初边值问题
u tt a 2u xx f ( x, t ), 0 x , t 0 u ( x, 0) ( x), ut ( x, 0) ( x), 0 x u (0, t ) (t ), u (l , t ) (t ), t 0 1 2
0
0
流体力学中的pde问题

流体力学中的PDE问题引言流体力学是研究流体运动规律的学科,广泛应用于各个领域,如天气预报、空气动力学、地下水流动等。
在流体力学中,偏微分方程(Partial Differential Equation,简称PDE)是描述流体运动的基本方程之一。
本文将介绍流体力学中的PDE问题,包括其定义、分类以及求解方法。
PDE问题的定义PDE是包含未知函数及其偏导数的方程,其中未知函数是多个自变量的函数。
在流体力学中,PDE用于描述流体的运动、能量传递和质量守恒等现象。
PDE问题的求解可以揭示流体运动的规律,进而为工程应用提供理论依据。
PDE问题的分类根据方程的类型和性质,PDE问题可以分为椭圆型、双曲型和抛物型三类。
椭圆型方程椭圆型方程的典型例子是泊松方程和拉普拉斯方程。
椭圆型方程主要用于描述稳态问题,如流体的静压力分布。
求解椭圆型方程可以通过有限差分法、有限元法等数值方法进行。
双曲型方程双曲型方程的典型例子是一维线性对流方程和二维波动方程。
双曲型方程主要用于描述流体的波动、振荡等动态过程。
求解双曲型方程可以通过特征线法、有限体积法等数值方法进行。
抛物型方程抛物型方程的典型例子是热传导方程和扩散方程。
抛物型方程主要用于描述流体的传热、扩散等过程。
求解抛物型方程可以通过差分法、变分法等数值方法进行。
PDE问题的求解方法对于一般的PDE问题,解析解往往难以获得,因此需要采用数值方法求解。
常用的数值方法包括有限差分法、有限元法、有限体积法等。
有限差分法有限差分法是一种基于离散化的数值方法,通过将连续的空间和时间域离散化成有限个网格点,将偏导数用差分近似表示。
有限差分法的求解过程包括网格生成、边界条件处理、差分方程离散化和迭代求解等步骤。
有限元法有限元法是一种基于变分原理的数值方法,通过将求解域分割成有限个单元,并在每个单元上构建适当的插值函数,将原始方程转化为一个代数问题。
有限元法的求解过程包括网格划分、单元刚度矩阵的计算、组装全局刚度矩阵和求解线性方程组等步骤。
pde偏微分方程

pde偏微分方程摘要:I.引言A.介绍PDE 偏微分方程B.说明PDE 在科学和工程领域的重要性II.PDE 的基本概念A.偏微分方程的定义B.典型的一阶和二阶偏微分方程C.偏微分方程的分类III.PDE 的解法A.分离变量法B.矩方法C.有限元法D.其他解法IV.PDE 的应用领域A.物理B.工程C.生物学D.金融V.结论A.总结PDE 偏微分方程的重要性B.展望PDE 在未来的发展正文:【引言】偏微分方程(Partial Differential Equation,简称PDE)是一种数学方程,用于描述物理、工程、生物学等领域的许多现象。
PDE 可以分为一阶和二阶,分别对应不同阶数的导数。
PDE 在科学和工程领域具有重要意义,例如在流体力学、传热、量子力学等领域都有广泛应用。
【PDE 的基本概念】偏微分方程是一种包含多个变量的方程,其中每个变量的导数可能有一个或多个。
典型的一阶偏微分方程包括一阶线性偏微分方程和一阶非线性偏微分方程,如波动方程和热传导方程。
二阶偏微分方程包括二阶线性偏微分方程和二阶非线性偏微分方程,如拉普拉斯方程和亥姆霍兹方程。
根据偏微分方程的特性,可以将其分类为不同的类型。
【PDE 的解法】有许多方法可以求解偏微分方程,其中一些常用的方法包括分离变量法、矩方法、有限元法等。
分离变量法适用于某些特殊类型的偏微分方程,例如波动方程和热传导方程。
矩方法是一种基于矩的积分方法,可以用于求解各种类型的偏微分方程。
有限元法是一种数值方法,可以将偏微分方程离散化为一个巨大的线性方程组,从而求解方程。
【PDE 的应用领域】偏微分方程在许多领域都有广泛应用。
在物理学中,PDE 用于描述电磁场、引力场、流体力学等现象。
在工程领域,PDE 用于解决结构分析、传热、流动控制等问题。
在生物学中,PDE 可以用于描述细胞生长、扩散和神经元信号传输等过程。
在金融领域,PDE 可以用于描述资产价格、利率和风险管理等现象。
pde偏微分方程

pde偏微分方程【最新版】目录1.PDE 简介2.PDE 与 ODE 的区别3.PDE 的分类4.PDE 的应用5.PDE 的求解方法正文1.PDE 简介偏微分方程(Partial Differential Equation,简称 PDE)是一种数学模型,用以描述多个变量之间关系的方程。
与普通微分方程(ODE)不同,PDE 涉及多个自变量,因此可以更准确地描述现实世界中复杂的数学问题。
2.PDE 与 ODE 的区别PDE 与 ODE 的主要区别在于涉及的自变量数量。
ODE 涉及一个自变量,而 PDE 涉及多个自变量。
这使得 PDE 能够描述更复杂的数学问题,如波动方程、热传导方程等。
3.PDE 的分类根据涉及的变量数量和方程形式,PDE 可以分为以下几类:- 一阶 PDE:涉及一个自变量的导数;- 二阶 PDE:涉及两个自变量的导数;- 高阶 PDE:涉及多个自变量的导数。
此外,根据方程中出现的偏导数类型,PDE 还可以分为线性 PDE 和非线性 PDE。
4.PDE 的应用PDE 在许多领域都有广泛应用,如物理学、工程学、生物学等。
著名的 PDE 问题包括波动方程(描述声波、光波传播)、热传导方程(描述物体温度分布)等。
解决这些问题对于理解和预测现实世界中的现象具有重要意义。
5.PDE 的求解方法求解 PDE 的方法有很多,如分离变量法、特征值法、有限差分法等。
根据 PDE 的性质和问题的具体情况,可以选择合适的方法进行求解。
对于某些复杂的 PDE 问题,可能需要多种方法相互结合,才能得到满意的解。
总之,PDE 是一种重要的数学模型,涉及多个自变量之间的关系。
它具有广泛的应用背景,如物理学、工程学等。
基于偏激分方程(PDE)的图像去噪的方法综述

基于偏激分方程(PDE)的图像去噪的方法综述摘要:偏微分方程(PDE)方法,是图像处理中的一种较新的方法,有着很强的数学基础,在图像处理中的应用发展非常快。
本文将近几年应用较多的几种图像去噪方法进行了系统的概括总结,指出了该领域的学者是如何一步步进行改进得到新方法的,并对该领域的发展做了新的展望。
关键词:图像去噪偏微分方程平滑滤波总变差1 引言图像去噪是数字图像处理中的一个经典问题。
随着数字图像处理技术的发展,大量数字图像经由信道传输或通过介质保存。
图像在传输或存储过程中受到外界物理条件的限制,所产生的噪声会影响图像的视觉效果。
而在众多的应用领域中,又需要清晰的、高质量的图像,因此,图像去噪是一类重要的图像处理问题,同时也是其它图像处理的重要预处理过程,对后继处理带来很大的影响。
基于偏微分方程(PDE)的方法进行图像处理因具有各向异性的特性,自适应性强,能够在平滑噪声的同时更好的保持边缘与纹理等细节性息,故在过去的二十几年中获得了巨大的发展。
这个领域的实质性的创始工作归功于和各自独立的研究。
他们严格地介绍了尺度空间理论并指出图像与具有递增方差的高斯函数做卷积实现低通滤波和求解以原图像为初值的热传导方程等价。
然而由于高斯滤波是各向同性扩散,在去除噪音的同时模糊了边界。
改进滤波技术,在去噪的同时能完好的保存边缘等重要信息,一直是这一领域的目标。
本文详细介绍了现存的基于PDE的图像去噪的主要方法,并指出了它们之间的联系。
2 图像去噪模型偏微分方程与图像去噪的结合产生了许多模型,大体上可以分为两大类:一种是基本的迭代格式,随着时间的变化更新,使得图像向所要得到的效果逐步逼近,这种算法的代表为的方程以及对其改进的后续工作。
该方法在前向扩散的同时具有向后扩散的功能,所以具有平滑图像和边缘锐化的能力,并且扩散系数有很大的选择空间。
但是该方法是病态问题,在应用中不稳定。
另一种是基于变分法的思想,确定图像的能量函数,通过求能量函数的最小值,使得图像达到平滑状态,现在得到广泛应用的总变差TV(Total Variation)模型[4]就是这一类。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
K=黏性或熱傳導 假設為常數
T T T 2 2 x y
2 2 2 2 2 T T 2 v T U 2 V 2 x y
有限差分近似及其符號表示
一個偏微分方程的有限差分近似由我們所 關心的區間上的網格所構成,採取矩形網 格結構,其間距為常量。
T v T k 2T t 2 2 T T T T T U V k 2 2 t x y y x 在空間交點ij處做離散 Tij 2 2 U 2 xTij V 2 yTij k x Tij y Tij t
偏微分方程的有限差分方法:介紹
謝謝大家~
偏微分方程(PDE)期末報告
-有限差分法簡單介紹
學生:李宗諺 B97520016 河工3A 指導教授:陳正宗 終身特聘教授
傳導-擴散方程
T 2 v T k T T T x , y , t t
v v x, y, t U x, y, t i V x, y, t j
Tijn 1 Tijn t
1 1 + 2 即可求解 2
運算元
Tijn T ix, jy, nt
一些常用的有限差分運算元:
1 2 xTij Ti 1 j Ti 1 j 中心差分 2x 1 xTij Tij Ti 1 j 向後差分 x 1 x Tij Ti 1 j Tij 向前差分 x 1 2 x Tij 2 Ti 1 j 2Tij Ti 1 j x
Tij t
U 2 xTij V 2 yTij k T T
2 x ij
2 y ij
由前向歐拉法可得 1 n 1 n Tij Tij 2 n n k x2Tijn y Tij U ij 2 xTijn Vijn 2 yTijn t 由後向歐拉法可得 2 Tijn1 Tijn 2 n 1 n 1 k x2Tijn1 y Tij U ij 2 xTijn1 Vijn1 2 yTijn1 t 再將求得的運算元代入
資料來源
•/zh-tw/CrankNicolson_%E6%96%B9%E6%B3%95
維基百科
Crank-Nicolson 方法
•/NR/rdonlyres/Aeronautics -and-Astronautics/16-901Computational-Methods-inAerospace-EngineeringSpring2003/60C5F02C-67F0490B-9651-1151A8077C12/0/Section3Article1.pdf
O x5
ij
可得 代入
T 2 xTij x
1 2 3T x 3 6 x ij
O x 4
ijFra bibliotekTijn 1 Tijn t
1 1 + 2 2
對這個演算法的一些注釋
2 2 O t , y , x •局部誤差為 •在無粘性限制時這個方法就不適用了,它 變得不再穩定。
這些運算元構成許多偏微分導數有限差分近似。
泰勒級數分析
1 2 xTij Ti 1 j Ti 1 j 2 x
Tij 泰勒級數展開式代入
T Tij x x
1 2 2T x 2 2 x ij
1 3 3T x 3 6 x ij
4 1 T 4 x 4 24 x ij
