最短路线(四年级)
最短路径问题练习题【优质】

最短路径问题Description:平面上有n个点(n<=100),每个点的坐标均在-10000到10000之间.其中的一些点之间有连线.若有连线,则表示可从一个点到达另一个点,即两点间有通路,通路的距离为两点间的直线距离.现在的任务是找出从一点到另一点之间的最短路径.Input:共n+m+3行第一行为整数n.第2行到第n+行,每行两个整数x和y,描述了一个点的坐标(以一个空格分开)第n+2行为一个整数m,表示图中连线的个数.以后的m行,每行描述一条连线,由两个整数i和j组成,表示第i个点和第j个点之间有连线.最后一行;两个整数s和t,分别表示源点和目标点.Output:仅一行,一个实数(保留两位小数),表示从s到t的最短路径长度Sample Input50 02 02 20 23 151 21 31 42 53 51 5Sample Output:3.41最小花费【问题描述】:在n个人中,某些人的银行账号之间可以互相转账。
这些人之间转账的手续费各不相同。
给定这些人之间转账时需要从转账金额里扣除百分之几的手续费,请问A 最少需要多少钱使得转账后B收到100元。
【输入数据】:第一行输入两个正整数n,m,分别表示总人数和可以互相转账的人的对数。
以下m行每行输入三个正整数x,y,z,表示标号为x的人和标号为y的人之间互相转账需要扣除z%的手续费 (z<100)。
最后一行输入两个正整数A,B。
数据保证A与B之间可以直接或间接地转账。
【输出数据】:输出A使得B到账100元最少需要的总费用。
精确到小数点后8位。
【输入样例】:3 31 2 12 3 21 3 31 3【输出样例】:103.07153164【数据规模】: 1<=n<=2000公园漫步(park.pas)【问题描述】小M 和小Z 饭后在公园散步,走着走着小Z 忽然想起来家中的水龙头没有关,于是他们要在最快的时间内走出公园赶到家中。
(精选)2021-2022学年人教版四年级上册数学竞赛培优专题-----统筹规划(附答案)

2021-2022学年人教版四年级上册数学竞赛培优专题-----统筹规划姓名:___________班级:___________考号:___________一、解答题1.小悦中午做烧豆腐,共需要七道工序,每道工序的时间如下:切豆腐2分钟,切肉片2分钟,准备葱姜蒜3分钟,准备佐料1分钟,烧热锅2分钟,烧热油2分钟,炒菜4分钟。
那么小悦烧好这道菜最短需要多少分钟?2.妈妈让小明给客人烧水沏茶。
洗开水壶要用1分钟,烧开水要用15分钟,洗茶壶要用1分钟,洗茶杯要用1分钟,拿茶叶要用2分钟。
小明估算了一下,完成这些工作要花20分钟。
为了使客人早点喝上茶,按你认为最合理的安排,多少分钟就能沏茶了?3.小杂货店里有一位售货员卖货,同时来了A、B、C、D、E五个顾客。
A买糖果需要2分钟;B买大米需要6分钟;C买香烟和啤酒需要4分钟;D买水果需要3分钟;E买蔬菜需要5分钟。
请问:售货员应该如何安排五个人的顺序,使得这五个人排队等候的时间总和最短?这个最短的时间是多少?(只计算每个人排队的时间,不计算买东西的时间。
)4.理发店里只有一位理发师,但同时来了五位顾客,理发师一次只能给一位顾客理发。
由于顾客要求的发型不同,理发师给这五位顾客理发分别需要10、12、16、20、25分钟。
怎样安排他们理发的顺序,才能使这五人排队等候所用时间的总和最少?最少是多少?5.如图是一张道路图,每段路旁标注的数值表示小悦走这段路所需的分钟数。
问:小悦从A出发走到B最快需要多少分钟?6.下图是某城市的道路图,每段路旁标注的数字表示走完这段路所需用的分钟数(单位:分钟)。
邮递员从A点沿道路到达B点至少要经过多长时间?7.如图,一条路上从西向东有A、B、C、D、E五所学校,分别有200人、300 人、400人、500人、600人。
任意相邻的两所学校之间的距离都是100米,现在要在某所学校的门口修建一个公共汽车站,要使所有人到达车站的距离之和最小,车站应该建在什么地方?距离的总和最少是多少?8.有八个村庄1A,2A,3A,4A,5A,6A,7A,8A分布在公路两侧,由一些小路与公路相连。
最短路线(四年级)

最短路线姓名邮递员叔叔每天都要送信,而且要穿过数以百计的大街小巷。
怎样设计一种科学的走法,使他完成送信任务后回到邮局所走的路最短?这个问题叫做最短邮递路线问题。
最短的邮递路线当然是从邮局出发,走遍每条街巷而且只走一次,最后回到邮局。
这样的路线由于没有重复,是最短的。
实际生活中是不是有这样的理想路线呢?当然没有。
那么,在什么情况下才能达到这样理想的路线呢?这还得从一种有名的数学游戏“一笔画”谈起。
如果在画图形时,笔不离纸而且每条线都不许重复,这种画法称为“一笔画”。
下面三个图形,请你试一试能不能将它们一笔画成?任何图形都是由点和线组成的,图形中的点可以分为两大类:(1)凡是从这点出发的线的数目是偶数的,称为偶点。
(2)凡是从这点出发的线的数目是奇数的,称为奇点。
一个图形能否一笔画成,关键在于图中奇点的个数的多少。
它的规律是:(1)凡是图形中没有奇点的,一定可以一笔画成。
画时,可以从任意一个偶点为起点,最后仍回到这点。
(2)凡是图形中只有两个奇点,一定可以一笔画成。
画时,必须以一个奇点为起点,另一个奇点为终点。
(3)当一个图形中奇点的个数多于两个时,此图形不能一笔画成。
例1、下图是国际奥委会的会徽,你能一笔把它画出来吗?及时练:1、下面图形可以一笔画成吗?如果可以,请你用一笔画成。
(1)(2)(3)(4)(5)例2、试判断下图中,哪一幅能一笔画?为什么??及时练:1、请将下列图形一笔画成,如果不行,请说明理由。
(1)(2)(3)(4)(5)(6)例3 下图是花园的平面图,你能走遍园中的小路,而路线不重复吗?及时练:1、下图是儿童游乐场的平面图。
要使游客能走遍每条路而不重复,在一张纸上出入口应设在哪里?甲例4、下图中线段代表小路,请你考虑一下,能够不重复地爬遍小路的是甲蚂蚁还是乙蚂蚁?该怎样爬?乙及时练:1、在一张纸上用剪刀能否一次连续剪下下图中三个正方形和两个三角形?如可以,请设计一种剪法。
例5、下图是某学校兴趣小组活动室分布图,共有ABCDEFGHIJKL十二个房间。
作新小学四年级数学上册第四单元线和角试题解析

作新小学四年级数学上册第四单元线和角试题解析姓名:_________班级:________ 得分:_________例1:如图所示已知∠1=32°,求∠2、∠3、∠4和∠5的度数。
解析:此题考察了运用推理法来解决稍复杂的求角度的问题。
根据题意通过观察可以先求出∠5的度数,∠1和∠5组成平角,和是180°,∠1=32°,所以∠5=180°—32°=148°;∠4与∠5的和也是180°,所以∠4=∠1=32°;∠1和∠2组成一个直角∠1=32°那么∠2=90°-32°=58°;∠3和∠4的和是90°,∠4是32°,那么∠3=90°-32°=58°。
答案:∠2=58°∠3=58°∠4=32°∠5=148°例2:数几条相交直线交点的个数。
3条直线相交,最多有多少个交点?4条直线相交,最多有多少个交点?你能自己寻找规律,发现10条直线相交最多有多少个交点吗?从图中可以看出,3条直线相交有3个交点,可以表示成1+2=3(条);4条直线相交有有6个交点,交点的个数可以表示为1+2+3=6(条);5条直线相交有10个交点,可以表示为1+2+3+4=10(个);10条直线有45个交点,可以表示为1+2+3+4+5+6+7+8+9=45(个);……n条直线相交,交点的个数可以表示成1+2+3+4+…+(n-1)=n×(n-1)÷2答案:3条直线相交有3个交点,4条直线相交有有6个交点,5条直线相交有10个交点,10条直线有45个交点。
例3:小猫要去小兔子家做客,请问走哪条路最近,为什么?解析:此题考查了两点间,线段最短这个知识点。
根据图意找出小猫家和小兔家之间的线段即可。
答案:通过观察图可知:路线①是一条线段,所以路线①是最近的一条路,因为两点之间,线段最短。
四年级组合计数

四年级名校第二讲组合计数——最短路线教学目标:1.让学生了解如何用标数法来解题。
2.让学生学会如何走最短路线。
3.让学生在学习中,学会数学的逻辑思维能力。
教学重点:如何用标数法解题。
教学难点:标数时我们应用什么样的方法去标数。
教学过程:导入:我们平时在出去玩的时候是不是有很多不同的路线可以选择,但是我们往往会选择一条最短的线路来走,但是事实上我们有的时候最短的路不止有一条。
这样就涉及到了我们数学当中一个非常有名的专题就是组合计数。
(出示课题)新授:例1下图是一个街道平面图,某人从A里走到B处(只能从南到北及从西到东)共有多少种不同的走法?分析:首先我们要看清楚题目,题目当中说的是只能从南到北及从西到东,那么我们只能怎么走呢?我们只能从下往上或者从左往右走。
我们可以这样想,从A点出发可以去2个地方,如果是这样我们是不是可以反过来想呢?到达那2个点只能从哪里来则我们可以这样标数。
那么从哪里来有几条路?(强调学生要注意标数的时候一定要一排一排的标,这样才能做到不重复不遗漏。
)那么我就可以这样标数,如图。
练习:演练一例2苏珊从A步行道Z,行走方向都是向东或向南,路线如图所示。
那么苏珊从A到Z有多少条不同的行走路线?分析:我们从A出发要到Z,可以随便走么?方向只能是向东或者向南,那么我们就可以用标数的方法将其标出来,这样就可以做出来了。
注意一定要一排一排的标,不能乱标。
要引导学生一个一个来。
练习:演练二例3 一直密封从A处出发,A回到家里B处,每次只能从一个蜂房爬向右侧邻近的蜂房而不准逆行,共有多少种回家的方法?分析:如果我们从蜂房的A出发回到B处,同学们可不可以将我们小蜜蜂的回家的路线试着画出来呢?将小蜜蜂的路线图画出来之后我们就可以用标数法将其做出来了。
例4如图所示科学家“爱因斯坦”的英文名拼写为“Einstein”,按见图所示方向有多少种不同的方法拼出英文单词“Einstein”?分析:我们在拼出英文单词的时候是不是可以随便拼写呢?我们一定要按照这个引文单词拼写的顺序来标数。
人教版四年级数学垂直的线段最短教案

课题:4.1平行与垂直课时:第3课时课型:新授课教学目标:1.通过探究掌握“垂直的线段最短”和“点到直线的距离”2.会根据“垂直的线段最短”解决最短路线问题3.了解“设疑-猜想-验证-归纳-应用”的数学学习过程4.继续培养学生的合作、互助习惯教学重点:通过探究掌握“垂直的线段最短”和“点到直线的距离”教学难点:会根据“垂直的线段最短”解决最短路线问题教学流程:一、复习旧知,做好铺垫二、创设情境,导入新课三、互助探究,获取新知四、课堂练习,巩固新知五、回顾反思,提升认识六、过关检测,了解效果活动1.复习旧知,做好铺垫1、复习过一点画这条直线的垂线的四个步骤,为后面的画垂直线段做好准备教师幻灯片演示,学生说出步骤2、过点A 画直线m的垂线要求:学师看着学友画在学案上,学友不会时,学师指导画完后,师生共同纠正活动2创设情境,导入新课1、在刚画出图形的基础上,创设小马喝水的情景,引起学生兴趣2、在小马喝水的情境中提出问题:哪条路线是最短的?学生可能立马会给出答案:线段AD最短。
3、学生补充小马过河图,为下面的探究做好准备。
活动3师友互助,探究新知1、在上个环节提出问题,学生做出猜想的基础上,老师给出理性的认知:根据实际,提出问题----观察图形,大胆猜想,同时教师板书。
2、提问学生,为什么说线段AD是最短的?然后告诉学生,仅凭眼睛观察,看出来的结论可能是不准确的,你能想办法验证你的猜想是准确的吗?请学生给出验证的方法。
3、师友合作,测量、验证,要求:师傅测量,学友记录,准备汇报。
测量完成后,请三组师友利用投影仪展示汇报。
教师板书。
4、教师出示不同的小马喝水图,引导寻找共同特点:垂直。
归纳结论,给出点到直线的距离的定义。
5、结合图形、内化知识。
师友互助,复述知识。
6、回顾解决小马喝水问题,强调,理由是“垂直的线段最短”而不是“看出来”的。
活动4课堂练习,巩固新知练习一,抢答主要针对基础的知识点的填空题练习二,画图、测量题,针对点到直线的距离的概念和垂线段的画法。
四年级下册数学讲义-奥数讲练: 最短路线问题
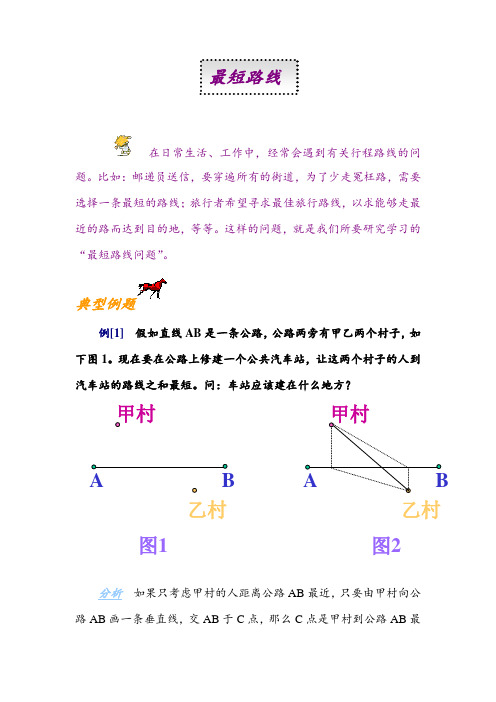
在日常生活、工作中,经常会遇到有关行程路线的问题。
比如:邮递员送信,要穿遍所有的街道,为了少走冤枉路,需要选择一条最短的路线;旅行者希望寻求最佳旅行路线,以求能够走最近的路而达到目的地,等等。
这样的问题,就是我们所要研究学习的“最短路线问题”。
典型例题例[1] 假如直线AB 是一条公路,公路两旁有甲乙两个村子,如下图1。
现在要在公路上修建一个公共汽车站,让这两个村子的人到汽车站的路线之和最短。
问:车站应该建在什么地方?分析 如果只考虑甲村的人距离公路AB 最近,只要由甲村向公路AB 画一条垂直线,交AB 于C 点,那么C 点是甲村到公路AB 最甲村 乙村AB 甲村乙村 图1图2最短路线近的点,但是乙村到C点就较远了。
反过来,由乙村向公路AB画垂线,交AB于D点,那么D点是乙村到公路AB最近的点。
但是这时甲村到公路AB的D点又远了。
因为本题要求我们在公路AB上取的建站点,能够兼顾甲村和乙村的人到这个车站来不走冤枉路(既路程之和最短),根据我们的经验:两个地点之间走直线最近,所以,只要在甲村乙村间连一条直线,这条直线与公路AB交点P,就是所求的公共汽车站的建站点了(图2)。
解用直线把甲村、乙村连起来。
因为甲村乙村在公路的两侧,所以这条连线必与公路AB有一个交点,设这个交点为P,那么在P 点建立汽车站,就能使甲村乙村的人到汽车站所走的路程之和最短。
例[2] 一个邮递员投送信件的街道如图3所示,图上数字表示各段街道的千米数。
他从邮局出发,要走遍各街道,最后回到邮局。
问:走什么样的路线最合理?全程要走多少千米?3分析选择最短的路线最合理。
那么,什么路线最短呢?一笔画路线应该是最短的。
邮递员从邮局出发,还要回到邮局,按一笔画问题,就是从偶点出发,回到偶点。
因此,要能一笔把路线画出来,必须途径的各点全是偶点。
但是图中有8个奇点,显然邮递员要走遍所有街道而又不走重复的路是不可能的。
要使邮递员从邮局出发,仍回到邮局,必须使8个奇点都变成偶点,就是要考虑应在哪些街道上重复走,也就是相当于在图上添哪些线段,能使奇点变成偶点。
最短线路问题

最短线路问题古希腊亚里山大里亚城有一位久负盛名的学者,名叫海伦.有一天,有位将军不远千里专程前来向海伦求教一个百思不得其解的问题:如图28-1,从甲地出发到河边饮马,然后再到乙地军营视察,显然有许多走法.问走什么样的路线最短呢?精通数理的海伦稍加思索,便作了完善的回答.这个问题后来被人们称作“将军饮马”问题.事实上,不仅是将军有这样的烦恼,运动着的车、船、飞机,包括人们每天走路都要遇到这样的问题.古今中外的任何旅行者总希望寻求最佳的旅行路线,尽量走近道,少走冤枉路.我们把这类求近道的问题统称最短线路问题.啊!原来这就是最短线路问题,我们已经在小学教科书上几次接触过.比如,三年级(第六册)书上说:“从学校到电影院有三条路(图28-2),小云要看电影走哪条路最近?”;又如,四年级(第八册)书上说:“通过度量可以知道‘从直线外一点到这条直线所画的各线段中,以和这条直线垂直的线段为最短’.”另外,从某种意义上说,上节的一笔画问题也属这类问题.看来最短线路问题在生产、科研和日常生活中确实重要且应用广泛.但是.怎样走才是近道呢?这可不是件容易的事.它慢慢地引起了数学家的兴趣,并用数学这个强有力的工具解决了它.下面来看看数学家是怎样解决的.问题28.1 假如直线AB是一条公路,在路两侧有甲、乙两个村子(如图28-3),现在要在公路上修一个公共汽车站,让这两村的人到车站的路线之和最短.问车站应修建在什么地方?分析如果只考虑甲村人距公路最近,由教材上的结论,只要由甲村向AB画一条垂线,交AB于C,那么C离甲村最近,但离乙村又远了.同样只考虑乙村近的线路乙—D—甲也不是最近的.怎样才能使甲、乙两村整体考虑时最近(即距离之和最短)呢?根据我们的经验:两个地点之间走直线最近.所以,在甲、乙之间连一条直线与AB相交于P点,则在P点建站就合要求了.注意:以上我们是凭经验作出的解答.但是数学家解决问题,总是要用一些公认的结论去对问题进行严格的证明才算正确,并把公认的结论称作公理.下面我们把解决最短线路问题时常用的公理列在下面.公理1 连接两点的所有线中,直线段最短.公理2 三角形的两边之和大于第三边.公理3 直线外一点到直线的所有线中垂线段最短.公理是从实践中总结出来的任何人都承认的原始道理.当然,有同学会想:“你那个公理我不承认行不行呢?”那可不行,比如图28-4(1)中,有一只鸡子在B点觅食,你在A点处放一些米,那么鸡子一定会沿直线AB跑过来吃食,决没有一只蠢鸡子沿B→C→A或沿B→D→A的路线跑过来.这表明:公理不但人类公认,连动物界也都遵循它.下面我们就用上述公理来解决一些最短线路问题.问题28.2 如图28-5,点A、B位于直线l的同侧,在l上找一点P,使得AP+PB最小.分析这就是“将军饮马”问题,我们看看海伦是怎么解决的.海伦发现这是一个求折线和最短的问题.从上面的公理1只知道两点间直线段最短.那么,显然要把折线变成直线再解.如果直接连AB,与l不会相交.怎么办呢?由问题28.1得到启发:当A、B位于l的异侧时,就有交点了.于是我们就希望在l的另一侧找一点A′,使得连A′B与l相交于P点后(这时A′P+PB最短)线段A′P与AP一样长.由对称的知识可知道,A关于l的对称点就有资格扮演A′的角色.解如图28-5,先作A关于l的对称点A′,连接A′B与l相交于P点,则AP+PB就最小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最短路线
姓名
邮递员叔叔每天都要送信,而且要穿过数以百计的大街小巷。
怎样设计一种科学的走法,使他完成送信任务后回到邮局所走的路最短?这个问题叫做最短邮递路线问题。
最短的邮递路线当然是从邮局出发,走遍每条街巷而且只走一次,最后回到邮局。
这样的路线由于没有重复,是最短的。
实际生活中是不是有这样的理想路线呢?当然没有。
那么,在什么情况下才能达到这样理想的路线呢?这还得从一种有名的数学游戏“一笔画”谈起。
如果在画图形时,笔不离纸而且每条线都不许重复,这种画法称为“一笔画”。
下面三个图形,请你试一试能不能将它们一笔画成?
任何图形都是由点和线组成的,图形中的点可以分为两大类:
(1)凡是从这点出发的线的数目是偶数的,称为偶点。
(2)凡是从这点出发的线的数目是奇数的,称为奇点。
一个图形能否一笔画成,关键在于图中奇点的个数的多少。
它的规律是:
(1)凡是图形中没有奇点的,一定可以一笔画成。
画时,可以从任意一个偶点为起点,最后仍回到这点。
(2)凡是图形中只有两个奇点,一定可以一笔画成。
画时,必须以一个奇点为起点,另一个奇点为终点。
(3)当一个图形中奇点的个数多于两个时,此图形不能一笔画成。
例1、下图是国际奥委会的会徽,你能一笔把它画出来吗?
及时练:
1
(1(2)(3)
(4)(5)
例2、试判断下图中,哪一幅能一笔画?为什么??
及时练:
1、请将下列图形一笔画成,如果不行,请说明理由。
(
1)
(2)
(3)
(4) (5) (6)
例3 下图是花园的平面图,你能走遍园中的小路,而路线不重复吗?
及时练:
1、下图是儿童游乐场的平面图。
要使游客能走遍每条路而不重复,在一张纸上出入口应设在哪里?
例4、下图中线段代表小路,请你考虑一下,能够不重复地爬遍小路的是甲蚂蚁还是乙蚂蚁?
该怎样爬?
及时练:
1、在一张纸上用剪刀能否一次连续剪下下图中三个正方形和两个三角形?如可以,请设计一种剪法。
例5、下图是某学校兴趣小组活动室分布图,共有ABCDEFGHIJKL十二个房间。
进出口都在A室,请你帮助设计一条路从进口进入A室,通过每一道门一次再回到A室而不重复。
及时练:
1、下图是一个展览厅的平面图,每个展览室的门如图。
你能够从室外不重复地走过每一道门进去参观,然后再离开吗?如果不能,适当关上哪两个展览室之间的门,就可以达到目的?
例6这是一个著名的数学问题——欧拉问题。
欧洲有一个哥尼斯城堡,有一条河穿过这个城市,河中有A、B两个岛,河上有七座桥连接这两个岛及河的两岸C、D,能不能从某一个地方出发走遍这七座桥,而且每座桥只准走一次?
及时练:
1、下图中有A、B、C、D、E、F六个小岛,各岛之间共有十五座桥。
现在要从A岛出发,不重复地走遍十五座桥,该怎样走?。
