2017年全国数学竞赛非数学类
2017年全国数学竞赛非数学类
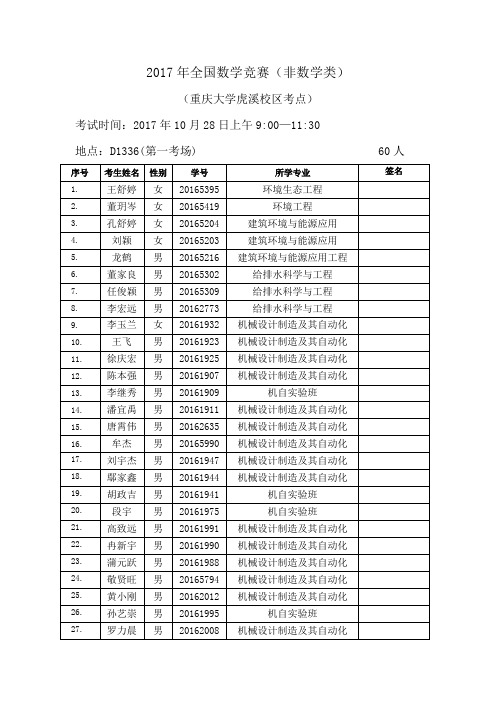
2017年全国数学竞赛(非数学类)(重庆大学虎溪校区考点)考试时间:2017年10月28日上午9:00—11:30地点:D1336(第一考场) 60人2017年全国数学竞赛(非数学类)(重庆大学虎溪校区考点)考试时间:2017年10月28日上午9:00—11:30地点:D1338(第二考场) 60人2017年全国数学竞赛(非数学类)(重庆大学虎溪校区考点)考试时间:2017年10月28日上午9:00—11:30地点:D1342(第三考场) 50人2017年全国数学竞赛(非数学类)(重庆大学虎溪校区考点)考试时间:2017年10月28日上午9:00—11:30地点:D1343(第四考场) 50人2017年全国数学竞赛(非数学类)(重庆大学虎溪校区考点)考试时间:2017年10月28日上午9:00—11:30地点:D1344(第五考场) 50人2017年全国数学竞赛(非数学类)(重庆大学虎溪校区考点)考试时间:2017年10月28日上午9:00—11:30地点:D1345(第六考场) 50人2017年全国数学竞赛(非数学类)(重庆大学虎溪校区考点)考试时间:2017年10月28日上午9:00—11:30地点:D1346(第七考场) 50人2017年全国数学竞赛(非数学类)(重庆大学虎溪校区考点)考试时间:2017年10月28日上午9:00—11:30地点:D1347(第八考场) 50人2017年全国数学竞赛(非数学类)(重庆大学虎溪校区考点)考试时间:2017年10月28日上午9:00—11:30地点:D1348(第九考场) 50人2017年全国数学竞赛(非数学类)(重庆大学虎溪校区考点)考试时间:2017年10月28日上午9:00—11:30地点:D1349(第十考场) 50人2017年全国数学竞赛(非数学类)(重庆大学虎溪校区考点)考试时间:2017年10月28日上午9:00—11:30地点:D1350(第十一考场) 50人2017年全国数学竞赛(非数学类)(重庆大学虎溪校区考点)考试时间:2017年10月28日上午9:00—11:30地点:D1351(第十二考场) 50人2017年全国数学竞赛(非数学类)(重庆大学虎溪校区考点)考试时间:2017年10月28日上午9:00—11:30地点:D1337(第十三考场) 99人。
2017年数学竞赛预赛(非数学类)试题评分标准及参考答案 .doc

2017年数学竞赛预赛(非数学类)试题评分标准及参考答案一 1. 已知可导函数满足, 则()f x解: 在方程两边求导得'()c o s +()s i n f x x f x x =,'()+()tan sec f x f x x x =.从而tan tan ()sec xdx xdx f x e xe dx c -⎛⎫⎰⎰=+ ⎪⎝⎭⎰l n c o sl n c o s211==cos cos cos x x ee dx c x dx c x x --⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭⎰⎰ ()=c o s t a n =s i n c o sx x c x cx ++ 由于(0)1f =,故()sin cos f x x x =+。
2.求()n n n +∞→22sin lim π解 由于 ()=+n n 22sin π()ππn n n -+22sin=2sin 1⎛⎫→。
3. 设(,)w f u v =具有二阶连续偏导数,且==+u x cy v x cy -,,其中c 为非零常数。
则21xx yy w w c-=_________。
解: 12+x w f f =,1112222xx w f f f =++,21()y w c f f =-,()()()22111122122111222=2yy w cf f c cf cf cf cf c f f f y∂=-=--+-+∂。
所以1221=4xx yy w w f c-。
4. 设()f x 有二阶导数连续,且(0)'(0)0,"(0)6f f f ===,则24(s i n )l i m x f xx →=______解:21()(0)'(0)"()2f x f f x f x ξ=++,所以241(sin )"()sin 2f x f x ξ=。
这样244400(sin )"()sin lim=lim 32x x f x f xx x ξ→→=。
中国大学生数学竞赛(非数学专业类)竞赛内容

5. 无穷小和无穷大的概念及其关系、无穷小的性质及无穷小的比较.
6. 极限的四则运算、极限存在的单调有界准则和夹逼准则、两个重要极限.
7. 函数的连续性(含左连续与右连续)、函数间断点的类型.
8. 连续函数的性质和初等函数的连续性.
1. 常微分方程的基本概念:微分方程及其解、阶、通解、初始条件和特解等.
5. 4.高阶导数的概念、分段函数的二阶导数、某些简单函数的n阶导数.
6. 5.微分中值定理,包括罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理.
7. 6. 洛必达(L’Hospital)法则与求未定式极限.
8. 7. 函数的极值、函数单调性、函数图形的凹凸性、拐点及渐近线(水平、铅直和斜渐近线)、函数图形的描绘.
9. 8. 函数最大值和最小值及其简单应用.
10. 9. 弧微分、曲率、曲率半径.
11. 一元函数积分学
12. 1. 原函数和不定积分的概念.
13. 2. 不定积分的基本性ห้องสมุดไป่ตู้、基本积分公式.
14. 3. 定积分的概念和基本性质、定积分中值定理、变上限定积分确定的函数及其导数、牛顿-莱布尼茨(Newton-Leibniz)公式.
中国大学生数学竞赛(非数学专业类)竞赛内容为大学本科理工科专业高等数学课程的教学内容,具体内容如下:
1. 函数、极限、连续
1. 函数的概念及表示法、简单应用问题的函数关系的建立.
2. 函数的性质:有界性、单调性、周期性和奇偶性.
3. 复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数.
15. 4. 不定积分和定积分的换元积分法与分部积分法.
第八届全国大学生数学竞赛决赛试题参考答案(非数学类,

(3)
∫∫∫( ) ∫ ∫ ∫ I = 1
1− (x2 + y2 + z2)
x2 + y2 + z2 dv = 1
2π dθ
π sin ϕ
1
(1 −
ρ 2 )ρ 3dρ
=
π
.
2Ω
20
0
0
6
3
五、设 n 阶方阵 A, B 满足 AB = A+B ,证明:若存在正整数 k ,使 Ak = O ( O 为零矩阵),则 行列式 B + 2017 A = B .
1 k
−
ln
n
.
(1)证明:极限
lim
n→∞
an
存在;
∞
∑ (2)记
lim
n→∞
an
=
C
,讨论级数
n =1
(an
−C)
的敛散性.
解 (1)利用不等式:当 x > 0 时, x < ln(1+ x) < x ,有 1+ x
1
an
−
an−1
=
1 n
−
ln
n n −1
=
1 n
−
ln
⎛⎜⎝1 +
1⎞ n −1⎟⎠
第八届全国大学生数学竞赛决赛试题参考答案
(非数学类, 2017 年)
一、填空题
1.过单叶双曲面
x2 4
+
y2 2
− 2z2
= 1 与球面
x2
+
y2
+
z2
=
4
的交线且与直线
⎧x = 0 ⎨⎩3y + z
第九届全国大学生数学竞赛非数类参考答案(白兔兔)

学校
由 α 的任意性得
"
fx p0, 0q “ 0 fy p0, 0q “ 0
, 从而 p0, 0q 是 f px, yq 的驻点.
˘ d2 gα pt q d` fx cos α ` fy sin α “ 2 dt dt ` ˘ ˘ ` “ fxx cos α ` fxy sin α cos α ` fyx cos α ` fyy sin α sin α 省市 “ fxx cos2 α ` 2 fxy sin α cos α ` fyy sin2 α “ ‰ “ sin α cos α fxx cot2 α ` 2 fxy ` fyy tan2 α
所以 f p0, 0q 是 f px, yq 极小值. 三、 (本题满分 14 分) 设曲线 Γ 为曲线 x ě 0, y ě 0, z ě 0 ∫ 上从点 Ap1, 0, 0q 到点 Bp0, 0, 1q 的一段. 求曲线积分 I “ y dx ` z dy ` x dz
Γ
x2 ` y2 ` z2 “ 1 ,
Γ1 Σ
第 4 页, 共 6 页
曲线 Γ 在 xOy 面上投影的方程为
` ˘2 x´ 1 y2 2 ` 1 ˘2 ` ` 1 ˘2 “ 1 座位号
2 ? 2
又该投影(半个椭圆)的面积得知 1 π 这样就有 I “ ´ ? 2 2 2
Σ
π dx dy “ ? . 同理, 4 2
Σ
π dy dz “ ? 4 2
密封线 答题时不要超过此线 姓名
一、 (本题满分 42 分, 共 6 小题, 每小题 7 分) ∫ x 1. 已知可导函数 f pxq cos x ` 2 f pt q sin t dt “ x ` 1 满足 则 f pxq “
附录:中国大学生数学竞赛(非数学专业类)竞赛内容

附录:中国大学生数学竞赛(非数学专业类)竞赛内容一、函数、极限、连续1.函数的概念及表示法、简单应用问题的函数关系的建立。
2.函数的性质:有界性、单调性、周期性和奇偶性。
3.复合函数、反函数、分段函数和隐函数、基本初等函数的性质及其图形、初等函数。
4.数列极限与函数极限的定义及其性质、函数的左极限与右极限。
5.无穷小和无穷大的概念及其关系、无穷小的性质及无穷小的比较。
6.极限的四则运算、极限存在的单调有界准则和夹逼准则、两个重要极限。
7.函数的连续性(含左连续与右连续)、函数间断点的类型。
8.连续函数的性质和初等函数的连续性。
9.闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理)。
二、一元函数微分学1. 导数和微分的概念、导数的几何意义和物理意义、函数的可导性与连续性之间的关系、平面曲线的切线和法线。
2. 基本初等函数的导数、导数和微分的四则运算、一阶微分形式的不变性。
3. 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法。
4. 高阶导数的概念、分段函数的二阶导数、某些简单函数的n阶导数。
5. 微分中值定理,包括罗尔定理、拉格朗日中值定理、柯西中值定理和泰勒定理。
6. 洛必达(L’Hospital)法则与求未定式极限。
7. 函数的极值、函数单调性、函数图形的凹凸性、拐点及渐近线(水平、铅直和斜渐近线)、函数图形的描绘。
8. 函数最大值和最小值及其简单应用。
9. 弧微分、曲率、曲率半径。
三、一元函数积分学1. 原函数和不定积分的概念。
2. 不定积分的基本性质、基本积分公式。
3. 定积分的概念和基本性质、定积分中值定理、变上限定积分确定的函数及其导数、牛顿-莱布尼茨(Newton-Leibniz)公式。
4. 不定积分和定积分的换元积分法与分部积分法。
5. 有理函数、三角函数的有理式和简单无理函数的积分。
6. 广义积分。
7. 定积分的应用:平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力及函数的平均值。
第十一届全国大学生数学竞赛(非数学类)试题

第十一届全国大学生数学竞赛(非数学类)试题参考解答及评分标准一、填空题(每小题6分)1. sin 014x x →=.解:sin sin 00x x x x x →→→=- sin 1/31/30022(e 1)1sin 1limlim 444422x x x x x x →→-=+-=⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭. 2. 设隐函数()y y x =由方程22()y x y x -=所确定,则232ln ||dx y y C y x x=-+⎰. 解:令y tx =,则21(1)x t t =-,1(1)y t t =-,3223(1)tdx dt t t -+=-, 这样,223332ln ||2ln ||dx t y ydt t t C C y t x x-+==-+=-+⎰⎰. 3. 定积分220(1sin )1cos x e x dx e xππ+=+⎰.解:222000(1sin )sin 1cos 1cos 1cos x xx e x e xdx dx de xx x πππ+=++++⎰⎰⎰ 2222200sin cos (1cos )+sin 1cos 1cos (1cos )xxxe xe x x x dx e dx x x x πππ+=+-+++⎰⎰2222000sin 1cos 1cos 1cos xxx e xe edx dx e x x x ππππ=+-=+++⎰⎰. 4. 已知22(,)323ydx xdy du x y x xy y -=-+,则1(,)()C 3x u x y y =-+. 解:22(,)323ydx xdy du x y x xy y -=-+21()233()3xd x yx x y y y ==--+().所以,1(,)()C 3x u x y y =-+.5. 设,,,0a b c μ>,曲面xyz μ=与曲面2222221x y z a b c ++=相切,则μ=.解:根据题意有:22x yz a λ=,22y xz b λ=,22zxy c λ=,以及 222x a μλ=,222y b μλ=,222z c μλ=,从而得:32228a b cλμ=,32μλ=,联立解得:μ=二、(14分)计算三重积分22d d d Ω+⎰⎰⎰xyzx y z x y,其中Ω是由曲面2222()2++=x y z xy 围成的区域在第一卦限部分.解:采用“球面坐标”计算,并利用对称性,得ππ3224222sin cos sin cos 2d d sin d sin I ρϕθθϕθϕρϕρρϕ=⎰⎰ -------5分ππ342002sin cos d sin cos d d θθθϕϕϕρρ=⎰⎰ππ3354202sin cos d sin cos d θθθϕϕϕ=⎰⎰ -------10分ππ354201sin 2d sin d(sin )4θθϕϕ=⎰⎰π3201121sin d 4848372t t ==⋅=⎰. -------14分 三、(14分)设()f x 在[0,)+∞上可微,(0)0f =,且存在常数0A >,使得|()||()|f x A f x '≤在[0,)+∞上成立,试证明:在(0,)+∞上有()0f x ≡.证明:设01[0,]2x A ∈,使得01|()|max |()|[0,]2f x f x x A ⎧⎫=∈⎨⎬⎩⎭, -------5分 000011|()||(0)+()||()||()|22f x f f x A f x f x A ξ'=≤=,只有0|()|0f x =. 故当 1[0,]2x A∈时,()0f x ≡. -------12分 递推可得,对所有的1[,]22k kx A A-∈,1,2,k =,均有()0f x ≡. -------14分四、(14分)计算积分2sin (cos sin )0sin I d e d ππθφφφθθ-=⎰⎰解:设球面 Σ:x 2+y 2+z 2=1, 由球面参数方程sin cos x θφ=,sin sin y θφ=,cos z θ=知sin dS d d θθφ=,所以,所求积分可化为第一型曲面积分I =∬e x−ydS Σ-------4分 设平面P t :√2=t,−1≤t ≤1,其中t 为平面P t 被球面截下部分中心到原点距离.用平面P t 分割球面Σ,球面在平面P t ,P t+dt 之间的部分形如圆台外表面状,记为Σt,dt .被积函数在其上为 e x−y =e √2t . -------8分由于Σt,dt 半径为r t =√1−t 2,半径的增长率为 d√1−t 2=√1−t 2 就是 Σt,dt 上下底半径之差. 记圆台外表面斜高为ℎt ,则由微元法知 dt 2+(d √1−t 2)2=ℎt 2, 得到ℎt =√1−t 2 ,所以 Σt,dt 的面积为 dS =2πr t ℎt =2πdt, -------12分I =∫e √2t 1−12πdt =√2√2t |−11=√2π(e √2−e −√2). -------14分 五、(14分)设()f x 是仅有正实根的多项式函数,满足 0()()n n n f x c x f x +∞='=-∑. 试证:0n c >,(0n ≥),极限lim n ()f x 的最小根. 证明:由f (x )为仅有正实根的多项式,不妨设()f x 的全部根为 0<a 1<a 2<⋯<a k ,这样,f (x )=A (x −a 1)r 1⋯(x −a k )r k ,其中 r i 为对应根a i 的重数 (i =1,⋯,k,r k ≥1). -------2分f ′(x )=Ar 1(x −a 1)r 1−1⋯(x −a k )r k +⋯+Ar k (x −a 1)r 1⋯(x −a k )r k −1,所以,f ′(x )=f (x )(r 1x−a 1+⋯+rkx−a k),从而, −f ′(x)f(x)=r 1a 1∙11−xa 1+⋯+r k a k∙11−x a k.-------6分若|x |<a 1, 则 −f ′(x)f(x)=r 1a 1∙∑(xa1)n∞n=0+⋯+r k a k∙∑(xak)n∞n=0=∑(r 1a 1n+1+⋯+r k a kn+1)∞n=0x n .而 −f ′(x)f(x)=∑c n x n∞n=0,由幂级数的唯一性知c n =r 1a 1n+1+⋯+r kak n+1>0, ------9分c ncn+1=r 1a 1n+1+⋯+r k a kn+1r 1a 1n+2+⋯+r k a kn+2=a 1∙r 1+⋯+(a1a k)n+1r kr 1+⋯+(a 1a k)n+2r k.limn→∞c nc =a 1∙r 1+0+⋯+0r +0+⋯+0=a 1>0, limn→∞c n+1c =1a , -----12分limn→∞1n ∙(ln c2c1+⋯+ln c n+1c n)=ln 1a 1,√c n n=elnc nn=elnc 1n +1n (ln c 2c 1+⋯+ln cn+1c n)→eln1a 1=1a 1.从而,lim√c nn=a 1,即f (x )的最小正根. -----14分六、(14分)设函数()f x 在[0, )+∞上具有连续导数,满足22223[3()]()2[1()]-'+=+x f x f x f x e ,且(0)1≤f .证明:存在常数0>M ,使得[0,)∈+∞x 时,恒有()≤f x M .证明:由于()0'>f x ,所以()f x 是[0, )+∞上的严格增函数,故+lim ()→∞=x f x L (有限或为+∞). 下面证明 ≠+∞L . -----2分记()=y f x ,将所给等式分离变量并积分得 222232d d (1)3-+=+⎰⎰x y y e x y ,即 2222arctan d 13-+=++⎰x t y y e t C y , ------6分 其中2(0)2arctan (0)1(0)=++f C f f . ------8分若=+∞L ,则对上式取极限→+∞x ,并利用2d 2+∞-=⎰t e t ,得π3=-C .-----10分 另一方面,令2()2arctan 1=++ug u u u ,则2223()>0(1)+'=+u g u u ,所以函数()g u 在(, )-∞+∞上严格单调增加. 因此,当(0)1≤f 时,1π((0))(1)2+=≤=C g f g , 但2π1π22+>>C ,矛盾, 这就证明了+lim ()→∞=x f x L 为有限数.最后,取max{(0),}=M f L ,则|()|≤f x M ,[0,)∀∈+∞x . -----14分。
第十届全国大学生数学竞赛决赛(非数学类)获奖名单
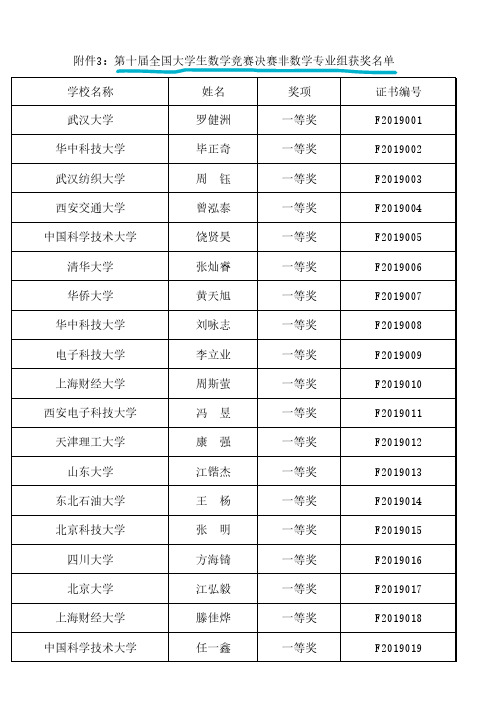
太原理工大学 北京大学 清华大学
华南理工大学 哈尔滨工业大学
丽水学院 燕山大学 电子科技大学 北京航空航天大学 厦门大学 合肥工业大学宣城校区 同济大学 华东理工大学 合肥工业大学 西安交通大学 湖北工业大学 华中科技大学 中国民航大学 陆军工程大学国防工程学院 陆军勤务学院 山东大学
王金宇 高铭齐 倪赞林 吴珍谦 李雨杭 苏文 张再哲 李诚佳 乐洋 何鸿光 陈家鑫 刘聪颖 詹研 朱基宏 潘翔宇 刘子文 阚腾 吴昊 曹晨 廖雪文 王一宁
二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖 二等奖
F2019083 F2019084 F2019085 F2019086 F2019087 F2019088 F2019089 F2019090 F2019091 F2019092 F2019093 F2019094 F2019095 F2019096 F2019097 F2019098 F2019099 F2019100 F2019101 F2019102 F2019103
张庆达
河海大学
石蕴
内蒙古科技大学
覃康朔
浙江大学
任梓洋
三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖
济南大学
胡广富
贵州大学
张繁盛
江苏大学
曾宇
长安大学
周星星
空军工程大学
涂捷
北京邮电大学
韩帅杰
上海财经大学
洪世哲
中国石油大学(北京)克拉玛依校区 郭 涛
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年全国数学竞赛(非数学类)
(重庆大学A区考点)
考试时间:2017年10月28日上午9:00—11:30
地点:B二415(第一考场) 60人
2017年全国数学竞赛(非数学类)
(重庆大学A区考点)
考试时间:2017年10月28日上午9:00—11:30
地点:B二416(第二考场) 90人
2017年全国数学竞赛(非数学类)
(重庆大学A区考点)
考试时间:2017年10月28日上午9:00—11:30
地点:B二417 (第三考场) 60人
2017年全国数学竞赛(非数学类)
(重庆大学A区考点)
考试时间:2017年10月28日上午9:00—11:30
地点:B二404(第四考场) 50人
2017年全国数学竞赛(非数学类)
(重庆大学A区考点)
考试时间:2017年10月28日上午9:00—11:30
地点:B二409(第五考场) 60人
2017年全国数学竞赛(非数学类)
(重庆大学A区考点)
考试时间:2017年10月28日上午9:00—11:30
地点:B二413(第六考场) 47人。
