九年级数学上册证明三测试题及答案C
九年级上册数学测试题(含答案)

九年级上册数学测试题(考试时间: 120 分钟分数: 120 )一、选择题(本大题共10 小题,共 30 分)1.某钢铁厂一月份生产钢铁 560 吨,从二月份起 ,由于改进操作技术 ,使得第一季度共生产钢铁1850 吨,问二、三月份平均每月的增长率是多少?若设二、三月份平均每月的增长率为 x,则可得方程A. B.C. D.2.若一元二次方程的常数项是 0,则 m 等于 ( )A. B. 3 C. D. 93.如图 ,AB 是的一条弦 ,于点 C,交于点 D,连接若,,则的半径为 ()A. 5B.C. 3D.4.若抛物线与 x 轴有交点 ,则 m 的取值X围是( )A. B. C. D.5.如图 ,A,B,C 是上三个点 ,,则下列说法中正确的是()A. B. 四边形 OABC 内接于C. D.6.中,于 C,AE 过点 O,连接 EC,若,,则 EC长度为( )A. B. 8 C. D.7.下列判断中正确的是 ( )A.长度相等的弧是等弧B.平分弦的直线也必平分弦所对的两条弧C.弦的垂直平分线必平分弦所对的两条弧D.平分一条弧的直线必平分这条弧所对的弦8. 如图 ,已知与坐标轴交于点A,O,B,点C在上,且,若点 B 的坐标为,则弧 OA 的长为 ( )A.B.C.D.9.将含有角的直角三角板 OAB 如图放置在平面直角坐标中 ,OB 在 x 轴上 ,若,将三角板绕原点 O 顺时针旋转,则点 A 的对应点的坐标为( )A.B.C.D.10.如图 ,在中 ,,,以点 C 为圆心 ,CB 的长为半径画弧 ,与 AB 边交于点 D,将绕点 D旋转后点 B 与点 A 恰好重合 ,则图中阴影部分的面积为 ()A. B.C. D.二、填空题(本大题共8 小题,共 24分)11.m 是方程的一个根 ,则代数式的值是______.12.已知,,是二次函数上的点 ,则, , 从小到大用“”排列是 ______.13.如图 ,在中 ,直径,弦于 E,若,则______.14.如图是一座抛物形拱桥 ,当水面的宽为 12m时,拱顶离水面 4m,当水面下降3m 时 ,水面的宽为 ______15.如图 ,正的边长为 4,将正绕点 B顺时针旋转得到,若点 D 为直线上的一动点 ,则的最小值是 ______.16.如图 ,在平面内将绕着直角顶点 C 逆时针旋转,得到,若,,则阴影部分的面积为 ______.17.如图,A、B、C、D 均在上 ,E 为 BC 延长线上的一点 ,若,则______.18.如图 ,内接于,于点 D,若的半径,则 AC 的长为 ______.三、解答题(本大题共7 小题,共66分)19. 已知关于 x 的一元二次方程有实数根.求 m 的取值X围;( 3+3=6分)若方程有一个根为,求 m 的值及另一个根.20. 如图 ,E 与 F 分别在正方形 ABCD 边 BC 与 CD 上,.以A 为旋转中心 ,将按顺时针方向旋转 ,画出旋转后得到的图形.( 4+4=8分)已知,,求 EF 的长.21. 平面上有 3 个点的坐标:,,.在 A,B,C 三个点中任取一个点 ,这个点既在直线上又在抛物线上的概率是多少?从A,B,C 三个点中任取两个点 ,求两点都落在抛物线上的概率.( 4+4=8分)22. 如图 ,抛物线与x轴交于A、B两点点A在点B的左侧,点 A 的坐标为,与 y 轴交于点,作直线动点P在x轴上运动,过点 P 作轴,交抛物线于点M,交直线BC于点N,设点P的横坐标为m.( 4+4+4=12)Ⅰ求抛物线的解析式和直线 BC 的解析式;Ⅱ当点 P 在线段 OB 上运动时 ,求线段 MN 的最大值;Ⅲ当以 C、O、M、N 为顶点的四边形是平行四边形时,直接写出 m 的值.23. 如图,内接于,,CD 是的直径 ,点 P 是 CD 延长线上的一点 ,且.( 5+5=10分)求证: PA 是的切线;若,,求的半径.24. 如图 ,AB 是的直径,四边形ABCD内接于,延长 AD,BC 交于点 E,且.求证:;若,,求的长.25. 如图 ,A、B、C 是圆 O 上三点 ,,点 D 是圆上一动点且,过点 D 作 BC 的平行线 DE,过点 A 作 AB 的垂线 AE,两线交于点 E.(1)求证: AB 是圆 O 的直径。
北师大版九年级数学上册 相似三角形解答题培优专题(含答案)

2019-2020相似三角形解答题培优专题(含答案)一、解答题1.如图,在Rt ABC ∆中,90B ︒∠=,6cm AB =,8cm BC =,点P 由点A 出发沿AB 方向向终点B 以每秒1cm 的速度匀速移动,点Q 由点B 出发沿BC 方向向终点C 以每秒2cm 的速度匀速移动,速度为2cm /s .如果动点同时从点A ,B 出发,当点P 或点Q 到达终点时运动停止.则当运动几秒时,以点Q ,B ,P 为顶点的三角形与ABC ∆相似?2.如图(1),已知点G 在正方形ABCD 的对角线AC 上,GE ⊥BC ,垂足为点E ,GF ⊥CD ,垂足为点F . (1)证明与推断:①求证:四边形CEGF 是正方形; ②推断:AGBE的值为 : (2)探究与证明:将正方形CEGF 绕点C 顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG 与BE 之间的数量关系,并说明理由: (3)拓展与运用:正方形CEGF 在旋转过程中,当B ,E ,F 三点在一条直线上时,如图(3)所示,延长CG 交AD 于点H .若AG=6,GH=22,则BC= .3.如图1,在Rt ABC 中,90,4,2B AB BC ∠︒===,点,D E 分别是边,BC AC 的中点,连接DE .将CDE △绕点C 逆时针方向旋转,记旋转角为α.1()问题发现①当0α=o 时,AE BD = ;②当180α=o 时,AEBD= . 2()拓展探究 试判断:当0360α︒≤︒<时,AEBD的大小有无变化?请仅就图2的情形给出证明. 3()问题解决 CDE △绕点C 逆时针旋转至,,A B E 三点在同一条直线上时,求线段BD 的长.4.在ABC ∆,CA CB =,ACB α∠=.点P 是平面内不与点A ,C 重合的任意一点.连接AP ,将线段AP 绕点P 逆时针旋转α得到线段DP ,连接AD ,BD ,CP . (1)观察猜想 如图1,当60α︒=时,BDCP的值是 ,直线BD 与直线CP 相交所成的较小角的度数是 . (2)类比探究如图2,当90α︒=时,请写出BDCP的值及直线BD与直线CP相交所成的小角的度数,并就图2的情形说明理由.(3)解决问题当90α︒=时,若点E,F分别是CA,CB的中点,点P在直线EF上,请直接写出点C,P,D在同一直线上时AD CP的值.5.如图1,在△ABC中,BA=BC,点D,E分别在边BC、AC上,连接DE,且DE=DC.(1)问题发现:若∠ACB=∠ECD=45°,则AEBD=.(2)拓展探究,若∠ACB=∠ECD=30°,将△EDC绕点C按逆时针方向旋转α度(0°<α<180°),图2是旋转过程中的某一位置,在此过程中AEBD的大小有无变化?如果不变,请求出AEBD的值,如果变化,请说明理由.(3)问题解决:若∠ACB=∠ECD=β(0°<β<90°),将△EDC旋转到如图3所示的位置时,则AEBD的值为.(用含β的式子表示)6.在矩形ABCD中,AB=4cm,BC=8cm,动点P从点A出发,以1cm/s的速度沿AB向点B运动,动点Q从点B出发,以2cm/s秒的速度沿BC向点C运动.P、Q分别从A、B同时出发,设运动时间为t秒.(如图1)(1)用含t 的代数式表示下列线段长度:①PB=__________cm,②QB=_____cm,③CQ=_________cm. (2)当△PBQ 的面积等于3 时,求t 的值.(3) (如图2),若E 为边CD 中点,连结EQ 、AQ.当以A 、B 、Q 为顶点的三角形与△EQC 相似时,直接写出满足条件的t 的所有值.7.如图l ,在ABCD 中,点M ,N 分别在边AD 和BC 上,点E ,F 在对角线BD 上,且AM CN =,12BE DF BD =<.(1)求证:四边形MENF 是平行四边形: (2)若6AB =,10BC =,8BD =.①当四边形MENF 是菱形时,AM 的长为______; ②当四边形MENF 是正方形时,BE 的长为______; ③当四边形MENF 是矩形且6AM =时,BE 的长为______.8.已知:如图,在平面直角坐标系中,△ABC 是直角三角形,∠ACB =90°,点A ,C 的坐标分别为A (﹣3,0),C (1,0),BC =34AC(1)求过点A,B的直线的函数表达式;(2)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m,使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.9.已知:如图,正方形ABCD中,P是边BC上一点,BE⊥AP,DF⊥AP,垂足分别是点E、F.(1)求证:EF=AE﹣BE;(2)联结BF,如果AFBF=DFAD.求证:EF=EP.10.如图,在△ C中,过点C作CD,E是AC的中点,连接DE并延长,交AB于点F,交CB的延长线于点G,连接AD,CF.求证:四边形AFCD是平行四边形.若, C,,求AB的长.11.已知:如图,点A .F ,E .C 在同一直线上,AB ∥DC ,AB=CD ,∠B=∠D . (1)求证:△ABE ≌△CDF ;(2)若点E ,G 分别为线段FC ,FD 的中点,连接EG ,且EG=5,求AB 的长.12.如图,直线 AB 与坐标轴交与点(0,6),(8,0)A B , 动点P 沿路线O B A →→运动.(1)求直线AB 的表达式;(2)当点P 在OB 上,使得AP 平分OAB ∠时,求此时点P 的坐标;13.如图,将矩形ABCD 沿AF 折叠,使点D 落在BC 边的点E 处,过点E 作EG ∥CD 交AF 于点G ,连接DG . (1)求证:四边形EFDG 是菱形; (2) 求证:21=2EG AF GF ⋅; (3)若AG=6,EG=25,求BE 的长.14.如图,在△ABC 中.AC=BC=5.AB=6.CD 是AB 边中线.点P 从点C 出发,以每秒2.5个单位长度的速度沿C-D-C 运动.在点P 出发的同时,点Q 也从点C 出发,以每秒2个单位长度的速度沿边CA 向点A 运动.当一个点停止运动时,另一个点也随之停止,设点P 运动的时间为t 秒.(1)用含t 的代数式表示CP 、CQ 的长度. (2)用含t 的代数式表示△CPQ 的面积.(3)当△CPQ 与△CAD 相似时,直接写出t 的取值范围.15.如图,AB ⊥BC ,DC ⊥BC ,垂足分别为B.C ,且AB=8,DC=6,BC=14,BC 上是否存在点P 使△ABP 与△DCP 相似?若有,有几个?并求出此时BP 的长,若没有,请说明理由.16.如图,正方形ABCD ,点P 为射线DC 上的一个动点,点Q 为AB 的中点,连接,PQ DQ ,过点P 作PE DQ 于点E .(1)请找出图中一对相似三角形,并证明;(2)若4AB ,以点,,P E Q 为顶点的三角形与ADQ △相似,试求出DP 的长.17.如图,正方形 ABCD 的边长为 8,E 是 BC 边的中点,点 P 在射线 AD 上, 过 P 作 PF ⊥AE 于 F .(1)请判断△PFA 与△ABE 是否相似,并说明理由;(2)当点 P 在射线 AD 上运动时,设 PA =x ,是否存在实数 x ,使以 P ,F ,E 为顶 点的三角形也与△ABE 相似?若存在,请求出 x 的值;若不存在,说明理由.18.已知:如图,△ABC 是等边三角形,点D 、E 分别在BC ,AC 且BD =CE ,AD 、BE 相交于点M ,求证:(1)△AME ∽△BAE ;(2)BD 2=AD×DM . 19.△ABC 中,AB =AC =5,BC =6,过AB 上一点D 作DE‖ C ,D ‖ C 分别交AC 、BC 于点E 和F(1)如图1,证明:△ADE∽△DBF;(2)如图1,若四边形DECF是菱形,求DE的长;(3)如图2,若以D、E、F为顶点的三角形与△BDF相似,求AD的长.20.如图,在矩形ABCD中,点E是AD的中点,连结BE,且BE⊥AC交AC于点F.(1)求证:△EAB∽△ABC;(2)若AD=2,求AB的长;(3)在(2)的条件下,求DF的长.21.如图,正方形ABCD中,M为BC上一点,F是AM上一点,EF⊥AM,垂足为F,交AD延长线于点E,交DC 于点N.(1)求证:△ABM∽△EFA;(2)若AB=12,BM=6,F为AM的中点,求DN的长;(3)若AB =12,DE =1,BM =5,求DN 的长.22.如图,在△ABC 中,AD 平分∠BAC ,按如下步骤作图:第一步,分别以点A 、D 为圆心,以大于12AD 的长为半径在AD 两侧作弧,交于两点M 、N ; 第二步,连接MN 分别交AB 、AC 于点E 、F ; 第三步,连接DE 、DF .若BD =6,AF =4,CD =3,求线段BE 的长.23.教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.例2 如图,在ABC ∆中,,D E 分别是边,BC AB 的中点,,AD CE 相交于点G ,求证:13GE GD CE AD ==, 证明:连结ED .请根据教材提示,结合图①,写出完整的证明过程.结论应用:在ABCD 中,对角线AC BD 、交于点O ,E 为边BC 的中点,AE 、BD 交于点F . (1)如图②,若ABCD 为正方形,且6AB =,则OF 的长为 . (2)如图③,连结DE 交AC 于点G ,若四边形OFEG 的面积为12,则ABCD 的面积为 .24.正方形ABCD的边长为4,M,N分别是BC,CD上的两个动点,当M点在BC上运动时,保持AM和MN垂直.(1)证明:△ABM∽△MCN;(2)若△ABM的周长与△MCN周长之比是4:3,求NC的长.25.如图,在△ABC中,AB=8,BC=16,点P从点A开始沿AB向点B以2m/s的速度移动,点Q从点B开始沿BC向点C以4m/s的速度移动,如果P,Q分别从AB,BC同时出发,经过几秒△PBQ与△ABC相似?26.如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.(1)求证:△APQ∽△CDQ;(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.当t为何值时,DP⊥AC?27.如图,在Rt△ABC中,∠ACB=90°,BC mAC n,CD⊥AB于点D,点E是直线AC上一动点,连接DE,过点D作FD⊥ED,交直线BC于点F.(1)探究发现:如图1,若m=n,点E在线段AC上,则DEDF=;(2)数学思考:①如图2,若点E在线段AC上,则DEDF=(用含m,n的代数式表示);②当点E在直线AC上运动时,①中的结论是否仍然成立?请仅就图3的情形给出证明;(3)拓展应用:若AC=,BC=2,DF=4,请直接写出CE的长.28.如图,已知△ABC是边长为6cm的等边三角形,动点P,Q同时从B,A两点出发,分别沿BA,AC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P,Q两点都停止运动,设运动时间为t(s),解答下列问题:(1)如图①,当t为何值时,AP=3AQ;(2)如图②,当t为何值时,△APQ为直角三角形;(3)如图③,作QD∥AB交BC于点D,连接PD,当t为何值时,△BDP与△PDQ相似?29.如图,在△ABC中,∠C=90°,点D是边AB上的动点,过点D作DE∥BC交AC于E,过E作EF∥AB交BC 于F,连结DF.(1)若点D是AB的中点,证明:四边形DFEA是平行四边形;(2)若AC=8,BC=6,直接写出当△DEF为直角三角形时AD的长.30.如图,四边形ABCD中,AC平分∠DAB,AC2=AB•AD,∠ADC=90°,E为AB的中点.(1)求证:△ADC∽△ACB;(2)CE与AD有怎样的位置关系?试说明理由;(3)若AD=4,AB=6,求的值.31.(1)观察发现:如图1,在Rt△ABC中,∠B=90°,点D在边AB上,过D作DE∥BC交AC于E,AB=5,AD =3,AE=4.填空:①△ABC与△ADE是否相似?(直接回答);②AC=;DE=.(2)拓展探究:将△ADE绕顶点A旋转到图2所示的位置,猜想△ADB与△AEC是否相似?若不相似,说明理由;若相似,请证明.(3)迁移应用:将△ADE绕顶点A旋转到点B、D、E在同一条直线上时,直接写出线段BE的长.32.如图1,一次函数y=12x+4与x轴、y轴分别交于A,B两点.P是x轴上的动点,设点P的横坐标为n.(1)当△BPO∽△ABO时,求点P的坐标;(2)如图2,过点P的直线y=2x+b与直线AB相交于C,求当△P AC的面积为20时,点P的坐标;(3)如图3,直接写出当以A,B,P为顶点的三角形为等腰三角形时,点P的坐标.33.如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,线段OA,OC的长是一元二次方程x2-12x+36=0的两根,BC=45,∠BAC=45°.(1)直接写出点A的坐标________点C的坐标________;(2)若反比例函数y=kx的图象经过点B,求k的值;(3)如图过点B作BD⊥y轴于点D;在y轴上是否存在点P,使以P,B,D为顶点的三角形与以P,O,A为顶点的三角形相似?若存在,直接写出满足条件的点P的坐标;若不存在,请说明理由.34.感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6 2,CE=4,则DE的长为______.35.已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的横坐标是一元二次方程x2+2x-3=0的两根(AO>OC),直线AB与y轴交于D,D点的坐标为9 04⎛⎫ ⎪⎝⎭,(1)求直线AB的函数表达式;(2)在x轴上找一点E,连接EB,使得以点A、E、B为顶点的三角形与△ABC相似(不包括全等),并求点E的坐标;(3)在(2)的条件下,点P、Q分别是AB和AE上的动点,连接PQ,点P、Q分别从A、E同时出发,以每秒1个单位长度的速度运动,当点P到达点B时,两点停止运动,设运动时间为t秒,问几秒时以点A、P、Q为顶点的三角形与△AEB相似.参考答案1.当运动2.4秒或1811秒时,以点Q ,B ,P 为顶点的三角形与ABC ∆相似 【解析】 【分析】设t 秒后,以Q ,B ,P 为顶点的三角形与△ABC 相似;则PB =(6−t )cm ,BQ =2tcm ,分两种情况:①当PB BQAB BC=时;②当BP BQBC BA=时;分别解方程即可得出结果. 【详解】解:设(04)t t <…秒后,以点Q ,B ,P 为顶点的三角形与ABC ∆相似,则(6)cm PB t =-,2cm BQ t =.∵90B ︒∠=,∴分两种情况讨论:①当PBQ ABC ∆∆∽时,PB BQ AB BC =,即6268t t-=,解得 2.4t =; ②当QBP ABC ∆∆∽时,BP BQBC BA=,即6286t t -=,解得1811t =. 综上所述,当运动2.4秒或1811秒时,以点Q ,B ,P 为顶点的三角形与ABC ∆相似. 【点睛】本题考查了相似三角形的判定方法、解方程;熟练掌握相似三角形的判定方法,分两种情况进行讨论是解决问题的关键.2.(1)①四边形CEGF 是正方形;②2;(2)线段AG 与BE 之间的数量关系为AG=2BE ;(3)35 【解析】 【分析】(1)①由GE BC ⊥、GF CD ⊥结合BCD 90∠=可得四边形CEGF 是矩形,再由ECG 45∠=即可得证;②由正方形性质知CEG B 90∠∠==、ECG 45∠=,据此可得CG2CE=、GE //AB ,利用平行线分线段成比例定理可得;(2)连接CG ,只需证ACG ∽△BCE 即可得; (3)证AHG ∽CHA 得AG GH AH AC AH CH ==,设BC CD AD a ===,知AC 2a =,由AG GHAC AH=得2AH a 3=、1DH a 3=、10CH a 3=,由AG AH AC CH =可得a 的值. 【详解】(1)①∵四边形ABCD 是正方形, ∴∠BCD=90°,∠BCA=45°, ∵GE ⊥BC 、GF ⊥CD , ∴∠CEG=∠CFG=∠ECF=90°,∴四边形CEGF 是矩形,∠CGE=∠ECG=45°, ∴EG=EC ,∴四边形CEGF 是正方形; ②由①知四边形CEGF 是正方形, ∴∠CEG=∠B=90°,∠ECG=45°,∴2CGCE=,GE ∥AB , ∴2AG CGBE CE==, 故答案为:2; (2)连接CG ,由旋转性质知∠BCE=∠ C =α, 在Rt △CEG 和Rt △CBA 中,CE CG =22、CB CA =22, ∴CG CE =2CACB=, ∴△ACG ∽△BCE ,∴2AG CABE CB==, ∴线段AG 与BE 之间的数量关系为AG=2BE ; (3)∵∠CEF=45°,点B 、E 、F 三点共线, ∴∠BEC=135°, ∵△ACG ∽△BCE , ∴∠AGC=∠BEC=135°, ∴∠AGH=∠CAH=45°, ∵∠CHA=∠AHG , ∴△AHG ∽△CHA , ∴AG GH AHAC AH CH==, 设BC=CD=AD=a ,则AC=2a ,则由AG GHAC AH=得6222AHa=,∴AH=23 a,则DH=AD﹣AH=13a,CH=22CD DH+=103a,∴由AG AHAC CH=得2632103aaa=,解得:a=35,即BC=35,故答案为:35.【点睛】本题考查了正方形的性质与判定,相似三角形的判定与性质等,综合性较强,有一定的难度,正确添加辅助线,熟练掌握正方形的判定与性质、相似三角形的判定与性质是解题的关键.3.(1)①5;②5;(2) 5;(3) 35 5【解析】【分析】(1)①根据勾股定理和三角形中位线的性质,即可得到答案;②根据平行线的性质即可得到答案;(2)根据相似三角形的性质和判定即可得到答案;(3) 根据勾股定理即可得到答案.【详解】解:()1①当0α︒=时,Rt ABC Q V 中,90B ∠︒=,22222425AC AB BC ∴++===,点,D E 分别是边,BC AC 的中点,115122AE AC BD BC ∴==,==,5AEBD∴=. ②如图1﹣1中,当180α︒=时, 可得//AB DE ,AC BCAE BD =Q , 5AE ACBD BC∴==. 故答案为:55①,②. 2()如图2,当0360α︒≤︒<时,AEBD的大小没有变化, ECD ACB ∠∠Q =, ECA DCB ∴∠∠=,又5EC ACDC BC==Q, ECA DCB ∴V V ∽,5AE ECED DC∴==. ()3①如图3﹣1中,当点E 在AB 的延长线上时,在Rt BCE V 中,5,2CE BC ==,22541BE EC BC ∴--===,5AE AB BE ∴+==,5AEBD=Q, 555BD ∴==.②如图3﹣2中,当点E 在AB 线段上时,易知1,413BE AE -===, 5AEBD=Q, 355BD ∴=, 综上所述,满足条件的BD 的长为355. 【点睛】本题考查勾股定理、三角形中位线的性质、平行线的性质和相似三角形的性质和判定,解题的关键熟练掌握勾股定理、三角形中位线的性质、平行线的性质和相似三角形的性质和判定. 4.(1)1,60︒(2)45°(3)22-,22+ 【解析】 【分析】(1)如图1中,延长CP 交BD 的延长线于E ,设AB 交EC 于点O .证明()CAP BAD SAS ∆≅∆,即可解决问题. (2)如图2中,设BD 交AC 于点O ,BD 交PC 于点E .证明DABPAC ∆∆,即可解决问题.(3)分两种情形:①如图3﹣1中,当点D 在线段PC 上时,延长AD 交BC 的延长线于H .证明AD DC =即可解决问题.②如图3﹣2中,当点P 在线段CD 上时,同法可证:DA DC =解决问题.【详解】解:(1)如图1中,延长CP 交BD 的延长线于E ,设AB 交EC 于点O .60PAD CAB ︒∠=∠=,CAP BAD ∴∠=∠,CA BA =,PA DA =,()CAP BAD SAS ∴∆≅∆, PC BD ∴=,ACP ABD ∠=∠, AOC BOE ∠=∠,60BEO CAO ︒∴∠=∠=,1BDPC∴=,线BD 与直线CP 相交所成的较小角的度数是60︒, 故答案为1,60︒.(2)如图2中,设BD 交AC 于点O ,BD 交PC 于点E .45PAD CAB ︒∠=∠=, PAC DAB ∴∠=∠,2AB ADAC AP ==, DABPAC ∴∆∆,PCA DBA ∴∠=∠,2BD ABPC AC==, EOC AOB ∠=∠,45CEO OAB ︒∴∠=∠=,∴直线BD 与直线CP 相交所成的小角的度数为45︒.(3)如图3﹣1中,当点D 在线段PC 上时,延长AD 交BC 的延长线于H .CE EA =,CF FB =,EF AB ∴∥,45∴∠=∠=,EFC ABC︒PAO︒∠=,45∴∠=∠,PAO OFH∠=∠,POA FOH∴∠=∠,H APO=,90∠=,EA ECAPC︒∴==,PE EA ECEPA EAP BAH∴∠=∠=∠,∴∠=∠,H BAH∴=,BH BA∠=∠=,ADP BDC︒45∴∠=,90ADB︒∴⊥,BD AHDBA DBC︒∴∠=∠=,22.5ADB ACB︒∠=∠=,90∴A,D,C,B四点共圆,DCA ABD︒∠=∠=,DAC DBC︒∠=∠=,22.522.5∴∠=∠=,22.5DAC DCA︒DA DC ∴=,设=AD a ,则DC AD a ==,22PD a =, 2222ADa CPa a∴==-+c .如图3﹣2中,当点P 在线段CD 上时,同法可证:=DA DC ,设=AD a ,则CD AD a ==,22PD a =,22PC a a ∴=-, 2222ADa PCa a∴==+-.【点睛】本题属于相似形综合题,考查了旋转变换,等边三角形的性质,等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.5.(1)2;(2)此过程中AE BD 的大小有变化,3AEBD=(3)2 osβ 【解析】 【分析】1)如图1,过E 作EF ⊥AB 于F ,根据等腰三角形的性质得到∠A=∠C=∠DEC=45°,于是得到∠B=∠EDC=90°,推出四边形EFBD 是矩形,得到EF=BD ,推出△AEF 是等腰直角三角形,根据等腰直角三角形的性质得到结论; (2)根据等腰三角形的性质得到∠ACB=∠CAB=∠ECD=∠CED=30°,根据相似三角形的判定和性质即可得到结论; (3)根据等腰三角形的性质得到∠ACB=∠CAB=∠ECD=∠CED=β,根据相似三角形的性质得到BC ACDC CE=,即BC DCAC EC =,根据角的和差得到∠ACE=∠BCD ,求得△ACE ∽△BCD ,证得AE AC BD BC=,过点B 作BF ⊥AC 于点F ,则AC=2CF ,根据相似三角形的性质即可得到结论. 【详解】解:(1)如图1,过E 作EF ⊥AB 于F ,∵BA=BC ,DE=DC ,∠ACB=∠ECD=45°, ∴∠A=∠C=∠DEC=45°, ∴∠B=∠EDC=90°, ∴四边形EFBD 是矩形, ∴EF=BD , ∴EF ∥BC ,∴△AEF 是等腰直角三角形,∴2BD EFAE AE==, 故填:2,(2)此过程中AEBD的大小有变化, 由题意知,△ABC 和△EDC 都是等腰三角形, ∴∠ACB=∠CAB=∠ECD=∠CED=30°, ∴△ABC ∽△EDC ,∴BC AC DC CE =,即BC DCAC EC=, 又∠ECD+∠ECB=∠ACB+∠ECB , ∴∠ACE=∠BCD , ∴△ACE ∽△BCD ,∴AE ACBD BC=, 在△ABC 中,如图2,过点B 作BF ⊥AC 于点F ,则AC=2CF ,在Rt △BCF 中,3cos302CF BC BC ︒=⋅=, ∴AC=3BC .∴3AE ACBD BC==; (3)由题意知,△ABC 和△EDC 都是等腰三角形,且∠ACB=∠ECD=β, ∴∠ACB=∠CAB=∠ECD=∠CED=β, ∴△ABC ∽△EDC ,∴BC AC DC CE =,即BC DCAC EC=, 又∠ECD+∠ECB=∠ACB+∠ECB , ∴∠ACE=∠BCD ,∴△ACE∽△BCD,∴AE AC BD BC=,在△ABC中,如图3,过点B作BF⊥AC于点F,则AC=2CF,在Rt△BCF中,C = C• osβ,∴ C=2 C osβ.∴AE ACBD BC==2 osβ,故答案为2 osβ.【点睛】本题考查了相似形的综合题、等腰直角三角形的性质、等腰三角形的性质、锐角三角函数、相似三角形的判定和性质等知识,解题的关键是灵活运用相似三角形的判定和性质解决问题,属于中考常考题型.6.(1)PB=4-t;QB=2t;CQ=8-2t;(2)1或3;(3)或或.【解析】【分析】(1)根据题意写出结果即可;(2)利用三角形的面积公式列方程求解即可;(3)根据相似三角形的性质,分两种情况列式求解即可.【详解】(1)由题意得,①PB=4-t;②QB=2t;③CQ=8-2t;(2)∵△PBQ的面积等于3,∴2t(4-t)=3×2,解之得,t=1或3;(3)当△ABQ~△QCE时,,∴,解之得,x1=,x2=;当△ABQ~△ECQE时,,∴,解之得,t=.∴满足条件的t的所有值为或或.【点睛】本题考查了列代数式,一元二次方程的应用,相似三角形的性质及分类讨论的数学思想,熟练掌握分类讨论的数学思想是解答本题的关键. 相似三角形的性质:如果两个三角形相似,那么它们的对应角相等,对应边的比,对应高的比,对应中线的比,对应角平分线的比,对应周长的比都等于相似比;它们对应面积的比等于相似比的平方.7.(1)证明见解析,(2)①5.②1.③41045 .【解析】【分析】(1)如图1中,设BD 的中点为O .连接AC ,AN ,CM ,MN .利用对角线互相平分的四边形是平行四边形证明即可.(2)①如图21-中,连接MN 交BD 于点O ,当MN BD ⊥时,四边形MENF 是菱形.利用平行线等分线段定理即可解决问题.②在①的基础上,OE OM =时,四边形MENF 是正方形.③如图32-中,连接MN 交BD 于点O ,作MH BD ⊥于H .当OE OF OM ON ===时,四边形MENF 是矩形. 【详解】(1)证明:如图1中,设BD 的中点为O .连接AC ,AN ,CM ,MN .四边形ABCD 是平行四边形, AC ∴与BD 互相平分且交于点O ,//AMCN ,AM CN =,∴四边形ANCM 是平行四边形,AC ∴与MN 互相平分且交于点O ,OM ON ∴=,OB OD =,BE DF =,OE OF ∴=,∴四边形MENF 是平行四边形.(2)①如图21-中,连接MN 交BD 于点O ,当MN BD ⊥时,四边形MENF 是菱形.6AB CD ==,10AD BC ==,8BD =, 222AD AB BD ∴=+,90ABD ∴∠=︒,90MOF ABD ∴∠=∠=︒,//OM AB ∴, OB OD =, 5AM DM ∴==.②在①的基础上,满足OM OE =时,四边形MENF 是正方形, 易知132OM AB ==, 3OE OF ∴==, 8BD =,1·(86)12BE DF ∴==-=.③如图32-中,连接MN 交BD 于点O ,作MH BD ⊥于H .//MH AB ,:::MH AB DM DA DH DB ∴== :64:10:8MH DH ∴==,125MH ∴=,165DH =, 164455OH ∴=-=, 224105OM MH OH ∴=+=, 当OE OF OM ON ===时,四边形MENF 是矩形,1810410(8)4255BE DF ∴==-=-. 故答案为:5,1,41045-. 【点睛】本题属于四边形综合题,考查了平行四边形的性质,矩形的判定,菱形的判定,正方形的判定,解直角三角形等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.8.(1)y =34x +94;(2)D 点位置见解析,D (134,0);(3)符合要求的m 的值为12536或259.【解析】 【分析】(1)先根据A(−3,1),C(1,0),求出AC进而得出BC=3求出B点坐标,利用待定系数法求出直线AB的解析式即可;(2)运用相似三角形的性质就可求出点D的坐标;(3)由于△APQ与△ADB已有一组公共角相等,只需分△APQ∽△ABD和△APQ∽△ADB两种情况讨论,然后运用相似三角形的性质建立关于m的方程,就可解决问题.【详解】解:(1)∵A(﹣3,0),C(1,0),∴AC=4,∵BC=34 AC,∴BC=34×4=3,∴B(1,3),设直线AB的解析式为y=kx+b,∴303k bk b-+=⎧⎨+=⎩,∴3494kb⎧=⎪⎪⎨⎪=⎪⎩,∴直线AB的解析式为y=34x+94;(2)若△ADB与△ABC相似,过点B作BD⊥AB交x轴于D,∴∠ABD=∠ACB=90°,如图1,此时ABAC=ADAB,即AB2= C• D.∵∠ACB=90°,AC=4,BC=3,∴AB=5,∴25=4AD,∴AD=25 4,∴OD=AD﹣AO=254﹣3=134,∴点D的坐标为(134,0);(3)∵AP=DQ=m,∴AQ=AD﹣QD=254﹣m.Ⅰ、若△APQ∽△ABD,如图2,则有APAB=AQAD,∴ P• D= • Q,∴254m=5(254﹣m),解得m=25 9;Ⅱ、若△APQ∽△ADB,如图3,则有APAD=AQAB,∴ P• = D• Q,∴5m=254(254﹣m),解得:m=125 36,综上所述:符合要求的m的值为12536或259.【点睛】此题是相似形综合题,主要考查了是待定系数法,相似三角形的判定与性质、勾股定理等知识,也考查了分类讨论的数学思想,属于中档题,解本题的关键是根据相似建立方程求解.9.(1)证明见解析;(2)证明见解析.【解析】【分析】(1)利用正方形的性质得AB=AD ,∠BAD=90°,根据等角的余角相等得到∠1=∠3,则可判断△ABE ≌△DAF ,则BE=AF ,然后利用等线段代换可得到结论;(2)利用AF DF BF AD =和AF=BE 得到BE BFDF AD=,则可判定Rt △BEF ∽Rt △DFA ,所以∠4=∠3,再证明∠4=∠5,然后根据等腰三角形的性质可判断EF=EP .【详解】(1)∵四边形ABCD 为正方形,∴AB=AD ,∠BAD=90°, ∵BE ⊥AP ,DF ⊥AP , ∴∠BEA=∠AFD=90°, ∵∠1+∠2=90°,∠2+∠3=90°, ∴∠1=∠3, 在△ABE 和△DAF 中12BEA AFDAB DA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ABE ≌△DAF , ∴BE=AF ,∴EF=AE ﹣AF=AE ﹣BE ;(2)如图,∵AF DFBF AD=, 而AF=BE ,∴BE DFBF AD =, ∴BE BFDF AD=, ∴Rt △BEF ∽Rt △DFA ,∴∠4=∠3,而∠1=∠3,∴∠4=∠1,∵∠5=∠1,∴∠4=∠5,即BE平分∠FBP,而BE⊥EP,∴EF=EP.【点睛】本题考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质,熟练掌握相关的性质与定理、正确添加辅助线是解题的关键.10.证明见解析;.【解析】【分析】由E是AC的中点知 E CE,由CD知 E CDE,据此根据“ S”即可证△ E ≌△CED,从而得CD,结合CD即可得证;证△∽△ CD得,据此求得CD,由CD及可得答案.C CD【详解】E是AC的中点,E CE , CD , E CDE , 在△ E 和△CED 中, ,△ E ≌△CED S , CD ,又 CD ,即 CD , 四边形AFCD 是平行四边形; CD , △ ∽△ CD ,CCD,即CD,解得:CD,四边形AFCD 是平行四边形, CD,. 【点睛】本题考查了平行四边形的判定与性质,全等三角形的判定与性质,相似三角形的判定与性质,熟练掌握相关的性质及定理是解题的关键.11.(1)证明见解析;(2)AB=10.【解析】分析:(1)根据平行线的性质得出∠A=∠C,进而利用全等三角形的判定证明即可;(2)利用全等三角形的性质和中点的性质解答即可.详解:(1)证明:∵AB∥DC,∴∠A=∠C,在△ABE与△CDF中===,∴△ABE≌△CDF(ASA);(2)∵点E,G分别为线段FC,FD的中点,∴ED=CD,∵EG=5,∴CD=10,∵△ABE≌△CDF,∴AB=CD=10.点睛:此题考查全等三角形的判定和性质,关键是根据平行线的性质得出∠A=∠C.12.(1)y=34x+6;(2)P(3,0).【解析】【分析】1)直接利用待定系数法即可得出结论;(2)方法1、利用角平分线判断出BC=AB=10,进而判断出△AOP∽△CBP,求出OP,即可得出结论;方法2、先判断出OP=PM,设OP=m,得出PM=m,BP=8-m,再求出AM=OA=6,进而得出BM=AB-AM=4,最后用勾股定理建立方程求解即可得出结论.【详解】解:(1)设直线AB的解析式为y=kx+b,∵A(0,6),B(8,0),∴680bk b⎧⎨+⎩==,∴346kb⎧=-⎪⎨⎪=⎩,∴直线AB的解析式为y=34-x+6;(2)方法1、如图1,∵A(0,6),B(8,0),∴OA=6,OB=8,AB=10,过点B作BC∥OA交AP的延长线于C,∴∠C=∠OAP,∵AP平分∠OAB,∴∠OAP=∠BAP,∴∠C=∠BAP,∴BC=AB=10,∵BC∥OA,∴△AOP∽△CBP,∴OP OA=BP BC=35,∴OP3=OB8,∴OP=3,∴P(3,0);方法2、如图3,过点P作PM⊥AB于M,∵AP是∠OAB的角平分线,∴OP=PM,设OP=m,∴PM=m,∴BP=OB-OP=8-m易知,△AOP≌△AMP,∴AM=OA=6,∴BM=AB-AM=4,在Rt△BMP中,根据勾股定理得,m2+16=(8-m)2,∴m=3,∴P(3,0).故答案为:(1)y=34x+6;(2)P(3,0).【点睛】本题是一次函数综合题,主要考查了待定系数法,角平分线的定义,相似三角形的判定和性质,正确作出辅助线构造出相似三角形是解题的关键.13.(1)证明见解析;(2)证明见解析;(3)BE的长为125 5.【解析】(1)先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF;(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF=12GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明D 2= O• ,于是可得到GE、AF、FG的数量关系;(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD﹣GH求解即可.解:(1)证明:∵GE∥DF,∴∠EGF=∠DFG.∵由翻折的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,∴∠DGF=∠DFG.∴GD=DF.∴DG=GE=DF=EF.∴四边形EFDG为菱形.“点睛”本题考查的是四边形与三角形的综合应用,解题应用了矩形的性质,菱形的性质和判定、相似三角形的判定和性质,掌握矩形的性质定理和相似三角形的判定定理、性质定理是解题的关键.14.(1)当0<t≤85时,CP=2.5t,CQ=2t;当8552t<≤时,CP=8-2.5t,CQ=2t.(2)当0<t≤85时,S△CPQ=12•PC•sin∠ CD•CQ=12×2.5t×35×2t=232t;当8552t<≤时,S△CPQ=12•PC•sin∠ CD•CQ=1 2×(8-2.5t)×35×2t=232425t t-+.(3)0<t≤85或80t41=s【解析】【分析】(1)分两种情形:当0<t≤85时,当85<t52≤时,分别求解即可.(2)分两种情形:当0<t≤85时,当85<t≤52时,根据S△CPQ=12•PC•sin∠ CD•CQ分别求解即可.(3)分两种情形:当0<t≤85,可以证明△QCP∽△DCA,当85<t52≤,∠QPC=90°时,△QPC∽△ADC,构建方程求解即可.【详解】解:(1)∵CA=CB,AD=BD=3,∴CD⊥AB,∴∠ADC=90°,∴CD=22AC AD-=2253-=4,当0<t≤85时,CP=2.5t,CQ=2t,当85t52<≤时,CP=8-2.5t,CQ=2t.(2)∵sin∠ACD=ADAC=35,∴当0<t≤85时,S△CPQ=12•PC•sin∠ CD•CQ=12×2.5t×35×2t=23t2当85t52<≤时,S△CPQ=12•PC•sin∠ CD•CQ=12×(8-2.5t)×35×2t=2324t t25-+.(3)①当0<t≤85时,∵CP=2.5t,CQ=2t,∴CQCP=45,∵CDCA=45,∴CQ CD CP CA=,∵∠PCQ=∠ACD,∴△QCP ∽△DCA ,∴0<t≤85时,△QCP ∽△DCA , ②当85t 52<≤时,当∠QPC=90°时,△QPC ∽△ADC , ∴CP CQ CD CA =, ∴8 2.5t 2t 45-=, 解得:80t 41=, 综上所述,满足条件的t 的值为:0<t≤85或80t 41=s 时,△QCP ∽△DCA . 【点睛】本题属于相似形综合题,考查了相似三角形的判定和性质,解直角三角形的应用等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.15.BC 上存在两个点P ,BP=6或8使△ABP 与△DCP 相似. 【解析】 【分析】设BP=x ,表示出PC=14-x ,然后分BP 与CP 是对应边,BP 与DC 是对应边两种情况,利用相似三角形对应边成比例列式求解即可. 【详解】设BP=x ,则PC=14−x ,BP 与CP 是对应边时,=BP ABCP DC, 即8146x x =-,解得x=8,BP 与DC 是对应边时,=BP ABDC CP, 即8=614x x-, 解得x1=6,x2=8,所以,BC 上存在两个点P ,BP=6或8使△ABP 与△DCP 相似. 【点睛】此题考查相似三角形的判定,解题关键在于根据相似三角形的性质对应边成比例列出方程. 16.(1)DPE QDA ∽,见解析;(2)2DP =或5DP =. 【解析】 【分析】(1)通过等角转换,可得出三角相等,即可判定DPE QDA ∽;(2)首先根据已知条件求出DQ ,由三角形相似的性质,列出方程,即可得解,注意分两种情况讨论. 【详解】(1)DPE QDA ∽根据已知条件,得∠DAQ=∠PED=90° 又∵∠ADQ+∠PDE=∠DPE+∠PDE=90° ∴∠ADQ =∠DPE ,∠AQD=∠PDE ∴DPE QDA ∽(2)由已知条件,得22224225DQ AD AQ =+=+=设DE 为x ∵DPE QDA ∽∴DA PEAQ DE= ∴PE 为2x ∵PEQADQ △△∴分两种情况:①AQ DAPE EQ = 即24225x x=- 解得255x =∴()2222DP x x =+=②AQ DAEQ PE= 即24225xx =- 解得5x =()2225DP x x =+=【点睛】此题主要考查三角形相似的性质,熟练掌握,即可解题.17.(1)见解析;(2)存在,x的值为2或5.【解析】【分析】(1)在△PFA与△ABE中,易得∠PAF=∠AEB及∠PFA=∠ABE=90°;故可得△PFA∽△ABE;(2)根据题意:若△EFP∽△ABE,则∠PEF=∠EAB;必须有PE∥AB;分两种情况进而列出关系式.【详解】(1)证明:∵AD∥BC,∴∠PAF=∠AEB.∵∠PFA=∠ABE=90°,∴△PFA∽△ABE.(2)若△EFP∽△ABE,则∠PEF=∠EAB.如图,连接PE,DE,∴PE∥AB.∴四边形ABEP为矩形.∴PA=EB=2,即x=2.如图,延长AD至点P,作PF⊥AE于点F,连接PE, 若△PFE∽△ABE,则∠PEF=∠AEB.∵∠PAF=∠AEB,∴∠PEF=∠PAF.∴PE=PA.∵PF⊥AE,∴点F为AE的中点.∵AE=22=25AB BE,∴EF=12AE=5.∵5==225,PE EF PEAE EB,即,∴PE=5,即x=5.∴满足条件的x的值为2或5.【点睛】此题考查正方形的性质,相似三角形的判定,解题关键在于作辅助线. 18.(1)见解析;(2)见解析.【解析】【分析】。
青岛版九年级上册数学第二章《解直角三角形》测试题

青岛版九年级上册数学第二章《解直角三角形》测试题一、单选题(共12题;共24分)1. 如图,在坡度为1:2的山坡上种树,要求相邻两棵树的水平距离是6m,则斜坡上相邻两棵树的坡面距离是()A.3mB.3√5mC.12mD.6m2. 如图,一架无人机航拍过程中在C处测得地面上A,B两个目标点的俯角分别为30∘和60∘.若A,B两个目标点之间的距离是100米,则此时无人机与目标点A之间的距离(即AC的长)为()A.100米B.100√3米C.50米D.50√3米3. 如图,轮船沿正南方向以30海里/时的速度匀速航行,在M处观测到灯塔P在西偏南68∘方向上,航行2小时后到达N处,观测灯塔P在西偏南46∘方向上,若该船继续向南航行至离灯塔最近位置,则此时轮船离灯塔的距离约为(由科学计算器得到sin68∘≈0.9272,sin46∘≈0.7193,sin22∘≈0.3746,sin44∘≈0.6947)()A.22.48海里B.41.68海里C.43.16海里D.55.63海里4. 如图,小明想要测量学校操场上旗杆AB的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;(2)量得测角仪的高度CD=a;(3)量得测角仪到旗杆的水平距离DB=b.利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )A.a+b tanαB.a+b sinαC.a+btanαD.a+bsinα5. 如图,一棵珍贵的树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,现采取以下措施:在地面上选取一点C,测得∠BCA=37∘,AC=28米,∠BAC=45∘,则这棵树的高AB约为()(参考数据:sin37∘≈,tan37∘≈,≈1.4)A.14米B.15米C.17米D.18米6. 如图,轮船在A处观测灯塔C位于北偏西70∘方向上,轮船从A处以每小时20海里的速度沿南偏西50∘方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25∘方向上,则灯塔C与码头B的距离是()A.10√2海里B.10√3海里C.10√6海里D.20√6海里7. 如图,A,B两景点相距20km,C景点位于A景点北偏东60∘方向上,位于B景点北偏西30∘方向上,则A,C两景点相距()A.10kmB.10√3kmC.10√2kmD.203√3km8. 如图,在距某居民楼AB楼底B点左侧水平距离60m的C点处有一个山坡,山坡CD的坡度(或坡比)i=1:0.75,山坡坡底C点到坡顶D点的距离CD=45m,在坡顶D点处测得居民楼楼顶A点的仰角为28∘,居民楼AB与山坡CD的剖面在同一平面内,则居民楼AB的高度约为( )(参考数据:sin28∘≈0.47,cos28∘≈0.88,tan28∘≈0.53)A.76.9mB.82.1mC.94.8mD.112.6m9. 如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45∘,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60∘和30∘,则该电线杆PQ的高度()A.6+2√3B.6+√3C.10−√3D.8+√310. 某游乐场新推出了一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度.其中斜坡轨道BC的坡度(或坡比)为i=1:2,BC=12米,CD=8米,∠D=36∘,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为()米.(精确到0.1米,参考数据:tan36∘≈0.73,cos36∘≈0.81,sin36∘≈0.59)A.5.6B.6.9C.11.4D.13.911. 某货站用传送带传送货物,为了提高传送过程的安全性,工人师傅将原坡角45∘的传送带AB,调整为坡度i=1:√3的新传送带AC(如图所示).已知原传送带AB的长是4√2米,那么新传送带AC的长是()A.8米B.4米C.6米D.3米12. 如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60∘,然后在坡顶D测得树顶B的仰角为30∘,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是()m.A.10B.15C.15√3D.15√3−5二、填空题(共8题;共9分)如图,航模小组用无人机来测量建筑物BC的高度,无人机从A处测得建筑物顶部B的仰角为45∘,测得底部C的俯角为60∘,若此时无人机与该建筑物的水平距离AD为30m,则该建筑物的高度BC为________m.(结果保留根号)如图,点C在线段AB上,且AC=2BC,分别以AC,BC为边在线段AB的同侧作正方形ACDE,BCFG,连接EC,EG,则tan∠CEG=________.如图,对折矩形纸片ABCD使AD与BC重合,得到折痕MN,再把纸片展平.E是AD上一点,将△ABE沿BE折叠,使点A的对应点A′落在MN上.若CD=5,则BE的长是________.如图,小明在距离地面30米的P处测得A处的俯角为15∘,B处的俯角为60∘.若斜面坡度为1:√3,则斜坡AB的长是________米.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则sin∠BAC的值为________.计算sin60∘tan60∘−√2cos45∘cos60∘的结果为________ 。
初中数学:利用旋转证明三角形全等综合证明题专题
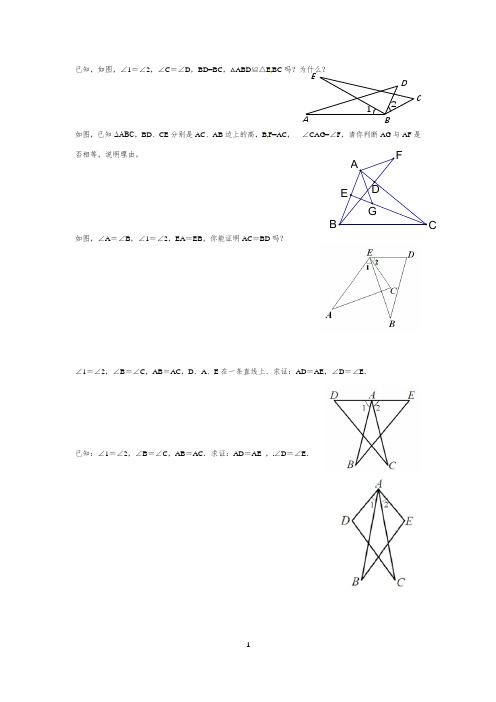
已知,如图,∠1=∠2,∠C =∠D ,BD=BC ,△ABD ≌△E BC 吗?为什么?如图,已知ΔABC ,BD 、CE 分别是AC 、AB 边上的高,B F=AC , ∠CAG=∠F ,请你判断AG 与AF 是否相等,说明理由。
如图,∠A =∠B ,∠1=∠2,EA =EB ,你能证明AC =BD 吗?∠1=∠2,∠B =∠C ,AB =AC ,D 、A 、E 在一条直线上.求证:AD =AE ,∠D =∠E .已知:∠1=∠2,∠B =∠C ,AB =AC .求证:AD =AE ,∠D =∠E .ABCDE1 2两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,AB=AC,AE=AD,∠BAC=∠EAD=90∘,B,C,E在同一条直线上,连接DC.(1)请找出图2中与△ABE全等的三角形,并给予证明(2)证明:DC⊥BE.如图,在Rt△ABC中,∠ACB=90∘,点D. F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90∘后得CE,连接EF.(1)求证:△BCD≌△FCE;(2)若EF∥CD,求∠BDC的度数。
如图,在正方形ABCD中,△PBC、△QCD是两个等边三角形,PB与DQ交于M,BP与CQ交于E,CP与DQ交于F. 求证:PM=QM.如图,已知长方形ABCD,过点C引∠A的平分线AM的垂线,垂足为M,AM交BC于E,连接MB,MD. (1)求证:BE=DC;(2)求证:∠MBE=∠MDC如图所示,已知△ABC和△DCE均是等边三角形,点B,C,E在同一条直线上,AE与BD与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC,FG,其中正确结论的个数是()①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC.如图,△ABD与△ACE均为正三角形,且AB<AC,则BE与CD之间的大小关系是()如图,在▱ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是()①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边三角形;④CG⊥AE.已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=.下列结论:①△APD≌△AEB;②点B到直线AE的距离为;③EB⊥ED;④S△APD+S△APB=1+;⑤S正方形ABCD=4+.其中正确结论的序号是()如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF.求证:DE=BF.如图,△ABC中,AB=AC,延长BC至D,使CD=BC,点E在边AC上,以CE,CD为邻边做▱CDFE,过点C作CG∥AB交EF于点G,连接BG,DE.(1)∠ACB与∠GCD有怎样的数量关系?请说明理由;(2)求证:△BCG≌△DCE.如图所示、△AOB和△COD均为等腰直角三角形,∠AOB=∠COD=90°,D在AB上.(1)求证:△AOC≌△BOD;(2)若AD=1,BD=2,求CD的长.如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD于点F,BD分别交CE、AE 于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.已知:如图,点C是线段AB的中点,CE=CD,∠ACD=∠BCE,求证:AE=BD.已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,点E在AC上,CE=BC,过E点作AC的垂线,交CD的延长线于点F.求证:AB=FC.如图,分别以Rt△ABC的直角边AC,BC为边,在Rt△ABC外作两个等边三角形△ACE和△BCF,连接BE,AF.求证:BE=AF.如图,已知,等腰Rt△OAB中,∠AOB=90°,等腰Rt△EOF中,∠EOF=90°,连接AE、BF.求证:(1)AE=BF;(2)AE⊥BF.如图,在△ABD和△ACE中,有下列四个等式:(1)AB=AC;(2)AD=AE;(3)∠1=∠2;(4)BD=CE.请你以其中三个等式作为题设,余下的作为结论,写出一个真命题.(要求写出已知,求证及证明过程)如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.(1)观察并猜想AP与CQ之间的大小关系,并证明你的结论;(2)若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.(1)求证:△ACE≌△BCD;(2)若AD=5,BD=12,求DE的长.如图,一个含45°的三角板HBE的两条直角边与正方形ABCD的两邻边重合,过E点作EF⊥AE交∠DCE 的角平分线于F点,试探究线段AE与EF的数量关系,并说明理由.如图,△ABC是等腰直角三角形,其中CA=CB,四边形CDEF是正方形,连接AF、BD.(1)观察图形,猜想AF与BD之间有怎样的关系,并证明你的猜想;(2)若将正方形CDEF绕点C按顺时针方向旋转,使正方形CDEF的一边落在△ABC的内部,请你画出一个变换后的图形,并对照已知图形标记字母,题(1)中猜想的结论是否仍然成立?若成立,直接写出结论,不必证明;若不成立,请说明理由.正方形ABCD和正方形AEFG有一公共点A,点G.E分别在线段AD、AB上(如图(1)所示),连接DF、BF.(1)求证:DF=BF,(2)若将正方形AEFG绕点A按顺时针方向旋转,连接DG、BE(如图(2)所示),在旋转过程中,请猜想线段DG、BE始终有什么数量关系和位置关系并证明你的猜想.(1)已知:如图①,在△AOB和△COD中,OA=OB,OC=OD,∠AOB=∠COD=60°,求证:①AC=BD;②∠APB=60度;(2)如图②,在△AOB和△COD中,若OA=OB,OC=OD,∠AOB=∠COD=α,则AC与BD间的等量关系式为_______;∠APB的大小为_______;(3)如图③,在△AOB和△COD中,若OA=k•OB,OC=k•OD(k>1),∠AOB=∠COD=α,则AC与BD 间的等量关系式为_______;∠APB的大小为_______.如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.(1)证明:∠BAE=∠FEC;(2)证明:△AGE≌△ECF;(3)求△AEF的面积.如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.△DAC, △EBC均是等边三角形,AE,BD分别与CD,CE交于点M,N,求证:(1)AE=BD (2)CM=CN (3) △CMN为等边三角形(4)MN∥BC已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2),其中结论正确的个数是()如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.(1)求证:CE=CF;(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.求证:BD=AE.某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.(1)求证:AM=AN;四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.(1)求证:△ADE≌△ABF;已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF(1)如图1,当点D在线段BC上时.求证CF+CD=BC;(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;①请直接写出CF,BC,CD三条线段之间的关系;②若正方形ADEF的边长为2,对角线AE,DF相交于点O,连接OC.求OC的长度.。
人教版2022-2023学年第一学期九年级数学第三次月考测试题(附答案)

2022-2023学年第一学期九年级数学第三次月考测试题(附答案)一、选择题(共40分)1.下列各曲线是在平面直角坐标系xOy中根据不同的方程绘制而成的,其中是中心对称图形的是()A.B.C.D.2.点P(2,﹣5)关于原点的对称点的坐标是()A.(﹣2,﹣5)B.(2,5)C.(﹣2,5)D.(﹣5,2)3.已知⊙O的半径为3,点M在⊙O上,则OM的长可能是()A.2B.3C.4D.54.如图所示,在⊙O中=,∠A=30°,则∠B=()A.150°B.75°C.60°D.15°5.平面上一点P与⊙O的点的距离的最小值是2,最大值是8,则⊙O的直径是()A.6或10B.3或5C.6D.56.如图,已知线段OA交⊙O于点B,且OB=AB,点P是⊙O上的一个动点,那么∠OAP 的最大值是()A.90°B.60°C.45°D.30°7.如图,△ODC是由△OAB绕点O顺时针旋转31°后得到的图形,若点D恰好落在AB 上,且∠AOC的度数为100°,则∠DOB的度数是()A.34°B.36°C.38°D.40°8.下列说法:①弧长相等的弧是等弧;②三点确定一个圆;③相等的圆心角所对的弧相等;④垂直于半径的直线是圆的切线;⑤三角形的外心到三角形三个顶点的距离相等.其中不正确的有()个.A.1B.2C.3D.49.某数学兴趣小组研究二次函数y=x2+bx+c的图象时,得出如下四个结论:甲:图象与x轴的一个交点为(1,0);乙:图象与x轴的一个交点为(3,0);丙:图象与x轴的交点在原点两侧;丁:图象的对称轴为过点(1,0),且平行于y轴的直线;若这四个结论中只有一个是不正确的,则该结论是()A.甲B.乙C.丙D.丁10.如图,AB是⊙O的直径,AB=4,C为的三等分点(更靠近A点),点P是⊙O上个动点,取弦AP的中点D,则线段CD的最大值为()A.2B.C.D.二、填空题(共24分)11.已知关于x的方程x2﹣3x﹣m=0的一个根是1,则m=.12.如图,若∠BOD=140°,则∠BCD=.13.在半径为10cm的⊙O中,圆心O到弦AB的距离为6cm,则弦AB的长是cm.14.如图,⊙O上三点A,B,C,半径OC=1,∠ABC=30°,⊙O的切线P A交OC延长线于点P,则PC的长为.15.在等边△ABC中,AB=5,点D是AB上的定点,点P是BC上的动点,DP绕点D逆时针旋转60°恰好落在AC上,已知BD=2,则此时DP=.16.如图,矩形ABCD中,E是BC上一点,连接AE,将矩形沿AE翻折,使点B落在CD 边F处,连接AF,在AF上取点O,以O为圆心,OF长为半径作⊙O与AD相切于点P,若AB=6,BC=3,则下列结论:①F是CD的中点:②⊙O的半径是2;③AE=CE,其中正确的是.(写序号)三、解答题(共86分)17.解方程:x2﹣2x﹣5=0.18.小晗家客厅装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏灯,在正常情况下,小晗按下任意一个开关均可打开对应的一盏电灯,因刚搬进新房不久,不熟悉情况.(1)若小晗任意按下一个开关,正好楼梯灯亮的概率是;(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图或列表法加以说明.19.已知关于x的一元二次方程x2﹣2x﹣m=0有两个不相等的实数根,且n+2m=4,求n 的取值范围.20.如图,在Rt△ABC中,∠ACB=90°,BD平分∠ABC.求作⊙O,使得点O在边AB 上,且⊙O经过B、D两点;并证明AC与⊙O相切.(尺规作图,保留作图痕迹,不写作法)21.如图,△ABC中,AB=AC,∠BAC=50°,P是BC边上一点,将△ABP绕点A逆时针旋转50°,点P旋转后的对应点为P′.(1)画出旋转后的三角形;(2)连接PP′,若∠BAP=20°,求∠PP′C的度数;22.某药店新进一批桶装消毒液,每桶进价35元,原计划以每桶55元的价格销售,为更好地助力疫情防控,现决定降价销售.已知这种消毒液销售量y(桶)与每桶降价x(元)(0<x<20)之间满足一次函数关系,其图象如图所示:(1)求y与x之间的函数关系式;(2)在这次助力疫情防控活动中,该药店仅获利1760元.这种消毒液每桶实际售价多少元?23.如图,△ABC内接于⊙O,AB是⊙O的直径,过点A作AD平分∠CAB,交⊙O于点D,过点D作DE∥BC交AC的延长线于点E.(1)依据题意,补全图形;(2)判断直线DE与⊙O的位置关系并证明;(3)若AB=10,BC=8,求CE的长.24.如图,△ABC内接于⊙O,弦BD⊥AC,垂足为E,点D、点F关于AC对称,连结AF 并延长交⊙O于点G.(1)连结OB,求证:∠ABD=∠OBC;(2)求证:点F、点G关于BC对称.25.已知抛物线y=x2+bx+c的顶点为P,与y轴交于点A,与直线OP交于点B.(1)若点P的横坐标为1,点B的坐标为(3,6).①求抛物线的解析式;②若当m≤x≤3时,y=x2+bx+c的最小值为2,最大值为6,求m的取值范围;(2)若点P在第一象限,且P A=PO,过点P作PD⊥x轴于D,将抛物线y=x2+bx+c 平移,平移后的抛物线经过点A、D,与x轴的另一个交点为C,试探究四边形OABC的形状,并说明理由.参考答案一、选择题(共40分)1.解:选项A、B、D均不能找到这样的一个点,使图形绕某一点旋转180度后和原图形完全重合,所以不是中心对称图形,选项C能找到这样的一个点,使图形绕某一点旋转180度后和原图形完全重合,所以是中心对称图形,故选:C.2.解:因为点P(2,﹣5)关于原点的对称点的坐标特点:横纵坐标互为相反数,所以对称点的坐标是(﹣2,5),故选:C.3.解:∵点M在⊙O上,⊙O的半径为3,∴OM=3,故选:B.4.解:∵=,∴AB=AC,∴∠B=∠C,∵∠A=30°,∴∠B=∠C=×(180°﹣30°)=75°.故选:B.5.解:当点P在圆内时,因为点P与⊙O的点的距离的最小值是2,最大值是8,所以圆的直径为10,当点P在圆外时,因为点P与⊙O的点的距离的最小值是2,最大值是8,所以圆的直径为6.故选:A.6.解:当AP与⊙O相切时,∠OAP有最大值,连接OP,如图,则OP⊥AP,∵OB=AB,∴OA=2OP,∴∠P AO=30°.故选:D.7.解:由题意得,∠AOD=31°,∠BOC=31°,又∠AOC=100°,∴∠DOB=100°﹣31°﹣31°=38°.故选:C.8.解:①弧长相等的弧是等弧,故该说法不正确;②不在同一直线的三点可以确定一个圆,故该说法不正确;③在同圆和等圆中,相等的圆心角所对的弧相等,故该说法不正确;④经过半径外端且垂直于这条半径的直线是圆的切线,故该说法不正确;⑤三角形的外心是三角形三边垂直平分线的交点,到三角形三个顶点的距离相等,故该说法正确.故选:D.9.解:若甲、乙成立,(1+3)÷2=1,∴图象的对称轴为过点(1,0),且平行于y轴的直线,图象与x轴的交点在原点右侧,故丁结论正确;图象与x轴的交点在原点右侧,故丙结论不正确,符合题意.故选:C.10.解:如图,连接OD,OC,∵AD=DP,∴OD⊥P A,∴∠ADO=90°,∴点D的运动轨迹为以AO为直径的⊙K,连接CK,AC,当点D在CK的延长线上时,CD的值最大,∵C为的三等分点,∴∠AOC=60°,∴△AOC是等边三角形,∴CK⊥OA,在Rt△OCK中,∵∠COA=60°,OC=2,OK=1,∴CK==,∵DK=OA=1,∴CD=+1,∴CD的最大值为+1,故选:D.二、填空题(共24分)11.解:把x=1代入方程可得:1﹣3﹣m=0,解得m=﹣2.故答案为:﹣2.12.解:由圆周角定理得,∠A=∠BOD=70°,∵四边形ABCD是圆内接四边形,∴∠BCD=180°﹣∠A=110°,故答案为:110°.13.解:连接OB.在Rt△ODB中,OD=6cm,OB=10cm.由勾股定理得BD===8.∴AB=2BD=2×8=16cm.14.解:连接OA,∵AP是⊙O的切线,∴OA⊥AP,∵∠ABC=30°,∴∠AOP=2∠ABC=60°,∴∠APO=30°,∵OA=OC=1,∴OP=2OA=2,∴PC=OP﹣OC=1.故答案为:1.15.解:如图,连接PP',过点D作DE⊥BC,∵DP绕点D逆时针旋转60°,∴DP=DP',∠PDP'=60°,∴△DP'P是等边三角形,∴DP=PP',∠DPP'=60°,∵△ABC是等边三角形,∴AB=BC=AC,∠A=∠B=∠C=60°,∵∠BPP'=∠C+∠PP'C=∠BPD+∠DPP',∴∠PP'C=∠BPD,且DP=PP',∠B=∠C,∴△BDP≌△CPP'(AAS)∴BD=CP=2,∴BP=3,∵∠B=60°,BD=2,DE⊥BC,∴BE=1,DE=BE=,∴PE=2,∴DP===,故答案为.16.解:①∵AF是AB翻折而来,∴AF=AB=6,∵矩形ABCD,则,∴,∴DF=CF,∴F是CD中点;故①正确;②如图,连接OP,∵⊙O与AD相切于点P,∴OP⊥AD,∵AD⊥DC,∴OP∥CD,∴△APO∽△ADF,∴,设OP=OF=x,则,解得:x=2,故②正确;③∵Rt△ADF中,AF=6,DF=3,∴,∴∠DAF=30°,∠AFD=60°,∴∠EAF=∠EAB=30°,∴AE=2EF;∵∠AFE=∠B=90°,∴∠EFC=90°﹣∠AFD=30°,∴EF=2EC,∴AE=4CE,故③错误;故答案为:①②.三、解答题(共86分)17.解:x2﹣2x=5,x2﹣2x+1=6,(x﹣1)2=6,x﹣1=±,所以x1=1+,x2=1﹣.18.解:(1)∵小晗家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,∴小晗任意按下一个开关,正好楼梯灯亮的概率是:;(2)画树状图得:∵共有6种等可能的结果,正好客厅灯和走廊灯同时亮的有2种情况,∴正好客厅灯和走廊灯同时亮的概率是:=.19.解:根据题意得Δ=(﹣2)2﹣4×(﹣m)>0,解得m>﹣1.∵n+2m=4,∴m=>﹣1,解得n<6,即n的取值范围为n<6.20.解:如图,⊙O为所作.证明:连接OD,如图,∵BD平分∠ABC,∴∠CBD=∠ABD,∵OB=OD,∴∠OBD=∠ODB,∴∠CBD=∠ODB,∴OD∥BC,∴∠ODA=∠ACB,又∠ACB=90°,∴∠ODA=90°,即OD⊥AC,∵点D是半径OD的外端点,∴AC与⊙O相切.21.解:(1)旋转后的三角形ACP'如图所示:(2)由旋转可得,∠P AP'=∠BAC=50°,AP=AP',△ABP≌△ACP',∴∠APP'=∠AP'P=65°,∠AP'C=∠APB,∵∠BAC=50°,AB=AC,∴∠B=65°,又∵∠BAP=20°,∴∠APB=95°=∠AP'C,∴∠PP'C=∠AP'C﹣∠AP'P=95°﹣65°=30°.22.解:(1)设y与x之间的函数关系式为:y=kx+b,将点(1,110)、(3,130)代入一次函数关系式得:,解得:,故函数的关系式为:y=10x+100(0<x<20);(2)由题意得:(10x+100)×(55﹣x﹣35)=1760,整理,得x2﹣10x﹣24=0.解得x1=12,x2=﹣2(舍去).所以55﹣x=43.答:这种消毒液每桶实际售价43元.23.解:(1)如图1即为补全的图形.(2)直线DE是⊙O的切线.理由如下:证明:如图2,连接OD,交BC于F.∵AD平分∠BAC,∴∠BAD=∠CAD.∴.∴OD⊥BC于F.∵DE∥BC,∴OD⊥DE于D.∴直线DE是⊙O的切线.(3)∵AB是⊙O的直径,∴∠ACB=90°.∵AB=10,BC=8,∴AC=6.∵∠BFO=∠ACB=90°,∴OD∥AC.∵O是AB中点,∴OF==3.∵OD==5,∴DF=2.∵DE∥BC,OD∥AC,∴四边形CFDE是平行四边形.∵∠ODE=90°,∴平行四边形CFDE是矩形.∴CE=DF=2.答:CE的长为2.24.证明:(1)连接OC,∵BD⊥AC,∴∠AEB=90°,∴∠EAB+∠ABE=90°,∵,∴∠BOC=2∠BAC,∵OB=OC,∴∠OBC=∠OCB,∵∠OBC+∠OCB+∠BOC=180°,∴2∠OBC+2∠BAC=180°,∴∠OBC+∠BAC=90°,∴∠OBC=∠ABE,即∠OBC=∠ABD,(2)连接BG,AD,GC,AG交BC于点H,∵点D,F关于AC对称,∴EF=ED,∵BD⊥AC,∴∠AEF=∠AED=90°,又∵AE=AE,∴△AEF≌△AED(SAS),∴∠EAF=∠EAD,∠AFE=∠ADE,即∠GAC=∠DAC,∵,∴∠DAC=∠DBC,∵,∴∠GAC=∠GBC,∴∠DBC=∠GBC,∵∴∠ADB=∠BGA,∵∠AFD=∠BFG,∴∠BFG=∠AGB,∴△BHF≌△BHG(AAS),∴FH=GH,∠BHF=∠BHG=90°,∴点F,点G关于BC对称.25.解:(1)①∵抛物线y=x2+bx+c的顶点P的横坐标为1,∴﹣=1,解得:b=﹣2.∴y=x2﹣2x+c,∵抛物线y=x2﹣2x+c经过点B(3,6),∴6=32﹣2×3+c,解得:c=3.∴抛物线的解析式为y=x2﹣2x+3;②由y=x2﹣2x+3=(x﹣1)2+2知,P(1,2).∴点(3,6)关于对称轴x=1的对称点B′的坐标为(﹣1,6),如图1,∵当m≤x≤3时,y=x2+bx+c的最小值为2,最大值为6,∴﹣1≤m≤1;(2)如图2,由P A=PO,OA=c,可得PD=.∵抛物线y=x2+bx+c的顶点坐标为P(﹣,),∴=.∴b2=2c.∴抛物线y=x2+bx+b2,A(0,b2),P(﹣b,b2),D(﹣b,0).可得直线OP的解析式为y=﹣bx.∵点B是抛物线y=x2+bx+b2与直线y=﹣bx的图象的交点,令﹣bx=x2+bx+b2.解得x1=﹣b,x2=﹣.可得点B的坐标为(﹣b,b2).由平移后的抛物线经过点A,可设平移后的抛物线解析式为y=x2+mx+b2.将点D(﹣b,0)的坐标代入y=x2+mx+b2,得m=b.则平移后的抛物线解析式为y=x2+bx+b2.令y=0,即x2+bx+b2=0.解得x1=﹣b,x2=﹣b.依题意,点C的坐标为(﹣b,0).则BC=b2.则BC=OA.又∵BC∥OA,∴四边形OABC是平行四边形.∵∠AOC=90°,∴四边形OABC是矩形.。
人教版九年级上册数学第三次月考试题及答案

人教版九年级上册数学第三次月考试卷一、单选题1.下列图形是中心对称图形的是()A.B.C.D.2.若⊙O的半径为5cm,OA=4cm,则点A与⊙O的位置关系是()A.点A在⊙O上B.点A在⊙O内C.点A在⊙O外D.无法确定3.如果-1是方程2x²-x+m=0的一个根,则m值()A.-1B.1C.3D.-34.如图,A,B,C是⊙O上的三个点,若∠C=35°,则∠AOB的度数为()A.35°B.55°C.65°D.70°5.在一个不透明的口袋中装有5个白球,若干个黑球,它们除颜色外其它完全相同,已知摸到白球概率为0.2,则袋子中黑球有多少个?()A.15B.10C.5D.206.将抛物线y=(x-1)²+2先向右平移3个单位,再向下平移5个单位得到的抛物线解析式是()A.y=(x-4)²+7B.y=(x-4)²-3C.y=(x+2)²+7D.y=(x+2)²-37.新能源汽车节能、环保,越来越受消费者喜爱,各种品牌相继投放市场,我国新能源汽车近几年销量全球第一,2016年销量为50.7万辆,销量逐年增加,到2018年销量为125.6万辆.设年平均增长率为x,可列方程为()A.50.7(1+x)2=125.6B.125.6(1﹣x)2=50.7C.50.7(1+2x)=125.6D.50.7(1+x2)=125.68.如图,AB是OO的直径,弦CD⊥AB,垂足为P,若CD=8,PB=2,则⊙O直径()A.10B.8C.5D.39.已知二次函数y=ax²+bx+c(a≠0)图象的一部分如图所示,给出以下结论:①abc<0;②当x=-1时,函数有最大值;③方程ax²+bx+c=0的解是x1=1,x2=-3;④4a+2b+c>0,⑤2a-b=0,其中结论正确的个数是()A.1B.2C.3D.410.如图,在菱形ABCD中,∠B=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿折线BA→AC运动到点C,同时动点Q从点A出发,以相同速度沿折线AC→CD 运动到点D,当一个点停止运动时,另一个点也随之停止.设△APQ的面积为y,运动时间为x秒,则下列图象能大致反映y与x之间函数关系的是()A.B.C.D.二、填空题11.一个盒子内装有大小、形状相同的6个球,其中红球3个、绿球1个、白球2个,任意摸出一个球,则摸到白球的概率是______12.已知圆锥的底面直径为4cm ,母线长为6cm ,则此圆锥的侧面积为____.13.若关于x 的一元二次方程kx²-x-1=0有两个实数根,则k 的取值范围______14.在Rt ABC 中,∠C=90°,BC=3,AC=4,则ABC 的外接圆半径是______15.如图,将△ABC 的绕点A 顺时针旋转得到△AED ,点D 正好落在BC 边上.已知∠C=80°,则∠EAB=____________°.16.如图,正六边形ABCDEF 内接于圆O ,边长AB=2,则正六边形的面积是______17.如图,点C 在以O 为圆心的半圆内一点,直径AB =4,∠BCO=90°,∠OBC=30°,将△BOC 绕圆心逆时针旋转到使点C 的对应点C′在半径OA 上,则边BC 扫过区域(图中阴影部分)面积为______(结果保留π)三、解答题18.解方程:(1)x 2+2x =2(2)4(3x ﹣2)(x +1)=3x +319.某幢建筑物从10米高的窗户A 用水管向外喷水,喷出的水流呈抛物线状(如图),若抛物线最高点M 离墙1米,离地面403米.问:(1)求抛物线的解析式;(2)求水流落地点B 离墙的距离20.已知:在ABC 中,AB AC =.(1)求作:ABC 的外接圆.(要求:尺规作图,保留作图痕迹,不写作法)(2)若ABC 的外接圆的圆心O 到BC 边的距离为4,6BC =,则O S = .21.为落实“垃圾分类”,环卫部门要求垃圾要按A 、B 、C 三类分别装袋投放,其中A 类指废电池、过期药品等有毒垃圾,B 类指剩余食品等厨余垃圾,C 类指塑料、废纸等可回收垃圾,甲、乙各投放了一袋垃圾.(1)直接写出甲投放的垃圾恰好是A 类的概率;(2)求甲乙投放的垃圾恰好是同类垃圾的概率(要求画出树状图)22.已知关于x 的一元二次方程x²-(2k+1)x+k 2+k=0(1)求证:无论k 为任何实数,方程总有两个不相等的实数根;(2)若两个实数根x 1,x 2满足()()121130x x ++=,求k 值.23.如图,已知正方形ABCD 的边长为3,E 、F 分别是边BC 、CD 上的点,∠EAF=45°(1)求证:BE+DF=EF(2)当BE=1时,求EF 的长24.如图:以ABC 的边AB 为直径作⊙O ,点C 在OO 上,BD 是⊙O 的弦,∠A=∠CBD ,过点C 作CF ⊥AB 于点交于点G 过作C ∥BD 交AB 的延长线于点E(1)求证:CG=BG(2)∠BAD=30°,CG=4,求BE 的长25.如图,已知抛物线25y ax bx =++经过A(5-,0),B(4-,3-)两点,与x 轴的另一个交点为C ,顶点为D ,连接CD .(1)求该抛物线的表达式;(2)点P 为该抛物线上一动点(与点B ,C 不重合),设点P 的横坐标为t .①当点P 在直线BC 的下方运动时,求PBC 的面积的最大值及点P 的坐标;②该抛物线上是否存在点P,使得∠PBC=∠BCD?若存在,求出所有点P的坐标;若不存在,请说明理由.参考答案1.A2.B3.D4.D5.D6.B7.A8.A9.C10.B11.1312.12π13.k≥14-且k≠0.14.52.15.20°.16.17.π18.(1)x 1=﹣1x 2=﹣1+(2)x 1=﹣1,x 2=1112.19.(1)210201033y x x =-++;(2)3米.20.(1)见解析;(2)25π21.(1)13;(2)13,作图见解析22.(1)见详解;(2)17k =-,24k =;23.(1)证明见解析;(2)52.24.(1)见解析;(2)25.(1)265y x x =++;(2)①278,P(52-,154-),②存在,P(32-,74-)或(0,5)。
2020届九年级中考数学知识点《三角形》强化练习卷含答案

三角形一、选择题1.(2019宿迁)一副三角板如图摆放(直角顶点C 重合),边AB 与CE 交于点F ,DE BC ∥,则BFC ∠等于A .105︒B .100︒C .75︒D .60︒【答案】A2.(2019临沂)如图,D 是AB 上一点,DF 交AC 于点E ,DE FE =,FC AB ∥,若4AB =,3CF =,则BD 的长是A .0.5B .1C .1.5D .2【答案】B3.(2019绍兴)如图,墙上钉着三根木条a ,b ,c ,量得∠1=70°,∠2=100°,那么木条a ,b 所在直线所夹的锐角是A .5°B .10°C .30°D .70°【答案】B4.(2019潍坊)如图,已知AOB ∠.按照以下步骤作图:①以点O 为圆心,以适当的长为半径作弧,分别交AOB ∠的两边于C ,D 两点,连接CD .②分别以点C ,D 为圆心,以大于线段OC 的长为半径作弧,两弧在AOB ∠内交于点E ,连接CE ,DE .③连接OE 交CD 于点M .下列结论中错误的是A .CEO DEO ∠=∠B .CM MD =C .OCD ECD ∠=∠D .12OCED S CD OE =⋅四边形 【答案】C5.(2019梧州)如图,DE 是ABC △的边AB 的垂直平分线,D 为垂足,DE 交AC 于点E ,且85AC BC ==,,则BEC △的周长是A .12B .13C .14D .15【答案】B6.(2019宁波)勾股定理是人类最伟大的科学发现之一,在我国古算书《周髀算经》中早有记载.如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积,则一定能求出A .直角三角形的面积B .最大正方形的面积C .较小两个正方形重叠部分的面积D .最大正方形与直角三角形的面积和 【答案】C7.(2019青岛)如图,BD 是△ABC 的角平分线,AE ⊥BD ,垂足为F .若∠ABC =35°,∠C =50°,则∠CDE 的度数为A .35°B .40°C .45°D .50°【答案】C9.(2019天水)如图,等边OAB △的边长为2,则点B 的坐标为A .(11),B .(1C .1)D .【答案】B10.(2019宁波)已知直线m ∥n ,将一块含45°角的直角三角板ABC 按如图方式放置,其中斜边BC 与直线n 交于点D .若∠1=25°,则∠2的度数为A .60°B .65°C .70°D .75°【答案】C11.(2019滨州)如图,在OAB △和OCD △中,,,,40OA OB OC OD OA OC AOB COD ==>∠=∠=︒,连接,AC BD 交于点M ,连接OM .下列结论:①AC BD =;②40AMB ∠=︒;③OM 平分BOC ∠;④MO 平分BMC ∠.其中正确的个数为A .4B .3C .2D .1【答案】B12.(2019陕西)如图,在△ABC 中,∠B =30°,∠C =45°,AD 平分∠BAC 交BC 于点D ,DE ⊥AB ,垂足为E .若DE =1,则BC 的长为A .B +C2 D .3【答案】A13.(2019衢州)“三等分角”大约是在公元前五世纪由古希腊人提出来的,借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒OA ,OB 组成,两根棒在O 点相连并可绕O 转动,C 点固定,OC =CD =DE ,点D 、E 可在槽中滑动.若∠BDE =75°,则∠CDE 的度数是A .60°B .65°C .75°D .80°【答案】D14.(2019重庆A 卷)如图,在△ABC 中,D 是AC 边上的中点,连接BD ,把△BDC ′沿BD 翻折,得到△,DC与AB交于点E,连接AC',若AD=AC′=2,BD=3则点D到BC的距离为BDC'A B C D【答案】B15.(2019南通)小明学了在数轴上画出表示无理数的点的方法后,进行练习:首先画数轴,原点为O,在数轴上找到表示数2的点A,然后过点A作AB⊥OA,使AB=3(如图).以O为圆心,OB的长为半径作弧,交数轴正半轴于点P,则点P所表示的数介于A.1和2之间B.2和3之间C.3和4之间D.4和5之间【答案】C16.(2019杭州)在△ABC中,若一个内角等于另外两个内角的差,则A.必有一个内角等于30° B.必有一个内角等于45°C.必有一个内角等于60° D.必有一个内角等于90°【答案】D17.(2019河南)如图,在四边形ABCD中,AD∥BC,∠D=90°,AD=4,BC=3.分别以点A,C为圆心,大于1AC长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长2为A .B .4C .3D 【答案】A18.(2019张家界)如图,在ABC △中,90C ∠=︒,8AC =,13DC AD =,BD 平分ABC ∠,则点D 到AB 的距离等于A .4B .3C .2D .1【答案】C19.(2019台州)下列长度的三条线段,能组成三角形的是 A .3,4,8 B .5,6,10 C .5,5,11D .5,6,11【答案】B20.(2019台湾)如图,△ABC 中,AC =BC <AB .若∠1、∠2分别为∠ABC 、∠ACB 的外角,则下列角度关系何者正确A .∠1<∠2B .∠1=∠2C .∠A +∠2<180°D .∠A +∠1>180°【答案】C21.(2019长春)如图,在ABC △中,ACB ∠为钝角.用直尺和圆规在边AB 上确定一点D .使2AD C B ∠=∠,则符合要求的作图痕迹是A .B .C .D .【答案】B22.(2019金华)若长度分别为a ,3,5的三条线段能组成一个三角形,则a 的值可以是 A .1 B .2C .3D .8【答案】C23.(2019广西)如图,在ABC ∆中,,40AC BC A =∠=︒,观察图中尺规作图的痕迹,可知BCG ∠的度数为A .40︒B .45︒C .50︒D .60︒【答案】C24.(2019大庆)如图,在△ABC 中,BE 是∠ABC 的平分线,CE 是外角∠ACM 的平分线,BE 与CE 相交于点E ,若∠A =60°,则∠BEC 是A .15°B .30°C .45°D .60°【答案】B25.(2019荆门)将一副直角三角板按如图所示的位置摆放,使得它们的直角边互相垂直,则1∠的度数是A .95︒B .100︒C .105︒D .110︒【答案】C26.(2019百色)三角形的内角和等于 A .90︒B .180︒C .270︒D .360︒【答案】B27.(2019徐州)下列长度的三条线段,能组成三角形的是 A .2,2,4 B .5,6,12 C .5,7,2 D .6,8,10【答案】D 二、填空题28.(2019临沂)如图,在ABC △中,120ACB ∠=︒,4BC =,D 为AB 的中点,DC BC ⊥,则ABC △的面积是__________.【答案】29.(2019南京)如图,在△ABC 中,BC 的垂直平分线MN 交AB 于点D ,CD 平分∠ACB .若AD =2,BD =3,则AC 的长为__________.30.(2019威海)如图,在四边形ABCD 中,AB CD ∥,连接AC ,BD .若90ACB ∠=︒,AC BC =,AB BD =,则ADC ∠=__________︒.【答案】10531.(2019北京)如图所示的网格是正方形网格,则∠PAB +∠PBA =__________°(点A ,B ,P 是网格线交点).【答案】4532.(2019成都)如图,在△ABC 中,AB =AC ,点D ,E 都在边BC 上,∠BAD =∠CAE ,若BD =9,则CE 的长为__________.【答案】933.(2019黄冈)如图,AC BD ,在AB 的同侧,288AC BD AB ===,,,点M 为AB 的中点,若120CMD ∠=︒,则CD 的最大值是__________.【答案】1434.(2019舟山)如图,一副含30°和45°角的三角板ABC和EDF拼合在一个平面上,边AC与EF重合,AC=12cm.当点E从点A出发沿AC方向滑动时,点F同时从点C出发沿射线BC方向滑动.当点E从点A滑动到点C时,点D运动的路径长为__________cm;连接BD,则△ABD的面积最大值为__________cm2.),()【答案】(24–35.(2019长沙)如图,要测量池塘两岸相对的A,B两点间的距离,可以在池塘外选一点C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=50 m,则AB的长是__________m.【答案】10036.(2019南京)在△ABC中,AB=4,∠C=60°,∠A>∠B,则BC的长的取值范围是__________.【答案】4<BC≤337.(2019枣庄)把两个同样大小含45︒角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个,,在同一直线上.若AB=2,则CD=__________.三角尺的直角顶点重合于点A,且另外三个锐角顶点B C D38.(2019兰州)在△ABC 中,AB =AC ,∠A =40°,则∠B =__________. 【答案】70°39.(2019盐城)如图,在ABC △中,BC =45C ∠=︒,AB =,则AC 的长为__________.【答案】240.(2019伊春)一张直角三角形纸片ABC ,90ACB ∠=︒,10AB =,6AC =,点D 为BC 边上的任一点,沿过点D 的直线折叠,使直角顶点C 落在斜边AB 上的点E 处,当BDE △是直角三角形时,则CD 的长为__________. 【答案】3或24741.(2019襄阳)如图,已知ABC DCB ∠=∠,添加下列条件中的一个:①A D ∠=∠,②A C D B =,③A B D C=,其中不能确定ABC △≌△DCB △的是__________(只填序号).【答案】②42.(2019南通)如图,△ABC 中,AB =BC ,∠ABC =90°,F 为AB 延长线上一点,点E 在BC 上,且AE =CF ,若∠BAE =25°,则∠ACF =__________度.【答案】7043.(2019哈尔滨)在ABC △中,50A ∠=︒,30B ∠=︒,点D 在AB 边上,连接CD ,若ACD △为直角三角形,则BCD ∠的度数为__________. 【答案】60︒或10︒44.(2019怀化)若等腰三角形的一个底角为72︒,则这个等腰三角形的顶角为__________. 【答案】36°45.(2019通辽)腰长为5,高为4的等腰三角形的底边长为__________. 【答案】6或46.(2019大庆)如图,在△ABC 中,D 、E 分别是BC ,AC 的中点,AD 与BE 相交于点G ,若DG =1,则AD =__________.【答案】347.(2019江西)如图,在ABC △中,点D 是BC 上的点,40BAD ABC ∠=∠=︒,将ABD △沿着AD 翻折得到AED △,则CDE ∠=__________°.【答案】20 三、证明题48.(2019南京)如图,D是△ABC的边AB的中点,DE∥BC,CE∥AB,AC与DE相交于点F.求证:△ADF ≌△CEF.证明:∵DE∥BC,CE∥AB,∴四边形DBCE是平行四边形,∴BD=CE,∵D是AB的中点,∴AD=BD,∴AD=EC,∵CE∥AD,∴∠A=∠ECF,∠ADF=∠E,∴△ADF≌△CEF.49.(2019益阳)已知,如图,AB=AE,AB∥DE,∠ECB=70°,∠D=110°,求证:△ABC≌△EAD.证明:由∠ECB=70°得∠ACB=110°,又∵∠D=110°,∴∠ACB=∠D,∵AB∥DE,∴∠CAB=∠E,∴在△ABC和△EAD中,==ACB DCAB E AB AE∠∠⎧⎪∠∠⎨⎪=⎩,∴△ABC≌△EAD.50.(2019山西)已知:如图,点B,D在线段AE上,AD=BE,AC∥EF,∠C=∠F.求证:BC=DF.证明:∵AD=BE,∴AD-BD=BE-BD,∴AB=ED,∵AC∥EF,∴∠A=∠E,在△ABC和△EDF中,C FA E AB ED∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ABC≌△EDF(AAS),∴BC=DF.51.(2019兰州)如图,AB=DE,BF=EC,∠B=∠E,求证:AC∥DF.证明:∵BF=EC,∴BF+FC=EC+FC,∴BC=EF,在△ABC 和△DEF 中,AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩,∴△ABC ≌△DEF (SAS ), ∴∠ACB =∠DFE , ∴AC ∥DF .52.(2019广州)如图,D 是AB 上一点,DF 交AC 于点E ,DE =FE ,FC ∥AB ,求证:ADE CFE △≌△.证明:∵FC ∥AB ,∴∠A =∠FCE ,∠ADE =∠F ,所以在△ADE 与△CFE 中,A FCE ADE F DE EF ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADE ≌△CFE .53.(2019泸州)如图,AB CD ∥,AD 和BC 相交于点O ,OA OD =.求证:OB OC =.证明:∵AB CD ∥,∴A D ∠=∠,B C ∠=∠,在AOB △和DOC △中,A D B C OA OD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴AOB DOC △≌△, ∴OB OC =.54.(2019重庆A 卷)如图,在△ABC 中,AB =AC ,D 是BC 边上的中点,连结AD ,BE 平分∠ABC 交AC 于点E ,过点E 作EF ∥BC 交AB 于点F .(1)若∠C =36°,求∠BAD 的度数.(2)若点E 在边AB 上,EF ∥AC 叫AD 的延长线于点F .求证:FB =FE .证明:(1)∵AB AC =,∴C ABC ∠=∠, ∵36C ∠=︒, ∴36ABC ∠=︒,∵D 为BC 的中点,∴AD BC ⊥,∴90903654BAD ABC ∠=-∠=-︒=︒︒︒. (2)∵BE 平分ABC ∠,∴ABE EBC ∠=∠, 又∵EF BC ∥,∴EBC BEF ∠=∠, ∴EBF FEB ∠=∠, ∴BF EF =.55.(2019桂林)如图,AB =AD ,BC =DC ,点E 在AC 上. (1)求证:AC 平分∠BAD ; (2)求证:BE =DE .证明:(1)在△ABC 与△ADC 中,AB AD AC AC BC DC =⎧⎪=⎨⎪=⎩∴△ABC ≌△ADC (SSS ), ∴∠BAC =∠DAC ,即AC 平分∠BAD .(2)由(1)∠BAE =∠DAE ,在△BAE 与△DAE 中,得BA DA BAE DAE AE AE =⎧⎪∠=∠⎨⎪=⎩,∴△BAE ≌△DAE (SAS ), ∴BE =DE .56.(2019黄石)如图,在ABC △中,90BAC ∠=︒,E 为边BC 上的点,且AB AE =,D 为线段BE 的中点,过点E 作EF AE ⊥,过点A 作AF BC ∥,且AF 、EF 相交于点F . (1)求证:C BAD ∠=∠; (2)求证:AC EF =.证明:(1)如图,∵AB AE =,∴ABE △是等腰三角形, 又∵D 为BE 的中点,∴AD BE ⊥, 在Rt ABC △和Rt DBA △中,∵B Ð为公共角,90BAC BDA ∠=∠=︒, ∴C BAD ∠=∠.(2)∵AF BC ∥,∴EAF AEB ∠=∠, ∵AB AE =,∴ABE AEB ∠=∠,∴EAF ABC ∠=∠,又∵90BAC AEF ∠=∠=∠︒, ∴BAC AEF △≌△, ∴AC EF =.57.(2019重庆)如图,在△ABC 中,AB =AC ,AD ⊥BC 于点D . (1)若∠C =42°,求∠BAD 的度数;(2)若点E 在边AB 上,EF ∥AC 交AD 的延长线于点F .求证:AE =FE .证明:(1)∵AB =AC ,AD ⊥BC 于点D , ∴∠BAD =∠CAD ,∠ADC =90°,又∠C =42°,∴∠BAD =∠CAD =90°-42°=48°. (2)∵AB =AC ,AD ⊥BC 于点D , ∴∠BAD =∠CAD , ∵EF ∥AC , ∴∠F =∠CAD , ∴∠BAD =∠F , ∴AE =FE .58.(2019苏州)如图,ABC △中,点E 在BC 边上,AE AB =,将线段AC 绕点A 旋转到AF 的位置,使得CAF BAE ∠=∠,连接EF ,EF 与AC 交于点G .(1)求证:EF BC =;(2)若65ABC ∠=︒,28ACB ∠=︒,求FGC ∠的度数.证明:(1)∵CAF BAE ∠=∠, ∴BAC EAF ∠=∠,∵AE AB AC AF ==,, ∴BAC EAF △≌△, ∴EF BC =.(2)∵65AB AE ABC =∠=︒,, ∴18065250BAE ∠=︒-︒⨯=︒, ∴50FAG ∠=︒, ∵BAC EAF △≌△, ∴28F C ∠=∠=︒, ∴502878FGC ∠=︒+︒=︒.59.(2019无锡)如图,在△ABC 中,AB =AC ,点D 、E 分别在AB 、AC 上,BD =CE ,BE 、CD 相交于点O . 求证:(1)DBC ECB △≌△; (2)OB OC =.证明:(1)∵AB =AC , ∴∠ECB =∠DBC ,在DBC △与ECB △中,BD CE DBC ECB BC CB =⎧⎪∠=∠⎨⎪=⎩,∴DBC △≌ECB △.(2)由(1)DBC △≌ECB △, ∴∠DCB =∠EBC , ∴OB =OC .60.(2019枣庄)在ABC △中,90BAC ∠=︒,AB AC =,AD BC ⊥于点D .(1)如图1,点M ,N 分别在AD ,AB 上,且90BMN ∠=︒,当30AMN =︒∠,2AB =时,求线段AM 的长; (2)如图2,点E ,F 分别在AB ,AC 上,且90EDF ∠=︒,求证:BE AF =;(3)如图3,点M 在AD 的延长线上,点N 在AC 上,且90BMN ∠=︒,求证:AB AN +=.证明:(1)∵90BAC ∠=︒,AB AC =,AD BC ⊥,∴AD BD DC ==,45ABC ACB ∠=∠=︒,45BAD CAD ∠=∠=︒, ∵2AB =,∴AD BD DC ===,∵30AMN ∠=︒,∴180903060BMD ∠=︒-︒-︒=︒, ∴30BMD ∠=︒,∴2BM DM =,由勾股定理得,222BM DM BD -=,即222(2)DM DM -=,解得DM =∴3AM AD DM =-=. (2)∵AD BC ⊥,90EDF ∠=︒,∴BDE ADF ∠=∠,在BDE △和ADF △中,B DAF DB DA BDE ADF ∠=∠=∠=∠⎧⎪⎨⎪⎩,∴BDE ADF △≌△, ∴BE AF =.(3)如图,过点M 作//ME BC 交AB 的延长线于E ,∴90AME ∠=︒,则AE =,45E ∠=︒,∴ME MA =,∵90AME ∠=︒,90BMN ∠=︒, ∴BME AMN ∠=∠,在BME △和AMN △中,E MAN ME MA BME AMN ∠=∠=∠=∠⎧⎪⎨⎪⎩,∴BME AMN △≌△,∴BE AN =,∴AB AN AB BE AE +=+==.61.(2019温州)如图,在△ABC 中,AD 是BC 边上的中线,E 是AB 边上一点,过点C 作CF ∥AB 交ED 的延长线于点F .(1)求证:△BDE ≌△CDF ;(2)当AD ⊥BC ,AE =1,CF =2时,求AC 的长.证明:(1)∵CF AB ∥, ∴B FCD BED F ∠=∠∠=∠,, ∵AD 是BC 边上的中线,∴BD CD =,∴△BDE ≌△CDF . (2)∵△BDE ≌△CDF , ∴2BE CF ==,∴123AB AE BE =+=+=. ∵AD BC BD CD ⊥=,, ∴3AC AB ==.62.(2019杭州)如图,在△ABC 中,AC <AB <BC .(1)已知线段AB 的垂直平分线与BC 边交于点P ,连接AP ,求证:∠APC =2∠B .(2)以点B 为圆心,线段AB 的长为半径画弧,与BC 边交于点Q ,连接AQ .若∠AQC =3∠B ,求∠B 的度数.证明:(1)∵线段AB 的垂直平分线与BC 边交于点P , ∴PA =PB , ∴∠B =∠BAP , ∵∠APC =∠B +∠BAP , ∴∠APC =2∠B ;(2)根据题意可知BA =BQ , ∴∠BAQ =∠BQA ,∵∠AQC =3∠B ,∠AQC =∠B +∠BAQ , ∴∠BQA =2∠B ,∵∠BAQ +∠BQA +∠B =180°, ∴5∠B =180°, ∴∠B =36°.四、解答题63.(2019河北)已知:整式A=(n2-1)2+(2n)2,整式B>0.尝试化简整式A.发现A=B2,求整式B.联想由上可知,B2=(n2-1)2+(2n)2,当n>1时,n2-1,2n,B为直角三角形的三边长,如图.填写下表中B的值:解:A=(n2-1)2+(2n)2=n4-2n2+1+4n2=n4+2n2+1=(n2+1)2,∵A=B2,B>0,∴B=n2+1,当2n=8时,n=4,∴n2+1=42+1=15;当n2-1=35时,n2+1=37.64.(2019大庆)如图,一艘船由A港沿北偏东60°方向航行10 km至B港,然后再沿北偏西30°方向航行10 km 至C港.(1)求A,C两港之间的距离(结果保留到0.1 km≈1.414 1.732);(2)确定C港在A港的什么方向.解:(1)由题意可得,∠PBC=30°,∠MAB=60°,∴∠CBQ=60°,∠BAN=30°,∴∠ABQ=30°,∴∠ABC=90°.∵AB=BC=10,∴AC=14.1.答:A、C两地之间的距离为14.1 km.(2)由(1)知,△ABC为等腰直角三角形,∴∠BAC=45°,∴∠CAM=15°,∴C港在A港北偏东15°的方向上.65.(2019金华)如图,在76⨯的方格中,ABC△的顶点均在格点上,试按要求画出线段EF(E,F均为格点),各画出一条即可.【答案】如图所示:。
初三上册数学试题及答案

初三上册数学试题及答案一、选择题(每题2分,共20分)1. 下列哪个数是无理数?A. -3.14B. √2C. 0.33333D. -22. 如果一个直角三角形的两条直角边分别为3和4,那么斜边的长度是:A. 5B. 6C. 7D. 83. 一个数的平方根是它本身,这个数是:A. 0B. 1C. -1D. 24. 一个多项式减去-3x等于2x^2 - 5x + 3,那么这个多项式是:A. 2x^2 + 2x + 6B. 2x^2 - 8x + 6C. 2x^2 - 2x - 3D. 2x^2 + 8x - 65. 一个圆的半径是5,那么它的面积是:A. 25πB. 50πC. 75πD. 100π6. 根据题目所给的选项,正确答案为:A. √2B. 5C. 0D. 2x^2 + 2x + 6E. 50π7. 如果一个数的相反数是-5,那么这个数是:A. 5B. -5C. 0D. 108. 下列哪个是二次根式?A. √3xB. 3xC. √x/3D. x√39. 一个数的立方根是它本身,这个数可以是:A. 1B. -1C. 0D. 所有选项10. 如果一个二次方程的判别式小于0,那么这个方程:A. 有唯一解B. 无实数解C. 有两个实数解D. 无法确定二、填空题(每题2分,共20分)11. 一个数的绝对值是5,这个数可以是______。
12. 如果一个角的余角是30°,那么这个角是______。
13. 一个数的相反数是它本身,这个数是______。
14. 一个数的平方等于9,这个数可以是______。
15. 一个圆的直径是10,那么它的半径是______。
16. 一个数的立方等于8,这个数是______。
17. 如果一个三角形的三个内角分别是40°、60°和80°,那么这个三角形是______。
18. 一个数的平方根是2,这个数是______。
19. 一个数的四次方等于16,这个数可以是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北九上第三章证明(三)水平测试(C )
一、耐心填一填(每小题5分,共25分)
1. 如图,EF 过平行四边形ABCD 的对角线的交点O ,交AD 于点E ,交BC 于点F ,已知AB = 4,BC = 5,OE = ,那么四边形EFCD 的周长是_______。
2. 在Rt ⊿ABC 中,∠C =︒90,周长为cm )325(+;斜边上的中线CD =cm 2,则Rt ⊿ABC 的面积为_______。
3. 如图所示,在△ABC 中,M 是BC 的中点,AN 平分∠BAC ,AN ⊥BN 于N 点,且AB =10,AC =16,则MN =_______。
4. 如图,过矩形ABCD 的四个顶点作对角线AC 、BD 的平行线,分别相交于E 、F 、G 、H 四点,则四边形EFGH 为_______。
5. 如图,在Rt ⊿ABC 中,∠C =︒90,AC = AB ,AB = 30,矩形DEFG 的一边DE 在AB 上,顶点G 、F 分别在AC 、BC 上,若DG :GF = 1:4,则矩形DEFG 的面积是
二、精心选一选(每小题5分,共25分)
1. 如图,在平行四边形ABCD 中,对角线AC 、BD 相交于点O ,若BD 、AC 的和为cm 18,CD :DA =2:3,⊿AOB 的周长为cm 13,那么BC 的长是 ( )
A .cm 6
B .cm 9
C .cm 3
D .cm 12
. 如图,有一矩形纸片ABCD ,AB =10,AD =6,将纸片折叠,使AD 边落在AB 边上,折痕为AE ,再将△AED 以DE 为折痕向右折叠,AE 与BC 交于点F ,则△CEF 的面积为( )
A .4
B .6
C .8
D .10
3. 如图,在等腰梯形ABCD 中,AB ∥CD ,AD =BC = A CM ,∠A =60°,BD 平分∠ABC ,则这个梯形的周长是( )
A .4A CM
B . 5A CM
C .6A CM
D . 7A CM
4. 如图:矩形花园ABCD 中,a AB =,b AD =,花园中建有一条矩形道路L MPQ 及一 条平行四边形道路RSTK 。
若c RS LM ==,则花园中可绿化部分的面积为( )
+bc +bc -c 2
C .(a -c )(b -c )
D . ac +bc +c 2
5. 给出下面四个命题:(1)一组对边平行的四边形是梯形;(2)一条对角线平分一个内角的平行四边形是菱形;(3)两条对角线互相垂直的矩形是正方形;(4)一组对边平行,另一组对边相等的四边形是平行四边形,其中真命题的个数有 ( )
个 个 个 个
三、用心想一想(本大题共50分)
1. 已知如图所示,平行四边形ABCD 的对角线AC 、BD 交于O ,GH 过点O ,分别交AD 、BC 于G 、H ,E 、F 在AC 上且AE =CF ,求证:四边形EHFG 是平行四边形.
2. 如图所示,已知等边△ABC的边长为A,P是△ABC内一点,PD∥AB,PE∥BC,PF∥AC,点D、E、F分别在BC、AC、AB上,猜想:PD+PE+PF=_________,并证明你的猜想.
90,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,3. 如图,在⊿ABC中,∠BAC =
EF⊥BC于F,求证:四边形AEFG是菱形;
如图所示,以△ABC的三边为边在BC的同侧分别作三个等边三角形
△ABD、△BCE、△ACF,猜想:四边形ADEF是什么四边形,试证明你的结论.
答案:
一、耐心填一填
1. 12;
2.√;
3. 3;
4. 菱形;
5. 100。
二、精心选一选
ACBBB
三、用心想一想
1.利用对角线互相平分证。
2. A;略。
3.先证四边形AEFG是平行四边形。
4. 四边形ADEF是平行四边形。
