第20章组合逻辑电路习题课
电工学20章 题库组合逻辑电路+答案

9、图 20-1-9 中全加器的输入 Ai=1,Bi=1,Ci-1=1,则全加和 Si =
,进位 Ci =
。
图 20-1-9
10、两个一位二进制数相加的全加器的输入分别为加数 Ai 和 Bi 以及低位送来的进位 Ci-1,
则全加和 Si =
。
11、用卡诺图化简逻辑函数时,合并最小项的每个圈中的最小项个数必须是________个。
D、Y=Σm(1,3,5,6)
17、8421BCD 码的 00011001 表示的十进制数为______。
A、16
B、13
C、19
D、25
18、图 20-2-18 所示逻辑电路的逻辑关系为__________。
图 20-2-18
A、 F = ABCA⋅ ABCBC
B、 F = ABCA + ABCBC
∑ ∑ (2) F ( A, B, C, D) = m(2, 3, 5, 6, 7,8, 9) + d (10,11,12,14,15)
(3) F = ABD + ABC + ABD + ABD (4) Y = AB + BC D + ABD + ABCD (5)Y ( A, B, C) = AB + ABC + ABC
15、 F = AB + AC + BC 的最小项表达式为 F=__________________________。
16、一般 TTL 门和 CMOS 门相比,
门的带负载能力强,
门的工作速度快。
17、四位二进制数输出的编码器应有__________个编码输入。
18、由 n 个变量构成的任意一个最小项,有
【数电】组合逻辑电路习题(含答案)
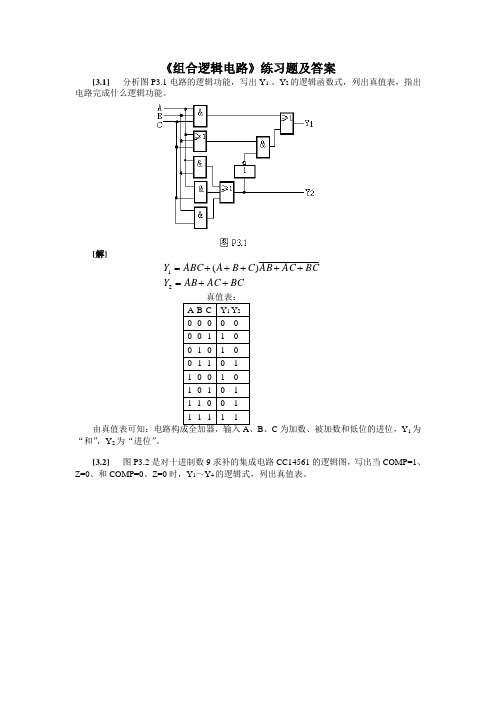
《组合逻辑电路》练习题及答案[3.1] 分析图P3.1电路的逻辑功能,写出Y 1、、Y 2的逻辑函数式,列出真值表,指出电路完成什么逻辑功能。
[解]BCAC AB Y BC AC AB C B A ABC Y ++=+++++=21)(B 、C 为加数、被加数和低位的进位,Y 1为“和”,Y 2为“进位”。
[3.2] 图P3.2是对十进制数9求补的集成电路CC14561的逻辑图,写出当COMP=1、Z=0、和COMP=0、Z=0时,Y 1~Y 4的逻辑式,列出真值表。
[解](1)COMP=1、Z=0时,TG 1、TG 3、TG 5导通,TG 2、TG 4、TG 6关断。
3232211 , ,A A Y A Y A Y ⊕===, 4324A A A Y ++=(2)COMP=0、Z=0时,Y 1=A 1, Y 2=A 2, Y 3=A 3, Y 4=A 4。
COMP =0、Z=0的真值表从略。
[题3.3] 用与非门设计四变量的多数表决电路。
当输入变量A 、B 、C 、D 有3个或3个以上为1时输出为1,输入为其他状态时输出为0。
[解] 题3.3的真值表如表A3.3所示,逻辑图如图A3.3所示。
ABCD D ABC D C AB CD B A BCD A Y ++++=BCD ACD ABC ABC +++=B C D A C D A B D A B C ⋅⋅⋅=[3.4] 有一水箱由大、小两台泵M L 和M S 供水,如图P3.4所示。
水箱中设置了3个水位检测元件A 、B 、C 。
水面低于检测元件时,检测元件给出高电平;水面高于检测元件时,检测元件给出低电平。
现要求当水位超过C 点时水泵停止工作;水位低于C 点而高于B 点时M S 单独工作;水位低于B 点而高于A 点时M L 单独工作;水位低于A 点时M L 和M S 同时工作。
试用门电路设计一个控制两台水泵的逻辑电路,要求电路尽量简单。
[解] 题3.4的真值表如表A3.4所示。
第20章组合逻辑电路习题课

6、题图所示电路试写出函数F的简化表达式。
A B 1 & 1 ≥1 & F
7、题图所示电路为数据比较器,试写出函数F的简化表达式。
(第二章习题-15)
8 、某产品有 A、 B、 C三项质量指标,其中 A为主要 指标,产品检验标准规定:当主要指标及一项次要 指标都合格时,产品定为合格品,否则定为不合格 品。试用与非门设计一个指标检验电路。 9.某汽车驾驶员培训班进行结业考试。有三名评判员, 其中A为主评判员,B和C为副评判员。在评判时按少 数服从多数原则通过。但若主评判员认为合格,亦可通 过。试用与非门设计逻辑门实现此逻辑电路。
表达式形式转换
F AB AC AB AC AB AC
(第二章习题-5)
卡诺图化简法的步骤
★
1.将函数式化为最小项之和的形式。(可省略) 2.填卡诺图。 3.找出可以合并的相邻项,用矩形框圈出。
①将相邻的1格圈出,圈的格数必须为2、4、8、16……,即2n。 ②圈的个数应最少,保证乘积项最少。 ③每个圈的格数应最多,保证乘积项中的因子最少。 ④可以重复圈,不能漏圈。
10
1
1
1
F F AC BC AD BD ABC
AC BC AD BD ABC
AD
AC
(第二章习题-8)
【例4】
试用卡诺图化简逻辑函数
Y=(A,B,C,D,E)=m5(1,5,9,13,16,18,20,22,27,31)
C B E A 000 001 011 010 110 111 101 100 D 1 00 1 01 11
7 4L U? B S00
Y ( B C )( A B) Y ( B C ) ( A B)
组合逻辑电路习题解

时输出0,输入为0时输出1。 只有当所有输入都为1时, 只要有一个输入为1,输出
输出才为0。
就为0。
逻辑代数基本定律
同一律
A+0=A,A·1=A
零律
A+1=1,A·0=0
互补律
A+¬A=1,A·¬A=0
交换律
A+B=B+A,A·B=B·A
结合律
(A+B)+C=A+(B+C),(A·B)·C=A·(B·C)
ga…
gat…
实现逻辑与运算,符号为“·” 实现逻辑或运算,符号为
或“∧”,只有当所有输入 “+”或“∨”,只要有一
都为1时,输出才为1。
个输入为1,输出就为1。
实现逻辑非运算,符号为
实现逻辑与非运算,即先与 实现逻辑或非运算,即先或
“¬”或“—”,输入为1 后非,符号为“⊕”或“↑”, 后非,符号为“↓”或“⊖”,
包括真值表、逻辑表达式、 卡诺图和逻辑图四种表示方 法,它们之间可以相互转换 。
组合逻辑电的 分析与设计方法
分析方法包括根据逻辑图写 出逻辑表达式、列出真值表 、分析电路功能等步骤;设 计方法包括根据实际需求确 定输入/输出变量、列出真值 表、化简逻辑表达式、画出 逻辑图等步骤。
拓展延伸内容探讨
复杂组合逻辑电路的设计
对于较复杂的组合逻辑电路,可以采用分级设计的方法,将整体功能划分为若干个相对简 单的子功能,分别设计子电路,最后将子电路组合起来实现整体功能。
组合逻辑电路中的竞争与冒险
当多个输入信号同时变化时,可能会在输出端产生瞬间的错误信号,这种现象称为竞争; 如果这种错误信号持续时间较长,且不能被后续电路所忽略,则称为冒险。为了避免竞争 和冒险,可以采取增加冗余项、引入选通脉冲等方法。
习题课PPT课件_OK

Y
F
D3
D4
D5
D6 D7
2021/7/28
30
(4) 函数有4个输入变量 ,而74151的地址端只有3个,即
A2 、A1 、A0 ,故须对函数的卡诺图进行降维,即降为3
维。
CD
AB 00 01 11 10
00 1
1
01
Ø
11 1 1 1
10 Ø
BC
A
00 01 11 10
0 D D00
1 0 0 D1
D1 =C⊙D,
相应的电路图如下图所示:
D2 = 0, D3 = CD,
B
A0
=1
A
A1
=
D0
1_ 2
7
41
5
3
D1
Y
F
D2
&
D3
EN
CD
2021/7/28
35
4.16 试在图4.2.31的基础上增加一片7485,构成25位数据比较器 。
A24A23A22A21 B24 B23B22B2 A19A18A17A16 B19 B18B17B1 A14A13A12A11 B14 B13B12B1 A9A8A7A6
F 1 ( A ,B ,C ,D ) m ( 0 , 4 , 8 , 1 )2
= m0 m4 m8 m12 = Y0 Y4 Y8 Y12
2021/7/28
24
F 2 ( A ,B , C ,D ) m ( 0 , 1 , 2 )
= m0 m1 m2
= Y0 Y1 Y2
F 3 ( A ,B , C ,D ) m ( 8 , 9 , 1 , 1 ) 0 1
解:(1) 函数有4个输入变量 ,而74151的地址端只有3个 ,即A2 、A1 、A0 ,故须对函数的卡诺图进行降维,即 降为3维。
组合逻辑电路的设计 题目

1
Z = RY G + YG + RG + RY
例题2.试分析如图所示的组合逻辑电路的功能。
G2 G1
A B
Z2 Z1 G3 Z3
G4 S
G5 C
解:(1)推出逻辑表达式
Z1 = ABZ 2 = Z1 ⋅ A = AB ⋅ A
JHR
解:(1)根据逻辑要求设定输入、输出变量。 用变量XY表示供血者代码。MN表示被输血者 代码。代码设定如下 XY=00 01 10 11 A型 B型 AB型 O型 MN=00 01 10 11 A型 B型 AB型 O型
设F1表示绿灯,F2表示红灯,依题意,可列出逻辑 真值表。
(2)列出真值表 (3)写出逻辑函数表达式 F1=∑m(0,2,5,6,10,12,13,14,15) (4)化简逻辑函数表达式 4
F1 = XY + M N + Y M N + X Y N = XY ⋅ M N ⋅ Y M N ⋅ X Y N
F2 = Y N ⋅ X MN ⋅ X Y M ⋅ X Y M N
设输入既有原变 量又有反变量
例7 有一火灾报警系统,设有烟感、温感、紫外光 感三种不同类型的火灾探测器。为了防止误报警, 只有当其中有两种或两种以上类型的探测器发出火 灾探测信号时,报警系统才产生报警控制信号,试 设计产生报警控制信号的电路。 [解](1)根据逻辑要求设置逻辑输入、输出变 量。 用A、B、C分别代表烟感、温感、紫外光感三种 探测器的探测输出信号,作为报警控制电路的输入 变量,以“1”表示高电平,“0”表示低电平,高电 平表示有火灾报警,低电平表示无火灾报警;
Y = A B C + AB C + AB C + ABC
组合逻辑电路习题(附答案)

例1 指出下图1所示电路的输出逻辑电平是高电平、低电平还是高阻态。
已知图(a)中的门电路都是74系列的TTL门电路,图(b)中的门电路为CC4000系列的CMOS门电路。
图1解: TTL门电路的输入端悬空时,相当于高电平输入,输入端接有电阻时,其电阻阻值大于1.4K时,该端也相当于高电平,电阻值小于0.8K时,该端才是低电平。
而CMOS逻辑门电路,输入端不管是接大电阻还是接小电阻,该端都相当于低电平(即地电位)。
所以有如下结论:(a) 1L为低电平状态;2L是低电平状态;3L是高电平状态;4L 输出为高阻状态;(b) 1L输出为高电平;2L输出是低电平状态;3L输出是低电平状态;例2 图例2所示为用三态门传输数据的示意图,图中n 个三态门连到总线BUS ,其中D 1、D 2、…、D n 为数据输入端,EN 1、EN 2、…、ENn 为三态门使能控制端,试说明电路能传输数据的原理。
图例2 解:由三态门电路符号可知,当使能端低电平时,三态门输出为高阻阻态,所以,只要给各三态门的使能端n EN EN EN ,,,21 依次为高电平时,则,1n D D 的数据就依次被传输到总线上去。
例3 某功能的逻辑函数表达式为L=∑m(1,3,4,7,12,14,15);(1)试用最少量的“与-非”门实现该函数;(2)试用最少量的“或-非”门实现该函数;解: (1)设变量为A 、B 、C 、D ,用卡诺图化简,结合“1”方格得:DBACDAABCDCBDBACDAABCDCBDCBAfL=+++==),,,((2)卡诺图中结合“0”方格,求最简的“或—与”表达式,得:DCADCBDBBADCADCBDBBAL+++++++++=++++++=))()()((例4 试用一片八选一数据选择器74LS151实现逻辑函数。
(1) ACD D ABC CD B A D C B A Z ++=),,,( (2) C B A C B A C B A C B A Z ++=),,(解:解例基本思路:选定多路选择器的地址输入变量,列出卡诺图,求出数据输入端的函数关系式;(1) 选定四变量函数中的ABC(A 2A 1A 0)为地址输入,卡诺图为画出的电路图为:(2) 选定多路选择器的地址变量为)(012A A A ABC ,由于地址数正好是变量数,所以数据输入端的逻辑关系一定是常量“0”和“1”。
(完整版)组合逻辑电路设计例题
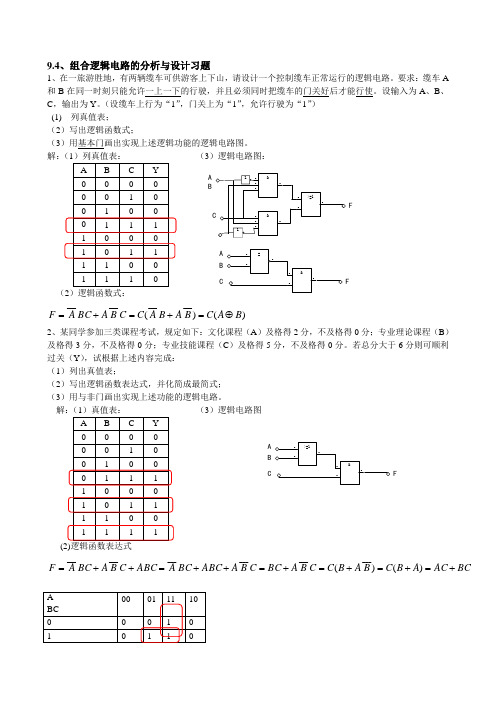
9.4、组合逻辑电路的分析与设计习题1、在一旅游胜地,有两辆缆车可供游客上下山,请设计一个控制缆车正常运行的逻辑电路。
要求:缆车A 和B在同一时刻只能允许一上一下的行驶,并且必须同时把缆车的门关好后才能行使。
设输入为A、B、C,输出为Y。
(设缆车上行为“1”,门关上为“1”,允许行驶为“1”)(1) 列真值表;(2)写出逻辑函数式;(3)用基本门画出实现上述逻辑功能的逻辑电路图。
解:(1)列真值表:(3)逻辑电路图:)()(____________BACBABACCBABCAF⊕=+=+=2、某同学参加三类课程考试,规定如下:文化课程(A)及格得2分,不及格得0分;专业理论课程(B)及格得3分,不及格得0分;专业技能课程(C)及格得5分,不及格得0分。
若总分大于6分则可顺利过关(Y),试根据上述内容完成:(1)列出真值表;(2)写出逻辑函数表达式,并化简成最简式;(3)用与非门画出实现上述功能的逻辑电路。
(3)逻辑电路图(2)逻辑函数表达式BCACABCBABCCBABCCBAABCBCAABCCBABCAF+=+=+=+=++=++=)()(__________________ABFAFBCAFBC3、中等职业学校规定机电专业的学生,至少取得钳工(A)、车工(B)、电工(C)中级技能证书的任意两种,才允许毕业(Y )。
试根据上述要求:(1)列出真值表;(2)写出逻辑表达式,并化成最简的与非—与非形式;(3)用与非门画出完成上述功能的逻辑电路。
解:(1(3)逻辑电路:(2)逻辑表达式:最简的与非—与非形式:ABC C AB C B A BC A F +++=_____________________________________________________________________________________________________________AB BC AC AB BC AC AB BC AC AB BC AC F ••=•+=++=++=4、用基本逻辑门电路设计一个一位二进制全加器,输入变量有:A 为被加数,B 为加数,C 为较低位的进位,输出函数为本位和S 及向较高位的进位H 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
D
个变量取值组 D. 2n
A.D 。
C. n2 C.逻辑图
A.C 。
2.逻辑函数的表示方法中具有唯一性的是 逻辑函数的表示方法中具有唯一性的是
D.卡诺图
3. F=A B +BD+CDE+ A D= A.
A B + D B.
( A + B ) D C.
( A + D)( B + D) D.( A + D)( B + D)
第21章 组合逻辑电路 习题课 章
1 (第二章习题-1)
逻辑符号
(第二章习题-2)
公式化简方法 我们通过一些例子说明如 何应用这些公式进行化简。 何应用这些公式进行化简。 Y=AB+A(C+D)B =AB Y=AC+AD+CD =AC+AC D =AC+ D 2式 式 1式 式
常用公式 吸收法 A + AB = A 2. A + AB = A+B 消因子法 1. 3. A B+AB = A 并项法 4. A B+AC+BC = AB+AC 5. A B+AC =A B+A C 消项法 Y=AB+AB+BC+BC =AB+AB+BC +BC+ AC
a D
C B
T337
f
b
c
e
d
A
g
•
R
2. 八路数据选择器,其地址输入端(选择控制端)有( C 八路数据选择器,其地址输入端(选择控制端) A.8个 B.2个 C.3个 D.4个 . 个 . 个 . 个 . 个 3.全加器具有 3 . 个输入端和 2 个输出端。 个输出端。
)个。
这种电路分为两大类, 4. 具有编码功能的电路称为 编码器 ,这种电路分为两大类, 一是 普通编码器 ,二是 优先编码器 。 ( ) ⒌半加器和全加器的区别在于 (A)是否考虑两个相加的数 (B)是否考虑相邻低位的进位 是否考虑两个相加的数 是否考虑相邻低位的进位 (C) 是否考虑电路的原状态 (D)是否考虑电路中有无记忆元件 是否考虑电路中有无记忆元件
Y=AC+BC+ BD+CD+A(B+C)+ABCD+ABDE =BC+BD+A 注意: 当有长非号时 应先化简非号下的式子,然后脱掉非号。 注意: 1.当有长非号时,应先化简非号下的式子,然后脱掉非号。 当有长非号时, 2.要十分注意冗余项公式的应用。 要十分注意冗余项公式的应用。 要十分注意冗余项公式的应用
(第二章习题-5)
代数法化简函数
例:试简化函数 F = AC+ AD + BD + BC 利用反演律 解: F = AC+ AD + BD + BC 配项加AB 配项加AB
= AC+ BC + D(A + B)
= AC + BC + DAB
消项AB 消项AB
消因律
= AC+ BC + AB+ DAB
例:
Y A 0 1 BC 00
Y = AB + BC
01 11 10
1 1 1 1
Y = BC + AB = BC • AB = B + C)(A + B) (
Y = ( B + C )( A + B) Y = ( B + C ) + ( A + B)
。
A
≥1
1
≥1
Y
B C
≥1
(第二章习题-12)
1.当逻辑函数有n个变量时,共有 当逻辑函数有n 当逻辑函数有 个变量时, 合? A. n A .真值表 B. 2n B.表达式
(第二章习题-8)
图形法化简函数
例:将F(A、B、C、D) = ACD + AB+ BCD + ABC+ AC F(A、 化为最简与非—与非式。 化为最简与非 与非式。 CD 与非式 AB 00Байду номын сангаас01 11 10 解: ACD 00 1 1 0 m14,m15 0 01 1 0 1 1 两次填1 两次填 1 1 AB 11 1 1 10 B CD AC ABC 0 1 1 1
(第二章习题-9)
图形法化简函数
例:将F(A、B、C、D) = ACD + AB+ BCD + ABC+ AC F(A、 化为最简与非—与非式 化为最简与非 与非式 A B C BC 解: CD AB 00 01 11 10 化简得: 化简得: 00 1 1
F = AC+ BC+ AD+ BD+ ABC
C。
B.A+C
C.(A+B)(A+C) A+B) A+C)
D.B+C
7.在何种输入情况下,“与非”运算的结果是逻辑0。 在何种输入情况下, 与非”运算的结果是逻辑0 D 在何种输入情况下 全部输入是0 任一输入是0 A . 全部输入是 0 B. 任一输入是 0 全部输入是1 入 是0 D.全部输入是1 C. 仅一输
(第二章习题-18)
6、题图所示电路试写出函数F的简化表达式。
A B
1 & 1 ≥1 &
F
7、题图所示电路为数据比较器,试写出函数F的简化表达式。 、题图所示电路为数据比较器,试写出函数 的简化表达式 的简化表达式。
(第二章习题-19)
8 、 某产品有A、 B、C三项质量指标, 其中A为主要 某产品有 、 、 三项质量指标, 其中 为主要 三项质量指标 指标, 产品检验标准规定: 指标 , 产品检验标准规定 : 当主要指标及一项次要 指标都合格时, 产品定为合格品, 指标都合格时 , 产品定为合格品 , 否则定为不合格 试用与非门设计一个指标检验电路。 品。试用与非门设计一个指标检验电路。 9.某汽车驾驶员培训班进行结业考试。有三名评判员, 某汽车驾驶员培训班进行结业考试。有三名评判员, 某汽车驾驶员培训班进行结业考试 其中A为主评判员 为主评判员, 和 为副评判员 为副评判员。 其中 为主评判员,B和C为副评判员。在评判时按少 数服从多数原则通过。但若主评判员认为合格,亦可通 数服从多数原则通过。但若主评判员认为合格 亦可通 试用与非门设计逻辑门实现此逻辑电路 逻辑门实现此逻辑电路。 过。试用与非门设计逻辑门实现此逻辑电路。
常用公式 1.
A + AB = A 2. A + AB = A+B
=ABC+ABC+ABC+ABC 3. A B+AB = A 3式 式 =AB+BC 4. A B+AC+BC = AB+AC 5. A B+AC =A B+A C .A Y=AB C+CD =(AB C+CD) .A =A C D 5式 5式 BC
最简与非—与非式为: 最简与非 与非式为: 与非式为
01 11 10
1 1 1 1 AD
1 1 1
1 1 1 AC
BD
F = F = AC+ BC+ AD+ BD+ ABC
= AC • BC • AD • BD • A BC
(第二章习题-10)
【例4】 】
试用卡诺图化简逻辑函数 试用卡诺图化简逻辑函数
(第二章习题-15)
例:
设计用3个开关控制一个电灯的逻辑电路, 设计用 个开关控制一个电灯的逻辑电路,要求改变任何 个开关控制一个电灯的逻辑电路
一个开关的状态都能控制电灯由亮变灭或者由灭变亮。 一个开关的状态都能控制电灯由亮变灭或者由灭变亮。要求用数 据选择器来实现。 据选择器来实现。 设三个开关为 ,灯为Z 解:设三个开关为ABC,灯为 根据题意, 中只有发生改变时, 根据题意,当A、B、C中只有发生改变时,输出应发生改变 、 、 中只有发生改变时 即相邻的最小项对应的输出应不同 得卡诺图如下 BC A 00 01 11 10 0 1 0 1 0 1 0 1 0 1
1
D0 D1 D2 D3
Y
Z
S
(第二章习题-17)
1. 图 示 为 采 用 共 阴 极 数 码 管 的 译 码 显 示 电 路, 若 显 示 码 数 是 2, 译 码 器 输 出 端 应 为 ( b ) 。
+10V
(a) a=b=d=e=“1”,g=c=f =“0” (b) a=b=d=e=g=“1”,c=f =“0” (c)a=b=c=d=e=g=“1”,c=f =“0”
Y=(A,B,C,D,E)=∑m5(1,5,9,13,16,18,20,22,27,31) ∑
C B E A 000 001 011 010 110 111 101 100 D 1 00 1 01 11 10 1
1 1 1 1 1
1
1
F = ABE + ADE + ABDE
(第二章习题-11)
用或非门实现函数的一般方法
= AC+ BC + AB+ D
= AC+ BC + D
(第二章习题-6)
函数表达式的常用形式
• 五种常用表达式 F(A、 F(A、B、C)= AB + AC
= (A + C)(A + B)
“与―或”式 与 “或―与”式 或 “与非―与非”式 与非―与非” 与非 基本形式
= AB • AC
或非― 或非 或非” = A + C + A + B “或非―或非”式 “与―或― 与 = A • 利用还原律 利用反演律 非”式 C+A•B • 表达式形式转换
